随着数据智能和数据处理技术的发展及广泛应用,多目标优化查询问题成为一个热点和难点问题.多目标优化查询帮助用户在一定约束条件下获得在多个目标对象下的查询结果以达到最优的结果集.Skyline查询是多目标优化查询中一类重要的查询问题.Skyline查询方法由Borzsony等人[1]提出,通过Skyline点的性质缩小结果集,提高并优化查询效率.
目前,Skyline查询方法的研究已经拓展到无线传感网络中的动态Skyline查询[2]、不确定数据Skyline查询[3]、移动K-支配最近邻查询[4]、反Skyline查询[5]、数据流Skyline查询[6]、子空间Skyline查询[7]、连续Skyline查询[8]、概率Skyline查询[9]、Top-k Skyline查询[10]、基于MapReduce的Skyline查询[11]、障碍空间中的Skyline查询[12]等方面.取得的研究成果解决了Skyline查询领域及延伸领域内的一系列重要的问题.上述研究的空间条件均没有考虑路网环境,但实际生活中人们很多时候均活动在道路网中,因此,道路网Skyline查询是一类重要的Skyline查询问题,道路网Skyline查询问题具有重要的应用价值.
相对于理想空间,道路网的空间拓扑结构更加复杂,数据对象之间的距离计算复杂度更高,传统的距离计算已不能很好地适用于道路网环境中.近年来针对道路网多目标优化查询的研究已经取得一些重要研究成果,潘晓等人[13]提出了在道路网络上基于时空相似性的连续查询隐私保护算法,该算法通过分组策略和共享机制防止连续查询攻击和位置依赖攻击.Bao等人[14]提出一种基于将道路边缘划分为子区间的基本算法,并通过检查子区间的端点来找到最佳位置.这些算法很好地处理了路网边缘区域的点,但是却忽略了数据点之间的空间支配关系,导致非边缘的数据对象之间的距离也需要通过复杂的计算得到结果.文献[15]对各个区域的数据点与查询点的位置关系均进行了处理,但是算法需要重复检查数据点之间的支配性,从而影响了算法查询效率.
Huang[16]出于用户隐私保护提出了基于位置范围的Skyline查询方法,设计了数据对象与道路网间的数据结构,将查询对象模糊化为一个位置范围用以保护用户隐私.该方法计算数据点与查询对象的网络距离时,只需计算数据点与位置范围边界交点的网络距离,再重新利用Dijkstra算法来计算距离,不再需要重复查询,因而可以节省实时计算开销.Miao等人[17]针对查询点推理确定更有潜力的Skyline点,方法具有一定的创新,但是算法对每个查询点的计算效率有待进一步提升.文献[18-19]提出了安全区域的概念,在安全区域内计算查询对象与目标对象之间的最短网络距离.但是安全区域需要对区域更新和维护.
对于K-支配Skyline查询问题,Lee等人[20]提出了一种在计算期间减少选择候选者和支配误报的方法.Miao等人[21]研究了不完整数据上K-支配Skyline查询的问题,提出利用位图索引缩小搜索空间的方法.这些算法可以有效减少数据点的k维属性支配判断的比较次数和减少I O代价次数,具有较好的性能.但忽略了数据对象的空间属性对查询结果的影响,当数据对象的空间位置属性改变时,则需要重新计算k维的结果.文献[22]考虑到数据对象的属性具有相关联性,通过查询预处理对空间属性必支配的属性进行处理使得查询效率提升.文献[23]基于MapReduce平台提出了一个有效的并行算法来处理K-支配Skyline查询问题.文献[24]提出了一种基于索引的K-支配Skyline查询算法,通过为数据集建立2个索引,算法可以高效地进行计算,在时间、空间和渐进性上具有一定的性能优势.
O代价次数,具有较好的性能.但忽略了数据对象的空间属性对查询结果的影响,当数据对象的空间位置属性改变时,则需要重新计算k维的结果.文献[22]考虑到数据对象的属性具有相关联性,通过查询预处理对空间属性必支配的属性进行处理使得查询效率提升.文献[23]基于MapReduce平台提出了一个有效的并行算法来处理K-支配Skyline查询问题.文献[24]提出了一种基于索引的K-支配Skyline查询算法,通过为数据集建立2个索引,算法可以高效地进行计算,在时间、空间和渐进性上具有一定的性能优势.
已有的道路网Skyline查询一般只有一个查询对象,但是查询对象往往是不唯一的,查询对象之间的相互影响可能导致数据对象的属性值发生变化.因此,使用单一的查询点会导致查询结果不符合实际需求.并且查询方法若不考虑数据点的非空间属性对查询的影响,则可能导致查询的结果不准确.在实际应用中,数据点的空间位置和非空间属性值都对用户的选择有影响,这就需要结合空间属性和非空间属性k维的支配关系来选择.如何将K-支配Skyline查询问题应用于道路网环境,特别当查询点的空间位置发生动态改变时还能准确提供最优化查询结果成为研究的难点.针对这些问题,本文将K-支配应用到道路网Skyline查询中以处理多属性数据对象,利用K-支配解决了道路网查询支配的问题.本文利用道路网Voronoi图的定义与相关性质对数据点进行约减和支配检查.在理论论证和分析的基础上提出了道路网K-支配空间Skyline查询方法.
1 定义与性质
道路网K-支配空间Skyline查询是道路网Skyline查询的变种问题,该问题涉及4个组成对象:数据点集、查询区域范围、查询属性范围以及道路网.本文假定数据点集P是一组具有k维属性的点的集合,其中k-1维为静态的非空间属性,k维属性为数据点在道路网中位置的坐标.
本节给出相关的定义与性质.
定义1. 非空间属性支配[22].给定2个数据点p1,p2,考虑所有的非空间属性,如果p1能被p2支配,称p2非空间属性支配p1,记为p2 p1.所有非空间属性支配p1点的集合称为p1的非空间属性支配集,记为Dom(p1).
p1.所有非空间属性支配p1点的集合称为p1的非空间属性支配集,记为Dom(p1).
定义2. 道路网支配[16].在道路网环境下给定一个查询点q和2个数据点p1,p2,d(q,p1)表示数据点p1距离查询点q的网络距离.当且仅当满足2个条件时,称p2道路网支配p1(简称“支配”),记为p2 p1:
p1:
1) p2在k-1维的空间中支配点p1,即![]()
2) d(p2,q)<d(p1,q),在道路网中,p2与点q的网路距离比p1与点q的网路距离更小.
定义3. 空间支配[7].空间中存在一个数据点p∈P,查询点qi,如果满足条件:对于P中任意一个数据点p′∈P,对于查询点qi存在d(qi,p)≤d(qi,p′)成立,则数据点p空间支配数据点p′.
定义4. 网络Voronoi图(network Voronoi diagram, NVD)[25].NVD与基本Voronoi图的区别在于NVD采用的是路网距离,而并非欧氏距离.在NVD中,由路网中的边和虚线所围成的区域称为网络Voronoi区域(network Voronoi polygon, NVP).由pi生成的NVP记为VNVP(pi).若给定生成点集合P={p1,p2,…,pn},边的集合E={e1,e2,…,ek}.pj为不同于pi的生成点,则VNVP(pi)可以形式化定义为
![]()
(1)
性质1[25]. 如果点q在网络Voronoi多边形VNVP(pi)中,则q到生成点pi的距离小于q到其他生成点的距离.
性质2[25]. 距离pi点最近的生成点一定在与VNVP(pi)有公共Voronoi边的Voronoi多边形中.
定义5. 道路网K-支配空间Skyline查询.给定一个查询点q和一个n维空间的对象集P,其中道路网K-支配空间Skyline查询结果返回P的一个子集,在此子集中的数据点都不能被P中的任何其他点在用户偏好的k-1个维度上非空间属性支配,并且在第k维空间属性上在道路网环境中也未被其他数据点空间支配,这样的数据点被称为道路网K支配空间Skyline点,记为K-PNS(q,P).道路网K-支配空间Skyline查询本文简称为K-PNS查询.
表1表示一个宾馆数据对象的非空间属性表.非空间属性是数据点的非空间地理位置的数据点自身存在的一些属性.这些信息不是地理位置上的空间坐标的位置,是非空间上数据点本身自有的属性,本文中的非空间属性是在一定范围内随机取得的模拟值.表1中,数据点p1,p2,p3,p4,p5为数据对象集中5个具有5维属性的宾馆,其中前4维为非空间属性,对应宾馆的价格、开业时间、用户评价和清洁情况.最后一维属性为宾馆距离查询点的道路网距离,如图1所示,图1给出了5个宾馆对象在道路网上的位置分布以及查询区域,需要查找的是在5维属性中数据点在4维属性维度上不被支配的查询结果,即道路网4-支配空间Skyline查询.
Table 1 Example of Non-spatial Attributes of Hotel Data Object
表1 宾馆数据对象的非空间属性示例

HotelPriceUser RatingOpening HoursCleanlinessp1175324p2226435p3198454p4300513p5156333
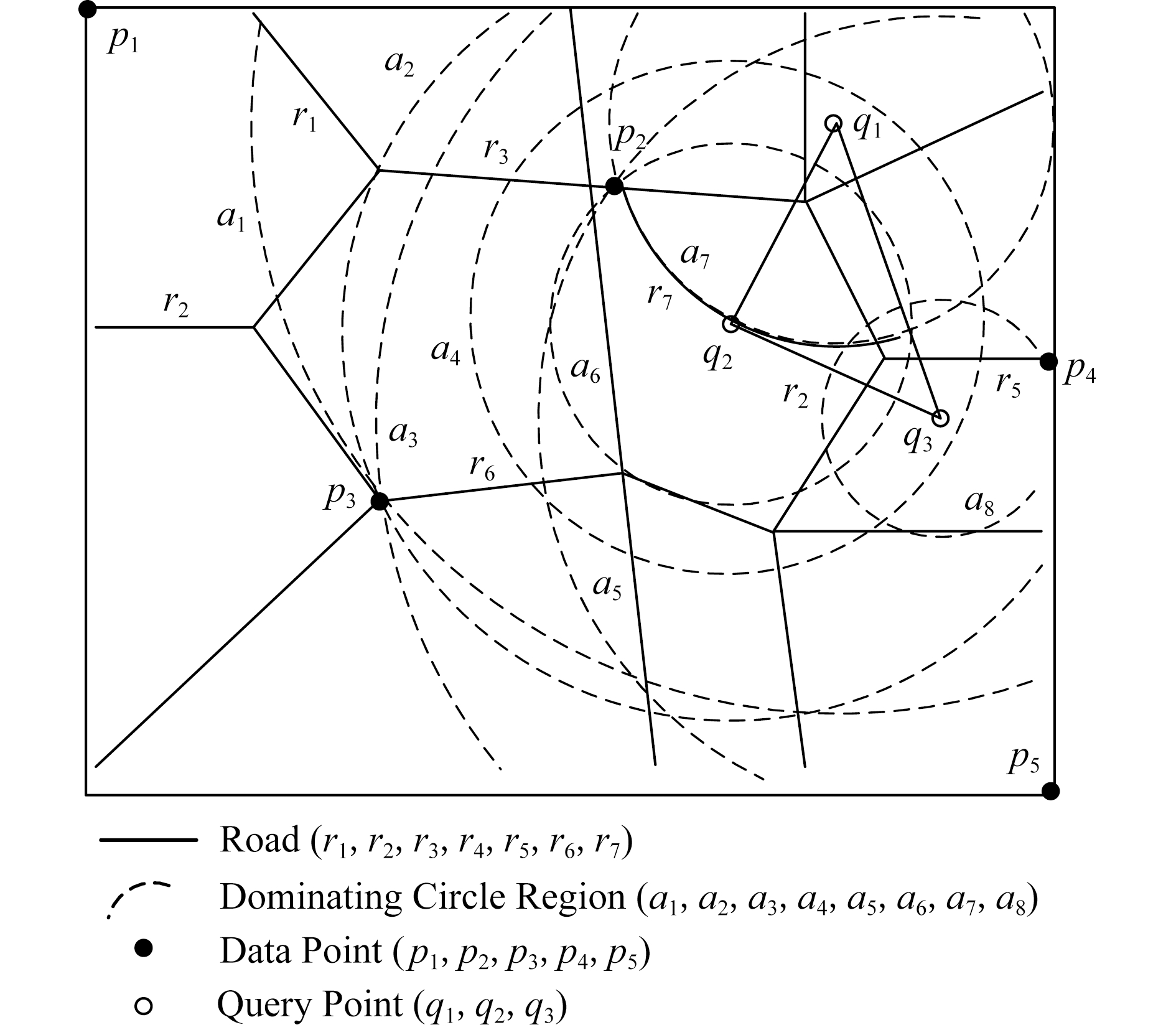
Fig. 1 Example of spatial attributes of hotel data object
图1 宾馆数据对象的空间属性的示例
首先对空间属性进行支配查询,图1中圆弧线a1,a2,a3,a4,a5,a6,a7,a8表示数据点p2,p3,p4相对查询点的支配圆域,由图1可以看出在支配圆域内的点支配生成该圆域的点,因此,数据点p2,p3,p4在道路网环境空间支配点p1和p5,即数据点在空间属性上不被支配的查询结果为{p2,p3,p4}.进一步对非空间属性进行3维支配的查询,基于查询区域的道路网Skyline查询需要查找对象集中既便宜,且用户评价好又距离用户当前位置近的宾馆.由表1可以看到在非空间属性中,在价格方面数据点p4和点p2被点p3支配,因此对于数据点在道路网4支配空间Skyline查询的结果为{p3}.即该例子中的道路网K-支配空间Skyline查询的结果为{p3}.
2 道路网K-支配空间Skyline查询
本文提出的道路网K-支配空间Skyline查询方法主要分为2个主要的过程:道路网中约减数据集过程和K-支配检查过程.首先通过约减大量的非候选数据点得到道路网环境中的候选集合,然后对候选集的非空间属性进行K-支配检查得到道路网精炼集合,最后对精炼集合进行支配检查得到最终的空间Skyline集合.本节优先处理数据点空间属性的道路网支配关系,由于数据点非空间属性往往较多,从而使得非空间属性间支配比较次数增加,如果优先处理非空间属性间的支配关系,在数据点数量较大时,算法的查询效率会降低.
2.1 约减数据集
约减数据集过程主要是对数据点进行过滤处理,通过道路网Voronoi图与查询点集合建立影响的查询区域间的空间位置关系来剪枝掉大量的被支配的数据点,用于获得精确的候选点集合.首先对空间数据点构建道路网Voronoi图,再对查询点建立一个查询的凸包.然后利用道路网Voronoi图及其查询区域形成的位置关系以及数据点之间的支配关系来约减大量被支配的数据点,从而缩小查询范围,剩下的数据点构成候选点集合.在此过程中通过对查询点集建立查询区域与建立数据点的道路网Voronoi图的方法来约减数据集,能够优化处理数据集并且有效地减少查询点重复搜索的现象,约减掉大量的非候选点,较大程度地缩小了查询的范围.
本文所研究的数据点与查询点之间的距离均采用道路网络中的网络距离.本节以定理的形式给出约减方法.假定数据点前n维的非空间属性是固定不变的,本节为了简化道路网非空间属性对空间支配的影响,用数据对象的非空间属性值的总和来表示非空间属性的支配能力,结合数据点的空间属性,查询结果得到的不被空间支配的候选集是固定的,使得查询效率更快.由于数据点为道路网上的静态点,故其道路网Skyline查询结果的变化是由查询位置与数据点之间的距离变化引起的.
定理1. 在由数据点构造的道路网Voronoi图中,若查询凸包CH(Q)内有一数据点p,则数据点p支配CH(Q)与该点所成圆相切区域外的数据点,则该区域外的数据点均被约减,区域内的数据点可加入候选集中.
证明. 已知在道路网Voronoi图中的数据点p与各查询点所成圆域外的一点数据点,2点所连接的线段的垂直平分线将2点分割为2个区域,p点与查询区域CH(Q)在同一边,根据垂直平分线性质,p点与各查询点的距离更近,则数据点p支配CH(Q)与该点所成圆相切区域外的数据点.在图2中,任意选取1组数据点和查询点,例如查询点集为Q={q1,q2,q3},数据点集为P={p1,p2,p3,p4,p5}.查询点组成的查询区域CH(Q)内任意位置有一数据点p,分别以各查询点q为圆心、以数据点p与各查询点间的距离为半径做圆.图2中的矩形区域表示数据点p与各查询点形成的圆(circle(p,q))相切的数据点p的支配区域,圆弧线l1,l2,l3表示数据点相对不同查询点的支配圆域.如图2所示,数据点p2是数据点p与各查询点形成的圆相切矩形区域外的任意一个数据点.从图2可以求得数据点p与查询点q1的道路网环境中的网络距离关系为:d(q1,p)<d(q1,p2),同理可得数据点p与另外2个查询点q1,q2的网络距离关系为:d(q2,p)<d(q2,p2),d(q3,p)<d(q3,p2).根据空间数据点支配的定义可得,点p在空间上支配区域外的点p2,则数据点p支配CH(Q)与该数据点所成圆相切区域外的点,则该区域外的点均被约减.
证毕.
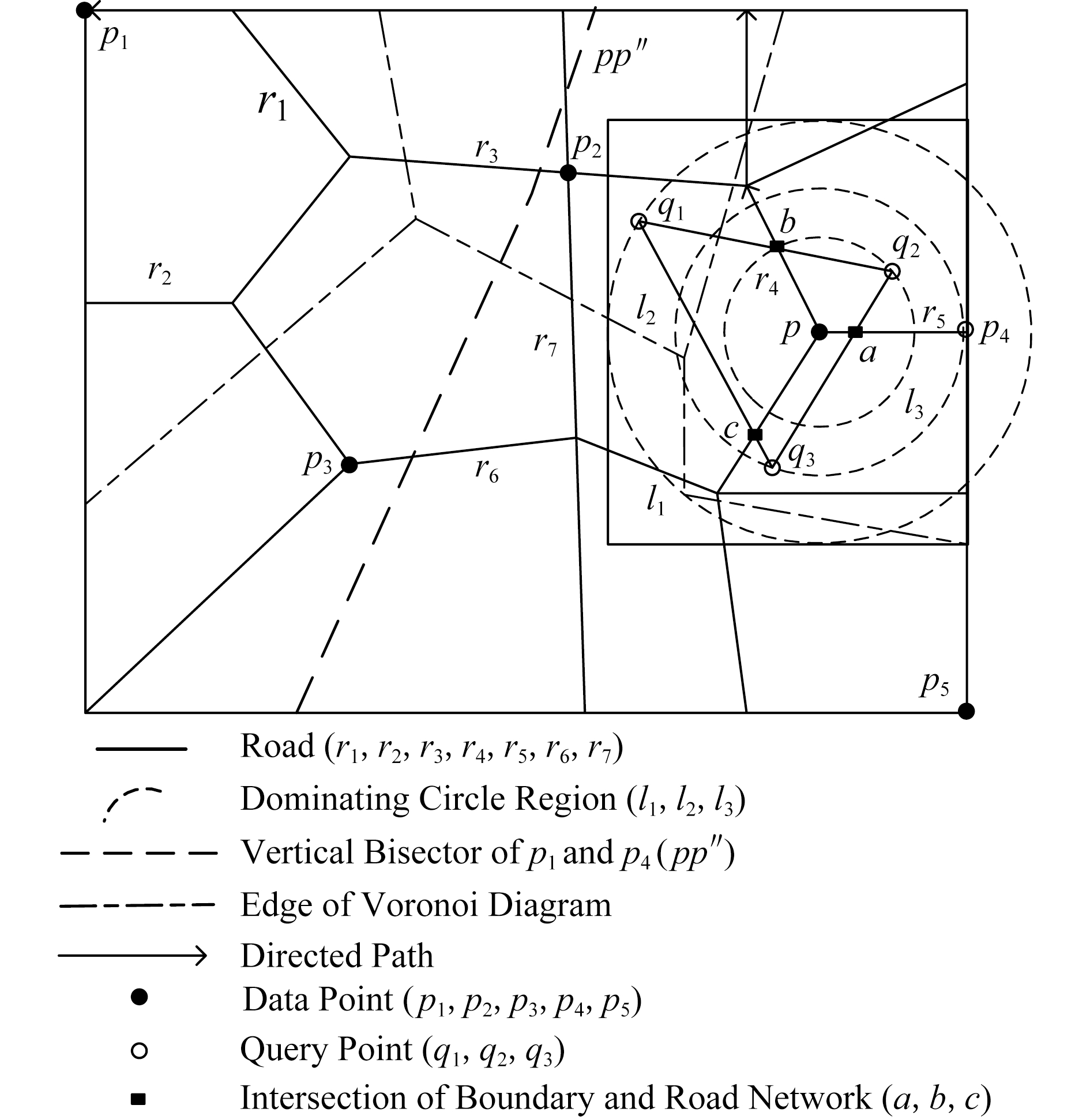
Fig. 2 Example based on theorem 1,2 and 3
图2 基于定理1,2,3的示例
定理2. 已知数据点p∈P,如果查询区域CH(Q)与该数据点所在的道路网Voronoi单元VC(p)相交,若数据点q为与数据点p所在道路网上任意一条不相交的道路网上的一个数据点,则数据点p支配点q,数据点q被剪枝.
证明. 任意连接与查询区域有关联的数据点p和与查询区域不相交的Voronoi单元内的数据点,则该2个数据点构成的线段的垂直平分线将与查询区域相交的Voronoi单元的数据点与查询点划分在一边.根据Voronoi图性质可知,在Voronoi单元内的数据对象点与形成该Voronoi单元的生成点之间的距离最短,因此与查询区域相交的数据点支配未与查询区域相交的数据点.如图2所示,任意选取数据点如p4,数据点p4∈P,数据点p4所在的Voronoi单元与查询区域CH(Q)相交,作线段pp″为数据点p1和数据点p4线段的垂直平分线,根据垂直平分线性质可知,同属一边的2点距离更近,由图2可以知道线段pp″与查询区域CH(Q)不相交,且该垂直平分线将数据点p4与CH(Q)划分到同一侧,已知垂直平分线上点到线段的两端点的距离相等,则对于qi∈CH(Q),一定有d(qi,p4)<d(qi,p1).因此,数据点p4支配点p1,故数据点p1被剪枝.因为与查询点的距离更近,所以圆域内的数据点支配圆域外的数据点,如数据点p.同样作线段pp4的垂直平分线,如图2所示,可以看到此垂直平分线与CH(Q)相交,则CH(Q)中距离p点更近的查询点之间的距离比p4更近,与p4同一侧的CH(Q)内的点之间的距离比与p点距离更近,即p点与p4点之间互补支配,故可以将2点都加入候选点集合中进行下一步的精炼,从而得到最终的空间道路网候选集.
证毕.
定理3. 对于给定的查询凸包区域CH(Q),若数据点所在的道路网与CH(Q)的边界相交,则该数据点与查询各点的网络距离更近,该数据点可加入到候选集中.
证明. 对于查询区域CH(Q)内任意查询点q,从q出发,要到达查询区域CH(Q)外的任意对象点pi,其最短路径必定经过查询区域CH(Q)与道路网的交点.由2点间线段最短定理可知,数据点pi与查询点q间的网络距离一定大于查询点q与相交路网上数据点的距离,故数据点pi被剪枝.如图2所示,要从对象数据点p1,p2,p3,p4到查询区域CH(Q)中任意一个查询点q,必定经过查询区域CH(Q)的边界与道路网的交叉点a,b,c这3个点之中的某一个.因此,对于数据点p1,存在有d(q1,p)=d(q,b)+d(b,p1).可见数据点p1到查询区域内部点q必经过查询区域的交点b,由此可知数据点所在的道路网与CH(Q)的边界相交,则该数据点与查询各点的网络距离更近,将该数据点加入到候选集中.
证毕.
只有当一个数据点在空间属性与非空间属性上均支配另一个数据点时,该数据点才可能是道路网中K-支配Skyline点,应该将这类数据点加入到候选集中.由于可能存在数据点的某些非空间属性值较大,影响K-支配查询的效率,因此在道路网环境中用数据点的非空间属性值的总和代表数据点非空间属性的支配能力,总体的支配能力可以初步约减掉部分非空间属性值较大的情况,便于约减非空间属性支配能力差的数据点.
约减策略1. 数据点在查询区域内或者查询点所在的道路网Voronoi单元与查询区域相交,则将查询点加入到候选集中.
在数据点构造的道路网Voronoi图中,若查询凸包CH(Q)内有一个数据点p,则数据点p支配CH(Q)与该点所成圆的相切区域外的数据点,则该区域外的数据点均被约减,区域内的数据点可加入候选集中.任意连接与查询区域有交集的数据点p和未与查询区域相交的Voronoi单元内的数据点,则该2个数据点构成的线段的垂直平分线将与查询区域相交的Voronoi单元内的数据点与查询点分在一边.根据Voronoi图性质,在Voronoi单元内的点与形成该Voronoi单元的点之间的距离最短,因此,与查询区域相交的数据点支配未与查询区域相交的数据点.
约减策略2. 数据点所在的道路网如果与查询区域相交,则将该数据点加入到候选集中.
任意连接与查询区域有关联的数据点p和未与查询区域相交的Voronoi单元的数据点,则该两个数据点够成的线段的垂直平分线将与查询区域相交的Voronoi单元的数据点与查询点化分在一边.根据Voronoi图性质可知在Voronoi单元内的点与形成该Voronoi单元的点之间的距离最短,因此各查询点与有关联的VNVP(p)内的数据点p的空间距离更短,即与查询区域相交的数据点支配未与查询区域相交的数据点.对于查询区域CH(Q)内的任意查询点q,从q开始到达查询区域CH(Q)外任意对象点pi,其最短路径必定经过查询区域CH(Q)与道路网的交点.因此,数据点pi与查询点q间的网络距离一定大于查询点q与相交路网上数据点的距离,故数据点pi被剪枝.
约减策略3. 对于候选集中数据点的非空间属性的支配能力进行比较,支配能力更强的数据点留在候选集,否则从候选集中删除.
用数据点的非空间属性值的总和来表示数据对象的非空间属性的支配能力,只有当一个数据点在空间属性与非空间属性上均支配另一个数据点时,该数据点才可能是道路网中K-支配Skyline点,应该将这类数据点加入到候选集中.
基于定理1、定理2和定理3及约减策略,本节进一步给出算法R-PNS,如算法1所示.
算法1. R-PNS(Q,P,R).
输入:查询区域Q、道路网路段集合R、数据集P;
输出:基于查询范围Q的道路网Skyline查询候选集resultSP.
① 以P中的数据点和道路网路段为生成点创建道路网Voronoi图;
② a[pi]←∅;
③ for i=0 to n do
④ 计算p点的前n维非空间属性值的和;
⑤ 将结果按升序结果存入a[pi]中;
⑥ end for
⑦ resultSP←∅;
⑧ 连接查询点组成最大的凸多边形查询区域CH(Q);
⑨ if p在CH(Q)内then
⑩ SR(p,Q)←circle(p,q1)∪…∪circle(p,qm); *以qi为圆心,p,qi之间的距离为半径做圆,m为查询点的数量*
*以qi为圆心,p,qi之间的距离为半径做圆,m为查询点的数量*
 BR=BR∩MBR(SR(p,Q));
BR=BR∩MBR(SR(p,Q));
 *获得内切矩形*
*获得内切矩形*
 if p在BR内then
if p在BR内then
 resultSP←resultSP+p;
resultSP←resultSP+p;
 *定理1*
*定理1*
 end if
end if
 end if
end if
 for j=1 to m do
for j=1 to m do
 if qj与VNVP(p)相交then
if qj与VNVP(p)相交then
 if p的路段与p所在的路段集合R相交then
if p的路段与p所在的路段集合R相交then
 resultSP←resultSP+p;
resultSP←resultSP+p;
 *定理2*
*定理2*
 end if
end if
 else if不相交then
else if不相交then
 找出查询区域CH(Q)与道路网集合R的相交的路段,记为r;
找出查询区域CH(Q)与道路网集合R的相交的路段,记为r;
 if p在路段r上then
if p在路段r上then
 resultSP←resultSP+p;
resultSP←resultSP+p;
 *满足定理3,加入候选集中*
*满足定理3,加入候选集中*
 end if
end if
 end if
end if
 end if
end if
 end for
end for
 for i=0 to |resultSP| do
for i=0 to |resultSP| do
 if a[p]>a[pi] then
if a[p]>a[pi] then
 resultSP←resultSP-p;
resultSP←resultSP-p;
 else if a[p]≤a[pi] then
else if a[p]≤a[pi] then
 resultSP←resultSP-pi;
resultSP←resultSP-pi;
 end if
end if
 end for
end for
 return resultSP.
return resultSP.
约减数据集由算法1实现.算法1首先对数据点集建立道路网Voronoi图并对数据点的非空间属性值进行计算,总和的值越小表示数据点的非空间属性的支配能力越强.再对查询点建立查询区域CH(Q),根据道路网Voronoi图与查询区域CH(Q)的位置关系,由定理1判断数据点是否在查询区域CH(Q)内,如果数据点在查询区域内,则直接将该数据点加入候选集中.再进行判断与查询区域有交集的道路网Voronoi单元的数据点,根据定理2将这些数据点加入候选集中,这些点在空间上支配那些所在的道路网Voronoi单元不与查询区域相交的数据点.再判断数据点所在的道路网路段与查询区域是否相交.根据定理3将道路网上相交的数据点加入候选集中,将不符合条件的数据点约减,减少计算大量非候选数据点.根据道路网Voronoi图查询区域CH(Q)与道路网集R路段的交点,将每一个交点所在路段上的数据点加入到候选集,再将所有的候选点进行合并.最后对resultSP集合中数据点的非空间属性值进行支配能力检查,值越小的数据点支配另一个数据点.在道路网环境中用数据点的非空间属性值的总和代表数据点的非空间属性的支配能力,总体的支配能力可以初步约减掉部分非空间属性值较大的情况,约减非空间属性支配能力差的数据点,获得最终的候选集.
2.2 精炼候选集
精炼候选集过程的主要处理对象是在约减过程中所得到的候选集resultSP.本节首先根据数据点K-支配的定义及支配关系给出定理4和定理5,再根据定理对候选集中的数据点进行非空间属性支配判断,若满足条件则加入候选集中,从而构成精炼候选集.本文中数据点的非空间属性是由数据点的前n维随机生成的,非空间属性值越小越好.
定理4[24]. 对于任意2个数据点pi和pj,若数据点pi在k维非空间属性上支配数据点pj,则数据点pi必定k-1维支配数据点pj.
本节将数据点的非空间维数属性值的范围定为相同的,并且属性值越小它的优势越大.数据点在k维上的最好和最差的支配能力分别为
(2)
(3)
定理5[24]. 如果对于数据集d维中的任意2个数据点p1和p2,若在k维上存在worstK(p1)≥bestK(p2),则数据点p2一定不会在k-1维非空间属性上支配数据点p1.
可以将候选点与各查询点间的距离总和作为空间属性的值,如果数据点在非空间和空间属性上均不被其他数据点支配,则将该点加入到精炼集合中.将数据点与查询点的空间距离总和作为空间属性与非空间属性进行K-支配判断,得到精炼集合Sk.由于数据点的空间属性同样需要检查K-支配,影响K-支配查询的效率,因此在道路网环境中用数据点与各查询点的空间距离总和作为空间属性代表数据点空间属性的支配能力,总体的支配能力可以约减掉部分空间属性值较大的情况,便于精炼数据点.
我们进一步给出道路网数据点K-支配的I-PNS算法如算法2所示.
算法2. I-PNS(resultSP,Q,t).
输入:候选集resultSP、查询集合Q、用户感兴趣的非空间属性值个数t;
输出:resultSP中的K-支配Skyline数据精炼候选集Sk.
① Sk←∅;
② for every point p∈resultSP do
③ 计算点p最好的支配能力值bestK(p)和最差的支配能力值worstK(p);
④ p初始化标记为p.isDominat=false;
⑤ 对resultSP中的数据点p的最好的支配能力值bestK(p)进行升序排序;
⑥ 将bestK(p)升序排序结果存储到数组AI[1,2,…,t]中; *数组AI[1,2,…,t]构成AI表*
*数组AI[1,2,…,t]构成AI表*
⑦ 对resultSP中的数据点p最差的支配能力值worstK(p)进行升序排序;
⑧ 将worstK(p)升序排序结果存储到数组BI[1,2,…,t]中; *数组BI[1,2,…,t]构成B表*
*数组BI[1,2,…,t]构成B表*
⑨ end for
⑩ for i=1 to t do *t是数组A和数组B中数据点的个数*
*t是数组A和数组B中数据点的个数*
 qi←AI[i];
qi←AI[i]; *p,q是数组中的点*
*p,q是数组中的点*
 if p.isDominat=false then
if p.isDominat=false then
 pi←BI[i];
pi←BI[i];
 if worstK(pi)<bestK(qi) then
if worstK(pi)<bestK(qi) then
 qi
qi pi;
pi;
 Sk←Sk+qi;
Sk←Sk+qi;
 else if worstK(pi)≥bestK(qi) then
else if worstK(pi)≥bestK(qi) then
 Sk←Sk+pi;
Sk←Sk+pi;
 end if
end if
 end if
end if
 end for
end for
 for i=0 to |Sk| do
for i=0 to |Sk| do
 for j=0 to m do
for j=0 to m do
 count d(pi,qj);
count d(pi,qj);
 d[pi]=d(pi,qj);
d[pi]=d(pi,qj);
 end for
end for
 if d[pi]>d[pi+1] then
if d[pi]>d[pi+1] then
 Sk←Sk-pi;
Sk←Sk-pi;
 else if d[pi]≤d[pi+1] then
else if d[pi]≤d[pi+1] then
 Sk←Sk-pi+1;
Sk←Sk-pi+1;
 end if
end if
 end for
end for
 return Sk.
return Sk.
算法2首先建立2个索引表来存储数据点的k维的最好和最坏支配能力值:AI表和BI表,根据对算法1中所得的候选集优化精炼的基本思想,首先要对候选集中的数据点计算其最好支配能力值和最差支配能力值,将结果按升序存储在表中,并对每一个数据点初始标记为未被支配.再根据定理4和5对表AI和BI中的数据点进行比较.如果worstK(pi)<bestK(qi),则点qi支配点pi,将点qi加入精炼候选集Sk中.再计算数据点空间支配的影响,被支配的数据点从候选集中删除,剩余的数据点组成最后的精炼集合,将数据点与各查询点的空间距离总和作为空间属性与非空间属性进行K-支配判断,最后得到精炼集合Sk.
2.3 查询算法
本节根据道路网K-支配空间Skyline查询的不同情况分别调用道路网空间Skyline情况下的R-PNS算法和K-支配空间Skyline查询情况下的I-PNS算法进行查询.
定理6. 确定数据点的支配判定圆区域的范围,数据点p与查询点qi之间通过道路网相互连接,当数据点p∈Sk时,则以查询点qi为圆心、查询点qi与数据点p间的网络距离d(qi,p)为半径做圆,若在多个圆域的相交区域中存在数据点pk,则数据点pk空间上支配数据点p,则将数据点p剪枝.
证明. 当数据点p∈Sk时,以查询点qi为圆心、以qi与数据点p之间的网络距离d(qi,p)为半径作圆,若在多个圆域的相交区域内存在数据点pk,则对于查询点qi,一定存在d(qi,pk)<d(qi,p),根据空间数据点支配定义可知,在空间上数据点pk支配数据点p,则数据点p就不是查询点q的空间Skyline点,故将数据点p删除.
证毕.
图3中,以qi点为中心、以候选集内的任意一数据点p之间的网络距离为半径做圆,圆弧线d1,d2,d3表示数据点相对不同查询点的支配圆域.若该圆域相关的相交区域内存在其他数据点p′,则相交区域内的数据点p′支配数据点p.根据定理2和3,{p1,p2,p4,p′}可加入候选集.以{q1,q2,q3}为圆心、以各候选集内的数据点的网络距离为半径做圆(如图3所示),点p′即处于这些圆域的相交区域中,根据定理6可知p2支配点p′.由此可知,数据点中不被空间支配的查询结果为Sk={p4,p′}.

Fig. 3 Example based on theorem 6
图3 基于定理6的示例
本节查询算法的主要思想为:首先调用算法1得到初步约减数据集后的候选集,再调用算法2对候选集进行非空间属性K-支配精炼处理,获得更精确的候选集.然后分别求出候选集中的点p到qi的网络距离d(p,qi).若满足d(qi,p1)<d(qi,p)时,候选点p被数据点p1支配,则从候选集中删除数据点p.最后剩下的候选点就构成查询结果集.
本节进一步给出K-PNS查询算法,如算法3所示.
算法3. K-PNS(Q,k,P,R).
输入:查询集Q、支配维数k、数据集P、道路网路段集R;
输出:道路网K-支配情况下的空间Skyline查询的结果集Sp.
① resultSp←∅,Sk←∅,Sp←∅;
② resultSp←call R-PNS(Q,P,R); *调用算法1,计算约减候选集合*
*调用算法1,计算约减候选集合*
③ Sk←call I-PNS(resultSp,Q,k); *调用算法2,计算精炼候选集合*
*调用算法2,计算精炼候选集合*
④ if p在Sk中then
⑤ for j=1 to m do
 *m是查询点的个数*
*m是查询点的个数*
⑥ C←Calculate_Circle(qj,pi); *计算支配判定圆的范围*
*计算支配判定圆的范围*
⑦ if p inside Sk并且p∩C≠∅ then
⑧ Sp←Sp-p;
⑨ else if p不在其他点的支配圆域内then
⑩ Sp←Sp+p;
 end if
end if
 end for
end for
 end if
end if
 return Sp.
return Sp.
算法3首先调用算法1求出PNS查询结果;在考虑数据点的k维属性时,则调用算法2得到精炼集.对精炼集合中的数据点再进行支配检查,对数据点与查询点做判定圆区域检查,在区域内若无其他数据点则加入Sp集,否则删除.最后算法对Sp集中的点进行k维检查,不满足条件的数据点从Sp集中删除,最终留下的数据点就是道路网K-支配空间Skyline查询的结果集.
3 实验比较与分析
本节通过实验对算法进行性能评估.由于道路网中K-支配空间Skyline查询问题是本文研究的一个新问题,已有研究成果无法直接处理道路网中K-支配空间Skyline查询问题,因此,为了构造对比算法,我们对文献[26-27]的曼哈顿道路网中空间Skyline查询的MSSQ算法和道路网基于距离的连续Skyline查询的Cknn-SQ算法进行了适当的修改,针对给定查询问题采用反复调用MSSQ算法和Cknn-SQ算法的策略,从而逐步得到数据点k维属性上的Skyline查询结果,从而与本文提出的K-PNS算法形成对比算法.得到的对比算法在本文称为MSSQ算法和Cknn-SQ算法.MSSQ算法分别对数据点集P和查询点集Q在一维上建立平衡二叉树,在其他维度上保存数据;Cknn-SQ查询算法从Skyline结果集中向用户返回s个Skyline点,这s个Skyline点在距离属性上要优于剩下的数据点.
本文使用的道路网数据集是来自美国加利福尼亚州空间信息网络,该网络中的数据集由地理信息组成.我们从该数据集中抽取10 000个节点对象和5 000个线段对象(线段作为道路网线段).为便于实验,对数据对象信息进行了适当调整和改动.查询集是由数据集中随机抽取的100个点的集合,数据点的非空间属性以数值来表示,数值在[0,20]上随机产生.
实验平台配置为:4 GB内存、2.0 GHz CPU、500 GB硬盘,Windows 10操作系统上用Microsoft Visual Studio2013实现.实验需要验证的是3个算法的查询性能,测试的指标是CPU时间和I O执行次数,两者反映各个算法的查询性能.实验测试中采用的合成数据为Skyline查询的测试数据集,测试过程中取执行30次查询的平均值作为结果.实验分别测试非空间属性维数k值、数据点数量和道路网路段数量对CPU执行时间和I
O执行次数,两者反映各个算法的查询性能.实验测试中采用的合成数据为Skyline查询的测试数据集,测试过程中取执行30次查询的平均值作为结果.实验分别测试非空间属性维数k值、数据点数量和道路网路段数量对CPU执行时间和I O执行效率的影响.
O执行效率的影响.
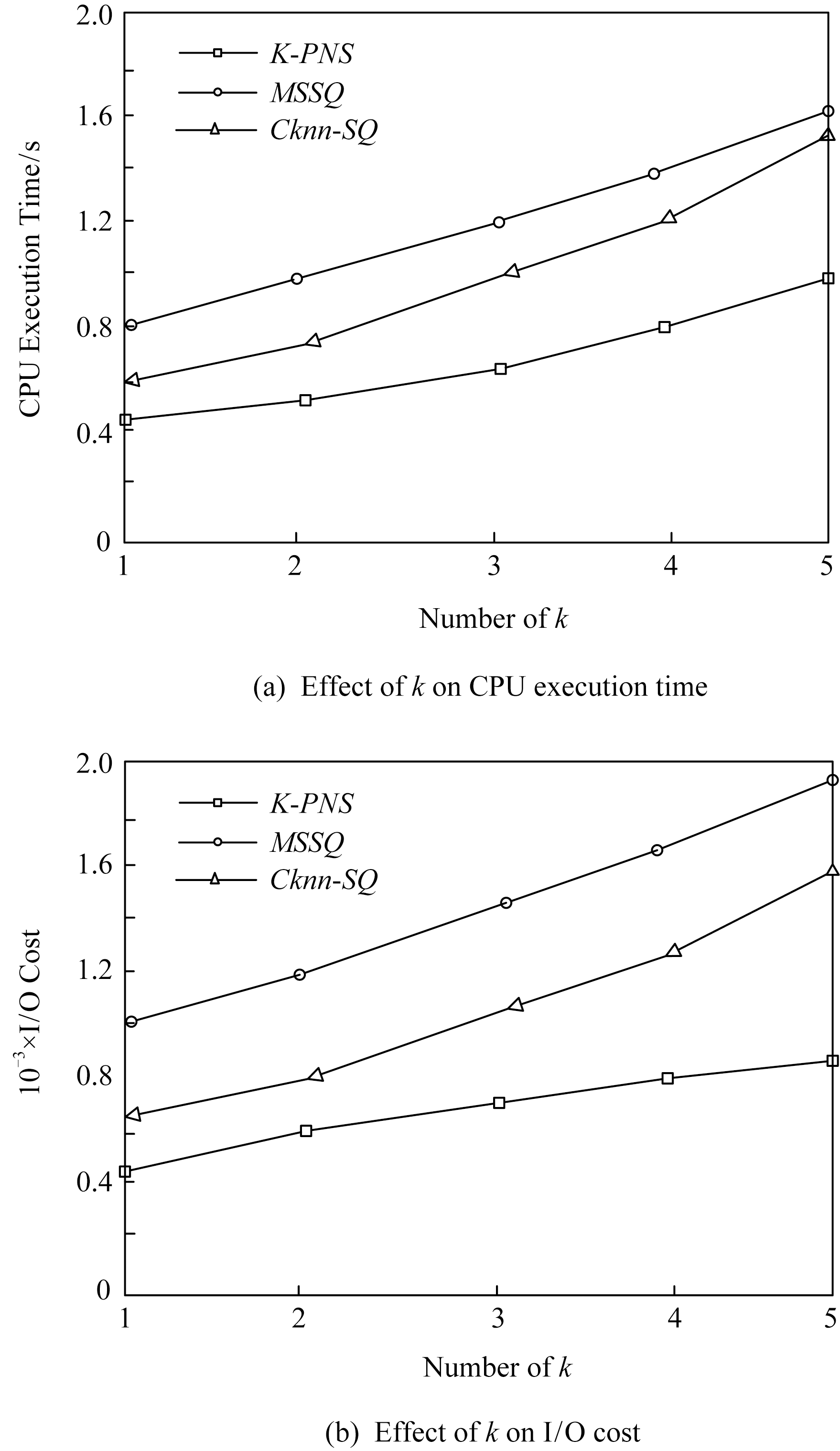
Fig. 4 Effect of k value on the efficiency ofthe query algorithms
图4 k值对查询算法效率的影响
如图4所示,实验测试了k值对算法的影响.在数据点的数量是10 000、查询点数量为100、道路网线段数量为1 000、数据点维数d=10、数据集的非空间属性维数k从1增加到5的情况下测试了3种查询算法的查询性能.从图4(a)中可以看出,K-PNS算法、MSSQ算法和Cknn-SQ算法的CPU执行时间都是随着k值的增大而呈上升趋势,K-PNS算法和Cknn-SQ算法的查询效率均优于MSSQ算法.但是Cknn-SQ算法上升趋势比K-PNS算法更显著,原因在于Cknn-SQ算法需要重新调用算法对视作数据点的道路网线段重新处理.图4(b)展示了k值增加对K-PNS算法、MSSQ算法和Cknn-SQ算法的I O代价的影响情况.由图4(b)可以看到随着k值的增加,3个算法的I
O代价的影响情况.由图4(b)可以看到随着k值的增加,3个算法的I O代价都逐渐增大,但K-PNS算法随着k值的增长速率先增大后减小,I
O代价都逐渐增大,但K-PNS算法随着k值的增长速率先增大后减小,I O代价的增幅最小.这是因为在数据点的非空间属性维数较小时,数据点的非空间属性的相互支配较多,所以I
O代价的增幅最小.这是因为在数据点的非空间属性维数较小时,数据点的非空间属性的相互支配较多,所以I O代价较高.
O代价较高.
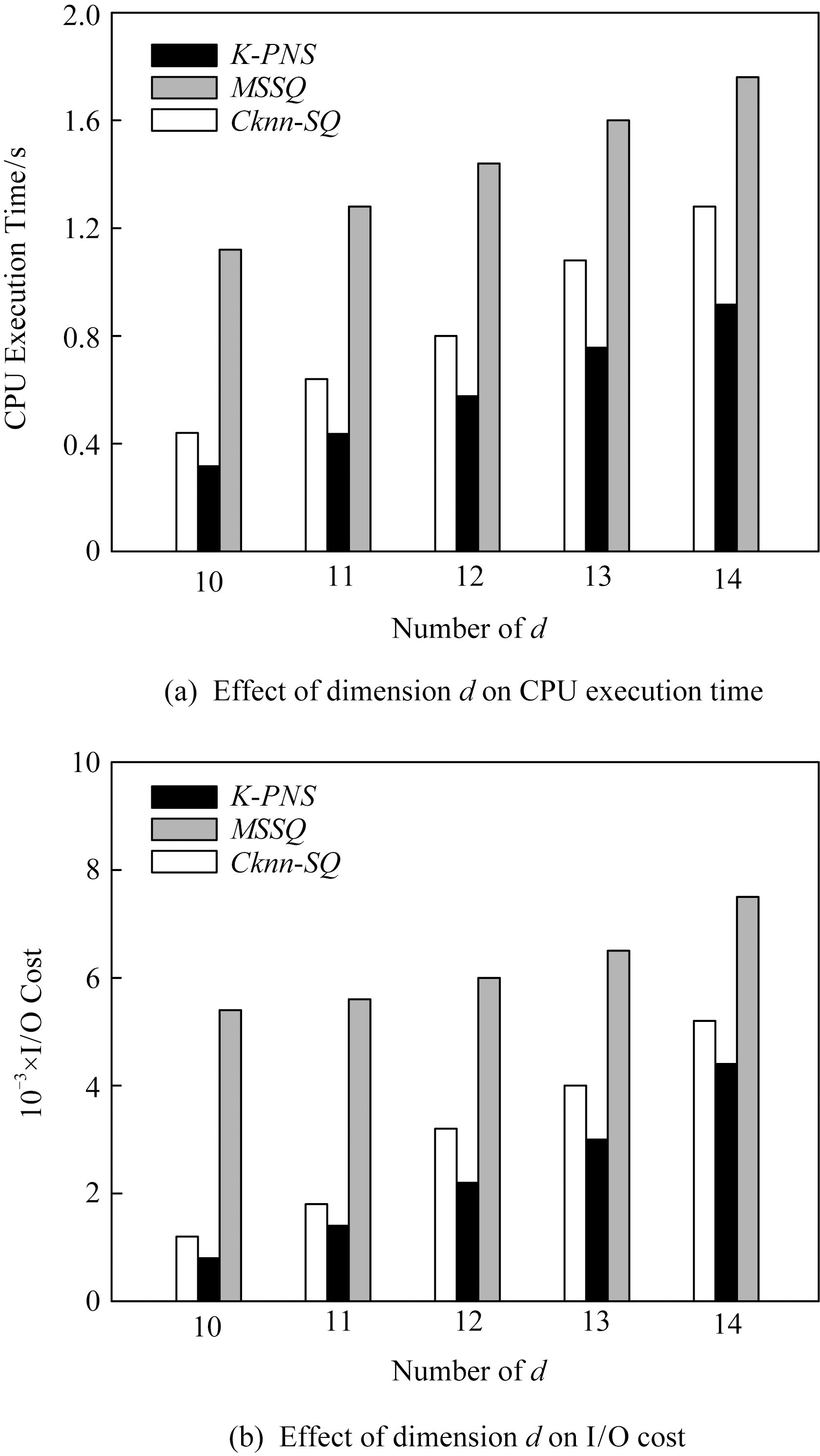
Fig. 5 Effect of dimension of data set onquery efficiency
图5 数据集维数对算法查询效率的影响
图5测试的是关于数据集维数变化对算法查询效率的影响.在数据点的数量是10 000、查询点数量为100、道路网线段数量为1 000、k=3的情况下测试了3种查询算法的查询性能.图5表示的是数据集维数d对算法的查询性能的影响.MSSQ算法采用平衡二叉树处理数据点间的道路网距离,随着数据集维数的增大,算法增加的趋势并不快,但是算法原本需要花费较多的时间和I O代价处理.Cknn-SQ算法采用网格索引对道路网和道路网上的数据点进行索引,维数的增多和距离增大使算法的查询性能有所降低.K-PNS算法在约减数据集的过程中,对空间属性和非空间属性分别进行了处理,因此随着维数的增加,算法的查询时间和I
O代价处理.Cknn-SQ算法采用网格索引对道路网和道路网上的数据点进行索引,维数的增多和距离增大使算法的查询性能有所降低.K-PNS算法在约减数据集的过程中,对空间属性和非空间属性分别进行了处理,因此随着维数的增加,算法的查询时间和I O代价变化较小.在数据集维数增加的情况下,K-PNS算法和Cknn-SQ算法优于MSSQ算法.
O代价变化较小.在数据集维数增加的情况下,K-PNS算法和Cknn-SQ算法优于MSSQ算法.

Fig. 6 Effect of data size on query performance
图6 数据点数量对查询性能的影响
图6测试数据点数量对算法查询性能的影响.设道路网线段数量为1 000、查询点为100、数据点维数d=10、k=3.由图6(a)可知,K-PNS算法和Cknn-SQ算法的时间耗费相对较少,MSSQ算法时间耗费较多.因为MSSQ算法需要对数据点进行重复调用来计算数据点k维非空间属性,在数据点增加的过程中反复调用算法花费时间较多,而K-PNS算法已经对数据点的非空间属性进行了处理,所以随着数据点的增加,CPU执行时间增加较小.从图6(b)中可以看出,随着数据点的增加,3个算法的I O代价都增加,本文所提的K-PNS算法比Cknn-SQ算法和MSSQ算法的CPU时间和I
O代价都增加,本文所提的K-PNS算法比Cknn-SQ算法和MSSQ算法的CPU时间和I O开销都要小.随着道路条数的增多,道路连通性更加复杂,Cknn-SQ算法计算全局Skyline点过程中,对道路网的访问以及对象之间的距离计算的复杂度都会增大.而K-PNS算法由于只需要维护固定对象序列的相邻对象点的距离关系,虽然其开销也会随着道路条数的增多而增大,但较MSSQ算法和Cknn-SQ算法的复杂度降低.
O开销都要小.随着道路条数的增多,道路连通性更加复杂,Cknn-SQ算法计算全局Skyline点过程中,对道路网的访问以及对象之间的距离计算的复杂度都会增大.而K-PNS算法由于只需要维护固定对象序列的相邻对象点的距离关系,虽然其开销也会随着道路条数的增多而增大,但较MSSQ算法和Cknn-SQ算法的复杂度降低.

Fig. 7 Effect of road network line segmentnumber on query performance
图7 道路网线段数量对查询性能影响
图7测试道路网线段对算法的查询性能的影响.设数据点数量为10 000、查询点数量为100、数据点集维数d=10、k=3.图7表示的是道路网线段数量对算法的查询性能的影响,w表示道路网线段数量.MSSQ算法采用平衡二叉树处理数据点间的道路网距离,随着道路网线段数量的增大,算法需要花费更多的时间和I O代价处理,而Cknn-SQ算法采用网格索引对道路网和道路网上的数据点进行索引,随着道路网线段增多,数据点与查询点之间的距离关系会发生变化,算法的查询性能减慢.但是K-PNS算法中在约减数据集的过程中,对不被支配路段的点及其路段进行了约减,所以道路网路段的增加对CPU执行时间和I
O代价处理,而Cknn-SQ算法采用网格索引对道路网和道路网上的数据点进行索引,随着道路网线段增多,数据点与查询点之间的距离关系会发生变化,算法的查询性能减慢.但是K-PNS算法中在约减数据集的过程中,对不被支配路段的点及其路段进行了约减,所以道路网路段的增加对CPU执行时间和I O代价增长的趋势不大.因此在道路网线段增加的情况下,K-PNS算法优于MSSQ和Cknn-SQ算法.
O代价增长的趋势不大.因此在道路网线段增加的情况下,K-PNS算法优于MSSQ和Cknn-SQ算法.
4 结束语
本文对道路网K-支配空间Skyline查询问题进行了系统研究.形式化定义了道路网环境下K-支配空间Skyline查询,提出了有效地处理道路网K-支配空间Skyline查询的算法,较大程度地减少了处理数据点和路段数量的时间,通过K-支配检查可得到精准的结果集.理论研究和实验表明,所提出的算法具有较好的性能.未来的研究重点主要集中在将障碍空间中的组反k最近邻查询技术[28]应用到障碍物的空间Skyline查询领域以解决复杂环境条件下的空间Skyline查询问题.
[1]Borzsony S, Kossmann D, Stocker K. The Skyline operator[C] //Proc of the 17th Int Conf on Data Engineering. Piscataway, NJ: IEEE, 2002: 421-430
[2]Ahmed K, Nafi N, Gregory M. Enhanced distributed dynamic Skyline query for wireless sensor networks[J]. Journal of Sensor & Actuator Networks, 2016, 5(1): 97-110
[3]Zhou Xu, Li Kenli, Zhou Yantao, et al. Adaptive processing for distributed Skyline queries over uncertain data[J]. IEEE Transactions on Knowledge & Data Engineering, 2016, 28(2): 371-384
[4]Cui Ningning, Yang Xiaochun, Wang Bin. Research on authentication of moving K-dominant NN queries[J]. Chinese Journal of Computers, 2018, 41(8): 1780-1797 (in Chinese)(崔宁宁, 杨晓春, 王 斌. 移动K-支配最近邻查询验证研究[J]. 计算机学报, 2018, 41(8): 1780-1797)
[5]Banaei-Kashani F, Ghaemi P, Movaqar B, et al. Efficient maximal reverse Skyline query processing[J]. Geoinformatica, 2017, 21(3): 549-572
[6]Qi Yafei, Wang Yijie, Li Xiaoyong. A Skyline query method over Gaussian model uncertain data streams[J]. Journal of Computer Research and Development, 2012, 49(7): 1467-1473 (in Chinese)(祁亚斐, 王意洁, 李小勇. 基于高斯模型的不确定数据流Skyline查询方法[J]. 计算机研究与发展, 2012, 49(7): 1467-1473)
[7]Wang Xiaoyi, Qin Xiaolin, Wang Ning, et al. Efficient algorithm for multiple subspace Skyline queries processing[J]. Journal of Frontiers of Computer Science & Technology, 2016, 10(5): 623-634
[8]Zheng Jiping, Chen Jialiang, Wang Haixiang. Efficient geometric pruning strategies for continuous Skyline queries[J]. ISPRS International Journal of Geo-Information, 2017, 6(3): 91-117
[9]Park Y, Min J K, Shim K. Processing of probabilistic Skyline queries using MapReduce[J]. VLDB Endowment, 2015, 8(12): 1406-1417
[10]Yang Linqing, Li Zhan, Mou Yanchao, et al. Algorithm of parallel Top-k Skyline queries for large data set[J]. Journal of Frontiers of Computer Science & Technology, 2015, 9(8): 182-193
[11]Ding Linlin, Cui Ziqiang, Yin Xiankun, et al. Augmented dynamic Skyline query processing method based on MapReduce[J]. Acta Electronica Sinca, 2018, 46(5): 1062-1070 (in Chinese)(丁琳琳, 崔子强, 尹显坤, 等. 基于MapReduce的增广动态Skyline查询处理方法[J]. 电子学报, 2018, 46(5): 1062-1070)
[12]Li Song, Li Shuang, Zhang Liping, et al. Spatial Skyline query method based on R+tree for obstructed spaces[J]. Journal of Frontiers of Computer Science and Technology, 2017, 11(12): 1886-1896(李松, 李爽, 张丽平, 等. 障碍空间中基于R+树的空间Skyline查询方法[J]. 计算机科学与探索, 2017, 11(12): 1886-1896)
[13]Pan Xiao, Chen Weizhang, Sun Yige, et al. Continuous queries privacy algorithm based over road networks[J]. Journal of Computer Research and Development, 2017, 54(9): 2092-2101 (in Chinese)(潘晓, 谌伟璋, 孙一格, 等. 道路网络上基于时空相似性的连续查询隐私保护算法[J]. 计算机研究与发展, 2017, 54(9): 2092-2101)
[14]Bao Jinling, Liu Xingshan, Zhou Rui, et al. Keyword-aware optimal location query in road network[C] //Proc of the 17th Int Conf on Web-Age Information Management. Berlin: Springer, 2016: 164-177
[15]Deng Ke, Zhou Xiaofang, Shen Hengtao. Multi-source Skyline query processing in road networks [C] //Proc of the 23rd Int Conf on Data Engineering. Piscataway, NJ: IEEE, 2007: 796-805
[16]Huang Y K. Within Skyline query processing in dynamic road networks[J]. ISPRS International Journal of Geo-Information, 2017, 6(5): 137-152
[17]Miao Xiaoye, Gao Yunjun, Guo Su, et al. On efficiently answering why-not range-based Skyline queries in road networks[J]. IEEE Transactions on Knowledge & Data Engineering, 2018, 30(9): 1697-1711
[18]Fu Xiaoyi, Miao Xiaoye, Xu Jianliang, et al. Continuous range-based Skyline queries in road networks[J]. World Wide Web-Internet & Web Information Systems, 2017, 20(6): 1443-1467
[19]Jiang Shunqing, Zheng Jiping, Chen Jialiang, et al. Efficient computation of continuous range Skyline queries in road networks[C] //Proc of the 12th Int Conf on Intelligent Computing Methodologies. Berlin: Springer, 2016: 520-532
[20]Lee G, Lee Y H. An efficient method of computing the k-dominant Skyline efficiently by partition value[C] //Proc of the 3rd Int Conf on Information Management. Piscataway, NJ: IEEE, 2017: 416-420
[21]Miao Xiaoye, Gao Yunjun, Chen Gang, et al. K-dominant Skyline queries on incomplete data[J]. Information Sciences, 2016, 367/368: 990-1011
[22]Awasthi A, Bhattacharya A, Gupta S, et al. K-dominant Skyline join queries: Extending the Join Paradigm to K-dominant Skylines[C] //Proc of the 33rd IEEE Int Conf on Data Engineering. Los Alamitos, CA: IEEE Computer Socity, 2017: 99-112
[23]Siddique M, Tian H, Morimoto Y. K-dominant Skyline query computation in MapReduce environment[J]. IEICE Transactions on Information and Systems, 2015, 98(5): 1027-1034
[24]Yin Jian, Yao Shuyu, Xue Shaoe, et al. An index based efficient k-dominant Skyline algorithm[J]. Chinese Journal of Computers, 2010, 33(7): 1236-1245 (in Chinese)(印鉴, 姚树宇, 薛少锷, 等. 一种基于索引的高效k-支配Skyline算法[J]. 计算机学报, 2010, 33(7): 1236-1245)
[25] Kolahdouzan M R, Shahabi C. Voronoi-based K nearest neighbor search for spatial network databases[C] //Proc of the 30th Int Conf on Very Large Data Bases. San Francisco, CA: Morgan Kaufmann, 2004: 840-851
[26]Son W B, Hwang S W, Ahn H K. MSSQ: Manhattan spatial Skyline queries[J]. Information Systems, 2014, 40(3): 67-83
[27]Huang Y K,Chang C H,Lee C. Continuous distance-based Skyline queries in road networks [J]. Information Systems, 2012, 37(7): 611-633
[28]Zhang Liping, Liu Lei, Hao Xiaohong, et al. Voronoi-based group reverse k nearest neighbor query in obstruct space[J]. Journal of Computer Research and Development, 2017, 54(4): 861-871 (in Chinese)(张丽平, 刘蕾, 郝晓红, 等. 障碍空间中基于Voronoi图 的组反k最近邻查询研究[J]. 计算机研究与发展, 2017, 54(4): 861-871)




