随着移动终端及网络技术的更迭,移动社交网络在世界范围内发展极为迅速,国内移动社交软件微信的注册用户已超10亿,微博的活跃用户数也日益增加至超大规模的数据量级.社交网络平台为人们提供分享、交流信息等服务,同时用户的真实信息和敏感数据要被社交网络收集和归档,随之而来的是各类的隐私泄露问题[1-2],例如Facebook的隐私泄露事件.传统的隐私保护理论和技术逐渐体现出疲软之态,已无法涵盖大数据隐私的内涵,大数据隐私保护问题需要重新思考与定位[3].其中,社交网络图结构数据的匿名发布及隐私保护问题已成为大数据及隐私保护领域备受关注的研究方向之一.而大规模社交网络数据的时效性和可用性与现存匿名保护算法的低执行效率之间的矛盾成为解决该问题的最大挑战之一.
关于社交网络中的隐私保护问题,现存的方法主要有2类:一是基于聚类的方法,如Casas-Roma等人[4]提出的基于k-匿名的保护方法,这一类方法主要是将节点(边)按规则分为不同组,并隐藏组内的详细信息,能实现较高的隐私保护程度,但隐藏子图的内部信息严重影响了社交网络的局部结构分析,从而降低了数据可用性,因此如何进行有效的分组以提高数据的可用性成为这类方法需要解决的最大问题.另一类是基于网络图结构的扰动算法,如通过添加、删除和交换等操作修改网络图结构[5-6],使得发布数据和原始数据产生差异从而起到隐私保护作用,同时也保持了社交网络的原有规模,相比于聚类方法往往具有更高的数据可用性.其后,Dwork[7]提出差分隐私的概念,能实现数据的强隐私保护.这2类方法均可很好结合差分隐私的模型和定义,例如通过添加、删除等操作修改网络结构图并使其满足差分隐私的需求[8-9].
然而,随着超大规模社交网络的出现,需要在大量的社交关系中划分出不同敏感程度的边关系,并为这些边关系赋予不同的权值.相比于无权值的社交网络处理方法,能有效减少需要扰动的边数量.然而,网络中的边权值也包含着许多重要的隐私信息.例如,对某个社交网络群体进行传染病或者遗传病研究时,个体间的关系强弱可能会决定传染或者遗传的扩散趋势,这对于个体而言是极其隐私的信息.针对带权值的社交网络的数据隐私保护,目前研究者们提出了多种对边权值扰动的方法[10-11],然而这些方法不能有效地解决图结构攻击的问题:当攻击者掌握某节点的邻接度序列时,仍然可以确定该节点在图中的位置,子图攻击仍然奏效.针对此,本文提出了一种非交互式的基于差分隐私的带权社交网络隐私保护方法,在对边权值扰动的同时,通过添加边和节点噪音对图结构进行扰动从而抵御图结构攻击.
本文的主要贡献有3个方面:
1) 针对带权值的社交网络图的特征,在约束模型下区分图中的关键边和非关键边,基于差分隐私模型,分别添加不同的噪音达到隐私保护的同时最大程度保留了数据的可用性;
2) 设计了带权社交网络中的节点和边的扰动策略,使得算法具有抵御图结构攻击的能力;
3) 将提出的隐私保护方法与已有方法进行比较,实验结果表明,本文方法具有更高的运行效率,有效解决了大规模数据集发布的隐私保护和数据可用性及时效性的问题.
1 相关工作
近年来针对无权值的社交网络隐私保护,研究者们提出了许多解决方案.Zhou等人[12]提出的基于k-匿名保护方法将图结构中的节点(边)按规则分组,隐藏组内的详细信息以达到保护目的,通过k-匿名和l-多样性来抵御社交网络中的邻域攻击.Zou等人[13]提出k-字同构方法来实现隐私保护,该方法也是先将原始图分割成若干组,不同于k-匿名方法的是它通过向组内添加边使得k个块同构,在可抵御图结构攻击的同时也保留了原始图的规模.Chen等人[8]提出了DER(density-based exploration and reconstruction)算法对社交网络图结构进行聚类划分,基于差分隐私模型添加噪音来保护数据安全,这类方法对于抵御携带背景知识的攻击有着显著的效果.
针对带权值的社交网络图的隐私保护,Sala等人[9]基于节点聚类的方法,通过构建超边和超点(其中超边的边权值为2个超点边权值的平均值)实现隐私保护,但是和无权值网络中的k-匿名方法有着相同的缺陷:较严重降低了数据的可用性.也有研究者提出了基于差分隐私策略的保护方法.Wang 等人[10]提出采用高斯随机乘法在权值中加入噪音,从而实现隐私保护.这种方法虽然对权值起到了很好的保护作用,但是社交网络的属性参数也容易被改变,不能很好地抵御图结构攻击.针对图结构的保护,Wang等人[14]提出一种新的k-匿名算法,扰动节点对之间的路径,使得存在k条相同长度的最短路径,当路径数小于k时,则扰动全部路径长度使其等于最短路径长度.该方法虽然能保持最短路径长度不变,然而却未能保存其他图属性参数.为解决图属性数据功用问题,Das等人[11]提出应用线性不等式捕获网络中的某些参数特征,对权值进行扰动,使得发布的社交网络图保持原有的线性属性.兰丽辉等人[15]设计了满足差分隐私的查询模型——WSQuery,该模型可以捕获社交网络的结构特征,并将结果集以三元组序列输出,降低了数据误差提高数据可用性.
2 约束模型和算法描述
2.1 差分隐私定义和模型
差分隐私是Dwork等人[7]提出的一种抵御背景知识攻击的强隐私保护模型.该模型最早应用于数据库隐私中.给定2个数据集D1和D2,其中只有1条数据记录不同,表示为|D1ΔD2|=1,即称D2为D1的邻近数据集,可表示为D2∈Nb(D1).
定义1. ε-差分隐私.对于随机算法M: D→SK,Range(M)用来表示算法的所有可能的输出结果集,即对于D1与D2的算法输出结果S∈Range(M),若满足ε-差分隐私,则有:
Pr[M(D1)∈S]≤eεPr[M(D2)∈S],
(1)
其中,概率Pr表示隐私被揭露的风险,由算法M进行随机性的控制,隐私保护程度由隐私预算参数ε表示,ε越小则隐私保护程度越高,表示邻近数据集结果越接近越不容易区分,但这却是以增加噪音为代价的[15].
定义2. 查询函数敏感度.假设查询函数定义为f: D→Rd,输入为数据集D,输出为一个d维的实数向量,对于2个邻近数据集D1和D2,有全局敏感度:
(2)
其中,Sf为查询函数f的查询敏感度,当f为计数查询时,f(D)=|D|,Sf=1;若f为计数求和时,则有![]()
定理1. 假设存在n个随机算法,其中Ai满足εi-差分隐私,则Ai (0<i<n+1)组合后的算法满足∑εi-差分隐私[15].
定理2. 假设存在n个随机算法,其中Ai满足εi-差分隐私,并且任意2个算法的操作数据集没有交集,则Ai (0<i<n+1)组合后的算法满足max(εi)-差分隐私[15].
上述性质将运用到本文的隐私算法设计中.
2.2 约束模型
假设在一个带有边权值的社交网络图中,图的一系列属性可以用边权值的线性组合来表示,则当我们改变边权值且保证它仍然满足原来的线性关系时,图的属性并不会被改变.在本文讨论的社交网络图中,权值均大于0,基于这一假设,Das等人[11]提出可以通过建立线性不等式模型来反映图属性.给定原加权图G=(V,E,W),其中E为图中全体边的集合,V为全体节点集合,W为边对应的权值集合,模型的目标是用边权值间的关系来模拟线性不等式系统.例如,在Dijkstra算法中,每次从可到达的节点中选择路径最短的节点,将其添加到集合S中.令v为在第i次迭代中选择的节点,f(u0,v)为源点u0到v的距离,同时f(u0,v′)为第i+1次迭代中选择的节点v′到源点的距离,则有f(u0,v)≤f(u0,v′).对于连续迭代过程中每次选择的边对(u,v)和(u′,v′),由于每次选择添加距离最小的节点到集合中,设w(u,v)和w(u′,v′)为2次迭代中更新的边,则有f(u0,v)+w(u,v)≤f(u0,v′)+w(u′,v′).显然除了距离约束,其他约束条件也可转化成该形式添加到模型中,如式(3)所示记作AX≤B,最终构建的模型可以通过其中1组或多组约束不等式体现出原图的属性.
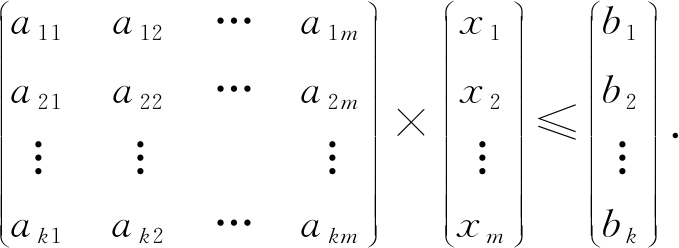
(3)
如果边权值被重新分配为式(3)中的不等式系统的任何解,则将确保被建模的算法的图属性保持不变.因此,该模型可以表示为线性规划问题:
(4)
其中F是线性目标函数对应于图的属性,因此图中任何能表示为边权值的线性组合的属性问题都可以转化为符合该模型的线性规划问题.而目前社交网络分析中使用的属性参数都可以用边权值的线性组合表示.因此这种模型可以完美应用于社交网络分析领域,并且在模型建立之后,有大量完善的线性规划问题求解方法来求得式(4)问题的解.通过这一模型可以轻易地解决传统隐私保护方式会改变图属性的问题,只需保证数据扰动之后仍然满足该模型约束即可.模型的复杂度是确定模型所必需的不等式的数量即矩阵A的规模.矩阵A的列对应于系统中的变量,即图中边的数量,行对应于模型产生的不等式,显然当不等式数量大于边数时即可认为图属性被保留.
3 差分隐私扰动模型
3.1 单源最短路径约束模型
在本节中,通过单源最短路径算法建立图的约束模型.设G为原始社交网络图,E为图中全体边的集合,V为全体节点集合,W为边对应的权值集合.初始化V0={v0},其中v0为给定的源点.通过改进的Dijkstra算法[16]在每一步选择节点添加到生成树的过程中构造约束不等式,具体算法如下:
算法1. 约束模型建立.
输入:G,E,V,W,V0={v0};
输出:约束矩阵A生成树序列T={t1,t2,…,ti,…}.
① FOR v∈V-V0且(v0,v)∈E
② Q=Q+{v};  *设置Q集合为下一步可到达的所有点集合*
*设置Q集合为下一步可到达的所有点集合*
③ END FOR
 *初始化各个联通区域*
*初始化各个联通区域*
④ IF Q=∅且V-V0≠∅  *当图G不联通时,遍历完1个联通区域后重新设置源点*
*当图G不联通时,遍历完1个联通区域后重新设置源点*
⑤ V=V-V0;
⑥ v0=rand(V);
⑦ V0={v0};
⑧ GOTO ①;
⑨ END IF
 *循环遍历联通区域*
*循环遍历联通区域*
⑩ WHILE Q≠∅
 u=minweight(Q);
u=minweight(Q);  *求集合Q中到V0边权值最小的点*
*求集合Q中到V0边权值最小的点*
 A=A+{f(v0,pre_u)≤f(v0,u)};
A=A+{f(v0,pre_u)≤f(v0,u)};
 *为矩阵A增加一行,对应位置的值为集合中的约束系数,pre_u记录上一步选择的节点*
*为矩阵A增加一行,对应位置的值为集合中的约束系数,pre_u记录上一步选择的节点*
 pre_u=u;
pre_u=u;
 V0=V0+{u};
V0=V0+{u};
 FOR v∈V-V0且(u,v)∈E
FOR v∈V-V0且(u,v)∈E
 IF D(v0,v)≥D(v0,u)+w(u,v);
IF D(v0,v)≥D(v0,u)+w(u,v);
 *D表示当前节点间的距离*
*D表示当前节点间的距离*
 A=A+{f(v0,v)≥f(v0,u)+
A=A+{f(v0,v)≥f(v0,u)+
w(u,v)};
 D(v0,v)=D(v0,u)+w(u,v);
D(v0,v)=D(v0,u)+w(u,v);
 ELSE
ELSE
 A=A+{f(v0,v)≤f(v0,u)+
A=A+{f(v0,v)≤f(v0,u)+
w(u,v)};
 END IF
END IF
 Q=Q+{v};
Q=Q+{v};
 END FOR
END FOR
 END WHILE
END WHILE
 build T;
build T;
 IF V≠∅
IF V≠∅
 GOTO ④;
GOTO ④;
 END IF
END IF
算法1的过程类似于Dijkstra算法.由于社交网络图的稀疏性,图G往往是非连通的,因此当算法执行到集合Q为空即从源点出发,剩余节点均不可到达时终止此次循环,将生成树ti添加到生成树序列T中,重新从未添加的节点集合中选择源点,重复上述过程直到所有节点均被添加到序列T中.每次构建生成树ti的过程与Dijkstra算法相同,从集合Q中选择出到集合V0权值最小的节点记作u,将节点u添加到集合V0中并更新V0到集合Q中节点的路径,根据更新的路径生成约束条件,同时pre_u为上一步从Q选择出添加到V0的节点,生成约束条件A(u,pre_u),最后使得pre_u=u,更新集合Q.其中生成约束不等式的规则如下:
1) Dijkstra算法的执行过程是贪心选择的过程,因此pre_u作为上次步骤中选择的节点,D(v0,pre_u)≤D(v0,u)将必然成立.所构建的约束不等式为
f(v0,pre_u)≤f(v0,u).
2) 若通过节点u可以优化D(v0,v),即D(v0,v)≥D(v0,u)+w(u,v),则将D(v0,v)更新为D(v0,u)+w(u,v),同时构建约束不等式为
f(v0,v)≥f(v0,u)+w(u,v).
3) 若通过节点u不可优化D(v0,v),即D(v0,v)≤D(v0,u)+w(u,v),则构建的约束不等式为
f(v0,v)≤f(v0,u)+w(u,v).
已知Dijkstra算法的时间复杂度为O(n2),考虑到社交网络图数据的稀疏性,可以对该算法进行优化.将边权值信息使用堆结构存储,则选择最短路径时可优化为O(m lb n),其中m表示边数,n表示节点数,建堆过程时间复杂度为O(n lb n),因此优化后的复杂度为O((m+n) lb n).
对Dijkstra算法的改进并没有增加它的复杂度,同为O((m+n) lb n).算法1中 ~
~ 步,选择最短路径时添加构造约束不等式过程,循环次数为O(m lb n),程序步增量为c,则有T(m,n)=m lb n+c lb n,当m,n趋向于无穷大时,由于c为常数,则T(m,n)(m lb n+c lb n)与T(m,n)(m lb n)同阶,则渐进时间复杂度可记为O(m lb n).建堆过程与Dijkstra算法一致,因此本方法与Dijkstra有相同的时间复杂度O((m+n) lb n).
步,选择最短路径时添加构造约束不等式过程,循环次数为O(m lb n),程序步增量为c,则有T(m,n)=m lb n+c lb n,当m,n趋向于无穷大时,由于c为常数,则T(m,n)(m lb n+c lb n)与T(m,n)(m lb n)同阶,则渐进时间复杂度可记为O(m lb n).建堆过程与Dijkstra算法一致,因此本方法与Dijkstra有相同的时间复杂度O((m+n) lb n).
生成的约束不等式分为2个部分,规则1和规则2生成的约束不等式为第1部分,规则3为第2部分.第2部分的数量计算很简单,每次选择节点时都会生成一个约束不等式,因此第2部分的不等式个数可看作节点数,记为O(n).第1部分的约束不等式是在每次选择节点之后生成的,设Ni为第i次迭代时生成的不等式数,nQ表示Q中的节点数,则Ni=nQ.Q中的节点数一直在改变而无法确定具体数值,但是我们可以计算出它的上界.若已知图中节点度的平均值为degree,集合V0中的节点个数为nV,当集合V0中边数最少时即边数等于nV-1(连通图边数最少为节点数减1),Q中节点数取得最大值,则Q中最大的节点数nQ=nV(degree-1)+1.![]() 带入nQ可得
带入nQ可得![]() V0每次迭代的值为1,2,…,n,因此化简
V0每次迭代的值为1,2,…,n,因此化简![]() 显然社交网络中图的平均度degree要远小于节点数N,因此可将degree看作常数项,则第1部分的约束不等式个数可记为O(n2).
显然社交网络中图的平均度degree要远小于节点数N,因此可将degree看作常数项,则第1部分的约束不等式个数可记为O(n2).
此外,还可以通过其他方式建立模型,如在构建最小代价生成树的Kruskal算法中,每次选择剩余边集合中权值最小的边,同时保证不产生回路,将其添加到生成树中.该过程建立的约束不等式类型只有1种,即w(u,v)≤w(u′,v′),其中(u,v)为在第i次迭代中选择的边,(u′,v′)为第i+1次迭代中选择的边.
另外度序列也可用来建立约束不等式模型,如Havel定理用于图重构时,设di为第i次迭代的节点度,di+1为第i+1次迭代的节点度,则有di≥di+1.当不等式组规模足够大时,所有满足约束模型且可简单图化的度序列都可以看作是同构的,只是该方法需要将图先度序列化,再将度序列重构为图.
相比于以上2种方式,针对带权值的社交网络数据而言,单源最短路径可以直接在图结构上操作执行,其简明性、应用广泛和较高的执行效率也使之成为各类隐私保护方案中最常用的模型,因此本文选择单源最短路径来建立模型.
3.2 差分隐私噪音添加
在带权值的社交网络图中的噪声添加不同于无权值图,一条边的权值改动将会影响整个图的结构,如最短路和最小代价生成树,都会发生相应的改变.因此本文采用算法1表示的约束模型对添加噪音进行线性约束.
在扰动过程中,由Laplace机制产生噪声,针对单源最短路径模型,查询函数f(u,v)的返回值是节点u和节点v间的最短路径,由定义2可知全局敏感度![]() 其中
其中
因此f的敏感度为
w(u′,v′)|,
(5)
其中,P(u,v)表示节点u和节点v间的最短路径的边集合,w′和w分别表示扰动前后边(u′,v′)和(u,v)的权值.
具体添加算法如下:
算法2. 约束噪音添加算法.
输入:G,E,V,W,A,T,ε1;
输出:G′.
① FOR (u,v) ∈ ET
② w′(u,v) =w(u,v)+laplace(S(f) ε1);
ε1);
③ END FOR
④ FOR (u,v) ∈ EN
⑤ w′(u,v)=value→answer(A)+laplace(S(f) ε1);
ε1);  *value→answer(A)为式(4)中线性规划的求解结果*
*value→answer(A)为式(4)中线性规划的求解结果*
⑥ END FOR
⑦ E=E+{(u,v)|rand(u,v)∩ET=∅};
 *随机选择几条不存在边的节点对u,v*
*随机选择几条不存在边的节点对u,v*
⑧ w(u,v)=min(ti,max wt).
算法2的输入是需要添加噪音扰动的原始图数据G,E,V,W,生成树序列T,以及约束矩阵A和隐私预算ε1,最终得到扰动图G′.首先我们将集合E分成ET和EN两个部分,其中ET为构成生成树的边集合;先对ET中的边权值添加Laplace噪声,再将加噪之后的权值带入约束不等式中,可解得EN中的边权值约束,并生成新的权值.在每个生成树ti中,我们选择若干原来不存在边的节点对(u,v)构造一条新边,比较ti中最大边权值与f(u,v),选择其中较小的一个作为边权值.
由于节点的添加或删除具有很大的敏感性,添加或者删除某个节点时,同时连接在该节点的边关系会随之改变,显然会引入大量的噪音.本文提出的虚假节点添加方法可以有效地降低对数据可用性的影响.对于节点u′的删除操作,函数f(u,v)的敏感度定义为
(6)
其中D′(u,v),D(u,v)表示删除节点后的最短路径长度和原最短路径长度,由此可见直接删除节点会造成巨大的影响.节点添加时只要保证边权值足够大即可极大程度地降低对数据可用性的影响,但是过大的边权值会很容易被攻击者识别出.本文的节点扰动方式分为2步:1)删除度低于阈值的节点,同时对于连接到该节点的所有节点,如果他们之间存在边关系,则修改其边权值;2)添加虚假节点,虚假节点的度等于定义的阈值.其中阈值由用户根据应用需求定义.具体算法流程如下:
算法3. 节点扰动算法.
输入:G,E,V,W,degree_value,ε2,ε3;
输出:G′.
① Nnoise=|laplace(ε2)|;  *通过用户定义的隐私预算计算扰动节点个数*
*通过用户定义的隐私预算计算扰动节点个数*
 *节点删除*
*节点删除*
② rand(v)∈V且v.degree≤degree_value;
 *随机选择度小于阈值degree_value的节点*
*随机选择度小于阈值degree_value的节点*
③ Nnoise=Nnoise-1;
④ FOR each node u1,u2∈V且(u1,v)∈E且(u2,v)∈E
⑤ IF f(u1,u2)≥w(u1,v)+w(u2,v)
⑥ IF {(u1,u2)}∩E=∅ THEN
E=E+{(u1,u2)};
⑦ w(u1,u2)= w(u1,v)+w(u2,v)+
laplace(S(f) ε3);
ε3);
⑧ END IF
⑨ END IF
⑩ END FOR
 delete(v);
delete(v);  *删除节点v,以及所有连接v的边*
*删除节点v,以及所有连接v的边*
 *插入噪音节点*
*插入噪音节点*
 rand(v)∈V且v.degree≤degree_value;
rand(v)∈V且v.degree≤degree_value;
 *随机选择度小于阈值degree_value的节点*
*随机选择度小于阈值degree_value的节点*
 Nnoise=Nnoise-1;
Nnoise=Nnoise-1;
 new(v1);
new(v1);  *新建一个虚假节点*
*新建一个虚假节点*
 V=V+{v1};
V=V+{v1};
 E=E+{(v1,v)};
E=E+{(v1,v)};
 w(v1,v)=average(v);
w(v1,v)=average(v);  *节点v的所有
*节点v的所有
边权值的平均值*
 FOR each u∈V且(u,v)∈E
FOR each u∈V且(u,v)∈E
 E=E+{(v1,u)};
E=E+{(v1,u)};
 w(v1,u)=w(u,v)+laplace(S(f)
w(v1,u)=w(u,v)+laplace(S(f) ε3);
ε3);
 END FOR
END FOR
算法3的输入包括了原始图数据G,E,V,W以及由用户自己定义的节点度的阈值degree_value和隐私预算ε2,ε3,输出为扰动图G′.首先执行删除扰动方式,由于查询函数对节点增删的敏感度很高,因此我们选择度小于degree_value的节点以减小对查询函数的影响,选择扰动节点个数Nnoise=|laplace(1 ε2)|(增加或删除节点的敏感度为1).当选择节点v之后对所有连接到节点v的节点两两进行如下操作:假设u1和u2都有到v的边且f(u1,u2)=w(u1,v)+w(v,u2),则令w(u1,u2)= w(u1,v)+w(v,u2);若u1和u2之间不存在边则构造一条边,最后删除节点v以及所有的边.虚假节点的插入也以度小于degree_value的节点为基准,选择到基准节点v之后添加虚假节点v1并且构造边(v1,v),该边权值可设置为v的边权值的平均值.为了使虚假节点v1的度不被攻击者识破,将所有与v连接的节点都构造一条边连接到节点v1.权值取值方式如下:设节点u与v直接存在边关系,则w(v1,u)=w(u,v)+laplace(S(f)
ε2)|(增加或删除节点的敏感度为1).当选择节点v之后对所有连接到节点v的节点两两进行如下操作:假设u1和u2都有到v的边且f(u1,u2)=w(u1,v)+w(v,u2),则令w(u1,u2)= w(u1,v)+w(v,u2);若u1和u2之间不存在边则构造一条边,最后删除节点v以及所有的边.虚假节点的插入也以度小于degree_value的节点为基准,选择到基准节点v之后添加虚假节点v1并且构造边(v1,v),该边权值可设置为v的边权值的平均值.为了使虚假节点v1的度不被攻击者识破,将所有与v连接的节点都构造一条边连接到节点v1.权值取值方式如下:设节点u与v直接存在边关系,则w(v1,u)=w(u,v)+laplace(S(f) ε3).
ε3).
由算法3所生成的边节点扰动对图的平均最短路径几乎没有影响,但是会增加三角计数,具体计算为
(7)
其中,Ctri表示原图中的三角计数,Vfake为添加的虚假节点集合.由式(7)可以看出,当添加的虚假节点度越高,三角计数越高.而虚假节点的度又与构建节点时的基准节点有关,因此我们选择度较小的节点作为基准节点.
3.3 隐私保护分析
差分隐私算法的隐私保护程度与添加噪声的过程有关,其中添加噪声的敏感度已在对应算法处给出分析.本文的扰动方法分为2个步骤:1)通过约束模型,对边权值添加差分隐私噪声,隐私预算为ε1;2)节点扰动,即节点的删除和虚假节点的添加,隐私预算为ε2,构造噪音边权值的隐私预算为ε3.首先,在算法2中步骤2是对组成生成树的边权值全部添加隐私预算为ε1的Laplace噪声,敏感度函数
![]() w(u′,v′)|,
w(u′,v′)|,
由定义1可知,算法2通过约束条件得出的扰动权值满足ε1-差分隐私.
同理,在算法3中,节点扰动数量由Laplace机制计算得出,是敏感度为1的ε2-差分隐私的直接应用.步骤⑦中,由Laplace机制产生敏感度函数![]() 的边权值噪音也满足ε3-差分隐私.
的边权值噪音也满足ε3-差分隐私.
在基于Laplace机制的噪音分配过程中算法2和算法3的噪音分配是相互独立的,由定理2可知,当算法2与算法3作用在图G时满足(ε1+ε2+ε3)-差分隐私,令ε=ε1+ε2+ε3,本文提出的带权值的大规模社交网络数据的隐私保护方法符合ε-差分隐私.
4 实验与结果
本节主要用仿真实验来分析本方法(在实验中简写为dp-noisy)的数据可用性、隐私保护程度和执行效率.如表1所示,本实验通过爬取新浪微博的社交网络参数,随机生成聚集系数为0.01的社交图模拟数据集:1 000节点、5 000节点、10 000节点和30 000节点.本方法的隐私预算ε1,ε2,ε3分配方式并不固定,可根据不同场景进行分配.多次实验中我们发现,取ε1∶ε2∶ε3=2∶1∶2时实验效果较好(ε2控制添加的节点噪音,因为节点数规模较大,需要添加大量节点噪音,所以ε2取值分配较小).
Table 1 Number of Nodes and Edges in 4 Data Sets
表1 4个不同数据集的节点数和边数

Data SetNumber of NodesNumber of Edgesdata1100028247data2500065940data310000212781data430000932974
4.1 性能分析
本文在表1中4个不同规模的数据集上将dp-noisy方法与Das等人[11]提出的lp-noisy方法,Wang等人[14]提出的K-MPNP(K-shortest path privacy)方法以及兰丽辉等人[15]提出的LWSPA(protection algorithm based on Laplace noise for weighted social networks)方法的运行效率进行了对比.如图1(a)所示,其中dp-noisy方法、lp-noisy方法和K-MPNP都是采用单源最短路径原理来扰动社交网络图中的边权值.图1中横坐标表示数据集的编号,纵坐标表示运行时间(单位s).

Fig. 1 Running time
图1 运行时间
由于K-MPNP方法中需要多次重复单源最短路径的计算过程,因此执行效率远低于其他2个方法.在较小规模数据集中,dp-noisy方法与lp-noisy方法的执行效率相当,当数据集规模不断扩大时,由于lp-noisy方法的扰动形式单一,因而具有更好的运行效率.而LWSPA方法通过向三元组查询模型中添加Laplace扰动,因而在数据规模较小时运行效率最优,然而当数据规模较大导致图结构复杂时,运行效率会急速下降.综上,dp-noisy方法与lp-noisy方法具有更好的执行效能.
由于带边权值的社交网络数据隐私保护的时空复杂度与无权值的相比更高,因此,为了进一步验证本方法的执行效率,我们将本方法的运行时间与同样采用差分隐私保护机制、但作用于无权值社交网络图的DER方法进行对比,实验中2种方法的隐私预算ε取值都为1.从图1(b)可以看出随着数据集规模的增加,2种方法的运行时间都在增加,但dp-noisy相较于DER方法有了较大程度的提高.因为DER方法的运行时间主要是在矩阵聚集上,这部分执行的过程中,每一次交换都需要计算曼哈顿距离,时间复杂度为O(n2),而dp-noisy方法的时间复杂度为O((m+n) lb n).这说明本方法可以运行在较大规模的数据集上,且对比传统扰动方法DER具有良好的可扩展性.同时,也说明了本方法在处理带权值的社交网络数据时也有着较好的运行效率.
4.2 隐私保护质量分析
针对边权值的识别攻击,本实验首先将dp-noisy方法与抵御边权值识别攻击的lp-noisy方法、LWSPA方法以及K-MPNP方法进行对比.其后,本实验选择了无向无权值的DER算法作对比,以验证本方法抵御图结构攻击的性能.
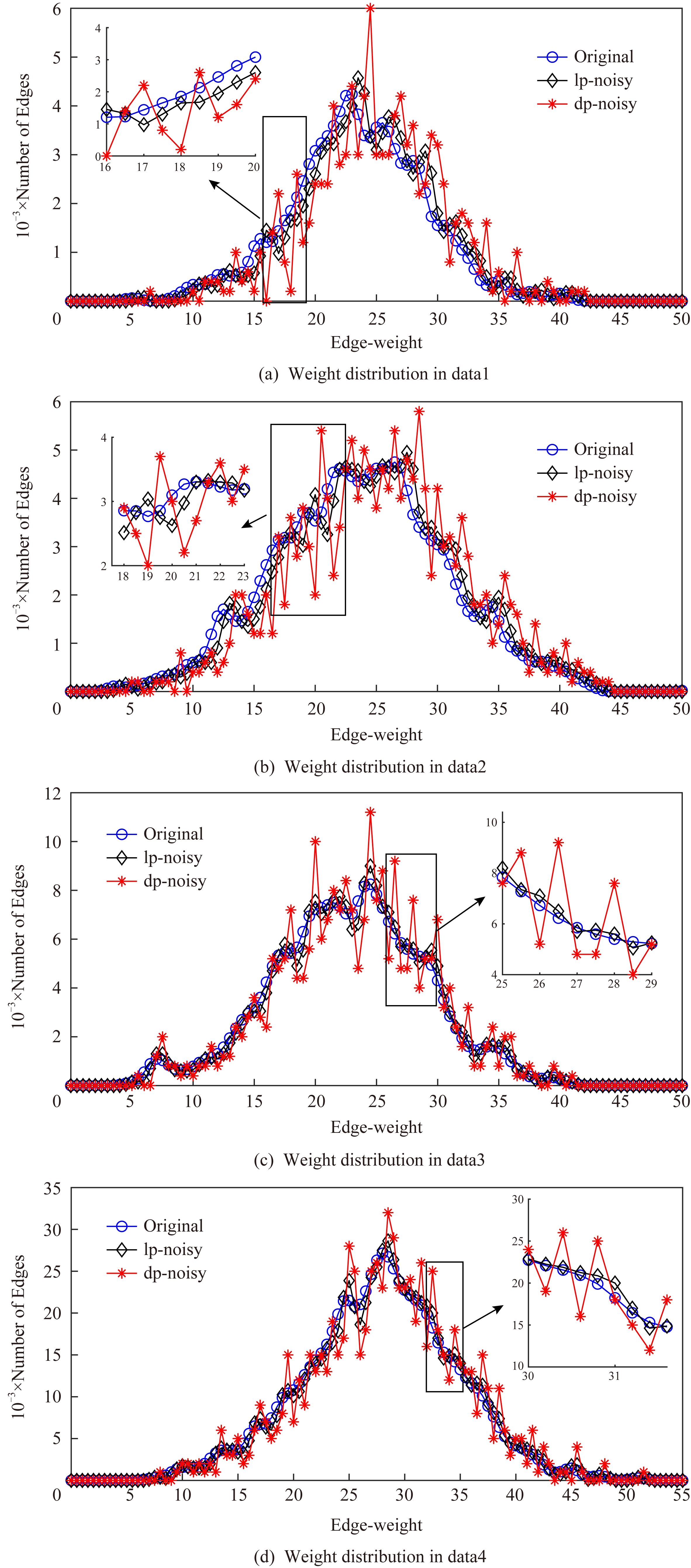
Fig. 2 Comparison of weight distribution before and after disturbance
图2 扰动前后权值分布对比
针对边权值的分析,本实验中dp-noisy的隐私预算ε=1.如图2所示,dp-noisy的扰动效果明显好于lp-noisy的扰动效果.当数据规模较小时,如图2(a)(b)所示,lp-noisy的扰动效果还比较明显,这是因为lp-noisy方法通过线性规划方法重新定义单源最短路径上的边权值,且只对不在路径上的权值加噪,虽然对于较低的权值并未实现很好的扰动,但由于数据规模小,依然取得了较好的扰动效果.如图2(c)(d)所示,当数据规模较大时,lp-noisy的扰动分布与原数据差异很小,尤其在权值极大和极小处,lp-noisy扰动后的分布几乎与原始数据一致.出现这种情况是因为数据规模较大时,边数的增加会引起约束集的增加,这使得线性规划求出的最优解无限接近于原始数据.而dp-noisy方法,除了对不在最短路径上的边权值扰动之外,还对线性规划的解添加差分隐私噪声,同时在节点扰动过程中也对权值分布产生了较大改变,由图2(a)~(d)可知,dp-noisy方法总能产生较明显的扰动.
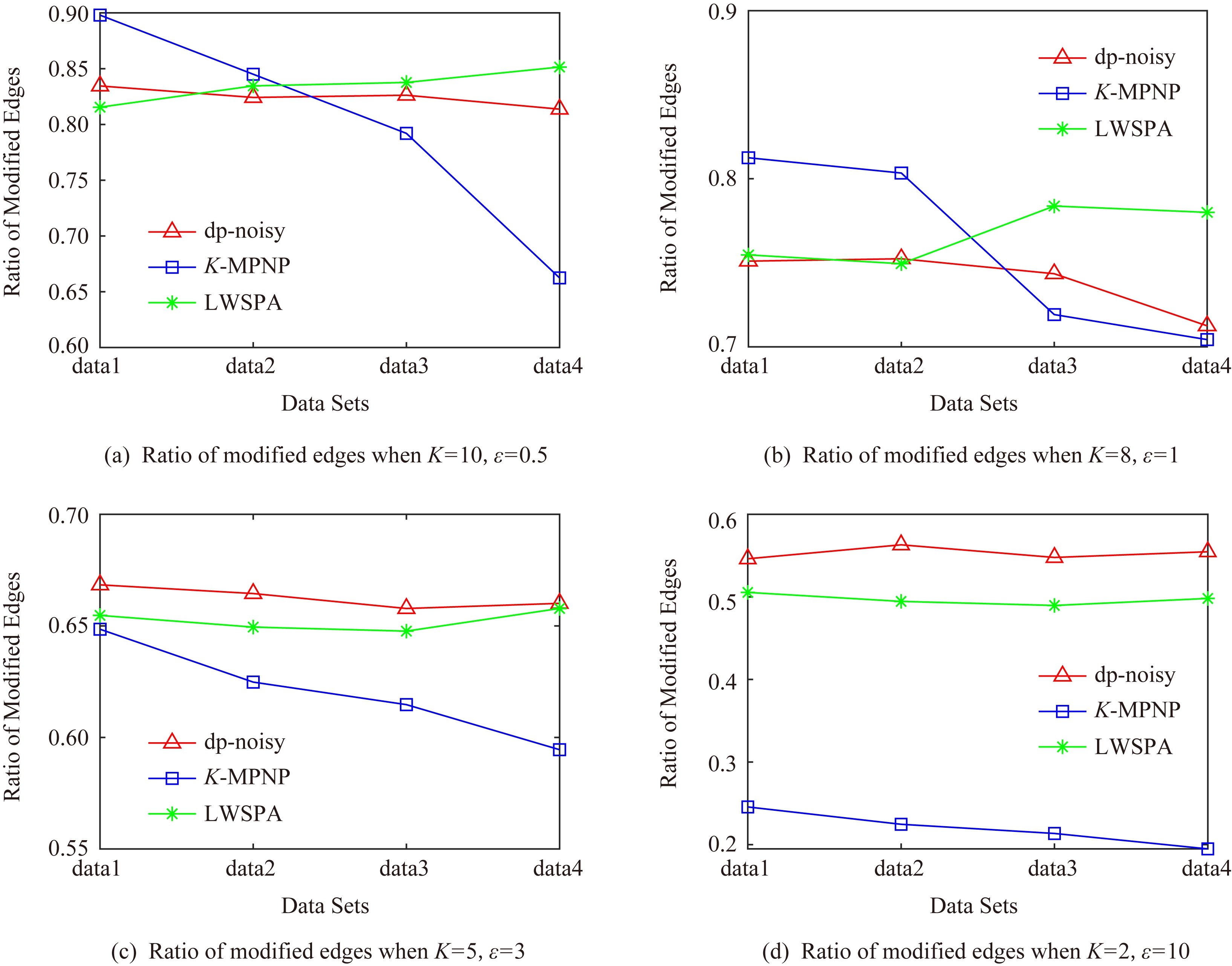
Fig. 4 Ratio of modified edges
图4 扰动边比例
另外攻击者通过边权值的识别方式还有可能识别节点间权值的大小关系来确定目标对象.因此,如果对权值扰动之后大小关系并未发生改变,攻击者依然能够识别出目标节点.本实验选择平均识别率R(式(8))来反映边权值的隐私保护强度.设图G扰动后为G′,wi ,wj为G的边权值,![]() 为G′对应位置的边权值.由图3可知,由于dp-noisy加入了差分隐私噪声,对图中的关键边与非关键边权值都进行了扰动,因此平均识别率要低于lp-noisy.
为G′对应位置的边权值.由图3可知,由于dp-noisy加入了差分隐私噪声,对图中的关键边与非关键边权值都进行了扰动,因此平均识别率要低于lp-noisy.

(8)
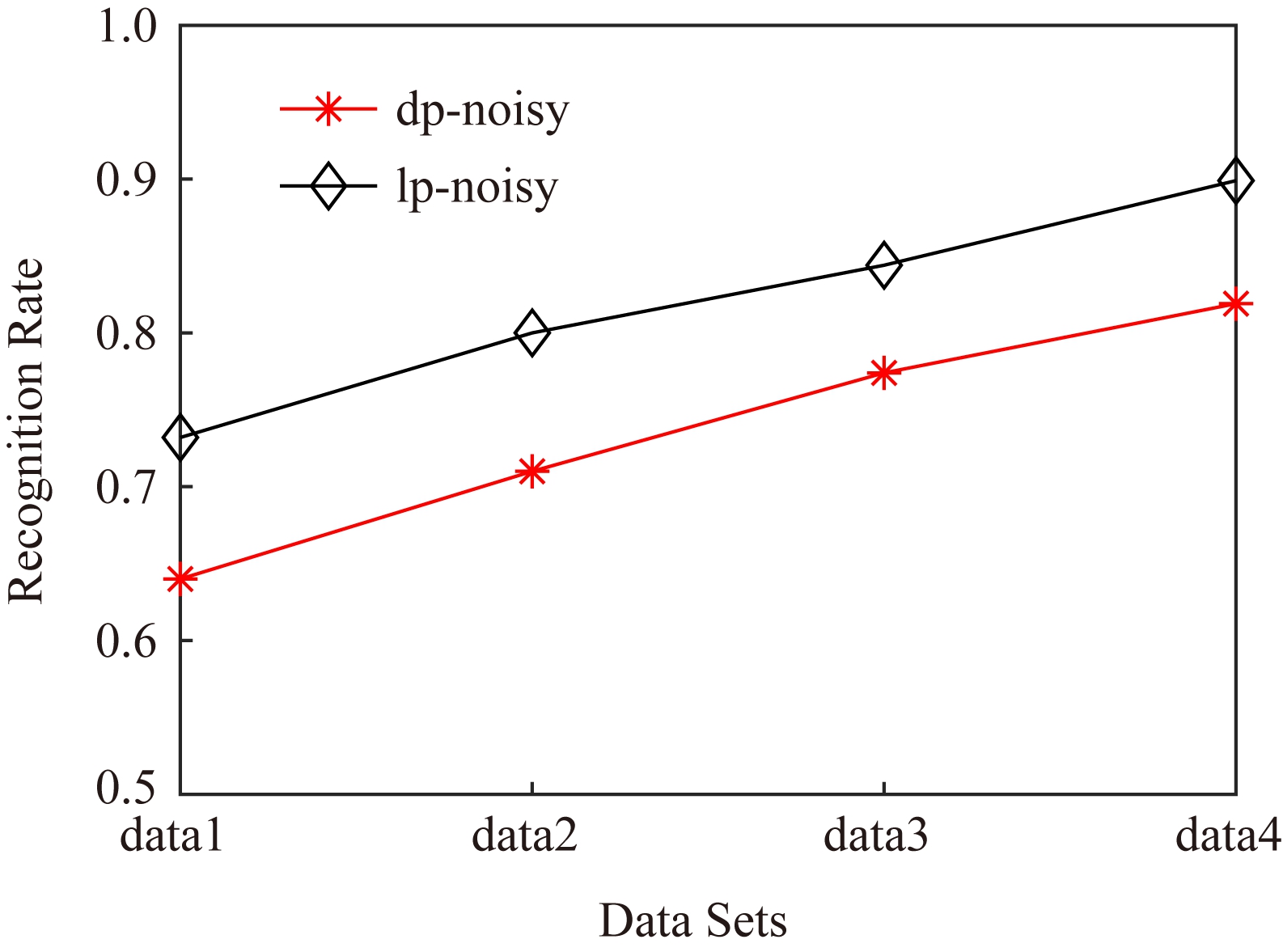
Fig. 3 Average recognition rate comparison
图3 平均识别率对比图
针对边权值的扰动质量,实验选择LWSPA方法与k-匿名方法K-MPNP 做对比,其中LWSPA方法是兰丽辉等人[15]提出的基于差分隐私的带权值的社交网络隐私保护方法.K-MPNP方法,是通过修改非最短路径中的边权值,使其等于最短路径长度,并且当路径数小于K时,则修改所有存在的路径.实验中,K-MPNP的|H|=10,当K分别取10,8,5,2时,其保护效果与另外2种差分隐私方法的ε取0.5,1,3,10时相当.在此基础上,对比实验结果如图4所示.
如图4(a)(b)所示,当数据规模较小时,K-MPNP取较大K值,即节点对之间被扰动的路径较多,因而大量的边权值被扰动.当数据集规模增加,由于社交网络图的“小世界”特征,最短路径不会发生较大改变,当|H|固定时,K-MPNP扰动的边权值数量并不会增加.LWSPA方法则通过三元组查询结构添加扰动噪声,因此当数据规模较大时,所添加的扰动最高.综上,在4个数据集中,隐私预算较小时,dp-noisy扰动比例较为平稳,LWSPA在数据规模较大时,扰动量有较大增加,而K-MPNP则在数据集3和数据集4中的扰动比例大幅度降低,其并不适合大规模数据集.
如图4(c)(d)所示,此时K的取值较小(隐私预算较大),会导致权值的扰动比例降低.在4个数据集中,dp-noisy都优于K-MPNP和LWSPA,尤其是当K=2,ε=10时,差异非常明显.这是由于,当K=2时,节点对之间只需要扰动1条路径的长度即可保证他们之间存在2条相等的最短路径,因此K-MPNP的扰动比例始终在30%以下.而dp-noisy则因为存在扰动边关系来扰动权值的过程,所以在4个数据集中都取得了最好的效果.
针对图结构的识别攻击是通过发布特殊形状的子图到网络中,在扰动后根据该子图确定扰动图中目标节点的位置.实验通过统计不同相似度的子图的匹配数来反映隐私保护质量.为了方便比较,隐私预算ε取值都为1,其中dp-noisy隐私预算分配为ε1∶ε2∶ε3=2∶1∶2.
如图5所示,在相同的隐私预算下,不论是何种数据集,同一相似度下DER扰动后的结果要小于dp-noisy,从而被攻击者识别的概率要高于dp-noisy.这是因为DER添加的边噪声过多,导致图结构变得复杂,攻击者一旦掌握了某一个子图信息便很容易确定目标在图中的位置.
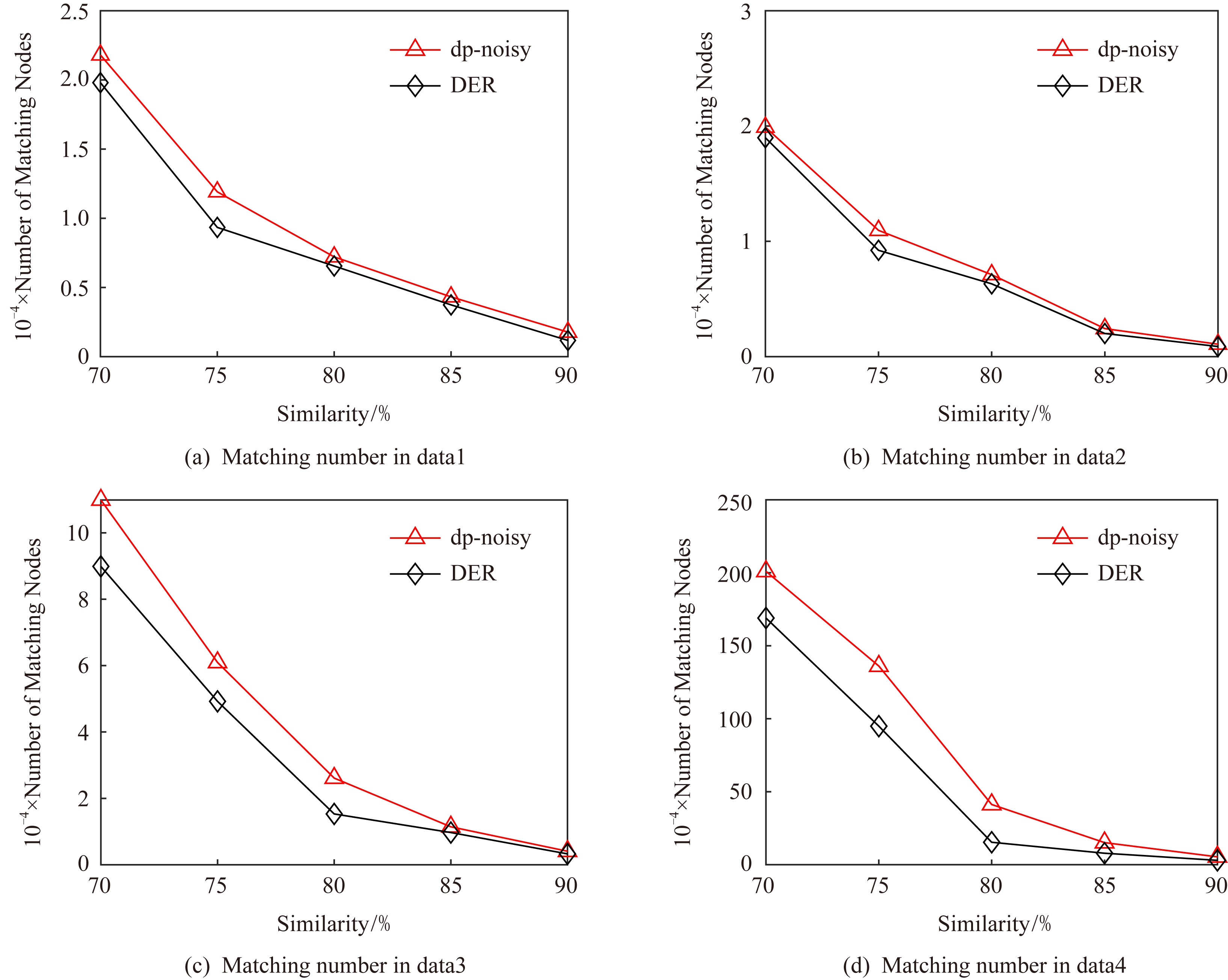
Fig. 5 Matching number comparison
图5 匹配数对比
4.3 数据可用性分析
对于带权值的社交网络图数据而言,数据可用性分析将分成2个部分进行:一是社交网络的结构特征参数分析,二是边权值分析.
对于结构特征参数,本实验通过将原始数据的图特征参数与扰动分布后社交网络数据的图特征参数进行比较分析,以验证在不同的隐私预算下本算法的数据可用性.本实验选择了聚集系数、三角形计数和边数这3个最重要的参数,用于统计图结构特征.实验选择同样使用差分隐私保护机制的LWSPA方法和DER方法在4个数据集上进行了对比,由于LWSPA不涉及边关系的扰动,因此三角形计数和边数2个参数只与DER方法进行对比.实验结果如图6~9所示:
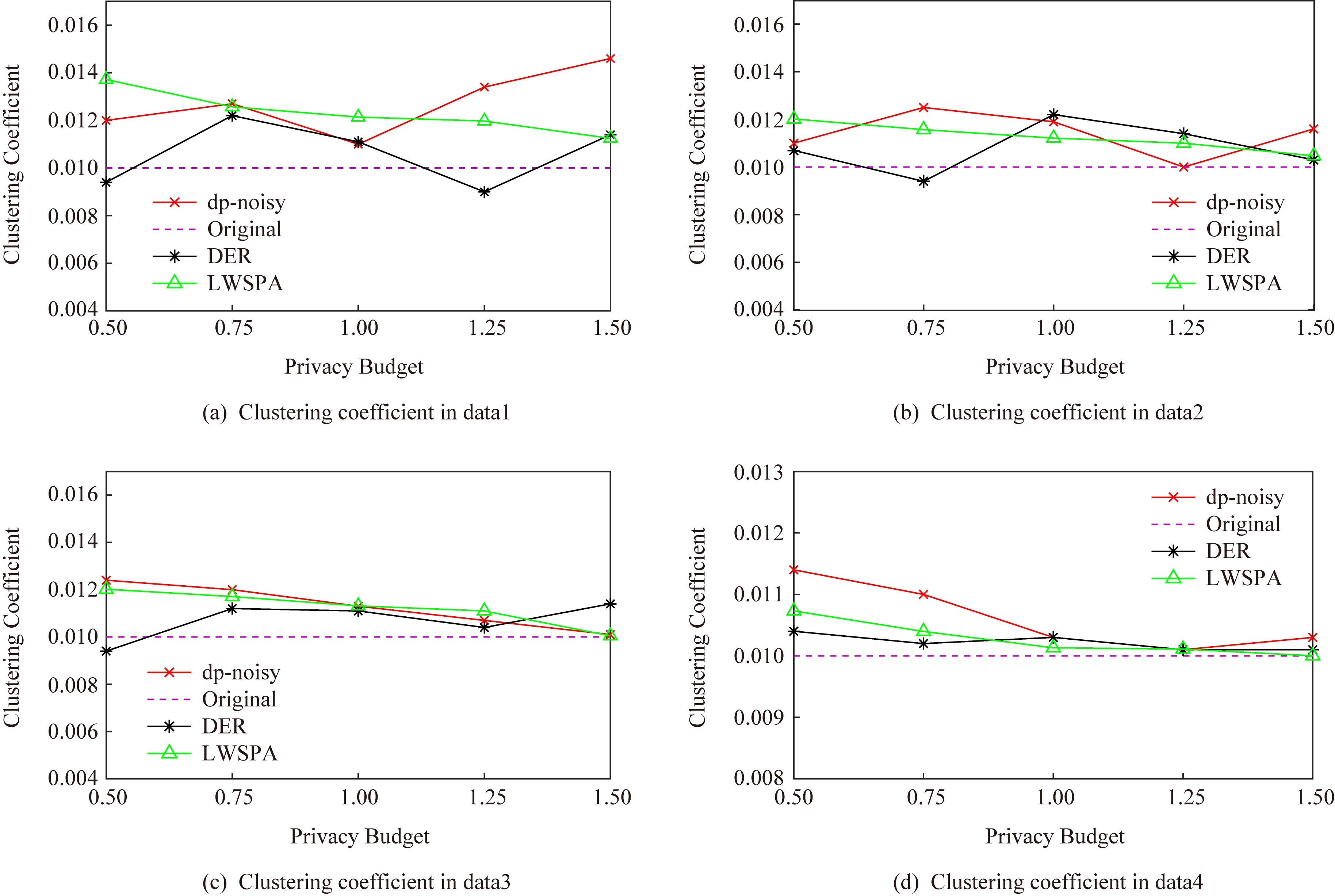
Fig. 6 Clustering coefficient comparison
图6 聚集系数对比
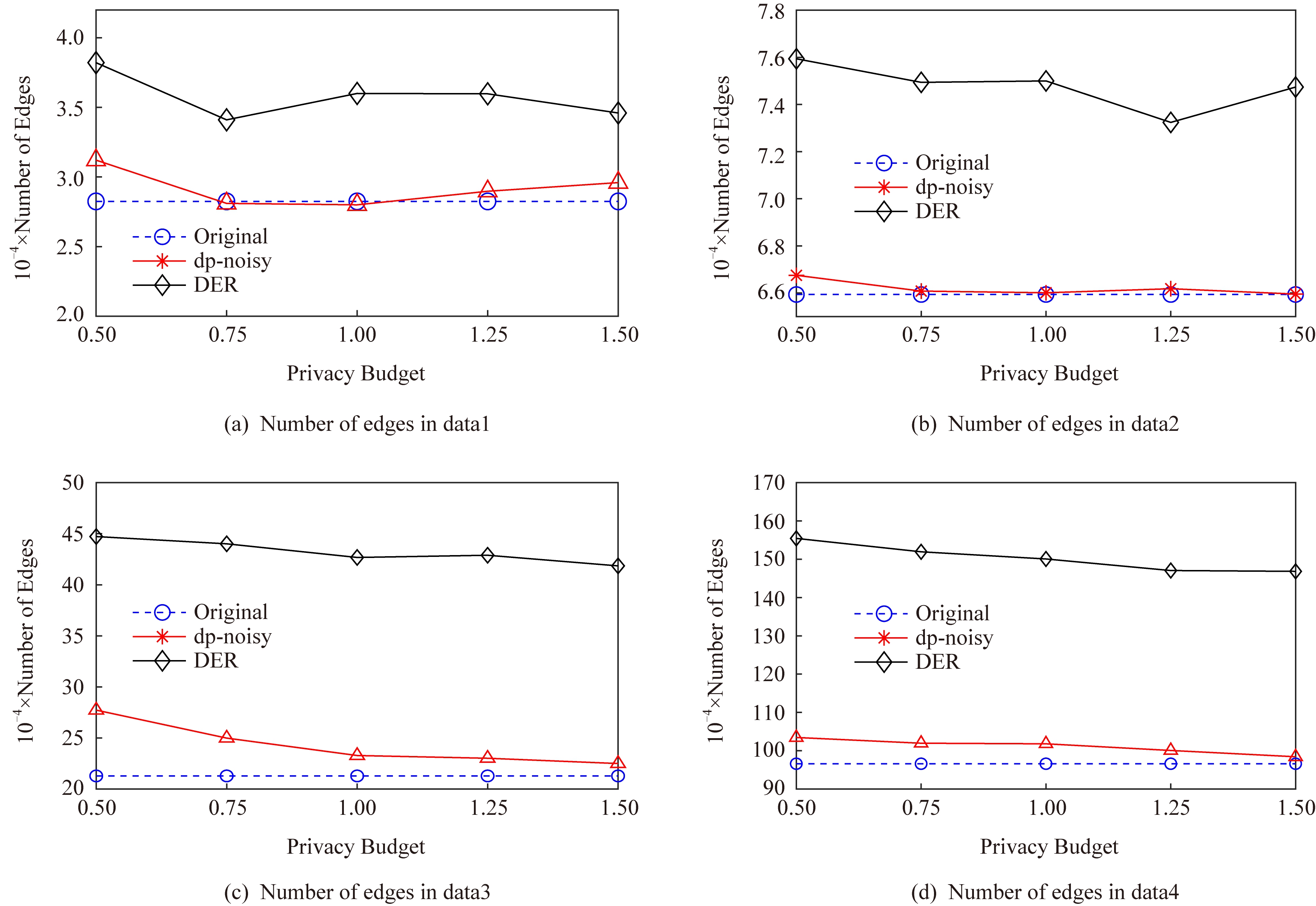
Fig. 7 Edge disturbance
图7 边数扰动对比

Fig. 8 Number of triangles
图8 三角形数量对比
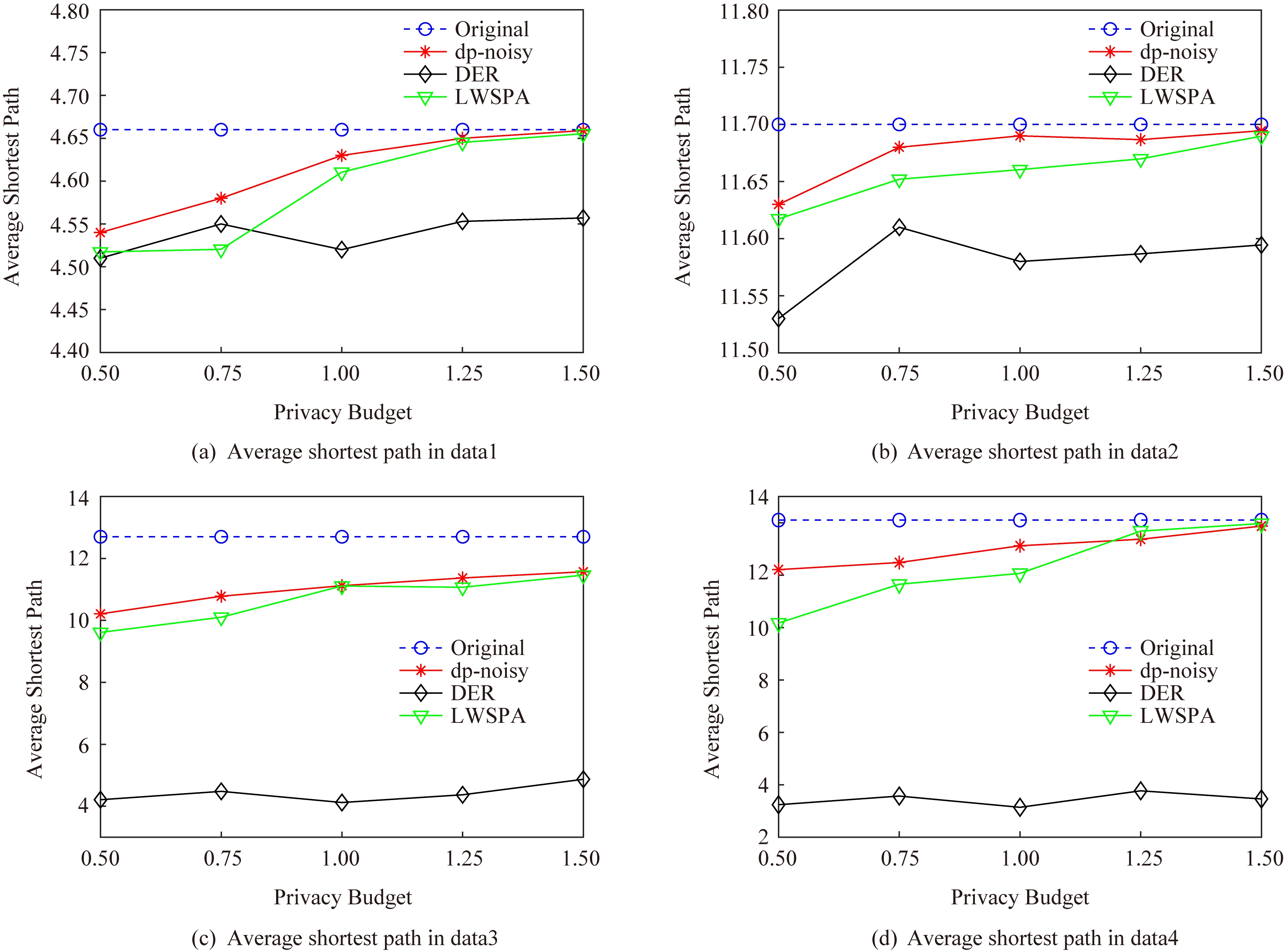
Fig. 9 Average shortest path
图9 平均最短路径对比
如图6所示,当选择不同的隐私预算时,使用这3种方法的聚集系数都不会发生大的改变且差异较小;其中dp-noisy和LWSPA的聚集系数大多数时候高于原始数据,但是随着隐私预算的增加,LWSPA的聚集系数更加接近于原始数据.由于dp-noisy方法会在2个互相可到达但是不存在边的节点对之间添加边关系,同时选择度较低的节点为基准点插入虚假节点,这在一定程度上增加了图的聚集程度.而DER方法则是通过聚类之后添加边噪声,这在一定程度上减少了对聚集系数的影响.对比图6(c)(d)还可以发现在更大规模的数据集上,3种方法对聚集系数的影响将会减小.对于稀疏矩阵而言,更大的数据集意味着噪音边有着更大的概率被添加到无效区域,从而对聚集系数的影响更小.
图7是每个数据集上,通过2种方法扰动之后的边数量对比,可以看到扰动后的边数量往往会高于原始数据.对比图7(a)~(d)可以发现,当数据集增大时DER算法的数据可用性越来越差,虽然dp-noisy方法也会增加边数量但影响远小于DER方法.这是因为DER通过添加大量的边噪音以达到保护效果,其中有相当一部分的冗余噪音边严重地破坏了数据的可用性.
同时由于边数量的增加,三角形数量也随之增加.如图8所示,DER方法产生的大量噪音边使得扰动后的三角形数量急剧增加,尤其是在大规模数据集data3和data4中,如图8(c)(d)所示,DER方法扰动后的三角形数量超过原数据的2倍.这是因为DER方法需要进行聚类划分,在社区密集处添加扰动边对三角形数量的影响要大于非密集处.对比DER,dp-noisy方法则可以在隐私预算取较大值时达到很好的数据可用性.
综上所述,在相同的隐私预算下,和LWSPA相比,dp-noisy的数据可用性与其相当; 与DER相比则有更好的数据可用性,尤其在大规模的数据集上具有显著的效果,同时也解决了现有带权图扰动方法无法抵御结构攻击的问题.
针对边权值的分析,实验通过对比图的平均最短路径来反映权值的数据有效性.如图9所示,随着隐私预算的增加,向数据集中添加的噪音将会减少,因此平均最短路径会更接近原始数据.而DER方法则因为聚类之后引入大量的噪音边导致平均最短路径长度低于原始数据,因此无论何种规模的数据集,其数据可用性均最差.当数据规模较小时,dp-noisy的数据可用性优于LWSPA方法; 当数据规模增大时,如图9(c)(d)所示,LWSPA的数据可用性有明显提升,但dp-noisy仍实现了效果最好的数据可用性.
针对dp-noisy生成的扰动图中权值及其属性要保持不变,需满足约束条件尽可能完整,约束不等式的数量在一定程度上决定了最终约束的完整性.表2记录了本实验在数据集data1,data2,data3,data4上每个阶段产生的约束不等式数.
Table 2 Number of Constraint Inequality
表2 约束不等式数量表
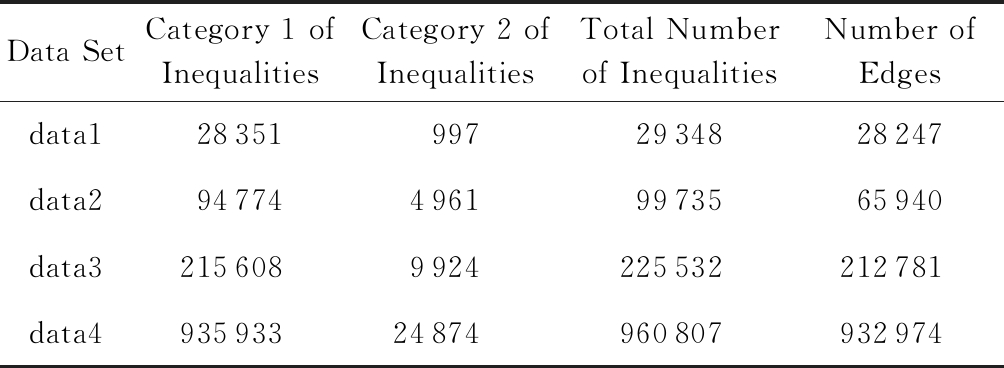
Data SetCategory 1 of InequalitiesCategory 2 of InequalitiesTotal Number of InequalitiesNumber of Edgesdata1283519972934828247data29477449619973565940data32156089924225532212781data493593324874960807932974
由表2可知,本方法执行过程中矩阵A中的约束不等式数量大于图中的边数量,则可认为本方法得出的边权值属性与原图保持一致.
5 结 论
由于大规模数据应用社交网络的普及,社交用户之间的边关系不能简单地同一化,其敏感度将直接影响到隐私的分布和保护方法的效能.本文针对带权值的社交网络提出了基于差分隐私机制的保护方法,该方法采用改进的单源最短路径约束模型构建边权值噪音,最大程度上保证扰动后的社交网络图的数据可用性.仿真实验表明,当数据集规模最大时(此时节点数目为30 000),本文所提出的方法在运行效率上比K-MPNP提高了47.3%,比LWSPA提高了41.8%,比DER提高了52.6%.在相似的数据隐私保护程度下,dp-noisy的数据可用性比lp-noisy提高了10%,显著优于DER的数据可用性,略好于LWSPA.当数据集规模最大时,dp-noisy的平均扰动质量比lp-noisy提高了14%,比DER提高了11.3%,比K-MPNP提高了27%,比LWSPA略低了3.6%; 而实际应用中为了保证数据效用,都会选择较高的隐私预算(例如苹果公司选择的隐私预算通常会在ε≤10时尽可能取最大值),因而当选择ε=10时,dp-noisy的扰动质量比LWSPA提升了6%.综上,dp-noisy具有较高的运行效率和数据效用,同时满足抵御图结构攻击的特性,且可适用于大规模的社交网络数据分析.
然而,本文提出的方法仍然存在一些问题有待深入研究.例如,单源最短路径模型是否可以进行优化,进一步减少不等式的数量从而提高算法的运行效率.后续工作将考虑根据对参数的不同需求优化模型,减少需求较低的属性约束.
[1]Rathore S, Sharma P K, Loia V, et al. Social network security: Issues, challenges, threats, and solutions[J]. Information Sciences, 2017, 421: 43-69
[2]Yin Chunyong, Shi Lingfeng, Sun Ruxia. Improved collabora-tive filtering recommendation algorithm based on differential privacy protection[J]. The Journal of Supercomputing, 2019, 14(7): 253-258
[3]Meng Xiaofeng, Zhang Xiaojian. Big data privacy manage-ment[J]. Journal of Computer Research and Development, 2015, 52(2): 265-281 (in Chinese)(孟小峰, 张啸剑. 大数据隐私管理[J]. 计算机研究与发展, 2015, 52(2): 265-281)
[4]Casas-Roma J, Herrera-Joancomartí J, Torra V. k-Degree anonymity and edge selection: Improving data utility in large networks[J]. Knowledge and Information Systems, 2017, 50(2): 447-474
[5]Abawajy J H, Ninggal M I H, Herawan T. Privacy preserving social network data publication[J]. IEEE Communications Surveys and Tutorials, 2016, 18(3): 1974-1997
[6]Wang Yue, Wu Xintao. Preserving differential privacy in degree-correlation based graph generation[J]. Transactions on Data Privacy, 2013, 6(2): 127-145
[7]Dwork C. Differential privacy[J/OL]. Encyclopedia of Cryptography and Security, 2011: 338-340[2018-12-20]. https://link.springer.com/referenceworkentry/10.1007%2F978-1-4419-5906-5_752
[8]Chen Rui, Fung B C, Yu P S, et al. Correlated network data publication via differential privacy[J]. The International Journal on Very Large Data Bases, 2014, 23(4): 653-676
[9]Sala A, Zhao Xiaohan, Wilson C, et al. Sharing graphs using differentially private graph models[C] // Proc of the 2011 ACM SIGCOMM Int Conf on Measurement. New York: ACM, 2011: 81-98
[10]Wang E K, Li Yueping, Ye Yunming, et al. A dynamic trust framework for opportunistic mobile social networks[J]. IEEE Transactions on Network and Service Management, 2017, 15(1): 319-329
[11]Das S, E![]() ecio
ecio![]() lu O, El Abbadi A. Anónimos: An LP-based approach for anonymizing weighted social network graphs[J]. IEEE Transactions on Knowledge & Data Engineering, 2012, 24(4): 590-604
lu O, El Abbadi A. Anónimos: An LP-based approach for anonymizing weighted social network graphs[J]. IEEE Transactions on Knowledge & Data Engineering, 2012, 24(4): 590-604
[12]Zhou Bin, Pei Jian. Preserving privacy in social networks against neighborhood attacks[C] //Proc of IEEE Int Conf on Data Engineering. Piscataway, NJ: IEEE, 2008: 506-515
[13]Zou Lei, Chen Lei, Özsu M T. K-automorphism: A general framework for privacy preserving network publication[J]. Proceedings of the VLDB Endowment, 2009, 2(1): 946-957
[14]Wang S L, Tsai Y C, Hong T P, et al. k-anonymization of multiple shortest paths[J]. Soft Computing, 2017, 21(15): 4215-4226
[15]Lan lihui, Ju Shiguang. Privacy preserving based on differential privacy for weighted social networks[J]. Journal on Communications, 2015, 36(9): 145-159 (in Chinese)(兰丽辉, 鞠时光. 基于差分隐私的权重社会网络隐私保护[J]. 通信学报, 2015, 36(9):145-159)
[16]Dijkstra E W. A note on two problems in connexion with graphs[J]. Numerische Mathematik, 1959, 1(1): 269-271




