近年来,全球存储的信息以每年近24%的速度增长[1],数据量的爆炸式增长加快了大数据时代的到来,这给各行各业带来了新的机遇和挑战.如何对大数据高效地进行自动分析和挖掘成为各行业面临的重大课题.
聚类算法是处理大数据的关键技术之一,它根据数据的相似特征对数据集进行自动划分,按一定规则根据对象属性把对象划分成不同的类别,同一个类别下的对象具有一定的相似性,而不同类别对象之间则差异性较大.聚类算法是机器学习中一种重要的无监督学习技术[2],已广泛应用于诸多领域,如计算机科学[3-5]、生物信息学[6-9]、图像处理[10-13]、社会网络[14-15]、天文学[16]以及许多其他领域[17].
目前,现有的聚类算法数以千计,且还在大量涌现.不同的聚类算法能很好地解决某些特定问题,但总体上仍然存在许多亟待解决的问题,比如聚类效果受数据分布影响大[18-19]、复杂度高、聚类数量需人工干预、聚类效果难以评价[20]等.
2014年在《Science》上发表了密度峰值聚类(density peak, DPeak)算法[21].该算法可识别出任意形状数据,能直观地找到簇(类别)数量,也能非常容易地发现异常点.此外,DPeak参数唯一、使用简单、具有非常好的鲁棒性,因而受到了广泛的关注.
本文针对DPeak算法进行介绍、分析,并总结了近年来的发展与应用动态,主要贡献有以下4个方面:1)介绍了DPeak算法,对其在聚类算法体系中的位置进行了讨论.特别地,对DPeak与mean shift[22]作了详细比较,并认为DPeak可能是一种特殊的mean shift算法或变种.2)讨论了DPeak算法的不足,并对相关改进算法的优缺点进行了分类讨论.3)梳理了DPeak及其改进算法在不同应用领域中所发挥的作用.4)讨论了DPeak与相关改进算法所存在的问题及挑战,并对其未来工作进行展望.
1 DPeak聚类算法的原理
DPeak是一种粒度计算模型[23],不仅在学术界产生了热烈的反响,同时也吸引了大量科研人员对该算法进行研究.DPeak算法基于2个假设:1)聚类中心被局部密度较低的近邻数据点包围;2)任意聚类中心与比它密度更高的数据点之间的距离都较远.
对于任意数据点i,DPeak需要计算2个量:i的局部密度ρi和它与具有更高密度的最近点的距离δi.数据点i的局部密度ρi定义为
(1)
其中,n为数据点个数;dij是数据点i和j的距离;χ是指示函数,当x<0时,χ(x)=1,否则χ(x)=0;dc是截断距离.可以看出,ρi等于分布在i的dc邻域范围内的数据点个数,即密度.δi则是通过计算点i与其他密度更高的点之间的最小距离来测量:
![]()
(2)
对于密度最高的点,则可以取![]()
除了式(1)的计算离散点的密度方式外,还有一种利用高斯核来计算连续点密度的方式,如下:
(3)
基于这2个量,DPeak通过“决策图”将数据点区分为3种不同的类型,即密度峰值点、正常点与离群点.如图1所示,数据点按密度递减的顺序排列.容易看出点1和10是非常突出,分布在图的右上角,具有非常高的δ值和ρ值,表明这2点在较大邻域范围内不存在比它们密度更高的数据点.因而这2个点正是所谓的密度峰值点,适合被选为簇(类别)中心.点7,8虽然具很高的ρ值,δ值却很小,分布在右下角,表明在它们近邻处存在密度更高的点,因而不是峰值点,不适合作为簇中心.点26,27,28具有较高的δ,ρ值却非常低,分布在偏左上角,表明它们是离群点.

Fig. 1 Two-dimensional mapping
图1 二维映射[21]
用户可以在决策图中手动选择簇中心,也可以选取前k个γ值最大的数据点作为簇中心,其中γ=ρ×δ.DPeak再将剩余的点分配到与其最近的密度较高的邻近区域的簇中.
2 DPeak与其他算法的比较
2.1 DPeak在聚类算法簇中的类别归属
聚类算法凭借其广泛的适用范围吸引了大量的研究人员,目前已存在大量的相关工作.为方便研究,人们对这些聚类算法进行了分类.基于现有聚类的分类方式[24-30],大致将聚类算法分为7类:划分聚类(division based)、层次聚类(hierarchical clustering)、网格聚类(grid based)、基于密度聚类(density-based)、模型聚类(model-based)、代表点聚类(exemplar)和图模型聚类(graph model),每种类型的聚类方式都有其优缺点.这些分类的方法并非是排他的,即一种聚类算法可以分别属于好几种不同类别.例如:均值漂移聚类(mean shift)[31]是基于密度梯度进行分析的,其中每个数据点迭代地向其局部密度中心漂移,所以可划分为基于密度聚类的算法.但其簇内数据点之间实际上是存在一定的层次关系,因而也可归到层次聚类.k均值聚类算法(k-means)虽然一般认为是划分聚类和代表点(质心)聚类,但它又是mean shift的一种特例[22].最大熵聚类[32]是一种基于统计物理的聚类方法,也是一种基于特殊内核的mean shift算法[22],所以也可划分到多种类别上.
对于DPeak而言,它是一种混合型聚类算法,可归为层次聚类、代表点聚类和密度聚类:
1) 层次聚类
与划分聚类相比,层次聚类[33]通过以自上而下或自下而上的方式递归地对数据进行分类来构建簇,可以更好地反映真实世界的数据集.层次聚类生成了一个嵌套簇的层次序列,可以用树状图来表示,输出的结果为层次结构,比平面结构含有更多的信息[34].然而,层次聚类缺乏鲁棒性,数据集小的扰动就会产生层次树状图结构较大的变化,而且算法的复杂度高[35].
Xu等人[36]提出了前导树的概念,除了根节点外,每个节点都是由其父节点引导加入同一个簇中的,即每个点的上一层节点是与其距离最近且密度更高的点,而整个数据集中密度最高的点是根节点.按前导树规则,DPeak算法生成的聚类结构实际上是一棵树状的层次结构,如图2所示.图2(a)是数据分布图;图2(b)是根据图2(a)画出来的树;图2(c)是假设簇数为3时,所生成的森林.点5是密度最大的点因此也是树的根节点.3,10,14,15,18为1个簇,其中3为密度峰值点;5,6,7,9,12,13,16,19,20为1个簇,其中5为密度峰值点;其余点为1个簇,其中8为密度峰值点.
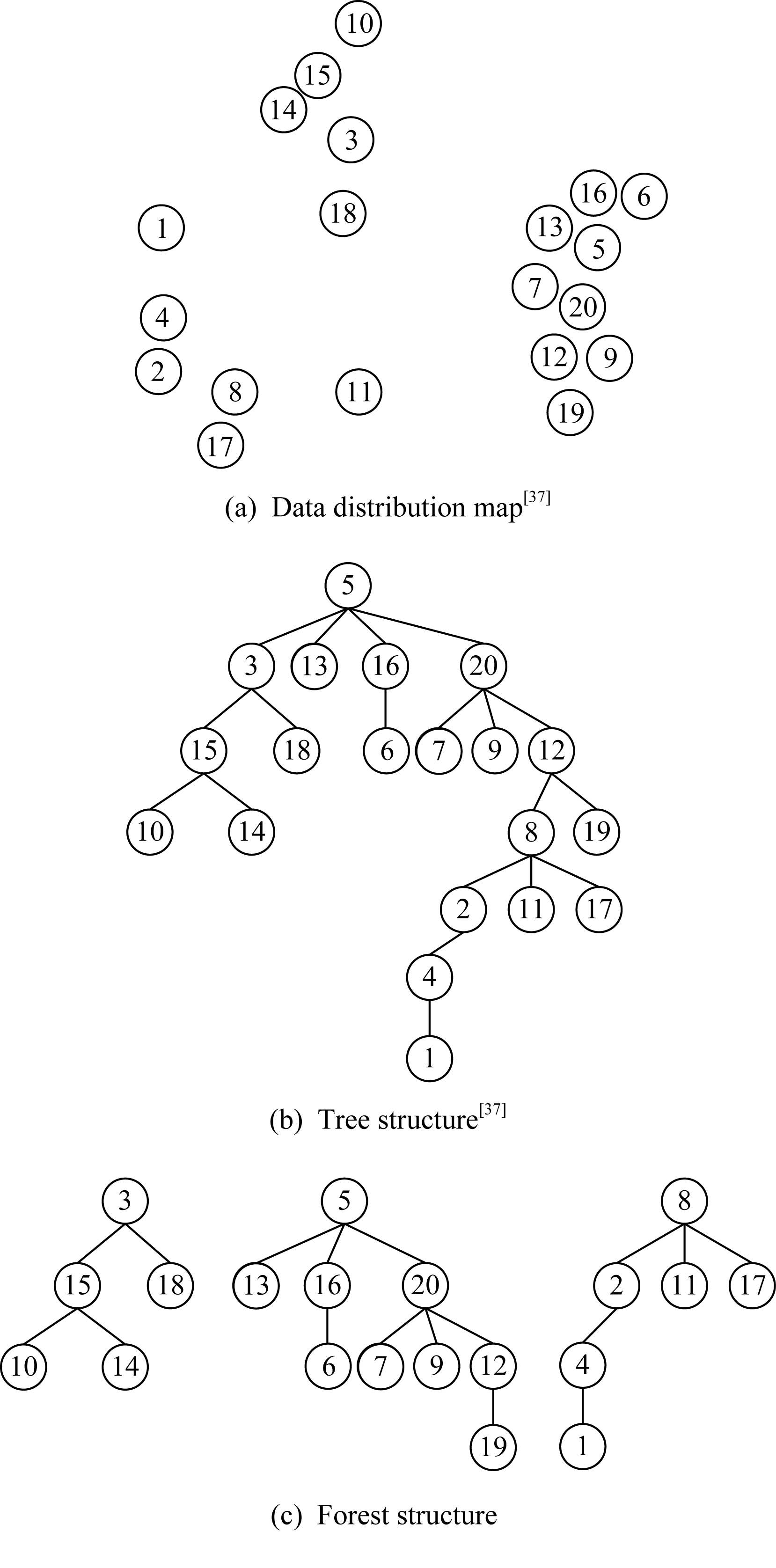
Fig. 2 Hierarchical structure of DPeak algorithm
图2 DPeak算法的层次结构
2) 代表点聚类
代表点聚类分为3类[38]:①把每个样本都视为潜在的簇中心,迭代更新其吸引度值和归属度值直到产生更好的代表点.如APCluster[39]中通过不断迭代使得每个类别产生的聚类中心为其代表点(exemplar).②随机选择代表点通过迭代调整来达到平方误差最小,如k-means.③采用密度估计来发现密度峰值点,用以当作代表点.
DPeak满足上述类型③,即选取一组密度高的远点来代表不同簇,如图2(c)中的3,5,8分别是3个簇的代表点.因而,DPeak可归为基于代表点聚类.
3) 密度聚类
密度聚类假设属于每个簇的点是从一个特定的概率分布[40]中提取出来的,该类算法可以发现任意形状的簇.基于密度聚类以DBSCAN[41]为代表,不需要先验知识来指定数据中的簇数,并且可以发现特征空间中具有任意形状的簇.但是它对用户定义的参数值非常敏感,即使参数设置稍有不同,通常也会在数据集中产生非常不同的聚类结果[24].
DPeak与DBSCAN(density-based spatial clustering of applications with noise)相比,两者的密度定义一致,DPeak中的截断距离参数dc与DBSCAN中的eps起相同作用.两者都将数据空间中密度较大的连续区域视为同一簇,因此DPeak算法是一种密度聚类算法.故密度聚类可以发现任意形状的簇这一优点也在DPeak算法中得以体现.
2.2 DPeak与5个主要聚类算法比较
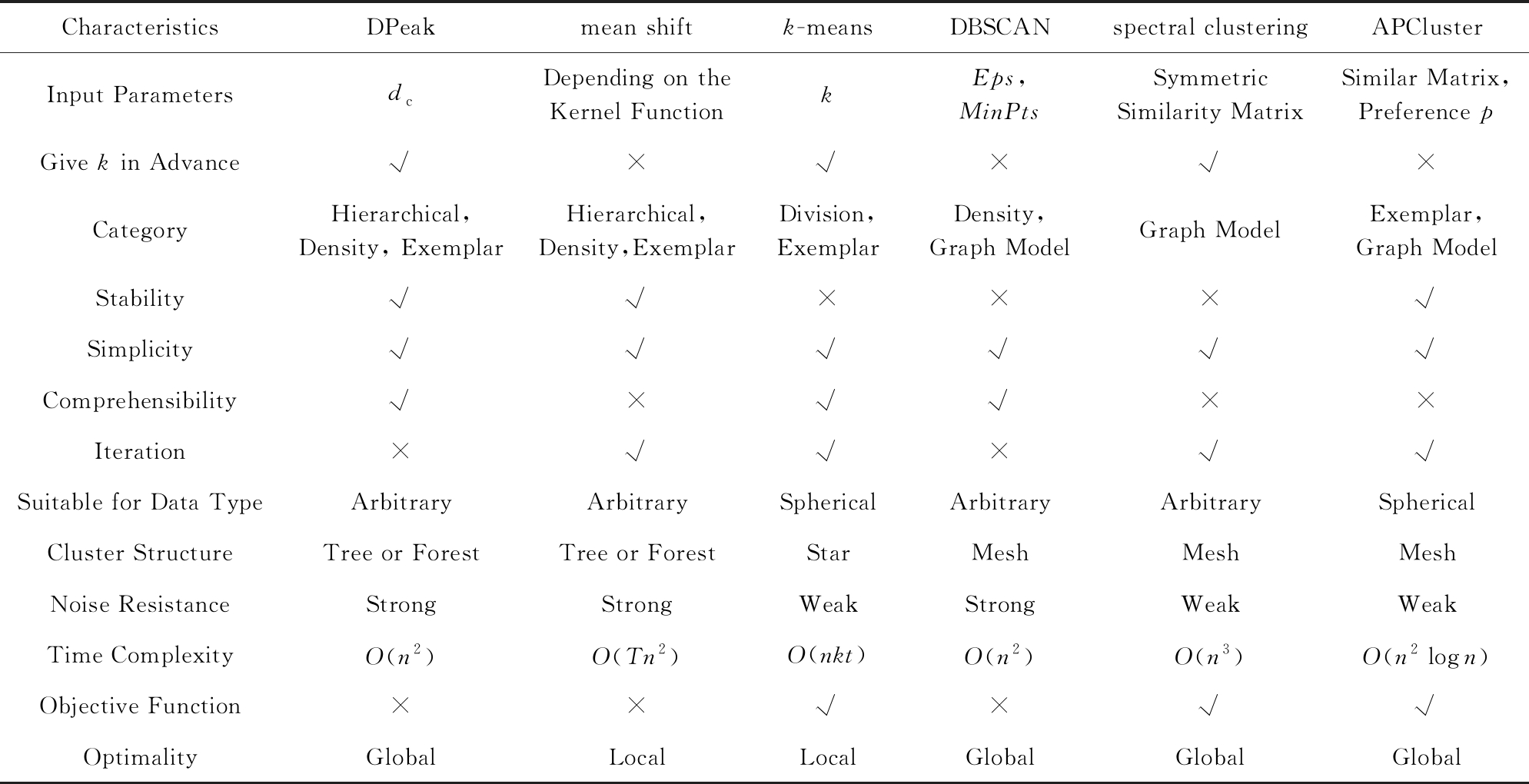
目前,比较常用的聚类算法主要是k-means[18-19]、DBSCAN[41-42]、mean shift[31]、谱聚类(spectral clustering)[43]和近邻传播聚类(affinity propagation cluster, APCluster)[39,44].相比于这些算法,DPeak算法的思想简单、参数要求少、能识别出任意形状的簇,缺点是复杂度较高.表1对上述这些算法进行了详细比较.可看出DPeak与mean shift算法最为接近.因此本文对两者进行详细比较,具体有6个方面:
1) 两者聚类过程都是自然过程.簇的形成是顺着数据密度变大的方向延展的,有明确的漂移轨迹.
2) 两者不同在于mean shift漂移的中间点可能是虚拟点,而在DPeak中,低密度点向上漂移到与其最近的高密度点,要求中间点必须是定义在数据集中的真实点.这个过程是一次搜索完成的,即不需迭代.
3) Fukunaga等人[45]提出mean shift算法,并认为该方法可能是梯度上升法.Cheng[22]指出mean shift是变步长的影子梯度上升法,当数据分布是理想状态下的高斯分布时mean shift是最速上升法.Fashing等人[46]进一步指明当核函数是分段常数(piecewise const)时,mean shift是牛顿法,而对于任意核函数,mean shift的均值漂移过程实际上是在使用影子函数对密度估计进行二次有界最大化.
直观而言,DPeak也应属于梯度上升法.按DPeak的定义可以理解为:每个点i向比其密度更高的最近邻(目标点)漂移,是跳跃式非连续的最小步长梯度上升法.目标点在i的最小步长邻域范围内密度最高,该最小步长不受参数dc约束,是全局最优.而mean shift则是在局部范围内寻找密度上升方向,其漂移过程是连续的、局部收敛和局部最优的.
Table 1 Comparisons on Several Typical Clustering Algorithms
表1 几种典型聚类算法的比较
CharacteristicsDPeakmean shiftk-meansDBSCANspectral clusteringAPClusterInput ParametersdcDepending on the Kernel FunctionkEps,MinPtsSymmetric Similarity MatrixSimilar Matrix,Preference pGive k in Advance√×√×√×CategoryHierarchical,Density, ExemplarHierarchical,Density,ExemplarDivision, ExemplarDensity,Graph ModelGraph ModelExemplar, Graph ModelStability√√×××√Simplicity√√√√√√Comprehensibility√×√√××Iteration×√√×√√Suitable for Data TypeArbitraryArbitrarySphericalArbitraryArbitrarySphericalCluster StructureTree or ForestTree or ForestStarMeshMeshMeshNoise ResistanceStrongStrongWeakStrongWeakWeakTime ComplexityO(n2)O(Tn2)O(nkt)O(n2)O(n3)O(n2logn)Objective Function××√×√√OptimalityGlobalLocalLocalGlobalGlobalGlobal
Note: √ means “Yes” or “Has”; × means “No”.
4) 虽然mean shift是无参算法,但当其核函数是平整函数(flat kernel)时需要输入参数,其作用与DPeak的参数dc等价.
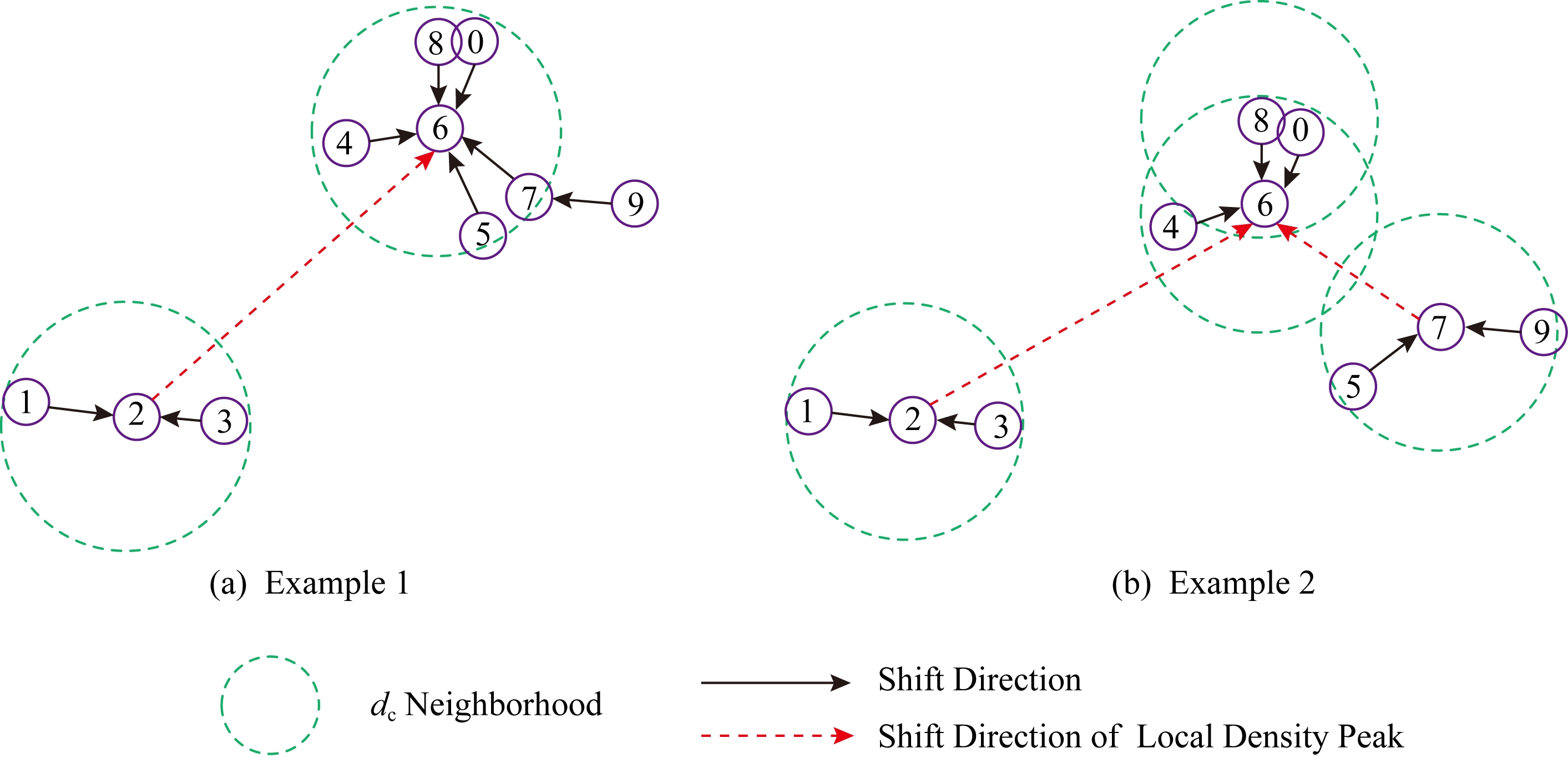
Fig. 3 Two examples of local peak of DPeak
图3 DPeak的局部峰值中心2个实例
5) mean shift无需指定聚类个数k,因为mean shift直接将均值漂移的收敛点视为一个簇的中心,也是局部密度中心点.DPeak算法虽然要指定k(或指定具体的聚类峰值点),但其与mean shift一样,在数据漂移的过程中存在一些数据点是局部中心点,这些点在dc邻域范围内是密度最高的,即局部峰值中心点.它们的密度更高且近邻在dc邻域范围之外.在没有指定k的情况下,可将这些点作为聚类中心,这与mean shift的寻找聚类中心方式是一致的.
以图3为例,图3(a)中局部峰值中心点有2和6,严格来说点2应该向点6继续漂移,如虚线箭头方向所示.若以局部峰值中心点为聚类中心,则该图可聚成2类:1,2,3一类;0,4,5,6,7,8,9为另一类.同理,图3(b)中局部峰值中心点有2,6,7,该图可聚成3类,分别是:1,2,3为第1类;0,4,6,8为第2类;5,7,9为第3类.
6) 在DPeak计算过程中,数据集S本身固定不变,是一个非模糊过程(non-blurring process)[21].在起始阶段,DPeak把所有数据点都看成是临时中心,并为每一个点迭代寻找最终中心.只不过在迭代程中有许多路径是重叠或重复的,可以省略,使DPeak看起来显得不用迭代,其复杂度相比mean shift较低.以图2(b)为例,对于数据点17而言,对其做完整迭代的路径是:17→8→12→20→5;对于数据点8而言,其路径则为:8→12→20→5,2条路径是交叉重叠的.因而,若数据点17的漂移路径计算完成后,点8的迭代过程可以省略,数据点12,20类似.
3 DPeak算法的优化
DPeak算法具有诸多优点,如不需要迭代、参数少、算法简单等,但仍存在一些亟待解决的问题.
1) 复杂度O(n2)较高.不适用于大规模数据的聚类分析.
2) 过程不是自适应的.不能自动调整内在参数.例如,不能自适应选择密度峰值与dc.
3) 精度易受影响.DPeak在计算局部密度时,如果没有考虑到数据的局部结构会导致许多簇的丢失、“假峰”[47-48]和“无峰值”[49]现象从而影响聚类的精度.
4) 高维数据适用性差.因为在高维数据中的许多维度相互无关,这会造成一些簇的丢失[50].
针对这些问题,近年来有许多算法从各方面对DPeak算法进行改进,下文选择具有代表性的算法进行汇总、分类和分析.
3.1 提升速度
DPeak在计算过程中产生了距离矩阵,因此增加了其空间复杂度.Wu等人[51]提出了DGB(density-and grid-based)聚类方法,先使用网格技术对数据空间按维度进行划分,每个单元格称之为一个Cell,再通过计算少量的非空Cell节点之间的距离来代替计算每个点之间的欧氏距离从而达到提升DPeak速度的目的.类似地,Xu等人[52]提出DPCG(density peaks clustering algorithm based on grid)算法,在计算局部密度时采用分团(clique)方法[53]中的网格思想来代替DPeak的原始方法,可将DPeak第1步计算数据点密度的复杂度大幅降低,也可将DPeak第2步寻找各点的密度更高近邻的复杂度降为O(m2),其中m为非空Cell数.PDPC(fast density peaks clustering algorithm based on pre-screening)[54]也采用网格(grid)技术来在前期过滤一部分计算,快速找到密度稠密区域.
然而,DGB和DPCG算法实验均只是在低维小规模数据集上有较好表现.在较高维数据集上,这2种方法效果并不佳,不能有效地对大规模数据进行聚类.究其原因在于:随着数据空间维度增大,Cell数成几何级数增长.非空Cell数越多,利用网格消除的欧氏距离计算量就越少.当非空Cell数接近于数据点总个数n时,网格技术失效[55].
我们随机生成若干个数据集,维度d分别取2,3,4,5,10,数据点每个维度上的取值范围为(0,1].对这些数据集进行网格划分,Cell宽度设为0.1.表2列出不同数据集上的Cell个数.从表2中可以看出随d的增长,非空Cell个数指数级增长.
Table 2 Cell Growth Trend with Dimension
表2 Cell随维度增长变化趋势表

nd=2d=3d=4d=5d=6d=7d=8d=9200061298942162619181978199919993000593371129220828002958299429995000653771407319144854891498149961000060401177748918134955099039985
另外,Li等人[56]引入CUDA技术,通过GPU实现DPeak算法的简单并行化,相比于在CPU上运行,该算法计算距离矩阵速度提升了4.39倍(其中线程数为1 000,有N个Blocks,Block size为32×32).当硬件条件更好时,速度还可以进一步提升.该算法复杂度降为O(αn2 t),其中t为线程数,α为GPU数据调度偶合系数.可以看出通过并行化处理,以硬件加速来改进DPeak是可行之道.
t),其中t为线程数,α为GPU数据调度偶合系数.可以看出通过并行化处理,以硬件加速来改进DPeak是可行之道.
在DPeak的计算过程中,每个点的ρ与δ值需要计算距离2n2次,计算量无疑是非常大的.Bai等人[26]提出了一种计算更少距离的加速算法CFSFDP+A,并且可以得到与原算法相同的聚类结果.该文作者发现簇往往存在于局部空间中,因此采用k-means来划分空间区域,使用近似算法和三角不等式精确地缩小了搜索空间.CFSFDP+A的时间复杂度为O(nkmt+nn1+nn2),其中km为划分的子集数,t为迭代次数,n1为计算所有点的密度时计算距离的平均次数,n2为划分空间时计算距离的平均次数.该算法的时间复杂度仍然接近O(n2),速度的提升并不显著.为了进一步扩展CFSFDP+A并提升算法的速度,该文作者还提出了一种基于代表点的近似算法CFSFDP+DE(clustering by fast search and find of density peaks based on exemplar clustering),使用k-means所产生的每个簇的代表点来代替样本点,利用代表点的密度关系来进行聚类.该算法的时间复杂度为O(nkmt+k2m)虽然速度相较于DPeak已经有所提升,但是复杂度大于O(n log n).
为提升DPeak的效率和可扩展性,巩树凤等人[57]提出了EDDPC(efficient distributed density peak clustering).该算法选择Voronoi分割所需要的种子,再用2个完整的MapReduce[58]作业分别计算ρ与δ值.首先,将数据分组并独立并行地处理各分组中的数据对象,在各分组内局部计算ρ值和δ值,以克服计算所有对象间的距离所造成的大量开销.该文作者给出了1个数据对象复制模型和2个数据对象过滤模型,将部分其他分组内的必要对象复制到本分组内来确保数据独立并行执行.此外,该文作者对比EDDPC和SDDPC(simple distributed density peak clustering)[57]后发现,EDDPC的运行速度明显小于SDDPC.值得注意的是,DPeak在单片机上运行数据量小的情况下运行时间优于SDDPC,但是在运行大规模数据时会出现内存溢出的现象.Zhang等人[59]在证明了Basic-DDP(basic distributed density park clustering)解决方案具有很高的通信开销后,提出了LSH-DDP(an app-roxima-tion algorithm for partitioning using local sensitive Hash).该算法利用局部敏感散列(local sensitive Hash, LSH)对输入数据进行分区,以便近邻点更有可能被分配到同一个分区,基于LSH的算法在每个分区内执行本地计算,然后聚合结果,得到最终的近似结果.该方法与EDDPC的聚类效果相似且速度是EDDPC的2倍,是Basic-DDP的1.7倍到70倍.
Chen等人[37]提出了FastDPeak(fast density peak clustering for large scale data based on KNN).基KNN搜索,该算法应用cover tree对密度计算进行加速.另外为避免在全局范围内计算各个点的δ值,提出了局部密度峰值与非局部密度峰值点概念,用以对δ值计算进行加速.若数据点p在其最近的k个近邻中密度最高,则称其为局部峰值点,否则为非局部密度峰值点.对于非局部密度峰值点而言,其父节点一定在其k个近邻内.对于局部密度峰值点,可逐渐增加k值来扩大搜索范围,来寻找它的上层节点.因而,FastDPeak大幅减少了δ值的计算复杂度,约为O(dk),其中d为与数据分布有关的常数.
综合来说,FastDPeak时间复杂度为O(n log n),空间复杂度为O(kn),其中k为KNN中的k值.如果k值较大,则需要大量的存储空间,因此该算法还需要改进从而优化算法.
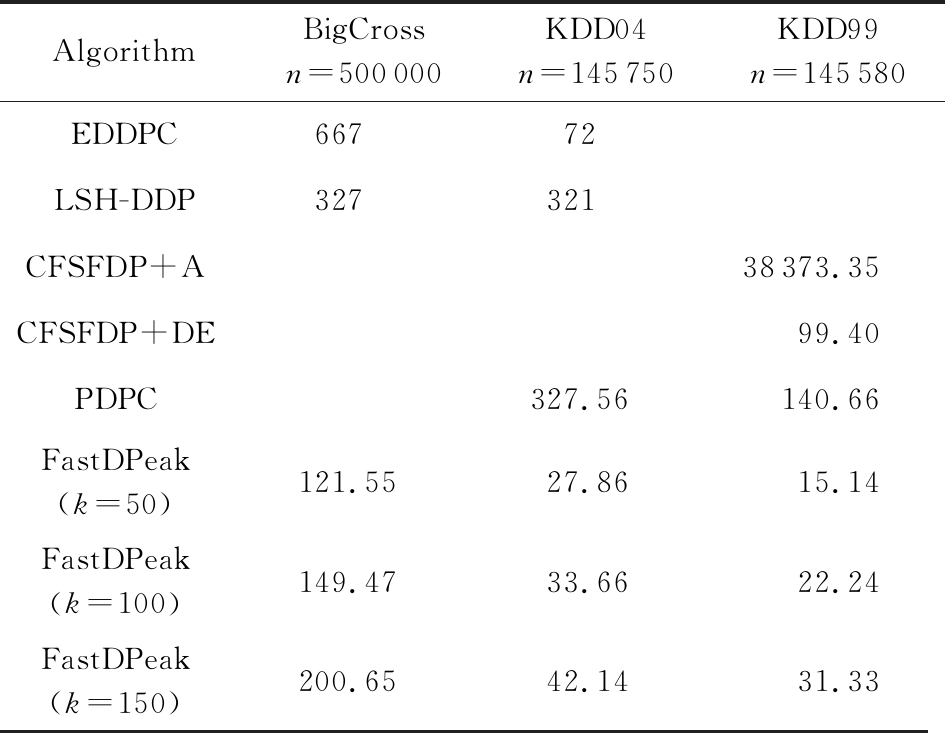
表3所示的是8种算法分别在BigCross,KDD99,KDD04[60]等数据集上的速度测试结果.可以看出,与CFSFDP+A[26],CFSFDP+DE[26],EDDPC[57],LSH-DDP[59]等算法比较,FastDPeak有较大改进.
Table 3 Runtime Comparison on Several Data Sets
表3 几个数据集上的运行时间比较 s
AlgorithmBigCrossn=500000KDD04n=145750KDD99n=145580EDDPC66772LSH-DDP327321CFSFDP+A 38373.35CFSFDP+DE 99.40PDPC 327.56140.66FastDPeak(k=50)121.5527.8615.14FastDPeak(k=100)149.4733.6622.24FastDPeak(k=150)200.6542.1431.33
3.2 参数自适应化
由于DPeak算法中局部密度的原始定义是基于截断计数测量的,因此很难推导出合理的参数估计准则和“最优”的参数.Wang等人[35]提出了ADPclust(fast clustering using adaptive density peak detection).首先,利用非参数的多元核估计来估计局部密度,并通过统计理论证明了模型参数的计算合理性.其次,该文作者在用户交互选择簇数目的基础上,提出了一种基于轮廓优化算法的簇中心自动选择方法.该方法无需迭代,在大数据分析中具有快速、实用的特点.dc的敏感性和密度的选择是影响DPeak聚类效果的两大问题.高斯核是一种局部密度估计方法,但是对于小簇的估计难以保证精度.虽然可以通过调整参数dc来提升精度,但是这要求dc适应不同的簇,显然难以实现.因此Hou等人[61]提出了一种新的局部密度估计方法,该方法仅采用最近邻来估计密度.局部密度主要用于将聚类中心与其他数据分离,该文利用最近邻数据中最远的那些点来突出聚类中心的唯一性,并建议使用密度归一化来处理簇之间的密度差异.该算法密度函数定义为
(4)
其中,![]() 是KNN中包含最远数据的子集.在给定簇数量的情况下,该算法能够在没有人为干预的情况下完成聚类过程并改善聚类结果,但是增加了计算的复杂度,且需要人工来确定簇的数目.
是KNN中包含最远数据的子集.在给定簇数量的情况下,该算法能够在没有人为干预的情况下完成聚类过程并改善聚类结果,但是增加了计算的复杂度,且需要人工来确定簇的数目.
DPeak算法在人工选择聚类中心的基础上能够得到满意的结果,但这种选择对于大量的聚类任务或具有复杂决策图的数据集来说都很难实现.Ding等人[29]提出了DPC-GEV(density peaks clustering based on generalized extreme value distribution).受到DPeak的视觉选择规则启发,该文作者提出了判断指数,并将其用于选择聚类中心.判断指数大致遵循广义极值(generalized extreme value, GEV)分布,每个聚类中心的判断指数要比其他点的判断指数高得多.因此,如果它们的判断指数大于GEV的上分位数,则选择这些点作为聚类中心是合理的.考虑到计算复杂性,该文还提出了DPC-CI(alternative method based on density peak detection using Chebyshev inequality).DPC-CI通过计算判断指标的期望和标准差,并根据切比雪夫不等式设置上界.DPC-GEV和DPC-CI在大多数数据集上可以达到与DPeak相同的精度,但消耗的时间要少得多.
参数选取不当会导致初始簇中心的选择错误,但在后续的分配过程中DPeak无法对其进行修正.在某些情况下,即使设定了dc的适当值,也很难从决策图中选取最优的初始聚类中心.为了准确地找到DPeak的簇中心,Liu等人[62]提出了ADPC-KNN(adaptive density peak clustering based on KNN).该方法通过使用高斯核![]() 提出了一种基于KNN的新密度度量方式.
提出了一种基于KNN的新密度度量方式.
(5)
(6)
(7)
其中,![]() 是点i与其第k个最近邻居KNNi之间的距离,由
是点i与其第k个最近邻居KNNi之间的距离,由![]() 定义.
定义.
ADPC-KNN只需一个参数就能自动聚类,总体时间复杂度与DPeak一样都为O(n2),其空间复杂度与DPeak也是相同的.该方法可以正确且不遗漏地找到簇中心,但是簇数目的选取仍是由人工实现的.
固定扫描半径主要有2个缺陷:1)对于高维数据来说,选择固定的扫描半径十分困难;2)对于存在假峰的数据集并不适合.如图4,在圆与中心点c之间存在空白区域,r1是外半径,r2是内半径.大部分点位于圆环范围内,从圆的内边缘到中心存在一个没有数据点的空白区域.显然,在扫描半径大于r1的情况下,点c为密度峰值.而扫描半径小于r2时,它实际上是一个被排除在圆之外的离群点.这种现象被称为“假峰”[47].因此,Chen等人[47]提出了DHeat(density heat-based algorithm for clustering with effective radius)方法,可以解决固定扫描半径造成的缺陷.该方法基于2个假设:1)如果密度分布均匀,一个点在其邻域半径内的密度与邻域的体积成正比.2)每个聚类可以划分为不同的密度层,如边缘、浅层、内层等.一个点所处的位置越是深入内层区域,这个点的密度就越高.
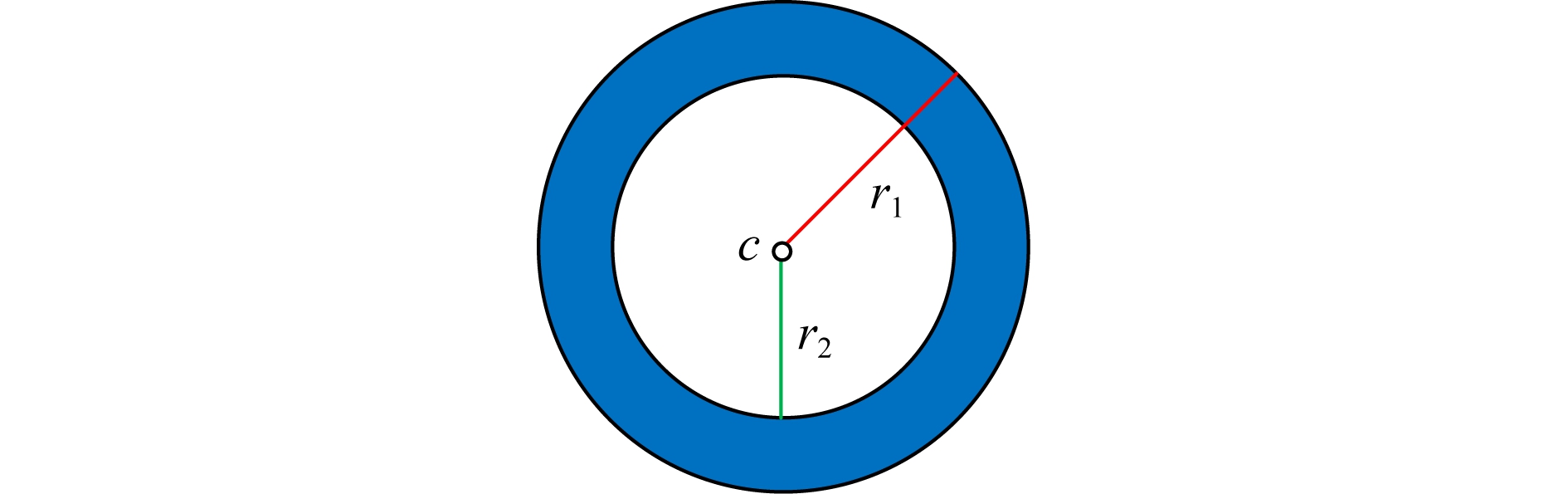
Fig. 4 “Fake Peak” illustration
图4 “假峰”说明图[47-48]
DPeak需要使用不同的方法来估计不同数据集的密度,并且dc的估计很大程度上取决于主观经验.为了克服DPeak的局限性,Mehmood等人[63]提出了CFSFDP-HD(clustering by fast search and find of density peaks via heat diffusion).该方法结合了截止距离选择和核密度估计的边界校正以便更好地估计密度,从而达到更精确的聚类效果,更有效地将聚类点的噪声分离出来.该方法对于大型数据集具有很好的鲁棒性,但是仍需要利用人机交互的方式来选择簇的数目.
基于以上分析,不难发现阻碍DPeak自动化的三大因素分别为中心的选择、dc的选择及簇数目的选取.其中已经有大量的相关研究对前2个因素进行改进,或采用非参数估计[63]来改善参数对聚类效果的影响.但是对于簇数目的选取仍然停留在人工干预选择阶段,缺少自动选择簇数目的相关工作.
3.3 改进聚类精度和鲁棒性
DPeak采用不同的方法确定不同数据集大小中点的局部密度.虽然DPeak对于大数据集的结果是稳健的,但对于小数据集则对dc非常敏感.此外,DPeak易产生多米诺骨牌效应,一旦一个点分配错误就会导致更多的点分配错误.为了增强DPeak的鲁棒性,Xie等人[28]提出了FKNN-DPC(robust clustering by detecting density peaks and assigning points based on fuzzy weighted KNN).由式(4)可以得到密度ρi,无论k最近邻点的数据集大还是小,该算法的局部密度ρi均与截止距离dc无关.将剩余点分配给最可能的簇有2种策略:1)通过从簇中心开始对每个点的k最近邻进行广度优先搜索来分配非异常值;2)使用模糊加权KNN技术,分配异常值和第1次分配过程未分配的点.主要技术如下:
定义点i和j之间的相似性wij,即
![]()
(8)
这意味着点i和j之间的距离越小,它们就越相似.计算点i属于簇a的概率![]() 即
即
(9)
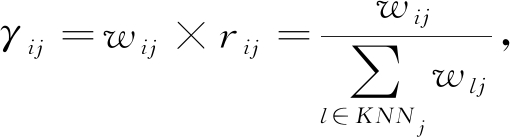
(10)
其中,yi是点j的簇标号.然后将点i分配给概率最高所对应的簇中.
Pang等人[64]提出了MrGDM(multi-granularity decomposition mechanism of complex tasks based on density peaks).首先,构建全局任务前导树,将该树看作是原始的求解空间,即包含全局信息概念的粗粒度层.该文作者对DPeak算法进行了改进,消除了DPeak算法难以准确定位聚类中心、分类困难等缺陷.然后,通过选择冗余子任务的中心,测量子任务集的相似性,定义粒度规则,从而生成几个多粒度任务求解空间.最后,根据实际问题来进行粒度优化,得到最优层来解决相应问题.该算法的时间复杂度为O(n2)+O(n)+O(st),其中s为初始可取的冗余初始中心的任务数,t为自动算法终止的循环指标.
要获得正确聚类,DPeak算法存在一个隐藏要求:数据集中的每个簇必须有且仅有一个密度峰值,否则DPeak将拆分为多个簇.当一个簇中有多个密度峰值,即“无峰值”时,此时的聚类效果并不好.为解决上述情况,Zhang等人[49]提出了E-CFSFDP(an extension of clustering by fast search and find of density peaks).该算法借鉴CHAMELEON[65]算法,根据数据点创建KNN图使得图分割成子类,然后合并子集.E_CFSFDP选择尽可能多的簇中心,以克服DPeak仅在数据集的每个簇具有唯一密度峰值时表现良好的不足.类似地,Chen 等人[48]认为在可聚类成不同簇的数据中,每一个簇由一个核心区确定,而非一个峰值点所能代表,这个核心区是由多个紧密相连的高密度点构成.基于这一思路提出了DCore(decentralized clustering by finding loose and distributed density cores)算法,通过与mean shift近似的漂移方法找出若干局部密度中心点,对这些中心点先完成聚类,再按漂移过程中形成的层次结构对其他数据点指派类别.如图5所示,红色点即为所谓的核心区,每一个红色数据点实际上都是一个局部密度中心点,它直接决定了一个簇的形状与分布区域.蓝色线条表示数据点的漂移轨迹,绿色点表示“假峰值点”.基于DCore思路,Xie等人[66]提出了DCNaN(a clustering algorithm based on the density core and the natural neighbor)算法,利用天然邻居(natural neighbors)完成实现dc动态化.
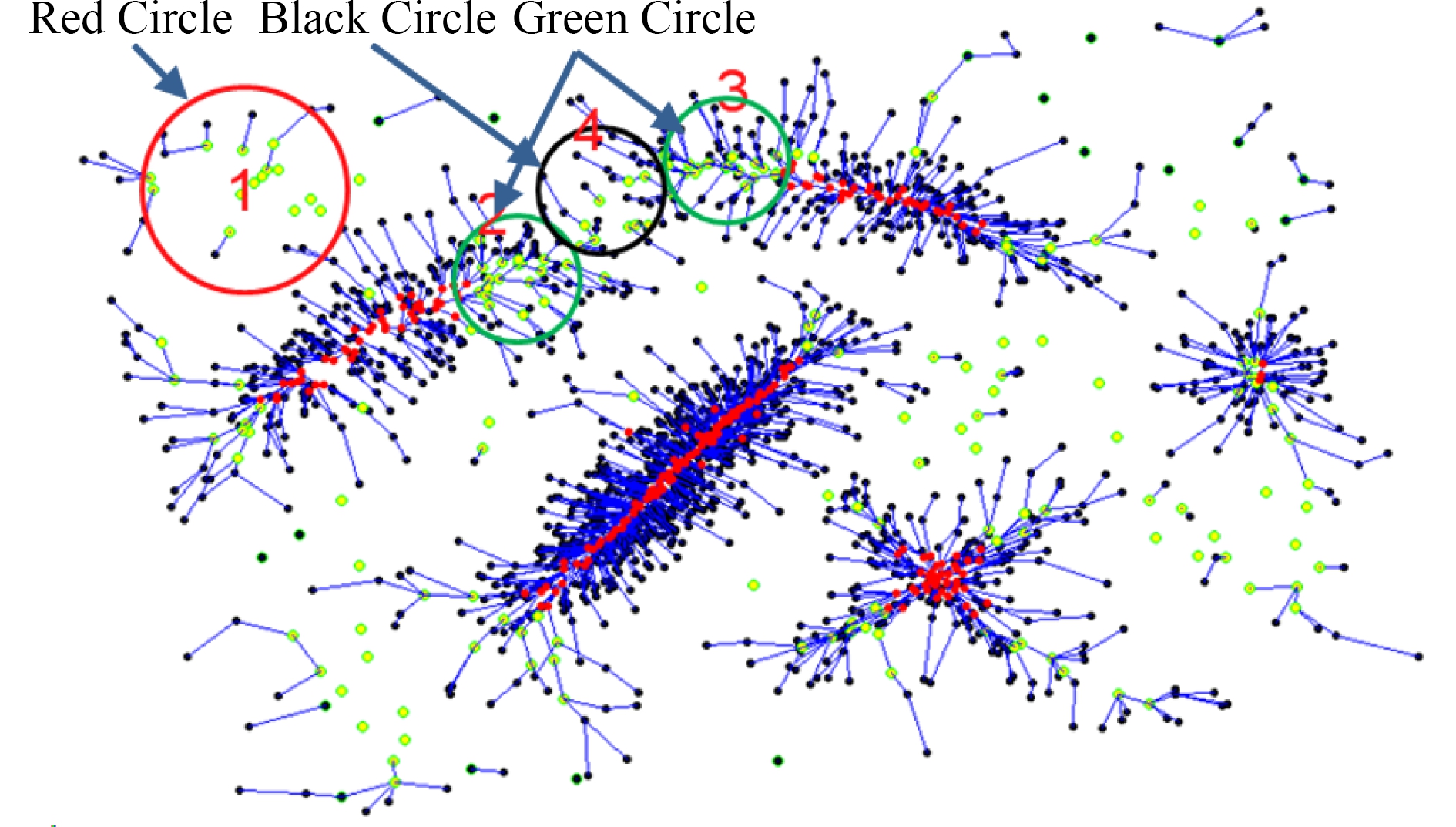
Fig. 5 The density cores and shift stream of DCore[48]
图5 DCore 的密度核心区与数据漂移[48]
影响DPeak聚类精度的情况通常有:产生“假峰”、“无峰值”、簇丢失及多米诺骨牌效应等.不难发现这些现象均由dc或簇中心选取不当或不规则的数据分布所产生,因此如何最优选择这2个参数,使其满足合适的数据集仍是DPeak研究的一个难点和热点.
3.4 高维数据处理
随着大数据时代的到来,数据维数越来越高,欧氏距离度量在高维数据中变得没有意义,基于距离计算的聚类效果也越来越差.如何有效处理高维数据已经成为一个亟待解决的难题.
Xu等人[34]提出了DenPEHC(density peak based hierarchical clustering method)引入网格粒度框架,使DenPEHC能够聚类大规模和高维的数据集,具有很好的鲁棒性、精确度和效率.Du等人[50]提出了DPC-KNN(a density peaks clustering based on KNN),它将KNN的思想引入DPeak,提出了一种局部密度计算的方法,其算法复杂度为O(n2).为了克服在高维数据上表现不佳的问题,该文将主成分分析(principal component analysis, PCA)引入到DPC-KNN模型中,并进一步提出了DPC-KNN-PCA(DPC-KNN based on PCA).该算法的时间复杂度为O(M3+M2n+n2),其中M为每个点的特征个数.DPC-KNN-PCA不仅具有良好的可行性,而且在聚类性能上优于经典的聚类算法(k-means和spectral clustering)和DPC算法.在低维数据集中,DPC-KNN的性能优于其他算法.在相对高维的数据集中,DPC-KNN-PCA取得了令人满意的结果.但是当数据集呈现垂直条纹时,这2个算法的聚类效果均不佳.另外,Xu等人[52]通过实验报告了基于Grid技术DPCG算法也具有较好的高维数据处理能力.FastDPeak[37]的实验中也表明在较高维数据集KDD04(77维)与BigCross(57维)上取得较好效果.
目前针对高维数据进行改进的DPeak算法较少,效果还不是太令人满意.这类问题需要针对具体应用场景选择合适的降维算法来解决,如PCA、网格粒度框架、LDA[67] 、流形学习[68-69]等,还有待进一步的研究.
3.5 主要改进算法汇总
表4汇总了DPeak的主要改进算法,通过对比不难发现:
1) DPeak的速度主要依靠KNN[28,37,50,61-62]算法、网格法[51-52]以及并行化[56]思想来提升.
2) DPeak的参数自动化研究主要通过密度估计[35,61]、自动计算参数dc[62]或通过KNN避开参数dc[37,61](但同时有可能带来新参数k的选择问题)、选择聚类中心[29,35,62]来实现的.
Table 4 Comparisons of Improved DPeak Algorithms
表4 DPeak的相关改进算法
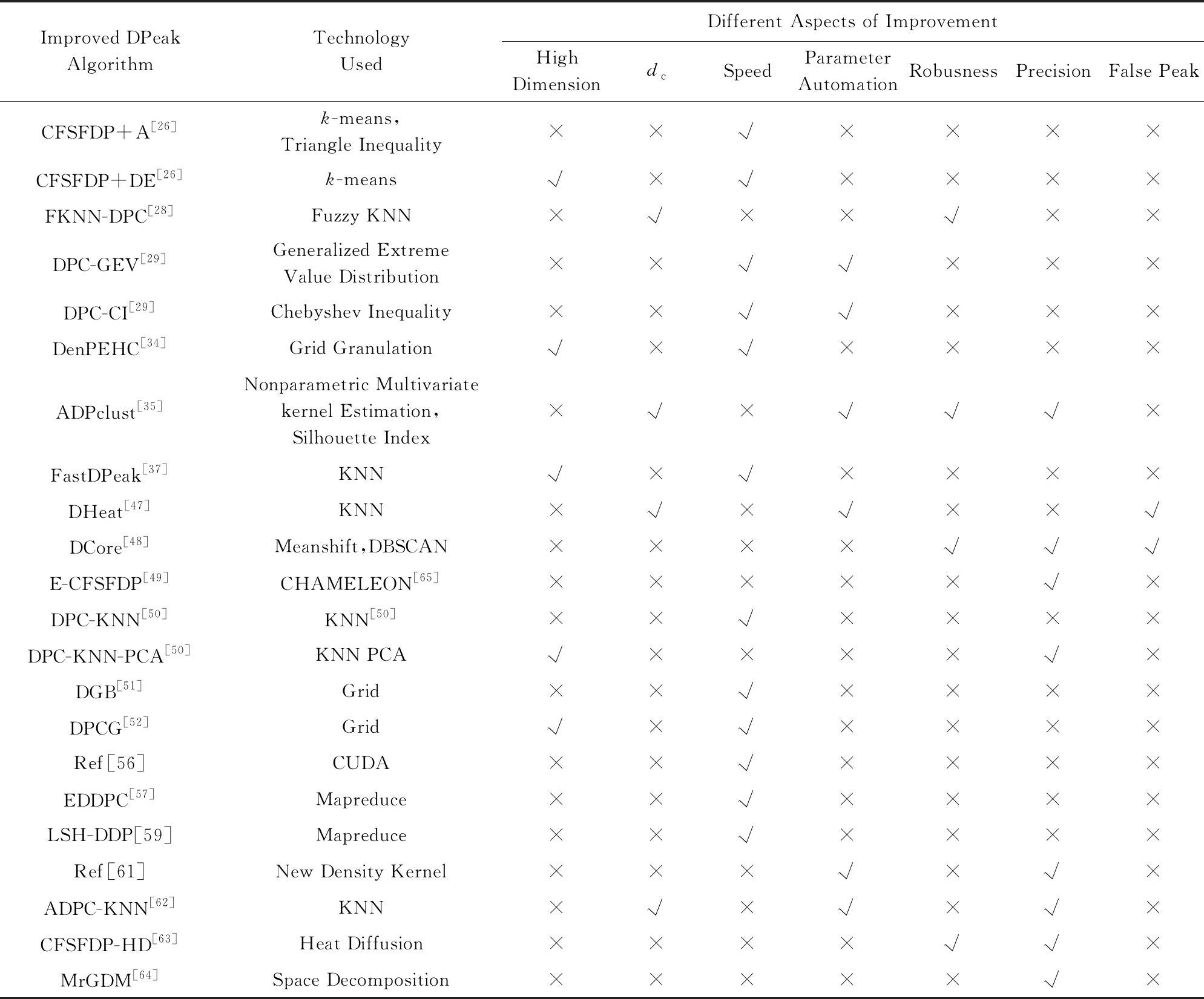
Improved DPeak AlgorithmTechnologyUsedDifferent Aspects of ImprovementHighDimensiondcSpeedParameterAutomationRobusnessPrecisionFalse PeakCFSFDP+A[26]k-means,Triangle Inequality××√××××CFSFDP+DE[26]k-means√×√××××FKNN-DPC[28]Fuzzy KNN×√××√××DPC-GEV[29]Generalized ExtremeValue Distribution××√√×××DPC-CI[29]Chebyshev Inequality××√√×××DenPEHC[34]Grid Granulation√×√××××ADPclust[35]Nonparametric Multivariatekernel Estimation,Silhouette Index×√×√√√×FastDPeak[37]KNN√×√××××DHeat[47]KNN×√×√××√DCore[48]Meanshift,DBSCAN××××√√√E-CFSFDP[49]CHAMELEON[65]×××××√×DPC-KNN[50]KNN[50]××√××××DPC-KNN-PCA[50]KNN PCA√××××√×DGB[51]Grid××√××××DPCG[52]Grid√×√××××Ref[56]CUDA××√××××EDDPC[57]Mapreduce××√××××LSH-DDP[59]Mapreduce××√××××Ref[61]New Density Kernel×××√×√×ADPC-KNN[62]KNN×√×√×√×CFSFDP-HD[63]Heat Diffusion××××√√×MrGDM[64]Space Decomposition×××××√×
Note: √ means “yes”; × means “No”.
3) 对于处理高维数据的改进方法中,目前主要以网格法[34,52]与PCA降维[50],但效果不是很好.
4) 此外,许多聚类算法使用模糊聚类[28,70-73]的方法来提升DPeak的鲁棒性.
4 DPeak算法的应用
虽然DPeak算法仍比较年轻,但具有过程较为简单、效果好等优势,已广泛应用于各个领域,例如:图像处理[74-76]、工业[77-79]、计算机[80-83]、生物医学[84-86]、光学[87-89]及其他方面[90-92]等.下文将对其中3个主要的应用领域展开简要介绍.
4.1 自然语言处理应用
近年来,交互可视化技术在分析文本文档方面的发展势头十分迅猛.然而,要对一篇文档进行抽象,并在相关的已作好标注的文档空间中进行检索仍然是个难题.面对这一问题,Heimerl等人[82]将DPeak算法用在高维空间中来估计给定文档集的最佳簇数,并且基于数据的密度结构将其他所有文档分配给其中一个峰值.但是DPeak在高维空间中的计算速度并不理想,存在速度较慢的问题.
多文档新闻摘要(MDNS)的目的是在保留原始新闻文档集的主要特征的同时,创建了一个浓缩的摘要.人们普遍认为,一个好的MDNS方法应该适当地考虑相关性和多样性.大多数MDNS方法都专注于其中一方面的研究,而Wang等人[83]提出的句子评分法综合考虑了相关性、多样性和长度约束.该方法用DPeak来度量句子层次的相关性和多样性,选择代表性较强的句子,生成冗余较少的摘要,保证了多文档新闻摘要的多样性和长度约束.但是,如果出现多个峰值的情况时,就会出现关键句子冗余的情况.
4.2 生物医学应用
通过计算机辅助折叠生物分子(特别是RNA)是计算结构生物学中最困难的难题之一.Kuhrova等人[84]引入了DPeak提出了一种新的算法,可以确定哪些分子力场破坏了折叠结构[93].造血干细胞(hematopoietic stem cell, HSC)出现在胚胎发育中的主动脉,目前已经可以通过移植的方法估计出HSC克隆的数量,但是在天然环境中生成的HSC的数量估计仍然具有挑战性.为解决这一挑战,在Henninger等人[85]所采用的方法中,使用DPeak聚类方法测量颜色空间中每个细胞的密度以及每个细胞距离密度更高细胞的距离,并绘制可以揭示聚类中心的结果图.对大量历史数据集进行分析可以得出疾病症状群.Chen等人[86]基于这2点,并根据目前疾病的阶段,向医生和患者推荐有价值的疾病诊断和治疗方案.该文作者采用DPeak来识别疾病症状,再采用Apriori算法进行关联分析,但是该方法对先验知识的要求较高.
4.3 光学应用
利用高光谱传感器在同一时刻对同一空间区域进行成像,获得的高光谱图像通常包含数百个波段图像,这为精确分析和识别地面物体提供了可能.然而,由于在实践中难以获得足够的标记训练样本,大量光谱带可能导致“维数灾难”.Jia等人[87]将DPeak算法进行改进,使其适用于高光谱波段选择.该方法不仅可以保证所选频带子集的稳定性,而且可以避免聚类过程中参数调优困难这一问题.Sun等人[88]基于DPeak算法中的2个假设,提出了一种新的波段选择方法(exemplar component analysis,ECA).ECA可以过滤掉许多噪声数据,这增加了其精度.此外,采用排名方法避免了子集的搜索过程,大大减少了计算量.Mai等人[89]提出了一种基于DPeak的相干光接收机技术,在改进后的DPeak中引入一个更适合于信号Stokes空间分布的新参数,从而达到了更好的分类效果且算法复杂度适中.
4.4 其他应用
预测“暗物质晕”的结构性质是现代宇宙学的基本目标之一.Klypin等人[90]采用MultiDark宇宙模拟来研究“暗物质晕”密度分布、浓度和速度各向异性的演化.该方法通过对密度峰值的研究证明了晕的演化经历了3个阶段且预测精度高.
智能手机已经成为每个人的不可或缺的一部分,越来越多的基于位置的内置应用程序可以丰富着我们的日常生活.Wang等人[91]提出了一种新的室内分区定位方案,采用DPeak算法将“指纹众包”聚类到不同的子区域,定位精度可以达到95%.
道路交通网络规模迅速扩大,复杂性日益增加.为了简化分析,保持交通顺畅,可以将大型城市公路网看作是一组小的子网络.Anwar等人[92]提出了一个基于DPeak算法的交通措施的大型城市道路网络空间划分框架,可将路况图转化为结构良好的压缩密度峰值图.在此基础上,将基于谱理论的图割应用于密度峰值图的划分,可得到不同的子网.
5 总结与展望
DPeak是目前最受关注的聚类算法之一,其算法思想简单且能够识别不同形状的簇,它的提出具有非常重要的理论和实际意义.该算法可以划归为层次聚类、密度聚类和代表点聚类,是一种混合型聚类算法.在对DPeak与经典的5种聚类算法进行详细比较后,我们发现DPeak算法和mean shift算法存在许多相似之处.两者最大的区别在于DPeak的漂移步长是跳跃的,而mean shift则是影子梯度上升法.
DPeak算法可以将不同维度和形状的数据进行聚类,但是该算法的复杂度高,在处理大规模数据时难以令人满意.此外,该算法只适用于每个簇的密度较为均匀的数据集.对于特殊形状的数据集可能会产生“假峰”或簇丢失等现象.目前,已经有大量学者对DPeak展开研究,也提出了许多改进的算法,主要优化方面有:提升速度、过程自适应、提高精度、适应高维数据.但仍然存在许多不足,还需要进一步深入研究,主要有5个方面.
1) 降低算法复杂度
在DPeak算法中,每个数据点都需要做2步计算:①在给定邻域内计算数据点密度,密度的计算是近邻搜索问题(RangeQuery),原始DPeak算法使用暴力法对每个点做RangeQuery的时间复杂度是O(n2).②对每个数据点寻找比其密度更高的最近邻,但原始DPeak算法仍然使用暴力法寻找每个点的密度更高的最近邻,其复杂度也是O(n2).
我们认为:①计算数据点密度与搜索近邻相关性很大,利用快速KNN算法如FLANN(fast library for approximate nearest neighbors)[94],cover tree[95],DCI(dynamic continuous indexing)[96],semi-convex hull tree[97], buffer kd tree[98], revised kd tree[99],可以有效地提升密度计算效率[37,49,100].②由于各个数据点之间的密度计算是相互独立的,因而利用GPU并行化DPeak算法是一个可行之道.可以通过高性能硬件,实现成倍提升计算速度,但还需在数据调度策略上做有针对性的设计.③此外,因为数据分布具有局部性的特点,即局部区域密度大,采用分布式方法对数据分区进行处理也是一种可行的方法.但是分布式环境复杂(如复杂不平衡、同步障碍、网络拥塞等)会影响聚类的精度[56],因此分布式方法中对参数的合理选取变得尤为重要.
目前,已经有学者在这方面做出了有意义的尝试与贡献.如前文所述,FastDPeak[37]通过快速KNN算法来加速密度和δ值计算,但k值不能取太大,对高维数据(如100维以上)效果不好,EDDPC[57]和LSH-DDP[56]则通过分布式方法来加速;Li等人[56]通过GPU来加速DPeak等.总的来说这些算法改进 DPeak手段比较单一,还有较大提升的空间,可以从上述3方面综合改进.
2) 过程自动化
随着数据量爆炸性增长,对数据处理的自动化要求成了必然趋势.DPeak的自动化实现存在2点挑战:自动确定簇数目和参数的自适应.首先,现有的大多数对于DPeak的自动化方面的改进算法只能做到给定簇的数目之后,进行自动聚类.然而簇的数目是通过人工来确定的,并非自动确定的,因此不能算是完全意义上的自动聚类.例如:Hou等人[61]提出了一种新的局部密度估计方法,该方法可以在给定簇的数量且没有人为干预的情况下完成聚类过程并改善聚类结果.其次,自动化的关键技术是要实现自适应的聚类.例如,Wang等人[35]提出了一种自适应密度峰值检测的聚类方法,该算法可以自动选择聚类中心.Hou等人[101]提出了将支配集和密度聚类相结合的方法,使得密度聚类无需提前输入参数.基于上述研究现状,将来可以从自动确定簇的数目和自适应的选择聚类中心、dc以及无参数输入方面来改进DPeak算法.
3) 提升精度和鲁棒性
在大数据时代,数据量激增、数据呈现丰富的多样性.不同的数据集适用于不同的算法,如何提升DPeak与数据集的匹配度已经成了当下的研究热门.DPeak算法由于其算法本身的固有性质导致其无法识别“假峰”现象,且对“无峰值”现象聚类效果差.此外,dc选取不当还会导致簇的丢失或簇过大,这些都是影响DPeak算法精度的因素.现有的密度峰值聚类算法更倾向于选择密集区域的聚类中心,从而容易忽略稀疏区域的聚类[102].如何将稀疏簇正确地检测出来,而不是将其合并到其他簇中,或者被当作噪声处理,这一问题还有待进一步的研究.改善上述这些问题也是DPeak未来研究的一个重要方向.
4) 高维数据处理
现有算法对于处理高维数据的表现仍不够理想.DPeak虽然可以把高维数据映射成2维,再在2维上完成聚类.但在映射过程仍然是基于距离计算完成的,而这恰恰是处理高维数据的弱点.因为高维数据往往是稀疏的,要在高维空间中选择一个合适的参数dc来计算密度是非常困难的.
现有算法对于处理高维数据的表现仍不够理想.面对“维度灾难”问题,对数据进行降维是一种有效可行的方法,如PCA在一定程度上揭示了高维数据的低维表达.此外,流形学习[68-69]是处理高维数据的有效手段.流形学习基于高维观测数据采样于一个潜在的低维流形上的假设,根据显式或隐式的映射关系学习出该假设中存在的流形,并将原始数据从观测空间投影到嵌入空间,在嵌入空间内保持原始数据的某些几何属性和内在结构.目前流形学习已经应用在了一些聚类算法的改进上[103],如Cai等人[104]针对流形特性提出了快速高性能的聚类新模式,构建了基于流形对高维数据进行低维表达与学习的理论体系.目前,DPeak对高维数据处理方面只出现了基于PCA的改进方法[50],基于流形学习的改进方式还未出现.
5) 与其他聚类的内在关系
对目前已有聚类算法的观测与分析,可以发现DPeak与mean shift比较相近.特别地,DPeak根据峰值进行漂移的方式,可以看成是一种变步长的梯度上升法.正如k-means可以归类为一种殊的mean shift一样[22],我们认为DPeak也可能是一种特定的means shift算法,或者至少是mean shift的一个非严格意义上的变种.DPeak是否可以在mean shift框架下进行解释还不能确定.因而,DPeak是否可以归类为mean shift算法族还有待进一步探索.
[1]Hilbert M, López P. The world’s technological capacity to store, communicate, and compute information[J]. Science, 2011, 332(6025): 60-65
[2]Rosenberger C, Chehdi K. Unsupervised clustering method with optimal estimation of the number of clusters: Application to image segmentation[C] //Proc of the 15th Int Conf on Pattern Recognition. Piscataway, NJ: IEEE, 2000: 656-659
[3]Frigui H, Krishnapuram R. A robust competitive clustering algorithm with applications in computer vision[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1999, 21(5): 450-465
[4]Achanta R, Shaji A, Smith K, et al. SLIC superpixels compared to state-of-the-art superpixel methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2274-2282
[5]Elhamifar E, Vidal R. Sparse subspace clustering[C] //Proc of 2009 IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2009: 2790-2797
[6]Li Weizhong, Godzik A. Cd-hit: A fast program for clustering and comparing large sets of protein or nucleotide sequences[J]. Bioinformatics, 2006, 22(13): 1658-1659
[7]King A D, Pržulj N, Jurisica I. Protein complex prediction via cost-based clustering[J]. Bioinformatics, 2004, 20(17): 3013-3020
[8]Huang Dawei, Sherman B T, Lempicki R A. Systematic and integrative analysis of large gene lists using DAVID bioinformatics resources[J]. Nature Protocols, 2009, 4(1): 44-57
[9]Rossant C, Kadir S N, Goodman D F M, et al. Spike sorting for large, dense electrode arrays[J]. Nature Neuroscience, 2016, 19(4): 634-641
[10]Moosmann F, Nowak E, Jurie F. Randomized clustering forests for image classification[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(9): 1632-1646
[11]Ducournau A, Bretto A, Rital S, et al. A reductive approach to hypergraph clustering: An application to image segmenta-tion[J]. Pattern Recognition, 2012, 45(7): 2788-2803
[12]Chaira T. A novel intuitionistic fuzzy C means clustering algorithm and its application to medical images[J]. Applied Soft Computing, 2011, 11(2): 1711-1717
[13]Zheng Miao, Bu Jiajun, Chen Chun, et al. Graph regularized sparse coding for image representation[J]. IEEE Trans-actions on Image Processing, 2011, 20(5): 1327-1336
[14]Chakrabarti S. Data mining for hypertext: A tutorial survey[J]. ACM SIGKDD Explorations Newsletter, 2000, 1(2): 1-11
[15]Chang MawShang, Chen LiHsuan, Hung Lingju, et al. Exact algorithms for problems related to the densest k-set problem[J]. Information Processing Letters, 2014, 114(9): 510-513
[16]Jones K M, Lacy M. Measuring the clustering around normal and dust-obscured quasars at 2 in the spitzer extragalactic representative volume survey (servs)[C/OL] //Proc of American Astronomical Society Meeting, 2014 [2019-03-01]. http://adsabs.harvard.edu/abs/2014AAS…22315019J
[17]Horng S J, Su Mingyang, Chen Y H, et al. A novel intrusion detection system based on hierarchical clustering and support vector machines[J]. Expert Systems with Applications, 2011, 38(1): 306-313
[18]MacQueen J. Some methods for classification and analysis of multivariate observations[C] //Proc of the 5th Berkeley Symp on Mathematical Statistics and Probability. Oakland, CA: University of California Press, 1967: 281-297
[19]Jain A K. Data clustering: 50 years beyond K-means[J]. Pattern Recognition Letters, 2010, 31(8): 651-666
[20]Färber I, Günnemann S, Kriegel H P, et al. On using class-labels in evaluation of clusterings[C/OL] //Proc of MultiClust: The 1st Int Workshop on Discovering, Summarizing and Using Multiple Clusterings Held in Conjunction with KDD. New York: ACM, 2010 [2019-03-01]. http://pdfs.semanti cscholar.org/5e38/fe4f14223716b8c70539e9943ee71f5350d2.pdf
[21]Rodriguez A, Laio A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496
[22]Cheng Yizong. Mean shift, mode seeking, and clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, 17(8): 790-799
[23]Wang Guoyin, Yang Jie, Xu Ji. Granular computing: From granularity optimization to multi-granularity joint problem solving[J]. Granular Computing, 2017, 2(3): 105-120
[24]Han Jiawei, Pei Jian, Kamber M. Data Mining: Concepts and Techniques[M]. Amsterdam: Elsevier, 1991
[25]Xu Rui, Wunsch D. Survey of clustering algorithms[J]. IEEE Transactions on Neural Networks, 2005, 16(3): 645-678
[26]Bai Liang, Cheng Xueqi, Liang Jiye, et al. Fast density clustering strategies based on the k-means algorithm[J]. Pattern Recognition, 2017, 71: 375-386
[27]Xu Dongkuan, Tian Yingjie. A comprehensive survey of clustering algorithms[J]. Annals of Data Science, 2015, 2(2): 165-193
[28]Xie Juanying, Gao Hongchao, Xie Weixin, et al. Robust clustering by detecting density peaks and assigning points based on fuzzy weighted K-nearest neighbors[J]. Information Sciences, 2016, 354: 19-40
[29]Ding Jiajun, He Xiongxiong, Yuan Junqing, et al. Automatic clustering based on density peak detection using generalized extreme value distribution[J]. Soft Computing, 2018, 22(9): 2777-2796
[30]Jain A K, Murty M N, Flynn P J. Data clustering: A review[J]. ACM Computing Surveys, 1999, 31(3): 264-323
[31]Comaniciu D, Meer P. Mean shift: A robust approach toward feature space analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(5): 603-619
[32]Rose K, Gurewitz E, Fox G C. Statistical mechanics and phase transitions in clustering[J/OL]. Physical Review Letters, 1990 [2019-03-01]. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.65.945
[33]Murtagh F, Contreras P. Algorithms for hierarchical clustering: An overview[J]. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 2012, 2(1): 86-97
[34]Xu Ji, Wang Guoyin, Deng Weihui. DenPEHC: Density peak based efficient hierarchical clustering[J]. Information Sciences, 2016, 373: 200-218
[35]Wang Xiaofeng, Xu Yifan. Fast clustering using adaptive density peak detection[J]. Statistical Methods in Medical Research, 2017, 26(6): 2800-2811
[36]Xu Ji, Wang Guoyin. Leading tree in DPCLUS and its impact on building hierarchies[J]. Computer Science, arXiv preprint, arXiv:1506.03879, 2015
[37]Chen Yewang, Hu Xiaoliang, Fan Wentao, et al. Fast density peak clustering for large scale data based on kNN[J/OL]. Knowledge-Based Systems, 2019 [2019-03-01]. https://doi.org/10.1016/j.kn
[38]Zhang Yuanpeng, Deng Zhaohong, Zhong Fuli, et al. Fast adaptive clustering algorithm for representative review sub-strategy[J]. Journal of Computer Research and Development, 2018, 55(1): 163-178 (in Chinese)(张远鹏, 邓赵红, 钟富礼, 等. 基于代表点评分策略的快速自适应聚类算法[J]. 计算机研究与发展, 2018, 55(1): 163-178)
[39]Frey B J, Dueck D. Clustering by passing messages between data points[J]. Science, 2007, 315(5814): 972-976
[40]Banfield J D, Raftery A E. Model-based Gaussian and non-Gaussian clustering[J]. Biometrics, 1993, 49(3): 803-821
[41]Ester M, Kriegel H P, Sander J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C] //Proc of KDD-96. Menlo Park, CA: AAAI, 1996: 226-231
[42]Campello R J G B, Moulavi D, Sander J. Density-based clustering based on hierarchical density estimates[G] //LNCS 7819: Pacific-Asia Conf on Knowledge Discovery and Data Mining. Berlin: Springer, 2013: 160-172
[43]Ng A Y, Jordan M I, Weiss Y. On spectral clustering: Analysis and an algorithm[C] //Proc of Advances in Neural Information Processing Systems. San Francisco: Morgan Kaufmann, 2002: 849-856
[44]Sun Leilei, Guo Chonghui. Incremental affinity propagation clustering based on message passing[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(11): 2731-2744
[45]Fukunaga K, Hostetler L. The estimation of the gradient of a density function, with applications in pattern recognition[J]. IEEE Transactions on Information Theory, 1975, 21(1): 32-40
[46]Fashing M, Tomasi C. Mean shift is a bound optimization[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(3): 471-474
[47]Chen Yewang, Tang Shengyu, Pei Songwen, et al. DHeat: A density heat-based algorithm for clustering with effective radius[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 48(4): 649-660
[48]Chen Yewang, Tang Shengyu, Zhou Lida, et al. Decentralized clustering by finding loose and distributed density cores[J]. Information Sciences, 2018, 433: 510-526
[49]Zhang Wenkai, Li Jing. Extended fast search clustering algorithm: Widely density clusters, no density peaks[J]. Computer Science, arXiv preprint, arXiv:1505.05610, 2015
[50]Du Mingjing, Ding Shifei, Jia Hongjie. Study on density peaks clustering based on k-nearest neighbors and principal component analysis[J]. Knowledge-Based Systems, 2016, 99: 135-145
[51]Wu Bo, Wilamowski B M. A fast density and grid based clustering method for data with arbitrary shapes and noise[J]. IEEE Transactions on Industrial Informatics, 2017, 13(4): 1620-1628
[52]Xu Xiao, Ding Shifei, Du Mingjing, et al. DPCG: An efficient density peaks clustering algorithm based on grid[J]. International Journal of Machine Learning and Cybernetics, 2016, 9(5): 743-754
[53]Wang Deqiang, Zhang Bin, Wang Kelun. A vertex-clustering algorithm based on the cluster-clique[G] //LNCS 8631: Proc of Int Conf on Algorithms and Architectures for Parallel Processing. Berlin: Springer, 2014: 376-385
[54]Xu Xiao, Ding Shifei, Sun Tongfeng. A fast density peaks clustering algorithm based on pre-screening[C] //Proc of 2018 IEEE Int Conf on Big Data and Smart Computing. Piscataway, NJ: IEEE, 2018: 513-516
[55]Chen Yewang, Tang Shengyu, Bouguila N, et al. A fast clustering algorithm based on pruning unnecessary distance computations in DBSCAN for high-dimensional data[J]. Pattern Recognition, 2018, 83: 375-38
[56]Li Mi, Huang Jie, Wang Jingpeng. Paralleled fast search and find of density peaks clustering algorithm on GPUs with CUDA[C] //Proc of the IEEE/ACIS Int Conf on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing. Piscataway, NJ: IEEE, 2016: 313-318
[57]Gong Shufeng, Zhang Yanfeng. EDDPC: An efficient distributed density center clustering algorithm[J]. Journal of Computer Research and Development, 2016, 53(6): 1400-1409 (in Chinese)(巩树凤, 张岩峰. EDDPC: 一种高效的分布式密度中心聚类算法[J]. 计算机研究与发展, 2016, 53(6): 1400-1409)
[58]Dean J, Ghemawat S. MapReduce: Simplified data processing on large clusters[J]. Communications of the ACM, 2008, 51(1): 107-113
[59]Zhang Yanfeng, Chen Shimin, Yu Ge. Efficient distributed density peaks for clustering large data sets in MapReduce[J]. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(12): 3218-3230
[60]Shindler M, Wong A, Meyerson A W. Fast and accurate k-means for large datasets[C] //Proc of Advances in Neural Information Processing Systems. New York: ACM, 2011: 2375-2383
[61]Hou Jian, Pelillo M. A new density kernel in density peak based clustering[C] //Proc of the 23rd Int Conf on Pattern Recognition. Piscataway, NJ: IEEE, 2016: 468-473
[62]Liu Yaohui, Ma Zhengming, Yu Fang. Adaptive density peak clustering based on K-nearest neighbors with aggregating strategy[J]. Knowledge-Based Systems, 2017, 133: 208-220
[63]Mehmood R, Zhang Guangzhi, Bie Rongfang, et al. Clustering by fast search and find of density peaks via heat diffusion[J]. Neurocomputing, 2016, 208: 210-217
[64]Pang Ziling, Wang Guoyin, Yang Jie. A multi-granularity decomposition mechanism of complex tasks based on density peaks[J]. Big Data Mining and Analytics, 2018, 1(3): 245-256
[65]Karypis G, Han E-H S, Kumar V. Chameleon: Hierarchical clustering using dynamic modeling[J]. Computer, 1999, 32(8): 68-75
[66]Xie Jiang, Xiong Zhongyang, Zhang Yufang, et al. Density core-based clustering algorithm with dynamic scanning radius[J]. Knowledge-Based Systems, 2018, 142: 58-70
[67]Pang Yanwei, Wang Shuang, Yuan Yuan. Learning regularized LDA by clustering[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(12): 2191-2201
[68]Nasibov E N, Ulutagay G. A new unsupervised approach for fuzzy clustering[J]. Fuzzy Sets and Systems, 2007, 158(19): 2118-2133
[69]Nasibov E N. A robust algorithm for solution of the fuzzy clustering problem on the basis of the fuzzy joint points method[J]. Cybernetics and Systems Analysis, 2008, 44(1): 7-17
[70]Nasibov E N, Ulutagay G. Robustness of density-based clustering methods with various neighborhood relations[J]. Fuzzy Sets and Systems, 2009, 160(24): 3601-3615
[71]Ulutagay G, Nasibov E N. Influence of transitive closure complexity in FJP-based clustering algorithms[J]. Turkish Journal of Fuzzy Systems, 2010, 1(1): 3-20
[72]Tenenbaum J B, De Silva V, Langford J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290(5500): 2319-2323
[73]Wang Yong. Classification and clustering method based on manifold learning and its application[D]. Changsha: National University of Defense Technology, 2011 (in Chinese)(王勇. 基于流形学习的分类与聚类方法及其应用研究[D]. 长沙: 国防科学技术大学, 2011)
[74]Chen Yewang, Lai Dehe, Qi Han, et al. A new method to estimate ages of facial image for large database[J]. Multimedia Tools and Applications, 2016, 75(5): 2877-2895
[75]Chen Guijun, Zhang Xueying, JohnWang Zizhong, et al. Robust support vector data description for outlier detection with noise or uncertain data[J]. Knowledge-Based Systems, 2015, 90: 129-137
[76]Chen Chen, Zhu Weixing, Ma Changhua, et al. Image motion feature extraction for recognition of aggressive behaviors among group-housed pigs[J]. Computers and Electronics in Agriculture, 2017, 142: 380-387
[77]Wang Yi, Chen Qixin, Kang Chongqing, et al. Clustering of electricity consumption behavior dynamics toward big data applications[J]. IEEE Transactions on Smart Grid, 2016, 7(5): 2437-2447
[78]Qin Yan, Zhao Chunhui, Gao Furong. An iterative two-step sequential phase partition (ITSPP) method for batch process modeling and online monitoring[J]. AIChE Journal, 2016, 62(7): 2358-2373
[79]Zhang Qingchen, Zhu Chunsheng, Yang L T, et al. An incremental CFS algorithm for clustering large data in industrial Internet of things[J]. IEEE Transactions on Industrial Informatics, 2017, 13(3): 1193-1201
[80]Wang Tao, Zhang Wenbo, Ye Chunyang, et al. FD4C: Automatic fault diagnosis framework for Web applications in cloud computing[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2016, 46(1): 61-75
[81]Wang Peipei, Liu Peiyu, Wang Ru, et al. A recommendation algorithm based on density peak clustering and key users[C] //Proc of the 13th Int Conf on Natural Computation, Fuzzy Systems and Knowledge Discovery. Piscataway, NJ: IEEE, 2017: 468-473
[82]Heimerl F, John M, Han Q, et al. DocuCompass: Effective exploration of document landscapes[C] //Proc of 2016 IEEE Conf on Visual Analytics Science and Technology. Piscataway, NJ: IEEE, 2016: 11-20
[83]Wang Baoyan, Zhang Jian, Ding Fanggui, et al. Multi-document news summarization via paragraph embedding and density peak clustering[C] //Proc of 2017 Int Conf on Asian Language Processing. Piscataway, NJ: IEEE, 2017: 260-263
[84]Kuhrova P, Best R B, Bottaro S, et al. Computer folding of RNA tetraloops: Identification of key force field deficiencies[J]. Journal of Chemical Theory and Computation, 2016, 12(9): 4534-4548
[85]Henninger J, Santoso B, Hans S, et al. Clonal fate mapping quantifies the number of haematopoietic stem cells that arise during development[J]. Nature Cell Biology, 2017, 19: 17-27
[86]Chen Jianguo, Li Kenli, Rong Huihui, et al. A disease diagnosis and treatment recommendation system based on big data mining and cloud computing[J]. Information Sciences, 2018, 435: 124-149
[87]Jia Sen, Tang Guihua, Zhu Jiasong, et al. A novel ranking-based clustering approach for hyperspectral band selection[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(1): 88-102
[88]Sun Kang, Geng Xiurui, Ji Luyan, et al. Exemplar component analysis: A fast band selection method for hyperspectral imagery[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(5): 998-1002
[89]Mai Xiaofeng, Liu Jie, Wu Xiong, et al. Stokes space modulation format classification based on non-iterative clustering algorithm for coherent optical receivers[J]. Optics Express, 2017, 25(3): 2038-2050
[90]Klypin A, Yepes G, Gottlöber S, et al. MultiDark simulations: The story of dark matter halo concentrations and density profiles[J]. Monthly Notices of the Royal Astronomical Society, 2016, 457(4): 4340-4359
[91]Wang Bang, Chen Qiuyun, Yang L T, et al. Indoor smartphone localization via fingerprint crowdsourcing: Challenges and approaches[J]. IEEE Wireless Communi-cations, 2016, 23(3): 82-89
[92]Anwar T, Liu Chengfei, Vu H L, et al. Partitioning road networks using density peak graphs: Efficiency vs accuracy[J]. Information Systems, 2017, 64: 22-40
[93]Varani G. Exceptionally stable nucleic acid hairpins[J]. Annual Review of Biophysics and Biomolecular Structure, 1995, 24(1): 379-404
[94]Muja M, Lowe D G. Scalable nearest neighbor algorithms for high dimensional data[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2014, 36(11): 2227-2240
[95]Beygelzimer A, Kakade S, Langford J. Cover trees for nearest neighbor[C] //Proc of the 23rd Int Conf on Machine Learning. New York: ACM, 2006: 97-104
[96]Li Ke, Malik J. Fast k-nearest neighbour search via dynamic continuous indexing[C] //Proc of Int Conf on Machine Learning. New York: ACM, 2016: 671-679
[97]Chen Yewang, Zhou Lida, Bouguila N, et al. Semi-convex hull tree: Fast nearest neighbor queries for large scale data on GPUs[C] //Proc of 2018 IEEE Int Conf on Data Mining. Piscataway, NJ: IEEE, 2018: 911-916
[98]Gieseke F, Heinermann J, Oancea C, et al. Buffer KD trees: Processing massive nearest neighbor queries on GPUs[C] //Proc of Int Conf on Machine Learning. New York: ACM, 2014: 172-180
[99]Chen Yewang, Zhou Lida, Tang Yi, et al. Fast neighbor search by using revised K-D tree[J/OL]. Information Sciences, 2018 [2019-03-01]. 10.1016/j.ins.2018.09.012
[100]Shi Bing, Han Lixin, Yan Hong. Adaptive clustering algorithm based on kNN and density[J]. Pattern Recognition Letters, 2018, 104: 37-44
[101]Hou Jian, Liu Weixue, Xu E. Density based clustering via dominant sets[C] //Proc of IAPR Workshop on Artificial Neural Networks in Pattern Recognition. Berlin: Springer, 2016: 80-91
[102]Guo Zhishuai, Huang Tianyi, Cai Zhiling, et al. A new local density for density peak clustering[C] //Proc of Pacific-Asia Conf on Knowledge Discovery and Data Mining. Berlin: Springer, 2018: 426-438
[103]Zhang Lijun, Chen Chun, Chen Wei, et al. Convex experimental design using manifold structure for image retrieval[C] //Proc of the 17th ACM Int Conf on Multimedia. New York: ACM, 2009: 45-54
[104]Cai Deng, He Xiaofei. Manifold adaptive experimental design for text categorization[J]. IEEE Transactions on Knowledge and Data Engineering, 2012, 24(4): 707-719





