粒计算以信息粒化简化复杂问题获得满意解而著称.目前，典型的粒计算方法包括模糊信息粒化[1]、熵空间法[2]、三支决策[3]等.近年来，粒计算被视作大数据分析与处理的有效工具[4-6]，应用于各个前沿领域，更多讨论见文献[7-12].
众所周知，形式概念分析[13]与粗糙集[14]是2种重要的粒计算方法.前者通过样本粒化、特征粒化、概念知识粒化等方式体现粒计算思想[15-19]，后者则是利用信息粒化、空间粒化、多粒度结构等实现粒计算功能的知识发现[20-27].实际上，如果撇开上述2种理论在体系结构上的差异，仅从实际需求出发，那么形式概念分析与粗糙集研究的诸多问题均存在共性，比如粒化准则、近似空间、属性冗余、规则挖掘等.另外，基于相同数据结构比较这2种理论的优劣也是一种增强互补性分析的重要方式.鉴于此，一些学者在讨论有关问题时频繁表现出研究内容上的互通性.也就是，从事形式概念分析研究的学者很自然会想到这一问题的粗糙集解决方法；反之，利用粗糙集讨论某一问题时，人们也会习惯性地联想到形式概念分析处理该问题的具体实效[28-29].
不仅如此，人们还从多粒度标记(或多尺度)角度基于形式概念分析和粗糙集建立了多种广义粒计算模型[22-23,27].需要指出的是，无论是形式概念分析还是粗糙集，多粒度标记数据的相关工作主要集中于粒度标记信息粒化、最优粒度选择和规则挖掘等研究方向[24-26,30-32].实际上，多粒度标记或多尺度思想的实际来源较为广泛.比如，类别等级意义下的数据表示[22]、尺度放缩环境下的数据采集[31]，以及属性特征值的合并与分解[33]等.目前，基于粗糙集的多粒度标记理论的研究已相对成熟，但针对形式概念分析的多粒度标记理论才刚建立，仍有一些富有挑战性的问题有待探讨，更多论述见文献[34].
为此，本文关注形式概念分析的多粒度标记理论框架的完善与扩展.具体地，在文献[34]建立的多粒度标记形式背景的基础上，进一步提出介粒度标记形式背景的概念，以满足多层次知识发现的需求.该问题可大致描述为：现有的多粒度标记形式背景均假设所有属性的粒度标记个数两两相同，它简单地将所有属性的粒度标记值通过多个单粒度标记形式背景的并置予以表示.这种表示方法延续了粗糙集理论中多粒度标记信息系统的惯用做法，因此一些共性问题依然会出现，即容易导致后续相关研究以单粒度标记数据为最小单位讨论相关问题，不利于多粒度标记数据进行多层次知识发现.然而，根据粗糙集理论中多粒度标记信息系统的研究经验，可以对单粒度标记数据的属性粒度标记值进行重组以获得重构数据结构，进而得到可行的解决方法.本文将采用完备格的扩充方式实现多层次知识发现.具体地，重构单粒度标记形式背景的属性粒度标记值，通过数据重构研究介粒度标记形式背景，包括介粒度标记形式背景的定义、语义解释、泛化、特化，以及介粒度标记决策形式背景的知识发现等.此外，实验分析说明了介粒度标记方法的一些优势，这为将来深入探讨多粒度形式概念分析的多层次知识发现、表示与处理奠定了基础.
1 相关工作
本文统一用U表示论域，即非空有限对象集.信息系统的非空有限属性集用C表示；形式背景的非空有限属性集用A表示.
定义1[14]. 一个经典的信息系统可表示成序对(U,C)，其中U={u1,u2,…,un}，C={a1,a2,…,am}.
定义2[22]. 若一个信息系统(U,C)的属性集
(1)
在p个粒度空间下取值，且每个属性粒度值相对于粒度粗细关系形成全序，则称(U,C)为多粒度标记信息系统.
需要指出的是，不宜将在p个粒度空间下取值简单理解为p个不同值，因为从大量的实例中发现，有些不同值可能来源于对某一取值的语义进行各种转化得到，即仅仅只是描述形式上的不同，实际上指的是同一个值.
定义3[13]. 一个形式背景可表示为三元组(U,A,I)，其中I是布尔关系，即任意u∈U，a∈A，要么uIa，要么
uIa，其中表示逻辑非运算.
为了使规则推理非平凡，本文仅讨论正则形式背景[35].
定义4[13]. 设(U,A,I)为形式背景，对于X⊆U， B⊆A，记
X*={a∈A|∀u∈X,uIa},
(2)
B*={u∈U|∀a∈B,uIa},
(3)
称映射序对(*,*)的不动点(X,B)(即X*=B，B*=X)为形式概念，该不动点的2个分量分别为外延和内涵.
依据上述定义，易得下列性质.
性质1[13]. 对于形式背景(U,A,I)的2个概念(Xs,Bs)和(Xt,Bt)(s,t∈T，T是指标集)，定义
(Xs,Bs)≤(Xt,Bt)⟺Xs⊆Xt,
(4)
(Xs,Bs)∨(Xt,Bt)=((Xs∪Xt)**,Bs∩Bt),
(5)
(Xs,Bs)∧(Xt,Bt)=(Xs∩Xt,(Bs∪Bt)**),
(6)
则(U,A,I)的所有概念构成一个完备格，称为概念格.
定义5[35]. 称属性不相交的2个形式背景(U,A,I)和(U,D,J)的并置为决策形式背景，记为(U,A,I,D,J).
注意，文献[36]也给出了与决策形式背景(U,A,I,D,J)相类似的数据结构，但命名为训练形式背景.尽管命名不同，但是通常均称A为条件属性集， D为决策属性集.
为了避免混淆，不妨用(·)*A与(·)*D表示算子(·)*作用于不同的形式背景(U,A,I)和(U,D,J).
定义6[37]. 对于(U,A,I,D,J)的条件属性子集E⊆A和决策属性子集F⊆D.若E*A⊆F*D，则称E→F为决策蕴涵，其中E为前件，F为结论.
2 多粒度标记形式背景及其语义解释
尽管文献[34]已给出多粒度标记形式背景的概念，但目前尚未就该概念进行语义解释，所以理解起来较为晦涩.为此，本节尝试从非交并集、非交融合属性、非交融合形式背景等多个角度对多粒度标记形式背景的语义作出解释，并结合一个实例辅助理解，便于第3节进一步引入介粒度标记形式背景并阐明其研究意义做好铺垫.
首先，介绍形式背景的反向尺度化方法，其核心思想是将(U,A,I)的若干布尔属性视作a∈C的取值，从而产生(U,C)[34].下面介绍形式背景的m可反向尺度化问题.
定义7[34]. 如果一个形式背景(U,A,I)经过反向尺度化得到具有m个属性的(U,C)，那么称其是m可反向尺度化的.
注意，是否能够反向尺度化与形式背景(U,A,I)的属性分块密切相关，即到底把(U,A,I)的哪几个属性视作(U,C)中某一属性的取值，直接关系到(U,A,I)能否成功反向尺度化到(U,C).
下面通过非交并集讨论属性和数据集的非交融合问题.虽然与文献[34]借助于布尔向量的叙述方式类似，但是非交并集的语义更加简洁直观.
定义8. 令(U,A,I)的2个属性b,c∈A对应的所有对象组成的集合分别为Ib与Ic.如果Ib和Ic的交集为空，那么记
为Ib和Ic的非交并集.
为了方便，记Tc为与参数c相关的一个指标集.
定义9. 给定形式背景(U,Ai,Ii)和(U,Aj,Ij)， c∈Aj，若存在br∈Ai(r∈Tc)满足
(7)
那么称c可由{br|r∈Tc}非交融合得到.
非交融合的语义可解释为将形式背景不相交的几列合并产生新的一列.显然，通过该合并方式可以由一个形式背景产生另一个形式背景.
定义10. 给定形式背景(U,Ai,Ii)和(U,Aj,Ij)，若Aj的每一个属性c均可由Ai的若干属性{br|r∈Tc}通过非交融合得到，且
(8)
那么称(U,Aj,Ij)可由(U,Ai,Ii)非交融合得到，简记为(U,Ai,Ii)
(U,Aj,Ij).
不难发现，由(U,Ai,Ii)出发，可以产生一系列非交融合形式背景(U,Aj,Ij)(j∈T，T是指标集).换言之，非交融合形式背景(U,Aj,Ij)的具体表现形式完全取决于非交融合方法所采取的特定融合模式.另外，(U,Ai,Ii)(U,Aj,Ij)也从侧面表明(U,Aj,Ij)的粒度标记值比(U,Ai,Ii)的更粗.也就是，原来分开细化各自表述的内容，被合并后使用更粗的标记值进行统一描述.注意，在此过程中原来可以区分的内容，现在可能变得无法区分.
定义11[34]. 设形式背景(U,Ak,Ik)(k=1,2,…,p)均m可反向尺度化，不妨令每个属性集Ak都可拆分为两两不相交的非空子集序列Ak1,Ak2,…,Akm，且每个属性块Akj所拥有的对象集构成U的划分.若对于1≤s<t≤p，有
(U,Asj,Isj)(U,Atj,Itj),j=1,2,…,m,
(9)
则称
为多粒度标记形式背景.
容易验证，多粒度标记形式背景的属性块Ak1,Ak2,…,Akm(k=1,2,…,p)一共有p×m个，每个属性块均描述了一个完整的属性特征(相当于经典信息系统的某一属性)，它们通过固定变量k的方式成批镶嵌于单粒度标记形式背景(U,Ak,Ik)中(即每个单粒度标记形式背景均可固定m个属性块)，但是这种表示方式很可能导致后续相关研究以单粒度标记形式背景(U,Ak,Ik)(k=1,2,…,p)为最小单位.实际上，这极大限制了数据的知识发现进一步延伸到更深层次，第3节将会给出详细解释.
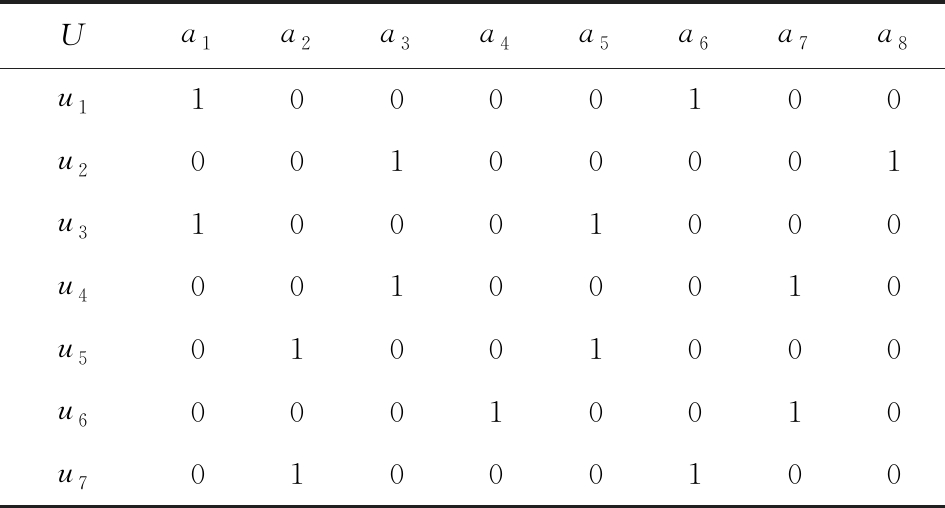
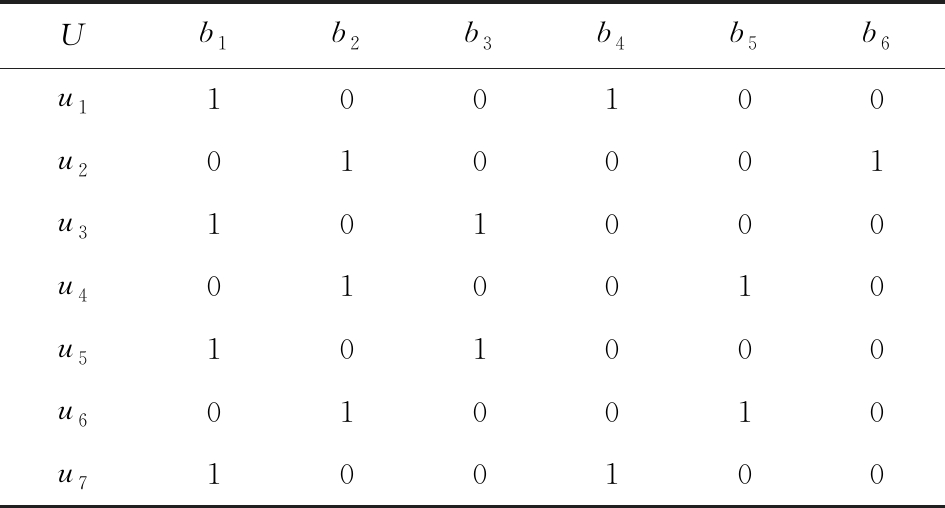
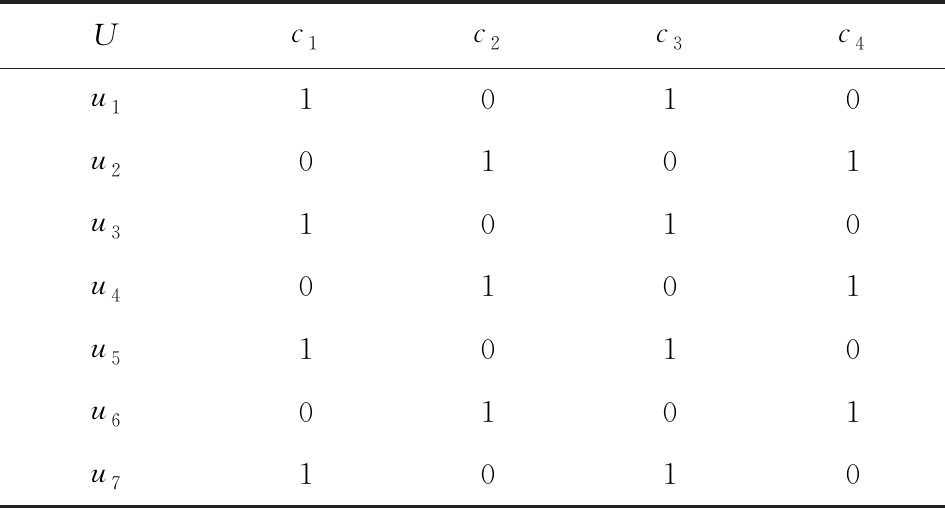
例1. 表1是一个形式背景(U,A1,I1)，其中对象集U={u1,u2,u3,u4,u5,u6,u7}代表7个时装模特，属性集A1={a1,a2,a3,a4,a5,a6,a7,a8}代表时装模特走秀时可能的着装搭配，具体语义是a1为黑点状裙子，a2为黑条纹裙子，a3为蓝点状裙子，a4为蓝条纹裙子，a5为白点状上衣，a6为白条纹上衣，a7为红点状上衣，a8为红条纹上衣.表2是另一个形式背景(U,A2,I2)，它的对象集与表1完全相同，但属性集不同，A2={b1,b2,b3,b4,b5,b6}，具体语义是b1为黑裙子，b2为蓝裙子，b3为白点状上衣，b4为白条纹上衣，b5为红点状上衣，b6为红条纹上衣.表3也是一个形式背景(U,A3,I3)，它的对象集也与表1完全相同，但属性集不同，A3={c1,c2,c3,c4}，具体语义是c1为黑裙子，c2为蓝裙子，c3为白上衣，c4为红上衣.
Table 1 The Formal Context (U,A1,I1)
表1 形式背景(U,A1,I1)
Ua1a2a3a4a5a6a7a8u110000100u200100001u310001000u400100010u501001000u600010010u701000100
Table 2 The Formal Context (U,A2,I2)
表2 形式背景(U,A2,I2)
Ub1b2b3b4b5b6u1100100u2010001u3101000u4010010u5101000u6010010u7100100
Table 3 The Formal Context (U,A3,I3)
表3 形式背景(U,A3,I3)
Uc1c2c3c4u11010u20101u31010u40101u51010u60101u71010
下面根据定义11判断表1、表2和表3的数据能否联合产生多粒度标记背景.依据表1、表2可得：
I2b3=I1a5={u3,u5}, I2b4=I1a6={u1,u7}, I2b5=I1a7={u4,u6}, I2b6=I1a8={u2}.
令A11={a1,a2,a3,a4}，A12={a5,a6,a7,a8}，A21={b1,b2}，A22={b3,b4,b5,b6}，那么(U,A21,I21)可由(U,A11,I11)通过非交融合得到，且(U,A22,I22)可由(U,A12,I12)通过非交融合得到.也就是，(U,A11,I11)(U,A21,I21)和(U,A12,I12)(U,A22,I22)均成立.
类似地，依据表2、表3可得：
I3c1=I2b1={u1,u3,u5,u7}, I3c2=I2b2={u2,u4,u6}, 
令A31={c1,c2}，A32={c3,c4}，那么(U,A31,I31)可由(U,A21,I21)通过非交融合得到，且(U,A32,I32)可由(U,A22,I22)通过非交融合得到.也就是，(U,A21,I21)(U,A31,I31)和(U,A22,I22)(U,A32,I32)均成立.
综上可知，表1、表2和表3的数据能够联合产生多粒度标记背景.此外，不难发现，属性块A11，A12，A21，A22，A31，A32均描述了一个完整的属性特征.比如，A31描述了裤子的特征，A32描述了上衣的特征.
3 介粒度标记形式背景
第2节给出了多粒度标记形式背景的语义解释，它可以由p个单粒度标记形式背景(U,A1,I1),(U,A2,I2),…,(U,Ap,Ip)组成.文献[34]建议研究这些单粒度标记形式背景的知识发现、表示与处理问题，以及由(U,As,Is)到(U,At,It)(1≤s<t≤p)的知识转换关系.这种研究方法与多粒度标记数据的采集过程基本一致，即现实中确实在多个粒度空间下成批采集数据(假设每个空间下均可产生一类单粒度标记数据).例如，地理信息系统的属性标记值在尺度放缩环境下采集的数据[31].但是，也有很多数据分析任务，其目标与数据采集方式存在差异.换言之，有些数据分析任务不仅仅局限于多粒度标记形式背景的单粒度标记数据，甚至需要的数据就不在这些单粒度标记数据之列.为了讨论这个问题，下面提出介粒度标记形式背景的概念.
定义12. 对于形式背景(U,Ak,Ik)(k=1,2,…,p)构成的多粒度标记形式背景S，设每个属性集Ak均可拆分为两两不相交的非空子集序列Ak1,Ak2,…,Akm，且每个属性块Akj所拥有的对象集构成U的划分，称(U,Ameso,Imeso)为介粒度标记形式背景，其中属性集Ameso由元素Ap11,Ap22,…,Apmm构成，下标满足pj∈{1,2,…,p}(j=1,2,…,m).
为了叙述方便，记S的所有介粒度标记形式背景组成的集合为δ(S).
根据定义12可知，介粒度标记形式背景的属性块允许来自各个单粒度标记形式背景.某种程度上，它也可以看作是属性粒度标记值重组产生的新数据结构.
性质2. 设(U,Ak,Ik)是S的某一单粒度标记形式背景，则(U,Ak,Ik)∈δ(S).
证明. 注意到(U,Ameso,Imeso)∈δ(S)的属性集Ameso由元素Ap11,Ap22,…,Apmm构成，其中下标满足pj∈{1,2,…,p}(j=1,2,…,m).特殊地，令
p1=p2=…=pm=k(k∈{1,2,…,p}),
则(U,Ameso,Imeso)退化为形式背景(U,Ak,Ik).也就是，(U,Ak,Ik)∈δ(S).
证毕.
为了叙述方便，本文用|·|表示集合的基数.
性质3. |δ(S)|=pm.
证明. 注意到多粒度标记形式背景S的属性块Ak1,Ak2,…,Akm(k=1,2,…,p)一共有p×m个.对于形成介粒度标记形式背景的属性粒度标记值重组问题，它实际上相当于m个填充位置，每个位置均有p种可能的填充方式的情形，故一共有pm种填充结果，所以介粒度标记形式背景的个数为pm.
证毕.
注意，与多粒度标记信息系统中组合粒度标记方法的语境略有不同[25]，多粒度标记形式背景的属性粒度个数是相同的(通过单粒度标记形式背景予以表示)，原因是现实中数据采集批次一般认为是相同的(当然，相邻2个单粒度标记形式背景的部分属性粒度标记值允许一样).实际上，即便属性粒度个数不同，也可以通过复制粒度标记值的方式将其视作属性粒度个数相同的情形.此外，需要指出的是，本文将属性粒度标记值进行重组得到的数据结构命名为介粒度标记形式背景，其原因是介粒度标记形式背景的属性集Ameso由元素Ap11,Ap22,…,Apmm构成，纵向来看它的粒度标记层恰好介于min{p1,p2,…,pm}和max{p1,p2,…,pm}之间，这对理解介粒度标记形式背景的粒度标记层所处的大致范围是有益的.
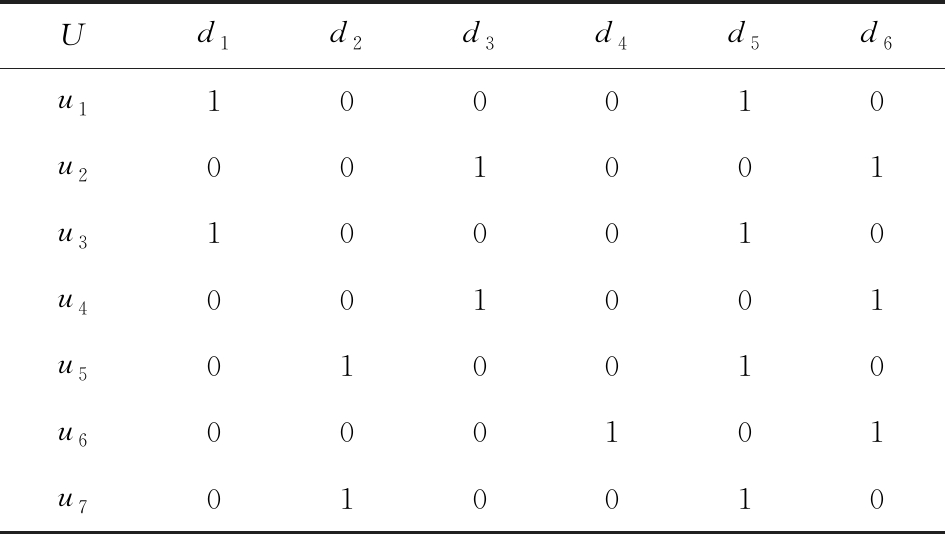
例2. 以表1、表2、表3构成的多粒度标记形式背景S为例.根据定义12可知，表4是一个介粒度标记形式背景(U,Ameso,Imeso)，它的属性粒度标记值来源于表1的第1个属性块和表3的第2个属性块.显然，它不属于原始数据的任一单粒度标记形式背景.不难发现，(U,Ameso,Imeso)的粒度标记层介于第1个粒度标记和第3个粒度标记之间.
不难看出，介粒度标记思想的引入使得多粒度标记形式背景的数据分析不再局限于各个单粒度标记形式背景，还包括原始的单粒度标记形式背景联合诱导出的数据结构.根据性质3，新诱导数据结构的规模远远大于原始的单粒度标记形式背景，这极大拓宽了多粒度标记形式背景进行知识发现的层度和广度.
Table 4 The Meso-granularity Labeled Formal Context(U,Ameso,Imeso)
表4 介粒度标记形式背景(U,Ameso,Imeso)
Ud1d2d3d4d5d6u1100010u2001001u3100010u4001001u5010010u6000101u7010010
4 介粒度标记形式背景的数据结构
由性质3可知，S的介粒度标记形式背景的个数众多，所以捋清它们之间的数据结构关系对于继续讨论S的多层次知识发现是必要的.为此，下面给出介粒度标记形式背景的泛化与特化，以揭示其数据结构形成一个完备格.为了书写方便，本节中的S均指
(10)
定义13. 对于多粒度标记形式背景S，设
其中
由元素Aλ11,Aλ22,…,Aλmm组成，
由元素Aμ11,Aμ22,…,Aμmm组成.如果对任意j∈{1,2,…,m}，有λj≤μj成立，则称
是
的泛化形式背景，或是的特化形式背景，记为
不难发现，介粒度标记形式背景的泛化与特化，实际上刻画的是属性粒度标记派生出的粗细关系，这种粒度粗细关系有可能不是数据采集或表示所自然形成的，而是通过属性标记值重构产生新的数据结构的方式，即人为诱导出的一种数据结构的粗细关系.在属性粒度标记值重构的过程中，它相当于打破了原有或故有的粒度标记层，从而有利于多层次知识发现.
例3. 以表1、表2、表3构成的多粒度标记形式背景S为例.对于表4的介粒度标记形式背景(U,Ameso,Imeso)∈δ(S)，表1的形式背景(U,A1,I1)是(U,Ameso,Imeso)的一个特化，而表3的形式背景(U,A3,I3)则是(U,Ameso,Imeso)的一个泛化.
性质4. δ(S)在关系≤下形成一个完备格.
证明. 对于假设由元素Aλ11,Aλ22,…,Aλmm组成，由元素Aμ11,Aμ22,…,Aμmm组成.为了叙述方便，记
其中
由元素Aα11,Aα22,…,Aαmm组成，
由元素Aβ11,Aβ22,…,Aβmm组成，且
αj=max{λj,μj},j=1,2,…,m,
βj=min{λj,μj},j=1,2,…,m.
那么
即
是介粒度标记形式背景
和
的上界.下面进一步表明为上确界.为此，假设
是和的任一上界，那么对任意j∈{1,2,…,m}，有
λj≤γj,μj≤γj,
其中γj表示
的第j个属性块Aγjj的第1个下标.所以max{λj,μj}≤γj，即αj≤γj，这就证得了是介粒度标记形式背景和的上确界.同理，容易证得
是介粒度标记形式背景和的下确界.因此，δ(S)形成一个格.注意，δ(S)的元素个数是有限的，所以δ(S)是完备格.
证毕.
实际上，完备格结构数据对于进一步考虑最优介粒度标记形式背景的选择(满足用户特定需求的前提下)是非常实用的.比如，可以利用格结构关系，通过渐进优化的方式逐步搜索最优介粒度标记形式背景.另一方面，由于搜索空间的规模较大，如何实现最优介粒度标记形式背景的有效搜索也是一个重要的研究课题.
最后，需要指出的是，从一个介粒度标记形式背景泛化到另一个介粒度标记形式背景，信息通常会出现损失；反之，从一个介粒度标记形式背景特化到另一个介粒度标记形式背景，信息会增加，当然该过程必须借助于额外信息才能完成.这是由于泛化过程是不可逆的，而特化过程是可逆的.因此，一个有趣的问题是，在介粒度标记形式背景的泛化过程中，如何刻画或度量信息的损失程度非常关键，这是传统粗糙集领域中尚未考虑的问题.
5 带决策信息的介粒度知识发现方法
定义14[34]. 称
与(U,D,J)的并置为多粒度标记决策形式背景，记为
(11)
文献[34]针对Q讨论了知识发现问题.然而，现有的知识发现方法仅限于原始单粒度标记数据本身或相互之间的推理关系，不涉及属性粒度标记值重构(即介粒度标记数据)的情形.换言之，现有方法仅仅考虑(U,Ak,Ik,D,J)(k=1,2,…,p)的知识发现.如前所述，单粒度标记数据或相互之间的知识发现的研究范围过于狭窄，不能较好地满足现实中复杂问题求解的需要，因为复杂问题求解通常会涉及属性粒度标记值重构的数据.
例4. 表5是一个形式背景(U,D,J)，其中U={u1,u2,u3,u4,u5,u6,u7}代表7个时装模特，D={e,f}代表时装模特走秀时的着装效果，具体语义是e代表“裙子和上衣搭配效果不满意”，f代表“裙子和上衣搭配效果满意”.
Table 5 The Formal Context (U,D,J)
表5 形式背景(U,D,J)
Uefu101u210u301u410u501u610u701
联合表1、表2、表3和表5的数据可得：
容易验证，Q是多粒度标记决策形式背景.
然而，根据现有的知识发现方法，只能从表1和表5、表2和表5，以及表3和表5组成的3个单粒度标记决策形式背景中挖掘知识，并不能从介粒度标记形式背景(如表4)和表5组成的决策形式背景中挖掘知识.
为了讨论该问题，下面引入介粒度标记决策形式背景的概念.
定义15. 对于多粒度标记决策形式背景Q，若
(12)
则称(U,Ameso,Imeso,D,J)是Q的介粒度标记决策形式背景，记为(U,Ameso,Imeso,D,J)∈δ(Q).
如第3节所述，如果(U,Ameso,Imeso)不属于任一原始的单粒度标记形式背景，那么(U,Ameso,Imeso,D,J)的决策蕴涵E→F(E⊆Ameso，F⊆D)通过现有的知识发现方法是无法直接获得的.但是，仍然可以通过原始的单粒度标记形式背景间接验证E→F是否成立，具体见算法1.
算法1. 单粒度标记方法判断决策蕴涵.
输入：多粒度标记决策形式背景Q，Qmeso=(U,Ameso,Imeso,D,J)∈δ(Q)，E⊆Ameso，F⊆D.
输出：E→F是否为Qmeso的决策蕴涵.
① 对于任意k∈{1,2,…,p}，j∈{1,2,…,m}，计算Ekj=E∩Akj.
② 对于任意k∈{1,2,…,p}，j∈{1,2,…,m}，如果Ekj≠∅(实际上最多存在一个k满足该条件)，那么在Ekj所属的原始形式背景(U,Ak,Ik)中计算
，其中(·)*k表示(·)*在(U,Ak,Ik)下的运算.
③ 对反复执行步骤②得到的取交集，记为ε=∩.
④ 若ε⊆F*D，则E→F是Qmeso的决策蕴涵；否则，E→F不是Qmeso的决策蕴涵.
容易验证，上述单粒度标记方法判断决策蕴涵的时间复杂度为
需要指出的是，根据定义6，也可以采用直接的方法在Qmeso=(U,Ameso,Imeso,D,J)中验证E→F是否为Qmeso的决策蕴涵，其时间复杂度为
因此，介粒度标记方法给决策蕴涵挖掘带来了计算上的便利，至少降低了算法的计算复杂性.第6节将通过数值实验进一步评估节省计算量的实际情况.
至此，针对介粒度标记数据，已给出直接和间接2种方法判断决策蕴涵.实际上，这里的“直接”与“间接”都是基于决策蕴涵E→F是否在(U,Ameso,Imeso,D,J)∈δ(Q)中进行验证做出的区分.因此，下文中统称它们为直接判断方法，以区别于即将讨论的推理演化间接方法.所谓推理演化是指随着介粒度标记形式背景的泛化与特化，借助于知识发现的演变规律间接判断决策蕴涵.
为了避免混淆，用(·)*λ与(·)*μ分别表示(·)*作用于和
定义16. 对于若
与
之间存在一个非交融合双射ρλμ，即任意eλ∈Eλ，有
则称Eμ是Eλ的属性提升.
需要强调的是，与定义10不同，这里的Eμ是通过双射ρλμ作用于Eλ得到，并不是完全合并更细的非交列产生.换言之，原像只是合并产生像的众多非交列之一(非交列唯一的情况除外).
为了讨论方便，记(U,Ameso,Imeso,D,J)的所有决策蕴涵为Δ(U,Ameso,Imeso,D,J).
性质5. 对于多粒度标记决策形式背景Q，设若条件属性集是的属性提升，决策属性集F⊆D，且
则
证明. 因为所以依据定义6可知(Eμ)*μ⊆F*D.进一步考虑到Eμ是Eλ的属性提升，那么由定义16可得:
因此，
证毕.
例5. 以例4的
为例，介粒度标记形式背景和分别来源于表3和表4的数据.
注意到({c2,c4})*μ⊆e*D和({c1,c3})*μ⊆f*D均成立.因此，
其语义解释为蓝裙子搭配红上衣效果不满意；类似地，
其语义解释为黑裙子搭配白上衣效果满意.
根据表3和表4可知，{c2,c4}=ρλμ({d3,d6})和{c2,c4}=ρλμ({d4,d6})均成立.因此，由性质5有
其语义解释为蓝点状裙子搭配红上衣效果不满意；类似地，
其语义解释为蓝条纹裙子搭配红上衣效果不满意.此外，不难发现{c1,c3}=ρλμ({d1,d5})和{c1,c3}=ρλμ({d2,d5})也均成立，所以
其语义解释为黑点状裙子搭配白上衣效果满意；同理，
其语义解释为黑条纹裙子搭配白上衣效果满意.
性质6. 对于多粒度标记决策形式背景Q，设
可由
通过非交融合得到.若对于任意r∈T，有
(13)
则
证明. 因为
所以
也有
立，故
那么
({aμ}∪E)*μ=({aμ})*μ∩E*μ= 
由定义6可知，
证毕.
性质5和性质6得到的间接推理关系是非常有意义的，它们提供了由
或
的决策蕴涵诱导出
或
的决策蕴涵的方法.换言之，并不是任何时候都需要重新计算一个介粒度标记数据的决策蕴涵，在条件允许、代价合理的情况下，不妨选择利用已知决策蕴涵诱导得到.因为该方法有效避免了重复计算，所以通常情况下比直接验证更有效.第6节的数值实验将会进一步表明这一点.
最后，需要指出的是，决策蕴涵只是形式概念分析进行知识发现的一种方式而已.除此之外，还有决策规则[38]、推理依赖[39]、关联规则[40]等.因此，基于这些规则深入研究随着介粒度标记数据的泛化与特化其知识推理的内在机理也是有意义的.
6 实验与结果
本节通过数值实验评估算法1、介粒度标记方法、性质5和性质6的性能表现，以表明介粒度标记方法的有效性与优势所在.
6.1 实验环境
实验使用的具体配置如下：CPU为Intel Core i3-2120 3.30 GHz,4.00 GB内存；JDK为jdk1.8.0_20,Eclipse使用32位的eclipse-4.2.实验选取的7个数据集均来源于UCI数据库(1)http://archive.ics.uci.edu/ml/的真实数据，即zoo,BC(breast cancer),monks2,wisconsin,SHD(semeion handwritten digit),mushroom,letter数据集，详见表6所示:
Table 6 The Data Sets for Experiments
表6 实验数据集
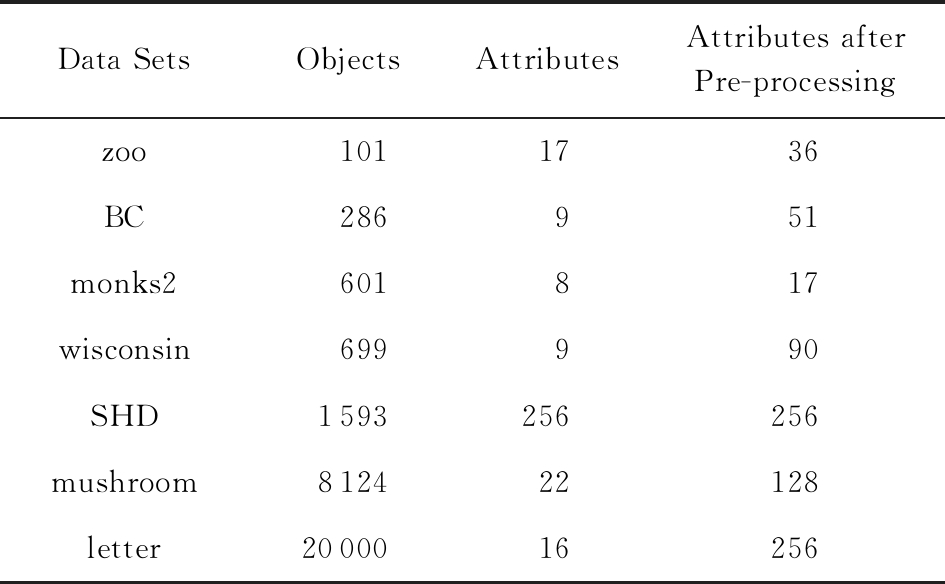
Data SetsObjectsAttributesAttributes afterPre-processingzoo1011736BC286951monks2601817wisconsin699990SHD1593256256mushroom812422128letter2000016256
在此基础上，将表6中的原始数据集通过尺度变换(scaling)[13]转化为标准形式背景格式的数据集，预处理后的属性情况如表6最后一列所示.类似于粗糙集理论中的惯用做法[30]，这里也选择合并相邻布尔属性的方式产生多粒度标记形式背景.为了叙述方便，本文将用于实验的7个数据集均处理成4个粒度标记层.具体如下：在尺度变换后得到的原始形式背景(记为第1粒度标记层)的基础上，依次通过属性距d1=2，d2=5，d3=10分别产生第2粒度标记层、第3粒度标记层和第4粒度标记层.比如，属性距d1=2表示通过合并相邻2个布尔属性的方式产生下一层粒度标记，其他属性距的语义可类似进行解释.注意，实验涉及的7个数据集均将样本类别标签信息视作决策属性，从而得到实验所需的标准数据集.在不引起混淆时，预处理后产生的标准数据集依旧沿用原始数据集的命名.
6.2 实验结果
首先，根据定义6、定义15和算法1，对比了单粒度标记方法(single-granularity labeled method, SLM)与介粒度标记方法(meso-granularity labeled method, MLM)的运行时间，以及它们在不同数据集上的表现.表7给出了在其他参数一定的情况下，决策蕴涵的前件属性集E与数据集类型对2种粒度标记方法产生的实际影响.
Table 7 Comparison of Meso-granularity andSingle-granularity Methods
表7 介粒度标记方法与单粒度标记方法的对比 ms
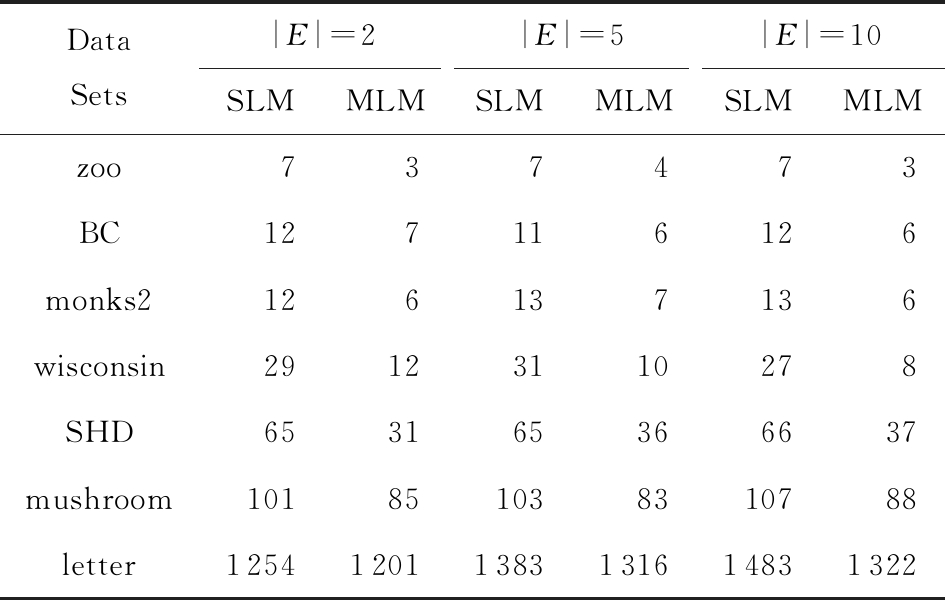
DataSets|E|=2|E|=5|E|=10SLMMLMSLMMLMSLMMLMzoo737473BC127116126monks2126137136wisconsin29123110278SHD653165366637mushroom101851038310788letter125412011383131614831322
从表7不难看出: 1)对于决策蕴涵挖掘,在不同的前件属性集E下，介粒度标记方法都比单粒度标记方法更加有效；2)2种粒度标记方法的运行时间都随着数据集规模的增大而变大；3)2种粒度标记方法的运行时间都对前件属性集E的变化表现不太敏感，这很可能是由于实验中E的元素个数相对于属性全集远远偏小的缘故.
其次，由性质5和性质6给出的2种决策蕴涵推理方法(decision implication inference method, DIIM)，可以间接进行跨粒度标记数据之间的决策蕴涵推理.为了区分性质5和性质6给出的决策蕴涵推理方法，将它们分别记为DIIM5和DIIM6.表8和表9给出了前件属性集E的元素个数为2(尽管E的元素个数与表7中的完全相同，但由于具体赋值不同，所以最终的实验结果基本不相同)，决策蕴涵推理方法的间接验证与单粒度标记方法和介粒度
Table 8 Comparison of the First Decision Implication
Inference Method and Recalculation
表8 第1种决策蕴涵推理方法与重新计算的对比
ms
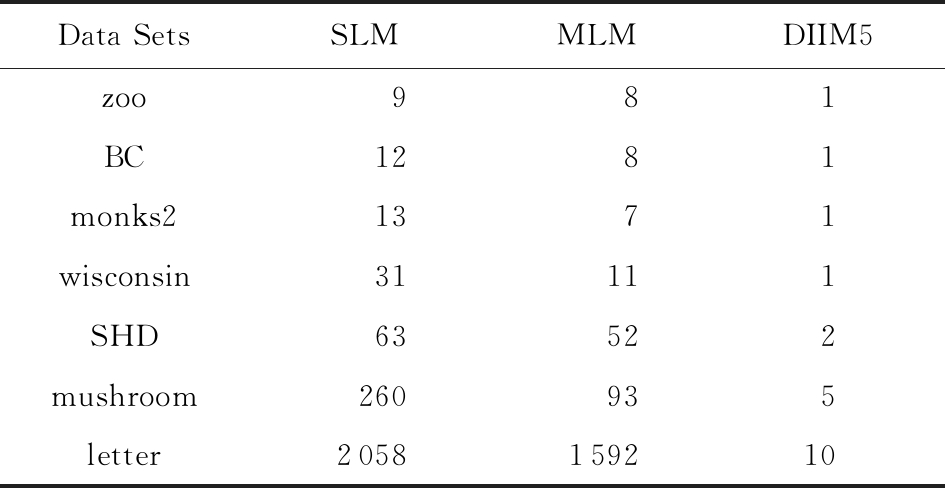
Data SetsSLMMLMDIIM5zoo981BC1281monks21371wisconsin31111SHD63522mushroom260935letter2058159210
Table 9 Comparison of the Second Decision Implication
Inference Method and Recalculation
表9 第2种决策蕴涵推理方法与重新计算的对比
ms
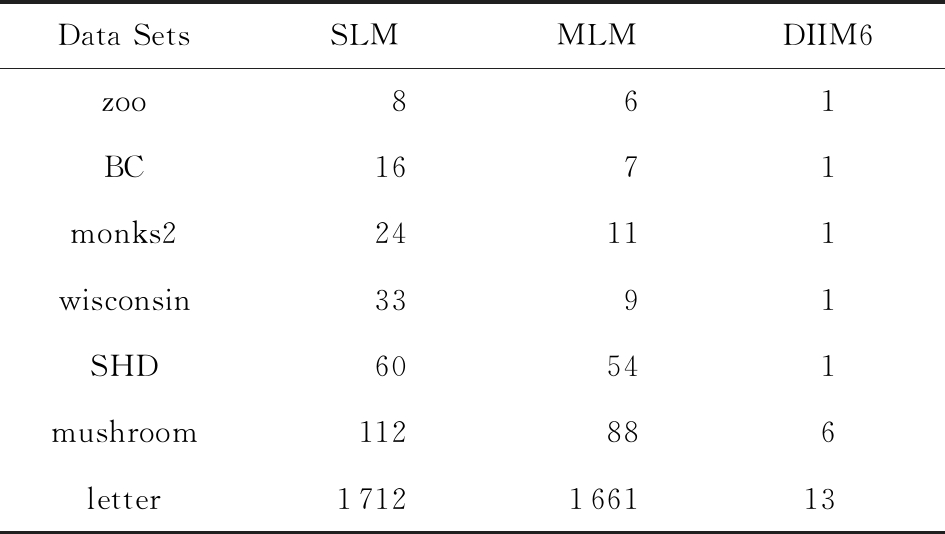
Data SetsSLMMLMDIIM6zoo861BC1671monks224111wisconsin3391SHD60541mushroom112886letter1712166113
标记方法重新计算的对比结果.从表8和表9不难看出，决策蕴涵推理方法的间接验证要比2种重新计算的方法更加高效.
最后，分析前件属性集E和数据集类型对决策蕴涵推理方法(这里仅以DIIM5为例)的影响.从图1与图2可以看出，随着数据集规模的增大进行决策蕴涵推理所需时间变长.除此之外，还显示出前件属性集E与决策蕴涵推理时间呈现正相关,其原因是前件属性集E越大，则其进行映射所需搜寻的范围也会越广.
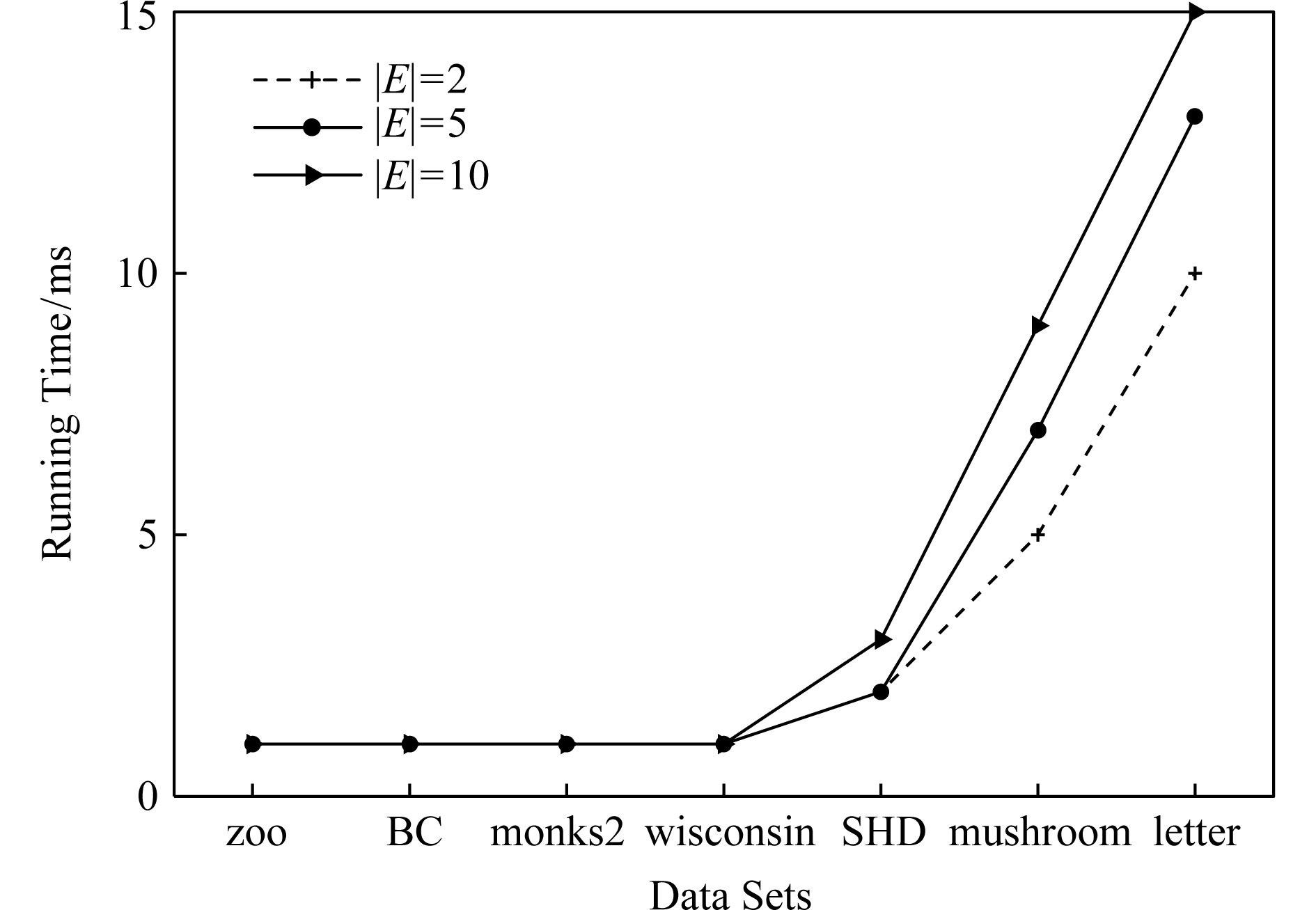
Fig. 1 The impact of data sets and attribute set E on DIIM5
图1 数据集与属性集E对DIIM5的影响
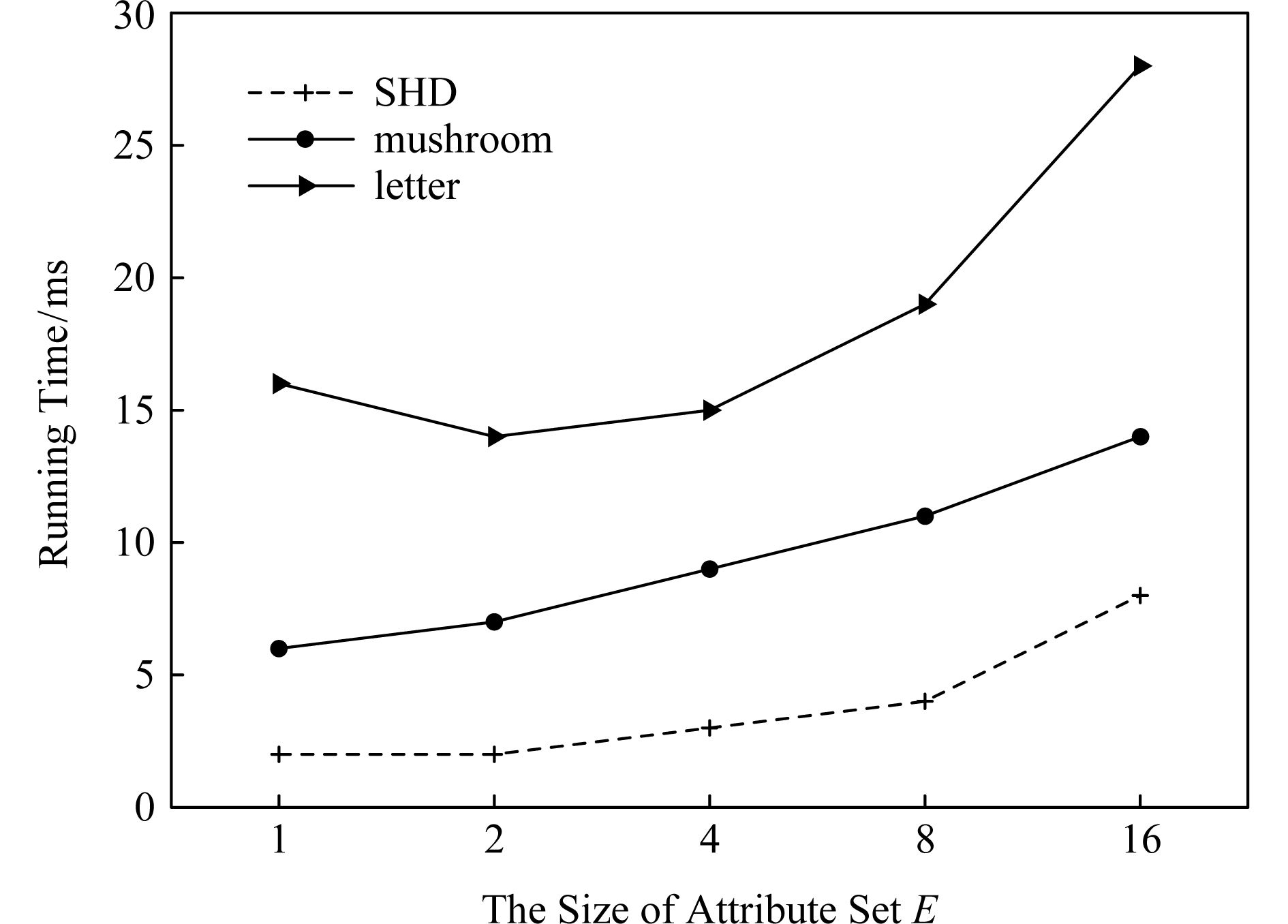
Fig. 2 The impact of attribute set E and data sets on DIIM5
图2 属性集E与数据集对DIIM5的影响
需要指出的是，前件属性集E和数据集类型对DIIM6的影响与DIIM5呈现的趋势基本一致，在此不再赘述.
注意，本文的实验都是针对判断一条决策蕴涵评估其计算代价，总的运行时间均较小，只是通过时间的相对大小表明介粒度标记方法的有效性.现实中，一个数据集的决策蕴涵的总数是相当庞大的，因为决策蕴涵的前件属性集E来源于属性全集的任一子集，所以它的个数与属性全集的幂集基本相当，均属于指数级别.换言之，尽管本文的实验都是针对判断一条决策蕴涵评估其计算代价，本文的方法与现有方法的运行结果貌似差异不大，但是一旦把决策蕴涵的前件属性集E的规模考虑进去，那么新旧方法的差异将会是显著的.
7 总 结
本文从实际应用出发，提出介粒度标记形式背景的概念，以表明重组属性粒度标记值呈现更多数据结构思想的重要性.尽管已存在类似的研究倡议[25]，但本文仍有一些值得归纳总结的新意：1)多粒度标记数据的粒度标记个数两两相同是有现实背景意义的，因为很多数据的采集都是成批进行的(假设每批数据均构成一类单粒度标记)；2)即使特殊时多粒度标记数据形成的粒度标记个数出现不同的情形，也可以通过扩充的方式使得粒度标记个数两两相同(允许部分属性的粒度标记值重复出现即可)；3)实际上，粒度标记个数相同与否不是该问题的关键所在，数据分析与处理的实际需求才是促使人们采用介粒度标记方法的重要因素；4)介粒度标记形式背景进行泛化时会导致信息出现损失，因为该过程是不可逆的.
本文在经典多粒度形式概念分析的基础上，提出介粒度标记方法以拓展现有的研究思路，使得数据分析与处理不再局限于数据采集或表示形成的自然粗细粒度标记关系.换言之，自然形成的粗细粒度标记数据结构，是数据存储表示的一种原始状态，如果要达到多层次知识发现的目的，那么充分利用各个单粒度标记数据相互交叉融合诱导出的介粒度标记数据是非常必要的.
除了与经典粗细粒度标记形式背景有类似的研究问题之外，介粒度标记方法有待继续探讨的课题如下：1)当用户提出具体的粒度标记层约束时，如何在满足用户需求的情况下，选择最优介粒度标记形式背景；2)由于选择最优介粒度标记形式背景的搜索空间庞大，所以探讨节省搜索空间的近似智能算法也是有必要的；3)介粒度标记数据在泛化过程中存在信息损失，如何度量其大小是一个重要的课题；4)介粒度标记方法带来诸多优势的同时，如何避免不足之处以充分发挥其积极作用？比如，精度和效率与计算代价之间的综合权衡关系.
致谢 感谢昆明理工大学闫梦宇博士对本文初稿提出的意见和建议！
[1]Zadeh L A. Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic[J]. Fuzzy Sets and Systems, 1997, 90(2): 111-127
[2]Zhang Yanping, Zhang Ling, Wu Tao. The representation of different granular worlds: A quotient space[J]. Chinese Journal of Computers, 2004, 27(3): 328-333 (in Chinese)(张燕平, 张铃, 吴涛. 不同粒度世界的描述法——商空间法[J]. 计算机学报, 2004, 27(3): 328-233)
[3]Yao Yiyu. Three-way decision and granular computing[J]. International Journal of Approximate Reasoning, 2018, 103: 107-123
[4]Liang Jiye, Qian Yuhua, Li Deyu, et al. Theory and method of granular computing for big data mining[J]. SCIENTIA SINICA Informationis, 2015, 45(11): 1355-1369 (in Chinese)(梁吉业, 钱宇华, 李德玉, 等. 大数据挖掘的粒计算理论与方法[J]. 中国科学: 信息科学, 2015, 45(11): 1355-1369)
[5]Xu Ji, Wang Guoyin, Yu Hong. Review of big data processing based on granular computing[J]. Chinese Journal of Computers, 2015, 38(8): 1497-1517 (in Chinese)(徐计, 王国胤, 于洪. 基于粒计算的大数据处理[J]. 计算机学报, 2015, 38(8): 1497-1517)
[6]Chen Philip C L, Zhang Chunyang. Data-intensive applications, challenges, techniques and technologies: A survey on big data[J]. Information Sciences, 2014, 275: 314-347
[7]Yao Yiyu. A partition model of granular computing[G] //LNCS 3100: Transactions on Rough Sets I. Berlin: Springer, 2004: 232-253
[8]Pedrycz W. From numeric to granular description and interpretation of information granules[J]. Fundamenta Informaticae, 2013, 127(1/2/3/4): 399-412
[9]Miao Duoqian, Zhang Qinghua, Qian Yuhua, et al. From human intelligence to machine implementation model: Theories and applications based on granular computing[J]. CAAI Transactions on Intelligent Systems, 2016, 11(6): 743-757 (in Chinese)(苗夺谦, 张清华, 钱宇华, 等. 从人类智能到机器实现模型——粒计算理论与方法[J]. 智能系统学报, 2016, 11(6): 743-757)
[10]Miao Duoqian, Xu Feifei, Yao Yiyu, et al. Set-theoretic formulation of granular computing[J]. Chinese Journal of Computers, 2012, 35(2): 2351-2363 (in Chinese)(苗夺谦, 徐菲菲, 姚一豫, 等. 粒计算的集合论描述[J]. 计算机学报, 2012, 35(2): 2351-2363)
[11]Wang Guoyin, Zhang Qinghua, Ma Xi’ao, et al. Granular computing models for knowledge uncertainty[J]. Journal of Software, 2011, 22(4): 676-694 (in Chinese)(王国胤, 张清华, 马希骜, 等. 知识不确定性问题的粒计算模型[J]. 软件学报, 2011, 22(4): 676-694)
[12]Xu Weihua, Sun Wenxin, Zhang Xiaoyan, et al. Multiple granulation rough set approach to ordered information systems[J]. International Journal of General Systems, 2012, 41(5): 475-501
[13]Wille R. Restructuring lattice theory: An approach based on hierarchies of concepts[G] //Ordered Sets. Dordrecht: Reidel, 1982: 445-470
[14]Pawlak Z. Rough sets[J]. International Journal of Computer and Information Sciences, 1982, 11(5): 341-356
[15]Guo Lankun, Huang Fangping, Li Qingguo, et al. Power contexts and their concept lattices[J]. Discrete Mathematics, 2011, 311(18/19): 2049-2063
[16]Wei Ling, Zhang Xiaohua, Qi Jianjun. Granular reduction of property-oriented concept lattices[G] //LNCS 6208: Proc of the 18th Int Conf on Conceptual Structures: From Information to Intelligence. Berlin: Springer, 2010: 154-164
[17]Kang Xiangping, Miao Duoqian. A study on information granularity in formal concept analysis based on concept-bases[J]. Knowledge-Based Systems, 2016, 105: 147-159
[18]Ma Yuan, Zhang Guozhi, Zhang Renqiu. On granulation based concept lattice of formal context[J]. Computer Applications and Software, 2010, 27(7): 11-13, 39 (in Chinese)(马垣, 张果枝, 张仁秋. 基于粒化的形式背景的概念格研究[J]. 计算机应用与软件, 2010, 27(7): 11-13, 39)
[19]Ma Jianmin, Zhang Wenxiu. Axiomatic characterizations of dual concept lattices[J]. International Journal of Approximate Reasoning, 2013, 54(5): 690-697
[20]Qian Yuhua, Liang Jiye, Dang Chuangyin. Incomplete multigranulation rough set[J]. IEEE Transactions on Systems, Man, and Cybernetics: Part A, 2010, 40(2): 420-431
[21]Qian Yuhua, Liang Jiye, Pedrycz W, et al. Positive approximation: An accelerator for attribute reduction in rough set theory[J]. Artificial Intelligence, 2010, 174(9/10): 597-618
[22]Wu Weizhi, Leung Yee. Theory and applications of granular labelled partitions in multi-scale decision tables[J]. Information Sciences, 2011, 181(18): 3878-3897
[23]Wu Weizhi, Leung Yee. Optimal scale selection for multi-scale decision tables[J]. International Journal of Approximate Reasoning, 2013, 54(8): 1107-1129
[24]She Yanhong, Li Jinhai, Yang Hailong. A local approach to rule induction in multi-scale decision tables[J]. Knowledge-Based Systems, 2015, 89: 398-410
[25]Li Feng, Hu Baoqing. A new approach of optimal scale selection to multi-scale decision tables[J]. Information Sciences, 2017, 381: 193-208
[26]Luo Chuan, Li Tianrui, Huang Yanyong, et al. Updating three-way decisions in incomplete multi-scale information systems[J]. Information Sciences, 2019, 476: 274-289
[27]Wu Weizhi, Chen Ying, Xu Youhong, et al. Optimal granularity selections in consistent incomplete multi-granular labeled decision systems[J]. Pattern Recognition and Artificial Intelligence, 2016, 29(2): 108-115 (in Chinese)(吴伟志, 陈颖, 徐优红, 等. 协调的不完备多粒度标记决策系统的最优粒度选择[J]. 模式识别与人工智能, 2016, 29(2): 108-115)
[28]Li Jinhai, Wu Weizhi. Granular computing approach for formal concept analysis and its research outlooks[J]. Journal of Shandong University: Natural Science, 2017, 52(7): 1-12 (in Chinese)(李金海, 吴伟志. 形式概念分析的粒计算方法及其研究展望[J]. 山东大学学报：理学版, 2017, 52(7): 1-12)
[29]Zhi Huilai, Li Jinhai. Granule description based on necessary attribute analysis[J]. Chinese Journal of Computers, 2018, 41(12): 2702-2719 (in Chinese)(智慧来, 李金海. 基于必然属性分析的粒描述[J]. 计算机学报, 2018, 41(12): 2702-2719)
[30]Hao Chen, Fan Min, Li Jinhai, et al. Optimal scale selection in multi-scale contexts based on granular scale rules[J]. Pattern Recognition and Artificial Intelligence, 2016, 29(3): 272-280 (in Chinese)(郝晨, 范敏, 李金海, 等. 多标记背景下基于粒标记规则的最优标记选择[J]. 模式识别与人工智能, 2016, 29(3): 272-280)
[31]Xie Junping, Yang Minhua, Li Jinhai, et al. Rule acquisition and optimal scale selection in multi-scale formal decision contexts and their applications to smart city[J]. Future Generation Computer Systems, 2018, 83: 564-581
[32]Zeng Wanglin, She Yanhong. Object-oriented multigranula-tion formal concept analysis[J]. Computer Science, 2018, 45(10): 51-53 (in Chinese)(曾望林, 折延宏. 面向对象的多粒度形式概念分析[J]. 计算机科学, 2018, 45(10): 51-53)
[33]Belohlavek R, De Baets B, Konecny J. Granularity of attributes in formal concept analysis[J]. Information Sciences, 2014, 260: 149-170
[34]Li Jinhai, Wu Weizhi, Deng Shuo. Multi-scale theory in formal concept analysis[J]. Journal of Shandong University: Natural Science, 2019, 54(2): 30-40 (in Chinese)(李金海, 吴伟志, 邓硕. 形式概念分析的多粒度标记理论[J]. 山东大学学报: 理学版, 2019, 54(2): 30-40)
[35]Zhang Wenxiu, Qiu Guofang. Uncertain Decision Making Based on Rough Sets[M]. Beijing: Tsinghua University Press, 2005(张文修, 仇国芳. 基于粗糙集的不确定决策[M]. 北京: 清华大学出版社, 2005)
[36]Kuznetsov S O. Complexity of learning in concept lattices from positive and negative examples[J]. Discrete Applied Mathematics, 2004, 142(1/2/3): 111-125
[37]Qu Kaishe, Zhai Yanhui, Liang Jiye, et al. Study of decision implications based on formal concept analysis[J]. International Journal of General Systems, 2007, 36(2): 147-156
[38]Li Jinhai, Mei Changlin, Lü Yuejin. A heuristic knowledge-reduction method for decision formal contexts[J]. Computers and Mathematics with Applications, 2011, 61(4): 1096-1106
[39]Xue Jinrong, An Qiusheng, Zheng Jun. Intent reduction of concept lattice and database inference dependence[J]. Journal of Computer Research and Development, 2014, 51(1): 96-103 (in Chinese)(薛金蓉, 安秋生, 郑军. 概念格的内涵缩减与数据库推理依赖[J]. 计算机研究与发展, 2014, 51(1): 96-103)
[40]Liang Jiye, Wang Junhong. An algorithm for extracting rule-generating sets based on concept lattice[J]. Journal of Computer Research and Development, 2004, 41(8): 1339-1344 (in Chinese)(梁吉业, 王俊红. 基于概念格的规则产生集挖掘算法[J]. 计算机研究与发展, 2004, 41(8): 1339-1344)
