近年来,由于大规模机器学习和数据分析的计算范式已经转向由单独的小型计算节点和不可靠的计算节点(即低端、商用硬件)组成的大型分布式系统,如像Apache Spark[1]这样的现代分布式系统和像MapReduce[2]这样的计算框架,使大规模机器学习集群受到了广泛的关注.然而,机器学习集群的性能普遍受到一种“系统噪音”——异常系统行为和瓶颈[3]的显著影响.考虑到这些分布式系统中节点的个体不可预测性,机器学习集群面临着如何在不确定性下保证快速高质量完成算法执行的挑战.
在最近的研究中,许多研究者使用编码技术来解决这个问题.几十年来,编码在提供抵抗系统噪声方面的作用已经在其他工程环境中得到了肯定,它是我们日常基础设施(智能手机、笔记本电脑、WiFi和蜂窝系统等)的一部分.本论文综述的是如何将编码技术应用于分布式机器学习算法以抵抗“噪声”对分布式算法的影响.如图1所示,分布式机器学习算法的工作流程可以分解为3个功能阶段:存储、通信和计算阶段.
分布式机器学习算法的工作流程如下:大规模系统接收输入数据,将它们存储在工作节点中,然后在分布式网络中通信数据;每个分布式节点在接收到所需数据后本地执行计算任务;系统将各个工作节点的计算结果进行聚合.工作过程中的主要瓶颈(通信、掉队节点、系统故障等)都被抽象成一种在这些阶段之间的延迟,用Δ表示.为了开发和部署复杂的解决方案以解决机器学习、科学、工程和商业中的大规模计算问题,了解和优化跨计算、通信、存储和结果准确性的多个维度的权衡是很重要的.近年来,分布式存储编码领域的再生码(regenerating codes)和本地可修复编码(local repairable codes)的提出,使得编码技术广泛用于分布式系统成为可能,并已开始改变现代数据中心分布式系统的存储层[4-12],对工业产生了重大影响[13-16].
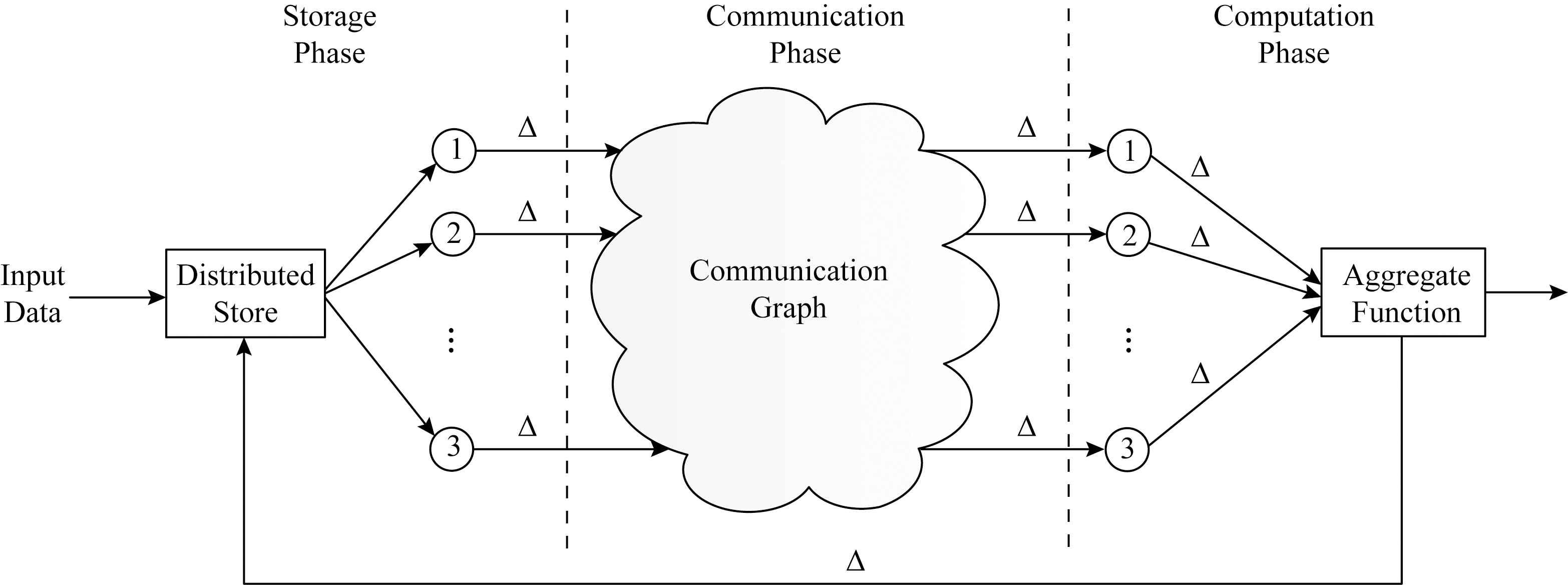
Fig.1 Conceptual diagram of the phases of distributed computation
图1 分布式计算阶段概念图
1 背景介绍
在硬件资源丰富的云计算时代,数据中心通过运行在大量商用服务器上的Hadoop分布式文件系统、Windows Azure存储、Amazon S3和Google文件系统等分布式存储系统存储了海量数据.由于对这些数据进行分析得到的结果可以为用户提供见解或建议,因此数据中心广泛部署了各种分布式计算系统(例如MapReduce,Spark,TensorFlow[17],MX Net[18])对数据进行大规模的分析.
在分布式存储系统中,数据通常被分为不同的区块,存储在不同的服务器上.另一方面,在分布式计算系统中进行的作业通常包含多个并行运行的任务,这种并行任务运行在不同的服务器上,每个任务处理整个输入数据的一小部分[19].因此,分布式计算系统与分布式存储系统通常是紧密交互的,例如,可以将作业中的任务分配给服务器,该服务器将尽可能就近存储相应的输入数据块,以利用数据局部性.
但是,分布式存储和计算系统在数据中心都会受到系统噪声的影响,这些噪声可能会影响系统的可用性或性能,造成系统故障、负载不平衡和资源争用等.例如在数千个服务器集群上运行的分布式存储系统每天可能会遇到20~100个由于系统噪声而导致的不可用事件.在分布式计算系统中,多个执行并行任务的服务器中可能存在某些节点的计算时间相较其他节点更长,该节点称为掉队节点,而完成整个计算任务的时间通常受制于最慢的计算节点.因此,掉队节点将成为作业的瓶颈.
为了减轻系统噪声的影响,可以采取在分布式存储系统中预先增加冗余数据或在分布式计算系统中增加冗余任务的方法,以容忍受系统噪声影响的数据或任务.为了确保数据完整性,将数据复制多份存储在不同的服务器上是实际生产中许多分布式存储系统采用的方法.同时,利用存储系统中的数据副本使得在分布式计算系统中以较小开销方便地复制计算任务成为可能.因此,受系统噪声影响的计算任务可以被容忍,因为该计算任务的结果仍然可以从另一台服务器获得.
但是,副本方式给计算和存储带来了非常高的资源开销.例如3副本(即将数据复制3次)的方式可以容忍任意2个不可用的副本出现,同时在分布式存储系统中产生3倍源文件大小的存储开销.为了减少资源开销,使用纠删码(erasure coding, EC)产生冗余数据或计算的方式受到了许多关注.纠删码起源于通信传输领域,后来逐渐应用到存储系统中的数据检错和纠错问题中,以提高存储系统的可靠性.在存储系统中,纠删码技术主要是通过利用纠删码算法将原始的数据进行编码得到冗余,并将数据和冗余一并存储起来,以达到容错的目的.与副本方式相比,纠删码允许以更少的资源开销来达到容忍同等系统噪声的效果.以目前广泛使用的一种纠删码方案RS码[20](Reed-Solomon code)的(n,k)=(4,2)编码为例,该编码将原文件分为k=2部分,然后按照RS码编码规则生成m=2个校验块,容错能力为2,数据收集节点可以选择任意2个块重建出原始文件,此编码方式仅需消耗2倍源文件大小的存储空间,就具有与3副本技术相同的容错能力,即可以容忍任意2个块丢失.同时,纠删码可以应用于其他的编码任务,来修改一些分布式计算算法,如矩阵乘法和数据洗牌等.编码任务将一部分编码数据作为输入,并且对所有任务的一个子集进行解码后即可得到作业的结果,从而实现了对掉队节点的容忍.
之前对EC编码技术的研究应用大多都集中于分布式存储领域,研究如何用这一编码技术增加相应的“冗余存储”以抵抗“erasure”节点对数据可靠性造成的影响,其中“erasure”节点是指由于各种原因导致的系统中失效的存储节点.本文则是聚焦于编码技术在分布式计算领域中的应用,介绍近几年对于如何用编码技术增加相应的“冗余计算”以改进大规模机器学习集群性能的研究进展,研究将大规模机器学习集群中的“straggler”看成是计算集群中的1个“erasure”节点,如何增加相应的“冗余计算”以抵抗“erasure”节点对分布式机器学习算法性能造成的影响.
目前基于编码技术改进大规模机器学习集群性能的研究,涉及在矩阵乘法、梯度计算、数据洗牌和其他一些机器学习领域的应用,本文将在后续章节中分别进行介绍.
2 编码技术应用于矩阵乘法
矩阵乘法是许多数据分析应用程序的关键操作之一,这些应用程序应用于各种领域,如机器学习、科学计算和图形处理等.此类应用程序需要大量的计算和存储资源来处理TB甚至PB级的数据量,而这是单台机器无法提供的.因此,在大规模分布式系统上部署矩阵乘法计算任务受到了广泛的关注[21-23].本文按照矩阵大小不同将矩阵乘法分成了矩阵-向量乘法和矩阵-矩阵乘法2种,分别介绍了实现对于掉队节点鲁棒性的2种矩阵乘法的编码方案,并对方案之间的部分性能进行了对比.
2.1 编码应用于矩阵-向量乘法
假设由于系统噪声,工作节点的延迟是不可预测的.目标是在有掉队节点存在的情况下尽可能快地计算矩阵-向量乘法AX,其中A是一个m×n的矩阵,X是一个n×1的一维矩阵,即向量.副本方案、MDS编码方案、无码率编码方案都是基于此目标来优化矩阵-向量乘法,下面分别介绍这3种方案,并进行分析和比较.
2.1.1 副本方案
对抗掉队节点的一种最基本的方法是使用副本方案,将每个计算任务以副本的形式在多个工作节点上并行执行,当任一节点完成工作后,该计算任务就被完成.本文把副本方案看作诸多编码方案中的一种特殊情况.图2给出了副本方案的简单示例.
首先将矩阵A分成2个子矩阵,即A=[A1A2],然后将A1,A2以2副本的形式分别存储在4个工作节点中.主节点将X发送给4个工作节点,工作节点执行计算任务AiX(i=1,2),并将计算结果返还给主节点.主节点接收到Worker1,Worker2和Worker3,Worker4这2组工作节点中每组的任一工作节点的计算结果即可计算出AX.例如,当节点Worker2,Worker3失效时,主节点接收到其他2个节点的计算结果可计算出AX.
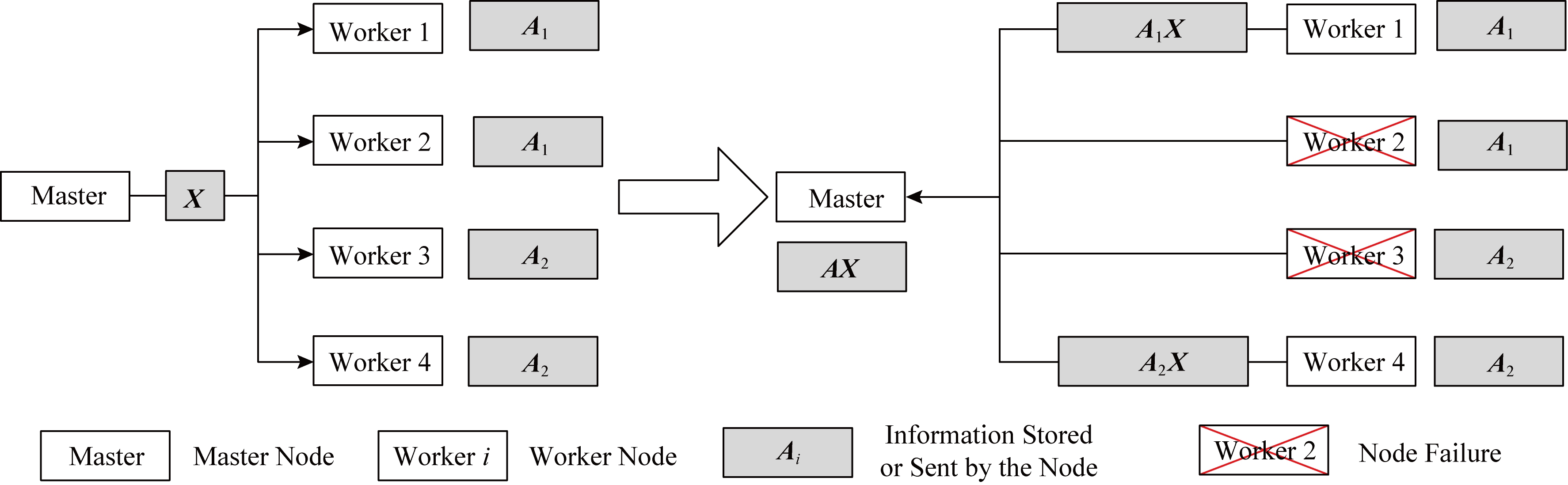
Fig.2 Illustration of replication scheme
图2 副本方案示例
2.1.2 MDS编码方案
在文献[24]中Lee等人提出了一种基于最大距离可分(maximum distance separable, MDS)码的编码计算方案,称为“MDS编码矩阵乘法”,关键思想如下.想象一个包含1个主节点(master)和3个工作节点(worker)的分布式计算系统,如图3所示,MDS编码方案首先将A分成2个子矩阵,即A=[A1A2],并计算2个子矩阵的奇偶校验,即A3=A1+A2,将A1,A2,A3预先存储在工作节点Worker1,Worker2,Worker3中.然后,主节点将向量X发送给每个工作节点,工作节点i(i=1,2,3)执行分配给该节点的计算AiX的任务.当工作节点i完成任务后,将结果发送回主节点.一旦主节点接收到3个计算结果中的任意2个,它就可以计算出AX.例如当节点Worker2失效时,主节点接收到A1X和A3X,它可以通过计算A2X=A3X-A1X得到A2X,然后计算出AX.
使用编码可以利用更多的节点缓解掉队节点的影响,Lee等人[24]通过分析表明:如果n个工作节点执行任务的时间属于独立同指数分布,那么最优的编码矩阵乘法会比未编码的矩阵乘法平均快Θ(lg n)倍.

Fig.3 Illustration of a system with 1 master and 3 workers
图3 拥有1个主节点和3个工作节点的系统示例
2.1.3 无码率编码方案
2.1.1节与2.1.2节中介绍的编码方案虽然实现了对掉队节点的容忍,但是对于掉队节点所完成的工作没有进行利用,这是对计算资源的浪费,Mallick等人[25]提出了一种基于LT码[26]的无码率喷泉编码(rateless fountain codes)[27]策略.编码思想如下:将m×n矩阵A的行a1,a2,…,am看作是基本块,并对这m个行进行编码生成me=αm个编码行并将其组成编码矩阵Ae,其中每个编码行是从矩阵A中随机均匀的选择d行并作异或运算得到的,选择d=i的概率正比于
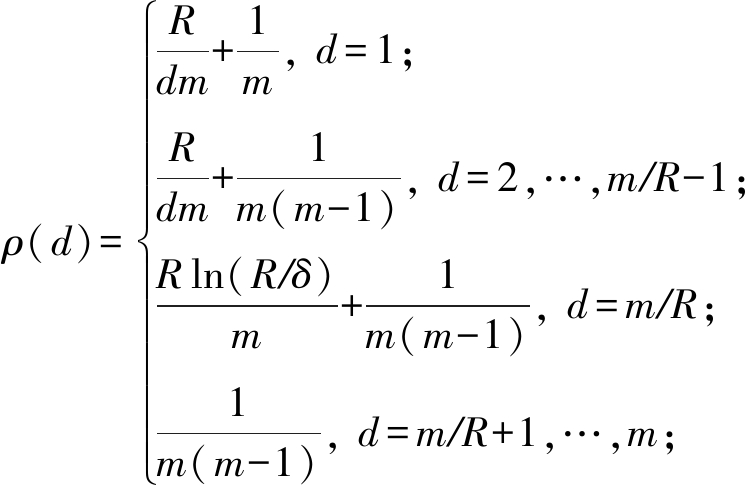
(1)
其中,![]() 和δ是设计参数,选择d=d0的概率等于
和δ是设计参数,选择d=d0的概率等于![]()
然后将编码矩阵Ae的me行分配给p个工作节点,每个工作节点分配的行的数量相等,分配给每个节点的αm/p行存储在其本地内存中,如图4所示.当需要将矩阵A与向量X相乘时,主节点就会把X发送给每个工作节点,每个工作节点将存储在各自本地内存中的编码矩阵Ae的每一行与X的乘积返还给主节点.另外,为了减少通信负载,工作节点可以只向主节点发送进度更新,来表明它已完成的计算任务的数量,并在主节点需要时发送乘积结果.

Fig.4 Illustration of rateless code
图4 无码率编码方案示例
根据编码策略,主节点利用从工作节点接收到的编码的行-向量积的子集(即Be=AeX的元素子集)中逐步恢复所需的矩阵-向量乘积B=AX.对于一个m行的矩阵,解码过程需要md=m(1+ε)个行-向量乘积,其中ε是一个很小的值,取决于编码时参数的设置,当m→∞时,ε→0.一旦主节点完成了对B=AX中所有元素的解码工作,它会向所有工作节点发送一个停止信号来停止它们的本地计算.在此期间,速度较快的工作节点比速度较慢的工作节点完成了更多的计算任务,p个计算节点共同完成了m(1+ε)个计算任务.
无码率编码方案与MDS编码方案相比具有4个优点:
1) 无码率编码方案相较于MDS编码具有更低的时延,MDS编码方案不适用于存在不同计算速度掉队节点的情况,仅仅使用了k个节点的计算结果,忽略了其他p-k个节点的工作;
2) 无码率编码方案最多只需完成m(1+ε)个计算任务,而MDS编码在没有掉队节点存在时,工作节点将会共同完成mp/k个计算任务;
3) 无码率编码方案可以容忍p-1个掉队节点,且冗余计算开销可以忽略不计,而一个(p, k) MDS编码方案(即将k个计算任务编码使用MDS码编码成p个编码任务,其中任意k个编码任务的计算结果即可解码出最终结果)对p-k个节点具有鲁棒性,k∈{1,2,…,p},当k降低时,可以容忍更多的掉队节点,但是会造成更多的计算冗余;
4) 无码率编码方案拥有O(m ln m)的极快解码速度,这使得在m的值非常大的时候仍然可以使用该编码方案.
表1给出了使用p个工作节点计算m×n矩阵A与n×1向量X相乘的3种策略之间的比较,其中时延是近似的,计算负载是在没有掉队节点的情况下给出的,τ为执行一次计算任务所用的时间,μ为延迟率且延迟的指数部分不随工作节点执行计算任务的次数而变化.
Table 1 Comparison of Different Strategies for Matrix-Vector Multiplication
表1 矩阵-向量乘法不同策略的对比
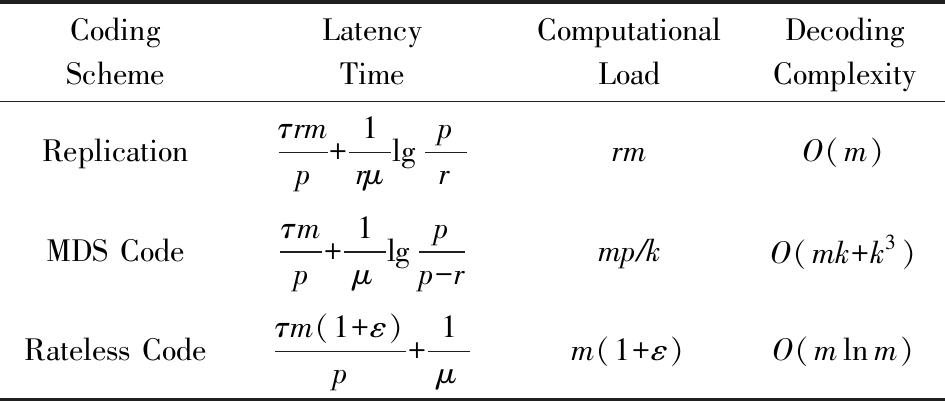
CodingSchemeLatencyTimeComputationalLoadDecodingComplexityReplicationτrmp+1rμlgprrmO(m)MDS Codeτmp+1μlgpp-rmp∕kO(mk+k3)Rateless Codeτm(1+ε)p+1μm(1+ε)O(mlnm)
2.2 编码应用于矩阵-矩阵乘法
文献[24]是在假设矩阵B足够小的前提下提出的矩阵乘法编码方案,否则在单独的工作节点上计算![]() 是不可行的,这一假设限制了该方案在涉及大规模矩阵乘法的现代应用中的适用性.因此基于矩阵乘法编码方案的研究,更多的是在文献[24]的基础上对A和B矩阵都很大的高维矩阵乘法进行的研究.
是不可行的,这一假设限制了该方案在涉及大规模矩阵乘法的现代应用中的适用性.因此基于矩阵乘法编码方案的研究,更多的是在文献[24]的基础上对A和B矩阵都很大的高维矩阵乘法进行的研究.
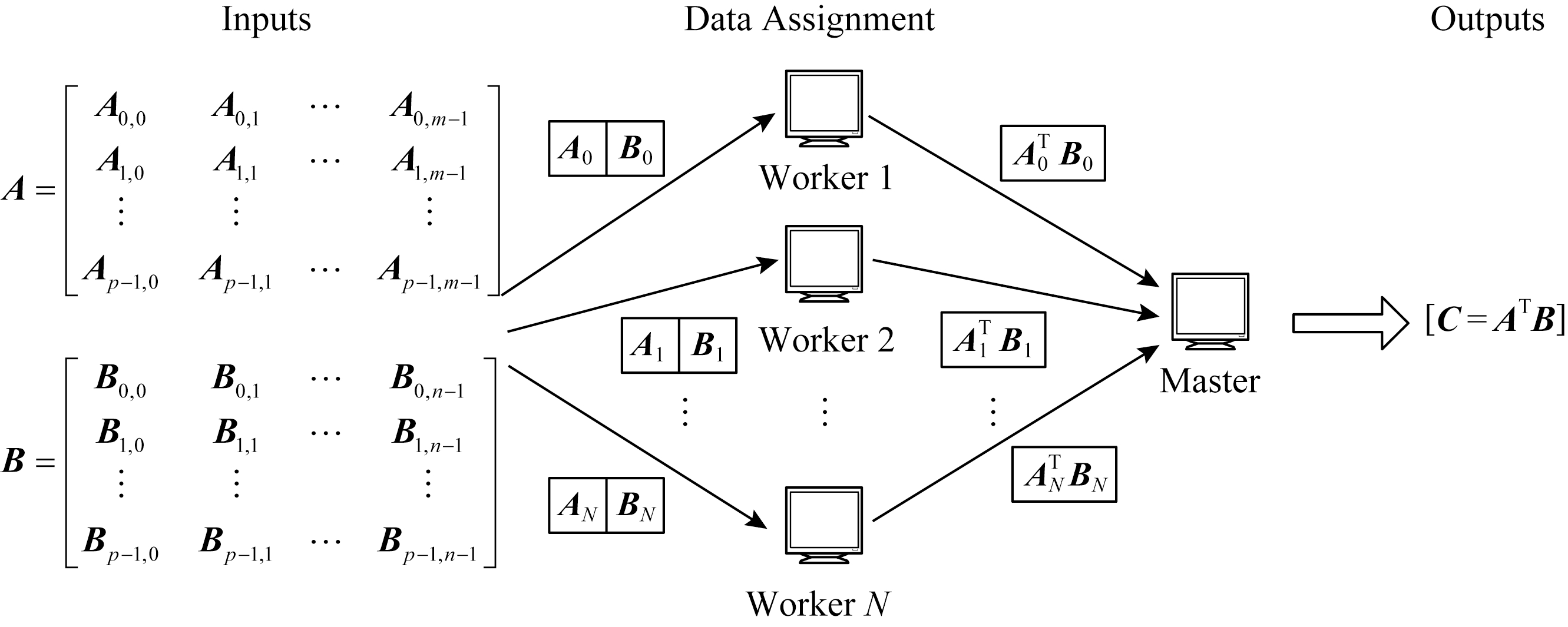
Fig.5 Example of high-dimensional matrix multiplication problem
图5 高维矩阵乘法问题示例
考虑一个如图5所示的高维矩阵乘法问题,目标是通过输入矩阵A和B计算出C=ATB.计算工作是在拥有1个主节点和N个工作节点的分布式系统中进行的.其中,2个输入矩阵分别被(任意)划分为p×m和p×n个子矩阵块,每一个输入矩阵划分的子矩阵大小是相同的.每个工作节点都有一个本地内存,可以用来存储每个矩阵的任意编码函数,用![]() 表示,每个函数的大小都与对应的子矩阵的大小相等.然后工作节点将2个已存储的(编码的)子矩阵相乘,并将结果返回给主节点.另外,通过设置参数p,m,n的值,可以对输入矩阵进行灵活的分区,从而支持对系统资源(即每个工作节点所需的存储量以及工作节点与主节点之间的通信量)的不同利用.因此,考虑到系统对可用存储和通信资源的限制,可以相应地选择p,m,n值.
表示,每个函数的大小都与对应的子矩阵的大小相等.然后工作节点将2个已存储的(编码的)子矩阵相乘,并将结果返回给主节点.另外,通过设置参数p,m,n的值,可以对输入矩阵进行灵活的分区,从而支持对系统资源(即每个工作节点所需的存储量以及工作节点与主节点之间的通信量)的不同利用.因此,考虑到系统对可用存储和通信资源的限制,可以相应地选择p,m,n值.
通过精心设计每个节点上的计算策略(即设计![]() 主节点在恢复输出矩阵C之前只需等待计算速度最快的工作节点子集,从而可以减轻掉队节点的影响.给定一种计算策略,将计算C所需等待的最小工作节点数定义为该计算策略的恢复阈值.也就是说,如果任何大小不小于恢复阈值的工作节点子集完成了它们的工作,主节点就能够计算出C.那么分布式矩阵乘法的最小恢复阈值是多少?能否找到一种最优的计算策略,既能达到最小恢复阈值,又能对主节点的最终输出进行有效解码?
主节点在恢复输出矩阵C之前只需等待计算速度最快的工作节点子集,从而可以减轻掉队节点的影响.给定一种计算策略,将计算C所需等待的最小工作节点数定义为该计算策略的恢复阈值.也就是说,如果任何大小不小于恢复阈值的工作节点子集完成了它们的工作,主节点就能够计算出C.那么分布式矩阵乘法的最小恢复阈值是多少?能否找到一种最优的计算策略,既能达到最小恢复阈值,又能对主节点的最终输出进行有效解码?
现今对这一问题提出了MDS码、乘积码、多项式码等编码解决方案,下面将对这些方案进行介绍.
2.2.1 MDS编码方案
应用于矩阵-矩阵乘法的MDS编码方案可以分为一维MDS编码方案和完全MDS编码方案
一维MDS编码方案是Lee等人[28]对文献[24]的编码思想进行扩展得出的,它仅使用MDS码在一个输入矩阵中加入冗余数据,因此将这种方法称为一维MDS码(1D MDS码).该编码方案的思想如下:将大矩阵乘法的问题看作k个小矩阵乘法的问题,即ATB=[ATb1ATb2…ATbk],然后对k个小矩阵中的每一个分别应用MDS编码矩阵乘法.假设N=nk,工作节点被分成大小为n的k个组,每个组都专门计算一个ATbj.例如对于第1个组,它用于计算ATb1,该方案首先使用(n,k) MDS编码对A的k列进行编码,以获得n个编码列,比如a1到an,然后将![]() 的计算分配给这组的第i个工作节点,以此类推.MDS编码计算的计算时间由k个组的计算时间中的最大值决定,每个组的计算时间由该组n个工作节点中第k个完成计算任务的工作节点决定.
的计算分配给这组的第i个工作节点,以此类推.MDS编码计算的计算时间由k个组的计算时间中的最大值决定,每个组的计算时间由该组n个工作节点中第k个完成计算任务的工作节点决定.
图6为1D MDS码的一个简单示例,编码方案的目标是使用3个工作节点计算出C=ATB,其中每个工作节点可以存储A的一半和全部的B.一维MDS码将A沿列均匀划分为2个子矩阵A0和A1,将它们编码为3个编码矩阵A0,A1,A0+A1,然后将这3个编码矩阵分配给3个工作节点.这一方案中,主节点接收到3个工作节点中的任意2个返回的计算结果后,即可计算出矩阵C,因此恢复阈值为2.例如,主节点接收到![]() 和(A0+A1)TB,剩余1个节点失效时,它可以通过计算
和(A0+A1)TB,剩余1个节点失效时,它可以通过计算![]() 得到
得到![]() 然后计算出AX.更一般地说,一维MDS码可以达到的恢复阈值为
然后计算出AX.更一般地说,一维MDS码可以达到的恢复阈值为
![]()
(2)
Fig.6 Illustration of 1D MDS code with 3 workers
图6 3个工作节点的1D MDS码示例
与一维MDS编码方案只在1个输入矩阵中加入冗余数据不同,完全MDS(full MDS)编码方案将所需计算的2个输入矩阵A和B相乘得到的矩阵C的m×n个任务看作是m×n个基本元素,并对这m×n个基本元素使用(N,m×n) MDS码得到N个编码计算任务,分别发送给每个工作节点进行计算.这一编码方案保证了最优的解码灵活性,任意m×n个任务的计算结果都足以恢复C,但是这种方法效率很低,因为显著增加了计算冗余任务的工作节点的计算量.例如当N=m×n+1时,对m×n个任务应用(m×n+1,m×n) MDS码得到m×n+1个计算任务:![]() 和
和![]() 其中ωij是编码系数.可以看出,虽然前m×n个计算任务每个只包含1个点积,但是最后1个计算节点需要计算m×n个点积和m×n-1次加法.
其中ωij是编码系数.可以看出,虽然前m×n个计算任务每个只包含1个点积,但是最后1个计算节点需要计算m×n个点积和m×n-1次加法.
2.2.2 乘积码编码方案
乘积码矩阵乘法是Lee等人在文献[28]中提出的一种基于乘积码的编码方案,它在2个输入矩阵中都加入了冗余,但是该方案只是针对m=n的情况设计的.MDS编码计算只沿着1个维度进行编码,而乘积码编码方案则沿着2个维度进行编码,与一维MDS编码方案相比,获得了更好的编码收益.乘积码是一种利用小编码块作为构建块构造更大的编码块的一种方法,例如当给定一个(n,k) MDS编码时,可以构造乘积码:将k2个符号放入一个k×k的数组中,然后对数组的每一行都使用(n,k) MDS编码进行编码,生成一个k×n的数组.最后对数组的每一列都使用(n,k) MDS编码进行编码,生成一个n×n的数组,包含n2个编码块.这个构造出的乘积码叫做(n,k)2乘积码.与上述构造过程类似,乘积码矩阵乘法编码方案先把工作节点分配成![]() 的矩阵,接着将矩阵A沿着列分成m个子矩阵,用
的矩阵,接着将矩阵A沿着列分成m个子矩阵,用![]() MDS码编码成
MDS码编码成![]() 个编码矩阵,然后分配给工作节点的
个编码矩阵,然后分配给工作节点的![]() 列.同理,将矩阵B沿着列分成m个子矩阵,编码后分配给工作节点的
列.同理,将矩阵B沿着列分成m个子矩阵,编码后分配给工作节点的![]() 行.根据MDS码的特性,主节点在获得该行/列中的任意m个结果后,即可对整行/列进行解码.因此,主节点可以在行和列上迭代地解码MDS编码块,直到输出完整的矩阵C为止.图7为乘积码矩阵乘法编码方案的简单示例,其中N=9,m=n=2.
行.根据MDS码的特性,主节点在获得该行/列中的任意m个结果后,即可对整行/列进行解码.因此,主节点可以在行和列上迭代地解码MDS编码块,直到输出完整的矩阵C为止.图7为乘积码矩阵乘法编码方案的简单示例,其中N=9,m=n=2.
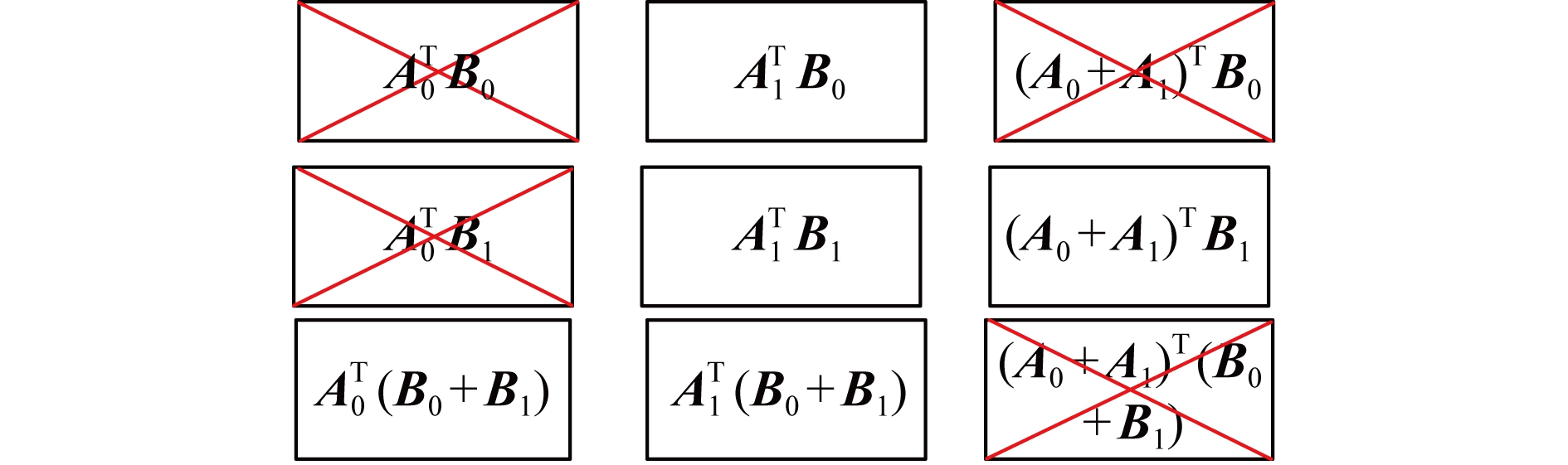
Fig.7 Illustration of product code with 9 workers
图7 9个工作节点的乘积码示例
主节点接收到的5个计算结果分别为![]() 其他4个节点无结果返回,那么主节点可以通过先后计算
其他4个节点无结果返回,那么主节点可以通过先后计算![]() 和
和![]() 来恢复所需的结果.更一般地说,乘积码可以达到的恢复阈值为
来恢复所需的结果.更一般地说,乘积码可以达到的恢复阈值为
![]()
(3)
该方案的恢复阈值相较于一维MDS码有着明显的改进.
2.2.3 多项式码编码方案
Yu等人[29]发现最优恢复阈值可以远远小于一维MDS编码和乘积码2种方案的恢复阈值,并指出恢复的最低阈值不与工作节点的数量成比例(即Θ(1)).他们通过设计一种新的编码计算策略,即多项式编码来证明这一观点,该编码策略实现了mn的恢复阈值,并显著提高了技术水平.图8为多项式码的简单示例.
在一个分布式矩阵乘法计算任务中,使用5个工作节点(即N=5)计算C=ATB,其中每个工作节点能存储每个输入矩阵的一半大小.沿着列将每个输入矩阵平均分成2个子矩阵:
A=[A0A1],
B=[B0B1].
(4)
因而,实际所需计算的内容就变成了4个未编码的部分:
![]()
(5)
现在设计一种计算策略来实现最优恢复阈值4,每个工作节点i(i∈{1,2,…,4})存储2个编码子矩阵:
![]()
(6)
为了证明该计算策略的恢复阈值为4,需要为拥有4个工作节点的任意子集设计一个有效的解码函数.通过一个具有代表性的场景来演示这种可解码性,其中主节点从工作节点1,2,3,4接收计算结果,工作节点0为掉队节点,如图8所示.类似地,其他4种可能场景的可解码性也可以证明.
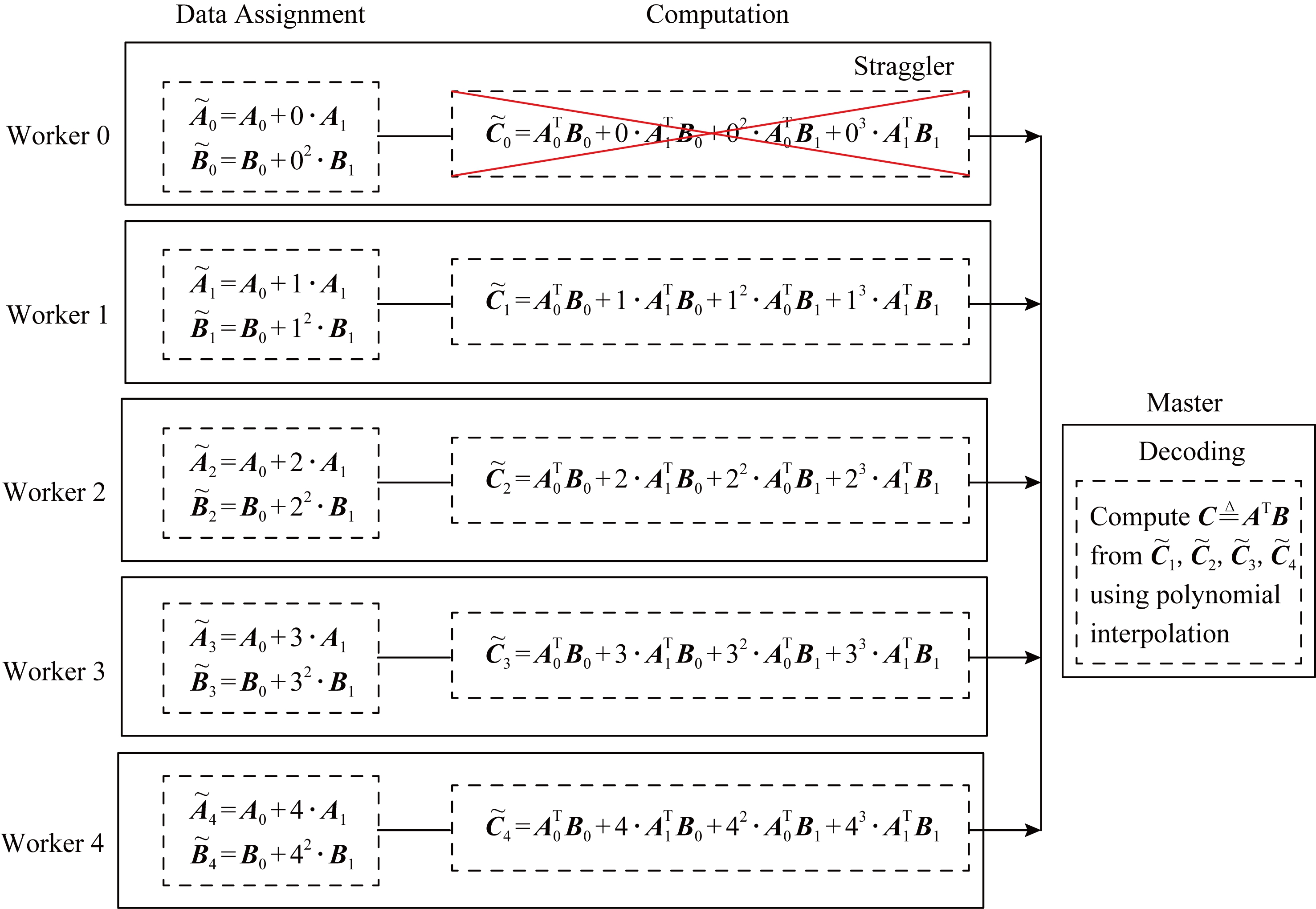
Fig.8 Illustration of polynomial code with 5 workers
图8 拥有5个工作节点的多项式码示例
根据设计的计算策略,可以得到:

(7)
式(7)中的系数矩阵是范德蒙德矩阵,由于它的参数1,2,3,4在有限域F7中是不同的,因此该矩阵是可逆的.因此恢复C的一种方法是直接对式(7)进行反求,这也证明了该式的可解码性.然而,在更一般的情况下,使用经典的反演算法直接计算这个逆可能比较复杂.Yu等人[29]认为,由于所设计的计算策略具有特殊的代数结构,解码过程可以看作是一个多项式插值问题(或是一个解码Reed-Solomon码的问题).
具体地说,在本例中,每个工作节点i都返回给主节点结果:
![]()
(8)
也就是多项式在x=i处的值:
![]()
(9)
因此,使用4个工作节点的计算结果恢复C等价于在给定值的情况下在第4个点处插值一个3次多项式.
Yu等人[29]得出的主要结论为:使用多项式码在N个工作节点上完成一个一般的矩阵乘法任务时,其中每个工作节点只能存储A的![]() 部分和B的
部分和B的![]() 部分,可以达到的恢复阈值为
部分,可以达到的恢复阈值为
Kpoly mn=Θ(1).
mn=Θ(1).
(10)
这种多项式编码的主要创新之处和优点在于,通过精心设计编码子矩阵的代数结构,可以确保工作节点上的任何mn个中间计算都足以在主节点上恢复矩阵乘法的最终乘积.从某种意义上来说,这是在中间计算中创建了一个MDS结构,而不是像以前的工作那样仅仅是对矩阵进行编码.此外,通过利用多项式码的代数结构,可以将在主节点上的最终输出的重构问题映射为一个多项式插值问题(或是一个RS码解码问题),并可有效求解.这种映射也架起了代数编码理论和分布式矩阵乘法之间的桥梁.
Yu等人[29]证明了多项式编码的最优性,指出它在恢复阈值上达到了信息理论的下界(至少需要工作节点返回的mn个矩阵块来恢复最终的输出,而最终输出的大小正好是mn块).因此,所提出的多项式编码本质上支持某种特定的计算策略,这样,从任何可恢复C所需的最小信息量的工作节点的子集中,主节点都可以成功地解码最终的输出.
在多项式编码的基础上,Yu等人[29]又在文献[30]中提出了一种新的编码策略,称为纠缠多项式码,对所有可能的参数值实现了pmn+p-1的恢复阈值.纠缠多项式码的构造是基于这样一个事实:当一个m×p矩阵和一个p×n矩阵相乘时,本质上是求一个由2个矩阵中元素的成对乘积张成的双线性函数的子空间.虽然可能存在总共p2mn对元素,但至多pmn对元素与矩阵乘积直接相关,存在p阶的缺失.纠缠多项式码的特殊结构将输入矩阵与输出相关联,使得系统几乎可以避免不必要的乘法,并且实现了pmn阶的恢复阈值.这种编码策略实现了用于抵抗掉队节点的传统非编码方法、随机线性编码和MDS编码类型的方法的有序改进.纠缠多项式编码是对多项式编码的推广,它是针对p=1的特殊情况而设计的.此外,Yu等人[30]利用双线性复杂度,通过改进纠缠多项式编码,在系数为2的范围内,描述了所有线性编码策略的最佳恢复阈值.此外,当评估双线性复杂度是一个众所周知的挑战性问题时,他们指出线性编码策略的最佳恢复阈值可以在这个基本量的2倍以内.
另外,Dutta等人[31]针对分布式矩阵乘法提供了一种新的编码计算策略——MatDot编码,该策略在恢复阈值方面优于文献[29]中提出的多项式编码.当每个矩阵的![]() 部分可以存储在每个工作节点中时,多项式编码需要m2个完成任务的工作节点,而MatDot编码只需要2m-1个完成任务的工作节点,但是这使得从每个工作节点到主节点的通信成本更高.此外,Dutta等人[32]提出了一种基于干扰对齐(即在编码计算中对齐不属于所需输出的计算)的新的编码矩阵乘法技术,称为一般PolyDot码,它在存储和通信约束下改进了现有的编码矩阵乘法方法.一般PolyDot码在多项式码和MatDot码之间架起了桥梁,权衡了恢复阈值和通信成本之间的关系.并用MatDot和PolyDot的编码思想提出了一种将n(n≥3)个矩阵相乘的编码技术.
部分可以存储在每个工作节点中时,多项式编码需要m2个完成任务的工作节点,而MatDot编码只需要2m-1个完成任务的工作节点,但是这使得从每个工作节点到主节点的通信成本更高.此外,Dutta等人[32]提出了一种基于干扰对齐(即在编码计算中对齐不属于所需输出的计算)的新的编码矩阵乘法技术,称为一般PolyDot码,它在存储和通信约束下改进了现有的编码矩阵乘法方法.一般PolyDot码在多项式码和MatDot码之间架起了桥梁,权衡了恢复阈值和通信成本之间的关系.并用MatDot和PolyDot的编码思想提出了一种将n(n≥3)个矩阵相乘的编码技术.
表2给出了上述6种编码策略之间的对比,这些编码策略的目标都是通过输入矩阵A和B计算出C=ATB,如图5所示.计算工作是在拥有1个主节点和N个工作节点的分布式系统中进行的.其中,2个输入矩阵分别被任意划分为p×m和p×n个子矩阵块,每一个输入矩阵划分的子矩阵大小是相同的,且每个工作节点只能在本地存储2个子矩阵.
Table 2 Comparison of Different Strategies for Matrix-Matrix Multiplication
表2 矩阵-矩阵乘法不同策略的对比

Coding SchemeLimitation on the ParametersRecovery Threshold1D MDS CodeN-Nn+mFull MDS CodeN-mnProduct Codem=n(2m-1)N-(m-1)2+1Polynomial CodemnEntangledPolynomial Codepmn+p-1MatDot Codem=n2m-1
另外,文献[24]中提出的编码计算方法忽略了计算速度最慢的的n-k个工作节点所做的工作,并将这些工作节点认定为掉队节点.对于持久的掉队节点,即永久不可用或非常长时间不可用的工作节点,这是理想的策略.然而,在实践中,有许多非持久性的掉队节点,他们的计算速度虽然缓慢,但能够做一些工作.此时对这些非持久性的掉队节点的忽略是对计算资源的浪费.因此Kiani等人[33]提出了一种利用掉队节点的计算能力的编码方案.他们首先考虑矩阵-向量乘法,并将MDS码应用于子矩阵的小块.工作节点按顺序处理块,一个块、一个块地工作,完成后将每个块的部分结果发送给主节点.这种工作策略允许一个更连续的处理过程,从而允许充分利用工作节点所做的工作并减少计算时间.然后,Kiani等人[33]使用乘积码将此技术应用于矩阵-矩阵乘法,证明了计算子任务的顺序是一种新的设计自由度,可以进一步利用它来减少计算时间,并提出了一种区别于传统顺序统计的新型分析结束时间的方法.仿真结果表明,与以前的方法相比,该方案预期的计算时间减少了至少67%.
此外,对于如何利用掉队节点的计算能力这一问题,Narra等人[34]和Ramamoorthy等人[35]也分别提出了不同的编码方案.
3 编码应用于梯度计算
在求解机器学习算法的无约束优化问题时,梯度下降(gradient descent)是最常采用的方法之一,求解损失函数的最小值时,可以通过梯度下降法来迭代求解,得到最小化的损失函数和模型参数值.针对基于梯度计算提出的编码方案,本文将编码方案分为精确梯度编码和近似梯度计算编码2种.
3.1 精确梯度编码方案
Tandon等人[36]研究了分布式系统中梯度计算的最优编码设计,他们注意到,在许多机器学习问题中,损失函数的梯度是更简单的梯度总和(这里更简单的梯度是指与每个数据点一起计算的每个梯度).在考虑到唯一重要的是总梯度的基础上,Tandon等人[36]提出了一种新的编码计算方案,用于计算函数的和,展示了对梯度进行编码可以提供同步梯度下降法对失效节点和掉队节点的容忍.他们根据工作节点运行速度变慢的程度将掉队节点分成完全掉队节点(full stragglers)和部分掉队节点(partial stragglers)两种,其中完全掉队节点是指完全失效的工作节点,即不提交任何计算结果;部分掉队节点是指没有完全失效的节点,即虽然要比正常节点计算速度慢但还是可以提交部分计算结果.针对完全掉队节点和部分掉队节点这2种情况,Tandon等人[36]分别提出了一种编码方案来实现机器学习集群对掉队节点的鲁棒性.
针对完全掉队节点,Tandon等人[36]提出的编码方案是通过复制工作节点所需完成的任务来实现的.但是这种副本策略仅适用于工作节点数量n是(s+1)的倍数,其中s是该方案能容忍的掉队节点的数量.编码方案过程:
1) 将n个工作节点分成大小为![]() 的(s+1)个组;在每个组中,将整个计算任务平均分成n份,给组中的每个工作节点分别分配(s+1)份;
的(s+1)个组;在每个组中,将整个计算任务平均分成n份,给组中的每个工作节点分别分配(s+1)份;
2) 所有的组都是彼此的副本;
3) 当计算完成时,每个工作节点传输其所计算部分的梯度的和到主节点.
图9为n=6,s=2时的构造实例,对2个掉队节点具有鲁棒性.
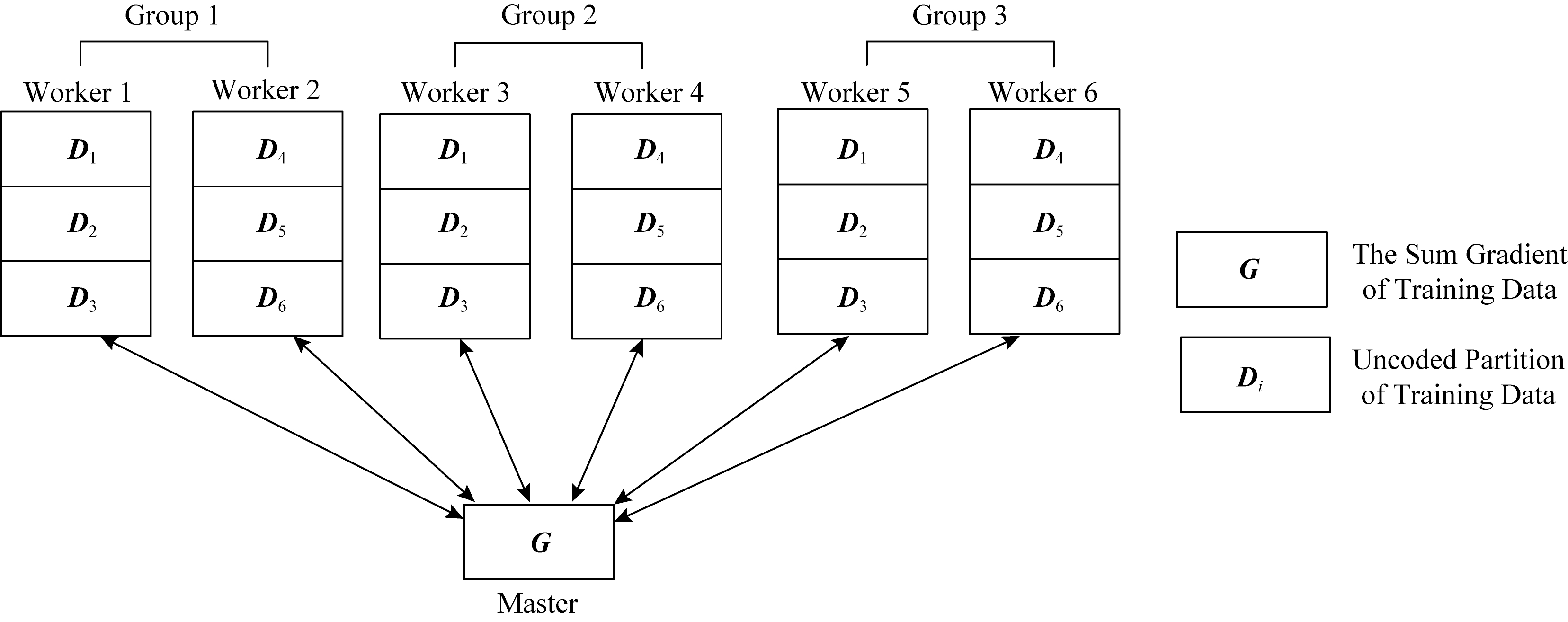
Fig.9 Illustration of full stragglers for n=6,s=2
图9 n=6,s=2时的full stragglers实例
针对部分掉队节点,Tandon等人[36]提出了一种编码块与未编码块结合起来的方案.该方案将数据分成编码部分和未编码部分,每当一个部分掉队节点处理完该节点上的未编码部分时,正常节点就处理完该节点上未编码部分和编码的部分.任意的(n,s,α)编码方案描述如下,其中α(α>1)是指部分掉队节点计算速度为正常节点的α倍:
1) 将初始数据分成![]() 个大小相同的块,其中n个块是编码块,其他的块是未编码块;
个大小相同的块,其中n个块是编码块,其他的块是未编码块;
2) 分别给每个工作节点分配![]() 个未编码的块,其中任意2个工作节点分配的块都不相同;
个未编码的块,其中任意2个工作节点分配的块都不相同;
3) 再给每个工作节点按照(A,B)分配方案分配(s+1)个编码块,这一分配方案对s个掉队节点具有鲁棒性;
4) 任意工作节点Worker i,首先处理该节点上所有的未编码块,并将它们的梯度和发送到主节点,然后再处理节点上的编码块,并根据(A,B)分配模式发送一个线性组合到主节点.
从编码方案中可以看出,每个工作节点要发送2部分梯度到主节点,而不是完全掉队节点方案中的1部分.但是,更快地处理较小部分数据时可能会减少通信开销,因为在这一编码方案中,每个正常节点只需要处理整个数据的![]() 部分,而完全掉队节点方案中每个正常节点需要处理整个数据的
部分,而完全掉队节点方案中每个正常节点需要处理整个数据的![]() 部分.如图10所示,为n=3,s=1,α=2时的构造示例,对1个掉队节点具有鲁棒性.
部分.如图10所示,为n=3,s=1,α=2时的构造示例,对1个掉队节点具有鲁棒性.
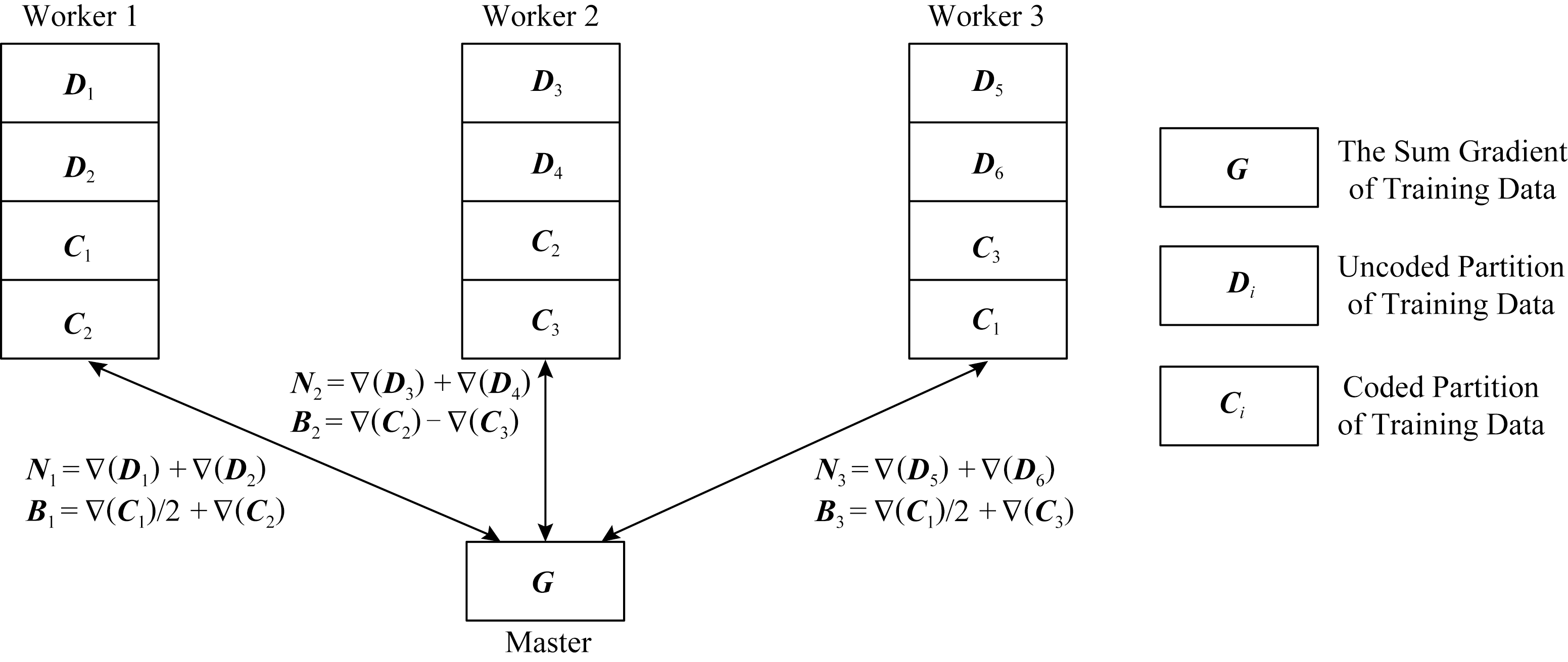
Fig.10 Illustration of partial stragglers for n=3,s=1,α=2
图10 n=3,s=1,α=2时的partial stragglers实例
Ye等人[37]提出了通信计算高效梯度编码方案,它从计算负载、掉队节点容忍和通信成本3个方面描述了梯度计算的基本权衡.为了有效地计算梯度(以及更一般的向量和),利用数据子集和向量之间的分布性,确定了这些参数之间的基本权衡:
![]()
(11)
其中,n为工作节点的数量,k为数据子集的数量,d为分配给每个工作节点的数据子集的数量,s为掉队节点的数量,m为通信下降因子.这一权衡概括了文献[36]中对应于m=1的结果.
Ye等人[37]进一步给出一种基于递归多项式构造的显式编码方案,实现了数据子集和向量分量的最优权衡,可以使梯度计算的运行时间最小化.编码方案的主要步骤:为了减少每个工作节点传输向量的维数,首先将梯度向量的坐标划分为m个相同大小的组;随后设计2个矩阵B和V,其中(n-s)×n的矩阵V的任意(n-s)×(n-s)的子矩阵是可逆,这一性质符合编码方案中能够容忍任意s个掉队节点的要求,并且可以通过将V设置为(非方)范德蒙德矩阵即可满足此要求.另外,mn×(n-s)的矩阵B满足2个性质:
1) B的最后m列由n个大小为n×n的单位矩阵组成;
2) 对于任意j∈[n],B的第i行与V的第j列的乘积必须为0,其中i为一组特定的值,基数为(n-d)m.
性质1可以保证梯度向量和的恢复,性质2确保每个工作节点最多分配d个数据子集.通过利用范德蒙德构造与多项式之间的本质联系,递归构造矩阵B,更精确地说,可以把B的每一行看作某个多项式的系数,且B和V的乘积只是由这些多项式在某一点的值组成.然后可以通过指定它们的根来定义这些多项式,从而满足B的2个性质.但是,Ye等人[37]的编码方案所构造的条件相较于文献[36,38-40]中的编码方案来说更为严格.文献[24]只要求B的最后m列最多包含n个非零项,对这些非零项的位置没有要求;文献[38-40]只处理m=1的特殊情况,不允许梯度向量降维.由于条件更为宽松,文献[36,38-40]中编码方案的构造不具有递归多项式结构,而这正是Ye等人[37]编码方案的主要技术创新所在.
通过使用带有mpi4py包的Python在Amazon EC2集群上运行,Ye等人[37]发现,与未编码方案相比,他们的方案保持了相同的泛化误差,同时使运行时间减少了32%,与只关注掉队节点的文献[24]中的编码方案相比减少了23%.
3.2 近似梯度编码方案
编码计算和梯度编码方面的前期工作主要集中在期望输出的完全精确恢复上,然而,稍微不精确的解决方案在抗噪声的应用中是可以接受的,例如通过基于梯度的算法进行模型训练.Charles等人[41]提出了基于稀疏图的简单梯度编码,以保证快速和近似精确的分布式计算,证明了牺牲少量的精度可以显著提高算法对掉队节点的鲁棒性.这一编码方案中,Charles等人[41]使用稀疏图来创建梯度编码,以一种分布式的方式高效准确地计算近似梯度.更一般地说,这些编码可用于以分布式方式近似计算函数的任何和.他们利用编码理论阐述并正式引入近似恢复问题,分析并提出了2种近似重建的解码技术:一种具有多项式时间复杂度的最优解码算法和一种输入稀疏性具有线性复杂度的快速解码方法.他们主要关注2种不同的编码,2种编码方案都可以有效地进行计算,并且每个计算节点只需要计算对数级的任务数.第1个是文献[42]中提出的部分重复码(fractional repetition code, FRC),即使一定比例的计算节点是掉队节点,部分重复码也能以较高的概率实现小误差甚至是零误差.然而,部分重复码易受敌对掉队节点的影响,即攻击者可以强迫部分工作节点成为掉队节点.为了解决这个问题,Charles等人[41]提出了基于稀疏随机图的贝努利梯度码(Bernoulli gradient code, BGC)和正则化贝努利梯度码(regularized Bernoulli gradient code, rBGC),证明了一般编码的敌对掉队节点的选择是NP难问题,表明这些随机的编码对多项式时间的掉队节点比部分重复码有更好的性能.他们对BGC和rBGC的误差给出了明确的界限,表明两者对攻击者的潜在容忍度是以比FRC更糟的平均情况误差为代价.模拟仿真的结果表明,梯度码的解码复杂度与其平均性能和最坏性能之间存在一定的权衡关系.
Raviv等人[40]利用经典编码理论中的工具设计了新的梯度码,即循环MDS码,以获得既在参数的适用范围内,又在所涉及算法的复杂度上,与现有解相比更优的确定性结构.好处之一是直接应用了这些编码的特性.其次,引入了梯度编码问题的一个近似变量,精确计算整个梯度的要求被一个近似的要求所代替.但是使用这种方法时,参数s不是系统结构的一部分,系统可以为任何s(s<n)提供一个近似的解决方案,其效率随着s的增加而逐渐降低(其中n与s分别为工作节点数量与能容忍的掉队节点的数量).通过扩展图的归一化邻接矩阵可以得出很好的近似梯度码,并且与精确梯度码相比,这种方法可以显著减少计算量.
4 编码应用于数据洗牌
数据洗牌是许多机器学习应用程序的核心元素,以提高学习算法的统计性能而著称.Lee等人在文献[24]中证明了在并行机器学习算法中,编码可以以一种新的方式来权衡额外的可用存储空间,从而降低并行机器学习算法中数据洗牌的通信成本.他们展示了当数据矩阵的常数部分可以缓存在每个工作节点上时(工作节点的总量为n),相比于未编码的洗牌,编码洗牌可以降低通信成本Θ(γ(n))倍,其中:
另外,如果将消息多播给n个用户和将消息单播给1个用户所需通信成本相同,那么γ(n)≈n.
4.1 编码降低洗牌阶段的通信开销
最近研究表明,编码可以为提高机器学习应用程序的运行时性能创造新的机会,通过利用精心设计的节点冗余本地计算,编码可以显著减少分布式计算的通信负载.特别地,Li等人[43]提出了一种MapReduce的编码框架,称为编码MapReduce(CMR),它在r(r∈![]() +)个精心选择的节点上分配每个任务的映射计算,以使网络内的节点减少r倍的通信负载.例如通过在2个精心选择的节点上对每个映射任务进行冗余计算,编码后的MapReduce可以将MapReduce的通信负载减少50%.
+)个精心选择的节点上分配每个任务的映射计算,以使网络内的节点减少r倍的通信负载.例如通过在2个精心选择的节点上对每个映射任务进行冗余计算,编码后的MapReduce可以将MapReduce的通信负载减少50%.
MapReduce是一个编程模型,它支持在一个商用服务器集群上对大规模数据集进行分布式处理.MapReduce的理想特性,例如可伸缩性、简单性和容错性[44-45],使得这个框架在文本/图形处理、机器学习和生物信息学中执行数据密集型工作时广受欢迎.考虑一个用于分布式计算的通用MapReduce框架,在该框架中,整个计算被分解为3个阶段:Map,Shuffle,Reduce,它们在许多计算节点上分步执行.在Map阶段,在1个(或多个)节点中本地处理每个输入文件,以生成中间值.在Shuffle阶段,对于要计算的每个输出函数,将该函数对应的所有中间值转移到其中一个节点上进行还原.最后,在Reduce阶段,将函数的所有中间值还原为最终结果.
考虑图11中的MapReduce问题,使用3个计算节点对6个输入文件F1~F6中的3个输出函数分别用圆、方、三角形表示,进行分布式计算.Node1,Node2,Node3分别负责最终还原圆、方、三角形输出函数.首先考虑没有对计算增加冗余的情况,即每个文件映射1次.如图11(a)所示,Nodei(i=1,2,3)映射文件2i-1和2i.这种情况下,每个节点本地映射2个输入文件,获得输出函数所需的6个中间值中的2个.因此,每个节点需要来自其他节点的4个中间值,从而产生4×3=12的通信负载.Li等人[43]提出的编码方案利用计算冗余通过网络内编码来减少通信负载.如图11(b)所示,增加计算负载的倍数,使每个文件映射到2个节点上.显然,由于增加了更多的本地计算,每个节点只需要另外2个中间值,因此一个未编码的洗牌方案的通信负载为2×3=6.但是,通过编码可以达到更好的效果.如图11(b)所示,每个节点不是将单个中间值进行单播,而是将2个中间值中的XOR运算结果(由⨁表示)多播给另外2个节点,同时满足它们的数据需求.例如,已知文件3中的三角形后,Node2可以从Node1发送的编码包中减去它,从而恢复所需文件1中的正方形.因此,该编码产生的通信负载为3,相较于未编码的洗牌方案实现了2倍的收益.
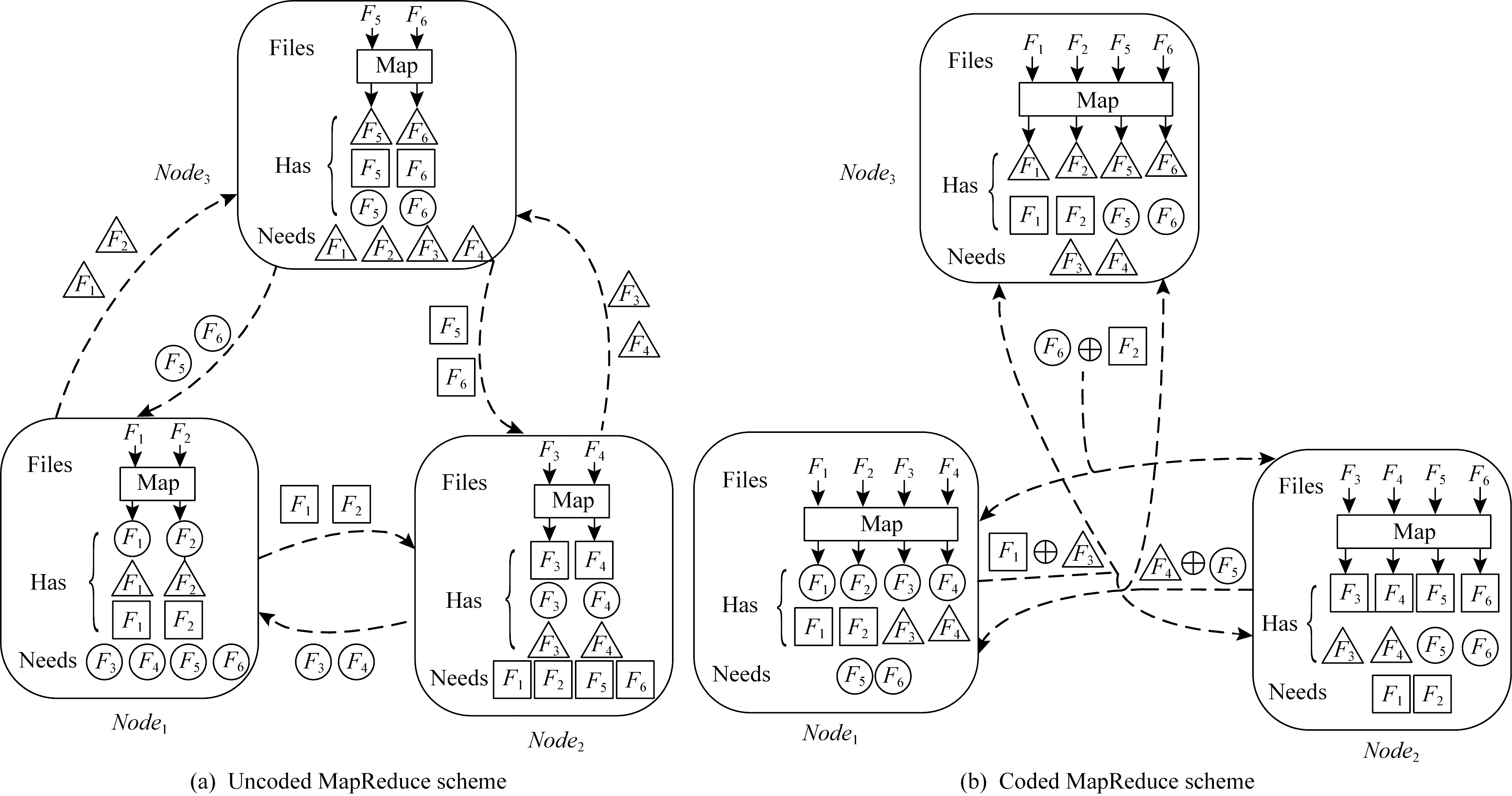
Fig.11 MapReduce scheme
图11 MapReduce框架
在文献[43,46]提出的一般CMR方案中,每个Map任务的计算在r个精心选择的节点上重复执行(即导致r的计算负载),以使节点能够发送对其他r个节点同时有用的编码多播消息.因此,CMR实现了1/r(正好为计算负载的倒数)的通信负载,即:
![]()
(12)
在文献[46]中,Li等人得到了最小可能通信负载的信息论下界L*(r),该下界与CMR的结果完全吻合,即![]() 这揭示了计算负载r和通信负载L之间的一个基本的反比线性关系,它可以利用网络中可用或未充分利用的计算资源来换取通信带宽.
这揭示了计算负载r和通信负载L之间的一个基本的反比线性关系,它可以利用网络中可用或未充分利用的计算资源来换取通信带宽.
Li等人[47]将文献[43]中提出的编码思想应用于TeraSort,提出了一种新的分布式排序算法“Coded TeraSort”,大大提高了Hadoop MapReduce中TeraSort基准的执行时间.排序不仅是Hadoop MapReduce和Spark等分布式计算系统的基本基准,也是推荐系统、SVD和许多图形算法等许多机器学习算法中的关键步骤,并以数据洗牌为主要瓶颈.TeraSort最初是为对TB大小的数据进行排序而开发的一种算法,是Hadoop MapReduce中常用的基准.与MapReduce执行的一般结构一致,在TeraSort执行过程中,每个服务器节点首先将其本地存储的每个数据点映射到密钥空间的特定分区中,然后将同一分区中的所有数据点转移到一个节点上,在该节点上进行分区内的排序,以减少最终的排序输出.而编码TeraSort的基本过程为:
1) 输入数据点被分割成不相交的文件,每个文件存储在多个精心选择的服务器节点上,以对数据创建结构化冗余.
2) 每个节点按照TeraSort的映射过程映射分配给它的所有文件.
3) 每个节点利用数据放置中强加的结构化冗余,为数据变换创建编码数据包,使得每个编码数据包的组播同时将数据点发送到多个节点,从而加快了数据洗牌速度.
4) 每个节点从接收到的编码报文中解码其Reduce阶段所需的数据点,并遵循TeraSort的Reduce过程.
4.2 一种数据洗牌的柔韧索引编码方法
如何利用索引编码提高分布式计算系统的通信效率,特别是迭代计算中的数据洗牌,是近年来出现的一个研究热点.Song等人[48]提出了一种与传统索引编码不同的柔韧索引编码,为数据洗牌提供一个更有效的框架,可以更好地利用许多可能的洗牌选择来减少传输量.他们分析了在数据洗牌的约束(希望每条消息最多传递给特定数量的工作节点,比如c,即每个节点都能接收任意它没有的信息,但是最多只有c个节点能接收一条相同的信息)下,柔韧索引编码的性能,实现看起来“类似随机”的无偏数据分布.Song等人[48]证明了:即使c=1,在某些情况下,仍然可以比索引编码获得O(n)的好处;证明了约束柔韧指数编码问题是NP难问题.另外还证明了,对于随机情况,当![]() 时,最优码长上界趋近于
时,最优码长上界趋近于![]() 当
当![]() 时,为
时,为![]()
其次,Song等人[48]还设计了一种以约束柔韧索引编码为组成部分的分层数据变换传输方案.引入汉明距离测度来量化洗牌性能,该方案在主节点具有线性编码复杂度的情况下,在传输优于索引编码方面可以达到O(ns/m),其中s是缓存大小,ns/m是缓存每个消息的平均工作节点的数量.
4.3 分布式学习的近最优编码数据洗牌
分布式节点集群之间的数据洗牌是实现大规模学习算法的关键步骤之一.在一组工作节点中随机地洗牌数据集,允许不同的节点在每个学习阶段获得新的数据分配.这一过程已被证明可以改善学习过程.然而,分布式数据洗牌的优点在于从主节点到工作节点的额外通信开销较少,但是也可能成为整个计算时间的主要瓶颈之一.目前不少研究者热衷于研究最小化通信开销的方法,一种方法是在计算节点上增加额外的存储.另一种新兴的方法是利用编码通信原理来最小化总体通信开销.
Attia等人[49]将重点放在主节点-工作节点设置的编码数据洗牌上,在主节点-工作节点设置中,编码机会是通过利用工作节点的额外存储空间来创建的.在每次训练开始之前,主节点对数据进行洗牌,以便在每个工作节点上分配不同的训练数据,这样会产生通信开销.在一种极端情况下,当所有工作节点都有足够的存储空间来存储整个数据集时,就不需要通过通信来进行任何随机洗牌.另一方面,当存储空间刚好能够存储分配的数据时(也称为无多余存储情况),那么通信开销将会达到最大.因此,目标是实现由洗牌产生的通信开销与分布式工作节点中的可用存储空间之间的基本权衡.
Attia等人[49]推导了最坏情况下数据洗牌问题通信开销的理论下界.这一工作的进行开始于在一些已选择洗牌的速率上得到了一组下界,由于任意洗牌的速率最好与最坏情况洗牌的速率一样大,因此得到的下界也可以作为最坏情况下速率的有效下界.然后得出所有选择洗牌的下界平均值,这里的关键步骤是选择那些导致作为存储函数的通信开销的最佳下界的洗牌.特别地,考虑一组循环洗牌,在随后的2次洗牌中,分配给任何工作节点的数据批处理之间没有重叠.基于一种新的边界方法[50-51],将下界表示为线性方程.然后,求解线性方程,以获得不同存储状态下通信开销的最佳下界.
Attia等人[49]介绍了基于放置/更新过程的可实现方案来维护存储结构,将其称为“结构不变的放置和更新”.存储放置涉及跨维度对数据点进行分区,这需要任意工作节点至少存储每个数据点的某些部分.通过精心设计的存储更新机制,可以随着时间的推移维护存储结构.这需要应用一种数据交付机制[52],当分布式工作节点的数量K增加时,在![]() 的消息间隙比内接近最优最坏情况下的通信存储权衡(基于所得到的下界).
的消息间隙比内接近最优最坏情况下的通信存储权衡(基于所得到的下界).
另外,Attia等人[49]还介绍了如何充分描述最坏情况下最优通信开销的新思想,他们证明,通过考虑更复杂的干扰对齐机制,可以使每个工作节点看到的干涉占据最小可能的维度,这个过程称为“对齐编码洗牌”方案.根据这一思想,可以缩小某些存储值所得到的界限之间的差距,缩小K<5时的差距,并使K≥5时最大空隙率降低到![]()
4.4 分布式数据洗牌最坏情况下的通信开销
用于处理大规模数据集的分布式学习平台正日益流行.在典型的分布式学习平台中,主节点将数据集分解成更小的快,以便跨分布式工作节点进行并行处理来实现速度和效率的收益.由于一些计算任务是顺序执行,涉及到数据的多次传递,在每次数据迭代中,通常的做法是在主节点上随机重新洗牌数据,为每个工作节点分配不同的批处理任务.这种随机的重新洗牌操作的代价是增加额外的通信开销,因为在每次洗牌时,需要将新的数据点交付给分布的工作节点.
Attia等人[53]研究了无冗余存储条件下的分布式数据洗牌问题的理论最优通信开销.
1) 给出了一个理论公式,借助一个描述工作节点中间数据流的洗牌矩阵,提出了一种新的方法来定义通信问题;
2) 提出了一种新的编码数据传递方案,在没有多余存储的情况下,每个工作节点只能存储分配的准备处理的数据,与现有的方法相比,它利用了一种新的编码方案来减少通信开销,该方案适用于任意的洗牌方式和任意数量的分布式工作节点;
3) 给出了数据洗牌最小通信开销的理论下界,并证明了所提方案符合最坏情况下通信开销的下界.
5 编码的其他应用
5.1 存在掉队节点的分布式计算统一编码框架
Li等人[46]提出了一个存在掉队节点的分布式计算的统一编码框架,在线性计算任务的计算延迟和通信负载之间进行权衡.通过考虑这种权衡的2个极端情况:分别最小化通信负载和计算延迟,他们证明,重复中间计算以创建编码多播机会以减少通信负载的文献[43,54]的编码方案,以及生成冗余中间计算以对抗掉队节点的文献[24]的编码方案,可以被视为所提出框架的特殊实例.此外,所提出的编码框架实现的权衡允许在该权衡上的任意一点进行操作,以执行分布式计算任务.这个统一的编码框架本质上是最小带宽码和最小延迟码的同时使用,在计算的不同阶段分别利用这2种编码技术.在Map阶段,使用MDS码创建编码任务,然后将这些任务以特定的冗余方式分配给节点,以便本地执行.根据Map阶段的特定计算延迟,只要有一定数量的节点完成本地计算,所有运行的Map任务就会终止(即最小延迟码).然后在Shuffle阶段,贪心地利用最小带宽码指定的编码组播机会,直到满足所有节点的数据需求.统一编码框架能够灵活地选择权衡点,以减少整个作业的执行时间.例如当网络速度较慢时,可以等待更多节点完成它们的映射计算,从而创造更好的多播机会来进一步削减通信数据量.另一方面,当检测到某些节点运行缓慢或响应缓慢时,只要执行了足够多的编码任务,就可以通过结束Map阶段将负载转移到网络上.Li等人[46]还证明了延迟负载权衡的一个理论下界,该下界与通信负载和计算延迟权衡关系之间存在一个不变的常量差.
5.2 分布式雾计算
Li等人[55]将文献[43,54]中提出的编码思想(称之为最小带宽码)、文献[24]中提出的编码思想(称之为最小延迟码)和文献[46]中提出的统一编码框架应用到分布式雾计算中,进行了探讨,并通过实例验证了这些编码思想、框架的优越性(可以加速总响应时间、计算时间、增强系统鲁棒性).
5.3 存在截止时间的并行和分布式计算的编码卷积
Dutta等人[56]考虑了存在掉队节点的情况下,使用并行处理器计算2个长向量的卷积问题,首先证明在简单的最坏情况下,将向量分割成更小的片段,并使用线性编码对这些片段进行编码,与基于副本的方案相比,具有更好的对抗掉队节点的效果.然后他们证明,在常用的计算时间模型下,编码可以显著提高在目标截止时间内完成计算的概率.与通常使用的预期计算时间分析技术不同,Dutta等人[56]量化了失效概率的指数.提出的指数度量显示了在指定的截止时间(即尾部行为)之前未能完成的概率.此外,还允许对更通用的计算时间模型使用简单的闭式表达式,例如移位威布尔模型,而不是对指数进行移位.通过编码卷积问题,Dutta等人建立了一种新的分布式系统用于分析渐近失效指数的实用性.
5.4 基于异构集群的编码计算
编码可以有效利用计算结果和存储冗余以减轻同构集群中的掉队节点和通信瓶颈的影响.但是虚拟数据中心中的计算环境是异构的,基于同构假设的算法会导致系统的性能大大降低.Reisizadeh等人[57]研究由各种不同性能的计算机组成的通用异构分布式计算集群,提出了一个编码框架,通过交换冗余来减少计算延迟,从而加速存在掉队节点的异构集群的分布式计算.他们提出了一种用于在异构集群中加速分布式矩阵乘法的编码框架,称为异构编码矩阵乘法(heterogeneous coded matrix multi-plication, HCMM),用于对可证明渐近最优的异构集群执行分布式矩阵乘法,证明了如果集群中的工作节点的数量为n,HCMM比任何未编码的框架要快Θ(lg n).
设TC为随机变量,表示接收至少r个内积的等待时间,即1组可解码结果,HCMM所需解决的核心问题是下面的优化问题:
minimize E[TC].
(13)
对于同构集群,为了实现编码解决方案,可以将原矩阵分成k个大小相等的子矩阵,并在这k个子矩阵中运用(n,k) MDS码进行编码.然后,主节点可以从任意k个编码子矩阵得到最终结果.在同构集群中,找到足够数量的内积的问题可以映射到找到一组最快响应的等待时间的问题,从而可以使用顺序统计来发现预期计算时间的封闭形式表达式.文献[24]找到了最小化平均运行时间的最优的k值.在异构集群中,使用同构集群中的求解方法是不可能的,因为负载分配是不均匀的(即给每个工作节点分配的矩阵大小不是完全相等的).在这种情况下,同构集群中求解式(13)显然不再适用.Reisizadeh等人[57]提出了一种式(13)的替代公式,并证明了该公式是易解的、渐进最优的.
5.5 多核装置的编码计算
在文献[24]中,应用纠删码可以加快线性函数的分布式计算,然而,目前还不清楚线性编码是否也能加快“非线性”函数的分布式计算.为了解决这个问题,Lee等人[58]提出了利用稀疏线性编码和现代多核(多核即一个工作节点有p个核心)的处理体系结构,指出1)编码解决方案达到顺序最佳运行时间;2)当工作节点的数量为n时至少比任何未编码的方案快![]() 倍,为任务分配和编码计算提供了建设性的框架和算法,以实现预期的最佳运行时间(直到常数因素).另外,Lee等人[58]的“逆向”结果表明,随着系统中工作节点数量的增加,如果任何任务分配(不管任务复制与否)在工作节点与主节点的通信中没有使用编码,那么这些作业的完成时间存在无限大的差距.
倍,为任务分配和编码计算提供了建设性的框架和算法,以实现预期的最佳运行时间(直到常数因素).另外,Lee等人[58]的“逆向”结果表明,随着系统中工作节点数量的增加,如果任何任务分配(不管任务复制与否)在工作节点与主节点的通信中没有使用编码,那么这些作业的完成时间存在无限大的差距.
5.6 分布式计算的层次编码
大多数现有的分布式计算编码都假定一个简单的主节点-工作节点模型,Park等人[59]提出了一个由工作节点组成的层次计算结构,其目的是反映现实世界分布式计算系统的体系结构.如图12所示,将所有的工作节点平均分成i个组,先对每个组使用![]() 编码,然后再对i个组使用(n2,k2) MDS编码.子的主节点收到任意k1个工作节点的计算结果可解码出子任务的计算结果,主节点收到任意k2个子的主节点的计算结果可解码出总任务的计算结果.
编码,然后再对i个组使用(n2,k2) MDS编码.子的主节点收到任意k1个工作节点的计算结果可解码出子任务的计算结果,主节点收到任意k2个子的主节点的计算结果可解码出总任务的计算结果.
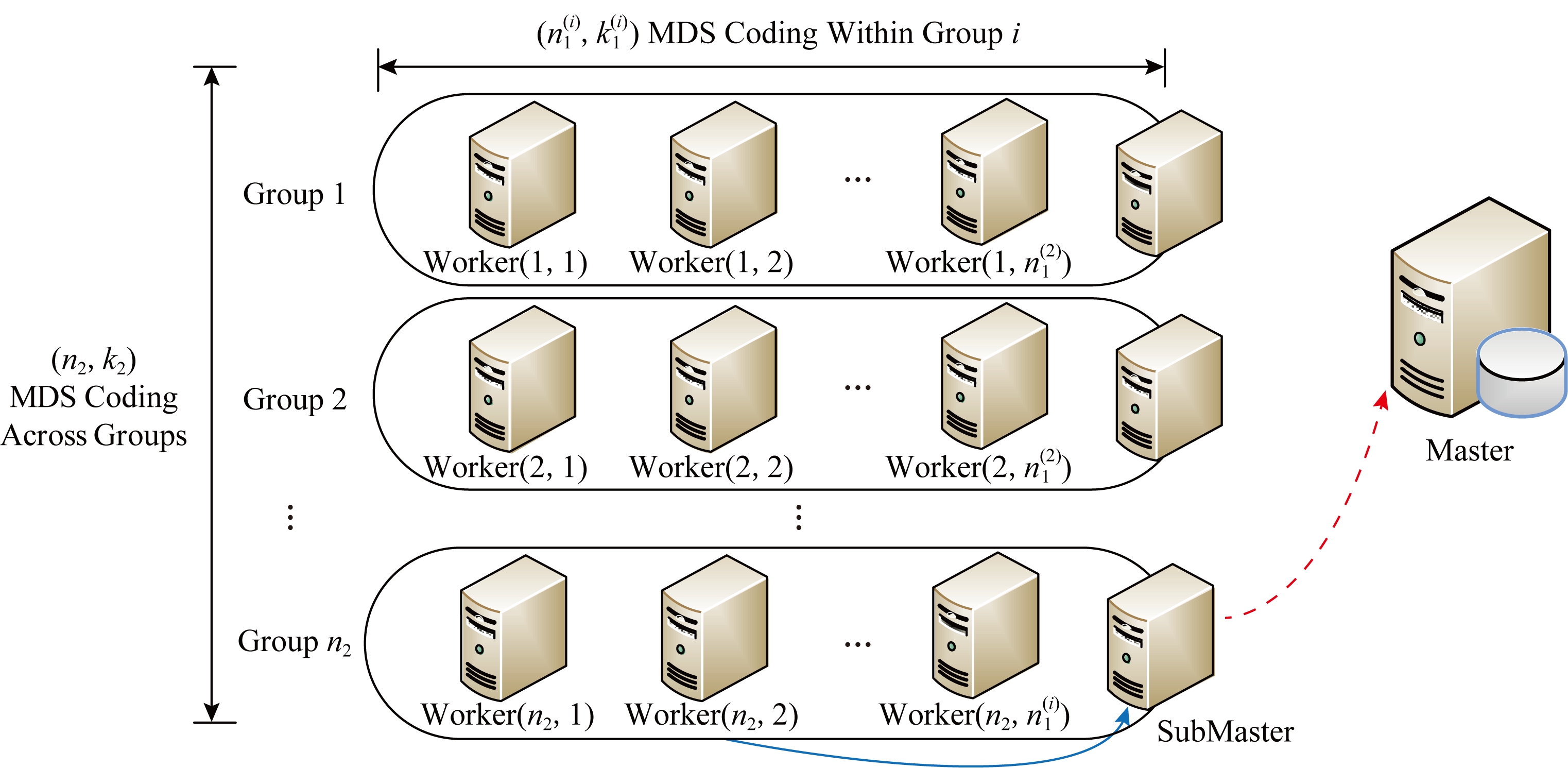
Fig.12 Illustration of hierarchical coding
图12 层次编码示例
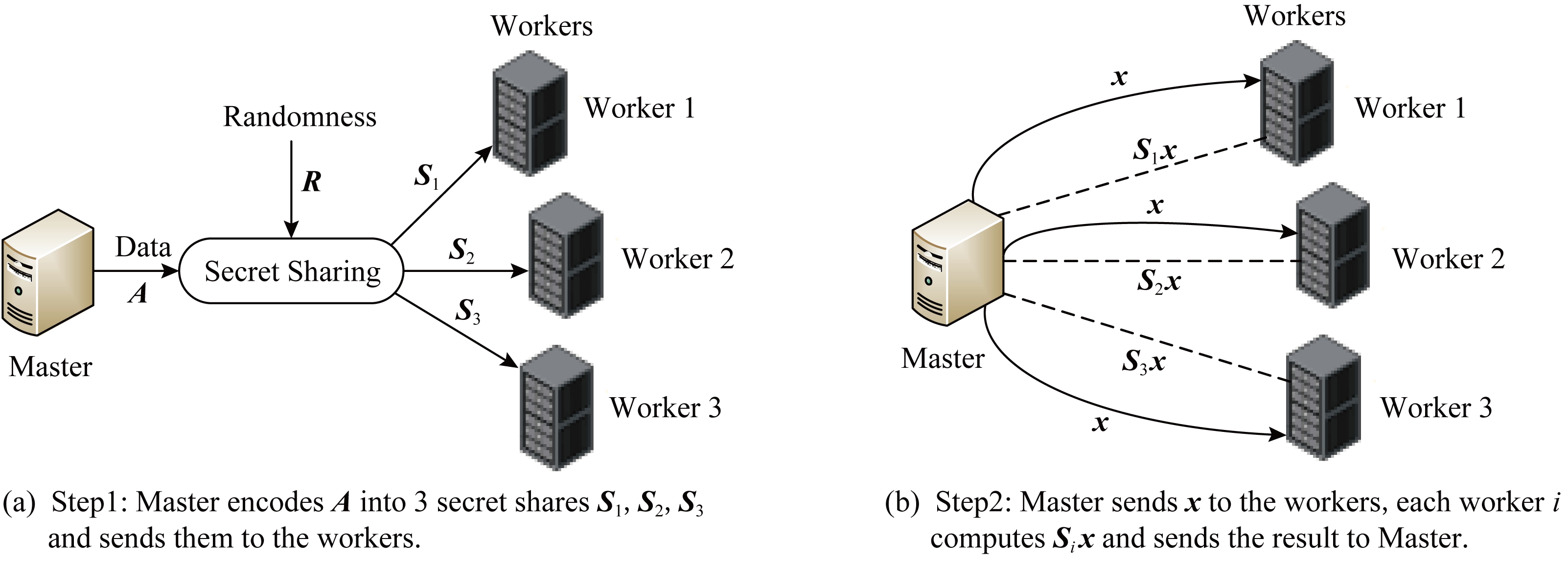
Fig.13 Illustration of secret sharing scheme with 3 workers
图13 3个工作节点的密钥共享方案示例
5.7 安全分布式计算的最小化延迟
在进行密集的计算(例如机器学习算法的一部分)时,主节点希望将这些计算任务分发给那些不受信任的工作节点,其中这些工作节点是自愿或受到激励来帮助完成这项任务的.然而,这些数据(即需要计算的任务)必须保持私密,不能透露给单个工作节点.另外,工作节点可能会忙于处理其他计算任务,甚至没有响应,它们会随机抽时间来完成分配给它们的任务.一个已知的解决方案是使用一个密钥共享的方案将数据划分为工作节点可以计算的密钥共享[60].Bitar等人[61]提出了一种新的安全编码,称为楼梯编码.图13是密钥共享方案的简单示例.
1) 文献[60]给出的密钥共享方案中计算任务由3个工作节点完成,最多允许1个工作节点未响应.如图13(b)所示,主节点Master生成一个随机矩阵R,其维数与A相同,在相同的域内,并将A和R编码为3个子矩阵S1=R,S2=R+A,S3=R+2A分别发送给3个节点.主节点收到任意2个节点的返回结果可解码出计算结果.
2) 文献[61]给出的楼梯编码方案中主节点Master将矩阵A和R分成A=[A1A2]T和R=[R1R2]T,将子任务A1+A2+R1和R1+R2发送给工作节点1,将子任务A1+2A2+4R1和R1+2R2发送给工作节点2,将子任务A1+3A2+4R1和R1+3R2发送给工作节点3.主节点有2种解码的可能:
① 主节点接收(A1+A2+R1)x,(A1+2A2+4R1)x,(A1+3A2+4R1)x可解码出计算结果,此时只需解码R1x,不需要解码R2x;
② 主节点接收任意2个节点的全部子任务结果可解码出计算结果,此时需解码R1x和R2x.
Bitar等人[61]提出了一个主节点Master拥有整个数据集的模型,在该模型上Master要执行分布式线性计算,引入了一种新的方法,将线性计算安全外包给不拥有该数据任何部分的n个工作节点.他们假设,最多n-k(k<n)个工作节点可能没有响应,其余的工作节点可以随时作出响应,这类似于掉队节点问题.Bitar等人[61]研究了在使用楼梯编码时,在指数模型下主节点的等待时间,即工作节点造成的总延迟.另外:1)推导了平均等待时间的上界和下界;2)推导出一个积分表达式,并使用这个表达式找到k=n-1和k=n-2时确切的平均等待时间;3)将楼梯编码与秘钥共享的方案进行了比较,结果表明,对于高速率、k=n和少量工作节点的情况,楼梯编码的方案能节省大约40%的等待时间,通过模拟来检查边界的严密性,并表明对于低速率的情况,对于任意的n楼梯编码方案节省了至少10%的等待时间.
5.8 近似矩阵编码
文献[24]的核心思想是利用MDS码生成冗余计算来减轻掉队节点的影响,这种方法的一个特点是直到得到精确解才会有最终输出,因此,过多处理器节点的输出延迟会显著影响总任务的时延.然而,如果放松对精确解的要求,那么这个问题就会得到有效缓解.针对这一情况,Nuwan等人[62]提出了一种用于近似矩阵乘法的任意时刻编码方案,通过近似计算的形式来加速分布式计算.将任务分解成优先级不同的若干子任务,在矩阵乘法中表现为矩阵的大小不同,越大的矩阵优先级越高;然后按优先级顺序分配工作节点,矩阵越大,分配的工作节点数量就越多.编码优点在于,可以在任意时刻结束处理任务,而且在任意时刻结束任务时都可以使用已完成任务的输出来产生一个近似解,并可以计算这个解的精度.显然,近似解的精度随着时间的推移而提高.文献[24]关注于得到精确的结果,而在Nuwan等人[62]的模型中,不需要等到输出的特定子集以找到精确的结果,相反,随着工作的完成,可以形成一个增量改进的过程,与现有编码方案相比,该方案能提高近似质量,便于近似计算.
6 总结与展望
本文将基于编码技术改进大规模机器学习集群性能的研究按照应用场景分成了应用于矩阵乘法、梯度计算、数据洗牌和一些其他应用,并分别进行了介绍并比对分析.
编码在存储领域的研究成果并不能直接应用在机器学习算法中,因为EC编码应用于存储领域抵抗“erasure”节点对数据可靠性造成的影响与应用于大规模机器学习集群中抵抗掉队节点对分布式机器学习算法性能造成的影响存在着很大的区别,前者增加的是数据的冗余,后者则是通过增加数据冗余来增加计算任务的冗余;后者关注于对掉队节点的鲁棒性,前者相较于对erasure节点的鲁棒性更加关注于如何对失效数据进行修复.
近几年,学术界对通过使用编码技术来解决分布式计算系统中的掉队节点问题,以及改进大规模机器学习集群性能等问题进行了研究,并取得了一定的成果,但仍然还存在很多问题需要进一步的研究.本文提出3个亟待解决的问题和该领域的研究趋势:
1) 目前提出的通过编码技术提高对掉队节点的鲁棒性的编码方案只是针对矩阵乘法等不需要进行迭代的机器学习算法,而对涉及到迭代的梯度下降算法只是采用了副本这一方式,因为副本之外的编码方案需要预先设计编码块来提供计算任务的冗余,从而实现对掉队节点的容忍,而涉及到迭代的机器学习算法的每一次迭代的数据是不同的,很难实现对每次迭代数据进行编码.如何使用其他编码方案而不只是副本改进存在迭代的机器学习算法的性能,在我们看来可以作为今后对基于编码技术改进大规模机器学习集群性能的研究方向之一.另外,将本文提到的编码方案拓展到更多的机器学习应用也是今后研究的一个趋势.
2) 现有的研究都是理论分析,所进行的实验与测试也只是模拟分布式场景对编码方案进行简单的实现和测试其性能,并没有具体应用于现有的机器学习算法.因此,对编码技术的实际应用还需要进一步研究,比如,多项式编码中涉及到很多参数,在实际应用中不同参数的设置对分布式机器学习集群的性能会产生不同的影响.
3) 利用计算机集群,使机器学习算法更好地从大数据中训练出性能优良的大模型是分布式机器学习的目标.为了实现这一目标,一般需要根据硬件资源与数据/模型规模的匹配情况,考虑对计算任务、训练数据和模型进行划分,考虑对计算任务、训练数据和模型进行划分,然后对划分后的计算任务等进行分布式存储和分布式训练.分布式机器学习可以分为计算并行模式、数据并行模式和模型并行模式.现有的编码技术目前只应用在数据并行模式上,对于如何应用在模型并行上尚未有相关讨论.另外,不同的数据并行和模型并行方法之间是可以互相结合的,而在此基础上如何应用编码技术更是需要今后进行研究与探讨.
[1]Zaharia M, Chowdhury M, Franklin M J, et al.Spark: Cluster computing with working sets[C] //Proc of the 2nd USENIX Conf on Hot Topics in Cloud Computing.Berkeley, CA: USENIX Association, 2010
[2]Dean J, Ghemawat S.MapReduce: Simplified data processing on large clusters[J].Communications of the ACM, 2008, 51(1): 107-113
[3]Dean J, Barroso L A.The tail at scale[J].Communications of the ACM, 2013, 56(2): 74-80
[4]Dimakis A G, Godfrey P B, Wu Yunnan, et al.Network coding for distributed storage systems[J].IEEE Transactions on Information Theory, 2010, 56(9): 4539-4551
[5]Rashmi K V, Shah N B, Kumar P V.Optimal exact-regenerating codes for distributed storage at the MSR and MBR points via a product-matrix construction[J].IEEE Transactions on Information Theory, 2011, 57(8): 5227-5239
[6]Tamo I, Wang Zhiying, Bruck J.MDS array codes with optimal rebuilding[C] //Proc of IEEE Int Symp on Information Theory.Piscataway, NJ: IEEE, 2011: 1240-1244
[7]Suh C, Ramchandran K.Exact-repair MDS code construction using interference alignment[J].IEEE Transactions on Information Theory, 2011, 57(3): 1425-1442
[8]Cadambe V R, Huang Cheng, Jafar S A, et al.Optimal repair of MDS codes in distributed storage via subspace interference alignment[J].arXiv preprint, arXiv: 1106.1250, 2011
[9]Papailiopoulos D S, Luo Jianqiang, Dimakis A G, et al.Simple regenerating codes: Network coding for cloud storage[C] //Proc of IEEE INFOCOM 2012.Piscataway, NJ: IEEE, 2012: 2801-2805
[10]Silberstein N, Rawat A S, Vishwanath S.Error resilience in distributed storage via rank-metric codes[C] //Proc of the 50th Annual Allerton Conf on Communication, Control, and Computing.Piscataway, NJ: IEEE, 2012: 1150-1157
[11]Papailiopoulos D S, Dimakis A G, Cadambe V R.Repair optimal erasure codes through hadamard designs[J].IEEE Transactions on Information Theory, 2013, 59(5): 3021-3037
[12]Kamath G M, Prakash N, Lalitha V, et al.Codes with local regeneration[C] //Proc of the Information Theory and Applications Workshop (ITA).Piscataway, NJ: IEEE, 2013: 1-5
[13]Huang Cheng, Simitci H, Xu Yikang, et al.Erasure coding in windows azure storage[C] //Proc of the USENIX Conf on Annual Technical.Berkeley, CA: USENIX Association, 2012: 15-26
[14]Sathiamoorthy M, Asteris M, Papailiopoulos D, et al.Xoring elephants: Novel erasure codes for big data[C] //Proc of the 39th Int Conf on Very Large Data Bases.New York: ACM, 2013: 325-336
[15]Rashmi K V, Shah N B, Gu Dikang, et al.A solution to the network challenges of data recovery in erasure-coded distributed storage systems: A study on the Facebook warehouse cluster[J].arXiv preprint, arXiv: 1309.0186, 2013
[16]Rashmi K V, Shah N B, Gu Dikang, et al.A hitchhiker's guide to fast and efficient data reconstruction in erasure-coded data centers[J].ACM SIGCOMM Computer Communication Review, 2015, 44(4): 331-342
[17]Abadi M, Barham P, Chen Jianmin, et al.Tensorflow: A system for large-scale machine learning[C] //Proc of the 12th USENIX Symp on Operating Systems Design and Implementation.Berkeley, CA: USENIX Association, 2016: 265-283
[18]Chen Tianqi, Li Mu, Li Yutian, et al.Mxnet: A flexible and efficient machine learning library for heterogeneous distributed systems[J].arXiv preprint, arXiv: 1512.01274, 2015
[19]Dean J, Corrado G, Monga R, et al.Large scale distributed deep networks[C] //Proc of the Neural Information Processing Systems (NIPS).New York: ACM, 2012: 1223-1232
[20]Reed I S, Solomon G.Polynomial codes over certain finite fields[J].Journal of the Society for Industrial & Applied Mathematics, 1960, 8(2): 300-304
[21]Choi J, Walker D W, Dongarra J J.PUMMA: Parallel universal matrix multiplication algorithms on distributed memory concurrent computers[J].Concurrency: Practice and Experience, 1994, 6(7): 543-570
[22]Van De Geijn R A, Watts J.SUMMA: Scalable universal matrix multiplication algorithm[J].Concurrency: Practice and Experience, 1997, 9(4): 255-274
[23]Solomonik E, Demmel J.Communication-optimal parallel 2.5D matrix multiplication and LU factorization algorithms[C] //Proc of European Conf on Parallel Processing.Berlin: Springer, 2011: 90-109
[24]Lee K, Lam M, Pedarsani R, et al.Speeding up distributed machine learning using codes[J].IEEE Transactions on Information Theory, 2018, 64(3): 1514-1529
[25]Mallick A, Chaudhari M, Joshi G.Rateless codes for near-perfect load balancing in distributed matrix-vector multi-plication[J].arXiv preprint, arXiv: 1804.10331, 2018
[26]Luby M.LT codes[C] //Proc of the 43rd Annual IEEE Symp on Foundations of Computer Science.Piscataway, NJ: IEEE, 2002: 271-280
[27]MacKay D J C.Fountain codes[J].IEEE Proceedings-Communications, 2005, 152(6): 1062-1068
[28]Lee K, Suh C, Ramchandran K.High-dimensional coded matrix multiplication[C] //Proc of Int Symp on Information Theory (ISIT).Piscataway, NJ: IEEE, 2017: 2418-2422
[29]Yu Qian, Maddah-Ali M, Avestimehr S.Polynomial codes: An optimal design for high-dimensional coded matrix multiplication[J].arXiv preprint, arXiv: 1705.10464, 2018
[30]Yu Qian, Maddah-Ali M A, Avestimehr A S.Straggler mitigation in distributed matrix multiplication: Fundamental limits and optimal coding[J].arXiv preprint, arXiv: 1801.07487, 2018
[31]Dutta S, Fahim M, Haddadpour F, et al.On the optimal recovery threshold of coded matrix multiplication[J].arXiv preprint, arXiv: 1801.10292, 2018
[32]Dutra S, Bai Ziqian, Jeong H, et al.A unified coded deep neural network training strategy based on generalized polydot codes[C] //Proc of IEEE Int Symp on Information Theory (ISIT).Piscataway, NJ: IEEE, 2018: 1585-1589
[33]Kiani S, Ferdinand N, Draper S C.Exploitation of stragglers in coded computation[C] //Proc of IEEE Int Symp on Information Theory (ISIT).Piscataway, NJ: IEEE, 2018: 1988-1992
[34]Narra K, Lin Zhifeng, Kiamari M, et al.Distributed matrix multiplication using speed adaptive coding[J].arXiv preprint, arXiv: 1904.07098, 2019
[35]Ramamoorthy A, Tang Li, Vontobel P O.Universally decodable matrices for distributed matrix-vector multi-plication[J].arXiv preprint, arXiv: 1901.10674, 2019
[36]Tandon R, Lei Qi, Dimakis A G, et al.Gradient coding: Avoiding stragglers in distributed learning[C] //Proc of the 34th Int Conf on Machine Learning.Sydney, Australia: PMLR, 2017: 3368-3376
[37]Ye Min, Abbe E.Communication-computation efficient gradient coding[J].arXiv preprint, arXiv: 1802.03475, 2018
[38]Dutta S, Cadambe V, Grover P.Short-dot: Computing large linear transforms distributedly using coded short dot products[J].arXiv preprint, arXiv: 1704.05181, 2017
[39]Halbawi W, Azizan N, Salehi F, et al.Improving distributed gradient descent using reed-solomon codes[C] //Proc of IEEE Int Symp on Information Theory (ISIT).Piscataway, NJ: IEEE, 2018: 2027-2031
[40]Raviv N, Tamo I, Tandon R, et al.Gradient coding from cyclic MDS codes and expander graphs[J].arXiv preprint, arXiv: 1707.03858, 2017
[41]Charles Z, Papailiopoulos D, Ellenberg J.Approximate gradient coding via sparse random graphs[J].arXiv preprint, arXiv: 1711.06771, 2017
[42]Tandon R, Lei Qi, Dimakis A G, et al.Gradient coding[J].arXiv preprint, arXiv: 1612.03301, 2016
[43]Li Songze, Maddah-Ali M A, Avestimehr A S.Coded mapreduce[C] //Proc of the 53rd Annual Allerton Conf on Communication, Control, and Computing.Piscataway, NJ: IEEE, 2015: 964-971
[44]Lee K H, Lee Y J, Choi H, et al.Parallel data processing with MapReduce: A survey[J].ACM SIGMOD Record, 2012, 40(4): 11-20
[45]Jiang Dawei, Ooi B C, Shi Lei, et al.The performance of mapreduce: An in-depth study[J].Proceedings of the VLDB Endowment, 2010, 3(1/2): 472-483
[46]Li Songze, Maddah-Ali M A, Avestimehr A S.A unified coding framework for distributed computing with straggling servers[J].arXiv preprint, arXiv: 1609.01690, 2016
[47]Li Songze, Supittayapornpong S, Maddah-Ali M A, et al.Coded terasort[C] //Proc of IEEE Int Parallel and Distributed Processing Symp Workshops (IPDPSW).Piscataway, NJ: IEEE, 2017: 389-398
[48]Song Linqi, Fragouli C.A pliable index coding approach to data shuffling[J].arXiv preprint, arXiv: 1701.05540, 2017
[49]Attia M A, Tandon R.Near optimal coded data shuffling for distributed learning[J].arXiv preprint, arXiv: 1801.01875, 2018
[50]Wan Kai, Tuninetti D, Piantanida P.On the optimality of uncoded cache placement[C] //Proc of IEEE Information Theory Workshop (ITW).Piscataway, NJ: IEEE, 2016: 161-165
[51]Yu Qian, Maddah-Ali M A, Avestimehr A S.The exact rate-memory tradeoff for caching with uncoded prefetching[J].IEEE Transactions on Information Theory, 2018, 64(2): 1281-1296
[52]Naderializadeh N, Maddah-Ali M A, Avestimehr A S.Fundamental limits of cache-aided interference management[J].IEEE Transactions on Information Theory, 2017, 63(5): 3092-3107
[53]Attia M A, Tandon R.On the worst-case communication overhead for distributed data shuffling[C] //Proc of the 54th Annual Allerton Conf on Communication, Control, and Computing.Piscataway, NJ: IEEE, 2016: 961-968
[54]Li Songze, Maddah-Ali M A, Yu Qian, et al.A fundamental tradeoff between computation and communication in distri-buted computing[J].IEEE Transactions on Information Theory, 2018, 64(1): 109-128
[55]Li Songze, Maddah-Ali M A, Avestimehr A S.Coding for distributed fog computing[J].IEEE Communications Magazine, 2017, 55(4): 34-40
[56]Dutta S, Cadambe V, Grover P.Coded convolution for parallel and distributed computing within a deadline[C] //Proc of IEEE Int Symp on Information Theory (ISIT).Piscataway, NJ: IEEE, 2017: 2403-2407
[57]Reisizadeh A, Prakash S, Pedarsani R, et al.Coded computation over heterogeneous clusters[J].arXiv preprint, arXiv: 1701.05973, 2017
[58]Lee K, Pedarsani R, Papailiopoulos D, et al.Coded computation for multicore setups[C] //Proc of IEEE Int Symp on Information Theory (ISIT).Piscataway, NJ: IEEE, 2017: 2413-2417
[59]Park H, Lee K, Sohn J, et al.Hierarchical coding for distributed computing[J].arXiv preprint, arXiv: 1801.04686, 2018
[60]Atallah M J, Frikken K B.Securely outsourcing linear algebra computations[C] //Proc of the 5th ACM Symp on Information, Computer and Communications Security.New York: ACM, 2010: 48-59
[61]Bitar R, Parag P, El Rouayheb S.Minimizing latency for secure distributed computing[C] //Proc of IEEE Int Symp on Information Theory (ISIT).Piscataway, NJ: IEEE, 2017: 2900-2904
[62]Ferdinand N S, Draper S C.Anytime coding for distributed computation[C] //Proc of the 54th Annual Allerton Conf on Communication, Control, and Computing.Piscataway, NJ: IEEE, 2016: 954-960



