在强化学习(reinforcement learning, RL)中,通常采用Markov决策过程(Markov decision processes, MDPs)作为不确定情况下的序贯决策问题的框架[1-2].RL的目标是通过最大化累积未来奖赏来获得最优策略.目前部分算法可以应用于带有明确样本转移和奖赏的强化学习问题中,而大多数的无模型算法可以直接学习到不同的动作值[3-5].其中,Q学习(Q-learning)是迄今为止最受欢迎的模型无关的强化学习算法[5-6],但由于在评估动作值过程中包含1个最大化操作,有时学习到的动作值比真实值会高很多,这直接导致了动作值的过高估计.
深度学习(deep learning, DL)已经成为机器学习领域的一大研究热点[7].其能够从原始图像中获取特征,通过线性或者非线性组合来获得更好的数据表征.DL已经在模型压缩、神经语言模型、情感分析等领域取得了很大的突破[8-10].深度学习和强化学习有着不同的特性,结合这两者得到深度强化学习(deep reinforcement learning, DRL)[11-12],可以帮助agent在一些复杂的环境中更好地学习和决策.
深度Q网络(deep Q-network, DQN)是第1个成功结合非线性函数逼近技术——深度神经网络(deep neural network, DNN)和Q学习的算法[13].DQN已经被证明能够在不同Atari 2600游戏中学习到人类级别的控制策略.DQN从当前游戏状态中评估每个可能动作的Q值.考虑到网络中的Q值估计足够精确,所以通常会在每个时间步选择具有最大Q值的动作来进行游戏.DQN以及基于DQN的改进算法已被证明可以在许多Atari 2600游戏中表现优异.
DQN将Q学习与灵活的深度神经网络相结合,并在各种各样的大量确定性Atari 2600游戏上进行测试,实验结果表明它在许多游戏中达到了人类级别的表现[14].虽然深度神经网络提供了灵活的函数逼近以及低渐进逼近误差的可能性,并且环境的确定性防止了噪声的有害影响,但是在这种相对有利的情况下,DQN有时也会大大高估动作值.
针对这种情况,Van Hasselt等人[15]提出了深度双Q网络(double deep Q-network, DDQN).这种算法不仅可以产生更准确的值估计,而且可以在部分游戏中获得更高的分数.这表明DQN的高估确实会影响策略的好坏,并且降低高估对于游戏性能来说是有益的.但是,DDQN有时会低估动作值从而产生偏差[15].章宗长等人[16]在双Q学习(double Q-learning, DQL)的基础上提出了基于权重的双Q学习(weighted double Q-learning, WDQ).该算法的目的是在单个估计器的高估和2个估计器的低估之间寻找平衡.实验结果表明,该算法能有效减少估计误差,并在大量的MDP问题中表现优异.Anschel等人[17]提出了另一种解决高估现象的方法——基于平均值的深度Q网络(averaged deep Q-network, Averaged-DQN),也就是计算先前学习到的Q值的平均值作为目标值.实验结果表明这种方法能有效提高训练的稳定性,且表现突出.
在本文中,我们将章宗长等人[16]提出的带权重的双估计器扩展到了深度强化学习中.为了缓解深度Q网络的高估和深度双Q网络的低估问题,我们将带权重的双估计器与深度双Q网络结合,形成新的基于权重的深度双Q网络算法(weighted double deep Q-network, WDDQN).此外,为了进一步减少目标值估计的方差,我们对Anschel等人[17]提出的Averaged-DQN方法进行了改进.具体地,计算之前学习到的动作估计值的平均值来产生目标值并且根据时间差分误差(temporal difference error, TD error)动态地确定平均动作值的数量,并将之整合到基于权重的深度双Q网络中,形成一个新的深度强化学习框架——基于权重平均值的深度双Q网络(averaged weighted double deep Q-network, AWDDQN).
本文的主要贡献有3个方面:
1) 将带权重的双估计器引入到深度双Q网络中,提出WDDQN算法.
2) 对Averaged-DQN中的Averaging方法进行了改进:通过计算之前学习到的动作估计值的平均值来产生目标值,并且根据时间差分误差动态地确定平均动作值的数量,将之与带权重的双估计器结合,产生更精确的动作值估计,并且提出AWDDQN算法.
3) 将AWDDQN应用于Atari 2600的4个经典游戏中,对比本文算法和其他相关算法的性能.实验结果表明,通过结合双估计器和改进的Averaging方法可以提升agent的性能.
1 背景知识
1.1 强化学习
强化学习能够解决agent在环境中自主采取动作以最大化标量奖赏信号的问题.在整个探索过程中,外界从未直接告知agent最优动作.在每个离散时间步t=0,1,…,环境为agent提供1个观察St,agent根据策略选择1个动作At作出响应,然后获得环境提供的立即奖赏Rt+1,并且转移到下一状态St+1.这种交互可以形式化地定义为MDPs模型[18],用元组〈S,A,T,R,γ〉表示,其中S表示有限状态集合,A表示有限动作集合,T(s,a,s′)=P[St+1=s′|St=s,At=a]表示转移函数,R(s,a)=E[Rt+1|St=s,At=a]表示奖赏函数,γ∈[0,1]表示折扣率.
agent的动作选择由策略π给出,该策略定义了每个状态的动作概率分布.在时刻t遇到状态st,当前agent获得的未来奖赏的折扣总和称为折扣回报,定义为
(1)
agent的目标是通过寻找一个最优策略来最大化期望折扣回报.
策略可以直接被学习,也可以通过函数构建.在基于值的强化学习[19]中,当从给定状态开始遵循策略π时,agent学习期望折扣回报的估计,可以是状态值,Vπ(s)=Eπ[Gt|St=s],表示在状态s遵循策略π到情节结束获得的期望回报.也可以是状态动作值,Qπ(s,a)=Eπ[Gt|St=s,At=a],表示在状态s根据策略π选择动作a,并一直遵循策略π到情节结束获得的期望回报.从状态动作值函数中推导出新策略的一种常见方法是采用关于动作值的ε-greedy策略,也就是以1-ε概率采取贪心动作,并且以ε概率随机均匀地采取任意动作.这种策略更有利于agent在环境中探索:根据当前估计随机选择次优动作,agent可以在适当的时候发现并纠正该估计.
在强化学习中,最优动作值函数被定义为![]() 同时,最优策略可以通过
同时,最优策略可以通过![]() 获得,表示最优策略选择可以最大化期望回报的动作.
获得,表示最优策略选择可以最大化期望回报的动作.
Q学习[5-6]是一种基于值迭代更新的算法,即直接估计最优动作值函数Q*.表格式的Q学习算法利用以下更新规则来对当前动作值函数的估计值进行更新:
![]()
Q(s,a)),
(2)
其中,s′表示在状态s采取动作a到达的下一个状态,a′表示在状态s′选择的动作,α∈[0,1]表示步长参数,r表示在状态s选择动作a后获得的立即奖赏.
当状态空间非常大的时候,存储所有状态动作对的值是难以实现的.对此常用的解决办法是使用函数逼近方法来近似求解动作值函数.一般采用参数θ[20],比如Q(s,a)≈Q(s,a;θ).Q(s,a;θ)表示使用参数θ近似估计的状态动作值函数,例如可用神经网络来求得.带有函数逼近参数θ的Q学习更新使用学习规则:
![]()
Q(s,a;θ)) θQ(s,a;θ).
θQ(s,a;θ).
(3)
1.2 深度Q网络
较大的状态空间或者动作空间使得agent难以独立学习每个状态动作对的Q值估计[21].在DRL中,策略π(a|s)或者Q(s,a)常用深层(即多层)神经网络表示.这些网络参数通过梯度下降进行训练以拟合一些合适的损失函数[22].
在DQN[13]中,通过使用卷积神经网络[23]将深度网络和强化学习成功地结合起来,以近似状态s的动作值,其通常以网络中的一些原始像素帧作为输入.DQN算法包含2个重要组成部分:1)使用目标网络;2)加入经验重放机制.在每个时间步上,agent基于当前状态选择1个动作,并将该转移(s,a,r,s′)添加到经验池中.神经网络的参数通过使用随机梯度下降以使损失最小化,损失函数表示为目标值和评估值之间的均方误差,定义为
L(θ)=Es,a,r,s′[(yDQN-Q(s,a;θ))2],
(4)
其中,目标值yDQN定义为
![]()
(5)
θ表示在线网络的参数,θ-表示目标网络的参数.Q(s,a;θ)表示在线网络的输出,用于更新值函数,Q(s′,a′;θ-)表示目标网络的输出,用于计算目标值.目标网络与在线网络的结构相同,只是它的参数是从在线网络中每τ步复制而来,在τ个时间步内目标网络的参数保持不变.Mnih等人[13]的实验研究发现,使用目标网络和经验重放可以相对稳定地学习Q值,并在几款Atari游戏中带来超出人类级别的表现.
算法1给出了DQN的具体流程.在每轮迭代i中,DQN算法通过利用近似动作值函数Q(s,a;θ)解决监督学习问题,这是对式(2)的函数逼近形式的一种延伸.
算法1.DQN算法.
输入:预处理后的图像特征向量;
输出:评估网络参数θ.
① 初始化Q(s,a;θ)、随机初始θ0;
② 初始化经验重放池D;
③ 初始化关于Q的探索性策略ε-greedy;
④ For i=1 to N
⑤ ![]()
⑥![]()
⑦ 将转移(s,a,r,s′)添加到D中;
⑧ End For
DQN使用指定的目标网络Q(s,a;θi-1)(使用先前的迭代参数θi-1)计算目标值![]() (行⑤),其中期望值ED取为关于重放池中经验转移的样本分布(s,a,r,s′)~D.使用随机梯度下降(SGD)变体来最小化DQN损失,即在重放池中小批量地采取样本.在每次迭代中,通过探索添加到重放池的新经验转移(s,a,r,s′)的数量很小,因此,θi-1可以在迭代i中作为θ的一个良好的初始值.
(行⑤),其中期望值ED取为关于重放池中经验转移的样本分布(s,a,r,s′)~D.使用随机梯度下降(SGD)变体来最小化DQN损失,即在重放池中小批量地采取样本.在每次迭代中,通过探索添加到重放池的新经验转移(s,a,r,s′)的数量很小,因此,θi-1可以在迭代i中作为θ的一个良好的初始值.
1.3 深度双Q网络
标准的Q学习和DQN的最大运算符使用相同的值进行评估和选择1个动作,这使得agent会选择高估值,导致过度乐观的估计.为了解决这种问题,最有效的办法是将选择与评估分离.
在双Q学习[5]中,通过随机分配经验来更新2个值函数中的1个,从而学习2个值函数,产生2组权重θ和θ′.对于每次更新,一组权重θ用于确定贪心策略,另一组权重θ′用于评估贪心策略的值.DQL的目标值更新可以写为
![]()
(6)
具有最大Q值的动作选择仍然是由在线权重θ引起的.这意味着,和深度Q网络一样,贪心策略的值还是需要根据θ定义的当前值来估计.
双Q学习的思想是通过将目标中的最大操作分解为动作选择和动作评估来降低过高估计.在DQN框架中,目标网络是第2个值函数的最佳选择,从而不必引入额外的网络.因此,在深度双Q网络中[15],通常根据在线网络评估贪心策略,根据目标网络评估其价值.DDQN的更新与DQN相同,但其用目标yDDQN替换:
![]()
(7)
与双Q学习式(6)相比,第2个网络的权重θ′被替换成目标网络的权重θ-,用于评估当前的贪心策略.目标网络的更新与DQN保持不变,并定期将在线网络的参数复制给目标网络.
Van Hasselt等人[15]的实验研究证明DDQN可以有效减少过高估计,从而获得更稳定的学习.并且DDQN算法在Atari 2600游戏中能够获得更好的表现,能得到比DQN更好的性能.
2 基于权重平均值的深度双Q网络
本节将主要阐述如何将带权重的双估计器整合到深度双Q网络中,以及怎样利用之前学习到的动作估计值的平均值来产生目标值,并且根据时间差分误差动态地确定平均动作值的数量.
我们提出AWDDQN算法的动机主要有2点:
1) 深度Q网络存在着高估动作值的缺陷,虽然深度双Q网络在一定程度上缓解了这一问题,但是依然存在着低估动作值的问题.高估和低估问题都会对学习到的策略产生影响,有可能会导致agent的性能变差.为了缓解高估和低估的问题,本文将最近提出的带权重的双估计器[16]整合到深度双Q网络中.
2) 目标值的计算偏差会对算法的性能有重要影响.虽然Averaged-DQN算法[17]利用之前学习到的K个动作Q值产生当前动作值估计,但是K值的大小会影响算法的性能,在Averaged-DQN算法中没有提出合适的确定K值的算法,只是简单地设置为5,10,15.为了改进这种Averaging方法,不同于Averaged-DQN算法中使用固定数量的平均动作值求得目标值,本文利用时间差分误差动态地确定平均动作值的数量.动态性体现在本文根据经验池抽取样本的时间差分误差大小的不同,具有较小时间差分误差的样本,K=5,反之,K的取值为10.因此不同样本计算目标值的K值并不是固定的,是根据样本的时间差分误差大小动态决定的.进一步地,本文还将之与基于权重的双估计器结合来进一步地减小动作值的估计偏差.
2.1 基于权重的双估计器
针对DDQN低估动作值的问题,WDDQN算法以权重的方式结合了深度Q网络和深度双Q网络.WDDQN的目标是减小目标值估计的误差,从而产生更精确的动作值估计.
不需要在DDQN中引入额外的网络,评估网络依然产生具有最大动作值的动作,目标网络则用于评估最大动作的值.
WDDQN使用Q(s′,a*;θ)和Q(s′,a*;θ-)的线性结合计算目标值,计算为
yWDDQN=r+γ[β Q(s′,a*;θ)+
(1-β)Q(s′,a*;θ-)],
(8)
其中,β定义为权重,计算为
![]()
(9)
动作a*表示为评估网络具有最大动作值的动作,aL表示评估网络具有最小动作值的动作,计算为
![]()
(10)
![]()
(11)
因此,Q(s′,a*;θ-)表示目标网络中在状态s′的最大动作值,Q(s′,aL;θ-)表示目标网络中状态s′的最小动作值.
式(9)中的c为超参数,用来计算权重β .在具有不同特征的问题中,c的最优值不一样.例如具有不同动作数量的赌博机问题最优的c值不同[16].因此,通常根据问题的特征自适应地设置c值.本文实验中采用的c值在多次实验的基础上选取.具体的WDDQN算法如算法2所示:
算法2.WDDQN算法.
输入:初始化评估网络参数θ、目标网络参数θ-、初始化经验池D;
输出:评估网络参数θ.
① For episode=1 to M do
② 初始化初始状态s0;
③ For t=0 to T do
④ 根据ε-greedy策略选择动作at;
⑤ 执行动作at,观察下一状态st+1和立即奖赏rt;
⑥ 将转移样本(st,at,rt,st+1)存入经验池中;
⑦ 从经验池D中抽取批量转移样本(sj,aj,rj,sj+1)进行更新;
⑧![]()
⑨![]()
⑩ 计算权重β:
 计算目标值:
计算目标值:
(1-β)Q(sj+1,a*;θ-)];
 随机梯度下降更新评估网络参数:
随机梯度下降更新评估网络参数:
 每经过C个时间步,将参数θ复制给θ-;
每经过C个时间步,将参数θ复制给θ-;
 End For
End For
 End For
End For
2.2 基于时间差分误差的Averaging方法
为了减少目标值计算的方差,获得更好的训练稳定性和性能,Averaged-DQN算法[17]利用先前学习的动作值来计算平均值从而产生目标值.然而,该算法仅仅只是将先前学习到的K个动作值求平均,K的取值为定值.若K值较小,算法的性能不理想.若K值较大,算法的性能有所提高,但大大增加了计算量.针对这个问题,本文对Averaging方法进行改进,利用转移样本的时间差分误差来动态地确定K值,并将之与基于权重的双估计器结合来进一步减少目标值估计的偏差和方差.
AWDDQN在更新网络参数时,从经验池中抽取n个转移样本.然后分别计算这n个样本的时间差分误差,时间差分误差表示该样本的目标值和评估值之间的差距.若时间差分误差较大,评估值不够准确,目标值存在较大的方差.AWDDQN算法将这n个样本的时间差分误差进行排序分成2组,对具有不同时间差分误差的样本进行区别对待.因为较小K值对算法的性能提升不大,较大K值会导致计算量增加,算法耗时久,所以本文的K值经验性地选取为5和10.
对于时间差分误差较小的样本,计算目标值时使用较少的K1=5个先前学习到的动作值的平均值来求目标值.对于时间差分误差较大的样本,使用K2=10个先前学习到的动作值的平均值计算目标值.这样的方式避免使用较大的K值,导致增加计算量,并且能够根据每个样本的时间差分误差动态地确定K值.AWDDQN计算目标值时使用基于权重的双估计器,计算为
![]()
![]()
(12)
AWDDQN将抽取的n个样本按照时间差分误差分成2组后,使用不同的K值进行目标值的计算,然后采用随机梯度下降方法对这一批量的样本进行网络参数的更新.
2.3 算法描述
在DDQN框架中,结合了基于权重的双估计器和基于时间差分误差的Averaging方法,形成了AWDDQN框架.
AWDDQN的实施过程如算法3所示:
算法3.AWDDQN算法.
输入:初始化评估网络参数θ、目标网络参数θ-、初始化经验池D;
输出:评估网络参数θ.
① For episode=1 to M do
② 初始化初始状态s0;
③ For t=0 to T do
④ 根据ε-greedy策略选择动作at;
⑤ 执行动作at,观察下一状态st+1和立即奖赏rt;
⑥ 将转移样本(st,at,rt,st+1)存放到经验池中;
⑦ 从经验池D中抽取n批量转移样本(sj,aj,rj,sj+1)进行更新;
⑧ 对抽取的n批量样本按照时间差分误差进行排序分成2组;
⑨ 具有较小时间差分误差的样本,K=5,具有较大时间差分误差的样本,K=10;
⑩![]()
 计算权重β:
计算权重β:
 计算目标值:
计算目标值:
 随机梯度下降更新评估网络参数θ:
随机梯度下降更新评估网络参数θ:
 每经过C个时间步,将参数θ复制给θ-;
每经过C个时间步,将参数θ复制给θ-;
 End For
End For
 End For
End For
首先输入初始化的超参数,agent在初始状态根据ε-greedy策略选择动作a0,并执行a0动作,得到下一状态和奖赏,随后将转移样本存入经验池中.训练网络时,从经验池中抽取n个样本,并按照时间差分误差将样本分成2组,然后使用基于时间差分误差的Averaging方法和基于权重的双估计器计算目标值,接着使用随机梯度下降更新网络的参数.agent在每个时间步根据网络输出的Q值来确定需要执行的动作,经过一定的时间步后,将当前评估网络的权重θ复制给目标网络.
3 实验及结果分析
本节主要介绍实验平台、实验参数设置、实验评估标准以及实验结果分析.
3.1 实验平台描述
本文将OpenAI开发的Gym[24]实验平台作为实验环境.Gym是一款用于研发和比较强化学习算法的工具包,它支持训练智能体agent完成多种任务——从行走到玩Pong或围棋之类的游戏.Gym实验平台包含了Atari 2600,MuJoCo等多种游戏环境.Atari 2600中每个游戏环境不同,且包含多种游戏类型.Gym提供了一个严格的测试平台,用来评估比较强化学习、模式学习、模仿学习、迁移学习以及深度强化学习这些方法.
DQN,DDQN使用了深度Q学习和双Q学习算法来训练agent,由于存在高估和低估动作值的问题,它们的性能并不是很令人满意.为了提升agent的性能,本文提出AWDDQN算法,并选取了4个Atari 2600游戏中具有代表性的游戏:Seaquest,Asterix,BeamRider,SpaceInvaders来设计实验.实验以DDQN为基准比较算法,根据实验结果评估AWDDQN算法在这些游戏上的表现,并与DDQN,WDDQN,ADDQN进行比较.
DDQN是Van Hasselt等人[15]提出的深度双Q网络.WDDQN是以加权的方式结合DQN和DDQN的算法.ADDQN是将基于时间差分误差的Averaging方法加入到深度双Q网络中,不使用基于权重的双Q学习算法更新网络参数,其目标值计算为
yADDQN=r+
![]()
(13)
AWDDQN是本文提出的将基于权重的双估计器和基于时间差分误差Averaging方法结合的深度双Q网络.
其中,AWDDQN的网络结构和DQN的网络结构相同,如图1所示:该网络由3个卷积层和2个全连接层构成;第1个卷积层为32个步幅为4的8×8的过滤器,第2个卷积层为64个步幅为2的4×4的过滤器,第3个卷积层为64个步幅为1的3×3的过滤器,最后隐藏层是由512个神经元组成的全连接线性层,输出层神经元数量和游戏合法动作数量相同.网络的输入是游戏的4帧画面,输出是该游戏状态下每个动作的Q值.
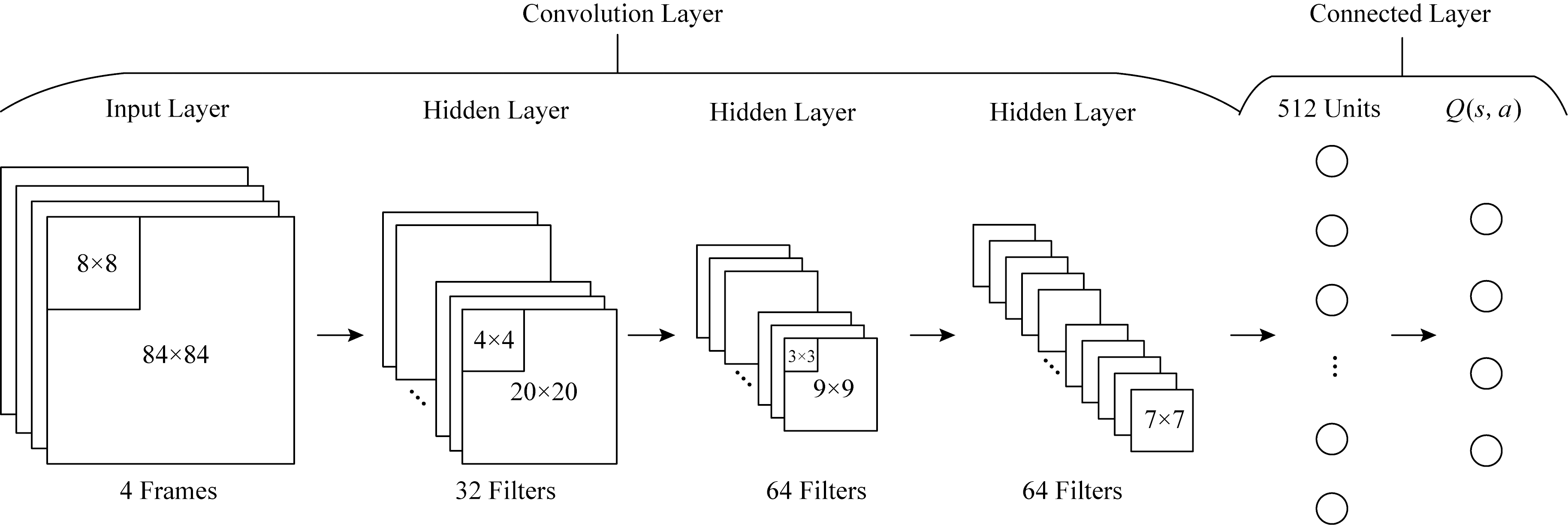
Fig.1 The architecture of AWDDQN
图1 AWDDQN网络结构示意图
3.2 实验参数设置
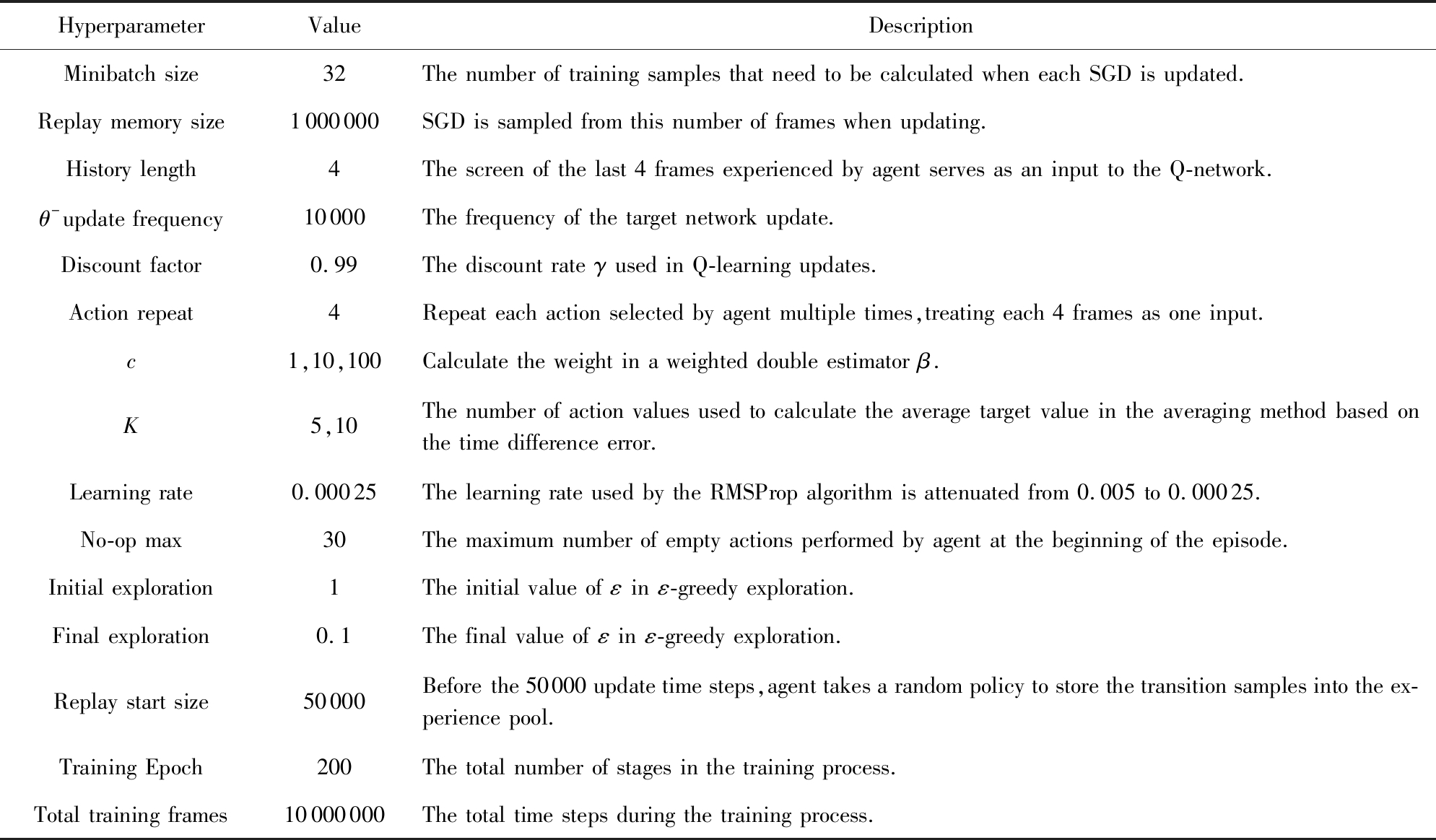
在本文设计的实验中,4种算法使用的大部分超参数是相同的,如表1所示.
上述4种算法的网络结构与DQN相同.在训练agent玩游戏的过程中,网络模型的输入通常是游戏的画面,因为模型中的卷积层能够自动学习到游戏画面的良好特征表达,所以在实验之前,不需要人工设计特征作为网络的输入数据.
在WDDQN中,使用了基于权重的双Q学习更新方式,用来计算权重的超参数c取值为1,10,100.在ADDQN中,使用基于时间差分的Averaging方法计算目标值进行更新,用来计算平均目标值的超参数K取值为5,10.而在AWDDQN中,使用基于权重的双Q学习和基于时间差分的Averaging方法结合计算目标值.其中,c=10,K取值为5,10.
样本池的最大容量为100万个转移样本.在训练的开始阶段,为了使agent在学习初期有足够的样本进行训练,在50 000更新时间步之前,agent采取随机的策略存储转移样本到样本池中.这样的方式使得agent的训练没有偏向性.
在实验中,还运用了一些常用方法[13]来减少不稳定现象.
1) 奖赏限界.在Atari 2600游戏中,因为每个游戏的环境不同,所得到的最终得分也有着较大差异.为了更清晰地比较实验效果,通常将每个游戏中的正奖赏设置为+1,负奖赏设置为-1,其余保持不变.
2) 误差裁剪.在深度强化学习中,一般使用基于均方根的随机梯度下降来逐步更新网络参数.在实验过程中,将动量系数设为0.95.不同游戏之间使用不同的学习率影响算法的稳定性,更有可能陷入局部最优.因此,在训练和测试过程中,将TD误差项裁剪到[-1,1]区间中,并且将梯度裁剪到[-5,5]区间中.
3) 批量更新.每次更新网络参数时,都需要从经验池中选取小批量的转移样本.在实验中,批量n设置为32.同时,设置折扣因子为0.99.学习率η与行为策略的参数ε设置为从情节开始到一定区间内递减的方式,学习率η从0.005逐渐递减到0.000 25,探索因子ε从1.0逐渐递减到0.1.
Table 1 The Detailed Explanation of Hyperparameters
表1 超参数的详细说明
HyperparameterValueDescriptionMinibatch size32The number of training samples that need to be calculated when each SGD is updated.Replay memory size1000000SGD is sampled from this number of frames when updating.History length4The screen of the last 4 frames experienced by agent serves as an input to the Q-network.θ-update frequency10000The frequency of the target network update.Discount factor0.99The discount rate γ used in Q-learning updates.Action repeat4Repeat each action selected by agent multiple times,treating each 4 frames as one input.c1,10,100Calculate the weight in a weighted double estimator β.K5,10The number of action values used to calculate the average target value in the averaging method based on the time difference error.Learning rate0.00025The learning rate used by the RMSProp algorithm is attenuated from 0.005 to 0.00025.No-op max30The maximum number of empty actions performed by agent at the beginning of the episode.Initial exploration1The initial value of ε in ε-greedy exploration.Final exploration0.1The final value of ε in ε-greedy exploration.Replay start size50000Before the 50000 update time steps,agent takes a random policy to store the transition samples into the ex-perience pool.Training Epoch200The total number of stages in the training process.Total training frames10000000The total time steps during the training process.
3.3 实验评估
在强化学习方法中,通常采用经历1个情节所获得的累积奖赏来作为评价标准.在Atari 2600游戏中,将agent玩1局游戏作为1个情节,因此,1局游戏所获得的得分就是累积奖赏.
训练深度Q网络往往需要很长时间,因此,一般深度Q网络的训练通过分阶段完成.在本文的实验中,将训练过程中各阶段得到的平均每情节奖赏数作为这4个算法性能的评估标准.
在Mnih等人[13]提出的DQN中,其训练过程是通过200个阶段来完成的.在每个阶段中,参数更新经历了250 000时间步,评估过程经历了125 000时间步.DQN在GPU上的训练大约需要2周的时间.为了保证不同算法之间的参数一致性和计算效率,虽然本文实验中的训练过程采用200个训练阶段,但是每个训练阶段只包含50 000时间步的参数更新过程以及25 000时间步的评估过程.这样的设置在GPU上只需要3天就能在1个游戏环境下训练出1个模型.
3.4 实验结果分析
本文首先比较了DDQN和WDDQN在训练玩Seaquest,Asterix,SpaceInvaders,BeamRider这4个游戏过程中的表现,探究超参数c对WDDQN算法性能的影响.
为了验证WDDQN算法在训练过程中的表现要优于DDQN算法[15]并探究超参数c对WDDQN算法的影响,首先进行实验来比较这2种算法在训练agent玩4种游戏时各阶段所获得的平均每情节奖赏.在WDDQN算法中,本文设置的超参数c,分别取值为1,10,100.图2展示这2种算法在训练4种游戏时各阶段平均每情节奖赏,其中x轴表示训练阶段,y轴表示平均每情节奖赏.
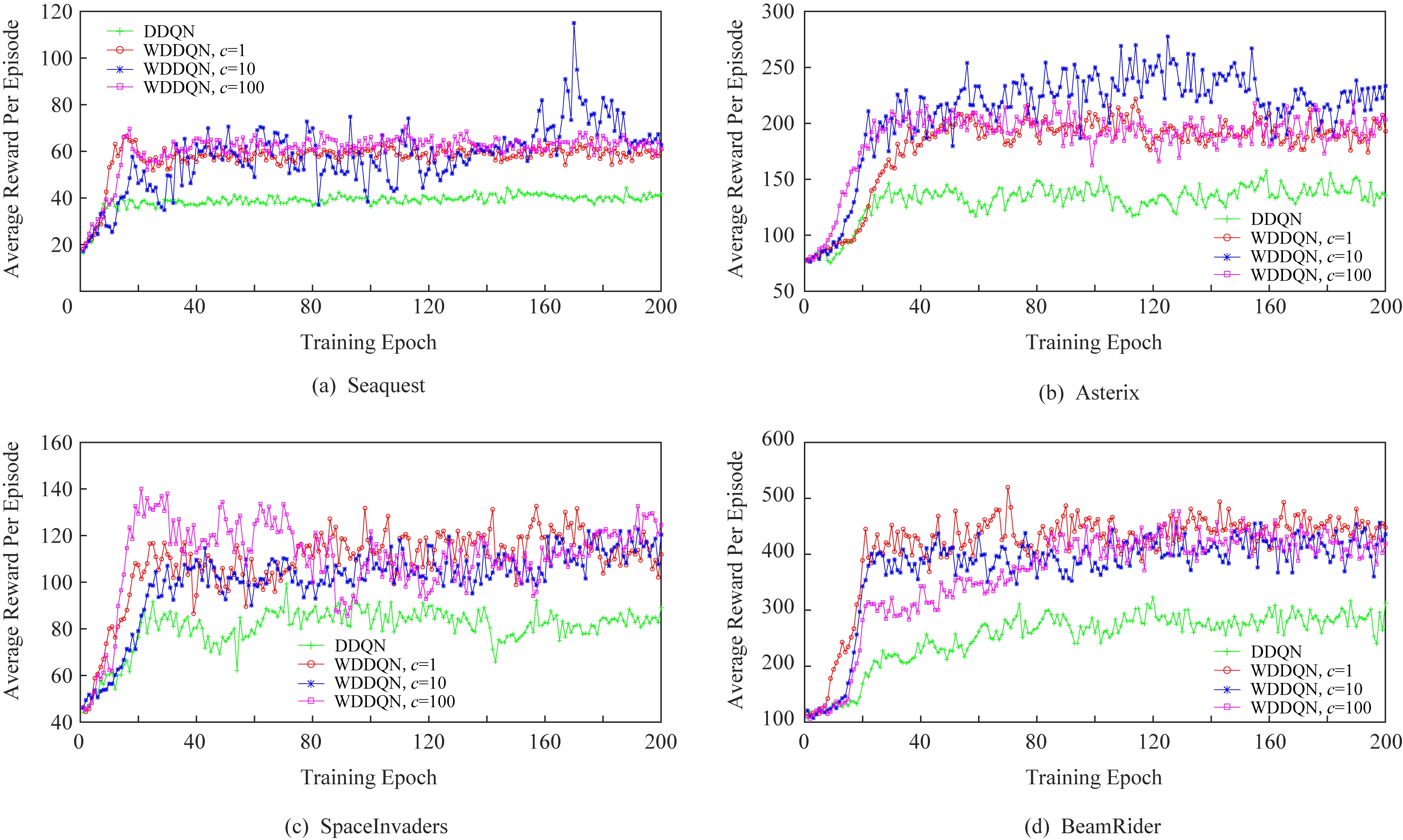
Fig.2 Comparisons of DDQN,WDDQN for Atari games
图2 采用DDQN,WDDQN训练Seaquest,Asterix,SpaceInvaders,BeamRider时各阶段平均每情节奖赏对比
图2表明在训练这4种游戏时,随着训练阶段的增加,WDDQN算法获得的平均每情节奖赏高于DDQN算法,尤其是在20个训练阶段之后表现更加明显.实验结果表明使用基于权重的双Q学习的WDDQN算法可以更大程度地减小目标值估计的误差,产生更精确的动作值估计,因此可以更加快速地学习到一些关键性策略,提高游戏得分.因此,WDDQN算法的性能好于DDQN,这说明了使用基于权重的双Q学习训练agent比只使用双Q学习训练更加有效.
WDDQN的3种算法在训练这4种游戏时的性能大致相当,没有太大的差距.但是从图2中的Asterix游戏对比图中看出,当c=10时,WDDQN算法性能稍微好于当c=1或100时,这说明WDDQN中计算权重的超参数c对算法性能存在着一定的影响.在第1组实验中当c取值为1,10,100时,WDDQN算法性能都要优于DDQN算法,然而这样的设置并不精确,可能还存在更优的c的取值,或许也可以根据动作值将超参数c表示成函数,使得c成为一个动态学习的参数.
另外,从图2可以看出,随着训练阶段的增加,尤其是在经历了180个训练阶段之后,WDDQN的3种算法获得的平均每情节奖赏趋于稳定.这在一定程度上保证了WDDQN算法的稳定性.
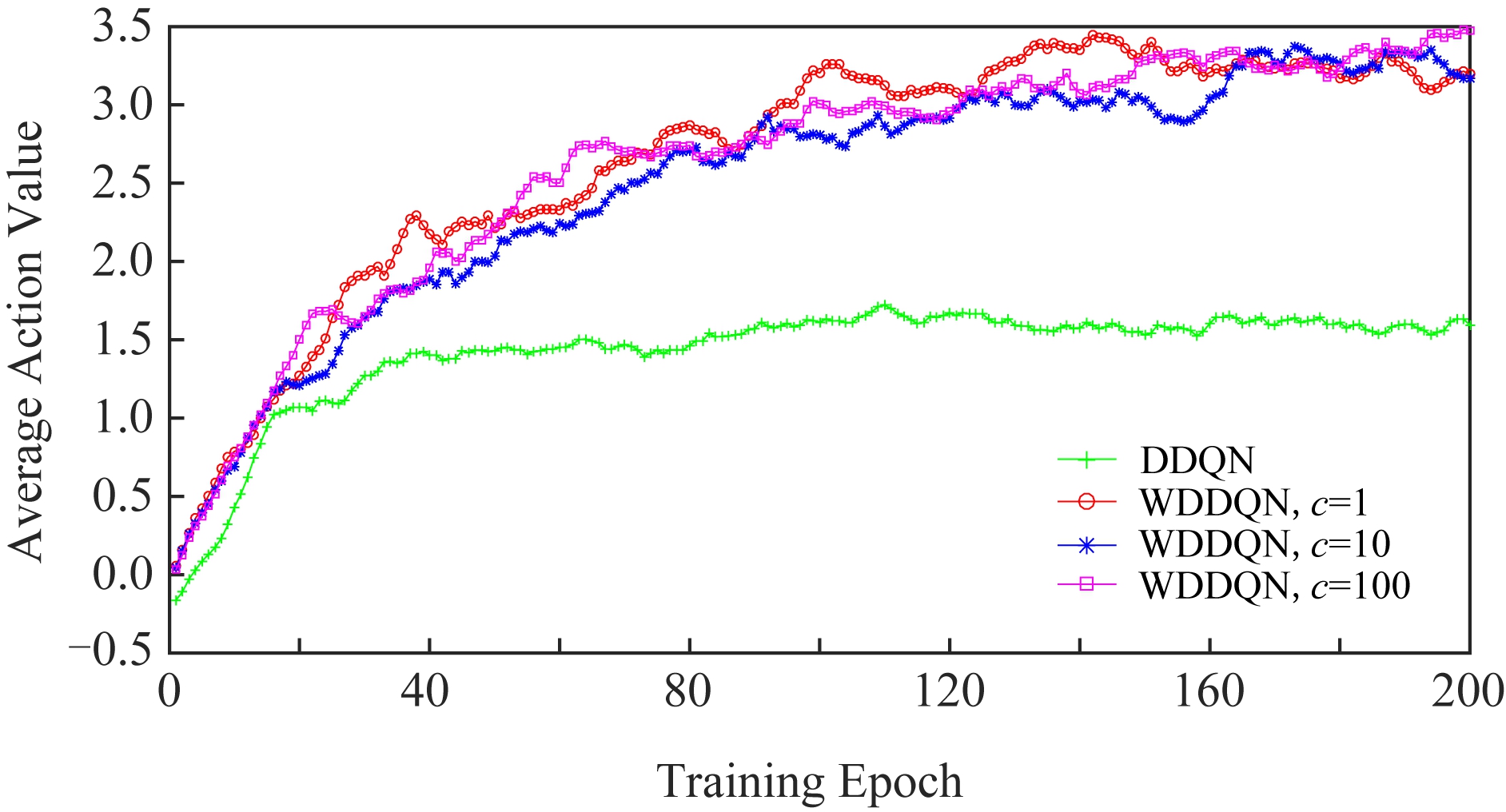
Fig.3 Average Q-values per episode for each stage of Seaquest
图3 训练Seaquest时各阶段平均每情节状态动作值
图3对比了DDQN和WDDQN算法在训练Seaquest游戏时各阶段获得的平均每情节的最大动作Q值.Seaquest游戏是一种战略性的游戏,提高得分的关键是agent是否能够及时学习到一些关键性策略.比如,当潜水艇在海底并且氧气不足时,agent应该选择多次上浮到水面储备氧气的动作.但是在游戏中有些动作需要在一个状态下重复执行多次,该动作带来的效益也会在较多时间步之后才会表现在游戏画面上并且被agent感知.如果agent不能学习到这个动作,那么得分会很低.
图3中WDDQN算法在训练过程中平均每情节最大Q值要比DDQN高3~4倍,这表明使用了基于权重的双Q学习方法,能够大幅度地减少动作值的低估,促进Q值的增长.而DDQN算法由于只使用双Q学习算法,存在低估动作值的不足,因此Q值曲线上升缓慢.

Fig.4 Comparisons of WDDQN,ADDQN,AWDDQN for Atari games(c=10)
图4 采用WDDQN,ADDQN,AWDDQN算法训练4种游戏时各阶段平均每情节奖赏对比(c=10)
WDDQN算法的Q值曲线一直处于上升趋势,这表明如果训练阶段增加,其平均每情节的最大Q值会越来越高,性能也会越来越好.从图3可以发现,WDDQN算法在训练时获得的Q值平缓上升并趋于收敛,充分说明WDDQN算法在训练过程中的稳定性和有效性.而相比于DDQN算法,WDDQN算法因为使用了基于权重的双Q学习方法,在训练时更加稳定,表现更好.
因此,在训练Seaquest游戏时,WDDQN算法可以有效地学习到关键性动作,在潜水艇氧气不足且还在海底深处时,重复执行向上动作多次直到储备了足够的氧气.在DDQN中,由于采用双Q学习的训练方式,对目标值的估计不够准确,会出现低估的情况,因此难以学习到玩Seaquest氧气不足时不断向上的动作,所以agent的性能不是很理想.
本文对WDDQN,ADDQN,AWDDQN在训练过程中的表现进行比较.为了验证AWDDQN算法在训练过程中的表现要优于WDDQN和ADDQN算法,进行实验来比较这3种算法在训练agent玩Seaquest,Asterix,SpaceInvaders,BeamRider等游戏时各阶段所获得的平均每情节奖赏.在这组实验中,WDDQN和AWDDQN算法均使用超参数c=10,ADDQN使用超参数K取值为5,10.图4展示3种算法在训练时各阶段的平均每情节奖赏.
图4表明AWDDQN算法的训练效果好于其余2种算法,随着训练阶段的增加,平均每情节获得的奖赏越来越大,并且和WDDQN和ADDQN算法的差距越发显著.这表明将基于权重的双估计器和基于时间差分误差的Averaging方法结合,能够更加准确地计算目标值,更准确地进行值估计.相对于单独使用其中任一方法,AWDDQN算法能够更加快速地学习一些关键性策略,提高游戏得分.因此在深度双Q网络中,将基于权重的双估计器和基于时间差分误差的Averaging方法结合是有效的,可以提升agent的性能,且性能超过这2个单一的方法.
ADDQN平均每情节获得的奖赏和WDDQN算法相比,两者之间差距不是很大.这能够说明基于时间差分误差的Averaging方法也可以改进DDQN算法的性能,其性能可以达到WDDQN的水平.然而,观察图4可以发现,在Asterix和BeamRider游戏中,ADDQN算法平均每情节获得的奖赏稍微低于WDDQN,这说明在某些游戏上ADDQN算法的性能会低于WDDQN.因此,ADDQN算法在一定程度上能够进行比较精确的动作值估计,提升自身的决策能力.
在训练过程中,3种算法各阶段的平均每情节奖赏值都存在一定波动,但是AWDDQN算法的波动相对较小,且平均每情节奖赏一直处于上升趋势中.奖赏值产生波动主要原因是在训练网络的过程中,每个时间步参数都在更新,虽然网络参数每次的变动都很小,但也会导致最终输出的动作值发生较大的变化,进而引起agent在下一阶段中学习到的策略发生较大变化.
为了进一步说明这3种算法在训练时的稳定性,图5对比了上述3种算法在Seaquest游戏中各阶段所获得的平均每情节的最大动作Q值.
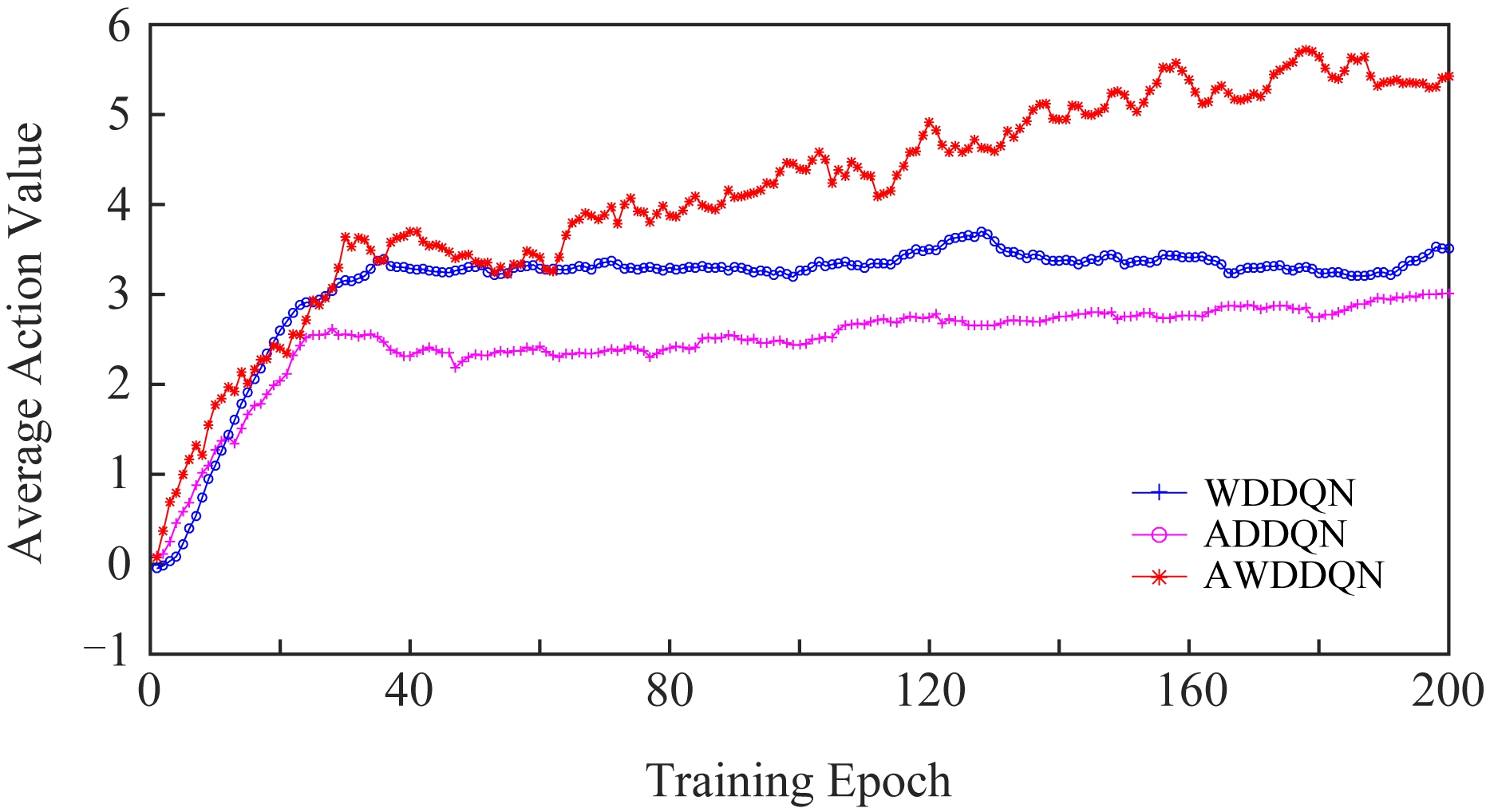
Fig.5 Average Q-values per episode for each stage of Seaquest(c=10)
图5 训练Seaquest时各阶段平均每情节状态动作值(c=10)
从图5可以看出AWDDQN在训练过程中平均每情节最大Q值函数的曲线高于WDDQN和ADDQN,这表明AWDDQN结合使用基于权重的双估计器和基于时间差分误差的Averaging方法,减少了动作值的低估,促进了Q值的增长.
AWDDQN的Q值曲线一直处于上升的趋势中,如果训练阶段增加,其性能会越来越好.而对于WDDQN和ADDQN算法,因为一直学习不到游戏中能够提高游戏得分的关键性策略,Q值曲线上升缓慢并趋于平缓.从图5可以看出,在训练后期,3种算法的Q值上升平缓并趋于收敛,表明这3种算法在训练时的稳定性,且AWDDQN算法在训练中表现更加稳定.
进一步地,本文比较了不同超参数K的取值对AWDDQN算法性能和运行时间效率的影响.本文进行了WDDQN,ADDQN,AWDDQN算法运行时间的对比.在AWDDQN算法中,K值分别选取了3组:K取值为5,10;K取值为10,15;K取值为15,20.运行时间对比结果如表2所示:
Table 2 Average Epoch Training Time of WDDQN, ADDQN,AWDDQN
表2 WDDQN,ADDQN,AWDDQN算法每训练阶段 平均运行时间对比

AlgorithmTraining Time∕minWDDQN21.6ADDQN24.5AWDDQN with K values of 5 and 1028.4AWDDQN with K values of 10 and 1536.8AWDDQN with K values of 15 and 2048.3
从表2可以看出,AWDDQN算法的训练时间比WDDQN和ADDQN算法所需的时间长.WDDQN和ADDQN算法所需要的训练时间相差不大.虽然AWDDQN算法的训练时间较长,但其获得的训练效果比其他2个算法更好.因此,AWDDQN算法的性能总体上优于WDDQN和ADDQN算法.从表2的后3行可以发现,选取不同K值来训练AWDDQN算法所花费的时间不同,对算法的影响较大.当K取值为15,20时,AWDDQN算法的每训练阶段平均运行时间为48.3 min,远高于其余2种AWDDQN算法.
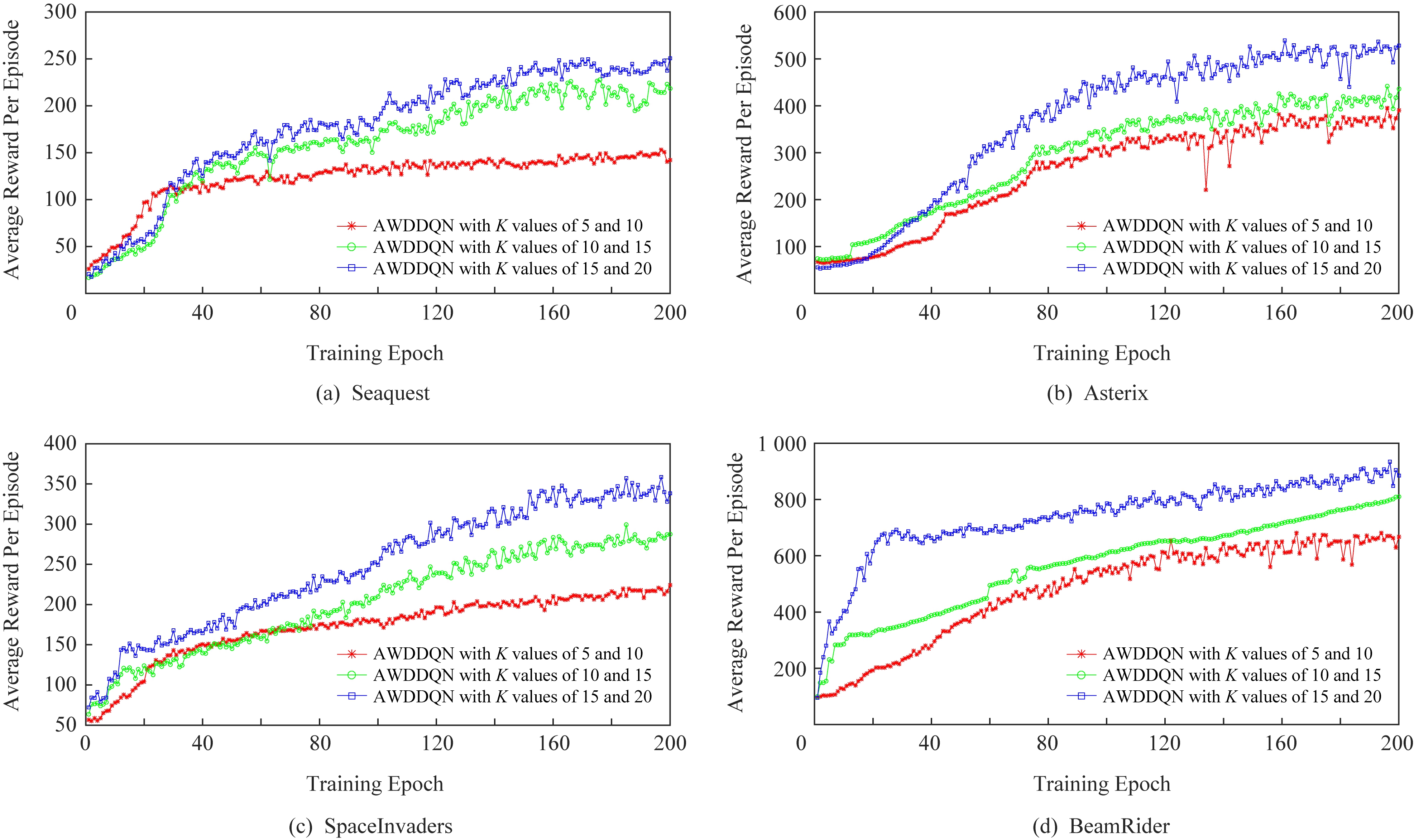
Fig.6 Comparisons of AWDDQN with different values of K for Atari games
图6 选取不同K值的AWDDQN算法训练4种游戏时各阶段平均每情节奖赏对比
另外,本文对比了具有不同K值的AWDDQN算法在训练Seaquest,Asterix,SpaceInvaders,Beam-Rider游戏时的表现.从图6可以看出,当K取值为15,20时,AWDDQN算法获得的各阶段平均每情节奖赏最大.K取值为10,15的AWDDQN算法获得的奖赏比K取值为5,10的算法大.在训练阶段后期,AWDDQN算法的奖赏曲线趋于平缓,表明该算法具有稳定性.因此,随着K值的增加,AWDDQN算法的性能越来越好,更好地减小估计值和目标值之间的误差.然而,虽然算法性能有所提升,但其所需的训练时间增加,导致计算量增加,从而降低算法的运行效率.所以,在特定的游戏环境中,综合考虑算法的运行效率和性能表现,选取适当的K值,有利于提高算法的效率,提升算法的性能.
最后本文还将训练完成后的DDQN,WDDQN,ADDQN,AWDDQN这4个算法用来玩这4个游戏,比较它们在测试过程中的性能.我们将训练完成后的模型经历1个步长为25 000的游戏测试过程来评估其性能的好坏.为了保证测试结果的多样性,每次游戏的初始状态都随机选取.不同游戏中agent在训练和测试过程中都采用ε-greedy策略,其中,ε=0.05.实验比较了4个模型在4种游戏中经历200次测试后得到的平均得分值和最大得分值.
实验结果详细如表3所示.从表3的平均值一列可以得到,与其他3种算法相比,训练完成后的AWDDQN算法在指导agent玩这4种游戏时的表现更好.这表明训练完成后的AWDDQN算法模型性能也优于DDQN,WDDQN,ADDQN算法.另一方面,从表3的最大值一列中可以看出, AWDDQN在玩这4种游戏时的最优表现也优于其他3种算法.与训练过程类似,针对这4种游戏,AWDDQN算法的测试性能好于DDQN,WDDQN,ADDQN算法,WDDQN算法和ADDQN算法测试性能相当,但都优于DDQN算法.
Table 3 The Scores of 4 Different Games After Different Training
表3 训练完成后的不同算法在4种游戏上的测试得分评估
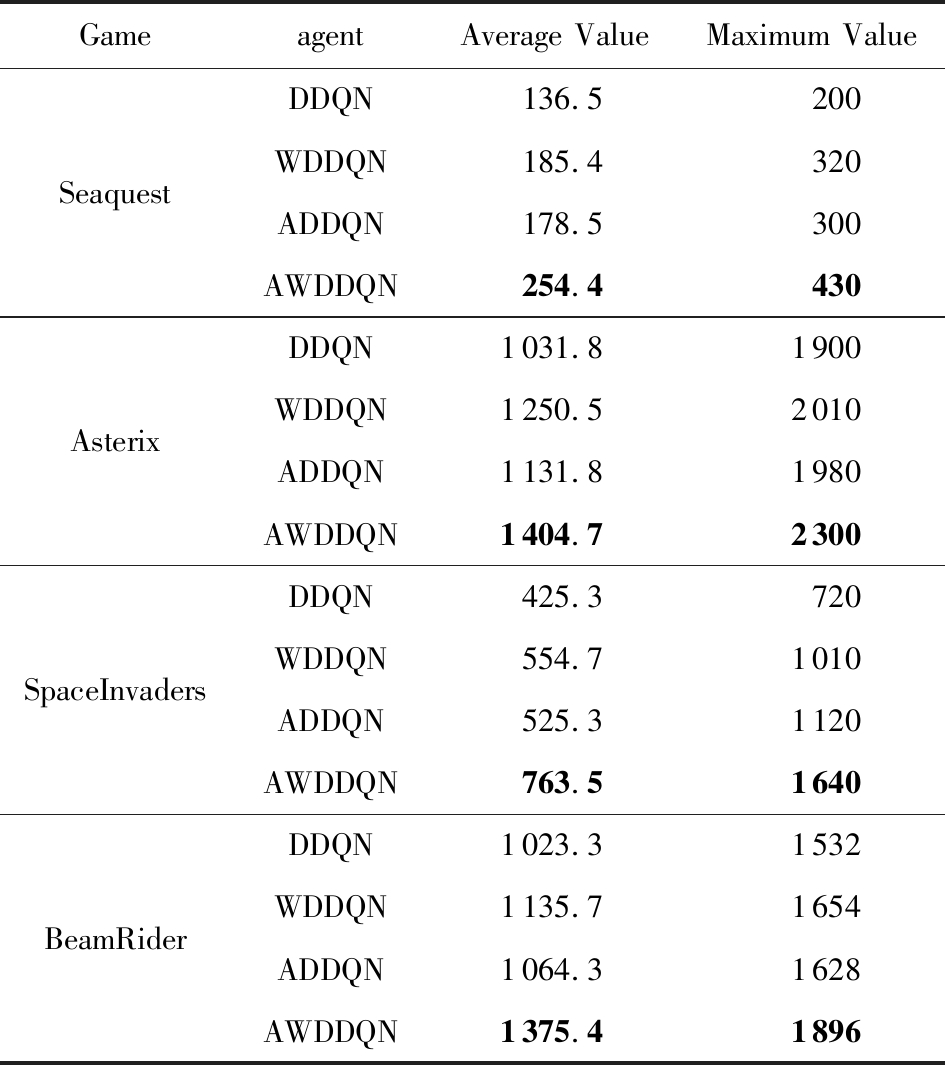
GameagentAverage ValueMaximum ValueSeaquestAsterixSpaceInvadersBeamRiderDDQN136.5200WDDQN185.4320ADDQN178.5300AWDDQN254.4430DDQN1031.81900WDDQN1250.52010ADDQN1131.81980AWDDQN1404.72300DDQN425.3720WDDQN554.71010ADDQN525.31120AWDDQN763.51640DDQN1023.31532WDDQN1135.71654ADDQN1064.31628AWDDQN1375.41896
Note:The bold numbers indicate the best results in each game.
3.5 实验总结
在本文实验中,一共进行了4组对比实验:第1组实验对比了DDQN和WDDQN算法,探究基于权重的双估计器是否能提高DDQN算法的性能并探究超参数c对WDDQN算法的影响;第2组实验使用WDDQN,ADDQN,AWDDQN这3种算法模型训练agent玩Seaquest,Asterix,Space Invaders,BeamRider游戏,并分析比较它们在训练阶段的表现,探究AWDDQN算法是否能够提高agent的性能;第3组实验探讨了不同超参数K的取值对AWDDQN算法的性能和运行时间效率的影响;在第4组实验中,将这4种训练完成后的算法模型用来测试玩这4种游戏,再次分析比较它们的测试性能.
通过分析比较实验结果,可以得出4个结论:
1) 基于权重的双估计器权衡了单估计器和双估计器的影响,能够产生更加精确的动作值估计,因此基于权重的双估计器方法提高了DDQN算法的性能,充分弥补DDQN存在低估动作值的不足.
2) 基于时间差分误差的Averaging方法根据抽取样本的时间差分误差的大小动态确定使用先前学习到的动作值的数量,然后求平均值产生目标值.在不增加算法计算量的基础上能够产生更精确的动作值估计,从而使得agent更加快速地学习到提高游戏得分的关键策略.
3) 在4种游戏中验证了WDDQN,ADDQN,AWDDQN算法的性能,它们在训练过程和训练完成后的测试过程中,表现都优于DDQN算法.并且AWDDQN算法的性能要优于WDDQN和ADDQN,充分说明AWDDQN算法的有效性,将基于权重的双估计器和基于时间差分误差的Averaging方法结合能够进一步提升agent的学习能力.
4) 在4种游戏中,具有3组不同K值的AWDDQN算法的性能表现不同.随着K值的增加,AWDDQN算法性能有所提升,但其所需的训练时间增加,降低了算法的运行效率.因此,综合考虑算法的运行效率和性能表现,选取适当的K值,有利于提高算法的效率,提升算法的性能.
4 总 结
本文将基于权重的双估计器整合到了深度双Q网络中,提出了WDDQN算法,并且改进了Averaging方法,提出基于时间差分误差的Averaging方法,形成新的ADDQN算法,最后为了进一步提升DDQN算法的性能,本文将这2种方法进行有效结合,提出AWDDQN算法.AWDDQN结合了基于权重双估计器和基于时间差分误差的Averaging方法的优势,能够计算出更加准确的目标值,产生更精确的动作估计值,从而快速学习到对决策更有帮助的策略.本文选取4个游戏来验证本文算法的有效性,同时对这4个游戏进行测试,结果表明AWDDQN算法平均每情节获得的奖赏最高,并且表现更稳定.
未来的研究工作包括如何将WDDQN算法中的超参数c变成一个可学习的参数,而不是简单地设置为一个常数.此外,尝试将本文提出的算法和其他网络模型结合,比如基于竞争的Q网络[25],深度循环网络模型[26]等.诸如此类的改进方法会进一步提高算法的性能,提高agent的学习能力.
[1]Bertsekas D P.Dynamic programming and optimal control[M].Belmont, MA: Athena Scientific, 1995
[2]Kochenderfer M J.Decision Making Under Uncertainty: Theory and Application[M].Cambridge, MA: MIT Press, 2015
[3]Littman M L.Reinforcement learning improves behaviour from evaluative feedback[J].Nature, 2015, 521(7553): 445-451
[4]Wiering M, Otterlo M V.Reinforcement Learning: State-of-the-art[M].Berlin: Springer, 2012
[5]Sutton R S, Barto A G.Reinforcement Learning: An Introduction[M].Cambridge, MA: MIT Press, 2018
[6]Kröse B J A.Learning from delayed rewards[J].Robotics & Autonomous Systems, 1995, 15(4): 233-235
[7]Yu Kai, Jia Lei, Chen Yuqiang, et al.Deep learning: Yesterday, today, and tomorrow[J].Journal of Computer Research and Development, 2013, 50(9): 1799-1804 (in Chinese)(余凯, 贾磊, 陈雨强, 等.深度学习的昨天、今天和明天[J].计算机研究与发展, 2013, 50(9): 1799-1804)
[8]Graves A, Mohamed A, Hinton G.Speech recognition with deep recurrent neural networks[C] //Proc of 2013 IEEE Int Conf on Acoustics, Speech and Signal Processing.Piscataway, NJ: IEEE, 2013: 6645-6649
[9]Sermanet P, Kavukcuoglu K, Chintala S, et al.Pedestrian detection with unsupervised multi-stage feature learning[C] //Proc of IEEE CVPR’13.Piscataway, NJ: IEEE.2013: 3626-3633
[10]Liang Bin, Liu Quan, Xu Jin, et al.Specific target sentiment analysis based on multi-attention convolutional neural network[J].Journal of Computer Research and Development, 2017, 54(8): 1724-1735 (in Chinese)(梁斌, 刘全, 徐进, 等.基于多注意力卷积神经网络的特定目标情感分析[J].计算机研究与发展, 2017, 54(8): 1724-1735)
[11]Lange S, Riedmiller M.Deep auto-encoder neural networks in reinforcement learning[C] //Proc of the 2010 Int Joint Conf on Neural Networks (IJCNN).Piscataway, NJ: IEEE, 2010: 1-8
[12]Liu Quan, Zhai Jianwei, Zhang Zongzhang, et al.Review of deep reinforcement learning[J].Chinese Journal of Computers, 2018, 41(1): 662-728 (in Chinese)(刘全, 翟建伟, 章宗长, 等.深度强化学习综述[J].计算机学报, 2018, 41(1): 662-728)
[13]Mnih V, Kavukcuoglu K, Silver D, et al.Human-level control through deep reinforcement learning[J].Nature, 2015, 518(7540): 529-533
[14]Mnih V, Kavukcuoglu K, Silver D, et al.Playing atari with deep reinforcement learning[J].arXiv preprint, arXiv: 1312.5602, 2013
[15]Van Hasselt H, Guez A, Silver D.Deep reinforcement learning with double q-learning[C] //Proc of the 13th AAAI Conf on Artificial Intelligence.Menlo Park, CA: AAAI, 2016: 2094-2100
[16]Zhang Zongzhang, Pan Zhiyuan, Kochenderfer M J.Weighted double q-learning[C] //Proc of the 26th Int Joint Conf on Artificial Intelligence.San Francisco, CA: Morgan Kaufmann, 2017: 3455-3461
[17]Anschel O, Baram N, Shimkin N.Averaged-dqn: Variance reduction and stabilization for deep reinforcement learning[C] //Proc of the 34th Int Conf on Machine Learning.New York: ACM, 2017: 176-185
[18]Filar J, Vrieze K.Competitive Markov Decision Processes[M].Berlin: Springer, 2012
[19]Ratitch B, Precup D.Sparse distributed memories for on-line value-based reinforcement learning[C] //Proc of European Conf on Machine Learning.Berlin: Springer, 2004: 347-358
[20]Busoniu L, Babuska R, De Schutter B, et al.Reinforcement Learning and Dynamic Programming Using Function App-roximators[M].Boca Raton, FL: CRC Press, 2017
[21]Irodova M, Sloan R H.Reinforcement learning and function approximation[C] //Proc of FLAIRS Conf.Menlo Park, CA: AAAI, 2005: 455-460
[22]Schorfheide F.Loss function-based evaluation of dsge models[J].Journal of Applied Econometrics, 2010, 15(6): 645-670
[23]Kim P.Convolutional Neural Network[M].Berkeley, CA: Apress, 2017
[24]Brockman G, Cheung V, Pettersson L, et al.Openai gym[J].arXiv preprint, arXiv: 1606.01540, 2016
[25]Wang Ziyu, Schaul T, Hessel M, et al.Dueling network architectures for deep reinforcement learning[J].arXiv preprint, arXiv: 1511.06581, 2015
[26]Liu Quan, Zhai Jianwei, Zhong Shan, et al.A deep recurrent q-network based on visual attention mechanism[J].Chinese Journal of Computers, 2017, 40(6): 1353-1366 (in Chinese)(刘全, 翟建伟, 钟珊, 等.一种基于视觉注意力机制的深度循环Q网络模型[J].计算机学报, 2017, 40(6): 1353-1366)



