信息时代的飞速发展,用户空间数据(例如移动用户位置、GPS位置、家庭住址等)的收集与分析能够改善IT企业的软件与服务质量,以及向用户提供更好的个性化体验.然而,不可信第三方对空间数据进行收集与分析时,个人的敏感信息有可能被泄露.例如不可信销售网站通过收集客户的位置信息,可以学习出客户的购物行为模式以及家庭住址.因此,在此情景下,用户通常无法掌控自己的空间隐私数据.本地差分隐私保护技术[1]的出现使得用户可以自己扰动自身数据之后再响应收集者的需求.目前基于本地差分隐私着眼于频率估计、均值估计等研究,而涉及空间范围查询的工作却很少.基于空间数据的范围查询是空间数据分析常用的技术之一.例如图1表示100万条纽约出租车位置数据(New York City data, NYC)散点图,查询框Q1要求返回曼哈顿医院附近范围内的乘客数量.该查询对应的SQL语句可以表示为Q1:Select Count(*) from NYC where -14≤lat≤23 and -10≤lon≤20.
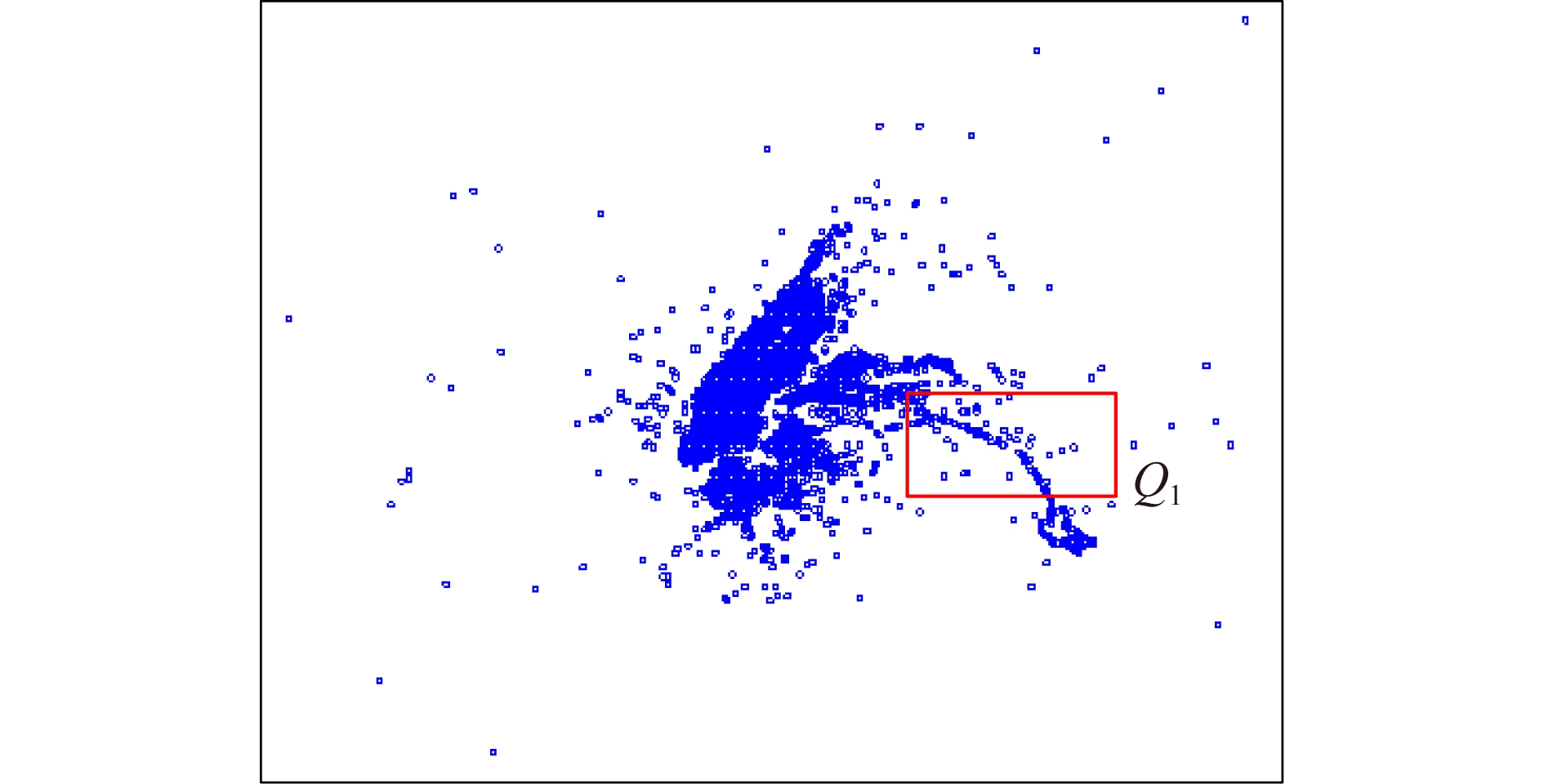
Fig. 1 Spatial range queries on NYC
图1 基于NYC的空间范围查询
在Q1查询中,用户位置所对应的经纬度为敏感信息.因此,用户在共享自身位置之前,需要本地化差分隐私保护处理.而在此过程中存在诸多挑战:1)收集者如何构建高效的空间索引结构收集用户的报告数据;2)由于空间数据的值域通常很大,用户采用什么样的编码机制与扰动机制处理自身的空间数据;3)如何设计高效的后置处理技术来提供空间范围查询精度.总而言之,目前还没有一个行之有效且满足本地差分隐私的空间范围查询方法能够同时克服上述3种挑战.为此,本文基于本地差分隐私技术提出了一种空间范围查询方法能够兼顾上述的查询需求.
本文主要贡献有4个方面:
1) 为了解决挑战1,本文首先结合网格与四分树结构提出了GT-R方法.在该方法中,收集者首先利用网格结构均分空间数据值域,并形成大小均等的空单元格区域;然后基于所有空单元格区域构建四分树索引结构,并共享给每个用户.
2) 为了有效解决挑战2,在GT-R方法中,每个用户结合收集者发来的四分树副本对自身位置数据进行编码,利用优化随机应答机制与随机采样技术本地扰动自身位置,并把所抽样的结点层次以及扰动值汇报给收集者.
3) 为了有效解决挑战3,GT-R方法结合四分树中父亲结点与其孩子结点所蕴含的逻辑关系,设计了一种有效的后置处理技术,该技术能够有效地提高空间范围查询精度.
4) 理论分析了GT-R方法满足ε-本地差分隐私,以及响应范围查询的误差边界.通过真实数据实验分析,该方法具有较高可用性和空间范围查询准确性.
1 相关工作
基于中心化差分隐私的空间范围查询已存在多种方法.文献[1]利用均分网格自适应地划分2维空间数据,对单元格添加相应的拉普拉斯噪音,然后结合噪音单元格响应范围查询;文献[2]采用kd-树对2维空间数据进行划分,利用指数机制选择分割中线以避免泄露实际空间点;文献[3]结合完全四分树划分空间数据,并通过结点计数的偏移值来减少噪音.上述这些方法均是在假设数据收集者是可信的前提下才成立,不能直接应用于本地差分隐私环境.此外,这些方法在进行扰动时常依赖于拉普拉斯机制与全局敏感度的大小.而拉普拉斯机制通常导致误差很大的本地差分隐私统计结果.
目前本地差分隐私研究主要集中于频率估计[4-5]、Heavy hitter[6]、均值估计[7-10]、频繁模式挖掘[11]以及图数据统计[12]等研究.而涉及空间范围查询的工作却很少.文献[5]结合随机应答与1元编码提出了基本Rappor方法,该方法被嵌入谷歌Chrome平台收集用户的会话记录,并估计会话项的频率.然而,1元编码无法应对较大的值域d,通信代价为Θ(d).为此,文献[5]利用布隆过滤把值域d散列到相对较小的值域中,通信代价为Θ(k).不同于文献[5],文献[6]采用随机矩阵投影技术对值域d进行编码,通讯代价为Θ(log m).此外,文献[6]利用2元本地散列技术对值域d进行编码,其通信代价同样为Θ(log d).为了取得更好的扰动精度,文献[7]结合1元编码,提出了优化1元编码与优化本地散列方法.尽管2种方法在较大的值域上取得同样的精度,但本地散列的通信代价较小.
不同于上述方法中的频率估计,文献[8-10]集中研究均值估计.文献[8]结合随机应答机制估计连续区间[-1,1]中均值.而文献[9]结合文献[8]的高通信代价与计算代价,提出了高维数据上的均值估计方法.该方法取得较好的估计精度.然而文献[8-9]方法的输出是离散的,并且与输入区间[-1,1]差别非常大.为此,文献[10]结合文献[8]与拉普拉斯机制的各自优点,提出了一种输出为连续区间的谱方法,该方法能够支持高维数据上的均值估计与SVM(support vector machines)分类.
上述的频率与均值估计均无法直接应用于空间范围查询.近期文献[13]结合完全2叉树与Hadamard编码响应1维范围查询,然而由于索引结构的不同,该方法无法直接应用于空间范围查询.文献[14]提出了基于本地差分隐私的空间数据聚集方法,该方法结合用户个性化隐私需求与分类树来分析所有用户的位置分布.尽管该方法能够响应范围查询,但与本文的需求存在不同:文献[14]中的层次结构划分空间数据只是在语义层面,缺少实际的空间索引结构.因此,针对上述方法的不足,本文提出了一种基于网格与四分树结构的空间范围查询方法,该方法不但能够适应于大规模空间数据,还能够比较精确地响应不同粒度的范围查询.
2 定义与问题
2.1 本地差分隐私
不同于中心化差分隐私保护技术,本地差分隐私技术通常要求用户在本地保护自己的数据,把扰动之后的数据报告给不可信的收集者,从而实现隐私不被泄露.本地差分隐私的形式化定义为:
定义1. ε-本地差分隐私.给定一个随机算法A及其定义域Dom(A)和值域Range(A),若算法A在任意2条不同空间位置l与l′(l,l′∈Dom(A))上得到相同输出结果O(O∈Range(A))的概率满足下列不等式,则A满足ε-本地差分隐私.
Pr[A(l)∈O]≤exp(ε)×Pr[A(l′)∈O],
(1)
其中ε为隐私预算,其值越小则算法A的隐私保护程度越高.
随机应答机制[15]与拉普拉斯机制[16]是实现本地差分隐私的常用技术.拉普拉斯机制通常需要计算出某操作的全局敏感性,利用拉普拉斯分布生成噪音对用户数值进行扰动.不同于拉普拉斯机制,随机应答机制在用户发送数据li之前,对其进行随机扰动.该机制的原始思想是用户在响应敏感的布尔问题时,以概率p真实应答,以1-p的概率给出相反的应答.为了使随机应答机制满足ε-本地差分隐私,通常设置p=exp(ε) (1+exp(ε))或者更大的值(例如1
(1+exp(ε))或者更大的值(例如1 2),收集者获得所有应答后,即可对真实应答进行分析估计.
2),收集者获得所有应答后,即可对真实应答进行分析估计.
定理1[17]. 给定空间数据集D和n个随机算法A1,A2,…,An,且Ai满足εi-本地差分隐私,则在D上的序列组合满足ε-本地差分隐私,且![]()
2.2 空间数据范围查询
空间数据通常包括空间位置信息、空间轨迹信息等,以2维散点图形式描述用户的空间位置.而空间范围查询是指在某一范围内所包含的用户位置个数.设Dom(D)为空间数据集D的值域,li(xi,yi)表示第i个用户的位置,其中xi与yi表示相应的经纬度.下面给出空间范围查询的形式化表示.
定义2. 空间范围查询.给定n个用户与一个空间范围查询框Q(Q∈D)且Q=[a,b]×[c,d],则Q的查询结果可以表示为
(2)
其中,I是标识函数,其值为1表示第i个用户的空间位置在Q内,其值为0表该用户位置不在Q内.
2.3 问题描述
给定多个用户与空间数据集D,设[a,b]×[c,d]为任意范围查询框,Q为查询框[a,b]×[c,d]中真实的响应结果,![]() 表示经过算法A处理后的结果.采用平方误差
表示经过算法A处理后的结果.采用平方误差![]() 度量[a,b]×[c,d]的查询精度.本文要解决的问题是在设计满足本地差分隐私的空间范围查询方法的同时,要尽可能获得精度较高的查询结果.
度量[a,b]×[c,d]的查询精度.本文要解决的问题是在设计满足本地差分隐私的空间范围查询方法的同时,要尽可能获得精度较高的查询结果.
3 基于本地差分隐私的空间范围查询方法
3.1 空间范围查询的原则
基于相关工作的分析,在设计新的基于本地差分隐私的空间范围查询方法时需要考虑2个原则:
1) 针对现有编码机制无法直接应对空间2维数据,所设计的方法尽可能利用空间几何结构对空间数据进行分割与索引;
2) 针对现有只对单个点的频率估计方法无法适应于2维空间范围查询,所设计的方法尽量能够保证较高的查询精度.
针对原则1与原则2,本文利用网格与四分树对大规模空间数据进行分割与编码,在此基础上提出了一种有效的空间范围查询方法GT-R,该方法能够满足本地差分隐私且输出较高精度的查询结果.
3.2 基于整个空间值域的范围查询方法
给定n个用户,每个用户拥有自己的空间位置.设c(li)表示li(li∈Dom(D))的用户计数.则式(2)可以重新表示为
(3)
在响应空间范围查询Q=[a,b] ×[c,d]时,最直接的方法是每个用户按照空间位置所在的值域Dom(D)进行2进制编码,结合随机应答机制扰动2进制编码,收集者汇总Dom(D)中所有的位置后再响应Q查询.假设error(A)表示某种随机应答机制A扰动用户位置所产生的误差.则采用A直接响应范围查询Q所产生的最坏误差为
![]()
(4)
其中,(b-a)×(d-c)表示查询框Q的面积.
响应查询Q的误差随着Q的面积呈线性增加.例如利用拉普拉斯机制报告每个位置并响应查询Q所产生的误差为8(b-a)(d-c)n ε2.由于直接方法是基于整个空间值域Dom(D)对用户位置进行编码,过大的值域导致范围查询误差与查询框面积线性相关.因此,本文基于网格划分技术将空间值域分割成均匀单元格区域,将每个用户的位置信息压缩到一个单元格区域中.每个用户结合单元格区域所构建的四分树对自身位置进行编码.收集者通过重构四分树来响应空间范围查询.
ε2.由于直接方法是基于整个空间值域Dom(D)对用户位置进行编码,过大的值域导致范围查询误差与查询框面积线性相关.因此,本文基于网格划分技术将空间值域分割成均匀单元格区域,将每个用户的位置信息压缩到一个单元格区域中.每个用户结合单元格区域所构建的四分树对自身位置进行编码.收集者通过重构四分树来响应空间范围查询.
3.3 基于网格分割的空间范围查询方法
网格分割是空间划分常用技术之一,其主要特点是在不涉及实际数据分布的情况下将空间分割成大小相等或不等的单元格区域.单元格区域是空间范围查询的最小响应单元.
3.3.1 基于均匀网格的空间范围查询方法
本节首先基于均匀网格提出GT-R算法,该算法包括基于网格与四分树结构的空间划分和索引、收集者重构四分树、用户利用四分树扰动自身位置以及响应查询4种操作.该算法具体细节详见算法1:

GT-R算法基于文献[2-3]中的UG方法均匀分割值域Dom(D),即![]() 例如图2所示,给定空间数据集D的域值范围为Dom(D)=32×32,利用均匀网格划分方法将其划分为4×4(m=4)的单元格.收集者创建空树T并共享给每个用户(行②③),如图2所示.每个用户通过LRR(local randomized response)方法本地扰动自己位置数据并报告给收集者(行④~⑥).收集者聚集所有用户的报告值后,重构四分树T(行⑦~
例如图2所示,给定空间数据集D的域值范围为Dom(D)=32×32,利用均匀网格划分方法将其划分为4×4(m=4)的单元格.收集者创建空树T并共享给每个用户(行②③),如图2所示.每个用户通过LRR(local randomized response)方法本地扰动自己位置数据并报告给收集者(行④~⑥).收集者聚集所有用户的报告值后,重构四分树T(行⑦~ ).遍历T获得最终的范围查询结果(行
).遍历T获得最终的范围查询结果(行 ).
).

Fig. 2 Grid decomposition and quadtree index
图2 网格划分与四分树索引
用户结合已被赋值的四分树T,向收集者报告自己的空间位置.LRR算法详见算法2:

收集者把空的四分树T共享给用户后,每个用户均拥有一棵T的副本(算法1行③).结合LRR算法,用户首先遍历四分树T,寻找到包含自身位置的路径,并判断自己的空间位置属于T中哪个叶子结点(算法2行②),找到所属叶子结点之后,该叶子结点至根结点路径的权重均被赋值为1,其他路径的权重为0(算法2行③~⑨).例如给定用户ui的空间位置li(xi=28,yi=12).ui结合图2中的四分树T,判断li(xi=28,yi=12)属于结点v12([24,32]×[8,16]),则路径v12-v3-v1上的权重均被赋值为1,如图2所示.接下来每个用户在T中随机选择一层,并产生由0 1构成的向量(算法2行⑩
1构成的向量(算法2行⑩ ).例如,随机选择图2中四分树的第2层,则所生成的向量为Vi=(0,1,0,0).最后利用优化随机应答机制[7]生成报告结果(算法2行
).例如,随机选择图2中四分树的第2层,则所生成的向量为Vi=(0,1,0,0).最后利用优化随机应答机制[7]生成报告结果(算法2行 ~
~ ).由于每个用户在T中随机选择一层报告,则LRR算法最坏的通信代价为
).由于每个用户在T中随机选择一层报告,则LRR算法最坏的通信代价为![]()
定理2. LRR算法满足ε-本地差分隐私.
证明. 假设Vi是用户ui基于四分树T随机生成的向量且结点个数![]() 其中
其中![]() 为该用户基于T随机选择的树层.Zi为LRR算法响应|Vi|次的输出结果.结合定理1则等式成立:
为该用户基于T随机选择的树层.Zi为LRR算法响应|Vi|次的输出结果.结合定理1则等式成立:
同理,给定![]() 等式成立:
等式成立:
则:
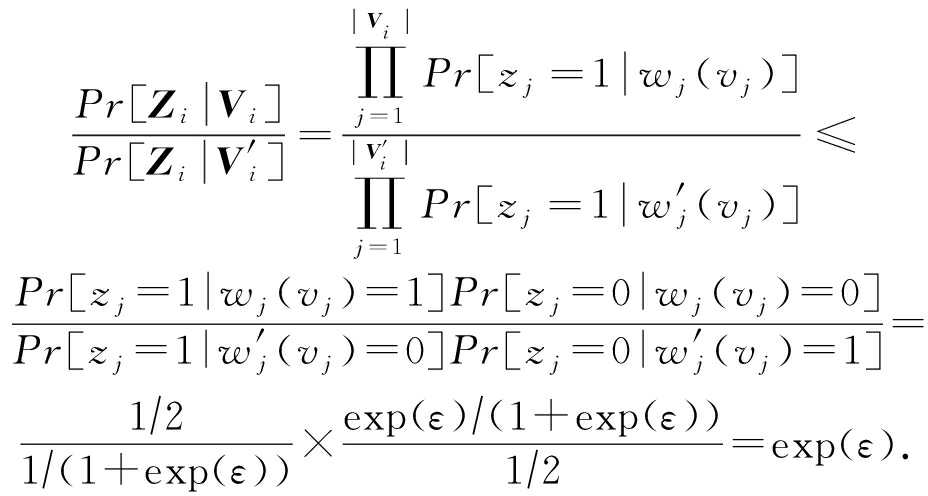
根据定义1可知,LRR算法满足ε-本地差分隐私.
证毕.
尽管通过LRR算法可以重构四分树T,但我们期望T中每个结点的噪音计数满足无偏性.
定理3. 假设vi是收集者重构四分树T中的任意结点,c(vi)与c′(vi)分别是结点vi中真实的用户位置数与估计数,则无偏估计E[c′(vi)]=c(vi)成立.
证明. 设l为结点vi所在的层次,nl为该层次中的用户数,也是结点vi中的用户报告数目.根据算法1的行 c′(vi)=c′(vi)+zi可知,nl个用户把自己的位置信息汇总到l层每个结点中去.设I(vi)表示结点vi中1的个数.为了证明方便,结合算法2设Pr[zi=1|wi(vj)]=p,以概率p生成zi=1,否则以概率Pr[zi=0|wi(vj)]=q生成zi=0.则I(vi)=p×c′(vi)+q×(nl-c′(vi))成立.进而可以获得随机变量c′(vi):
c′(vi)=c′(vi)+zi可知,nl个用户把自己的位置信息汇总到l层每个结点中去.设I(vi)表示结点vi中1的个数.为了证明方便,结合算法2设Pr[zi=1|wi(vj)]=p,以概率p生成zi=1,否则以概率Pr[zi=0|wi(vj)]=q生成zi=0.则I(vi)=p×c′(vi)+q×(nl-c′(vi))成立.进而可以获得随机变量c′(vi):
则:
成立.
根据I(vi)=p×c′(vi)+q×(nl-c′(vi))可知:
E[c′(vi)]=![]()
我们期望E[c′(vi)]=c(vi),则:
E[c′(vi)]=![]()
![]()
成立.
证毕.
由于每个用户本地扰动自身的空间位置,T中每个结点的计数不可避免地产生误差.定理4给出了每个结点所产生的方差.
定理4. 假设vi是收集者重构四分树T中的任意结点,nl为l层次中的用户数,p=1 2,q=1
2,q=1 (1+exp(ε)),c(vi)与c′(vi)分别是结点vi中真实的用户位置数与估计数,则:
(1+exp(ε)),c(vi)与c′(vi)分别是结点vi中真实的用户位置数与估计数,则:
证明. 根据定理3可知,![]() 则:
则:
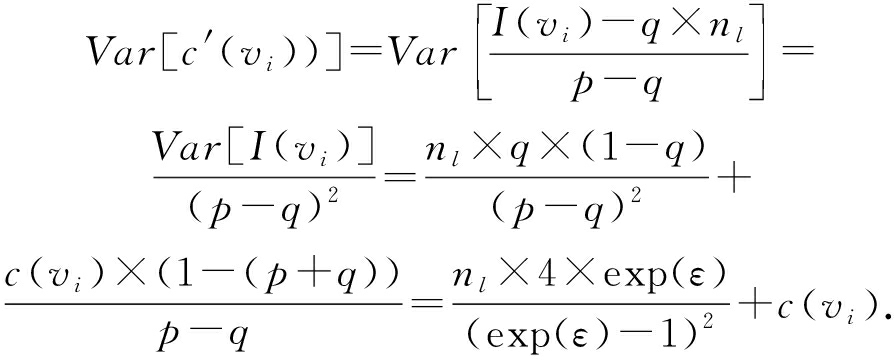
证毕.
由文献[12]可知,T中很多结点真实位置计数非常小,因此,Var[c′(vi)]≈nl×4×exp(ε) (exp(ε)-1)2.进而可知每个结点的方差仅与四分树每层所分配的用户个数nl线性相关.
(exp(ε)-1)2.进而可知每个结点的方差仅与四分树每层所分配的用户个数nl线性相关.
尽管通过定理4可以估算出每个结点产生的方差,而如何度量c(vi)与c′(vi)之间的最大偏差是个挑战性问题.
定理5. 假设vi是收集者重构四分树T中的任意结点,设lj是第j个用户的位置.c(vi)与c′(vi)分别是结点vi中真实的用户位置数与估计数,则等式至少以概率1-β成立:
其中,n为用户个数,ћ=1+2log4m为四分树高度.
证明. 设c′(vi)-c(vi)为一个随机变量,根据定理3可知其均值为0.根据算法1与算法2可知:
|c′(vi)-c(vi)|=![]()
![]()
(5)
其中,wj(vi)与zj分别表示第j个用户的真实值与估计值.
同理可知zj-wj(vi)也是一个随机变量.由于zj∈{0,1},wj(vi)∈{0,1},则zj-wj(vi)∈{-1,0,1}.
随机变量zj-wj(vi)的方差可以表示为
Var[zj-wj(vi)]=E[(zj-wj(vi))2]-
(E[zj-wj(vi)])2=E[(zj-wj(vi))2]=![]()
![]()
此外,由式(5)可知:
|zj-wj(vi)|≤2(exp(ε)+1) (exp(ε)-1)
(exp(ε)-1)
成立.根据Bernstein不等式可知:
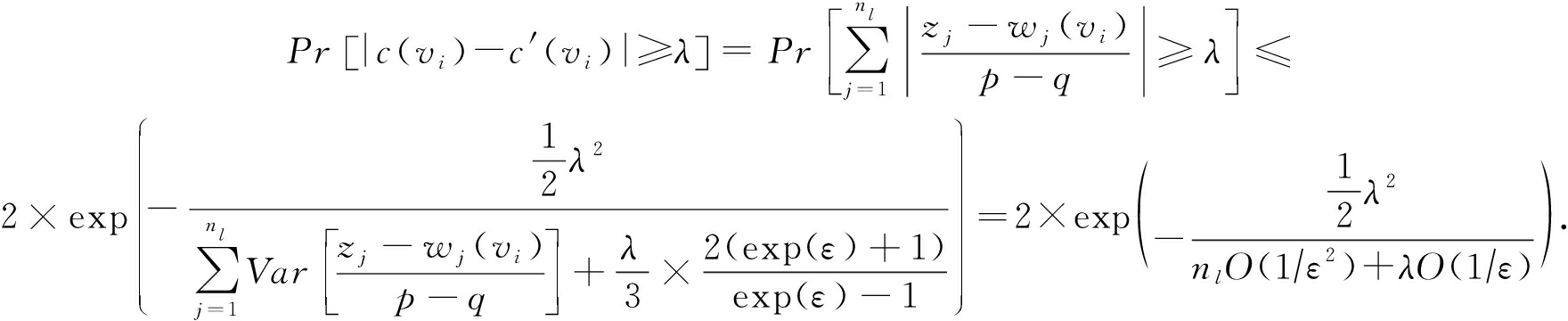
结合上述不等式可知![]() 此时nl=n
此时nl=n ћ.则可知|c′(vi)-c(vi)|<λ至少以概率1-β成立.
ћ.则可知|c′(vi)-c(vi)|<λ至少以概率1-β成立.
证毕.
结合收集者重构的四分树T响应空间范围查询Q,具体细节如算法3描述.

收集者利用GT-R算法重构四分树T之后,首先进行后置处理(行①),再利用TDT算法自动向下遍历T即可响应空间范围查询Q.如果某结点与Q无交叉,则忽略该结点(行⑤⑥).若Q完全包含该结点,即可把该结点中的空间点数添加响应结果中(行⑦⑧).若Q部分包含该结点且该结点不是叶子结点,则重新遍历该结点的孩子结点(行⑨~ ).否则计算Q与该结点的重合部分,并把重合部分中的空间点数添加响应结果中(行
).否则计算Q与该结点的重合部分,并把重合部分中的空间点数添加响应结果中(行 ~
~ ).
).
定理6. 结合算法1与算法3,任意空间范围查询Q的最大误差error(Q)满足:
其中,η为某一常数.
证明. 四分树中每个结点产生的误差只与该结点所在层次中用户个数线性相关.因此,只要自顶向下估算出每一层最多有多少个结点响应Q,即可估算出Q的查询误差上界.任意给定T中一层l(1≤l≤ћ),cl表示该层中响应查询Q的最多结点个数.设C(Q)表示T中能够响应查询Q的结点总数,则![]() 成立.T为四分树,则cl≤8×2ћ-l.其原因是Q查询框与l-1层中至多有8个结点相交.因此,每一层最多产生的误差为8×2ћ-l×Var[c′(vi)].
成立.T为四分树,则cl≤8×2ћ-l.其原因是Q查询框与l-1层中至多有8个结点相交.因此,每一层最多产生的误差为8×2ћ-l×Var[c′(vi)].
结合Var[c′(vi)]≈nl×4×exp(ε) (exp(ε)-1)2,可知不等式成立:
(exp(ε)-1)2,可知不等式成立:
![]()
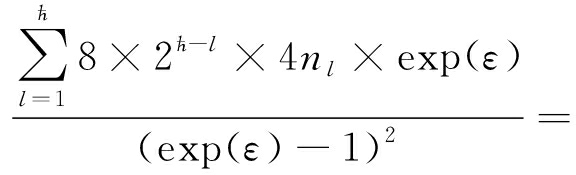
![]()
(6)
为了估算error(Q),设![]() 为了使不等式(6)成立,可以利用优化技术解决该问题.
为了使不等式(6)成立,可以利用优化技术解决该问题.
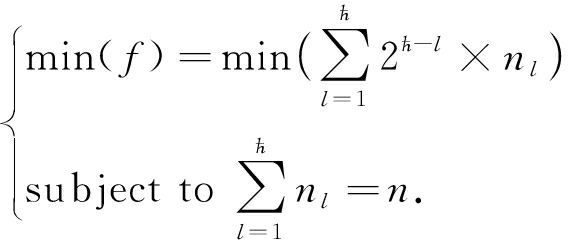
基于目标函数min(f)与柯西-施瓦茨不等式可知不等式成立:
(7)
当nl=η×2ћ-l×nl时,则不等式(7)中的等号成立.可知2ћ-l=1 η .该等式说明四分树中响应查询Q的结点个数是定值,则min(f)=n
η .该等式说明四分树中响应查询Q的结点个数是定值,则min(f)=n η.进而可知:
η.进而可知:
证毕.
结合定理6与式(4)可知,GT-R算法与最直接方法均可以采用方差度量误差.若在最直接方法中每个用户也利用优化随机应答机制扰动自身位置,可知error(A)=4n×exp(ε) (exp(ε)-1)2.因此,只要范围查询Q的查询面积大于8
(exp(ε)-1)2.因此,只要范围查询Q的查询面积大于8 η,即可知GT-R算法优于最直接方法.
η,即可知GT-R算法优于最直接方法.
3.3.2 基于重构四分树的求精处理方法
四分树本身蕴含着内在的计数特征,即任何一个非叶子结点中的计数等于其孩子结点中计数的和.随机给定一个非叶子结点vi,c(vi)为其计数,uj是vi的孩子结点,则![]() 成立.此外,结点vi中的计数与其孩子结点计数之和满足无偏估计,即
成立.此外,结点vi中的计数与其孩子结点计数之和满足无偏估计,即![]() 成立.然而,由于算法2中的本地扰动噪音与用户基于四分树的随机采样,打乱了四分树本身内在的约束机制.因此,本文利用文献[18]中的一致性约束处理方法,对四分树结点中的计数进行求精处理(算法3行①).设c′(vi)和
成立.然而,由于算法2中的本地扰动噪音与用户基于四分树的随机采样,打乱了四分树本身内在的约束机制.因此,本文利用文献[18]中的一致性约束处理方法,对四分树结点中的计数进行求精处理(算法3行①).设c′(vi)和![]() 分别表示结点vi中的用户位置的估计数与求精处理之后的计数.求精处理包含2种操作:
分别表示结点vi中的用户位置的估计数与求精处理之后的计数.求精处理包含2种操作:
1) 自底向上的平均化处理
c″(vi)=
其中,uj表示结点vi的孩子结点.
2) 自顶向下的均值一致性处理
![]()

其中,p(vi)表示结点vi的父亲结点.
结合图2,以例子说明求精处理过程.给定只有2层的四分树T,vi为其根结点.假设c′(vi)=5,其孩子结点的计数分别为c′(u1)=2,c′(u2)=1,c′(u3)=1,c′(u4)=2.由于c′(vi)≠c′(u1)+c′(u2)+c′(u3)+c′(u4),则需要求精处理.处理之后c′(vi)=3.9,c′(u1)=2,c′(u2)=1,c′(u3)=1,c′(u4)=2.
4 实验结果与分析
实验平台是4核Intel i7-4790 CPU(4 GHz)、8 GB内存、Win7系统.所有算法均采用Python实现.实验采用2个数据集Checkin与Landmark,其中Checkin数据集从基于地理位置的社交网站Gowalla获取,该数据集记录了在2009-02—2010-10期间,Gowalla用户签到的时间和位置信息,包含100万条记录;Landmark数据集从infochimps平台获得,该数据集记录了2010年人口普查时用户到过的美国48个州的地标位置,总共包含87万条数据.2种数据集具体细节与可视化结果分别如表1与图3所示.
结合上述数据集,采用相对误差(relative error, RE)度量 KRR[19],RAPPOR[5],PSDA[14],OUE[7],GT-R,N-PSDA,N-GT-R,QT-RAPPOR,QT-KRR方法的范围查询精度.其中N-PSDA与N-GT-R表示无空间结构索引下的方法;QT-RAPPOR与QT-KRR表示四分树索引下的RAPPOR与KRR方法.RE的表示为
![]()
(8)
其中,Q(D)表示D上真实的范围查询结果,![]() 表示D上范围查询的噪音结果.
表示D上范围查询的噪音结果.
Table 1 Characteristics of Datasets
表1 数据集的属性

DatasetCoordinate RangeReal SizeSample SizeLandmark[-124.4,-67.0]×[24.6,49.0]8.70051×1055×105Checkin[-176.3,177.46]×[-48.2,90.0]1×1065×105

Fig. 3 Visualization of two datasets
图3 2种数据集可视化结果
本文设置的隐私预算参数ε的取值为0.1,0.3,0.5,0.7,0.9.实验中范围查询Q的查询范围分别覆盖Landmark与Checkin这2种数据集的[10%,50%],[15%,55%],[20%,60%],在每种查询范围内随机生成500次查询.
1) 基于Landmark数据集的多种方法RE值比较
图4(a)~(f)描述了KRR,RAPPOR,OUE,N-PSDA以及N-GT-R算法的RE值比较结果.由图4(a)~(c)的实验结果可以发现,当范围查询Q固定时,ε从0.1变化到0.9,5种方法的RE值均减少.然而,N-GT-R的范围查询精度优于其他4种方法.在ε=0.7,Q为[15%,55%]时,N-GT-R所取得的查询精度远优于KRR方法和RAPPOR方法,从实验结果可以看出,其精度是KRR方法的近3倍,是RAPPOR方法的2倍多,是N-PSDA与OUE方法的近1倍.从图4(d)~(f)的实验结果可以发现,当ε固定,Q的范围从[5%,45%]变化到[20%,60%]时,5种方法的RE值均增大,其原因在于范围查询的查询范围越大,包含的查询单个点数越多,累计误差越大,导致精度随着查询范围的增大而降低.从图4(d)~(f)中还可以发现N-GT-R方法的精度优于其他4种方法,其原因在于N-GT-R算法采用均匀网格分割整个值域,缩小了值域空间.
图4(g)~(l)描述了QT-KRR,QT-RAPPOR,PSDA,GT-R 这4种方法的RE值比较结果.由图4(g)~ (i)可以发现,当范围查询Q固定时,ε从0.1变化到0.9,4种方法的RE值均减少,且GT-R方法明显优于其他3种方法.当ε=0.5且Q为[20%,60%]时,GT-R所取得的精度是QT-RAPPOR的近4倍,是QT-KRR和PSDA的近3倍.其原因是GT-R方法采用均匀网格与四分树对空间值域进行重新编码与索引,而其他3种方法均是基于整个值域响应范围查询.此外,GT-R通过后置处理使结果不仅达到了无偏还保证了结果的一致性.由图4(j)~(l)还发现,当固定ε,查询范围Q从[5%,45%]变化到[15%,55%]时,4种方法的查询精度随着查询范围的增大而降低.但查询范围Q从[15%,55%]变化到[20%,60%]时,4种方法的查询精度出现随着查询范围的增大而提高的现象,其原因在于使用四分树索引后,Q的查询精度与其所含盖的树中结点个数成反比,随着查询面积的增大,查询范围在四分树中含盖的索引结点个数可能变少,反而使精度更加精准.
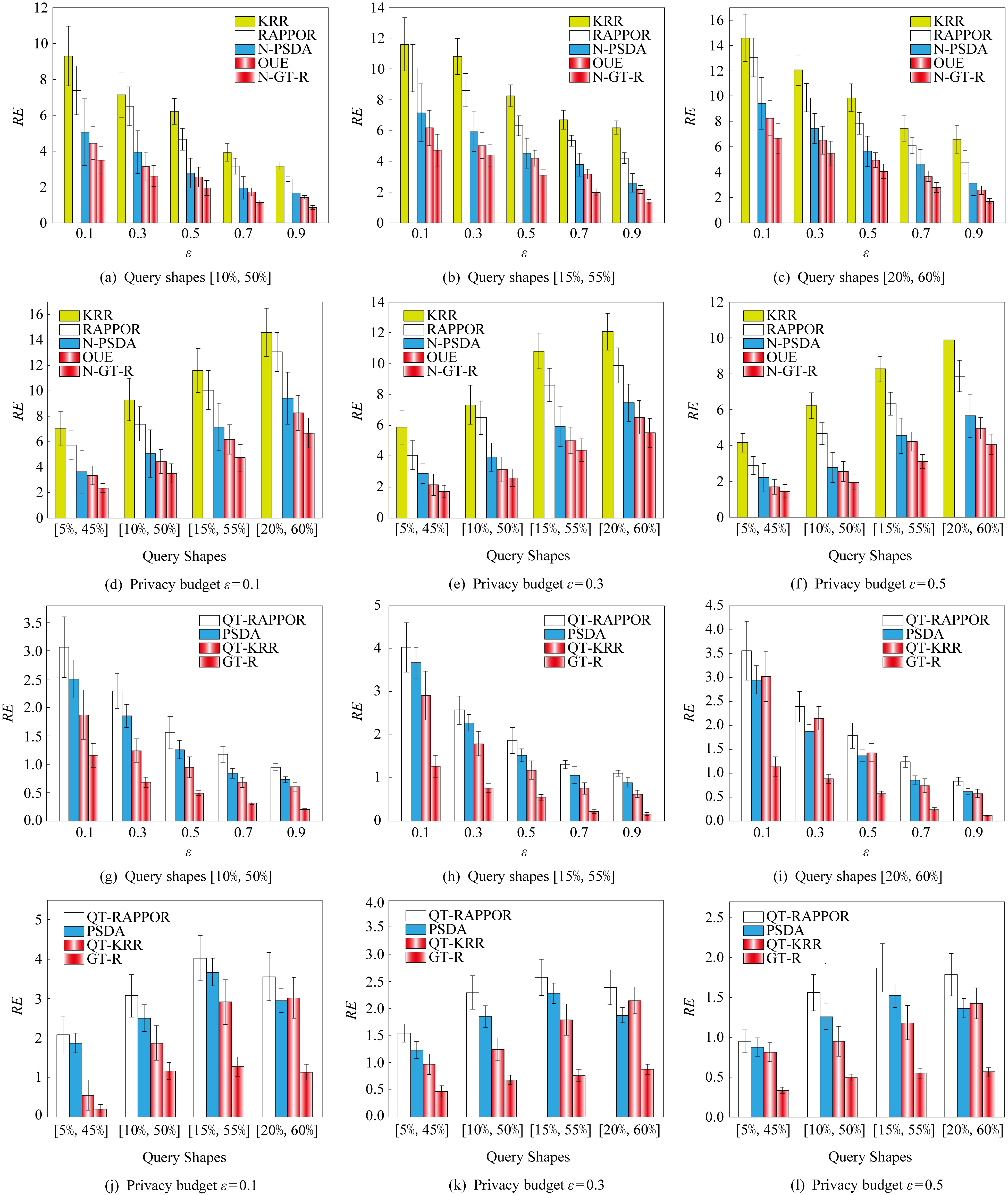
Fig. 4 Results of range queries on Landmark
图4 Landmark数据集范围查询结果
2) 基于Checkin数据集的多种方法RE值比较
图5(a)~(f)描述了KRR,RAPPOR,OUE,N-PSDA,N-GT-R 这5种方法的RE值比较结果.由图5(a)~(f)可以发现,当范围查询Q固定,ε从0.1变化到0.9时,5种方法的RE值均减少,然而N-GT-R的查询误差的稳定性与查询精度优于其他5种方法.当ε=0.3且查询范围为[15%,55%]时,N-GT-R方法所取得的查询精度是KRR方法的近4倍,是RAPPOR方法的近3倍,是OUE方法和N-PSDA的近0.5倍.当ε固定,随着查询范围扩大,5种方法查询精度均呈现下降趋势,但N-GT-R方法的查询精度与误差稳定性同样优于其他4种方法.其主要原因是N-GT-R方法减小了值域空间,在做相同的范围查询时比其他方法所累积的误差少.
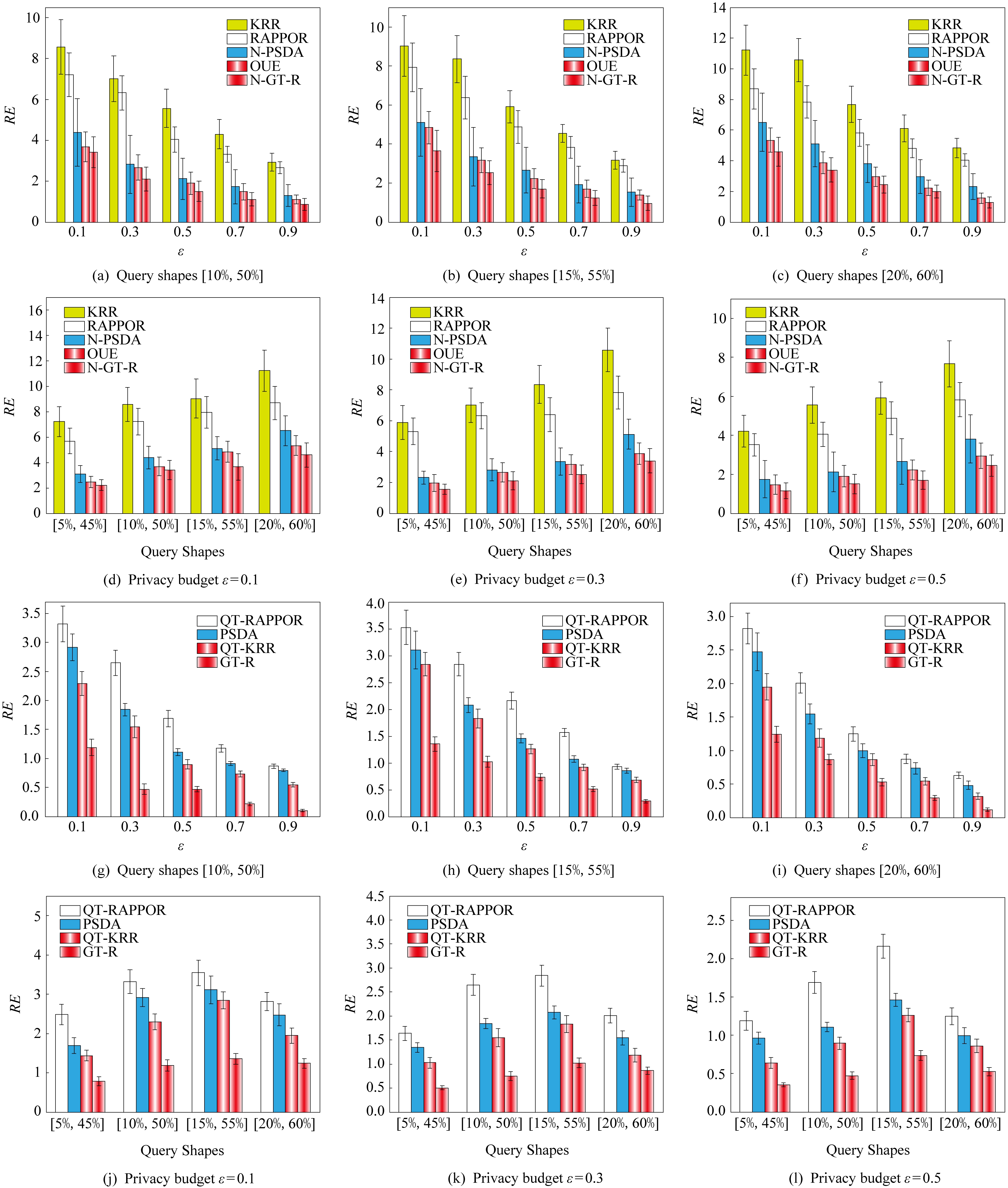
Fig. 5 Results of range queries on Checkin
图5 Checkin数据集范围查询结果
图5(g)~(l)描述了QT-KRR,QT-RAPPOR,PSDA,GT-R 这4种方法的RE值比较结果.由图5(g)~(i)可知,当范围查询Q固定且ε增大时,4种方法的误差均减小.特别是查询范围为[10%,50%]且ε=0.9时,GT-R方法的精度是PSDA方法和QT-RAPPOR方法的近7倍,是QT-KRR的近6倍.此外,由图5(j)~(l)显示,当ε固定,查询范围Q从[5%,45%]变化到[20%,60%]时,GT-R方法在各个范围的查询精度虽然变化相对不大,但优于其他3种方法.在ε=0.5时,GT-R方法取得的精度是其他3种方法的1倍以上.其主要原因是GT-R方法利用网格与四分树对整个空间值域进行压缩与重新编码,既缩减了值域空间又减少了统计时的累计误差点数,因此精度优于其他方法.
5 结束语
针对本地差分隐私保护下收集用户空间位置存在的问题,本文结合现有的用户数据收集方法存在的不足,提出了基于网格与四分树索引的空间位置收集方法GT-R.该方法通过均匀网格缩小空间值域,通过四分树对用户位置进行重新编码.从本地差分隐私定义角度分析GT-R满足ε-本地差分隐私.最后通过2种真实的大规模数据集验证了GT-R方法的范围查询精度.实验结果表明:GT-R明显优于现有的同类方法.未来工作考虑动态环境下的隐私空间数据收集与分析问题.
[1] Qardaji W H, Yang Weining, Li Ninghui. Differentially private grids for geospatial data [C] //Proc of the 29th IEEE Int Conf on Data Engineering. Piscataway, NJ: IEEE, 2013: 32-33
[2] Cormode G, Procopiuc C M, Srivastava D, et al. Differentially private spatial decompositions [C] //Proc of the 28th IEEE Int Conf on Data Engineering. Piscataway, NJ: IEEE, 2012: 20-31
[3] Zhang Jun, Xiao Xiaokui, Xie Xing. PrivTree: A differentially private algorithm for hierarchical decompositions [C] //Proc of the 2016 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2016: 155-170
[4] Erlingsson  , Pihur V, Korolova A. Rappor randomized aggregatable privacy-preserving ordinal response [C] //Proc of the 2014 ACM SIGSAC Conf on Computer and Communications Security. New York: ACM, 2014: 1054-1067
, Pihur V, Korolova A. Rappor randomized aggregatable privacy-preserving ordinal response [C] //Proc of the 2014 ACM SIGSAC Conf on Computer and Communications Security. New York: ACM, 2014: 1054-1067
[5] Bassily R, Smith A. Local, private, efficient protocols for succinct histograms [C] //Proc of the 47th Annual ACM on Symp on Theory of Computing. New York: ACM, 2015: 127-135
[6] Wang Tianhao, Bloci J, Li Ninghui, et al. Locally differentially private protocols for frequency estimation [C] // Proc of the 26th USENIX Security Symp. Berkeley, CA: USENIX Association, 2017: 729-745
[7] Duchi J C, Jordan M I. Local privacy and statistical minimax rates [C] // Proc of the 54th Annual IEEE Symp on Foundations of Computer Science. Piscataway, NJ: IEEE, 2013: 429-438
[8] Duchi J C, Jordan M I, Wainwright M J. Minimax optimal procedures for locally estimation [J]. Journal of the American Statistical Association, 2018, 113(521): 182-201
[9] Nguyên T T, Xiao Xiaokui, Yang Yin, et al. Collecting and analyzing data from smart device users with local differential privacy[OL]. (2016-06-05) [2019-05-03]. https://arxiv.org/abs/1606.05053
[10] Wang Ning, Xiao Xiaokui, Yang Yin, et al. Collecting and analyzing multidimensional data with local differential privacy [C] // Proc of the 35th IEEE Int Conf on Data Engineering. Piscataway, NJ: IEEE, 2019: 638-649
[11] Wang Tianhao, Li Ninghui, Jha S. Locally differentially private frequent itemset mining [C] //Proc of IEEE Symp on Security and Privacy. Piscataway, NJ: IEEE, 2018: 127-143
[12] Qin Zhan, Yu Ting, Yang Yin, et al. Generating synthetic decentralized social graphs with local differential privacy [C] //Proc of ACM Conf on Computer and Communications Security. New York: ACM, 2017: 425-438
[13] Kulkarni T, Cormode G, Srivastava D. Answering range queries under local differential privacy [C] //Proc of the 2019 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2019: 1832-1834
[14] Chen Rui, Li Haoran, Qin Kai, et al. Private spatial data aggregation in the local setting [C] //Proc of the 32nd IEEE Int Conf on Data Engineering. Piscataway, NJ: IEEE, 2016: 289-300
[15] Warner S L. Randomized response: A survey technique for eliminating evasive answer bias [J]. The American Statistical Association, 1965, 60(309): 63-69
[16] Dwork C, McSherry F, Nissim K, et al. Calibrating noise to sensitivity in private data analysis [C] //Proc of the 3rd Theory of Cryptography Conf. Berlin: Springer, 2006: 363-385
[17] Dwork C, Lei Jing. Differential privacy and robust statistics [C] //Proc of the 41st Annual ACM Symp on Theory of Computing. New York: ACM, 2009: 371-380
[18] Michael H, Vibhor R, Gerome M. Boosting the accuracy of differentially private histograms through consistency [J]. Proceedings of the VLDB Endowmen, 2010, 3(1): 1021-1032
[19] Kairouz P, Oh S, Viswanath P. Extremal mechanisms for local differential privacy [J]. Journal of Machine Learning Research, 2016, 17(17): 43-51


