Facebook,Twitter等大规模社交网络的兴起,为社会网络研究提供了数据支撑,而复杂网络工具的引入,为社会网络分析提供了定量基础.节点重要性研究作为社会网络分析的关键问题之一,迄今发展起来的理论框架主要面向单关系网络结构.作为一种简化的网络科学框架,单关系网络结构不足以准确刻画现实世界中相互关联、彼此依存的复杂系统,即网络的网络(networks of networks, NoN),对NoN的研究已逐渐成为复杂网络分析领域富有挑战性的研究热点[1-2].多关系网络(multi-relational networks)作为NoN的一种典型存在方式,已成为刻画现实世界各类关系构成复杂系统的常用模型.近年来,国内外学者面向多关系网络,围绕基本度量[3-6]、社团结构[7-10]、传播扩散[11]、谱特征分析[12]等基础问题进行了大量研究,也形成了较为丰富的理论成果.但针对多关系网络节点重要性的研究,大多仍是通过构建多个单关系网络,并通过某种规则进行复合的方式进行建模和分析,这种处理方式会丧失各类关系之间的特定结构信息.如何精确刻画多关系网络,探索推广单个网络上已有的节点重要性度量方法到多关系网络中,研究设计符合多关系网络结构特点和动力学特征的节点重要性分析方法,具有重要的理论价值和应用价值.
本文针对多关系社交网络的节点重要性问题,着眼于在线社交平台产生的海量关系数据,通过构建多关系有向网络模型,应用基于张量代数的多层网络数学框架对其进行表示和分析,融合刻画节点中心性、声望、传递性等影响社交网络节点重要性因素的度量指标,借鉴单关系网络ClusterRank,IO-ClusterRank等节点重要性方法和基于D-S(Dempster-Shafer)证据理论的信息融合方法,对多关系有向网络的节点重要性进行了系统研究,提出了面向多关系有向网络的IOMCR(in-degree out-degree multiplex ClusterRank)和IOMEC(in-degree out-degree multiplex evidential centrality)方法.在4个大规模多关系真实网络数据集上的实验结果表明,由于受多关系网络耦合信息和传递机制的影响,直接借鉴ClusterRank和IO-ClusterRank所提出的IOMCR方法,会对节点重要性测量的准确性造成影响,而运用D -S证据理论进行多元信息融合的IOMEC方法能够有效规避这种影响,相比于其他方法,能够更加准确地测量节点的重要程度.在时间复杂度方面,相对于IOMCR,IOMEC方法由于引入了信息融合技术,具有更低的时间复杂度.本文所做工作不仅丰富了多关系网络节点重要性的度量方法,也扩展了多关系网络的基本度量和D -S证据理论的实际应场景.
1 相关工作
多关系网络[13]的概念起源于社会学领域,社会学家根据行动者(actor)之间的关系属性,对网络中的边进行分类[14-15].Mitchell[16]将此类网络称之为拥有“多重(multi-stranded)”关系的网络.被用来研究多关系社会网络的方法包括指数随机图模型、元网络(meta-networks)、元矩阵(meta-matrices),以及通过块模型(block modeling)和关系代数(relational algebras)来确定社会角色的其他方法等[17-18].但社会学领域所研究的网络规模相对较小,定量分析复杂度较低,且常采用调查的方法对结果进行统计分析,不适用于大规模网络.
对大规模多关系网络进行研究,一个基本问题是如何对其进行建模和表示.随着复杂网络分析技术的不断发展,对于单个网络,已经建立了较为完备的理论分析框架.鉴于此,对多关系网络的处理,起初的处理思路是利用“降维”的思想,围绕特定领域网络,针对性地运用社会学、可拓学等其他学科理论,通过构建加权网络的方式将多关系网络转化为单关系网络[19-20];或是借助矩阵分解、多子网复合等理论方法对已有网络进行时间划分或快照处理,对单个网络分别进行研究后再进行复合[21-22].此类简化的处理方式,会导致原始数据中包含的特定结构信息和不同类型关系之间关联信息的丧失,不利于后续研究的开展.一些研究围绕“全连通网络”,运用超图理论开展分析[20],虽能够对网络进行融合,保留了信息的完整性,但“超图”模型通常用于刻画“全连通网络”,局限性较强.
在计算机科学和计算机线性代数领域,研究者们运用张量分解(tensor-decomposition)[23-24]和多路数据(multiway data)分析[25]的方法研究了不同类型的多层网络.在物理学领域,物理学家们围绕多层网络[26-29]、网络的网络[30-31]和节点着色网络(node-colored networks),已经开展了许多重要的基础性工作.Boccaletti等人[32]于2014年首次提出了多层网络的基本数学定义,该定义统一了迄今文献上关于多层网络的不同提法.经过近几年的发展,多层网络模型已逐渐成熟,形成了一系列符合复杂网络基本特征和动力学机制的理论方法,为后续研究奠定了基础.对于多关系网络,可将每一类关系对应于一个网络层,同时考虑各类关系间的关联信息,建立多层网络模型开展相关研究.因此,多层网络模型是表示多关系网络的理想形式,将多层网络模型运用到多关系网络中,在应用层面进行拓展,是值得深入研究的一个基本问题.
在社会网络分析领域,中心性、声望和传递性是制约社会网络中行动者显著性或重要性的关键因素[13].在复杂网络分析领域,对于单个网络节点中心性的度量,已经建立了较完备和丰富的指标和方法[33].根据局部性质划分,可分为全局中心性、局部中心性、半局部中心性3类.全局中心性的经典指标有介数中心性(betweenness centrality, BC)[34]、接近中心性(closeness centrality, CC)[35]、特征向量中心性(eigenvector centrality, EC)[36]等.局部中心性的典型指标有度中心性(degree centrality, DC)[37].为平衡全局中心性的复杂度和局部中心性的因素单一,Chen等人[38]提出了一种半局部中心性(semi-local centrality, SLC),通过考虑节点的4阶邻居信息来度量节点重要程度,Gao等人[39]在其基础上通过引入D-S证据理论,提出了一种证据半局部中心性(evidential semi-local centrality, ESC).但上述经典指标都只关注了节点的中心性,而忽略了传递性在度量重要节点的关键作用.通常用节点的局部聚集系数刻画节点的传递能力,Chen等人[40]综合考虑了节点的中心性和传递性因素,同时考虑了节点的二阶邻居对节点重要性造成的影响,提出了ClusterRank指标,该指标在运行效率和准确度上都要优于前者.声望的概念,主要通过可以区分行动者发出或者接收“选择”关系的行为进行量化,因此只能利用有向网络进行研究.在复杂网络分析中,通常用节点的出度来刻画中心性,用节点的入度来刻画声望[13].遗憾的是,声望除用于早期社会网络分析外,现阶段对有向网络节点重要性的研究中,研究者们更加关注节点的出度信息,关注节点的入度信息的研究很少.值得一提的是,Wang等人[41]研究了有向网络节点出度和入度的分布关系,针对有向加权的单关系网络提出了IO-ClusterRank指标,其对节点重要性的度量效果要优于传统的ClusterRank指标.
面向多关系网络,如何借用已有的物理量去描述其基本拓扑结构和性质尚面临巨大挑战,将单关系网络中的成熟工具和方法扩展到多关系网络中已成为当前复杂网络研究的一大热门方向.最初的做法是将不同关系的节点和连边以不同权重的方式进行合并,从而将多关系网络转化成为单关系网络,再利用传统物理量去分析其各种结构属性.将多关系网络合并成单关系网络,会导致一些关系间重要信息的丢失,同时还存在如何设定各种权重的问题[42].因此,发现一套适合多关系网络的网络理论框架的必要性开始凸显.多层网络模型的提出为多关系网络的研究奠定了理论基础,国内外学者针对多层网络度量指标的研究做了大量研究工作,也取得了一些成果,多层网络的中心性、路径长度、聚集系数等概念被相继提出,为后续研究奠定了基础.但多层网络的度量指标,大多数是在特定条件和应用场景下提出的,尚未形成类似于单关系网络丰富经典的度量指标体系,其可扩展性需进一步增强.值得一提的是,Battiston等人[43]在向量的基础上提出了多层网络节点度(node degree)、节点强度(node strength)等概念,Cozzo等人[44]从路径和环的概念出发,基于多层网络的传递性提出了一种多层网络聚集系数(clustering coefficient)的概念,二者都是从多层网络的基本表征和动力学特性出发的,具有较好的可扩展性,成为目前比较经典的多层网络度量指标,为后续研究提供了基本遵循.特别是在传递性研究方面,通过在实际数据上进行实验和分析,表明在社会网络和交通网络中,层内聚集性和层间聚集性的差异是不同的,这实际上反映了在这些网络中节点传递性的起源机制大不一样.他们提供的聚集系数定义表达式为不同类型的网络传递性研究提供了新的思路.
综上,现阶段对于多关系网络的研究比较理想的处理方式是构建多层网络模型并运用相关指标进行分析,而对于多层网络2种较为经典的度量指标,主要是围绕多层网络的拓扑结构和传递机制进行研究,如何从多层网络的基本模型和表示框架出发,运用这些指标对多关系网络的节点重要性开展研究还存在很多问题,也是本文工作的出发点之一.
2 基础理论
本节主要对文中用到的基础理论和符号记法进行介绍和说明.
2.1 爱因斯坦求和约定和符号记法
在张量计算体系中,为使计算公式简洁,通常将求和符号∑省略,即采用爱因斯坦求和约定.满足2个规则[45]:
1) 哑指标规则
① 在同一项中,以一个上标与一个下标成对地出现,表示遍历其取值范围求和.如:
![]()
(1)
![]()
(2)
(3)
② 每一对哑指标的字母可以用相同取值范围的另一对字母任意替换,其意义不变(必须指代明确).如:
AαBα=AβBβ,
(4)
![]()
(5)
在式(5)中,由于已经存在β,若将γ替换为β,则会造成指代不明.
③ 涉及张量积之间比率的方程式,应将爱因斯坦求和约定分别应用到分子与分母.如:
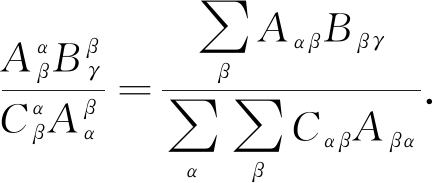
(6)
2) 自由指标规则
若一个指标在表达式的各项中都在同一水平上出现并且只出现一次,或者全为上标,或者全为下标,表示该表达式在该自由指标的N维取值范围内都成立,即代表了N个表达式:
(7)
其中,β为哑指标,α和γ均为自由指标.
同理,一个表达式中的某个自由指标可以全体地换用相同取值范围的其他字母,意义不变.
在欧几里德空间中,张量的协变向量通常用列向量a∈![]() N来表示,其分量记为aα,(α=1,2,…,N),对偶向量(逆变向量)可用对应的转置向量(行向量)表示,其分量记为aα.
N来表示,其分量记为aα,(α=1,2,…,N),对偶向量(逆变向量)可用对应的转置向量(行向量)表示,其分量记为aα.
为避免混淆,本文对张量代数框架下的符号记法做2个约定:
1) 用拉丁字母(如i,j,k…)来表示张量;用希腊字母(如α,β,γ…)来表示张量分量.例如![]() 表示第i个张量的分量.
表示第i个张量的分量.
2) 用不带波浪线的字母(如i,α…)指代网络中的节点;用带波浪线的字母![]() 指代网络中的关系类别.
指代网络中的关系类别.
2.2 ClusterRank与IO-ClusterRank指标
节点的局部聚集系数与信息传播的范围及网络进化中节点的度增长能力均呈负相关.鉴于此,Chen等人[40]提出的ClusterRank指标是一种针对有向网络节点重要性的半局部中心性指标,该指标不仅将邻居节点数量作为衡量中心性的一个指标,同时考虑了传递性对节点重要程度的影响,即聚集系数越大节点的传播能力越弱.ClusterRank算法定义为
(8)
![]()
(9)
其中,![]() 为节点vj的出度,Γi为节点vi的邻居集合,f(ci)为vi的局部聚集系数ci的线性负相关函数,ci越大,f(ci)越小.式(9)中,Njk为Γi中节点vj和vk存在连边的数量.通过实验对比,ClusterRank算法优于PageRank和LeaderRank算法,并且计算复杂度与后二者比较相对较低.
为节点vj的出度,Γi为节点vi的邻居集合,f(ci)为vi的局部聚集系数ci的线性负相关函数,ci越大,f(ci)越小.式(9)中,Njk为Γi中节点vj和vk存在连边的数量.通过实验对比,ClusterRank算法优于PageRank和LeaderRank算法,并且计算复杂度与后二者比较相对较低.
但是,ClusterRank指标只考虑了节点的出度,并没有考虑节点的入度信息,Wang等人[41]通过对有向网络出入度的分析,基于ClusterRank提出了一种针对加权有向网络的节点重要性度量指标IO-ClusterRank,定义为
![]()
(10)
![]()
(11)
(12)
其中,![]() 和
和![]() 分别为节点vi的出度和入度,
分别为节点vi的出度和入度,![]() 和
和![]() 分别为节点vi出聚集系数和入聚集系数,wij为节点vi和vj的权重,
分别为节点vi出聚集系数和入聚集系数,wij为节点vi和vj的权重,![]() 和
和![]() 分别为节点vj的出强度和入强度.实验结果表明:IO-ClusterRank指标在出入度差异较大的网络中具有明显优势,从而说明在节点重要性研究中考虑入度信息的必要性.
分别为节点vj的出强度和入强度.实验结果表明:IO-ClusterRank指标在出入度差异较大的网络中具有明显优势,从而说明在节点重要性研究中考虑入度信息的必要性.
2.3 D-S证据理论
D-S证据理论是由Dempster和Shafer[46]建立的一套数学理论,是对概率论的进一步扩充,在表示和处理有限个不确定问题时具有明显优势,适用于专家系统、人工智能、模式识别和系统决策等领域的实际问题.本节主要介绍证据理论处理流程涉及到的辨识框架(frame of discernment)、基本概率指派(basic probability assignment, BPA)以及Dempster-Shafer证据组合规则等基本概念和计算方法.
定义1. 辨识框架.在证据理论中,通常将所考察判断对象的全体用一个两两互斥的有限完备集合来表示,该集合称为辨识框架,记为
Ψ={ψ1,ψ2,…,ψN},
(13)
Ψ的幂集2Ψ记为
2Ψ={∅,ψ1,…,ψN,ψ1∪ψ2,…,ψ1∪
ψ2∪ψ3,…,Ψ}.
(14)
定义2. 基本概率指派.设Ψ是辨识框架,2Ψ构成命题集合,∀A⊆Ψ,若函数m:2Ψ→[0,1]满足2个条件:
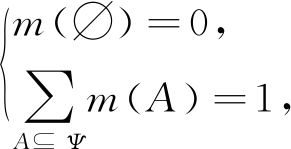
(15)
则称m为基本概率指派,m(A)为命题A的基本概率数,被视为准确分配给A的信度.
定义3. Dempster-Shafer组合规则.设m1和m2为2组基本概率指派,对应的对象分别为A1,A2,…,Ak和B1,B2,…,Bl,用m表示m1和m2组合后的新证据.Dempster-Shafer组合规则定义:
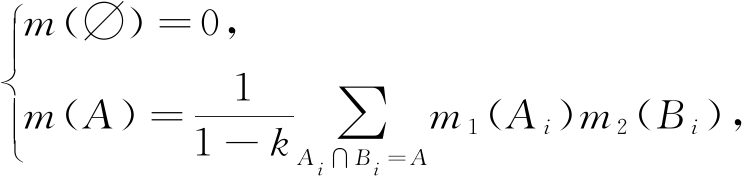
(16)
其中,![]() 称为冲突系数,用于衡量证据对象间的冲突程度,k越大,则冲突越大.当k=1时,组合规则无法使用,即BPA存在矛盾.
称为冲突系数,用于衡量证据对象间的冲突程度,k越大,则冲突越大.当k=1时,组合规则无法使用,即BPA存在矛盾.
3 多关系网络的张量表示和基本度量
为研究多关系网络,首先需构建一种精确的数学表示方法,以及与之配套的分析工具.本文采用基于张量代数的多层网络表示框架对多关系网络进行建模和分析.该框架的优势在于可扩展性强,多重网络、时序网络、相互依赖网络等均可用多层网络模型进行构建.本节主要介绍多关系网络的基本模型和张量表示方法,以及本文中所用到的一些基本度量指标的计算方法.
3.1 多关系网络的基本模型
参考Boccaletti等人[32]提出的多层网络数学定义,给出多关系网络的图定义:
定义4. 多关系网络.一般地,多关系网络的图结构可用一个二元组表示,记为GR=(V,ER).其中,V={v1,v2,…,vN}表示顶点集,N为网络中顶点个数,边集![]() 其中
其中![]() 表示第α类关系的边集,M表示关系类别数量.
表示第α类关系的边集,M表示关系类别数量.
进一步,针对多关系有向网络,可将其分层表示为层内网络(intra-layer network)和层间网络(inter-layer network)两部分,每一层对应于一种关系.其中,层内网络用GRI=(V,ERI)表示,层内边集可记为
![]()
(17)
其中,![]() 表示层α内,节点vi指向节点vj的有向边的集合.层间网络用GRC=(V,ERC)表示,层间边集可记为
表示层α内,节点vi指向节点vj的有向边的集合.层间网络用GRC=(V,ERC)表示,层间边集可记为
![]()
(18)
不同于层内网络,由于多关系网络各层间均存在彼此的交互关系,故层间边集中各层对应节点间为一种双向关系(也可视为无向关系).
为避免与节点标号混淆,在多关系网络的抽象定义中,我们用带有[]的希腊字母([α],[β]等)的上标来指示多层网络的层标号.E[α]组成元素称为多层网络层内连边,区别于每个E[α,β]的表示层间连边的组成元素.
由定义4可得,用于构建多关系网络的多层网络模型是一种“层间节点对齐”型的多层网络,称之为多重网络(multiplex network).图1展示了一个具有3层的无向多层网络和多重网络的示意图,可以看出,多重网络属于多层网络的特殊类型,其唯一的层间连接模式是来自不同层之间对应节点的连接.
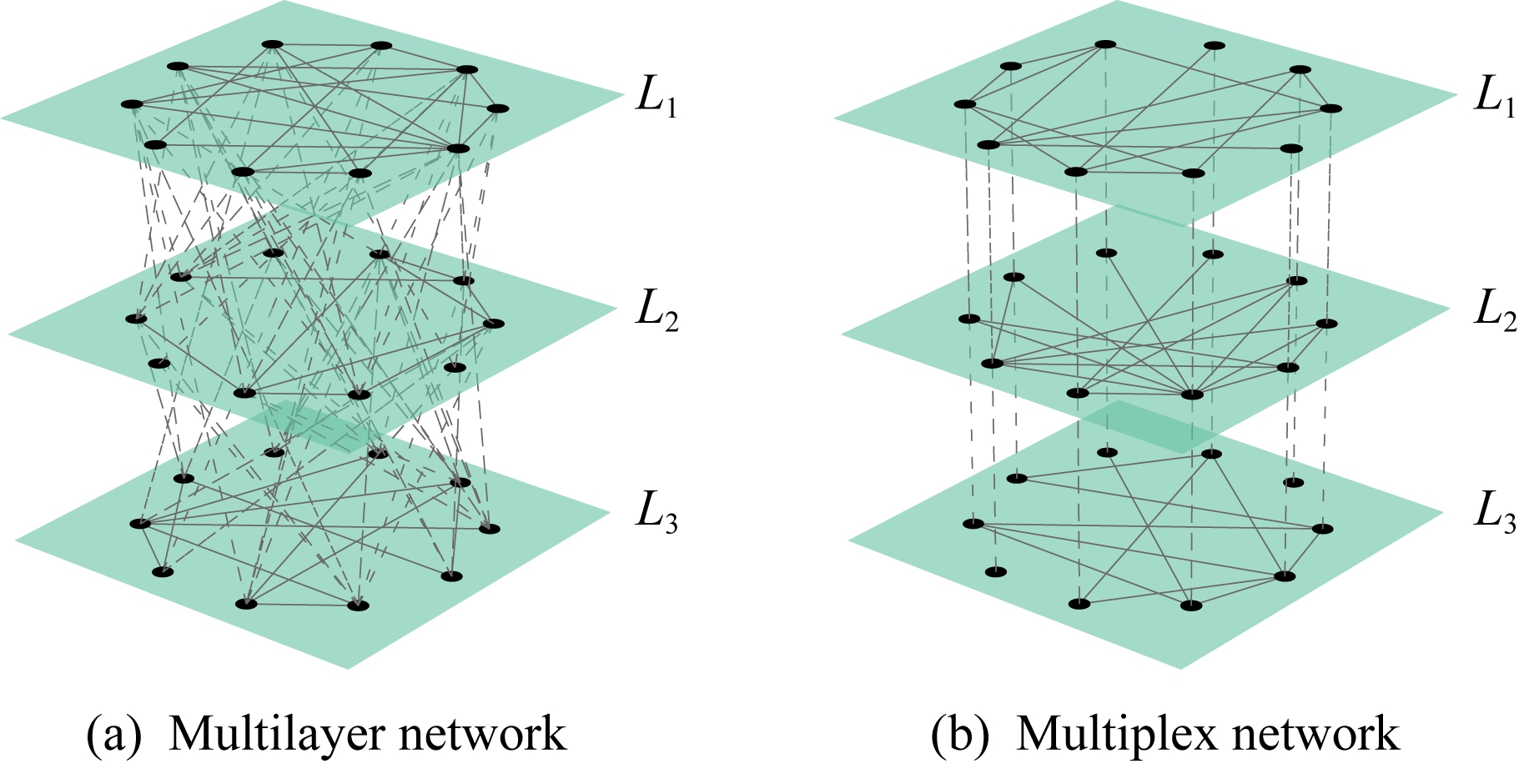
Fig. 1 Schematics of multilayer and multiplex networks
图1 多层网络与多重网络原理图
3.2 多关系网络的张量表示框架
由3.1节可知,可用多重网络模型对多关系网络进行建模,本节主要介绍基于张量代数的多关系网络框架,本文中关于张量运算的公式符号记法采用2.1节介绍的爱因斯坦求和约定.下面分别介绍单层网络和多层网络的张量表示方法[47]:
1) 单层网络的张量表示
有别于通常情况下的单关系网络,本文中所讨论的单层网络(monoplex networks)属于多层网络的特殊情况,需满足与时间无关和同构2个条件.
记单层网络为Gmonoplex={V,E},节点集记为V={v1,v2,…,vN},将节点集中每一个节点与向量空间 ![]() N 中状态向量相对应,例如,节点vi所对应的状态向量分量为:
N 中状态向量相对应,例如,节点vi所对应的状态向量分量为:![]() 此式中第i个元素为1,其余元素全为0,它在向量空间
此式中第i个元素为1,其余元素全为0,它在向量空间![]() N中所对应的逆变(对偶)向量分量记为:
N中所对应的逆变(对偶)向量分量记为:![]() 通过克罗内克积来构建描述节点间关系的张量空间,即:
通过克罗内克积来构建描述节点间关系的张量空间,即:![]() N⊗
N⊗![]() N=
N=![]() N×N.由此,二阶标准基张量可定义为
N×N.由此,二阶标准基张量可定义为
![]()
(19)
为描述简洁,通常省略符号⊗,式(19)可记为![]() 本文后续部分将采用省略⊗的通用记法.
本文后续部分将采用省略⊗的通用记法.
进一步,用![]() 来表示节点vi与vj间的连接情况(连接为1,反之为0),则对应的邻接张量(在矩阵理论框架下称之为邻接矩阵)可由二阶张量来表示:
来表示节点vi与vj间的连接情况(连接为1,反之为0),则对应的邻接张量(在矩阵理论框架下称之为邻接矩阵)可由二阶张量来表示:
![]()
![]()
![]()
(20)
同理,对于加权网络,可用![]() 来表示节点vi与vj间的连接权重,则所对应的加权邻接张量为
来表示节点vi与vj间的连接权重,则所对应的加权邻接张量为
![]()
![]()
![]()
(21)
2) 多层网络的张量表示
对于多关系网络,可用多层框架对其进行描述,其中每一类关系用单独一层![]() 来表示
来表示![]() 用二阶张量
用二阶张量![]() 表示第
表示第![]() 层层内邻接张量(即同一层内节点间的关系).
层层内邻接张量(即同一层内节点间的关系).
对于多层网络,来自层![]() 的节点vi可以连接到任意一层
的节点vi可以连接到任意一层![]() 的任意节点vj,为了表示包含多个层关系的信息,引入二阶层间邻接张量,记为
的任意节点vj,为了表示包含多个层关系的信息,引入二阶层间邻接张量,记为![]() 特别地,对应于一对表示相同层
特别地,对应于一对表示相同层![]() 的层间邻接张量等于该层的层内邻接张量,即:
的层间邻接张量等于该层的层内邻接张量,即:![]()
类似于单层网络,在空间![]() M中,引入标准基向量,其分量记为
M中,引入标准基向量,其分量记为![]() 其中
其中![]() 对于空间
对于空间![]() M×M,可构造二阶标准基张量,记为:
M×M,可构造二阶标准基张量,记为:![]()
根据上述定义,多层邻接张量可用层间邻接张量![]() 和二阶标准基张量来表示,即:
和二阶标准基张量来表示,即:
![]()
(22)
其中,![]() 为一实数,表示
为一实数,表示![]() 层节点vi与
层节点vi与![]() 层节点vj之间的连接情况(可能不对称);
层节点vj之间的连接情况(可能不对称);![]() 为空间
为空间 ![]() N×N×M×M中4阶标准基张量(即秩4张量).
N×N×M×M中4阶标准基张量(即秩4张量).
由上述讨论可得,基于张量代数的表征框架适用于有向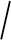 无向、有权
无向、有权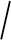 无权各类网络.
无权各类网络.
为在某些情况下便于计算,在空间![]() N×N×M×M中,可将多层邻接张量
N×N×M×M中,可将多层邻接张量![]() 通过矩阵化(或称为展开运算)表示为一个NM×NM的矩阵,这对于计算算法的实现是非常有用的[23].在已有研究中,关于多层网络的社区检测、扩散、聚集系数等研究都使用了矩阵表示法进行计算和分析[43-44,48-50].
通过矩阵化(或称为展开运算)表示为一个NM×NM的矩阵,这对于计算算法的实现是非常有用的[23].在已有研究中,关于多层网络的社区检测、扩散、聚集系数等研究都使用了矩阵表示法进行计算和分析[43-44,48-50].
事实上,根据定义4和克罗内克积的运算规则,可以很方便地得到该矩阵,所得结果与通过动力学扩散方程得到的矩阵是一致的[49].下面以构造多关系网络的邻接矩阵为例,对其构造方法予以说明:
根据定义4,可分别构建层内网络和层间网络所对应的邻接矩阵.
定义5. 层内邻接矩阵.多关系网络第α类关系所对应的层内连接可由一个邻接矩阵来表示,记为A[α]∈![]() N×N,则多关系网络的层内邻接矩阵定义为
N×N,则多关系网络的层内邻接矩阵定义为
![]()
![]() MN×MN.
MN×MN.
(23)
定义6. 层间邻接矩阵.多关系网络所对应的层间连接可由一个加权邻接矩阵来表示,记为WC∈![]() M×M,取单位矩阵E∈
M×M,取单位矩阵E∈![]() N×N,则多关系网络的层间邻接矩阵定义为
N×N,则多关系网络的层间邻接矩阵定义为
WRC=WC⊗E∈![]() MN×MN.
MN×MN.
(24)
由定义5和定义6可得到多关系网络的邻接矩阵,即:
AR=ARI+WRC∈![]() MN×MN.
MN×MN.
(25)
3.3 多关系网络的基本度量
1) 多关系网络的度中心性
在张量代数框架下首先给出单层网络度中心性的表示方法[47],并在多层网络上进行推广:
① 单层网络的度中心性
首先定义“1-向量”,即分量元素全为1的向量,记为
uα=(1,1,…,1)T∈![]() N.
N.
同理,![]() 为元素全为1的二阶张量,称之为“1-张量”.
为元素全为1的二阶张量,称之为“1-张量”.
对于无向无权网络而言,其对应的邻接张量![]() 可以解释为应用于“1-向量”的1个算子,由此可定义无权无向网络的度中心性向量(度向量)为
可以解释为应用于“1-向量”的1个算子,由此可定义无权无向网络的度中心性向量(度向量)为
![]()
![]() N.
N.
(26)
通过将度向量投影到对应于节点vi的标准基向量上,可得到节点vi的度中心性,即:
![]()
(27)
② 多关系网络的度中心性
与单层网络相似,通过使用适当阶的“1-张量”对单层网络情况进行相同的投影,可以得到多关系网络的度中心性张量(multiplex degree centrality, MDC),即
![]()
(28)
其中,![]() 为对应于层
为对应于层![]() 和
和![]() 之间连接的中心性向量.类似地,可在多关系网络上得到相应的节点度、平均度、度的二阶矩、度的方差的定义.
之间连接的中心性向量.类似地,可在多关系网络上得到相应的节点度、平均度、度的二阶矩、度的方差的定义.
节点度(node degree):
![]()
(29)
平均度(mean degree):
![]()
(30)
度的二阶矩(the second moment of the degree):
![]()
(31)
度的方差(the variance of the degree):
![]()
(32)
对于有向网络,使用不同的克罗内克积,可分别得到出度中心性和入度中心性的张量表示:
![]()
(33)
![]()
(34)
由式(33)和式(34)可得,使用张量代数的网络表征框架有助于理解有向网络中的方向性,因为入度与出度的克罗内克积的运算规则是不同的.
2) 多关系网络的局部聚集系数
Cozzo等人[44]从路径和环的概念出发,提出了多层网络局部聚集系数和全局聚集系数的概念.在单层网络中,可用邻接矩阵来计算网络中路径和环的数量[51-52].类似地,将多层网络中的行走称之为“超行走(supra-walk)”,并通过层内邻接矩阵和层间邻接矩阵来计算多层网络的局部聚集系数.按照Cozzo等人提出的多层网络聚集系数的计算方法,本文给出一种多关系网络局部聚集系数(multiplex local clustering coefficient, MLCC)的简化计算方法.由3.1节可知,本文运用多重网络模型来表示多关系网络,则在多关系网络中,通过“超行走”得到的三元闭环结构有且仅有图2所示的5种基本形式,其中较大节点(红色)代表闭环的起始节点,层内路径用实线表示,层间路径用虚线表示,较粗实线(橙色)代表层内第2步行走路径.通过“超行走”所构成的三元闭环可通过将各网络层聚合到一层得到.

Fig. 2 Sketch of elementary cycles
图2 基本闭环结构
根据3.2节多关系网络邻接矩阵的构造方法,可得到多关系网络节点聚集系数的定义.
定义7. 多关系网络的局部聚集系数.令M,I,C分别表示多关系网络的邻接矩阵、层内邻接矩阵、层间邻接矩阵,
Ω={III,IICIC,ICIIC,ICICI,ICICIC}
为多关系网络中基本三元闭环结构集合,ξ为集合Ω中的元素,
为在构成基本三元闭环结构的“超行走”过程中,层内第2步发生在一个完全图上的闭环结构集合.其中,F=⊕αF[α],F[α]=J[α]-E[α]为层α中一全连接网络的邻接矩阵,![]() 表示
表示![]() 中的元素,则多关系网络节点vi的局部聚集系数可定义为
中的元素,则多关系网络节点vi的局部聚集系数可定义为

(35)
其中,ωξ和![]() 代表“超行走”分别跨越1层、2层和3层所占的贡献,在无特定背景情况下,一般设
代表“超行走”分别跨越1层、2层和3层所占的贡献,在无特定背景情况下,一般设![]()
4 融合多元信息的节点中心性度量方法
现实世界的社交数据中存在许多有向关系,比如微博网络中的转发、关注关系,引文网络中的引用和被引用关系,都可以用有向边予以刻画.因此,本节基于第2节和第3节介绍的基础理论,用有向多重网络的张量表示框架刻画多关系社交网络,综合考虑社交网络中节点中心性、声望、传递性对节点重要性造成的影响,分别用多关系网络中节点的出度中心性、入度中心性、局部聚集系数进行量化,运用信息融合的思想,对多关系网络中的节点重要性度量方法进行了研究.
4.1 基于IO-ClusterRank的节点重要性排序方法
借鉴2.2节介绍的ClusterRank和IO-ClusterRank的思想方法,并利用多关系网络的度量指标进行推广,提出了一种基于ClusterRank的多关系社交网络节点的半局部中心性度量方法IOMCR.IOMCR在考虑节点本身及其邻居节点中心性和声望的同时,还考虑了节点的传递能力.IOMCR的定义:
(36)
节点的局部聚集系数与其传递能力一般呈负相关关系,即其局部聚集系数越小,说明该节点传递能力越强.式(36)中,f(CM,i)为节点vi的局部聚集系数CM,i的非线性负相关函数,本文取f(CM,i)=10CM,i.Ki为节点vi的度中心性值,![]() 的计算:
的计算:
![]()
(37)
![]()
(38)
(39)
其中,![]() 和
和![]() 分别代表节点vi的出度和入度,用以刻画该节点的中心性和声望.
分别代表节点vi的出度和入度,用以刻画该节点的中心性和声望.![]() 和
和![]() 分别刻画了节点vi邻居的中心性和声望强度,
分别刻画了节点vi邻居的中心性和声望强度,![]() 和
和![]() 分别为vi的邻居节点集合Γi中节点vj的出度中心性和入度中心性.
分别为vi的邻居节点集合Γi中节点vj的出度中心性和入度中心性.
4.2 融合多元信息的节点重要性排序方法
4.1节提出的IOMCR指标采用了一种正相关性融合方法,即认为节点的中心性和声望越显著,其传递性也就越强.但在真实网络中,很多节点往往不具备这种正相关关系,例如在微博网络中,一些用户虽然中心性和声望都很显著(即关注和被关注的用户都很多),其可以接收到很多消息,但却不喜欢转发(即传递性很弱),还有一些用户热衷于转发自己的消息(即传递能力较强),但关注和被关注的用户却很少(即中心性和声望不显著).综上,中心性、声望、传递性之间往往呈现出的是一种不确定性关系,而IOMCR方法往往需要在中心性、声望、传递性三者之间具有相对明确的正相关性条件下,才能表现出较好性能.而在多关系网络中,由于传递机制具有差异性,往往三者之间不具备明确的正相关关系.故IOMCR指标具有一定的局限性,其在度量节点重要性程度时,节点中心性、声望、传递性三者信息之间有可能会相互抵消,从而对度量节点重要程度造成影响.
考虑到D-S证据理论[39,46,53]是处理不确定性问题的理想办法,本文引入D-S证据理论,对IOMCR进行了改进,分别将节点的中心性和声望信息与节点的传递性信息进行融合,进一步提出了IOMEC方法:
![]()
(40)
其中,υOMEC,i为中心性信息和传递性信息进行融合后的度量值,υIMEC,i为声望信息和传递性信息融合后的度量值,取二者的平均值作为最终的度量值.以计算υOMEC,i为例,介绍D-S证据理论融合节点中心性和传递性信息的方法步骤:
1) 计算节点中心性和传递性量化指标
分别计算节点的出度中心性向量Kα和节点的聚集系数向量CM,记Ki和CM,i分别为Kα和CM中对应第i个位置的元素值,分别计算f(CM,i)=10-CM,i,所得结果向量记为F.统计Kα和F中元素的最大值和最小值,分别记为KM,Km,FM,Fm.一般情况下,KM≠Km,FM≠Fm.
2) 确定节点重要程度的辨识框架
按照2.3节中D -S证据理论的处理流程,首先应确定考察对象的辨识框架Ψ.本文所考察的是节点的重要程度,简单起见,可将网络中节点的重要性分为节点重要和节点不重要2类,用I表示节点重要,NI表示节点不重要,则记Ψ={I,NI}.显然,Ψ中的元素两两互斥且为有限完备集合.
3) 构建基本概率指派函数
令mK,I(i)和mK,NI(i)分别为在Ki下节点vi重要和不重要的概率,mF,I(i)和mF,NI(i)分别代表在f(CM,i)下节点vi重要和不重要的概率.在无特定条件情况下,通常约定该概率指派服从均匀分布,根据均匀分布的概率密函数,可定义上述4个指标的BPA函数:
![]()
(41)
![]()
(42)
![]()
(43)
![]()
(44)
μ和λ为修正参数,取值对节点排序没有影响,通常取μ,λ∈(0,1).
4) 进行D -S证据组合
首先定义考察对象的集合,记为
M(i)={mI(i),mNI(i),mΨ(i)},
(45)
其中,mI(i)为表示节点vi重要的概率,mNI(i)表示节点vi不重要的概率,mΨ(i)表示节点vi或者重要或者不重要的概率.根据式(16),可分别计算mI(i),mNI(i),mΨ(i).
5) 计算OMEC.
根据贝叶斯理论,在无其他先验知识的情况下,将mΨ(i)等可能分配给mI(i)和mNI(i),进一步修正节点vi重要的概率MI(i)和不重要的概率MNI(i),即:
![]()
(46)
![]()
(47)
由式(46)和式(47)可得,当MI(i)越大、MNI(i)越小时,说明节点vi越重要.鉴于此,对MI(i)和MNI(i)进行组合,可得到υOMEC,i的度量值:
υOMEC,i=MI(i)-MNI(i)=mI(i)-mNI(i).
(48)
为保证概率的非负性和归一性,将式(48)进行标准化处理,进一步修正为
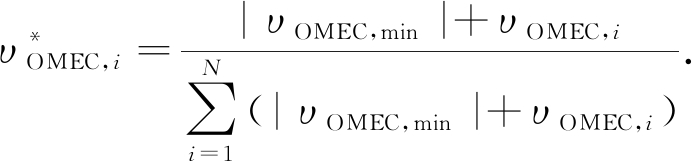
(49)
类似地,将υOMEC,i计算过程中的出度中心性向量Kα改为计算入度中心性向量Kα,即可得到融合声望和传递性的υIMEC,i度量指标.
4.3 时空复杂度分析
多关系网络中,记节点数为n,关系数为m.
1) 时间复杂度分析
计算多关系网络出度中心性和入度中心性的时间复杂度均为O(mn),计算节点的局部聚集系数时间复杂度为O(m3n3).由于IOMCR方法和IOMEC方法的计算均考虑了衡量节点中心性、声望和传递性的度量指标,故二者的计算复杂度均依赖于计算节点出度中心性、入度中心性和局部聚集系数的时间复杂度.在已知节点出度中心性、入度中心性和局部聚集系数的条件下,IOMCR方法由于考虑了节点的一阶邻居信息,其时间复杂度为O[mn(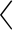 Kα
Kα +
+ Kα
Kα )],而IOMEC方法将层间信息通过D-S证据理论进行了融合,仅关注了节点本身,故其时间复杂度为O(n).在单独计算二者的时间复杂度方面,IOMEC方法要优于IOMCR方法,但综合考虑节点的出度中心性、入度中心性和聚集系数的时间复杂度后,二者的时间复杂度均为O(m3n3).
)],而IOMEC方法将层间信息通过D-S证据理论进行了融合,仅关注了节点本身,故其时间复杂度为O(n).在单独计算二者的时间复杂度方面,IOMEC方法要优于IOMCR方法,但综合考虑节点的出度中心性、入度中心性和聚集系数的时间复杂度后,二者的时间复杂度均为O(m3n3).
2) 空间复杂度分析
鉴于通过构建4阶张量对多关系网络进行表征,故其空间复杂度为O(m2n2).在代码实现过程中,由于考虑到邻接张量的稀疏性,采用稀疏张量对其进行压缩处理,可以有效降低多关系网络的空间复杂度.
5 实验与讨论
通过在4个真实社交网络数据集上进行相关实验,从运行时间和度量节点重要程度准确性2个方面对所提出方法进行了评测,并选取多关系网络的度中心性和特征向量中心性[47] 2种经典指标进行对比来说明提出方法的有效性,为避免与单关系网络中的度量指标进行混淆,将多关系网络中的度中心性度中心性记为MDC、特征向量中心性记为MEVC.实验平台为Intel Core i9-9900K 3.6 GHz,64 GB RAM,操作系统为CentOS 7,代码由Python实现.
选取了4个规模不同的真实社交网络数据集[54]MoscowAthletics2013,NYClimateMarch2014,MLKing2013,Cannes2013,这4个数据集均是围绕特定事件从Twitter平台获得的,包含转发、提及、回复3种有向关系.4个数据集的基本统计信息如表1所示:
Table 1 The Basic Information of Experimental Data
表1 实验数据集的基本信息

Data SetNrNuNlKK2MoscowAthletics201338880421025010.693286.23NYClimateMarch2014310243935349512.856785.34MLKing201333277073966718.401559.62Cannes2013343853799185410.463160.37
5.1 评价标准
在节点重要性研究中,通常利用传播动力学模型对节点重要性的排序结果进行评价,本文采用SIR模型[11,32,55-57].SIR模型包括3个状态:
1) 易感(susceptible)状态S(t).表示易感染但尚未感染疾病的个体数量.
2) 感染(infected)状态I(t).表示已经感染,并且能够将疾病传播给易感个体的个体数量.
3) 恢复(recovered)状态R(t).表示感染个体已经恢复,并且不会被再次感染的个体数量.
在SIR模型中,节点重要性的评价标准一般有2项:一种为节点的平均传播范围,即达到稳态时感染态I(t)和恢复态R(t)的数量之和,数量越大,说明该节点越重要.另一种为传播速率,可从传播初始阶段感染态I(t)和恢复态R(t)的数量和达到稳态时所用时间2方面来评判,数量越大、所用时间越小,说明该节点越重要;为方便说明,将第t个时间迭代步时的感染态和恢复态的数量之和记为F(t),感染态的平均数量记为Fi(t),达到稳态时的数量记为F(tc).
由于网络规模不同,SIR模型的传染概率和恢复概率依赖于各层层内网络的拓扑结构.通常,传染概率的设置依赖于各层内网络的渐近传播阈值![]() .渐进传播阈值为传播过程中应取的最小传播概率[33],定义为
.渐进传播阈值为传播过程中应取的最小传播概率[33],定义为
![]()
(50)
根据贝叶斯理论和条件概率,各层传染概率设置为
![]()
(51)
其中,λi为放大系数,Nr为多关系网络的关系数.恢复概率通常依赖于各层的平均度,类似地,各层恢复概率设置为
![]()
(52)
由于传播过程是依概率进行感染传播,即使2组实验条件完全相同,最终得到的结果也会存在一定差异.为此,为此选取100次独立实验所得结果的期望值作为评价结果.
5.2 运行时间分析
通过统计4个真实网络数据集上各算法的实际运行时间来比较提出方法的运行速率,并对4.3节中的时间复杂度分析结果进行验证.为方便说明,记tK,tL,tI,tIE,tE分别为多关系网络中计算多重度中心性、多重局部聚集系数、IOMCR方法、IOMEC方法以及多重特征向量中心性的运行时间,![]() 和
和![]() 分别为单独计算IOMCR方法和IOMEC方法的运行时间.根据4.3节对各算法的时间复杂度分析可知,tI和tIE依赖于tK和tL,即:
分别为单独计算IOMCR方法和IOMEC方法的运行时间.根据4.3节对各算法的时间复杂度分析可知,tI和tIE依赖于tK和tL,即:
![]()
(53)
![]()
(54)
由于4个网络规模不同,我们通过统计各方法运行时间占总运行时间的比重来说明算法运行时间的长短,即:
(55)
其中,tmethod表示计算指定方法时所消耗的时间,ttotal表示计算各方法所消耗的总时间.
如图3所示,在单独计算IOMCR方法和IOMEC方法时,![]() 要明显少于
要明显少于![]() 图4描述了5种指标在4个网络上的运行时间,可以看出,tI,tIE,tK三者之间差别不大,说明在计算IOMCR方法和IOMEC方法的过程中,主要时间消耗在计算多重局部系数的环节上,而多重度中心性和多重特征向量中心性由于都是线性时间复杂度,故二者运行时间很短,在整个计算过程中基本可以忽略不计.综上,实验结果与4.3节中时间复杂度的分析是一致的,在运行时间上,IOMEC方法要优于IOMCR方法.
图4描述了5种指标在4个网络上的运行时间,可以看出,tI,tIE,tK三者之间差别不大,说明在计算IOMCR方法和IOMEC方法的过程中,主要时间消耗在计算多重局部系数的环节上,而多重度中心性和多重特征向量中心性由于都是线性时间复杂度,故二者运行时间很短,在整个计算过程中基本可以忽略不计.综上,实验结果与4.3节中时间复杂度的分析是一致的,在运行时间上,IOMEC方法要优于IOMCR方法.
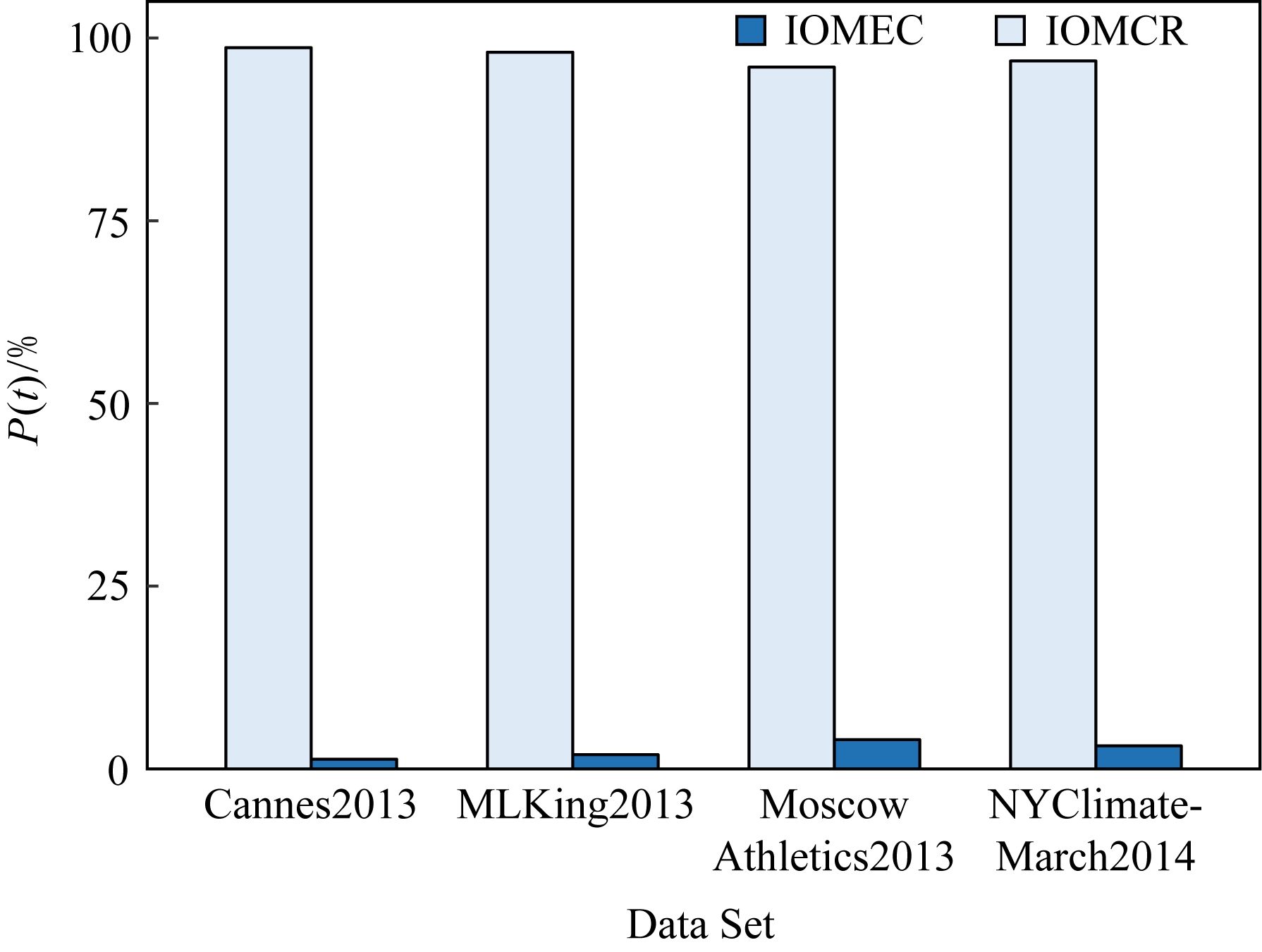
Fig. 3 The run time of IOMCR and IOMEC
图3 IOMCR方法和IOMEC方法运行时间统计图
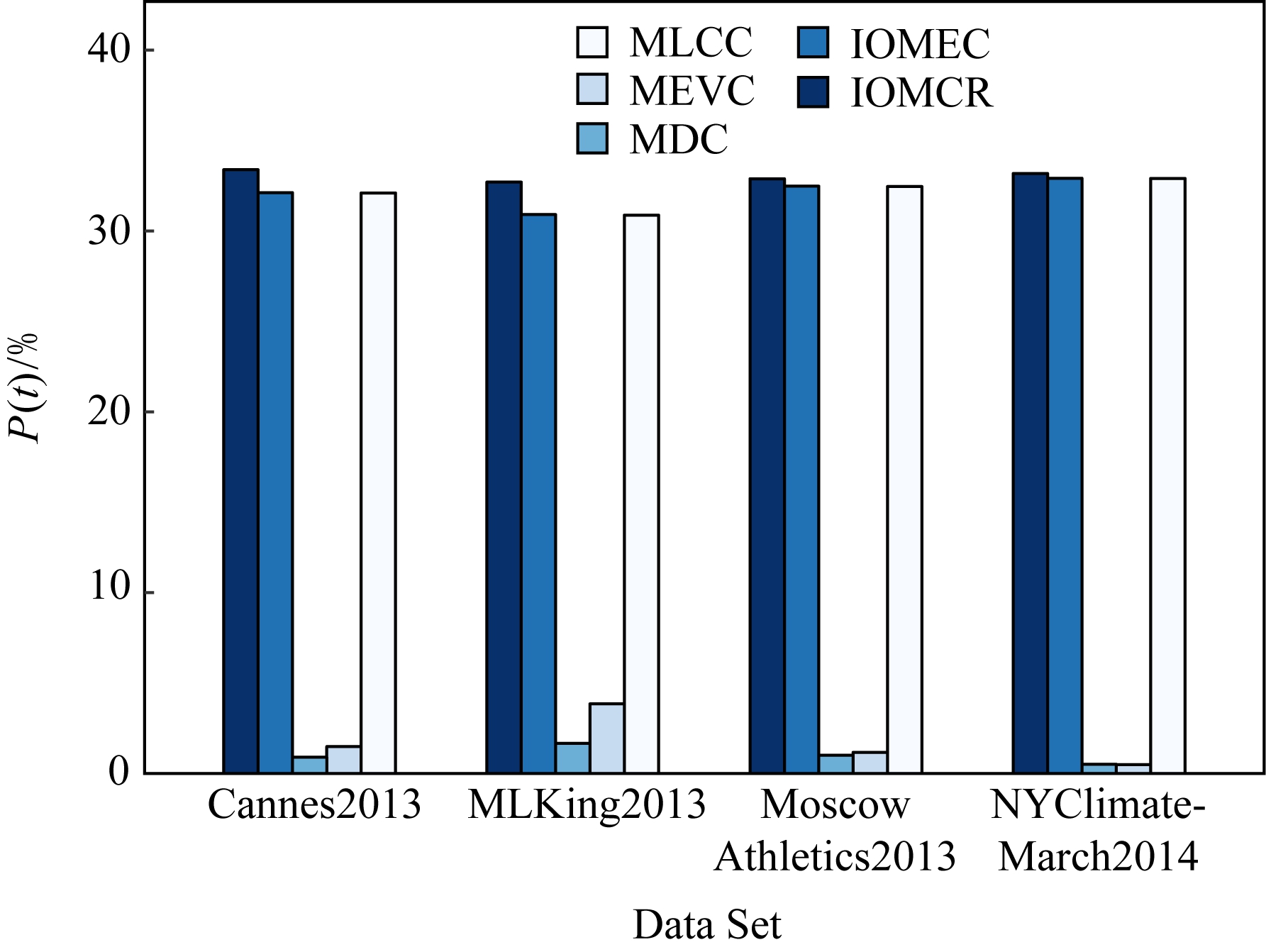
Fig. 4 The run time of measures
图4 各度量方法运行时间统计图
5.3 度量准确性分析
本节在4个数据集上进行了4组不同的实验,并通过SIR进行评测,分别从传播范围和传播速率2方面对各度量方法进行评价来验证提出算法在度量节点重要程度的准确性.
实验1. 通过观测SIR传播曲线的传播范围和传播速率,对各方法度量节点重要性的准确性进行评测.在4个网络中,按照各方法对节点重要程度的度量值进行降序排序,分别选取前1%的节点作为初始传染源节点,统计给定时间迭代步的F(t),并绘制SIR传播曲线,其中横轴代表时间迭代步数,在前3个网络中,设定最大迭代步数为200,而由于Cannes2013规模较大,设置最大迭代步为500.纵轴代表对应的F(t),通过观测曲线达到稳态时的时间和对应的F(tc)来说明传染源节点的传播范围,通过观测曲线的斜率变化来说明传染源节点的传播速率.图5所示的实验结果显示:
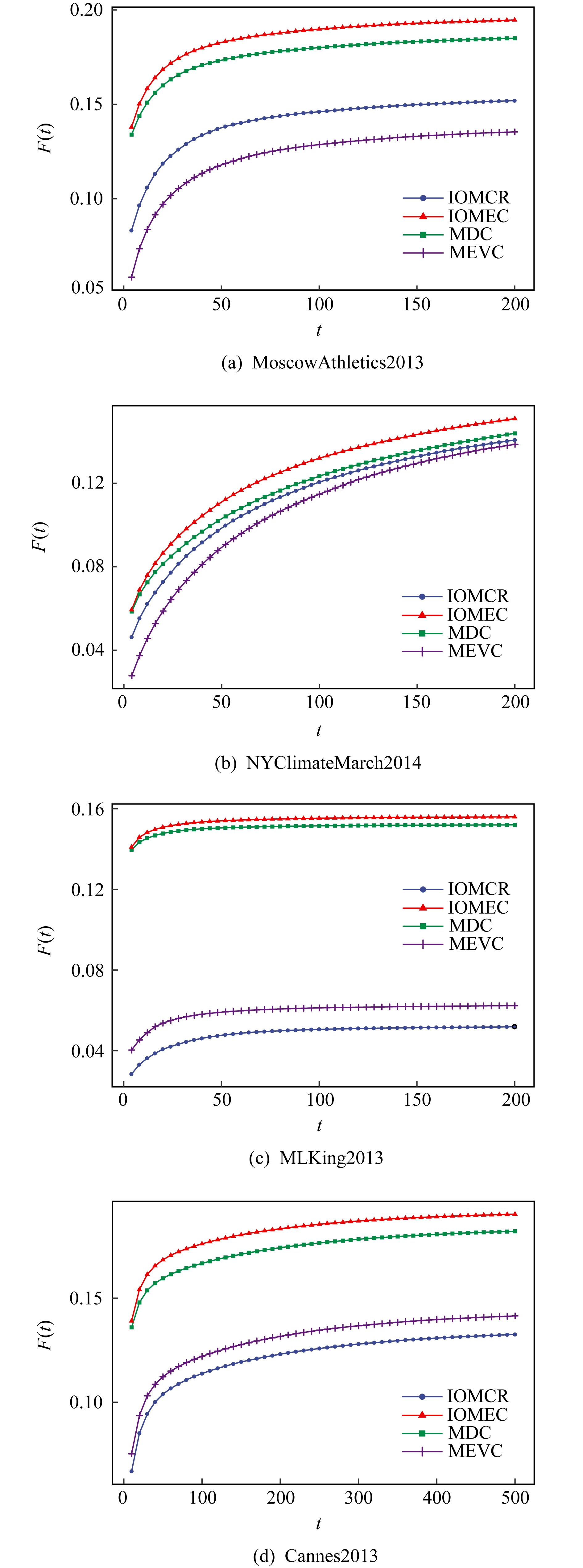
Fig. 5 SIR spreading curves of the top 1% nodes obtained by each method as the initial infectious nodes
图5 各度量方法所得前1%的节点作为初始传染源节点时的SIR传播曲线
1) 在4个网络上,无论是传播时间还是传播范围,IOMEC方法相比于其他方法,都能表现出较好结果,特别是随着网络规模的增加,该优势愈发明显,而多重特征向量中心性表现最差;
2) IOMCR方法的评测结果要劣于IOMEC方法和多重度中心性,特别是在MLKing2013数据集上表现最为突出,IOMEC方法和多重度中心性得到的重要节点的传播范围,约是IOMCR方法得到重要节点传播范围的3倍;
3) 多重度中心性总体表现良好,但要劣于提出的IOMEC方法,并且随着网络规模的增大,二者差距愈发明显.
实验2. 由于在传播过程中,传染源节点在早期的传播中起到主要作用,即对于节点传播能力的评测,早期的传播更为重要.本实验主要通过观测各节点传播初期的F(t)与各方法测量值之间的相关关系,来说明节点的传播能力.本实验设置t=10.在理想状态下,F(t)与对应的测量值应呈现正相关关系.
4个数据集上的实验结果如表2所示.表2中,每列子图分别对应同一数据集下4种不同方法,坐标轴采用双对数坐标,横轴表示每种方法下各节点的度量值,纵轴表示各节点作为传染源节点,所对应的F(t)(t=10).由于网络规模较大,故选取各方法得到前1 000个重要节点的并集作为实验节点集合.
Table 2 The Correlation Between F(t)(t=10) and Its Measure
表2 t=10时,F(t)与各方法度量值间的相关关系

Method MoscowAthletics2013 NYClimateMarch2014MLKing2013Cannes2013MDCMEVCIOMCRIOMEC
实验结果表明:多重度中心性和IOMEC方法在4个网络中都呈现出一定的正相关性,而另2种方法均未呈现出明显的正相关性.在多重度中心性方法中,一些度量值较低的节点反而F(t)更大且分布较为稠密,而在IOMEC方法中这类节点分布稀疏,故IOMEC方法总体上要优于多重度中心性方法.
实验3. 为进一步讨论各方法节点的测量值与其传播能力之间的相关关系,并评测各方法对节点重要性度量的准确性.本实验对各节点在SIR模型中得到的稳态值F(tc)进行排序,并以此为基准,比较其与各方法对节点重要性度量值之间的相关关系.表3描述了在4个网络中,各节点在SIR模型中的传播能力与4种方法对节点度量值间的相关关系,表3中每一列子图对应同一数据集的不同方法,坐标轴采用双对数坐标,横轴表示各节点在对应方法下的测量值,纵轴表示各节点在SIR模型中得到的稳态值F(tc),每一个数据点代表网络中的一个节点,节点的颜色表示在传播过程中,t=10时的传播能力,即F(10).类似地,分别选取各方法得到前1 000个重要节点的并集作为实验节点集合.
Table 3 The Correlation Between Each Measure and Spreading Ability of SIR
表3 节点度量值与SIR传播能力间的相关关系
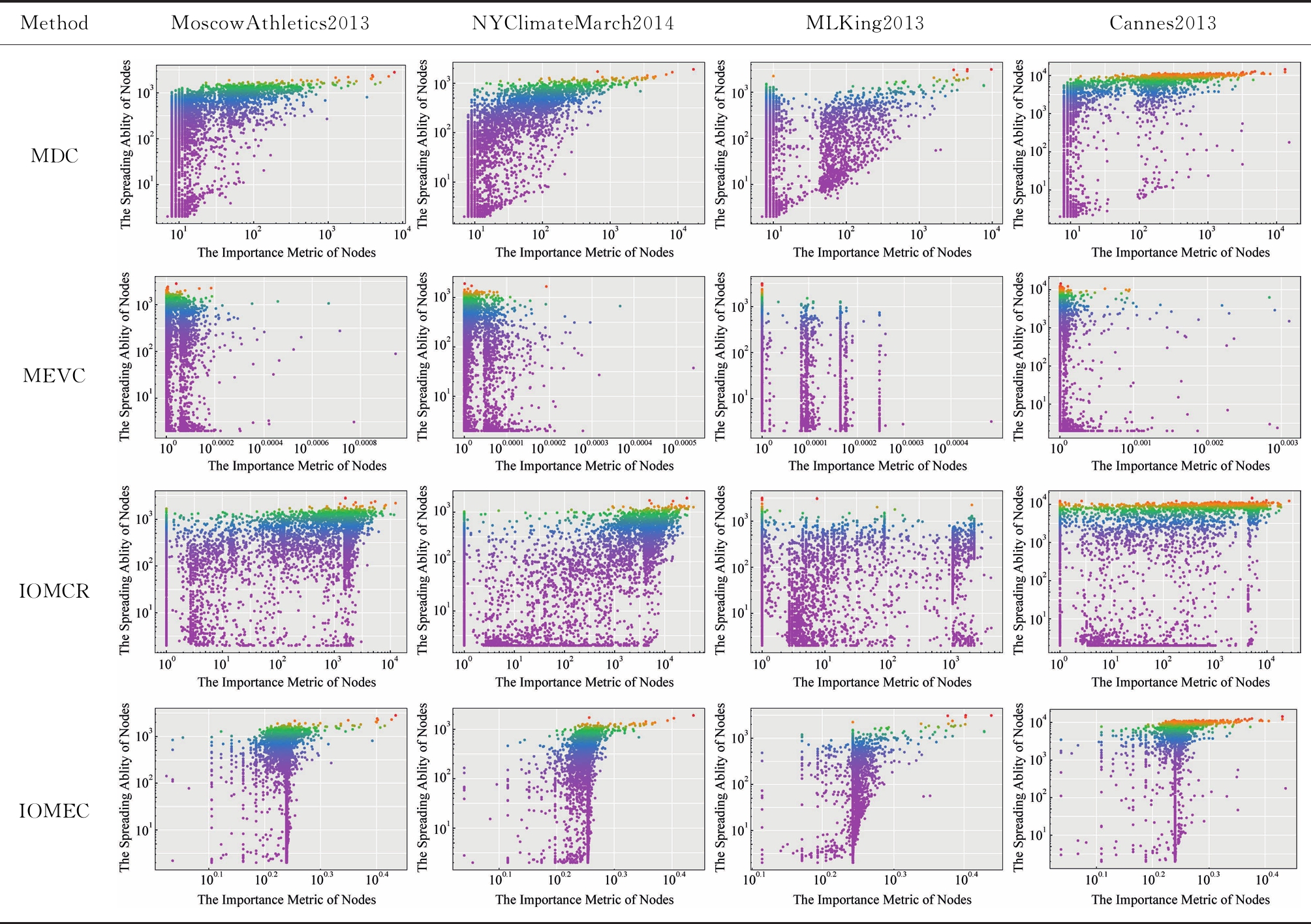
Method MoscowAthletics2013 NYClimateMarch2014MLKing2013Cannes2013MDCMEVCIOMCRIOMEC
实验结果表明:表3所示的各节点相关性分布与表2所示的节点分布基本一致,说明各节点传播能力在传播过程初期起主要作用.从结果上分析,IOMEC方法和多重度中心性仍然能够呈现出正相关态势,IOMEC方法所得到的节点相关性分布要优于多重度中心性;IOMCR方法和多重证据中心性所得到的结果较差,没有呈现出明显的相关性态势.
实验4. 为了进一步验证各方法的性能,本实验研究了按照某种度量方法对节点的重要程度进行排序后,节点排序与在SIR传播过程中所对应的平均感染数量 F(t)
F(t)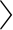 (t=10)之间的关系.从理论上分析,性能较好的度量指标,其图像应该呈现递减关系,即随着节点重要程度的降低,对应的受感染节点的平均数会减少.为了对比,本实验特意增加了随机排序(random ranking)这种极端情况.实验结果如图6所示,其中横轴代表各节点排序,纵轴代表对应的受感染节点平均数量.类似地,分别选取各方法得到前1 000个重要节点的并集作为实验节点集合.4个网络上的实验结果表明:
(t=10)之间的关系.从理论上分析,性能较好的度量指标,其图像应该呈现递减关系,即随着节点重要程度的降低,对应的受感染节点的平均数会减少.为了对比,本实验特意增加了随机排序(random ranking)这种极端情况.实验结果如图6所示,其中横轴代表各节点排序,纵轴代表对应的受感染节点平均数量.类似地,分别选取各方法得到前1 000个重要节点的并集作为实验节点集合.4个网络上的实验结果表明:
1) 随机排序和多重证据中心性情况最差.二者除未呈现出较好的递减态势外,平均感染数量也非常少,说明二者所得到的节点的传播能力很弱.
Fig. 6 The relation between the node ordering given by five measures and average infected number in SIR(t=10)
图6 通过5种方法得到的节点排序与SIR中对应t=10时的平均感染数间的关系
2) IOMEC方法和多重度中心性在4个网络上均能够呈现出良好的递减态势,并且在平均感染数量上,IOMEC方法所得到的结果要优于多重证据中心性,进一步验证了本文提出方法对节点重要程度度量的准确性.
3) 在MoscowAthletics2013和NYClimateMarch 2014上,IOMCR方法所得到的结果能够呈现出较好的递减态势,并且筛选出部分节点的传播能力要优于多重度中心性所得到的结果.但在其他2个网络上,IOMCR方法所得到的结果表现较差,筛选出的节点传播能力与IOMEC方法和多重度中心性得到的结果差距明显,尤其在MLKing2013中,未呈现出明显的递减趋势,并且平均感染数量很低.进一步说明,随着网络规模的增大,节点传递性的因素愈发重要,并且节点的中心性、声望、传递性之间不具备绝对的正相关性,传统的ClusterRank思想存在一定的局限性.
6 总 结
本文针对多关系社交网络的节点重要性问题进行了研究,应用有向多重网络模型和基于张量代数的数学框架对其进行建模和分析,综合分析中心性、声望和传递性对节点重要性的影响,提出了IOMCR节点重要性度量方法,并针对其存在问题,引入D-S证据理论信息融合方法对其进行改进,进一步提出了面向多关系网络的IOMEC节点重要性度量方法.在4个真实网络上的实验表明4个主要结论:
1) 在多关系社交网络中,由于受耦合信息和传递机制差异性的影响,节点的中心性、声望和传递性之间不具有绝对的相关关系,对三者进行相关性融合的IOMCR度量方法会对计算结果造成误差,降低了度量节点重要性的准确度,随着网络规模的增大,该问题会更加突出,说明传统的ClusterRank思想具有局限性.
2) 通过引入D-S证据理论,对节点中心性、声望、传递性进行依概率融合所提出的IOMEC度量方法,可以有效消除多关系网络耦合信息和传递机制的差异性对节点重要信息造成的影响,相比于只关注中心性和声望的多重度中心性和只关注节点传递能力的多重特征向量中心性,能够更加准确地挖掘网络中的重要节点,特别是在大规模网络中优势更为明显.
3) 通过IOMEC方法、多重度中心性和多重特征向量中心性3种方法所得结果的横向对比分析,说明在多关系网络的节点重要性研究中,基于网络拓扑结构的中心性和声望因素占主导地位,而只关注节点传递特性,直接扩展单个网络节点特征向量中心性的思路方法到多关系网络上,并未得到理想效果.为更加准确的度量节点的重要性程度,在关注节点中心性和声望的同时,也应该关注节点的传递特性,特别是在大规模网络中,节点的传递性作用更加突出.
4) 由于考虑了节点的传递性指标,故提出方法总体具有较高的时间复杂度,相比于IOMCR方法,改进的IOMEC方法具有更低的时间复杂度.故本文提出方法适用于需要精准挖掘网络中重要节点的应用场景,对于准确度不高的应用场景,可以考虑只关注节点中心性和声望的多重度中心性.
综上,本文所做工作不仅对多关系社交网络的节点重要性研究提供了新的思路方法,也进一步拓展了D-S证据理论的应用场景.然而,本文的工作也并不完美,受实验环境的限制,尚不适用于超大规模的多关系网络.近年来,复杂网络呈现出大规模、高维度和动态性的特点,如何建立合理的模型对网络进行表示,设计有效的度量指标或算法识别大规模高维动态复杂网络的关键节点是当前复杂网络节点重要性研究面临的一项挑战,也是我们今后研究工作的重点.
[1]Fang Jinqing. From a single network to “network of networks” development process: Some discussions on the exploration of multilayer supernetwork models and challenges[J]. Complex Systems and Complexity Science, 2016, 13(1): 40-47 (in Chinese)(方锦清. 从单一网络向《网络的网络》的转变进程——略论多层次超网络模型的探索与挑战[J]. 复杂系统与复杂性科学, 2016, 13(1): 40-47)
[2]Battiston F, Nicosia V, Latora V. The new challenges of multiplex networks: Measures and models[J]. The European Physical Journal Special Topics, 2017, 226(3): 401-416
[3]Tu Xiao, Jiang Guoping, Song Yurong, et al. Novel multiplex PageRank in multilayer networks[J]. IEEE Access, 2018, 6: 12530-12538
[4]Ding Cangfeng, Li Kan. Centrality ranking in multiplex networks using topologically biased random walks[J]. Neurocomputing, 2018, 312: 263-275
[5]De Arruda G F, Cozzo E, Moreno Y, et al. On degree-degree correlations in multilayer networks[J]. Physica D: Nonlinear Phenomena, 2016, 323/324: 5-11
[6]Solé-Ribalta A, De Domenico M, Gómez S, et al. Random walk centrality in interconnected multilayer networks[J]. Physica D: Nonlinear Phenomena, 2016, 323/324: 73-79
[7]Liu Yangyang, Zhao Chengli, Zhang Xue, et al. Core structure: The coupling failure procedure in multiplex networks[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 507: 1-11
[8]Ma Lijia, Gong Maoguo, Yan Jianan, et al. Detecting composite communities in multiplex networks: A multilevel memetic algorithm[J]. Swarm and Evolutionary Computation, 2018, 39: 177-191
[9]Ding Rui, Ujang N, Hamid H B, et al. Detecting the urban traffic network structure dynamics through the growth and analysis of multi-layer networks[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 503: 800-817
[10]Pan Lulu, Shao Haibin, Mesbahi M, et al. Structural balance of multiplex signed networks: A distributed data-driven approach[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 508: 748-756
[11]Zheng Chunyuan, Xia Chengyi, Guo Quantong, et al. Interplay between SIR-based disease spreading and awareness diffusion on multiplex networks[J]. Journal of Parallel and Distributed Computing, 2018, 115: 20-28
[12]Pedroche F, García E, Romance M, et al. On the spectrum of two-layer approach and multiplex PageRank[J]. Journal of Computational and Applied Mathematics, 2018, 344: 161-172
[13]Faust K, Wasserman S. Social Network Analysis: Methods and Applications[M]. Cambridge, MA: Cambridge University Press, 1994
[14]Gluckman M. The Judicial Process Among the Barotse of Northern Rhodesia[M]. Manchester, Engliand: Manchester University Press, 1955
[15]Verbrugge L M. Multiplexity in adult friendships[J]. Social Forces, 1979, 57(4): 1286-1309
[16]Mitchell J C. Social Networks in Urban Situations: Analyses of Personal Relationships in Central African Towns[M]. Manchester, England: Manchester University Press, 1969
[17]Pattison P, Wasserman S. Logit models and logistic regressions for social networks: Ⅱ. Multivariate relations[J]. British Journal of Mathematical and Statistical Psychology, 1999, 52(2): 169-193
[18]Lusher D, Koskinen J, Robins G. Exponential random graph models for social networks[J]. Social Networks, 2009, 31(1): 12-25
[19]Wang Nana, Gao Hong, Liu Wei. Research on a heterogeneous edge multi-graph network model[J]. CAAI Transactions on Intelligent Systems, 2017, 12(4): 475-481 (in Chinese)(王娜娜, 高红, 刘巍. 异质边多重图网络模型研究[J]. 智能系统学报, 2017, 12(4): 475-481)
[20]Wang Nana, Gao Hong, Li Shanshan, et al. A research on hypergraph of heterogeneous edge[J]. Journal of Guangdong University of Technology, 2017, 34(1): 6-10 (in Chinese)(王娜娜, 高红, 李珊珊, 等. 基于异质超边的超图[J]. 广东工业大学学报, 2017, 34(1): 6-10)
[21]Huang Ruiyang, Wu Qi, Zhu Yuhang. Community detection in dynamic heterogeneous network with joint nonnegative matrix factorization[J]. Application Research of Computers, 2017, 34(10): 2989-2992 (in Chinese)(黄瑞阳, 吴奇, 朱宇航. 基于联合矩阵分解的动态异质网络社区发现方法[J]. 计算机应用研究, 2017, 34(10): 2989-2992)
[22]Bing Sheng, Sun Gengxin. Important node detection algorithm for multiple relationships on line social network based on multi-subnet composited complex network model[J]. Journal of Nanjing University: Natural Sciences, 2017, 53(2): 378-385 (in Chinese)(宾晟, 孙更新. 基于多子网复合复杂网络模型的多关系社交网络重要节点发现算法[J]. 南京大学学报: 自然科学, 2017, 53(2): 378-385)
[23]Kolda T G, Bader B W. Tensor decompositions and applications[J]. SIAM Review, 2009, 51(3): 455-500
[24]Jo H, Moon H, Ki Baek S. Immunization dynamics on a 2-layer network model[J]. Physica A: Statistical Mechanics and Its Applications, 2006, 361(2): 534-542
[25]Acar E, Yener B. Unsupervised multiway data analysis: A literature survey[J]. IEEE Transactions on Knowledge and Data Engineering, 2009, 21(1): 6-20
[26]Kurant M, Thiran P, Hagmann P. Error and attack tolerance of layered complex networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2006, 76(2): 26103
[27]Kurant M, Thiran P. Layered complex networks[J]. Physical Review Letters, 2006, 96(13): 138701
[28]Wei Xiang, Chen Shihua, Wu Xiaojun, et al. A unified framework of interplay between two spreading processes in multiplex networks[J]. EPL: A Letters Journal Exploring the Frontiers of Physics, 2016, 114(2): 26006
[29]Mei Guofeng, Wu Xiaoqun, Wang Yingfei, et al. Compressive-sensing-based structure identification for multilayer networks[J]. IEEE Transactions on Cybernetics, 2018, 48(2): 754-764
[30]Zhou Changsong, Zemanová L, Zamora-López G, et al. Structure-function relationship in complex brain networks expressed by hierarchical synchronization[J]. New Journal of Physics, 2007, 9(6): 178
[31]Zamora-López G, Zhou Changsong, Kurths J. Structural characterization of networks using the cat cortex as an example[G] //Lectures in Supercomputational Neurosciences: Dynamics in Complex Brain Networks. Berlin: Springer, 2008: 77-106
[32]Boccaletti S, Bianconi G, Criado R, et al. The structure and dynamics of multilayer networks[J]. Physics Reports, 2014, 544(1): 1-122
[33]Lü Lingyuan, Chen Duanbing, Ren Xiaolong, et al. Vital nodes identification in complex networks[J]. Physics Reports, 2016, 650: 1-63
[34]Freeman L C. A set of measures of centrality based on betweenness[J]. Sociometry, 1977, 40(1): 35-41
[35]Sabidussi G. The centrality index of a graph[J]. Psychometrika, 1966, 31(4): 581-603
[36]Bonacich P. Factoring and weighting approaches to status scores and clique identification[J]. The Journal of Mathematical Sociology, 1972, 2(1): 113-120
[37]Albert R, Jeong H, Barabasi A. Diameter of the World-Wide Web[J]. Nature, 1999, 401(6749): 130-131
[38]Chen Duanbing, Lü Lingyuan, Shang Mingsheng, et al. Identifying influential nodes in complex networks[J]. Physica A: Statistical Mechanics and Its Applications, 2012, 391(4): 1777-1787
[39]Gao Cai, Wei Daijun, Hu Yong, et al. A modified evidential methodology of identifying influential nodes in weighted networks[J]. Physica A: Statistical Mechanics and Its Applications, 2013, 392(21): 5490-5500
[40]Chen Duanbing, Gao Hui, Lü Linyuan, et al. Identifying influential nodes in large-scale directed networks: The role of clustering[J]. PLoS ONE, 2013, 8(10): e77455
[41]Wang Yafei, Yan Guanghui, Ma Qingqing, et al. Identifying influential spreaders on weighted networks based on ClusterRank[C] //Proc of Int Symp on Computational Intelligence and Design. Piscataway,NJ: IEEE, 2017: 476-479
[42]Zhang Xin. Multilayer networks science: Concepts, theories and data[J]. Complex Systems and Complexity Science, 2015, 12(2): 103-107 (in Chinese)(张欣. 多层复杂网络理论研究进展:概念、理论和数据[J]. 复杂系统与复杂性科学, 2015, 12(2): 103-107)
[43]Battiston F, Nicosia V, Latora V. Structural measures for multiplex networks[J]. Physical Review E, 2014, 89(3): 32804
[44]Cozzo E, Kivelä M, Domenico M D, et al. Structure of triadic relations in multiplex networks[J]. New Journal of Physics, 2015, 17(7): 73029
[45]Huang Kezhi, Xue Mingde, Lu Mingwan. Tensor Analysis[M]. 2nd ed. Beijing: Tsinghua University Press, 2003 (in Chinese)(黄克智, 薛明德, 陆明万. 张量分析[M]. 2版. 北京: 清华大学出版社, 2003)
[46]Han Chongzhao, Zhu Hongyan, Duan Zhansheng. Multi-source Information Fusion[M]. 2nd ed. Beijing: Tsinghua University Press, 2010 (in Chinese)(韩崇昭, 朱洪艳, 段战胜. 多源信息融合[M]. 2版. 北京: 清华大学出版社, 2010)
[47]De Domenico M, Solé-Ribalta A, Cozzo E, et al. Mathematical formulation of multilayer networks[J]. Physical Review X, 2013, 3(4): 41022
[48]Gómez S, Díaz-Guilera A, Gómez-Garde es J, et al. Diffusion dynamics on multiplex networks[J]. Physical Review Letters, 2013, 110(2): 028701
es J, et al. Diffusion dynamics on multiplex networks[J]. Physical Review Letters, 2013, 110(2): 028701
[49]Solé-Ribalta A, De Domenico M, Kouvaris N E, et al. Spectral properties of the Laplacian of multiplex networks[J]. Physical Review E, 2013, 88(3): 032807
[50]Estrada E, Gómez-Garde es J. Communicability reveals a transition to coordinated behavior in multiplex networks[J]. Physical Review E, 2014, 89(4): 042819
es J. Communicability reveals a transition to coordinated behavior in multiplex networks[J]. Physical Review E, 2014, 89(4): 042819
[51]Newman M E. Properties of highly clustered networks[J]. Physical Review E: Statistical, Nonlinear, and Soft Matter Physics, 2003, 68(2): 26-121
[52]Newman M E. Networks: An Introduction[M]. Oxford, England: Oxford University Press, 2010
[53]Wei Daijun, Deng Xinyang, Zhang Xiaoge, et al. Identifying influential nodes in weighted networks based on evidence theory[J]. Physica A: Statistical Mechanics and Its Applications, 2013, 392(10): 2564-2575
[54]Omodei E, De Domenico M D, Arenas A. Characterizing interactions in online social networks during exceptional events[J]. Frontiers in Physics, 2015, 3(15): 59
[55]Reng Xiaolong, Lü Linyuan. Review of ranking nodes in complex networks[J]. Chinese Science Bulletin, 2014, 59(13): 1175-1197 (in Chinese)(任晓龙, 吕琳媛. 网络重要节点排序方法综述[J]. 科学通报, 2014, 59(13): 1175-1197)
[56]Yagan O, Qian Dajun, Zhang Junshan, et al. Conjoining speeds up information diffusion in overlaying social-physical networks[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(6): 1038-1048
[57]Salehi M, Sharma R, Marzolla M, et al. Spreading processes in multilayer networks[J]. IEEE Transactions on Network Science and Engineering, 2015, 2(2): 65-83







