密码S盒是许多对称密码算法的核心部件,通常决定算法的安全强度.最优密码S盒通常具有双射性、高非线性、低差分均匀性等代数性质.分组密码S盒的构造,早期主要从数学结构方面考虑,比如高级加密标准(advanced encryption standard, AES)与Camellia所使用的S盒均基于幂映射方法.但这种构造方法难以同时兼顾S盒的多种密码安全性质,比如透明阶指标[1-3]即抵御差分功耗攻击(diff-erential power attack, DPA)[4]的能力等.如何设计并确保密码S盒具有一定能力抵御侧信道攻击一直是业界研究的难点.在密码S盒的设计中,除了传统的代数构造外,采用智能化搜索算法进行搜索设计也是当前的研究热点之一.这些智能化搜索能够在更大空间高效搜索最优解,提高全局寻优效率,并克服了传统密码S盒构造方法的缺陷.目前,遗传算法、遗传规划、元胞自动机等相继被应用于S盒构造.1999年Millan等人[5]利用启发式算法更快地找到密码性质更强的S盒;2004年陈华等人[6]利用基因算法对S盒的密码特性作局部优化,再通过遗传算法产生性能良好的S盒;2014年Picek等人使用遗传算法分别搜索到含有较小透明阶值的布尔函数[7],4×4 S盒[8]和8×8 S盒[9];2015年Kumar等人[10]提出一种基于可逆CA规则的AES的S盒设计方法,降低了实现成本;2017年Picek等人[11]利用遗传规划演化了大量的CA规则,产生了具有良好密码特性的S盒,并在硬件上实现了最优S盒的性能测试;2018年Ghoshal等人[12]利用CA规则构造了4×4最优S盒,降低了基于门限实现(threshold implementation, TI)占用的芯片面积和功耗;2019年关杰等人[13]通过实验找到一类新的基于CA的S盒,其具有代替Keccak杂凑函数S盒的潜力.注意到,文献[12]没有讨论所构造S盒的透明阶大小,并且其搜索到的4×4最优S盒数量偏少.如何设计低透明阶的最优密码S盒是目前有待解决的问题.
本文基于CA规则,采用变元分量部分固定和分别搜索的策略,提出一种S盒新搜索方法.首先,分析CA规则下生成的4×4 S盒,对CA规则下12类S盒数量进行分类统计,并测试了其透明阶值;其次,使用S盒的新自动搜索方法设计出大量的4×4 S盒,对设计出的新S盒的密码学性质进行安全性分析,相对于CA规则生成的S盒,获得了数量更多且透明阶值更低的4×4最优S盒,这说明这些新的S盒具有更好抵御DPA攻击的能力.
1 预备知识
设n,m为正整数,即n,m∈N,域F2中所有n元组元素的集合表示为![]() 其中F2是包含2个元素的二元有限域.(n,m)-函数是函数F从
其中F2是包含2个元素的二元有限域.(n,m)-函数是函数F从![]() 的任意映射,称为S盒.对于(n,m)-函数表示为F(x)=(f1(x),f2(x),…,fi(x),…,fm(x)),其中
的任意映射,称为S盒.对于(n,m)-函数表示为F(x)=(f1(x),f2(x),…,fi(x),…,fm(x)),其中![]() 称为F的坐标函数,其分量函数都是非零系数坐标函数的线性组合.
称为F的坐标函数,其分量函数都是非零系数坐标函数的线性组合.
本文考虑具有相同输入和输出数量的S盒,即:n×n S盒.目前,对n×n S盒的安全性评估指标较多,本文主要从传统安全性指标和抵抗侧信道攻击的安全性新指标透明阶做简要描述.
1.1 S盒安全性指标
1) 代数次数
定义1[14]. 对于任意的n元布尔函数![]() 其多项式表示形式唯一,即:
其多项式表示形式唯一,即:
(1)
其中,βu∈F2,u=(u1,u2,…,un).则称式(1)为f的代数正规型(algebraic normal form, ANF).
布尔函数f的代数次数定义为布尔函数的ANF中最大乘积项的变量个数,用degf表示:
![]()
(2)
其S盒的代数次数是其分量函数f代数次数的最大值,用degF表示;wt(u)表示函数f的汉明重量,即真值表中“1”的个数.理想情况下,一个密码学上有用的S盒具有较高的代数次数,以抵御代数攻击.
2) 平衡性
对于函数![]() 若
若![]() 域中的每一个值恰好取一次,则F是平衡的.
域中的每一个值恰好取一次,则F是平衡的.
3) 非线性度
定义2[15]. 对于n×n S盒函数F的非线性度定义为其所有分量函数组合v·F的最小非线性值,其中![]() 即:
即:
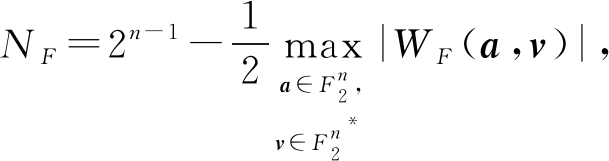
(3)
其中
(4)
是函数F的一个Walsh谱.a·b是a,b的内积,![]() 且
且![]()
4) 差分均匀性
定义3[16]. 设函数F是从![]() 的非线性映射(S盒),对于
的非线性映射(S盒),对于![]() 函数F的差分分布表定义为
函数F的差分分布表定义为
![]()
(5)
其差分均匀度为
![]()
(6)
5) 透明阶
在2005年FSE会议上,法国学者Prouff[1]在汉明重量模型下,提出了S盒透明阶(transparency order, TO)的定义,这是第1次在多位的条件下,量化S盒抵御DPA攻击的能力.2017年Chakraborty等人[2]指出TO定义的不足之处,并得到了改进透明阶(modified transparency order, MTO)的新定义.
定义4. 令F为一个平衡的n×m函数,改进的透明阶TMTO(F)计算为
![]()
![]()
(7)
其中,β表示寄存器初始状态,![]() 为Fi(x),Fj(x)的互相关谱
为Fi(x),Fj(x)的互相关谱![]()
2019年Li等人[3]提出了修订的透明阶(revised transparency order, RTO),以更好地度量密码S盒抵御DPA攻击的能力.
定义5. 令F为一个平衡的n×m函数,修订的透明阶TRTO(F)计算为
![]()
![]()
(8)
由式(3)(7)(8)可知,2个指标都与Walsh谱有关,当Walsh谱的值越大,透明阶越小,S盒的NF也越小.但在理论上,透明阶越小越好,NF越大越好,抵抗DPA的能力越强,所以二者存在一种对立的关系.
1.2 元胞自动机
元胞自动机是用于模拟和分析各种离散复杂系统的并行计算模型.CA主要由元胞、元胞空间、邻域和规则组成,一个CA在每一个时间状态中,元胞空间上的每一个元胞都按照局部规则同步更新其状态,其中该局部规则应用于元胞的邻域.本文只考虑一维布尔周期型边界元胞自动机(periodic boundary cellular automata, PBCA).其中,CA是一个矢量布尔函数,每个元胞处于0或1状态,即F2={0,1}.
定义6[17]. 对于任意![]() 位输入元胞
位输入元胞![]() 的PBCA定义为
的PBCA定义为
F(x1,x2,…,xn)=(f(x1,…,xd),…,
f(xn-d+2,…,x1),…,f(xn,…,xd-1)),
(9)
其中,xi(i=1,2,…,n)为元胞,d为邻域半径,f是变量d(d≤n)上的布尔函数,称为局部规则.
2 基于CA规则的4×4 S盒
2.1 基于CA规则的4×4 S盒设计
CA规则可作为S盒的设计策略,该规则具有良好的密码学性质和较低的实现成本.根据PBCA的定义,Ghoshal等人[12]给出了4×4 S盒的如下表示形式:
定义7. 选择CA规则,给出一个4×1的CA规则f,则相应的4×4的S盒表示为
S(X,Y,Z,W)=(f(X,Y,Z,W),f(Y,Z,W,X),
f(Z,W,X,Y),f(W,X,Y,Z)).
(10)
基于定义7,在S盒构造中,先选择一个局部CA规则,其本质是一个4×1的布尔函数,将该局部CA规则的输入位进行4种不同的循环置换,得到4×4的S盒映射,使得其能够在硬件中实现一个低成本的等价迭代.
基于CA规则的S盒可看作一种特殊类型的向量布尔函数,其中每个坐标函数对应于局部邻域的CA规则.在此规则下生成的S盒总数利用德布莱英图(De Bruijn graph)技术表示,其首先给定一个德布莱英图G=(V,E),其中V表示顶点,E表示边,E的数量|E|=2n;其次将图的每条边与一个位{0,1}关联,得到局部CA规则,与此图相关联的CA规则总数为22n.基于上述方法,对于n=4,所产生的CA规则总数为224=216,每一个CA规则产生一个唯一的4×4函数;对这些函数进行穷搜索得到1 536个双射S盒,考虑其非线性度和差分均匀度的密码性质最优,最终搜索到512个候选S盒.
2.2 基于CA规则的4×4 S盒分析
针对基于CA规则生成的512个4×4候选S盒,文献[12]根据S盒的代数正规型(ANF)表示的性质进行了分类:其首先把S盒用ANF形式表示,由于每一个4×4 S盒的最优代数次数为3,其划分每一类的ANF都具有相同数量的三次项、二次项和线性形式,最终划分了12类.这些S盒在硬件实现中具有类似的占用面积和功耗,由于每一类都有相同的代数结构,则有几乎相同的TI电路表示,减少了硬件面积消耗,提高了运行速度.
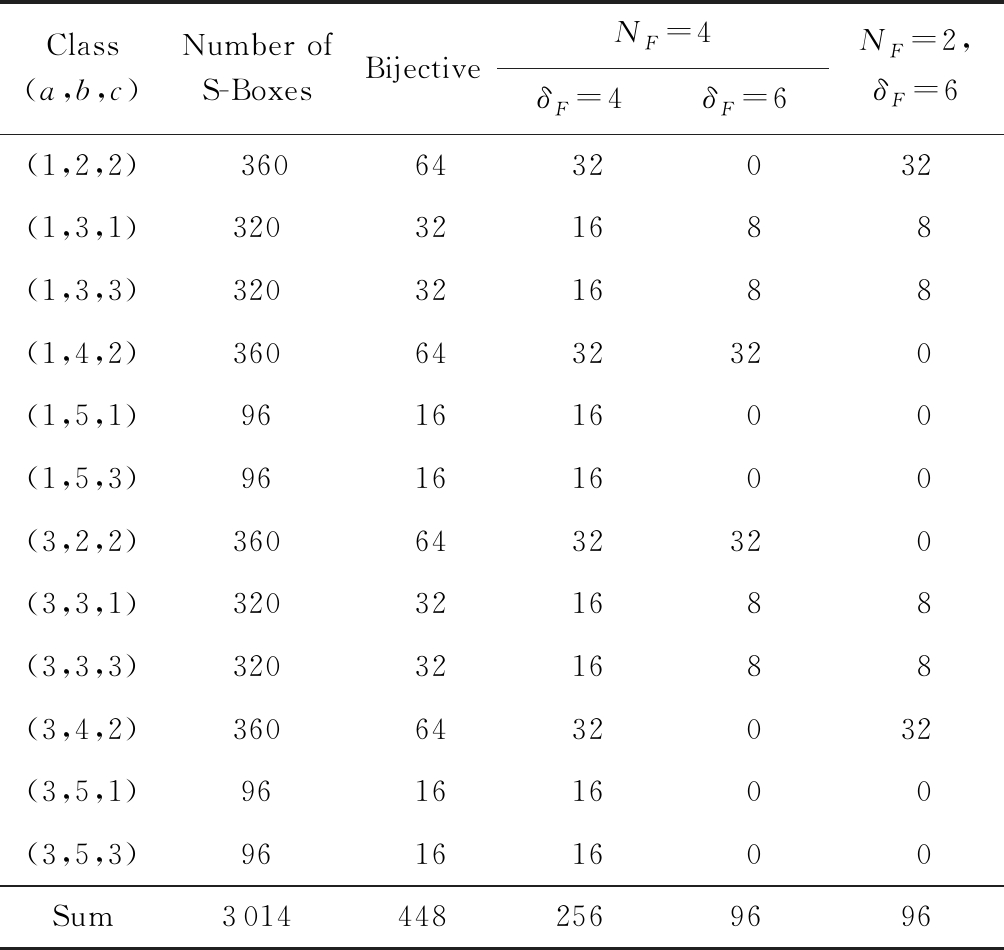
在对文献[12]的分类分析中发现:每一类的项数之和为奇数(记为奇数类),则满足双射性;若为偶数(记为偶数类),则不满足双射性.因此,在进行分类时判断哪一类存在最优S盒不用考虑偶数类,这将有效减少搜索时间.基于该方法,最终对基于CA规则生成的S盒划分为同样的12类,如表1所示[12].
表1显示,满足这12类的双射S盒有448个,考虑其非线性度、差分均匀度和代数次数的密码性质最优,得到256个最优S盒.
传统安全性指标可作为衡量经典密码分析的标准,透明阶则是评估S盒抵抗DPA攻击的能力.文献[12]没有考虑抵抗DPA攻击的能力,特别是MTO和RTO指标.
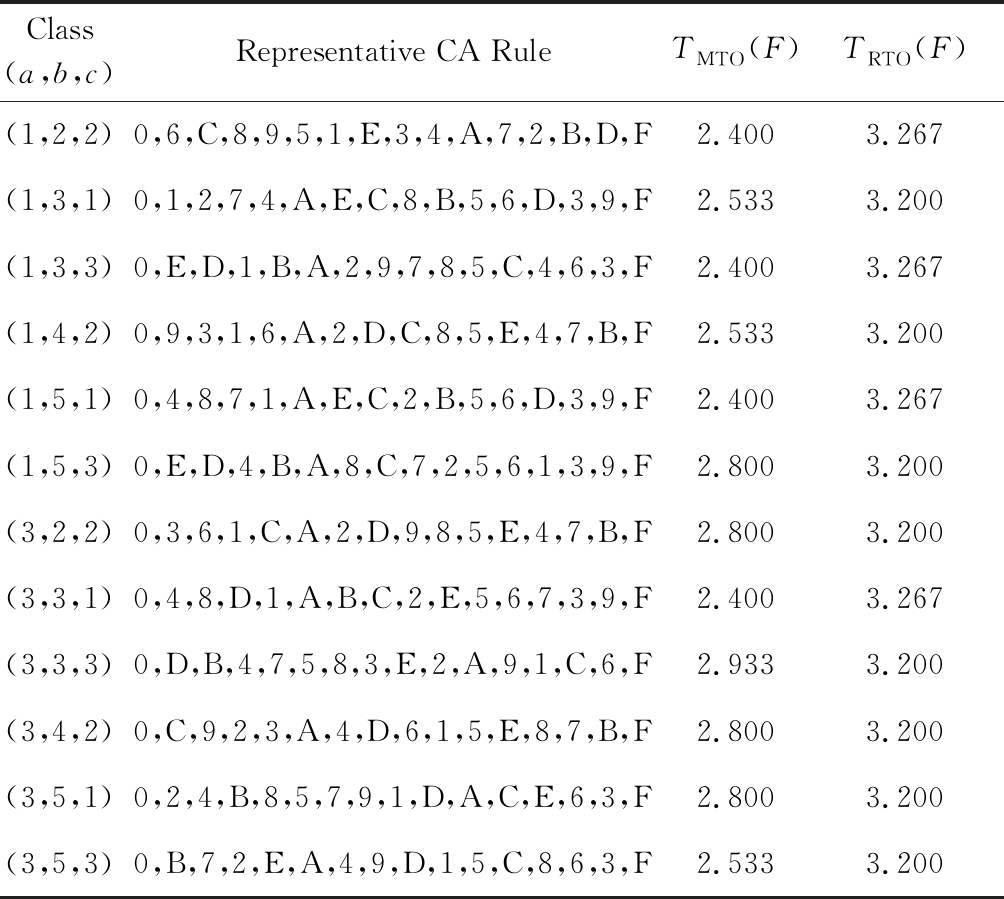
利用式(7)(8)定义的透明阶,测试了每一个S盒的透明阶值.因篇幅有限,在此仅列出每一类代表元最优S盒的MTO,RTO值,具体如表2所示.
Table 1 Statistics Table of 12 Classes of 4×4 S-Boxes
表1 12类4×4 S盒数量统计表
Class(a,b,c)Number ofS-BoxesBijectiveNF=4δF=4δF=6NF=2,δF=6(1,2,2)3606432032(1,3,1)320321688(1,3,3)320321688(1,4,2)3606432320(1,5,1)96161600(1,5,3)96161600(3,2,2)3606432320(3,3,1)320321688(3,3,3)320321688(3,4,2)3606432032(3,5,1)96161600(3,5,3)96161600Sum30144482569696
Note: a is cubic terms, b is quadratic terms, and c is linear terms.
Table 2 Transparent Order Value of 12 Classes of 4×4 S-Boxes Representatives
表2 12类4×4 S盒代表元的透明阶值
Class(a,b,c)Representative CA RuleTMTO(F)TRTO(F)(1,2,2)0,6,C,8,9,5,1,E,3,4,A,7,2,B,D,F2.4003.267(1,3,1)0,1,2,7,4,A,E,C,8,B,5,6,D,3,9,F2.5333.200(1,3,3)0,E,D,1,B,A,2,9,7,8,5,C,4,6,3,F2.4003.267(1,4,2)0,9,3,1,6,A,2,D,C,8,5,E,4,7,B,F2.5333.200(1,5,1)0,4,8,7,1,A,E,C,2,B,5,6,D,3,9,F2.4003.267(1,5,3)0,E,D,4,B,A,8,C,7,2,5,6,1,3,9,F2.8003.200(3,2,2)0,3,6,1,C,A,2,D,9,8,5,E,4,7,B,F2.8003.200(3,3,1)0,4,8,D,1,A,B,C,2,E,5,6,7,3,9,F2.4003.267(3,3,3)0,D,B,4,7,5,8,3,E,2,A,9,1,C,6,F2.9333.200(3,4,2)0,C,9,2,3,A,4,D,6,1,5,E,8,7,B,F2.8003.200(3,5,1)0,2,4,B,8,5,7,9,1,D,A,C,E,6,3,F2.8003.200(3,5,3)0,B,7,2,E,A,4,9,D,1,5,C,8,6,3,F2.5333.200
Note: a is cubic terms, b is quadratic terms, and c is linear terms.
表2显示,基于CA规则生成的12类代表元S盒的MTO值在2.4~2.933之间,未列出的S盒也在这个范围之内;RTO值均为3.200或3.267,其他未列出的S盒的RTO值也均为3.200或3.267.发现基于CA规则生成的12类S盒的透明阶值普遍不低,抵御DPA攻击相对较弱,如何构造新型最优S盒,且在满足传统安全性指标的同时还有较低的透明阶是目前需要解决的问题.
3 基于改进CA规则的4×4 S盒
3.1 基于改进CA规则4×4最优S盒
3.1.1 4×4最优S盒设计
基于CA规则下生成的12类4×4最优S盒,本文提出一种新的搜索方法,实现S盒的扩展,以搜索具有更低透明阶的最优S盒.
注意到基于CA规则生成的12类4×4最优S盒无法直接降低透明阶值,则考虑在CA规则的基础上实现S盒的扩展,再搜索具有更低透明阶的最优S盒.首先考虑4×4 S盒的本质特征,为此我们通过以下2个性质进行改进.
性质1. 对于4×4 S盒,X∈{0,1,…,15},fi∈{0,1}(i=0,1,2,3),F=(f0,f1,f2,f3),F3=(f0,f1,f2).令4×4 S盒输入输出坐标对为(X,F),参考坐标对为(X,F3),则输入输出坐标对可表示为(X,F3,f3).则任意双射4×4 S盒可由16对(X,F)均互不相同的输入输出坐标对唯一表示.
性质2. 设有双射4×4 S盒,对于任意给定函数![]() 根据该S盒真值表,均可得到确定的2对参考坐标对:
根据该S盒真值表,均可得到确定的2对参考坐标对:![]() 和
和![]() 相应地,输入输出坐标对可表示为
相应地,输入输出坐标对可表示为![]() 及
及![]() 其中a,b∈{0,1}且a≠b.
其中a,b∈{0,1}且a≠b.
由性质2可知,若已知![]() 则a或b任意一个元素确定取值后,即确定任意一组输入输出坐标对
则a或b任意一个元素确定取值后,即确定任意一组输入输出坐标对![]() 或
或![]() 便可得到4×4 S盒的2对输入输出坐标对(Xa,Fa)和(Xb,Fb).结合性质1,若将
便可得到4×4 S盒的2对输入输出坐标对(Xa,Fa)和(Xb,Fb).结合性质1,若将![]() 取值遍历GF(23)域,即可唯一确定4×4 S盒.
取值遍历GF(23)域,即可唯一确定4×4 S盒.
基于性质1和性质2,通过变化最后一位f3,S盒的真值表发生变化,可能对Walsh谱有影响.由定义4和定义5知,透明阶与NF存在对立的关系,且都与Walsh谱有关,Walsh谱的变化,导致在满足传统安全性指标的情况下引起透明阶发生改变.
基于上述性质,首先将定义7的CA规则简化为F=(f0,f1,f2,f3);将F3换成CA规则下的前3个局部规则,即F3=(f0,f1,f2),并令最后一个规则f3未知,则变更后的CA规则输入输出坐标对为(X,F′),其中F′=(F3,f3);全遍历第4个局部规则f3,实现S盒的自动搜索.
基于改进CA规则的S盒一种新自动搜索方法具体过程为:
1) 将基于CA规则生成的12类256个4×4最优S盒分别按类排列,每一个S盒![]() 输入变量
输入变量![]() 其中x0为最高位,x3为最低位;
其中x0为最高位,x3为最低位;
2) 对于变量(x0,x1,x2,x3)按照字典的顺序取完所有值,列出该S盒F的真值表(f(0,0,0,0),f(0,0,0,1),…,f(1,1,1,1));
3) 根据F的真值表,确定F3=(f0,f1,f2)的真值表,其中F3为前3个分量函数的集合,即![]()
4) 根据分量函数F3的真值表,确定函数f3的真值.当输入变量为(x0,x1,x2,x3)时,分量函数F3从000到111变化,这时F3会出现2个相同的值,则f3的值分别取0或者1,从而得到28个新的函数F′;
5) 判断新生成的28个S盒是否满足平衡性.若某个S盒不满足平衡性,则剔除,保留所有满足平衡性的S盒;
6) 队列前移,若队列为空则结束,转7);否则,转2);
7) 结束自动搜索,输出所有新生成的S盒.
基于CA规则生成的12类4×4最优S盒有256个,基于本文的S盒新搜索方法,一个S盒就可以生成28个新的S盒,则一共生成256×28=216个不同的新S盒,扩展了生成的S盒数量,在扩展的基础上找寻透明阶较低的最优S盒.
以表2中(1,5,3)类代表元4×4最优S盒为例,说明新的自动搜索过程如下.
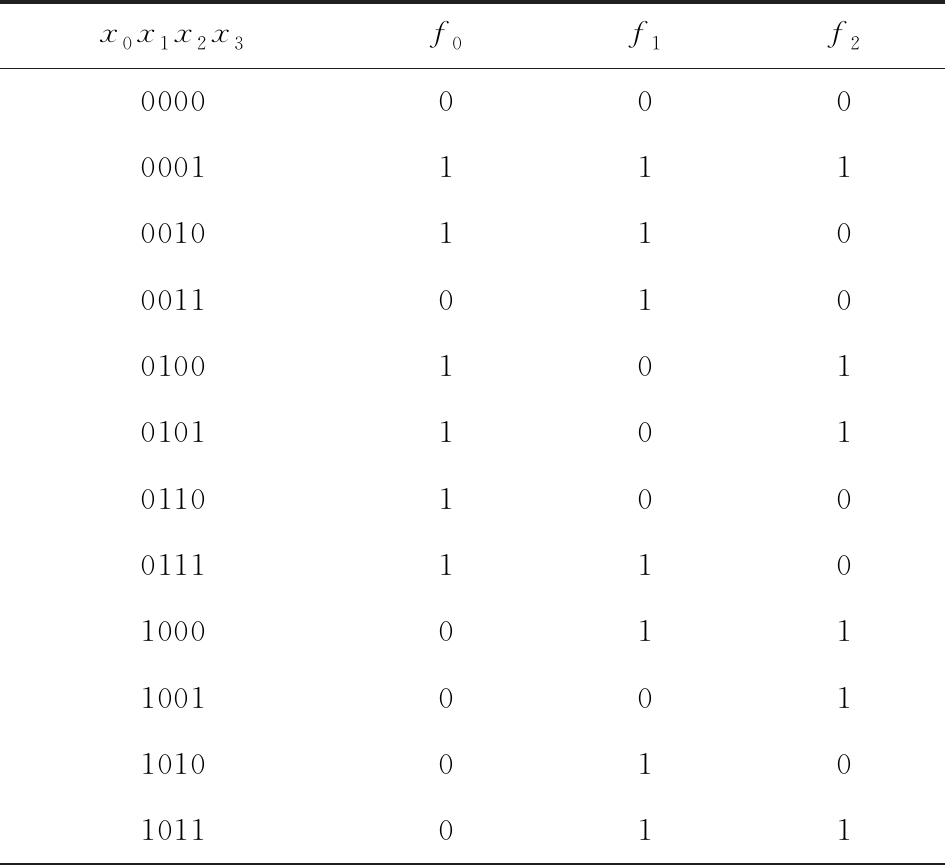
由函数F3=(f0,f1,f2)来进一步的确定分量函数f3.首先,根据(x0,x1,x2,x3)的取值,函数F3=(f0,f1,f2)的真值表如表3所示:
Table 3 Truth Table for Function F3=(f0,f1,f2)
表3 函数F3=(f0,f1,f2)的真值表
x0x1x2x3f0f1f2000000000011110010110001101001001010101101011010001111101000011100100110100101011011
Continued (Table 3)

x0x1x2x3f0f1f21100000110100111101001111111
其次,根据函数F3=(f0,f1,f2)的取值情况,分量函数f3的真值分别变化,如表4所示:
Table 4 Value Form of Component Function f3
表4 分量函数f3取值形式

x0x1x2x3f0f1f2f300101100or100110100or1︙︙︙01111101or0︙︙︙10100101or0
对于2个相同的分量函数F3=110,分量函数f3的值按0或1变化.当输入变量(x0,x1,x2,x3)遍历![]() 时,函数
时,函数![]() 的真值不会重复,并生成28个新的函数F′,即生成新的28个S盒.
的真值不会重复,并生成28个新的函数F′,即生成新的28个S盒.
3.1.2 4×4最优S盒分析与对比
对于新生成的4×4 S盒,考虑其双射性、差分均匀度和非线性度最优,利用密码算法随机测试平台,搜索4×4最优S盒;根据定义4和定义5的透明阶公式编写的程序,测试新生成的每一个最优S盒的透明阶值.
由表1可知,文献[12]生成的12类最优S盒有256个.本文通过改进,对文献[12]中生成的每一个最优S盒,分别生成包含32~72个不同数量的最优S盒.由于采用上述方法生成的S盒数量较多,因篇幅有限,在此主要以表2所列的12类代表元4×4最优S盒为例,统计该代表元下新生成的4×4最优S盒数量及最小的MTO,RTO值,如表5所示:
Table 5 Statistics Table of the Newly Generated 4×4 Optimal S-Boxes Representatives
表5 新生成4×4最优S盒代表元统计表
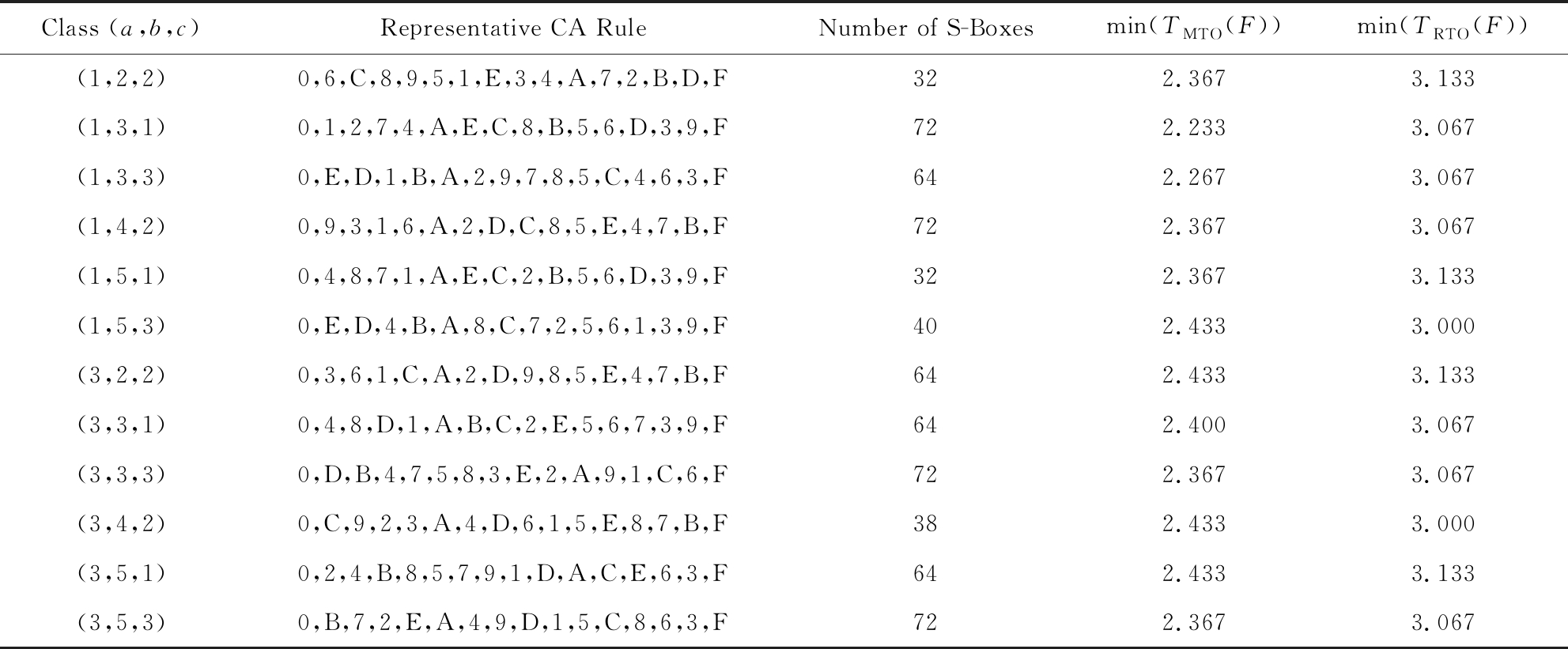
Class (a,b,c)Representative CA RuleNumber of S-Boxesmin(TMTO(F))min(TRTO(F))(1,2,2)0,6,C,8,9,5,1,E,3,4,A,7,2,B,D,F322.3673.133(1,3,1)0,1,2,7,4,A,E,C,8,B,5,6,D,3,9,F722.2333.067(1,3,3)0,E,D,1,B,A,2,9,7,8,5,C,4,6,3,F642.2673.067(1,4,2)0,9,3,1,6,A,2,D,C,8,5,E,4,7,B,F722.3673.067(1,5,1)0,4,8,7,1,A,E,C,2,B,5,6,D,3,9,F322.3673.133(1,5,3)0,E,D,4,B,A,8,C,7,2,5,6,1,3,9,F402.4333.000(3,2,2)0,3,6,1,C,A,2,D,9,8,5,E,4,7,B,F642.4333.133(3,3,1)0,4,8,D,1,A,B,C,2,E,5,6,7,3,9,F642.4003.067(3,3,3)0,D,B,4,7,5,8,3,E,2,A,9,1,C,6,F722.3673.067(3,4,2)0,C,9,2,3,A,4,D,6,1,5,E,8,7,B,F382.4333.000(3,5,1)0,2,4,B,8,5,7,9,1,D,A,C,E,6,3,F642.4333.133(3,5,3)0,B,7,2,E,A,4,9,D,1,5,C,8,6,3,F722.3673.067
Note: a is cubic terms, b is quadratic terms, and c is linear terms.
表5显示,对于12类代表元,本文搜索到的4×4最优S盒数量,多于表1中列出的12类所有4×4最优S盒的数量;同时,新生成的最优S盒的透明阶值也有一定程度的下降,在抵抗差分密码分析、线性密码分析等攻击的同时,可以更好地抵抗DPA攻击.
进一步地,将基于CA规则生成的12类最优S盒与本文改进CA规则提出的S盒新搜索方法所生成的最优S盒进行比较如下.因采用本文方法生成新的密码S盒数量太多,无法一一列出,在此以表2中列出的12类代表元对应的S盒进行对比,结果如表6所示:
Table 6 Results of the Number of 12 Classes of Optimal S-Boxes Representatives and Newly Generated
表6 12类代表元最优S盒与新生成最优S盒数量对比结果

ClassNFδFdegFNumber of S-BoxesSource12 ClassesCA Rules44312Ref[12]443686Our Method
表6显示,本文改进CA规则S盒的自动搜索方法能够通过遍历第4个规则快速地生成更多的最优S盒.
基于上述统计结果,同样以表2中的某2类代表元,采用本文改进CA规则生成新的最优S盒,对比测试文献[12]与本文方法所生成S盒的MTO,RTO值,结果如表7所示.
表7表明,本文方法在满足传统安全指标的同时,能够在新生成的最优S盒中找到具有更低透明阶值的最优S盒.
Table 7 Results of Transparent Order Values of 2 Classes of Optimal S-Boxes and Newly Generated S-Boxes
表7 2类最优S盒与新生成S盒透明阶值对比结果

Class (a,b,c)RepresentativeNFδFTMTO(F)TRTO(F)Source(1,5,3)0,E,D,4,B,A,8,C,7,2,5,6,1,3,9,F442.8003.200Ref[12]1,E,C,5,B,A,8,D,6,2,4,7,0,3,9,F442.4333.000Our Method(3,4,2)0,C,9,2,3,A,4,D,6,1,5,E,8,7,B,F442.8003.200Ref[12]1,D,9,2,3,A,5,C,7,0,4,E,8,6,B,F442.4333.000Our Method
Note: a is cubic terms, b is quadratic terms, and c is linear terms.
3.2 基于改进CA规则4×4次优S盒优化
基于CA规则划分了12类并生成最优S盒,但在这划分的12类之外,同样还存在其他的CA规则.为了能够充分利用每个规则,搜索更多的有价值的S盒,对12类规则外的其他规则进行搜索.
在2.2节的分类分析中表明了基于CA规则划分的12类均为奇数类,因偶数类不满足双射性未被考虑.针对其他奇数类,采用2.2节中设计的自动化搜索方法,搜索到除了12类规则外的3类规则,即(1,1,1)(3,1,1)(3,1,3),搜索出每一类的所有局部规则;进一步地,统计这3类规则下的S盒数量,结果如表8所示:
Table 8 Statistics Table of 3 Classes of 4×4 S-Boxes
表8 3类4×4 S盒数量统计表
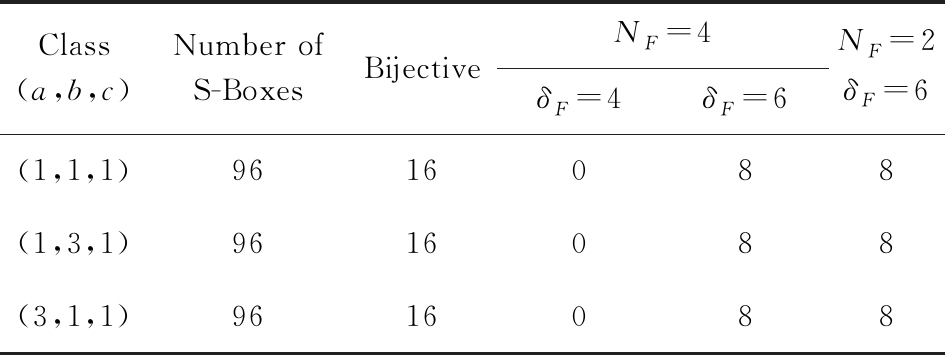
Class(a,b,c)Number ofS-BoxesBijectiveNF=4δF=4δF=6NF=2δF=6(1,1,1)9616088(1,3,1)9616088(3,1,1)9616088
Note: a is cubic terms, b is quadratic terms, and c is linear terms.
表8表明,这3类规则不存在4×4最优S盒,但存在密码性质稍弱的S盒.对表8中的这些S盒,测试其透明阶值,发现最小的MTO值为2.333,RTO值为3.200.
针对表8搜索到的S盒,由于NF=2且δF=6的S盒性质较差,本文没有考虑;但对NF=4且δF=6的S盒,采用本文改进CA规则自动搜索方法,搜索新的S盒.由于每个S盒可生成28新的S盒,一共生成24×28个不同的新S盒.
对于新生成的4×4 S盒,利用密码算法随机测试平台,从中搜索4×4最优S盒,并测试新生成的每一个最优S盒的透明阶值.
采用上述方法生成的S盒数量较多,因篇幅有限,在此主要以表8所列的3类代表元NF=4且δF=6的4×4 S盒为例,统计该代表元下新生成的4×4最优S盒数量及最小的MTO,RTO值,如表9所示.
表9显示,每一类代表元S盒生成了56个新的4×4最优S盒.同时,新生成的最优S盒的透明阶值也有一定程度的下降,具有更好的抵抗DPA攻击的能力.
Table 9 Statistics Table of the Newly Generated 4×4 Optimal S-Boxes
表9 新生成4×4最优S盒统计表

Class (a,b,c)Representative CA RuleNumber of S-Boxesmin(TMTO(F))min(TRTO(F))(1,1,1)0,2,4,E,8,A,D,3,1,7,5,9,B,C,6,F562.4333.000(3,1,1)0,4,8,E,1,5,D,6,2,7,A,3,B,9,C,F562.3333.000(3,1,3)0,E,D,1,B,5,2,3,7,8,A,9,4,C,6,F562.4333.133
Note: a is cubic terms, b is quadratic terms, and c is linear terms.
进一步地,统计基于CA规则生成的(1,1,1)(3,1,1)(3,1,3)类S盒与本文改进CA规则S盒的新搜索方法所生成的最优S盒,经过验证,对12类以外的每一个NF=4且δF=6的次优S盒,都改进搜索到56个新的4×4最优S盒,对比如表10所示.
基于上述统计结果,同样以(3,1,1)类代表元,采用本文改进CA规则生成新的最优S盒,对比测试文献[12]与本文方法所生成S盒的透明阶值,结果如表11所示.
表11表明,本文方法基于CA规则生成的S盒基础上,能够生成新的具有更低透明阶值的最优S盒.
Table 10 Results of the Number of 3 Classes of S-Boxes and Newly Generated Optimal S-Boxes
表10 3类S盒与新生成最优S盒数量对比结果

Class (a,b,c)NFδFdegFNumber of S-BoxesSource(1,1,1)(3,1,1)(3,1,3)46324Ref[12](1,1,1)(3,1,1)(3,1,3)4431344Our Method
Note: a is cubic terms, b is quadratic terms, and c is linear terms.
Table 11 Results of Transparent Order Values of Sub-Optimal S-Boxes and Newly Generated S-boxes
表11 次优S盒与新生成最优S盒透明阶值对比结果

Class (a,b,c)RepresentativeNFδFTMTO(F)TRTO(F)Source(3,1,1)0,4,8,E,1,5,D,6,2,7,A,3,B,9,C,F462.3333.200Ref[12]0,4,9,F,1,5,C,7,3,6,A,2,B,8,D,E442.3333.000Our Method
Note: a is cubic terms, b is quadratic terms, and c is linear terms.
4 结束语
基于CA规则,采用变元分量部分固定和分别搜索的策略,给出了一种设计密码S盒的新自动搜索方法.搜索结果发现:通过改进CA规则自动搜索,不仅能够生成更多的4×4最优S盒,也有效降低了最优S盒的透明阶值;基于CA规则给出的12类之外的3类规则,并对基于这3类规则生成的4×4次优S盒进行搜索,同样获得了较多的具有较低透明阶值的4×4最优S盒.在将来的工作中,将重点研究8×8高强度密码S盒的设计问题.
[1]Prouff E. DPA attacks and S -boxes[C] 
 Proc of Int Workshop on Fast Software Encryption. Berlin: Springer, 2005: 424-441
Proc of Int Workshop on Fast Software Encryption. Berlin: Springer, 2005: 424-441
[2]Chakraborty K, Sarkar S, Maitra S, et al. Redefining the transparency order[J]. Designs, Codes and Cryptography, 2017, 82(1 2): 95-115
2): 95-115
[3]Li Huizhong, Zhou Yongbin, Ming Jingdian, et al. The notion of transparency order, revisited[EB OL]. 2019 [2019-06-08]. https:
OL]. 2019 [2019-06-08]. https:
 eprint.iacr.org
eprint.iacr.org 2019
2019 683
683
[4]Kocher P, Jaffe J, Jun B. Differential power analysis[C] 
 Proc of Annual Int Cryptology Conf. Berlin: Springer, 1999: 388-397
Proc of Annual Int Cryptology Conf. Berlin: Springer, 1999: 388-397
[5]Millan W, Burnett L, Carter G, et al. Evolutionary heuristics for finding cryptographically strong S-boxes[C] 
 Proc of Int Conf on Information and Communications Security. Berlin: Springer, 1999: 263-274
Proc of Int Conf on Information and Communications Security. Berlin: Springer, 1999: 263-274
[6]Chen Hua, Feng Dengguo, Wu Wenling. An effective algorithm for improving cryptographic properties of bijective S-boxes[J]. Journal of Computer Research and Development, 2004, 41(8): 1410-1414 (in Chinese)(陈华, 冯登国, 吴文玲. 一种改善双射S盒密码特性的有效算法[J]. 计算机研究与发展, 2004, 41(8): 1410-1414)
[7]Picek S, Batina L, Jakobovic D. Evolving DPA-resistant boolean functions[C] 
 Proc of Int Conf on Parallel Problem Solving from Nature. Berlin: Springer, 2014: 812-821
Proc of Int Conf on Parallel Problem Solving from Nature. Berlin: Springer, 2014: 812-821
[8]Picek S, Ege B, Papagiannopoulos K, et al. Optimality and beyond: The case of 4× 4 S-boxes[C] 
 Proc of 2014 IEEE Int Symp on Hardware-Oriented Security and Trust (HOST). Piscataway, NJ: IEEE, 2014: 80-83
Proc of 2014 IEEE Int Symp on Hardware-Oriented Security and Trust (HOST). Piscataway, NJ: IEEE, 2014: 80-83
[9]Picek S, Ege B, Batina L, et al. On using genetic algorithms for intrinsic side-channel resistance: The case of AES S-box[C] 
 Proc of the 1st Workshop on Cryptography and Security in Computing Systems. New York: ACM, 2014: 13-18
Proc of the 1st Workshop on Cryptography and Security in Computing Systems. New York: ACM, 2014: 13-18
[10]Kumar K J J, Karthick V. AES S-box construction using one dimensional cellular automata rules[J]. International Journal of Computer Applications, 2015, 110(12): 35-39
[11]Picek S, Mariot L, Yang Bohan, et al. Design of S-boxes defined with cellular automata rules[C] 
 Proc of the Computing Frontiers Conf. New York: ACM, 2017: 409-414
Proc of the Computing Frontiers Conf. New York: ACM, 2017: 409-414
[12]Ghoshal A, Sadhukhan R, Patranabis S, et al. Lightweight and side-channel secure 4×4 S -boxes from cellular automata rules[J]. IACR Transactions on Symmetric Cryptology, 2018, 2018(3): 311-334
[13]Guan Jie, Huang Junjun. Research on cryptographic properties of a new S-box based on cellular automaton[J]. Journal on Communications, 2019, 40(5): 192-200 (in Chinese)(关杰, 黄俊君. 一类新的基于元胞自动机的S盒的密码学性质研究[J]. 通信学报, 2019, 40(5): 192-200)
[14]Leander G, Poschmann A. On the classification of 4 bit S-boxes[C] 
 Proc of Int Workshop on the Arithmetic of Finite Fields. Berlin: Springer, 2007: 159-176
Proc of Int Workshop on the Arithmetic of Finite Fields. Berlin: Springer, 2007: 159-176
[15]Nyberg K. On the construction of highly nonlinear permutations[C] 
 Proc of Workshop on the Theory and Application of of Cryptographic Techniques. Berlin: Springer, 1992: 92-98
Proc of Workshop on the Theory and Application of of Cryptographic Techniques. Berlin: Springer, 1992: 92-98
[16]Nyberg K. S-boxes and round functions with controllable linearity and differential uniformity[C] 
 Proc of Int Workshop on Fast Software Encryption. Berlin: Springer, 1994: 111-130
Proc of Int Workshop on Fast Software Encryption. Berlin: Springer, 1994: 111-130
[17]Mariot L, Picek S, Leporati A, et al. Cellular automata based S-boxes[J]. Cryptography and Communications, 2019, 11(1): 41-62



