近年来,涌现出一大批知识图谱(knowledge graph, KG),诸如YAGO[1],DBpedia[2],Knowledge Vault[3],NELL[4]以及中文的CN-DBpedia[5],Zhishi.me[6]等,这些大规模知识图谱在问答系统、个性化推荐等智能服务中起到重要作用.此外,为满足特定领域相关需求,衍生出越来越多的领域知识图谱,如医疗知识图谱(1)https:
 flowhealth.com
flowhealth.com 和科学知识图谱(2)https:
和科学知识图谱(2)https:
 www.aminer.cn
www.aminer.cn scikg.在知识图谱构建过程中,无法避免地需要在覆盖率和正确率间作权衡.而任何一个知识图谱都无法达到完备或者完全正确.
scikg.在知识图谱构建过程中,无法避免地需要在覆盖率和正确率间作权衡.而任何一个知识图谱都无法达到完备或者完全正确.
为提升知识图谱的覆盖率及正确率,一种可行方法是从其他知识图谱中引入相关知识,因为以不同方式构建得到的知识图谱间存在知识的冗余以及互补.例如从网页上抽取构建的通用知识图谱中可能仅包含药品的名字,而更多的信息可在基于医疗数据构建的医疗知识图谱中找到.为将外部知识图谱中的知识整合到目标知识图谱中,最重要的一步是对齐不同的知识图谱.为此,实体对齐(entity alignment, EA)任务[7]被提出并受到广泛关注.该任务旨在找到不同知识图谱中表达同一含义的实体对.而这些实体对则作为链接不同知识图谱的枢纽,服务于后续任务.
目前,主流实体对齐方法[7-21]主要借助知识图谱结构特征判断2实体是否指向同一事物.这类方法假设不同知识图谱中表达同一含义的实体具有类似的邻接信息.在人工构建的数据集上,这类方法取得了最好的实验结果.但最近一项工作[20]指出,这些人工构建的数据集中的知识图谱比真实世界的知识图谱更加稠密,而基于结构特征的实体对齐方法在具有正常分布的知识图谱上效果大打折扣.
事实上,通过分析真实世界知识图谱中的实体分布可知,超过半数的实体只与一两个其他实体相连.这些实体被称为长尾实体(long-tail entities),占据了知识图谱实体的大部分,使得图谱整体呈现较高的稀疏性.这也符合人们对真实世界知识图谱的认知:只有很少一部分实体被经常使用并具有丰富的邻接信息;绝大部分实体很少被提及,包含微少的结构信息.因此,当前基于结构信息的实体对齐方法在真实世界数据集[20]上的表现不尽人意.
此外,标注数据的缺乏也大大限制了实体对齐的效果.为将不同知识图谱的表示向量映射到同一空间,需要足够的标注数据作为链接.然而,已知的实体对数量是有限的.为解决此问题,部分方法[8,10]提出采用迭代训练(iterative training, IT)从测试集结果中选出高置信度实体对(confident pairs)用作下一轮训练,但存在易引入错误样本[8]以及效率过低[10]等问题.此外,在具有真实世界度数分布的数据集上,这些迭代训练框架只能引入少量高置信度实体对,无法带来明显的效果提升.
鉴于此,为克服当前方法的不足之处,本文提出结合实体结构特征以及实体名特征,实现初步的实体对齐.其中实体结构特征向量由图卷积神经网络(graph convolutional network, GCN)生成,而实体名特征向量则由平均词向量(averaged word embedding)表示.由于实体名与结构信息相互补充,且实体名不受实体节点度数的影响,此基本框架能大幅提升长尾实体的对齐结果,进而优化整体对齐效果.
此外,针对标注数据的缺乏,在本文基本实体对齐框架上,设计了一种基于课程学习(curriculum learning, CL)的迭代训练策略,在保证训练效率的同时,能显著提升实体对齐的效果.该方法受课程学习思想的启发,以实体节点度数为衡量指标,将度数较高的实体视为简单课程,长尾实体视为困难课程,以从简至难的方式将高置信度实体对加入到训练集中,优化迭代训练方式,提升结构特征表示准确性,并使得模型训练更容易达到最优.
最后,不难发现,将实体名用平均词向量表示,虽然提升了其易操作性,但平均化过程难免会造成一定程度上的语义损失,进而无法完全表示实体名的语义信息.为此,提出基于词移距离(word mover’s distance, WMD)的重排序模型,即在前2步生成的实体排序结果上,利用词移距离模型进一步挖掘实体名信息,并与结构信息结合,优化实体对齐效果.
本文的主要贡献有3个方面:
1) 设计了一个融合结构特征和实体名特征的实体对齐基本框架.在此之上,提出基于课程学习的迭代训练策略,通过改变高置信度实体对添加方式,使得训练过程更容易达到最优.
2) 采用词移距离模型将前序对齐结果进行重排序,以充分挖掘实体名信息,提升对齐准确性.
3) 利用跨语言和单语言实体对齐数据集验证本文提出方法的有效性.而实验结果也证实了本文提出的模型取得了比当前最好方法更好的效果.
1 相关工作
由于不同知识图谱间具有知识的互补性,通过引入外部知识图谱中的相关知识,能够大大提升目标知识图谱的覆盖率以及正确率.在此过程中,最重要的1步便是对齐知识图谱.其中,实体对齐任务旨在找到不同知识图谱中表示同一事物的实体,在近年来得到广泛研究.
传统的实体对齐方法[22-23]多依赖本体模式对齐,利用字符串相似度或者规则挖掘等复杂的特征工程方法[24]实现对齐,但在大规模数据下准确率及效率显著下降.而当前实体对齐方法[7,13,25]大多依赖知识图谱向量,因为向量表示具有简洁性、通用性以及处理大规模数据的能力.这些工作具有相似框架:首先利用TransE[7-8,12],GCN[11]等知识图谱表示方法编码知识图谱结构信息,并将不同知识图谱中的元素投射到各自低维向量空间中.接着设计映射函数,利用已知实体对对齐这些向量空间.有些方法[9-10,20]通过在数据准备阶段融合不同知识图谱中的元素,进而直接将不同知识图谱映射到同一向量空间.最后根据向量空间中实体之间的距离或者相似度,生成实体对齐结果.
上述方法仅考虑到实体在全局中的结构表示,为充分利用实体的局部结构信息,文献[15]提出为每一个实体构建1个主题图(topic graph),进而直接将局部结构信息融入实体表示中,并将实体对齐问题转化为主题图之间的图匹配问题;类似地,文献[17]同样也指出之前的方法忽略了邻接子图信息,并称其能为实体对齐提供更多的线索,因此提出基于邻接信息的注意力表示模型,利用注意力机制对实体邻接信息加权求和得到实体的结构表示;此外,文献[14]提出多通道图神经网络,从多个角度生成面向实体对齐的知识图谱嵌入向量.每一个通道能学到不同的加权方法,并从基于自注意力的知识图谱补全和基于跨图谱注意力的互斥实体剪枝这2个角度生成知识图谱表示,最后通过池化操作进行结合.
除了生成并优化结构表示之外,部分方法[9,11,13]提出引入属性信息以补充结构信息.文献[9]提出利用属性类型生成属性向量;而文献[11]则将属性表示成最常见属性名的one-hot向量;最近,文献[13]设计了字符嵌入模型以充分挖掘属性值信息,并借此将不同知识图谱中的实体向量映射到同一空间.这类工作均假设图谱中存在大量属性三元组;但文献[26]指出,在大多数知识图谱中,69%~99%的实体至少缺乏1个同类别实体具有的属性.类似地,虽然实体描述也能提供文本特征[12],但这类信息在大多数知识图谱中也是缺乏的.这也限制了这些方法的通用性以及在处理长尾实体时的有效性.
还有一些工作[8,10]注意到标注数据的不足限制了模型效果,进而提出迭代训练方法,从对齐结果中选出高置信度实体对以扩增训练集.文献[8]根据结构向量空间中实体间距离选择高置信度实体对,并采用直接对齐以及软对齐2种方式将这些实体对加入到训练集中.但直接对齐易引入错误样本,而软对齐则会增加模型训练复杂度;文献[10]提出自举训练(bootstrapping)框架,在选择高置信度实体对时,设计了全局优化目标以提升高置信度实体对的准确率.但全局优化过程过于复杂,大幅降低了实体对齐的效率.而本文设计的基于课程学习的迭代训练策略,以从简至难的方式将高置信度实体对加入到训练集中,优化迭代训练方式,在保证训练效率的同时,显著提升实体对齐的效果.
文献[20]指出当前实体对齐数据集中的知识图谱比真实世界中的知识图谱更加稠密.在具有正常分布的数据集上,存在大量长尾实体,此时结构信息只能发挥有限作用,而外部信息(属性、实体描述等)也往往缺失.因此,需要设计针对长尾实体的对齐方法.目前,暂未发现直接解决此问题的措施.而本文提出的基本实体对齐框架,由于利用了广泛存在但又不受实体节点度数影响的实体名特征,能在一定程度上提升长尾实体对齐效果.此外,基于实体度数的迭代训练框架以及基于词移距离模型的重排序,均能在很大程度上缓解长尾实体问题.
2 问题定义与总框架
本节主要介绍实体对齐任务的定义以及本文所提出的框架.
2.1 基本定义
给定2个知识图谱,G1=(E1,R1,T1)以及G2=(E2,R2,T2),其中E代表实体,R代表关系,T⊆E×R×E代表图谱中的三元组.已知实体对表示为![]() 实体对齐任务旨在利用已知的实体对信息找到新的实体对,并生成最终对齐结果
实体对齐任务旨在利用已知的实体对信息找到新的实体对,并生成最终对齐结果![]() 其中等号代表2实体指向同一真实世界实体.
其中等号代表2实体指向同一真实世界实体.
给定某一实体,寻找其在另一知识图谱中对应实体的过程可视为排序问题.即在某一特征空间下,计算给定实体与另一知识图谱中所有实体的相似程度(距离)并给出排序,而相似程度最高(距离最小)的实体可被视为对齐结果.
当前,实体对齐任务面临2个方面的挑战:
1) 已知实体对能够链接不同知识图谱,在实体对齐过程中起到不可或缺的作用.但其数量往往有限,进而限制了当前实体对齐模型效果;
2) 文献[20]指出,在正常分布的数据集中,长尾实体占据较大比例,使得在之前工作中广泛使用的结构信息无法充分发挥作用.
针对上述缺陷,本文做出3项改进:
1) 提出基于课程学习的迭代训练方法,挑选高置信度实体对用于下一轮训练,解决训练数据过少问题;
2) 充分利用实体度数信息,通过课程学习从简至难展开训练;
3) 采用不受实体度数影响的实体名特征并进行2阶段排序,提升长尾实体对齐效果.具体模型框架图1所示.相关符号表1所示.
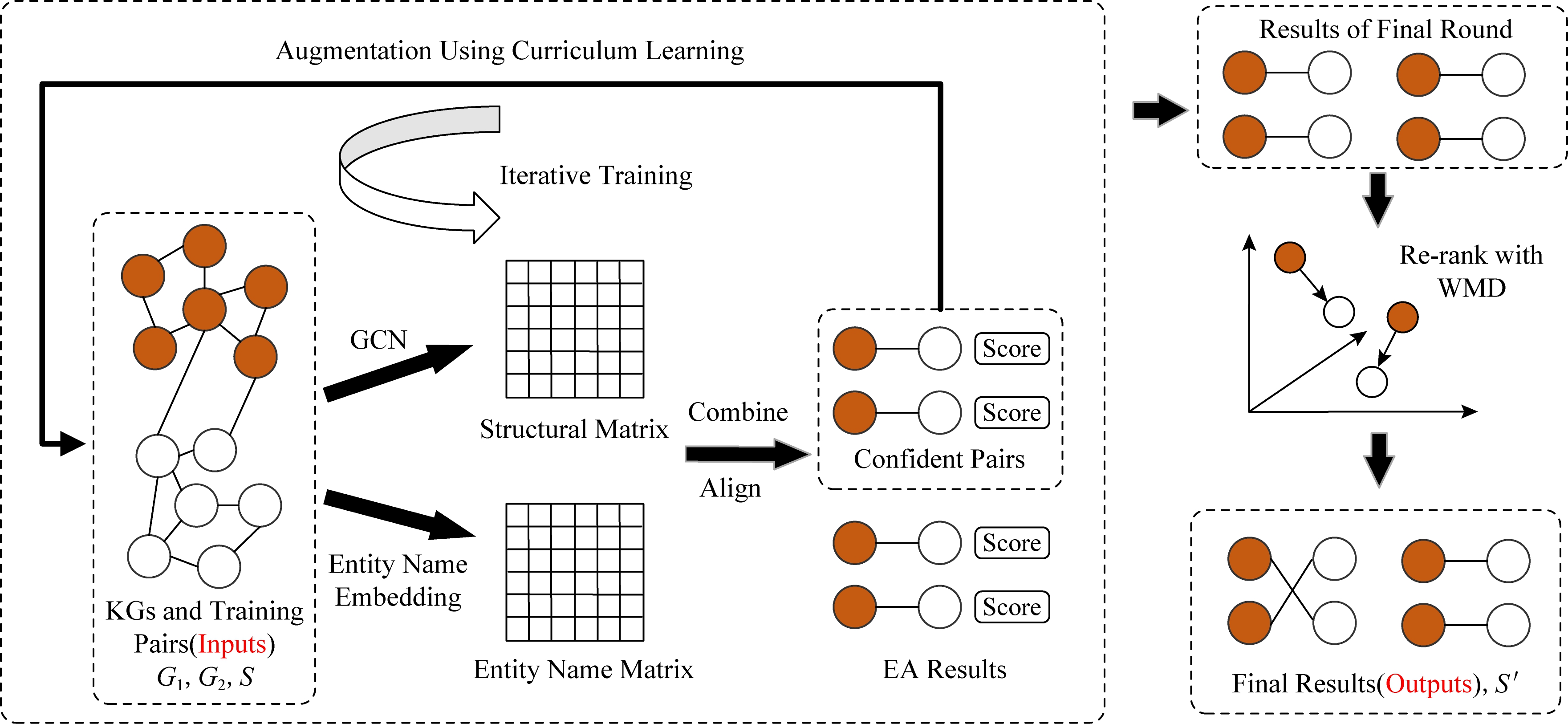
Fig. 1 Our proposed EA framework
图1 本文实体对齐框架
2.2 总框架
如图1所示,本工作首先设计了1个基本的实体对齐框架:利用图卷积网络学习实体结构向量,生成结构特征矩阵(structural matrix),并将实体名字表示为平均词向量,生成实体名特征矩阵(entity name matrix).进一步结合2种向量生成实体表示向量,并根据表示向量的相似程度,实现实体对齐(combine & align);接着提出基于课程学习的迭代训练框架(iterative training),从易至难地选择高置信度实体对加入到训练数据中(augmentation using curriculum learning),优化实体结构表示并不断提升实体对齐效果;最后,利用词移距离模型(re-rank with WMD)对前一步输出结果(results of final round)重排序,融合更精准的实体名信息,进一步提高实体对齐的效果.
Table 1 Notation
表1 符号表

SymbolMeaningHlFeature (Structural) Matrix of the l th LayerXInitial Feature (Structural) MatrixZFinal Feature (Structural) MatrixNEntity Name MatrixAAdjacency MatrixWlParameter Matrix of the l th LayerseStructural Vector of Entity eneEntity Name Vector of Entity eG1KG1G2KG2e1Entity in G1 e2Entity in G2γ1Distance Gap Between the Two Closest Entities to e1γ2Distance Gap Between the Two Closest Entities to e2θ1Threshold of γ1 and γ2θ2Threshold of Number of Newly Added Entity PairsSSeed Entity PairsdsDimension of Structural MatrixDsDistance Between Entities in Structural SpacednDimension of Entity Name MatrixDnDistance Between Entities in Entity Name SpaceDDistance Between EntitiesPDimension of Initial Feature MatrixFDimension of Final Feature MatrixnNumber of Nodes
3 实体对齐基本框架
本节主要介绍实体对齐的基本框架,包括实体结构特征和实体名特征以及如何有效结合不同特征进行实体对齐.
3.1 实体结构特征
本文采用GCN[27]捕捉实体邻接结构信息并生成实体结构表示向量.
GCN基本结构:GCN是一种直接作用在图结构数据上的卷积网络,通过捕捉节点周围的结构信息生成相应的节点结构向量.GCN的输入是实体的特征矩阵X∈Rn×P,以及图的邻接矩阵A.输出是融入了结构信息的特征矩阵Z∈Rn×F.n代表图谱中节点的数目,而P和F分别代表输入和输出矩阵特征的维度.
GCN模型通常包含多个GCN层.特别地,假设第l层的输入为节点的特征矩阵Hl∈Rn×dl,其中dl代表第l层特征矩阵的维度(对于第1层,H1=X,d1=P).第l层输出为![]() 其中
其中![]() 为单位矩阵,
为单位矩阵,![]() 为
为![]() 的对角矩阵.Wl∈Rdl×dl+1为第l层的参数矩阵,dl+1是下一层特征矩阵的维度.激活函数σ常被设为ReLU.对于最后一层,Hl+1=Z,dl+1=F.
的对角矩阵.Wl∈Rdl×dl+1为第l层的参数矩阵,dl+1是下一层特征矩阵的维度.激活函数σ常被设为ReLU.对于最后一层,Hl+1=Z,dl+1=F.
实体对齐中GCN设置:在实体对齐任务中,利用GCN生成实体结构向量.本文构建了2个2层的GCN,各用来处理1个知识图谱并生成相应的实体向量.其中初始特征矩阵X从L2正则化的截尾正态分布中抽样得到,并通过GCN各层训练更新,进而充分捕捉知识图谱中的结构信息并生成输出特征矩阵Z.值得注意的是,特征矩阵的维度一直设置为ds(P=F=dl=ds),而2个GCN在2层中共享特征矩阵W1和W2.关于GCN初始特征阵X的设置,在6.4节中有详细讨论与分析.
此外,构建矩阵A:首先考虑到知识图谱中存在多种关系,为每一个关系r定义正向重要度和反向重要度.其中正向重要度fun(r)是包含关系r的所有三元组中不重复头实体的数目与包含关系r的所有三元组的数目的比值;反向重要度ifun(r)则是包含关系r的所有三元组中不重复尾实体的数目与包含关系r的所有三元组的数目的比值.接着定义矩阵A中元素
其中,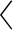 ei,r,ej
ei,r,ej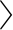 ,
,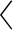 ej,r,ei
ej,r,ei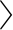 为包含实体ei,ej的三元组.
为包含实体ei,ej的三元组.
不同知识图谱的实体结构向量并不在同一空间中,因此需要利用已知实体对S将它们对齐到同一空间中.具体的训练目标为最小化下述损失值
![]()
![]()
(1)
其中,![]() 代表基于已知实体对(e1,e2),将e1或者e2替换成随机实体生成的负样本集合.se代表实体e的结构向量.τ代表将正负样本分隔的端距.采用随机梯度下降进行模型优化.
代表基于已知实体对(e1,e2),将e1或者e2替换成随机实体生成的负样本集合.se代表实体e的结构向量.τ代表将正负样本分隔的端距.采用随机梯度下降进行模型优化.
给定最终结构特征矩阵Z,e1∈G1和e2∈G2在结构空间下的距离为![]() 若只考虑结构特征,和目标实体e距离Ds最近的实体将被视为e的对应实体.
若只考虑结构特征,和目标实体e距离Ds最近的实体将被视为e的对应实体.
3.2 实体名特征
区别于当前主流的仅基于结构特征的方法,本文提出同时利用文本特征进行对齐.具体地,采用实体名这一文本形式,考虑到:1)实体名常被用来标识实体并广泛存在;2)通过比较实体名,能直观的判断2实体是否相同;3)其不受训练集规模的影响,具有较强的稳定性.
虽然传统的字符串比较方法能用来衡量2实体名相似度,本文选用实体名的语义相似度,因为其在知识图谱差异很大时亦能适用,如多语言知识图谱对齐.具体地,考虑到平均词向量表示具有简洁性和通用性,不需要特别的训练语料便能表达语义信息,所以将其用作实体名向量.假设实体e名字中包含词语w1,w2,…,wp,那么实体名向量可表示为这些词向量的平均,即![]() 其中ωi是wi的词向量.所有实体的名字向量可表示为N.
其中ωi是wi的词向量.所有实体的名字向量可表示为N.
和词向量类似,相似的实体名将在向量空间里十分接近.e1∈G1和e2∈G2在文本特征空间下的距离为![]() 若只考虑实体名特征,和目标实体e距离Dn最近的实体将被视为e的对应实体.对于跨语言实体对齐,可利用预训练跨语言词向量(3)https:
若只考虑实体名特征,和目标实体e距离Dn最近的实体将被视为e的对应实体.对于跨语言实体对齐,可利用预训练跨语言词向量(3)https: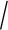
 github.com
github.com facebookresearch
facebookresearch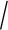 MUSE,进而确保跨语言实体名向量在同一空间中.
MUSE,进而确保跨语言实体名向量在同一空间中.
3.3 特征融合
考虑到结构特征和名字特征分别从结构和语义2个不同的方面对实体进行刻画,可进一步结合以提供更全面的对齐线索.具体地,2实体e1∈G1和e2∈G2之间的距离为
D(e1,e2)=αDs(e1,e2)+(1-α)Dn(e1,e2),
(2)
其中,α是用来调整2种特征权重的超参数.在特征融合后的空间下,和目标实体e距离D最近的实体将被视为e的对应实体.对超参数α的讨论详见6.4节.
4 基于课程学习的迭代训练框架
已标注数据的数量是有限的,无法有效地将不同知识图谱的向量映射到同一空间中,进而限制了实体对齐的效果.因此,本文提出将具有高置信度的实体对齐结果从简至难地添加到下一轮训练数据中,迭代式地扩增训练集规模并提升实体对齐结果.本节首先介绍基本迭代训练框架,接着阐述如何将课程学习的思想运用到迭代框架中以优化训练效果.
4.1 迭代训练框架
每一轮迭代训练的输入为待对齐知识图谱和已对齐实体对(训练集),输出为对齐结果和扩增后训练集.一种最简单的扩增方式是,对于G1中的每一个待对齐实体e1,假设G2中距离其最近的实体为e2;而对于e2来说,G1中距离其最近的实体正好也为e1,那么可认为(e1,e2)为高置信度实体对,并将其添至训练数据中.但在此过程中,无法避免地会引入一部分错误的实体对,进而对后续训练造成负面的影响.而一旦加入了错误实体对,很难再次评估这些实体对的正确性或是将其从训练数据中移除[28].
为此,本文设计了一种简单但能大大减少引入错误实体对概率的方法.对于G1中的每一个待对齐实体e1,假设G2中距离其最近的实体为e2,第2近实体为![]() 距离差值为
距离差值为![]() 而对于e2来说,若G1中距离其最近的实体恰好为e1,第2近实体为
而对于e2来说,若G1中距离其最近的实体恰好为e1,第2近实体为![]() 距离差值为
距离差值为![]() 并且γ1≥θ1,γ2≥θ1,那么可认为(e1,e2)为高置信度实体对,并将其添至训练数据中用于下一轮训练.上述方法对高置信度实体对有较高选择标准:2实体的距离从2侧来说均为最近,并且最相近实体和第2相近实体间存在一定距离差.这在一定程度上确保了新加入实体对的正确率.上述迭代训练将会一直持续,直到新加入的实体对数目低于给定阈值θ2.
并且γ1≥θ1,γ2≥θ1,那么可认为(e1,e2)为高置信度实体对,并将其添至训练数据中用于下一轮训练.上述方法对高置信度实体对有较高选择标准:2实体的距离从2侧来说均为最近,并且最相近实体和第2相近实体间存在一定距离差.这在一定程度上确保了新加入实体对的正确率.上述迭代训练将会一直持续,直到新加入的实体对数目低于给定阈值θ2.
值得注意的是,在本文设计的迭代训练框架中,当测试集中高置信度实体对加入到训练集后,将不会出现在下一轮的测试集中,即测试集中实体数量是不断减少的.这在一定程度上能够提升测试集中剩余实体的对齐效果,因为其候选实体数目与原始相比大幅减少.而在文献[8,10]中,高置信度实体对加入到训练集后,仍会出现在下一轮的测试集中.实验结果表明,本文提出的迭代训练框架能带来更好的效果.
4.2 基于课程学习的迭代策略
课程学习主要思想是模仿人类学习的特点,由简单到困难学习,这样能使得模型更容易找到局部最优,同时加快训练速度[29].在实体对齐任务中,课程的难易程度可由实体节点度数高低来刻画:度数较高的实体具有更为丰富的结构信息,更容易对齐;而对齐度数低的长尾实体则相对而言颇具难度.为此,在迭代训练过程中,首先添加容易的实体对,再加入较难的实体对,从而实现由易至难地对模型进行训练,使得训练更容易达到最优.
具体地,假设有从简至难的δ个课程,c1,c2,…,cδ,分别代表从大到小的一系列实体节点度数值,那么在每一次迭代训练得到的高置信度实体对中,只选择节点度数大于c1的加入到训练集中,并保持该条件一直循环迭代训练,直到符合要求的实体对数目低于给定阈值θ2时,停止该课程难度的训练.
在接下来的训练中,调整课程难度,将条件改为从高置信度实体对中选择度数大于c2的加入到训练集中,并保持该课程难度一直循环迭代训练,直到符合要求的新增实体对数目低于给定值θ2时,停止该课程难度的训练.最后重复上述步骤,遍历剩下的课程难度c3,c4,…,cδ.需要注意的是,对于不同课程难度下的迭代训练,均采用4.1节中介绍的方法.
基于课程学习的迭代训练通过优化高置信度实体对的添加方式,生成更准确的实体表示向量,进而提升对齐效果.这也通过第6节的实验结果得到验证.
5 基于词移距离模型的重排序
基于课程学习的迭代训练框架已大幅提升实体对齐的准确率,在此基础上,提出进一步挖掘实体名信息,采用词移距离模型对前序结果进行重排序,优化实体对齐效果.
如图2所示,词移距离模型旨在衡量不同句子间的差异性,其表示为1个句子中所有词的嵌入向量需要移动到达另一个句子中所有词的嵌入向量的最小距离值[30].与平均词向量间的距离相比,词移距离能更好地刻画句中每个词对整个句子的影响,避免了平均操作造成的语义损失.然而,由于需要计算词级别的距离,该模型耗时较长,不适用于大规模数据.为此,并未在一开始就使用该方法计算实体名之间的距离,而是利用其对前序结果进行重排序.具体算法细节可参见文献[30].
具体地,在基于课程学习的迭代训练结束后,对于测试集中的每一个待对齐实体,保留另一个知识图谱中距离其最近的h个实体,并将其作为输入送入到词移距离模型中,重新计算实体名空间下实体间的距离.最后利用更新后的实体名距离,结合式(2),计算得到新的实体间距离以及重排序后的对齐结果.
Fig. 2 Word mover’s distance model
图2 词移距离模型
6 实验与结果
本节首先介绍实验的基本设置,包括参数设置,数据集、对比方法以及度量指标.接着展示在跨语言实体对齐以及单语言实体对齐2个任务上的实验结果.随后进行特征分析以验证各个模块的有效性.最后通过案例分析,对本文框架有更清晰的认识.
6.1 参数设置及度量指标
对于实体结构特征,ds=300,τ=3,训练300轮,为每个正例生成5个负例.对于实体名特征,利用fastText[31]预训练词向量生成实体名向量,而跨语言词向量则通过MUSE获得.其中fastText向量采用CBOW模型训练得到,维度为300(即dn=300),字符长度为5,窗口大小为5,负正例比为10.通过验证集上实验,将设置超参数α=0.3.对于基于课程学习的迭代训练框架,θ1=0.03,θ2=20.c1,c2,…,cδ={10,6,4,2,0}且δ=5.词移距离模型中,h=100.
采用Hits@k(k=1,10),以及平均排序倒数(mean reciprocal rank, MRR)作为衡量指标.对于测试集中的每一个实体,根据与该实体之间的距离D,从低至高地将另一个知识图谱中的实体进行排序.Hits@k反映了前k个实体中包含正确实体的比例.特别地,Hits@1代表对齐的准确率.MRR表示正确实体平均排名的倒数.虽然Hits@1是最重要的衡量指标,Hits@10可被视为对Hits@1的补充.假设某种方法未能成功将正确实体排为距离最近实体,但若其将正确实体排为距离前10近实体,那么这种方法至少好于未将正确实体排为距离前10近实体的方法.MRR亦能提供类似的信息补充.注意到,高的Hits@k和MRR值代表更好的实验结果,实验中的Hits@k由百分数表示.
6.2 数据集及对比方法
本文将在EN-FR,EN-DE2个跨语言实体对齐数据集以及DBP-WD,DBP-YG2个单语言实体对齐数据集上测试提出的方法[20].详细数据集信息如表2所示.值得注意的是,文献[20]指出,之前构建的实体对齐数据集中的实体节点度数分布整体偏高,并不符合真实世界知识图谱情况,而其构建的数据集则具有正常分布以及更高的对齐难度.
Table 2 Statistics of Triples and Entities
表2 三元组及实体统计信息
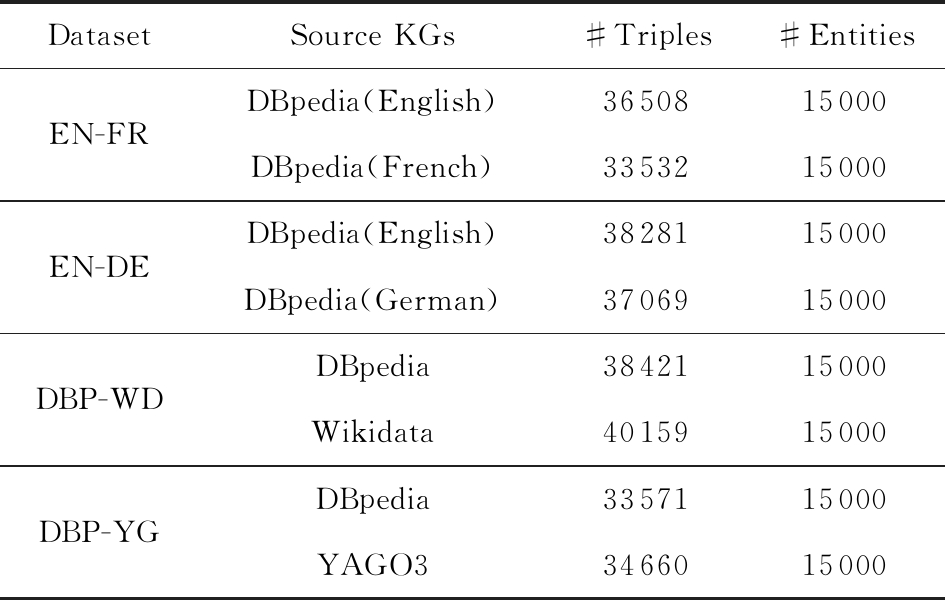
DatasetSource KGs#Triples#EntitiesEN-FREN-DEDBP-WDDBP-YGDBpedia(English)3650815000DBpedia(French)3353215000DBpedia(English)3828115000DBpedia(German)3706915000DBpedia3842115000Wikidata4015915000DBpedia3357115000YAGO33466015000
此外,与7种方法进行对比:
1) MTransE[7].最先提出采用知识图谱嵌入(TransE)进行实体对齐的方法.
2) IPTransE[8].采用迭代训练框架提升对齐效果.
3) BootEA[10].设计了一种基于对齐的知识图谱嵌入方法以及自举策略.
4) JAPE[9].利用属性信息对结构信息进行优化.
5) GCN-Align[11].利用GCN生成实体向量,并与属性向量相结合以对齐实体.
6) RSNs[20].采用基于残差学习的循环神经网络来有效捕捉知识图谱内部以及知识图谱间的长距离关系依赖.
7) GM-Align[15].为每个实体构建1个局部的实体图以捕捉更多的局部信息.实体名信息用来初始化整个框架.
6.3 实验结果
表3展示了实验结果.在第1组只采用结构信息的方法中(MTransE,IPTransE,BootEA,RSNs),BootEA及RSNs取得了更好的实验结果.这是因为BootEA利用了针对实体对齐任务设计的知识图谱表示向量,并且其提出的自举策略也能提升对齐结果.而RSNs通过挖掘长距离依赖关系以解决邻接结构信息的局限性,进而提升整体对齐效果.然而在所有数据集上,这些方法的Hits@1值均未超过50%,揭示了只利用结构特征的不足之处.
第2组方法采用了实体属性特征来补充结构特征,但JAPE 与GCN-Align均未取得比第1组更好的效果,这可归因于属性信息效果的局限性.此外,这2种方法中使用的结构特征模型均不如BootEA以及RSNs.
Table 3 Entity Alignment Results
表3 实体对齐结果
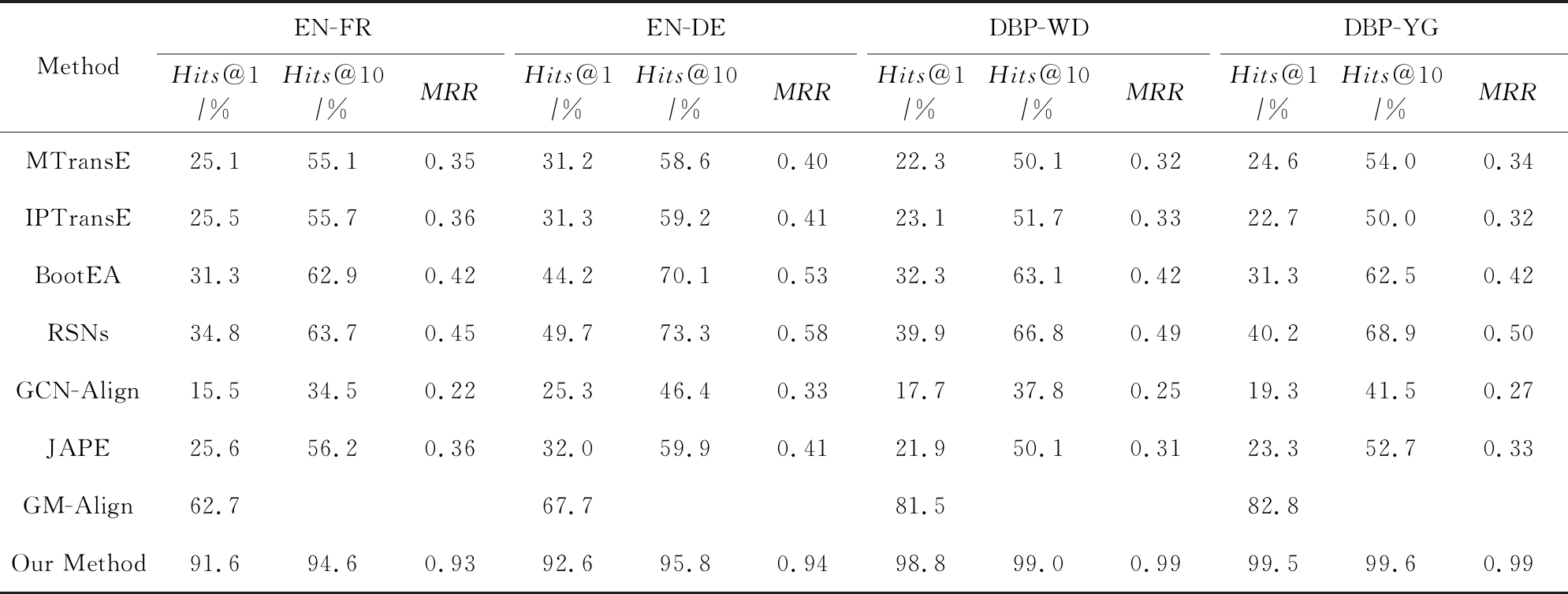
MethodEN-FREN-DEDBP-WDDBP-YGHits@1∕%Hits@10∕%MRRHits@1∕%Hits@10∕%MRRHits@1∕%Hits@10∕%MRRHits@1∕%Hits@10∕%MRRMTransE25.155.10.3531.258.60.4022.350.10.3224.654.00.34IPTransE25.555.70.3631.359.20.4123.151.70.3322.750.00.32BootEA31.362.90.4244.270.10.5332.363.10.4231.362.50.42RSNs34.863.70.4549.773.30.5839.966.80.4940.268.90.50GCN-Align15.534.50.2225.346.40.3317.737.80.2519.341.50.27JAPE25.656.20.3632.059.90.4121.950.10.3123.352.70.33GM-Align62.767.781.582.8Our Method91.694.60.9392.695.80.9498.899.00.9999.599.60.99
第3组方法利用了实体名信息,与第1组相比,大大提升了对齐效果,证明了实体名信息的重要性,特别是对于长尾实体.此外,本文提出的方法与GM-Align相比,在Hits@1指标上取得了近20%的提升,并且所有指标均逾九成,展示了整体框架的有效性(对实验结果大幅提升的原因分析可参见6.5节).其中单语言数据集上的结果要优于跨语言对齐结果,因为单语言下的实体名信息更有助于判断实体的等价性.
需要注意的是:GM-Align无法给出没有有效实体名字向量的实体的对齐结果,因此认为GM-Align不能对齐这些实体.由于无法知晓这些实体的具体排序结果,因而表3中未提供其Hits@10和MRR值.
6.4 参数分析
此节对超参数α以及GCN初始特征矩阵X进行实验分析.
如3.3节指出,超参数α旨在调整结构和文本特征权重.为分析其对实验效果的影响,在验证集上进行了相关实验.如图3所示,只使用文本特征(α=0)已取得较高实验结果(在所有数据集上均超过60%).当α增加时,Hits@1结果有一定幅度的提升,并在α≈0.3时达到最优效果.当结构特征占据更大比重时(α>0.3),整体对齐结果开始逐步下降,并在α=1时达到最低值.
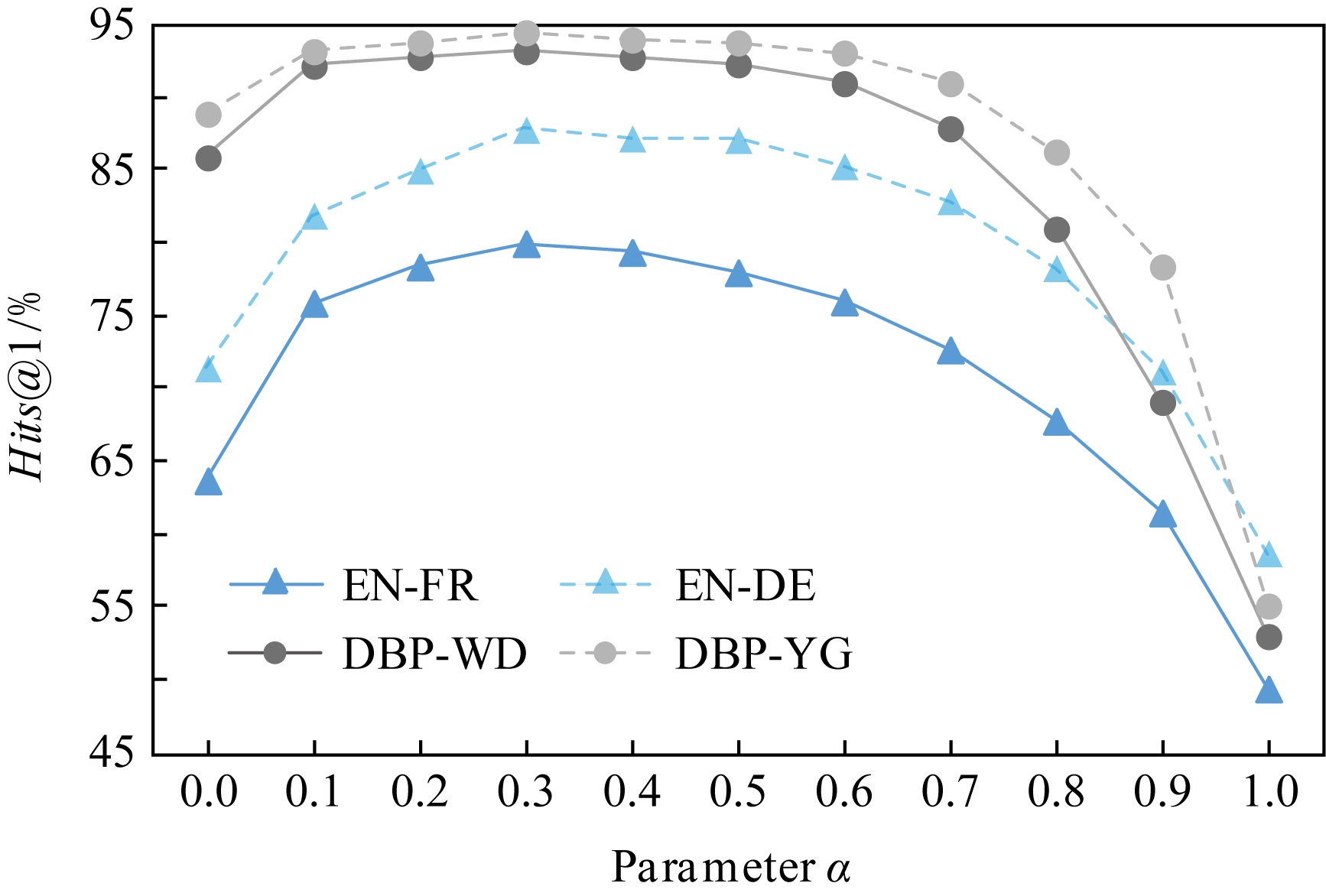
Fig. 3 Analysis of parameter α
图3 超参数α分析
由此可知,结合结构和文本特征确实能提升整体对齐结果.相对于结构特征,文本特征能提供更多的对齐线索.此外,对GCN训练过程中初始特征矩阵X进行分析,具体结果如表4所示:
Table 4 Analysis of GCN Initialization Matrix
表4 GCN 初始化特征矩阵分析
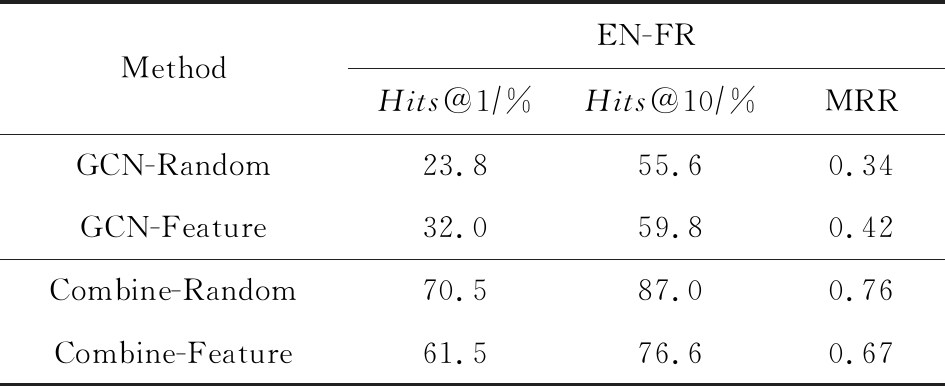
MethodEN-FRHits@1∕%Hits@10∕%MRRGCN-Random23.855.60.34GCN-Feature32.059.80.42Combine-Random70.587.00.76Combine-Feature61.576.60.67
在本文设置中,X通过随机初始化得到,具体从L2正则化的截尾正态分布中抽样生成,并通过GCN各层训练更新,进而使得输出矩阵能充分体征结构信息.另一种思路是将初始特征矩阵X设置为有意义的特征信息,并通过GCN各层训练更新,根据结构信息在各个节点之间交换特征,进而学到更有用的表示.为验证这2种不同思路的有效性进行对比实验,具体结果如表4所示.
考虑到实体对齐任务中特征的局限性(绝大多数情况下仅存在结构和文本特征),将初始特征矩阵X设置为实体名向量矩阵(有意义的特征信息),并送入GCN中进行更新.而利用最终输出矩阵生成的对齐结果(GCN-Feature)的确好于随机初始化特征矩阵X后的对齐结果(GCN-Random).
然而,融合GCN生成的结构特征矩阵与实体名特征矩阵后的实验结果表明,将初始特征矩阵X设置为实体名向量矩阵(有意义的特征信息)的对齐结果(Combine-Feature)并不如随机初始化的结果(Combine-Random),即便相关参数已在验证集上调到最优.这表明通过随机初始化特征矩阵X,能够使得GCN学到更“纯粹”的结构信息,这也在文献[27]中得到印证.在实体对齐任务上,将这样学到的结构信息与其他特征信息融合,比将其他特征信息作为GCN的初始特征进行学习训练以及融合更加有效.
当然,可以认为将X设置为实体名向量矩阵学习得到的结构特征矩阵,在后续与实体名向量矩阵结合过程中存在信息冗余,进而导致Combine-Feature结果较差.但在整个对齐过程中用到的特征只有结构特征与实体名特征,因而在此条件下,Combine-Random是比Combine-Feature更好的一种解决方案.
6.5 结果讨论与特征分析
通过表3可以明显看出,本文提出的方法要远好于现有方法.为对实验结果进行深入分析,首先验证各个特征的有效性以及其对实验结果带来的提升.
具体地,表5中给出了结合了结构信息和实体名信息的基本实体对齐模型(Basic)、基本迭代训练框架(Basic+IT)、基于课程学习的迭代训练框架(Basic+IT-CL)以及基于词移距离的重排序模型(Basic+IT-CL+WMD)的相关实验结果.
1) 基本实体对齐模型(Basic).不难看出,结合了结构和实体名信息的基本实体对齐模型已取得了比RSNs, GM-Align等方法更好的效果,如Basic在EN-FR上取得了70.5%的Hits@1值(如表5所示),而GM-Align仅取得62.7%(如表3所示).这不仅体现了实体名这一特征的重要性,也揭示了本文提出的特征融合方法要优于之前的模型.具体案例如表6所示.
Table 5 Feature Analysis of Our Method
表5 本文模型的特征分析
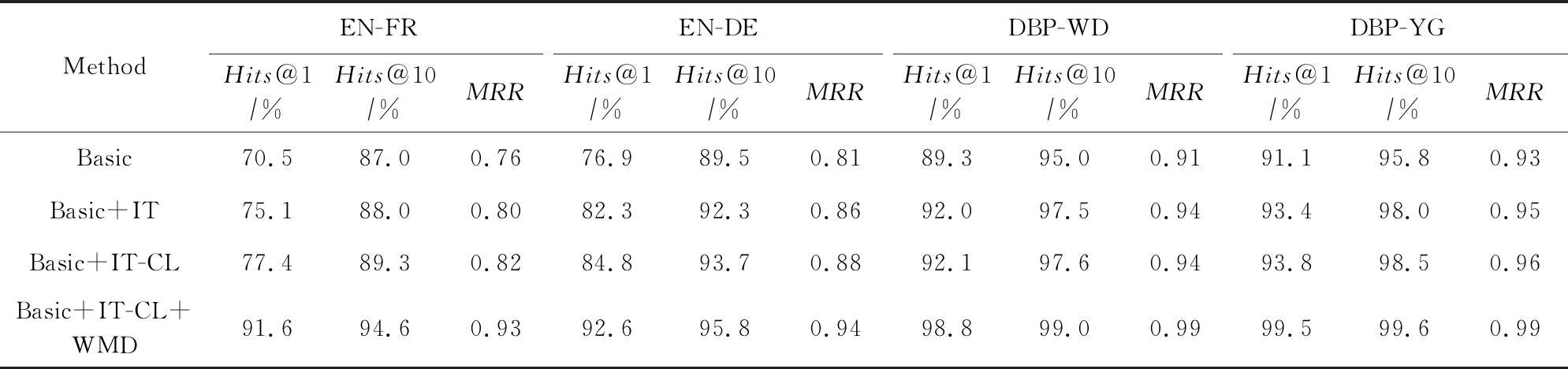
MethodEN-FREN-DEDBP-WDDBP-YGHits@1∕%Hits@10∕%MRRHits@1∕%Hits@10∕%MRRHits@1∕%Hits@10∕%MRRHits@1∕%Hits@10∕%MRRBasic70.587.00.7676.989.50.8189.395.00.9191.195.80.93Basic+IT75.188.00.8082.392.30.8692.097.50.9493.498.00.95Basic+IT-CL77.489.30.8284.893.70.8892.197.60.9493.898.50.96Basic+IT-CL+WMD91.694.60.9392.695.80.9498.899.00.9999.599.60.99
Table 6 Case Study of Entity Pair (Guerre De Laponie,Lapland War)
表6 关于实体对(Guerre De Laponie,Lapland War)的案例分析
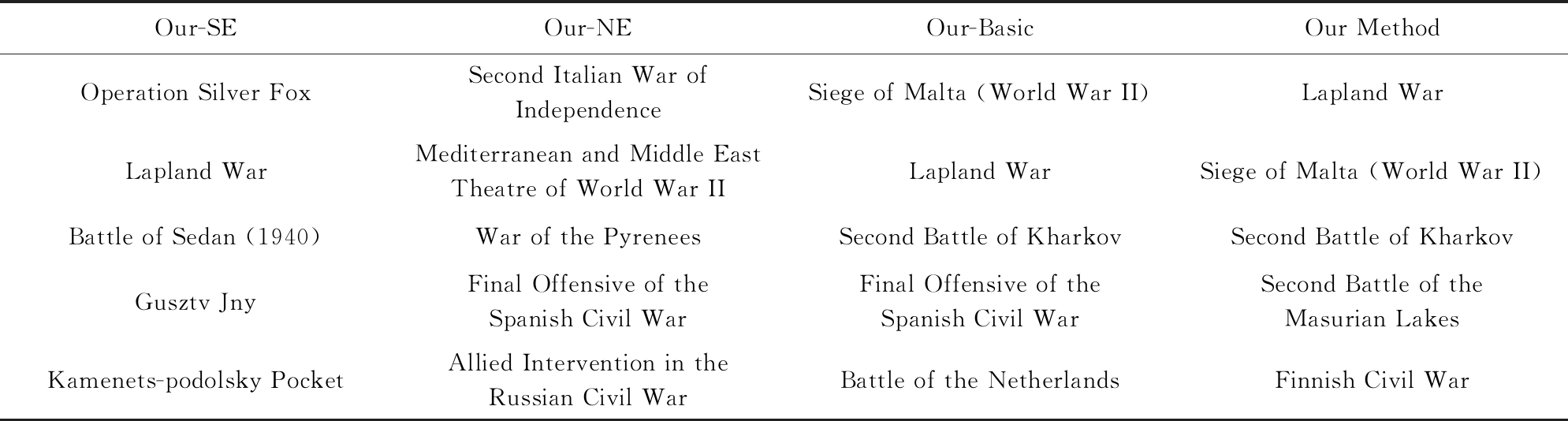
Our-SEOur-NEOur-BasicOur MethodOperation Silver FoxSecond Italian War of IndependenceSiege of Malta (World War II)Lapland WarLapland WarMediterranean and Middle EastTheatre of World War IILapland WarSiege of Malta (World War II)Battle of Sedan (1940)War of the PyreneesSecond Battle of KharkovSecond Battle of KharkovGusztv JnyFinal Offensive of the Spanish Civil WarFinal Offensive of the Spanish Civil WarSecond Battle of the Masurian LakesKamenets-podolsky PocketAllied Intervention in the Russian Civil WarBattle of the NetherlandsFinnish Civil War
2) 基本迭代训练框架(Basic+IT).与基本实体对齐模型(Basic)相比,本文提出的迭代训练框架进一步提升了各项指标,证实了扩增训练数据对整体对齐效果产生的正面影响,以及高置信度实体对选择方法的有效性.
3) 基于课程学习的迭代训练框架(Basic+IT-CL).与基本迭代框架(Basic+IT)相比,课程学习策略在EN-FR和EN-DE数据集上带来了超过2%的Hits@1值提升,证明其能使得迭代训练模型达到更优的效果.而其在单语言实体对齐数据集上的效果则不太明显,因为单语言数据集中绝大部分实体在前几轮便被添至训练数据中,而改变加入顺序对整体结果影响不大.
4) 基于词移距离的重排序模型(Basic+IT-CL+WMD).最后,与基于课程学习的迭代训练框架(Basic+IT-CL)相比,基于词移距离的重排序模型使得Hits@1指标有了显著提升,特别是在跨语言实体对齐数据集上.这验证了进一步挖掘实体名信息确实能带来对齐准确率的提升.至此,所有数据集上的各项指标均达到了90%以上,展现了本文提出方法性能的优越性.
由上述分析可见,与当前其他方法相比,本文提出的基本实体对齐模型、基于课程学习的迭代训练框架以及基于词移距离的重排序模型均能带来实验结果的提升.其中结合了实体名信息的基本实体对齐模型带来的效果提升最为明显(奠定了基础),而其他几个模块(特别是基于词移模型的重排序)则进一步大幅优化对齐结果.此外,使用词移距离模型,迭代训练策略等算法带来效果提升的具体量化分析可参见表5的实验结果.而本文代码(4)https:
 github.com
github.com DexterZeng
DexterZeng CL也已公开供读者复现与验证.
CL也已公开供读者复现与验证.
6.6 案例分析
通过案例分析进一步揭示各个模块对最终结果的影响.如表6所示,以En-Fr数据集中的(Guerre De Laponie, Lapland War)实体对为例,分别给出只使用结构特征(Our-SE)、只使用实体名特征(Our-NE)、基本对齐框架(Our-Basic)以及整体框架(Our Method)生成的与Guerre De Laponie最接近实体.通过结果分析可知,Our-SE旨在找到与Guerre De Laponie(Lapland War)相关的实体,但并不知道寻找方向,因此返回的最相关结果中既包含战役,也包含军事行动以及有名军官.Our-NE则抓住了关键词Guerre(War),因此其生成的最相关实体的名字中均包含War,但这些战役大部分甚至不是在第二次世界大战发生.
充分结合结构特征与实体名特征,Our-Basic将Lapland War排到了第2,因为其既与第二次世界大战相关,本身也是1次战役.但Our-Basic仍将错误实体Siege of Malta(World War II)排到第1.这个错误进一步被后续基于课程学习的迭代训练以及词移距离模型消除,而本文提出的方法最终为Guerre De Laponie找到正确的对应实体Lapland War.
此例充分展现了本文提出的实体对齐框架能够有效结合不同特征及策略,以提升实体对齐的准确率.
7 总 结
针对知识图谱结构信息在真实世界数据集上匮乏的问题,本文将不受实体节点度数影响的实体名信息与结构信息结合,构建实体对齐基本框架.此外,注意到标注数据的不足限制了模型效果,设计基于课程学习的迭代训练方法,由易至难地扩增训练数据,提升对齐准确度.最后,在前2步基础上,利用词移距离模型进一步挖掘实体名信息,对前序结果重排序,进而生成最终的对齐结果.该模型在广泛使用的实体对齐数据集上取得了最好的效果.
后续工作将主要研究关系对齐、融合降噪等知识图谱对齐的余留问题,并构建高效可行的知识图谱融合系统.
[1]Suchanek F M, Kasneci G, Weikum G. YAGO: A core of semantic knowledge[C] 
 Proc of the 16th Int Conf on World Wide Web. New York: ACM, 2007: 697-706
Proc of the 16th Int Conf on World Wide Web. New York: ACM, 2007: 697-706
[2]Auer S, Bizer C, Kobilarov G, et al. DBpedia: A nucleus for a Web of open data[C] 
 Proc of Int Semantic Web Conf (ISWC). Berlin: Springer, 2007: 722-735
Proc of Int Semantic Web Conf (ISWC). Berlin: Springer, 2007: 722-735
[3]Dong Xin, Gabrilovich E, Heitz G, et al. Knowledge vault: A web-scale approach to probabilistic knowledge fusion[C] 
 Proc of the 20th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2014: 601-610
Proc of the 20th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2014: 601-610
[4]Carlson A, Betteridge J, Kisiel B, et al. Toward an architecture for never-ending language learning[C] 
 Proc of the 24th AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2010: 1306-1313
Proc of the 24th AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2010: 1306-1313
[5]Xu Bo, Xu Yong, Liang Jiaqing, et al. CN-DBpedia: A never-ending Chinese knowledge extraction system[C] 
 Proc of Int Conf on Industrial, Engineering and Other Applications of Applied Intelligent Systems. Berlin: Springer, 2017: 428-438
Proc of Int Conf on Industrial, Engineering and Other Applications of Applied Intelligent Systems. Berlin: Springer, 2017: 428-438
[6]Niu Xing, Sun Xinruo, Wang Haofeng, et al. Zhishi.me—weaving Chinese linking open data[C] 
 Proc of Int Semantic Web Conf (ISWC). Berlin: Springer, 2011: 205-220
Proc of Int Semantic Web Conf (ISWC). Berlin: Springer, 2011: 205-220
[7]Chen Muhao, Tian Yingtao, Yang Mohan, et al. Multilingual knowledge graph embeddings for cross-lingual knowledge alignment[C] 
 Proc of the 26th Int Joint Conf on Artificial Intelligence (IJCAI). Menlo Park, CA: AAAI, 2017: 1511-1517
Proc of the 26th Int Joint Conf on Artificial Intelligence (IJCAI). Menlo Park, CA: AAAI, 2017: 1511-1517
[8]Zhu Hao, Xie Ruobing, Liu Zhiyuan, et al. Iterative entity alignment via joint knowledge embeddings[C] 
 Proc of the 26th Int Joint Conf on Artificial Intelligence (IJCAI). Menlo Park, CA: AAAI, 2017: 4258-4264
Proc of the 26th Int Joint Conf on Artificial Intelligence (IJCAI). Menlo Park, CA: AAAI, 2017: 4258-4264
[9]Sun Zequn, Hu Wei, Li Chengkai. Cross-lingual entity alignment via joint attribute-preserving embedding[C] 
 Proc of Int Semantic Web Conf (ISWC). Berlin: Springer, 2017: 628-644
Proc of Int Semantic Web Conf (ISWC). Berlin: Springer, 2017: 628-644
[10]Sun Zequn, Hu Wei, Zhang Qingheng, et al. Bootstrapping entity alignment with knowledge graph embedding[C] 
 Proc of the 27th Int Joint Conf on Artificial Intelligence (IJCAI). Menlo Park, CA: AAAI, 2018: 4396-4402
Proc of the 27th Int Joint Conf on Artificial Intelligence (IJCAI). Menlo Park, CA: AAAI, 2018: 4396-4402
[11]Wang Zhichun, Lü Qingsong, Lan Xiaohan, et al. Cross-lingual knowledge graph alignment via graph convolutional networks[C] 
 Proc of the 2018 Conf on Empirical Methods in Natural Language Processing (EMNLP). Stroudsburg, PA: ACL, 2018: 349-357
Proc of the 2018 Conf on Empirical Methods in Natural Language Processing (EMNLP). Stroudsburg, PA: ACL, 2018: 349-357
[12]Chen Muhao, Tian Yingtao, Chang Kaiwei, et al. Co-training embeddings of knowledge graphs and entity descriptions for cross-lingual entity alignment[C] 
 Proc of the 27th Int Joint Conf on Artificial Intelligence (IJCAI). Menlo Park, CA: AAAI, 2018: 3998-4004
Proc of the 27th Int Joint Conf on Artificial Intelligence (IJCAI). Menlo Park, CA: AAAI, 2018: 3998-4004
[13]Trisedya B D, Qi Jianzhong, Zhang Rui. Entity alignment between knowledge graphs using attribute embeddings[C] 
 Proc of the AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2019, 297-304
Proc of the AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2019, 297-304
[14]Cao Yixin, Liu Zhiyuan, Li Chengjiang, et al. Multi-channel graph neural network for entity alignment[C] 
 Proc of the 57th Conf of the Association for Computational Linguistics (ACL). Stroudsburg, PA: ACL, 2019: 1452-1461
Proc of the 57th Conf of the Association for Computational Linguistics (ACL). Stroudsburg, PA: ACL, 2019: 1452-1461
[15]Xu Kun, Wang Liwei, Yu Mo, et al. Cross-lingual knowledge graph alignment via graph matching neural network[C] 
 Proc of the 57th Conf of the Association for Computational Linguistics (ACL). Stroudsburg, PA: ACL, 2019: 3156-3161
Proc of the 57th Conf of the Association for Computational Linguistics (ACL). Stroudsburg, PA: ACL, 2019: 3156-3161
[16]Wu Yuting, Liu Xiao, Feng Yansong, et al. Relation-aware entity alignment for heterogeneous knowledge graphs[C] 
 Proc of the 28th Int Joint Conf on Artificial Intelligence (IJCAI). Menlo Park, CA: AAAI, 2019: 5278-5284
Proc of the 28th Int Joint Conf on Artificial Intelligence (IJCAI). Menlo Park, CA: AAAI, 2019: 5278-5284
[17]Zhu Qiannan, Zhou Xiaofei, Wu Jia, et al. Neighborhood-aware attentional representation for multilingual knowledge graphs[C] 
 Proc of the 28th Int Joint Conf on Artificial Intelligence (IJCAI). Menlo Park, CA: AAAI, 2019: 1943-1949
Proc of the 28th Int Joint Conf on Artificial Intelligence (IJCAI). Menlo Park, CA: AAAI, 2019: 1943-1949
[18]Pei Shichao, Yu Lu, Zhang Xiangliang. Improving cross-lingual entity alignment via optimal transport[C] 
 Proc of the 28th Int Joint Conf on Artificial Intelligence (IJCAI). Menlo Park, CA: AAAI, 2019: 3231-3237
Proc of the 28th Int Joint Conf on Artificial Intelligence (IJCAI). Menlo Park, CA: AAAI, 2019: 3231-3237
[19]Zhang Qingheng, Sun Zequn, Hu Wei, et al. Multi-view knowledge graph embedding for entity alignment[C] 
 Proc of the 28th Int Joint Conf on Artificial Intelligence (IJCAI). Menlo Park, CA: AAAI, 2019: 5429-5435
Proc of the 28th Int Joint Conf on Artificial Intelligence (IJCAI). Menlo Park, CA: AAAI, 2019: 5429-5435
[20]Guo Lingbing, Sun Zequn, Hu Wei. Learning to exploit long-term relational dependencies in knowledge graphs[C OL]
OL] 
 Proc of the Int Conf on Machine Learning (ICML). 2019 [2019-11-01]. http:
Proc of the Int Conf on Machine Learning (ICML). 2019 [2019-11-01]. http:
 proceedings.mlr.press
proceedings.mlr.press v97
v97 guo19c
guo19c guo19c.pdf
guo19c.pdf
[21]Pei Shichao, Yu Lu, Hoehndorf R, et al. Semi-supervised entity alignment via knowledge graph embedding with awareness of degree difference[C] 
 Proc of the World Wide Web Conf. New York: ACM, 2019: 3130-3136
Proc of the World Wide Web Conf. New York: ACM, 2019: 3130-3136
[22]Zhuang Yan, Li Guoliang, Feng Jianhua. A survey on entity alignment of knowledge base[J]. Journal of Computer Research and Development, 2016, 53(1): 165-192 (in Chinese)(庄严, 李国良, 冯建华. 知识库实体对齐技术综述[J]. 计算机研究与发展, 2016, 53(1): 165-192)
[23]Huang Junfu, Li Tianrui, Jia Zhen, et al. Entity alignment of Chinese heterogeneous encyclopedia knowledge base[J]. Journal of Computer Applications, 2016, 36(7): 1881-1886 (in Chinese)(黄峻福, 李天瑞, 贾真,等. 中文异构百科知识库实体对齐[J]. 计算机应用, 2016, 36(7): 1881-1886)
[24]Qiao Jingjing, Duan Liguo, Li Aiping. Entity alignment algorithm based on multi-features[J]. Computer Engineering and Design, 2018, 39(11): 103-108 (in Chinese)(乔晶晶, 段利国, 李爱萍. 融合多种特征的实体对齐算法[J]. 计算机工程与设计, 2018, 39(11): 103-108)
[25]Zhu Jizhao, Qiao Jianzhong, Lin Shukuan. Entity alignment algorithm for knowledge graph of representation learning[J]. Journal of Northeastern University: Natural Science, 2018, 39(11): 18-22 (in Chinese)(朱继召, 乔建忠, 林树宽. 表示学习知识图谱的实体对齐算法[J]. 东北大学学报: 自然科学版, 2018, 39(11): 18-22)
[26]Galárraga L, Razniewski S, Amarilli A, et al. Predicting completeness in knowledge bases[C] 
 Proc of the 10th
Proc of the 10th
ACM Int Conf on Web Search and Data Mining (WSDM). New York: ACM, 2017: 375-383
[27]Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint, arXiv:1609.02907, 2016
[28]Li Ming, Zhou Zhihua. SETRED: Self-training with editing[C] 
 Proc of the Pacific -Asia Conf on Knowledge Discovery and Data Mining (PAKDD). Berlin: Springer, 2005: 611-621
Proc of the Pacific -Asia Conf on Knowledge Discovery and Data Mining (PAKDD). Berlin: Springer, 2005: 611-621
[29]Bengio Y, Louradour J, Collobert R, et al. Curriculum learning[C] 
 Proc of the 26th Annual Int Conf on Machine Learning (ICML). New York: ACM, 2009: 41-48
Proc of the 26th Annual Int Conf on Machine Learning (ICML). New York: ACM, 2009: 41-48
[30]Kusner M, Sun Yu, Kolkin N, et al. From word embeddings to document distances[C OL]
OL] 
 Proc of Int Conf on Machine Learning (ICML). 2015[2019-11-01]. http:
Proc of Int Conf on Machine Learning (ICML). 2015[2019-11-01]. http:
 proceedings.mlr.press
proceedings.mlr.press v37
v37 kusnerb15.pdf
kusnerb15.pdf
[31]Bojanowski P, Grave E, Joulin A, et al. Enriching word vectors with subword information[J]. Transactions of the Association for Computational Linguistics, 2017, 5: 135-146




