极小冲突集问题是基于模型诊断(model-based diagnosis, MBD)[1]中的重要组成部分,基于模型诊断一直是人工智能领域中一个热门的研究问题.Reiter[2]于1987年首次提出了模型诊断方法,首先生成所有极小冲突识别,然后生成候选极小碰集,最终得到所有诊断解;Genesereth[3]提出DART(device-independent diagnostic program)方法来进行冲突识别,并使用独立于设备的语言来描述设备;2002年Haenni[4]提出使用归结的方法生成冲突集,用于在基于逻辑的论证或诱导推理的背景下计算论证或解释;栾尚敏等人[5]提出极小冲突集问题可以根据系统结构特征进行求解,进而由极小冲突求得诊断解;方敏[6]结合工业控制系统,提出先离线识别极小冲突候选,后根据测量和约束,在线确定极小冲突的方法;张立明等人[7]利用ATMS(assumption-based truth maintenance system)将所有极小冲突集导出,并将其分为2类极小冲突.经过对冲突集问题的深入研究,国内外学者发现通过集合枚举树(set enumeration tree, SE-Tree)求解极小冲突集是一种很高效的方法,将元件集合映射为树节点,进而遍历整棵枚举树进行冲突判别;Hou[8]在1994年提出的CS-Tree(conflict set tree),是最早利用枚举树求解极小冲突集的方法,,但其剪枝策略不能保证算法的完备性.
随着SAT(propositional satisfiability problem)求解器应用研究的扩展,部分学者发现可以把求解冲突集问题转化为命题可满足问题.冲突元件集从命题可满足问题角度可以解释为:在该集合内所有元件均假设为正常行为的模式下,不能找到一组赋值使得系统是一致可满足的.于是可以调用SAT求解器判断该集合中元件均正常的逻辑表示公式是否与系统是可满足的.首次使用SAT求解器求解冲突集问题的是赵相福等人提出的HSSE-Tree(hitting set on set enumeration tree)[10],CSSE-Tree(conflict set on set enumeration tree)[10],CSISE-Tree(conflict set on inverse set enumeration tree)[11]方法;陈荣等人[12]在求解诊断问题时,先调用SAT求解器识别冲突后,由所有冲突集的极小碰集得到诊断解;刘伯文等人[13]提出反向深度遍历SE-Tree,并用SAT求解器判别冲突集的方法CSRDSE;徐旖旎等人[14]在对比正常输出与实际输出情况后,结合故障输出特征提出MCS -SFFO(minimal conflict set-structural feature of fault output)方法,将故障无关元件集及其子集剪枝,求解效率提高.
本文在对MCS -SFFO方法分析的基础上,提出结合故障逻辑关系的有解剪枝以及无解剪枝方法MCS -FLR(fault logic relationship).提出单元件非冲突集定理以及非极小冲突定理:单元件集合都是非冲突的、故障输出相关元件集的真超集都是冲突集,且都不是极小冲突集.因此,对故障输出相关元件集的严格超集都不需要进行冲突判定,可以直接将其加入冲突集集合中.MCS -FLR方法在MCS -SFFO方法的基础上进一步对SE-Tree进行单元件无解空间以及故障输出相关元件真超集有解空间的剪枝,提高了冲突集求解效率、节省求解时间.
1 预备知识
本节首先介绍诊断的相关定义,然后介绍命题可满足问题的基本概念,并将诊断相关问题转化为命题可满足问题.
定义1. 诊断系统[15].一个系统可以形式地定义为一个三元组(SD,COMPS,OBS),其中:SD(system description)代表系统描述,是一阶谓词公式的集合;COMPS(system components)代表系统中元件的集合,是一个有限常量集合;而OBS(system observation)代表一观测集合,是一阶谓词公式构成的有限集合.在下面我们使用一元谓词AB(·)表示“Abnormal”,AB(c)为真当且仅当c反常,其中c∈COMPS.
定义2. 基于一致性诊断[15].设一元件集合Δ⊆COMPS,称Δ为关于(SD,COMPS,OBS)的一个基于一致性诊断,如果SD∪OBS∪{AB(c)|c∈Δ}∪{ AB(c)|c∈COMPS-Δ}是一致的.
AB(c)|c∈COMPS-Δ}是一致的.
定义3. 冲突集[13].系统(SD,COMPS,OBS)的冲突集CS是1个元件集合{c1,c2,…,ck}⊆COMPS,使得SD∪OBS∪{ AB(c1),
AB(c1), AB(c2),…,
AB(c2),…, AB(ck)}不一致.
AB(ck)}不一致.
一个元件集如果是极小冲突集,则其任意真子集都不是冲突集[10].
推论1. 当元件集C是冲突集时,C除自身以外的任意超集都不是极小的冲突集[10].
推论2. 当元件集C不是冲突集时,C的任意真子集与C具有同样的冲突性质,也都不是冲突集[13].
SE-Tree是求解极小冲突集的基本逻辑存储结构.利用SE-Tree求解极小冲突集的问题与元件个数呈指数级相关,所以对树中每一个节点都调用SAT求解器判别冲突显然是效率低下的,为了缩减搜索空间进一步减少求解次数,结合上述冲突集的概念以及推论可知,对冲突集的所有真超集以及非冲突集的所有真子集,可不必再对其进行冲突判定.
在命题可满足问题中,用xi(i=1,2,…,n)表示布尔变量.xi及 xi称作称作变量xi的正文字及负文字.X={x1,x2,…,xn}表示变量的集合.Ci(i=1,2,…,m)表示子句,每一个子句是由一组文字组成的析取式.Φ代表CNF公式,CNF公式是由子句Ci的合取构成,即合取范式CNF:Φ=C1∧C2∧…∧Cr,而命题可满足问题就是寻找是否存在一组X的赋值,使其满足CNF.命题可满足问题又称作SAT问题,即判断一个命题公式Φ是不是可以被满足的.
xi称作称作变量xi的正文字及负文字.X={x1,x2,…,xn}表示变量的集合.Ci(i=1,2,…,m)表示子句,每一个子句是由一组文字组成的析取式.Φ代表CNF公式,CNF公式是由子句Ci的合取构成,即合取范式CNF:Φ=C1∧C2∧…∧Cr,而命题可满足问题就是寻找是否存在一组X的赋值,使其满足CNF.命题可满足问题又称作SAT问题,即判断一个命题公式Φ是不是可以被满足的.
定义4. 命题可满足问题(propositional satis-fiability problem, SAT)[15].针对给定的一个命题公式Φ,X={x1,x2,…,xm}是该公式的变量集合,SAT问题可以描述为是否存在1组X的赋值使得给定的命题公式Φ的取值为真.如果能找到至少一组这样的赋值,那么我们则称命题公式Φ是可满足的,若不存在这样的赋值,则该命题公式是不可满足的.
那么,要判断一个元件集合S是否是某系统的一个冲突集,只需要假设S中的元件都为正常行为模式,将S中每一个元件正常状态的行为描述、与该元件相关的系统描述以及观测描述一起编写成一个CNF文件,之后调用SAT求解器对当前CNF文件进行冲突判定.如果SAT求解器得到不可满足,那么S是系统的一个冲突解,反之S为非冲突解.
2 MCS -SFFO方法
本节主要介绍当前求解极小冲突集问题效率较高的MCS -SFFO方法,并给出算法的一些相关概念与基本实现思想.
定义5. 集合枚举树[16].S为一个集合,将S中各个元素不重复的所有组合映射为树中的节点,并以树的形式按一定顺序枚举排列出来,称这样的树为集合枚举树.
定义6. 故障输出元件[14].对于一个电路的诊断系统{SD,COMPS,OBS},若存在元件c∈COMPS,c没有后继元件,且c的输出是系统的输出且是故障输出,即该输出与系统不一致,c为该系统的故障输出元件.
定义7. 故障输出相关元件集[14].称Rel为系统的一个故障输出相关元件集,当且仅当Rel中每一个元件的输出都会传播到故障输出(包含故障输出元件c).
定义8. 故障输出无关元件集[14].Rel为系统的一个故障输出相关元件集,称集合COMPS-Rel为系统的故障输出无关元件集.
MCS -SFFO方法提出与诊断系统故障输出无关的元件集合的所有子集都不是冲突集,所以对SE-Tree中与故障输出无关的电路元件的所有组合进行剪枝,缩小了SAT求解问题的规模.下面给出一些求解极小冲突集的相关概念及SE-Tree遍历节点的剪枝规则.
设Node为SE-Tree中当前正在遍历的节点,以下为剪枝规则及标识规则.
剪枝规则1[13]. 若Node是冲突集且Node是其父节点的最左孩子节点,则向上回溯判断其父节点;否则,跳转判断Node的下一个兄弟节点的最左孩子节点;若Node没有下一个兄弟节点,则跳转判断下一个叶节点.
剪枝规则2[14]. 若Node不是冲突集,且Node是由其子孙节点回溯的节点,(此时Node的最左孩子节点为极小冲突集)则跳转判断Node的左侧下一个孩子节点的最左孩子节点;否则,跳转判断Node的下一个兄弟节点;若Node没有下一个兄弟节点则跳转至以同层非同根节点的最左孩子节点.
剪枝规则3[13]. 在对Node判断其是否冲突之前,先判断Node是否为非冲突集合簇中集合的子集.若是,则其一定是非冲突的,直接调用剪枝规则2跳转判断即可;否则,对Node调用SAT求解器.
标示规则[13]. 当Node是冲突集时,将Node加入到冲突集合簇中,将其标示“0”,并将冲突集合簇中Node的超集标示“1”.
下面给出MCS -SFFO方法的伪代码.
算法1. MCS -SFFO.
输入:SD.cnf、OBS.cnf、故障输出相关元件集onABCompS、故障输出无关元件集unOnABCompS;
输出:极小冲突集合MCSRes.
① 初始化SE-Tree,CSRes=∅,UCSRes=∅,Node=∅;
② Node=SE-Tree的最左节点;
③ While (Node≠∅)
④ If (Node⊆unOnABCompS)
⑤ Break;
⑥ Else
⑦ If (Node是UCSRes元素的子集)
⑧ 剪枝规则3;
⑨ Else
⑩ If (Node是冲突集)
 剪枝规则1;
剪枝规则1;
 Else
Else
 剪枝规则2;
剪枝规则2;
 EndIf
EndIf
 EndIf
EndIf
 EndIf
EndIf
 EndWhile
EndWhile
 将CSRes中所有标示为“0”的节点加入到MCSRes;
将CSRes中所有标示为“0”的节点加入到MCSRes;
 Return MCSRes.
Return MCSRes.
3 MCS -FLR方法
MCS -SFFO方法通过对故障输出无关元件组合的所有子集进行剪枝减少了调用SAT求解器次数,使问题规模变小.结合实际问题进一步分析,与故障输出端相关的电路元件集的超集都是冲突集,不必对其进行可满足性判断,且故障输出相关元件真超集一定不是极小冲突集,故可以将故障输出相关元件真超集剪枝,进一步减少SAT求解器调用次数.因此,提出结合故障逻辑关系的MCS -FLR方法对MCS -SFFO方法改进.
定理1. 单元件非冲突集定理:在多元件电路中,任何单元件集合都不是冲突集.
证明. ci为诊断多元件电路中的任一单元件,ci∈COMPS.首先,根据冲突集的定义,判断ci是否为冲突集,即判断系统中SD∪OBS∪{ AB(ci)}是否一致.然后将ci在系统中的观测描述、ci元件正常行为的子句描述构成CNF文件,最后调用SAT求解器进行求解.已知在保证ci为正常行为的情况下,多元件电路中其他元件可以是故障模式,即存在一组赋值使CNF公式取值为真,SAT返回可满足,进而可知SD∪OBS∪{
AB(ci)}是否一致.然后将ci在系统中的观测描述、ci元件正常行为的子句描述构成CNF文件,最后调用SAT求解器进行求解.已知在保证ci为正常行为的情况下,多元件电路中其他元件可以是故障模式,即存在一组赋值使CNF公式取值为真,SAT返回可满足,进而可知SD∪OBS∪{ AB(ci)}是一致的,元件集非冲突.得证单元件集合都不是冲突集.
AB(ci)}是一致的,元件集非冲突.得证单元件集合都不是冲突集.
证毕.
定理2. 非极小冲突集定理:系统的故障输出相关元件集的任意超集(包含自身)都是冲突集.
证明. 反证法.Rel为系统的一个故障相关元件集,ARel是Rel的任意一个严格超集.假设ARel不是冲突集,则根据推论2可以得出Rel也不是冲突集.已知Rel是故障相关的,即Rel是在所有元件正常情况下,与系统观测及系统描述的输出不一致的元件集合.由冲突集定义可知,Rel一定是冲突集.由此推出矛盾,假设不成立.得出ARel为冲突集,即故障相关元件集Rel的任意超集(包括自身)都是冲突集.进而可推出,Rel的任意真超集都不是极小冲突集.
证毕.
求解故障输出无关元件集方法是通过给定的CNF文件,先调用SAT求解器求得预计的正常输出,然后根据输入将实际输出与正常输出中的元素一一比较,与正常输出不一致的输出即为故障输出端,进而可以从故障输出的输入推出与之相联系的元件集合.
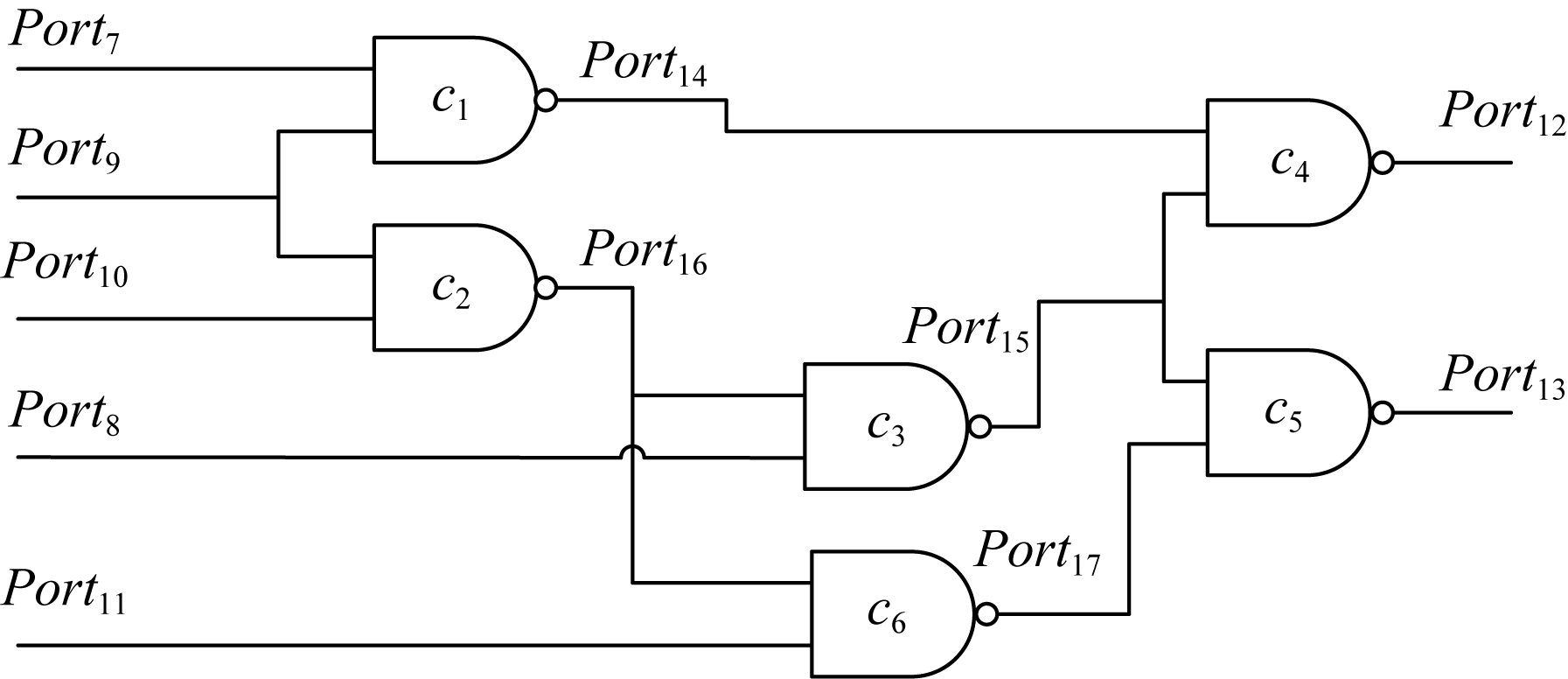
Fig. 1 C17 circuit
图1 C17电路
例1. 在图1所示的C17电路中,输出端口12异常,端口13正常,如图1所示,与13端相联系的元件集合为{c2,c3,c5,c6},因为它们的输出都会传播到13端.其中c2,c3的输出既传播到12端又传播到13端,故无法确定是否为故障输出无关,而c5与c6元件的输出仅传播到13端,则可以明确判断{c5,c6}为故障输出无关元件集.故根据定义9可知{c1,c2,c3,c4}为故障输出相关集合.由此我们可以得到,{c5,c6}是非冲突的,且它的任意子集都是非冲突集,{c1,c2,c3,c4}是冲突的,根据定理2可知,它的任意超集也是冲突集.对于已经明确该集合是否冲突时,不必再调用SAT求解器对其求解.
在同一实例上分别执行MCS -SFFO方法及MCS -FLR方法,将通过这2种方法剪枝后的待遍历节点数进行对比来说明MCS -FLR方法求解效率的提高.已知在当前系统中,有元件集{c1,c2,c3,c4,c5},根据故障输出可以得到,其中{c2,c4}为故障输出相关元件集,{c1,c3,c5}为故障输出无关元件集.
图2为完整的SE-Tree,非空节点31个.图3为MCS -SFFO方法将故障输出无关集合{c1,c3,c5}及其子集剪枝后的枚举树,非空节点23个.图4为MCS -FLR方法在MCS -SFFO方法基础上将单元件集合{c2}及{c4}、故障输出相关集合{c2,c4}真超集剪枝后的枚举树,非空节点15个.图2及图3是未执行剪枝规则前初始化的枚举树.由此可以看出,MCS -FLR方法在MCS -SFFO方法的基础上减少了近1 2的待遍历节点,进而减少大量求解次数,使得求解效率更高.下面给出MCS -FLR方法的伪代码.
2的待遍历节点,进而减少大量求解次数,使得求解效率更高.下面给出MCS -FLR方法的伪代码.
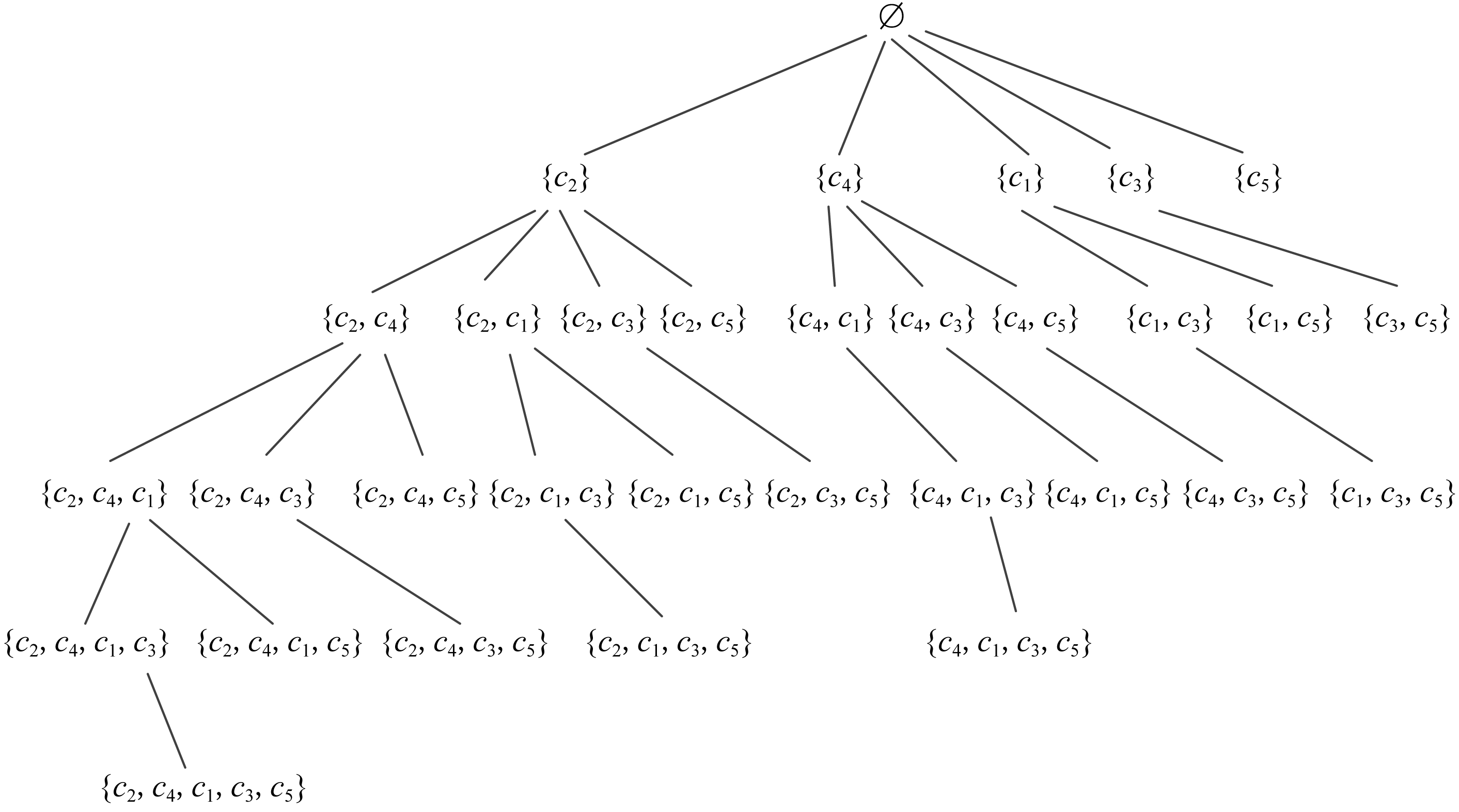
Fig. 2 SE-Tree
图2 集合枚举树
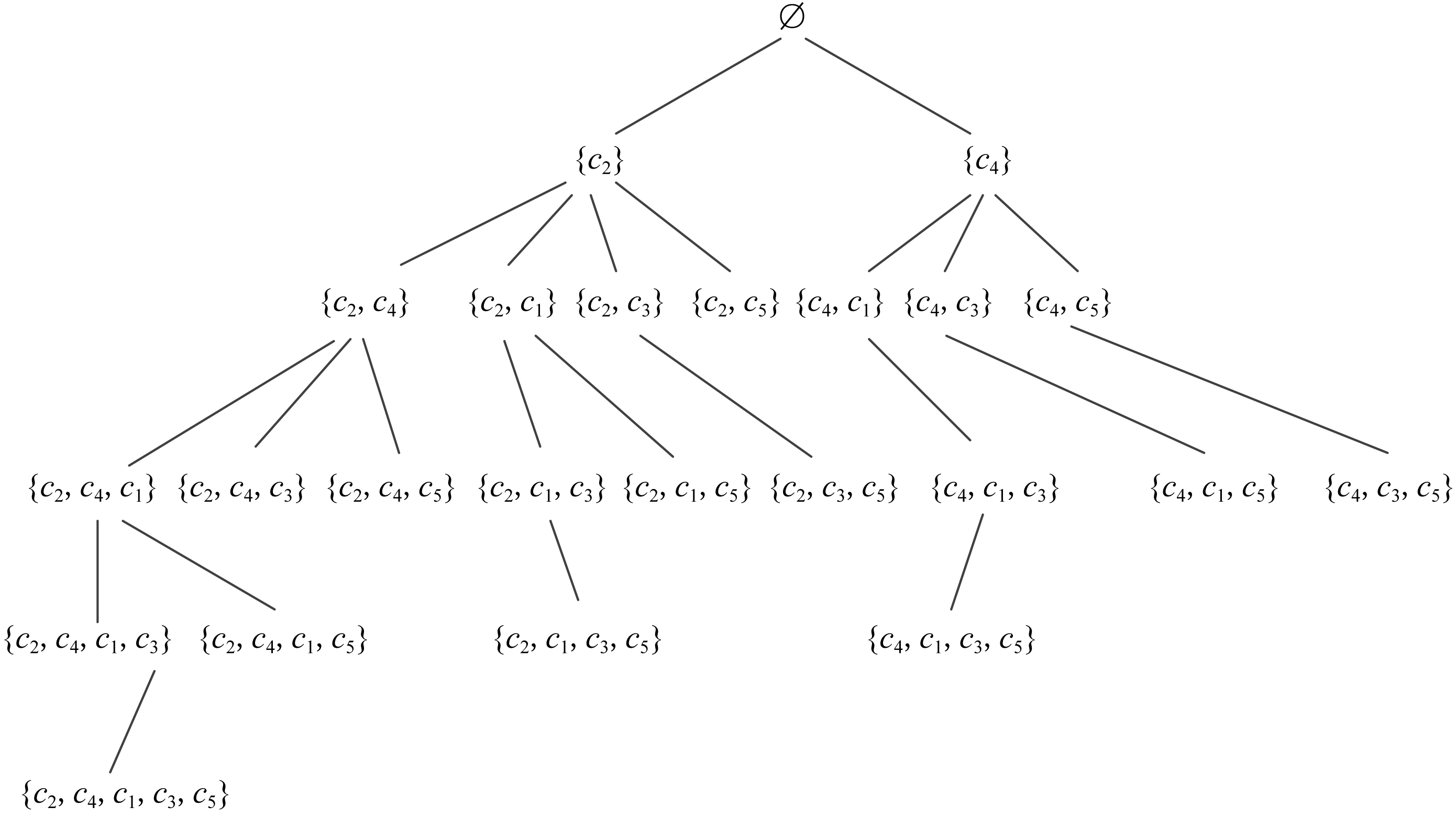
Fig. 3 SE-Tree after pruning by MCS -SFFO method
图3 MCS -SFFO方法剪枝后的SE-Tree
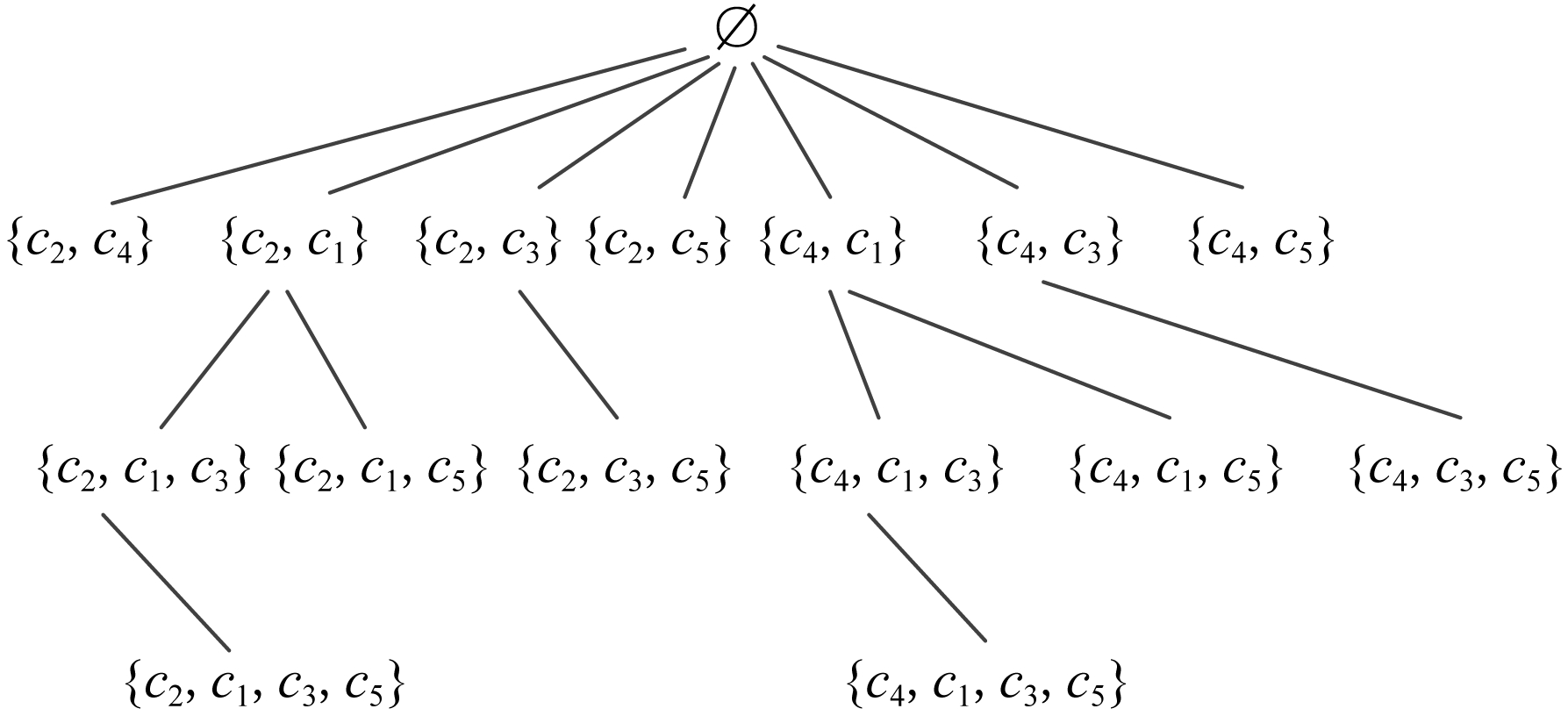
Fig. 4 SE-Tree after pruning by MCS -FLR method
图4 MCS -FLR方法剪枝后的SE-Tree
算法2. MCS -FLR.
输入:系统观测文件circuit.cnf、故障相关元件集合Rel、故障输出无关元件集合UnRel;
输出:极小冲突集合MCSes.
① 初始化冲突集CS=∅,非冲突集UCS=∅,当前遍历节点Node=∅;
② 生成集合{Rel[0],…,Rel[N1-1],UnRel[0],…,UnRel[N2-1]}的集合枚举树CSTree.其中,NUM1是故障输出相关的元素个数,NUM2是故障输出无关的元素个数;
③ Node赋值为CSTree的最左节点;
④ While (Node≠∅)
⑤ If (Node是故障输出无关集合的子集‖Node为单元件集合)
⑥ 将Node及其子集加入到UCS中;
⑦ Break;
⑧ EndIf
⑨ If (Node是故障输出相关集合的超集)
⑩ 将Node及其超集加入到CS中;
 下一个Node依照剪枝规则1;
下一个Node依照剪枝规则1;
 Break;
Break;
 EndIf
EndIf
 If (Node是非冲突集的子集)
If (Node是非冲突集的子集)
 下一个Node依照剪枝规则3;
下一个Node依照剪枝规则3;
 Else
Else
 If (SAT(Node)=0)
If (SAT(Node)=0)
 *当前Node为冲突集*
*当前Node为冲突集*
 将Node加入到CS中,依照标示规则标记;
将Node加入到CS中,依照标示规则标记;
 下一个Node依照剪枝规则1;
下一个Node依照剪枝规则1;
 Else
Else
 *当前Node为非冲突集*
*当前Node为非冲突集*
 将Node加入到UCS中;
将Node加入到UCS中;
 下一个Node依照剪枝规则2;
下一个Node依照剪枝规则2;
 EndIf
EndIf
 EndIf
EndIf
 EndWhile
EndWhile
 将CS中所有标示为极小冲突集的节点加入到MCSes中;
将CS中所有标示为极小冲突集的节点加入到MCSes中;
 Return MCSes.
Return MCSes.
算法2是以输入的circuit.cnf,Rel,UnRel构造集合枚举树,并用CS存放冲突集,UCS存放非冲突集(行①),Node为当前遍历的枚举树中的最左节点(行③).当枚举树中仍有节点没有被遍历时,对当前Node节点进行判断,分为4种情况:1)若为故障输出无关元件集子集或单元件集合,则其可满足性已知,不必再判断(行⑤~⑧);2)若为故障输出相关集合的超集,则直接将其加入冲突集合CS,调用剪枝规则1(行⑨~ );3)若为非冲突集的子集,则不进行判断,直接将其加入UCS,按照剪枝规则3对其赋值(行
);3)若为非冲突集的子集,则不进行判断,直接将其加入UCS,按照剪枝规则3对其赋值(行
 );4)若以上3种情况都不满足,则利用SAT求解器判断,若其是冲突集,按照剪枝规则1对其赋值(行
);4)若以上3种情况都不满足,则利用SAT求解器判断,若其是冲突集,按照剪枝规则1对其赋值(行 ~
~ ),否则若其是非冲突集,按照剪枝规则2对其赋值(行
),否则若其是非冲突集,按照剪枝规则2对其赋值(行 ~
~ ).SE-Tree遍历完成后,将CS中所有标示为“0”的节点加入MCSes,得到所有极小冲突集(行
).SE-Tree遍历完成后,将CS中所有标示为“0”的节点加入MCSes,得到所有极小冲突集(行 ~
~ ).
).
根据算法2的描述可知,MCS -FLR方法为完备算法,除了被剪枝掉的节点,其余节点均被遍历到,且在整棵SE-Tree遍历完成之后会得到所有的极小冲突集.
MCS -FLR方法与MCS -SFFO算法的主要区别在于MCS -SFFO方法是结合故障输出无关集合特征的无解剪枝,MCS -FLR方法是在MCS -SFFO方法的基础上,又结合故障输出相关集合逻辑关系新增有解及无解剪枝.MCS -FLR方法提出了非极小冲突集定理以及单元件非冲突定理,将大量单元件集合和故障输出相关元件真超集剪枝,不必对故障输出相关元件的真超集及单元件集合调用SAT求解器,使得调用SAT求解器次数大大减少,求解效率明显提高.
4 实验结果
本节将对MCS -FLR方法与MCS -SFFO方法进行比较,并给出2种方法在同样测试用例下的实验结果.实验平台为64 b Ubantu 16.04.3 LTS系统,Intel® CoreTM i5-3337U CPU@1.80 GHz×4.MCS -FLR方法与MCS -SFFO方法同时调用的求解器均为Picosat[17].
本次测试的用例[10-11]包括c17,FullAdd_1,FullAdd_2,Polybox_5,Polybox_9,FullAdd_3,FullAdd_4,FullAdd_8.实验对每一个电路设置多观测进行测试,同时每组测试都存在冲突.在使用MCS -FLR方法及MCS -SFFO方法求解时,首先根据CNF文件获取系统描述和系统观测,求出故障输出相关元件集Rel与故障输出无关元件集UnRel,然后将其作为输入构造SE-Tree,作为实现MCS -FLR方法以及MCS -SFFO方法求解极小冲突集的预处理.
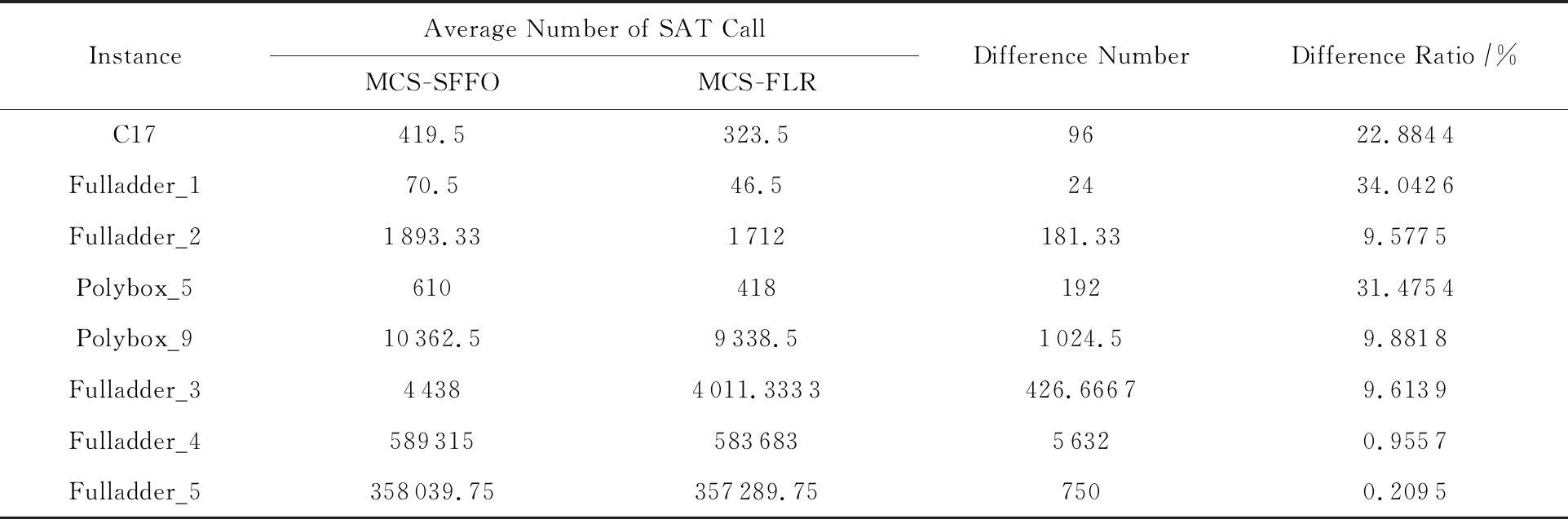
表1中列1为实例名称,列2,3分别是MCS -SFFO方法与MCS -FLR方法在求解用例时平均调用SAT求解器的次数(多个不同故障电路测试用例调用求解器的总次数 故障电路个数),其中每个输出端口都会被设定为故障输出,分别求得一个故障电路.列4是MCS -SFFO方法与MCS -FLR方法调用求解器次数之差,差值越大说明节省的求解器调用次数越多,效率提高越多.列5是MCS -FLR方法较MCS -SFFO方法减少的求解次数百分比,即Difference Ratio=(列2-列3)
故障电路个数),其中每个输出端口都会被设定为故障输出,分别求得一个故障电路.列4是MCS -SFFO方法与MCS -FLR方法调用求解器次数之差,差值越大说明节省的求解器调用次数越多,效率提高越多.列5是MCS -FLR方法较MCS -SFFO方法减少的求解次数百分比,即Difference Ratio=(列2-列3) 列2×100%.以C17电路为例说明,MCS -FLR方法节省了MCS -SFFO方法22.884 4%的求解器次数.可以看出,在所有测试用例中MCS -FLR方法都较MCS -SFFO方法有提高,求解器次数有或多或少的减少,甚至在实验效果较好的用例中(如FullAdd_1,Polybox_5)中,MCS -FLR方法节省了MCS -SFFO方法1
列2×100%.以C17电路为例说明,MCS -FLR方法节省了MCS -SFFO方法22.884 4%的求解器次数.可以看出,在所有测试用例中MCS -FLR方法都较MCS -SFFO方法有提高,求解器次数有或多或少的减少,甚至在实验效果较好的用例中(如FullAdd_1,Polybox_5)中,MCS -FLR方法节省了MCS -SFFO方法1 3的求解器调用次数,求解效率大大提高.不同的电路结构以及同一电路中设置故障输出端口的不同都是影响MCS -FLR方法优化程度的因素.例如在FullAdd_5电路中,故障输出端口的相关元件个数较多,可剪枝的故障输出相关元件真超集的个数较少,故效率提高不明显.在FullAdd_1电路中,由于故障输出端口的相关元件个数较少,所以剪枝掉的故障输出相关元件真超集的个数较多,求解效率提高明显.
3的求解器调用次数,求解效率大大提高.不同的电路结构以及同一电路中设置故障输出端口的不同都是影响MCS -FLR方法优化程度的因素.例如在FullAdd_5电路中,故障输出端口的相关元件个数较多,可剪枝的故障输出相关元件真超集的个数较少,故效率提高不明显.在FullAdd_1电路中,由于故障输出端口的相关元件个数较少,所以剪枝掉的故障输出相关元件真超集的个数较多,求解效率提高明显.
Table 1 Average Number of Calls to SAT Solver and its Difference Ratio
表1 平均调用SAT求解器次数及其加速比
InstanceAverage Number of SAT CallMCS-SFFOMCS-FLRDifference NumberDifference Ratio ∕%C17419.5323.59622.8844Fulladder_170.546.52434.0426Fulladder_21893.331712181.339.5775Polybox_561041819231.4754Polybox_910362.59338.51024.59.8818Fulladder_344384011.3333426.66679.6139Fulladder_458931558368356320.9557Fulladder_5358039.75357289.757500.2095
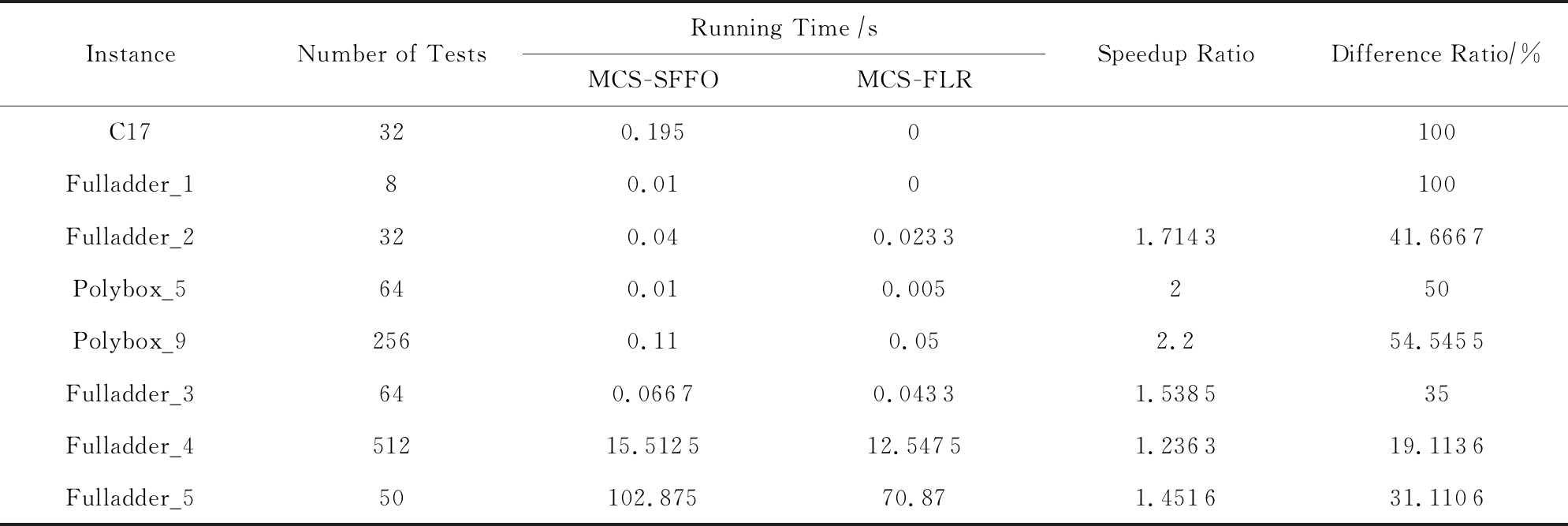
表2是MCS -SFFO方法与MCS -FLR方法求解极小冲突集的时间对比结果.列1为实例名称;列2为测试的组数,即赋值的次数,例如对于C17电路来说,共有5个输入端口,则有25,共计32组赋值.为了保证测试的时限,将测试次数作为输入参数来控制算法的执行,例如FullAdd_5电路中,输入端口共有10个,即应有210,共计1 024组赋值,程序运行时间过长,可以截取一部分结果作为比较的衡量,故设置测试次数为50;列3,4分别为MCS -SFFO方法及MCS -FLR方法的求解时间,本文所有数据均保留4位小数;列5为MCS -SFFO方法与MCS -FLR方法的加速比,是列3求解时间与列4求解时间的比值.加速比越大说明时间效率提高越多;列6为差值加速比,即使用MCS -FLR方法减少了MCS -SFFO方法的时间占MCS -SFFO方法总时间的比,例如在FullAdd_2用例中,MCS -FLR方法减少了MCS -SFFO方法41.666 7%的时间使用.显然,节省求解器次数越多的用例两项加速比也越高,MCS -FLR方法求解极小冲突集的效率也越高.但也存在特殊情况,比如在Polybox_9用例中,节省的求解器次数百分比为9.881 8%,但节省时间百分比却高达54.545 5%,这是因为SAT求解器对元素个数较多的子集判断其是否满足时会更加耗时.
Table 2 Running Time and its Difference Ratio
表2 求解时间及其差值加速比
InstanceNumber of TestsRunning Time ∕sMCS-SFFOMCS-FLRSpeedup RatioDifference Ratio∕%C17320.1950100Fulladder_180.010100Fulladder_2320.040.02331.714341.6667Polybox_5640.010.005250Polybox_92560.110.052.254.5455Fulladder_3640.06670.04331.538535Fulladder_451215.512512.54751.236319.1136Fulladder_550102.87570.871.451631.1106
5 结束语
极小冲突集问题是模型诊断问题中的重要分支.MCS -SFFO方法是目前求解极小冲突集效率较好的方法.本文在深入研究分析MCS -SFFO方法无解剪枝方法的基础上,结合故障的逻辑关系,在SE-Tree上做进一步的无解空间以及大量有解空间的剪枝.提出针对单元件进行无解剪枝以及对故障输出相关元件集的真超集进行有解剪枝的MCS -FLR方法.该方法首先提出了单元件非冲突集定理,推证出单元件构成的集合节点一定是非冲突的,故不进行可满足性判断.之后,提出非极小冲突定理,即系统故障输出相关元件集的超集都是冲突集,且其真超集都非极小冲突,根据此定理将故障输出相关元件集的真超集剪枝,直接加入冲突集中,减少大量求解器调用次数,降低了算法的时间消耗.实验结果表明:在故障输出相关元件占元件总数较大时,剪枝次数较少,效果一般,但调用SAT求解器次数已明显减少.若故障输出相关元件占元件总数比例较小时,其超集个数较多,有解空间剪枝次数较多,求解器效率对比与MCS -SFFO方法提升近1 3,算法效率提高明显.并且,在大规模电路中,有解剪枝的节点个数大幅增加,MCS -FLR方法有更好的剪枝效果.
3,算法效率提高明显.并且,在大规模电路中,有解剪枝的节点个数大幅增加,MCS -FLR方法有更好的剪枝效果.
[1]Liu Meng, Ouyang Dantong, Liu Bowen, et al. Grouped diagnosis approach using the feature of problem[J]. Acta Electronica Sinica, 2018, 46(3): 589-594 (in Chinese)(刘梦, 欧阳丹彤, 刘伯文, 等. 结合问题特征的分组式诊断方法[J]. 电子学报, 2018, 46(3): 589-594)
[2]Reiter R. A theory of diagnosis from first principles[J]. Artificial Intelligence, 1987, 32(1): 57-96
[3]Genesereth M R. The use of design descriptions in automated diagnosis[J]. Artificial Intelligence, 1984, 24(1): 411-436
[4]Haenni R. A query-driven anytime algorithm for argumentative and abductive reasoning[C] 
 Proc of the 1st Int Conf on Computing in an Imperfect World. Berlin: Springer, 2002: 114-127
Proc of the 1st Int Conf on Computing in an Imperfect World. Berlin: Springer, 2002: 114-127
[5]Luan Shangmin, Dai Guozhong. An approach to diagnosing a system with structure information[J]. Chinese Journal of Computers, 2005, 28(5): 801-808 (in Chinese)(栾尚敏, 戴国忠. 利用结构信息的故障诊断方法[J]. 计算机学报, 2005, 28(5): 801-808)
[6]Fang Min. A practical method to identify the minimal conflict sets[J]. Journal of Hefei University of Technology: Natural Science, 1999, 22(1): 39-43 (in Chinese)(方敏. 一种识别最小冲突集的实用方法[J]. 合肥工业大学学报: 自然科学版, 1999, 22(1): 39-43)
[7]Zhang Liming, Ouyang Dantong, Zhao Xiangfu. A new ATMS-based method for deriving all minimal conflict sets[J]. Computer Engineering & Science, 2007, 29(11): 127-130 (in Chinese)(张立明, 欧阳丹彤, 赵相福. 一种基于 ATMS 的求解所有极小冲突集的新方法[J]. 计算机工程与科学, 2007, 29(11): 127-130)
[8]Hou A. A theory of measurement in diagnosis from 1st principles[J]. Artificial Intelligence, 1994, 65(2): 281-328
[9]Yan Xiaolang, Zheng Feijun, Ge Haitong, et al.Combining binary decision diagrams and Boolean satisfiability for equivalence checking[J]. Acta Electronica Sinica, 2004, 32(8): 1233-1235 (in Chinese)(严晓浪, 郑飞君, 葛海通, 等. 结合二叉判决图和布尔可满足性的等价性验证算法[J]. 电子学报, 2004, 32(8): 1233-1235)
[10]Zhao Xiangfu, Ouyang Dantong. A method of combining SE-Tree to compute all minimal hitting sets[J]. Progress in Natural Science, 2006, 16(2): 169-174
[11]Zhao Xiangfu, Ouyang Dantong. Deriving all minimal conflict sets using satisfiability algorithms[J]. Acta Electronica Sinica, 2009, 37(4): 804-810 (in Chinese)(赵相福, 欧阳丹彤. 使用 SAT 求解器产生所有极小冲突部件集[J]. 电子学报, 2009, 37(4): 804-810)
[12]Chen Rong, Gao Jian, Zhang Weishi, et al.Digital circuit fault diagnosis method and system based on logic compatibility: Chinese, CN102156772A[P]. 2011-08-17 (in Chinese)(陈荣, 高健, 张维石, 等. 基于逻辑相容性的数字电路故障诊断方法及系统: 中国, CN102156772A[P]. 2011-08-17)
[13]Ouyang Dantong, Liu Bowen, Zhou Jianhua, et al. A method of computing minimal conflict sets combining the structure property with the anti-depth SE-Tree[J]. Acta Electronica Sinica, 2017, 45(5): 1175-1181 (in Chinese)(欧阳丹彤, 刘伯文, 周建华, 等. 结合问题特征利用SE-Tree反向深度求解冲突集的方法[J]. 电子学报, 2017, 45(5): 1175-1181)
[14]Xu Yini, Ouyang Dantong, Liu Meng. Algorithm of computing minimal conflict sets based on the structural feature of fault output[J]. Journal of Computer Research and Development, 2018, 55(11): 46-54 (in Chinese)(徐旖旎, 欧阳丹彤, 刘梦, 等. 结合故障输出结构特征的极小冲突求解算法[J]. 计算机研究与发展, 2018, 55(11): 46-54)
[15]Ouyang Dantong, Zhou Jianhua, Liu Bowen, et al. A new algorithm combining with the characteristic of the problem for model-based diagnosis[J]. Journal of Computer Research and Development, 2017, 53(3): 502-513 (in Chinese)(欧阳丹彤, 周建华, 刘伯文, 等. 基于模型诊断中结合问题特征的新方法[J]. 计算机研究与发展, 2017, 53(3): 502-513)
[16]Rymon R. Search through systematic set enumeration[C] 
 Proc of the 3rd Int Conf on Principles of Knowledge Representation and Reasoning. San Francisco, CA: Morgan Kaufmann, 1992: 539-550
Proc of the 3rd Int Conf on Principles of Knowledge Representation and Reasoning. San Francisco, CA: Morgan Kaufmann, 1992: 539-550
[17]Biere A. PicoSAT essentials[J]. Journal on Satisfiability, Boolean Modeling and Computation, 2008, 4(20): 75-97



