在决策过程中,当人类缺乏足够的证据或详细的知识时,可能会进行逻辑欠缺的随机猜测[1-6].例如学生在面对困难的多项选择题时喜欢选择自己幸运的选项.有时,这些随机猜测可能与实际情况形成一致性,我们称这种一致性为随机一致性.随机一致性的存在会误导逻辑形成方向,导致决策结果无意义、信息含量少、扩展能力差.在随机猜测与真实情况的分布相同时,这些缺点尤为明显.
基于智能算法的机器学习系统本质上是一种由数学表达与逻辑运算构成的决策函数,被认为具有较强的客观性与确定性,不像人类容易受外部因素的影响,出现主观臆断的现象.然而,1)智能学习算法是数据驱动的.机器学习算法面对的历史数据通常具有数量有限、类别分布不平衡、含噪音等特质[7-9],这使得学习机所面对的学习证据缺乏完备性、充分性与准确性.那么,基于历史数据所得的决策知识与数据蕴涵的潜在模式可能会出现偏差;2)智能学习算法是目标导向的[10-11].智能算法的设计目的、数据运用、结果表征等都是开发者、设计者的主观价值选择,算法设计者在把算法逻辑输入机器的同时,也将具有随机性的判断方式带到了学习机中.基于上述分析,智能算法也会呈现随机一致性,并且在自我提升的反馈循环中又可能会把随机一致性带来的后果进一步放大或者固化,严重影响到自身泛化性能的提升.
目前,大多数机器学习算法以准确度为目标导向.例如,决策树所采用的信息熵,k近邻算法中所采用的投票准则,以及支持向量机,Adaboost等经典学习算法所使用的损失函数都与准确度有着密切的关系[12-13].然而,简单的准确度指标作为反馈或启发准则包含了由于偏差所导致的随机一致性,这对于学习机泛化性能的评价是不合理的.
因此,研究如何消除学习过程中的随机一致性,从而建立基于纯一致性度量(消除随机一致性的一致性度量)的机器学习算法与理论体系已成为人工智能研究领域的一个重要科学问题[14-17].
支持向量机(support vector machine, SVM)是传统机器学习中泛化能力较强、理论保障较为完善的方法之一,被广泛应用在故障诊断、文本分类等各个领域.本文首先给出纯准确度的定义,然后提出基于纯准确度的支持向量机分类方法PASVM,并通过KEEL数据集验证PASVM的泛化性能.
1 纯准确度指标
本文考虑二分类问题.设X∈![]() d为d维特征空间,Y∈{-1,+1}为标签空间.二分类问题的任务是建立从X映射到Y的二值分类器h(X).为了评价分类器的性能,引入混淆矩阵,如表1所示.其中:
d为d维特征空间,Y∈{-1,+1}为标签空间.二分类问题的任务是建立从X映射到Y的二值分类器h(X).为了评价分类器的性能,引入混淆矩阵,如表1所示.其中:
Table 1 Confusion Matrix
表1 混淆矩阵

Y∕h(X)h(X)=+1h(X)=-1Total(Y)Y=+1TPFNpY=-1FPTN1-pTotal(h)q(h)1-q(h)1
TP(true positive)表示正类样本被分为正类的比例;
FN(false negative)表示正类样本被分为负类的比例;
FP(false positive)表示负类样本被分为正类的比例;
TN(true negative)表示负类样本被分为负类的比例;
p表示真实类别中正类的比例;
q(h)表示分类器输出正类的比例.
基于混淆矩阵,准确度A和错误率L的定义分别为
A(h)=TP(h)+TN(h),
(1)
L(h)=FN(h)+FP(h).
(2)
1.1 随机准确度指标和纯准确度指标的定义
如引言所述,分类器构建过程中存在着不可避免的随机因素.本文引入置换划分集来刻画随机因素对分类结果的影响.
定义1. 置换划分集Hq(h)为类别分布与待评估分类器h(X)相同的所有可能的二值划分组成的集合:
Hq(h)={h′:P(h′(X)=+1)=
q(h),h′(X)=±1}.
(3)
例1. 对于只包含3个样本的数据集,假设待评估分类器的类别分布为q(h)=2/3,那么置换划分集为包含3种二值划分的集合:
Hq(h)={h1=(-1,+1,+1),h2=(+1,-1,+1),
h3=(+1,+1,-1)}.
当分类器视被视为一个随机变量时,其分类结果的随机性可以通过类别分布来体现.置换划分集包含了与当前分类器输出分布相同的所有可能的划分结果.基于此,置换划分集的某些数字特征可用来刻画随机性导致的一致性.本文使用置换划分集中所有划分的平均准确度来衡量随机一致性,并且因缺乏划分对数据偏好信息的先验(倾向划分哪些样本为正类),我们假设所有的划分以相同的概率出现.
引理1. 当置换划分集中的所有划分是均匀分布的,其平均准确度为
Eh′:h′∈Hq(h)(A(h′))=pq(h)+
(1-p)(1-q(h)).
(4)
证明. 不失一般性,假设q<p,样本量为N.由于混淆矩阵的自由度为3,我们只需要考虑TP(h)或者TN(h)来证明.现以TP(h)为例.当![]() 时,
时,
当置换划分集中的划分服从均匀分布时,TP(h)服从参数为(N,Np,Nq(h))的超几何分布,即从N个样本中(其中包含Np个正类样本)中不放回地抽出Nq(h)个样本,TP(h)表示其中包含正类样本的个数.于是,我们有:
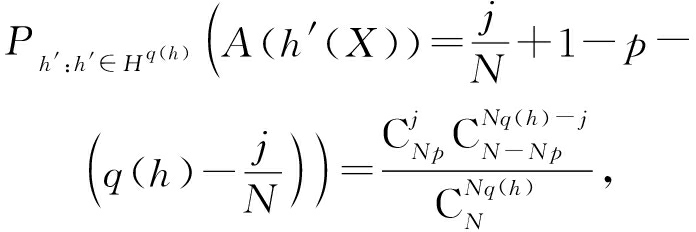 (5)
(5)
其中j=0,1,…,Nq(h).进一步基于超几何分布的2个重要公式:
![]()
![]()
(6)
我们有:
Eh′:h′∈Hq(h)(A(h′(X))=![]()
pq(h)+(1-p)(1-q(h)).
(7)
证毕.
假设例1中3个样本的真实标签为Y=(-1,-1,+1),那么例1中置换划分集的平均准确度为:![]() 这与按照引理1计算的结果
这与按照引理1计算的结果![]() 相同.
相同.
定义2. 分类器h(X)的随机准确度定义为
RA(h)=pq(h)+(1-p)(1-q(h)).
(8)
定义3. 分类器h(X)的纯准确度定义为
![]() (9)
(9)
需要指出的是,纯准确度与统计学中的κ指标形式相同,不同的是κ指标从评估者独立时的一致性来刻画随机一致程度[16].随机准确度的定义更具有启发意义,可指导其他指标中随机一致程度的定义,也可以扩展置换划分集的定义形式和概率分布来定义新的形式.
纯准确度从准确度中减去随机一致的部分,再除以上界使得最大值归一化,其定义框架与聚类中的调整兰德指数[4-5,7-8]相同.图1展示了纯准确度指标以随机准确度值为基准线(零值线);准确度指标以绝对零值为基准线.纯准确度指标是相对指标,衡量算法优于随机划分的程度,而准确度指标是绝对指标,衡量算法取得的分数.在机器学习中,不同任务的数据集,不同类型的运行环境,不同的算法,导致分类器产生程度不同的随机一致性.因此纯准确度指标作为评价指标更为合理客观,具有更多的信息量.
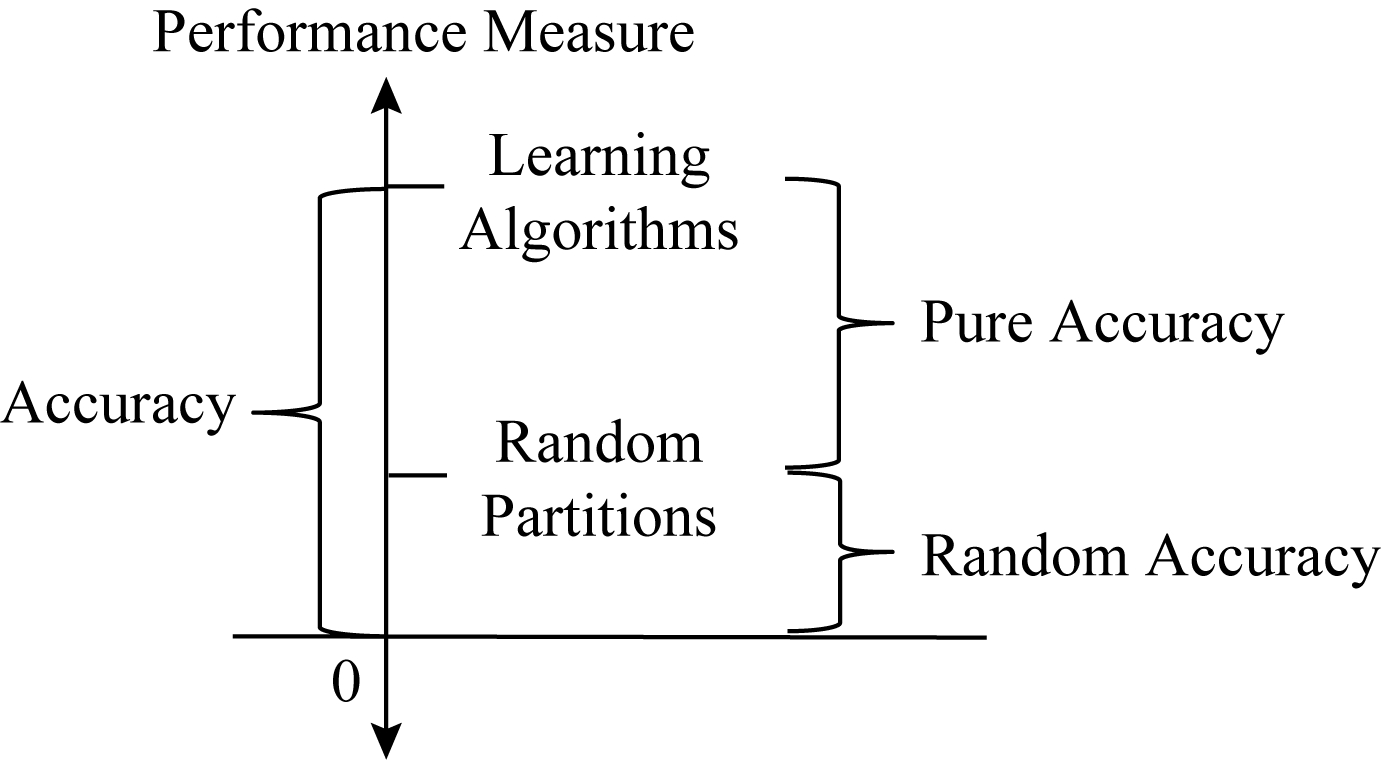
Fig. 1 The diagram of the baseline
图1 基准线示意图
定义4. 分类器h(X)的纯错误率定义为
![]() (10)
(10)
进一步,纯错误率还可以表示为
![]() (11)
(11)
![]() (12)
(12)
纯准确度指标和纯错误率指标属于线性分式指标.线性分式指标是指形式如(13)的指标:
![]() (13)
(13)
其中,ai,bi(i=0,1,2)是不为零的常数.类似指标还包括F1-measure和精确率Precision等.
1.2 随机准确度的进一步分析
本节进一步分析随机准确度在评价过程中的作用及意义.图2展示了随机准确度值RA与真实标签的类别分布p及输出标签的类别分布q之间的曲线图.可以看到,(0.5,0.5)是纯准确度曲面的鞍点:在p=q方向,0.5是曲面的最小值点;在p+q=1方向,0.5是曲面的最大值点.
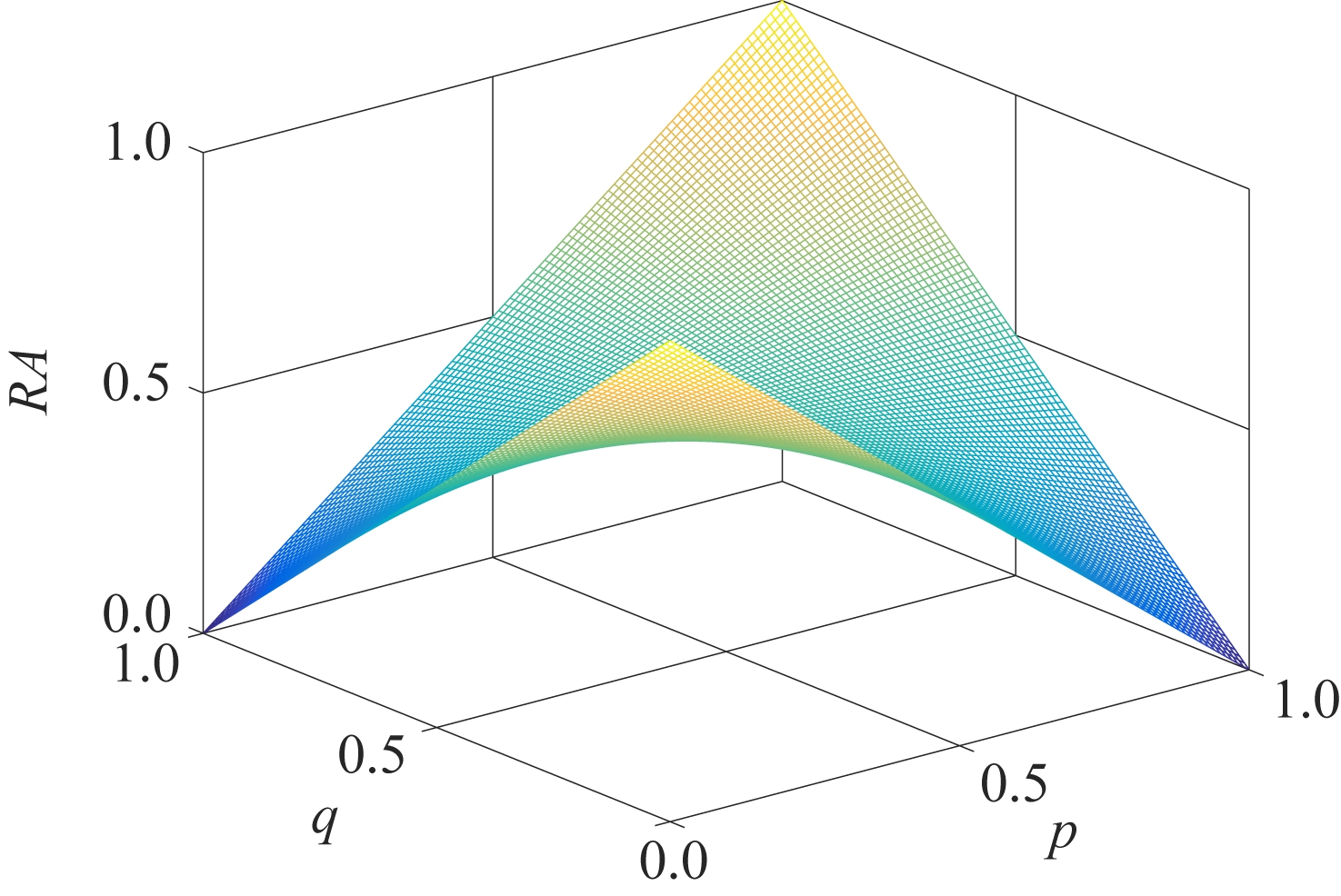
Fig. 2 The relationship between the random accuracy and the class distribution
图2 随机准确度与类别分布的关系
准确度指导的分类器往往过度拟合大类样本.纯准确度值随着准确度的增加而增加,随着随机准确度的减少而增加.在纯准确度指导下,为了保证较高的准确度,分类器与真实标签类别分布趋势应该相同(同时小于或大于0.5);为了保证达到较低的随机准确度,分类器应该趋近于无偏的(输出分布接近于0.5),进而有望更加接近于真实分布.基于上述分析,可以看到随机准确度使得纯准确度追求完全的输出随机性(输出概率为0.5),而不是依赖于经验数据的有偏差的随机性.
在实际任务场景中,机器学习算法面对的数据越复杂,所得到的分类模型与真实模式之间的偏差越大,相对于真实模式的随机性越强,从而产生更高的随机一致性.表2展示了10种不同任务的数据集.我们通过改变数据的不平衡度和噪音水平来验证随机准确度是否能捕捉到偏差造成的随机一致性.具体地,通过对每个数据集的小类样本欠抽样,得到不同IR(imbalance ratio)的数据集.IR表示大类与小类样本的数量比例.通过数据的标签加入单边噪音,得到不同噪音水平的数据集.这里,单边噪音是指小类样本的标签随机均匀地被污染为大类.在人工标注中,这种单边噪音相较于另一侧的单边噪音(大类标注为小类)更为常见.
然后,每个数据集按照7∶3的比例划分为训练集和测试集,使用训练集建立SVM分类器.实验进行30次,图3和图4的记录了测试随机准确度值(箱线)及其平均值(紫色圈),从图3和图4可以看到,随着IR和噪音水平的升高,随机准确度的值升高,这说明随机准确度的定义是有意义的.
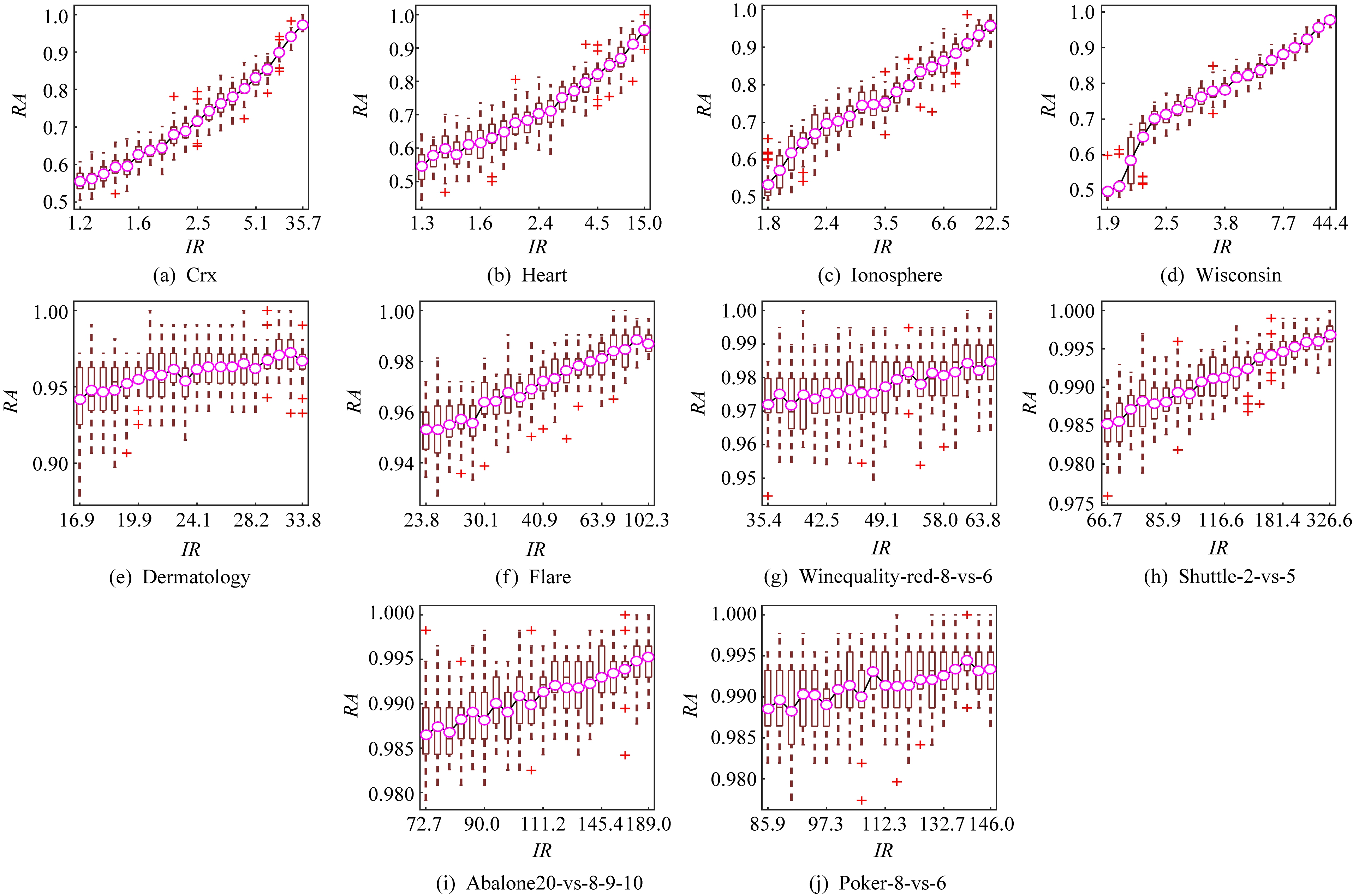
Fig. 3 The random accuracy increases with the increase of imbalance degree
图3 随机准确度随着不平衡程度的增加而增加
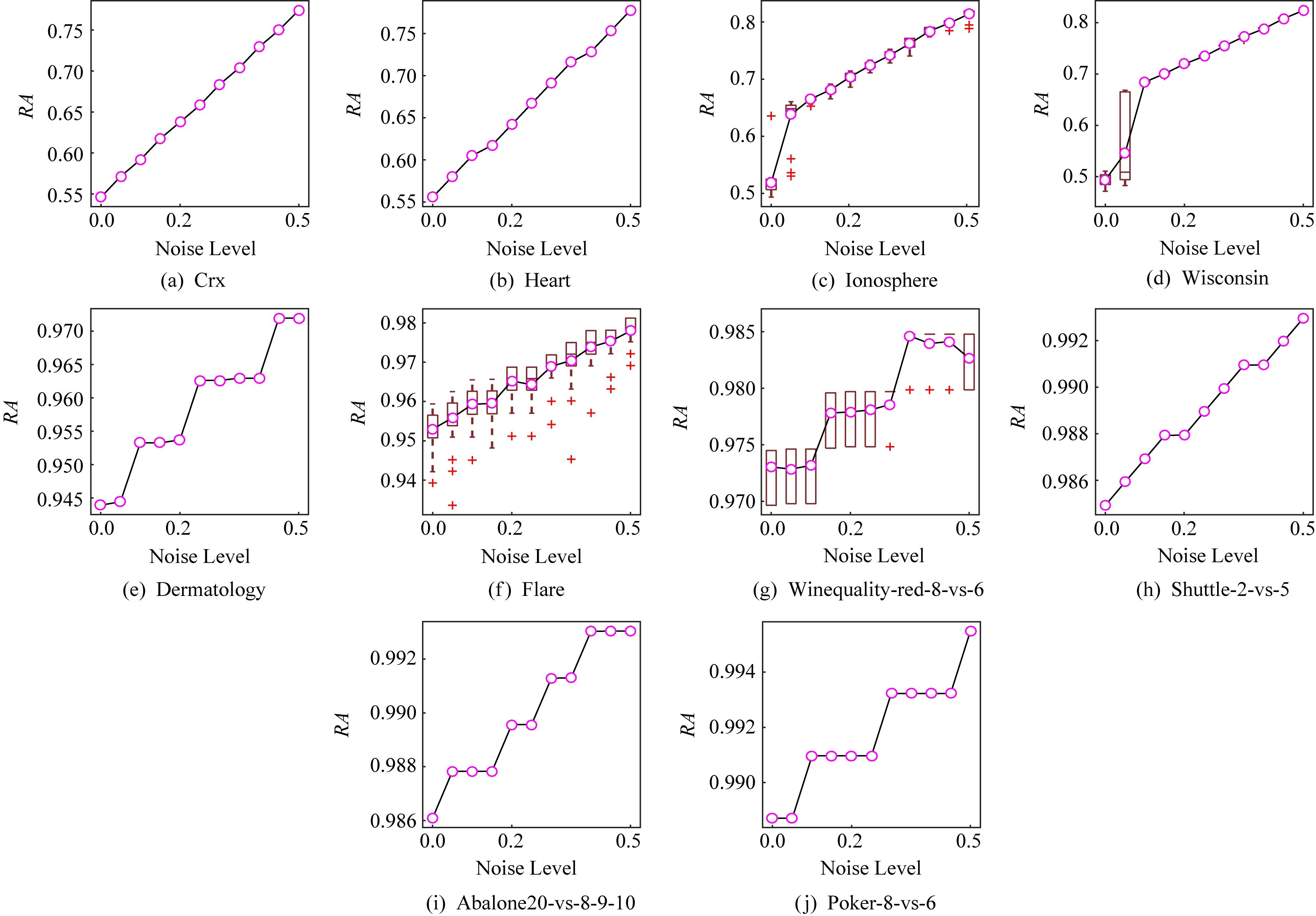
Fig. 4 The random accuracy increases with the increase of the one-size noise level
图4 随机准确度随着单边标签噪音水平的增加而增加
2 基于纯准确度的支持向量机模型
为了消除SVM模型的随机一致性,本文提出优化纯准确度的SVM模型.首先,简要回顾SVM模型,可用来优化纯准确度指标的SVMperf(support vector machine for multivariate performance measures)模型及梯度下降法.然后,给出基于纯准确度指标的SVM模型PASVM及其求解过程.
2.1 SVM、SVMperf及梯度下降法回顾
SVM模型是传统机器学习中泛化能力较强的分类方法之一,该方法的基本思想是样本点不仅能够正确分类并且所有样本点到分类器界面的距离要尽可能大.
设w∈![]() d为分类界面的参数,分类函数为
d为分类界面的参数,分类函数为
![]() (14)
(14)
SVM模型为
s.t. ∀i:ξi≥0,yi(wTxi)≥1-ξi,
(15)
其中,ξi是错误率的上界.参数C为错误率和权重项的折中参数.SVM模型也可以等价表示为
为了构建优化F1-measure,Precision等多元复杂指标的SVM模型,文献[18]提出SVMperf模型.SVMperf模型可以用来优化纯准确度.其基本思想是将所有训练数据看作一个整体,然后要求真实标签向量与其他所有可能标签向量之间的间隔要超过它们之间的评价指标值.
具体地,令![]() 为标签向量空间,
为标签向量空间,![]() 为真实标签向量,
为真实标签向量,![]() 为其余标签向量.设Ψ是定义在标签向量组
为其余标签向量.设Ψ是定义在标签向量组![]() 和
和![]() 上的性能度量.SVMperf模型为
上的性能度量.SVMperf模型为
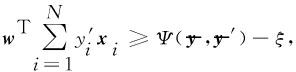 (17)
(17)
其中ξ可证明是目标度量Ψ的上界.参数C为错误率和权重项的折中参数.
与传统的SVM模型相比,SVMperf的待解变量减少,然而约束条件的个数为2N-1个,与样本数量呈现指数增长关系.
梯度下降法[19]是SVMperf的扩展方法,对于线性分式指标Ψ,该方法首先推断一组标签向量![]() 与
与![]()
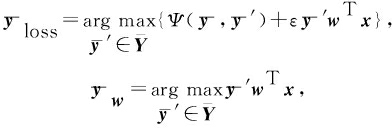
其中ε为折中参数.在二类分类问题中,线性分式指标Ψ的梯度定义为
![]()
![]()
据此,模型参数w的更新公式为
wt+1=wt-λ![]()
![]()
其中λ为更新步长.
梯度下降法中的ε值较难确定,当ε值较大时,推测得到的![]() 与
与![]() 相近,容易出现梯度为零的现象;当ε值较小时,性能度量Ψ在
相近,容易出现梯度为零的现象;当ε值较小时,性能度量Ψ在![]() 的推测中占据主导地位,容易出现在每轮迭代中推测得到的
的推测中占据主导地位,容易出现在每轮迭代中推测得到的![]() 与真实标签向量
与真实标签向量![]() 相近的现象,使得梯度的定义取决于
相近的现象,使得梯度的定义取决于![]() 进而导致参数更新与目标函数无关.
进而导致参数更新与目标函数无关.
2.2 PASVM模型
构建基于纯准确度指标的支持向量机模型最直观的方法之一是使用纯错误率指标替代传统SVM模型中的错误率指标:
![]() (18)
(18)
其中,L=EX,YI[Yh(X)<0],q=EYI[Y>0],I[·]为示性函数.
这个目标函数的难点在于纯错误率指标呈分式形式,并且L和q中存在不连续的非凸的示性函数.L中的示性函数表征样本是否被错误分类,q中的示性函数表征样本是否属于正类.在本文所采用的优化方法中L出现在目标函数中,q出现在约束条件中.因此,本文使用连续的凸的hinge函数和有界的sigmoid函数分别近似L和q中的示性函数:
![]()
![]()
![]()
(19)
那么,基于纯准确度指标的SVM模型为
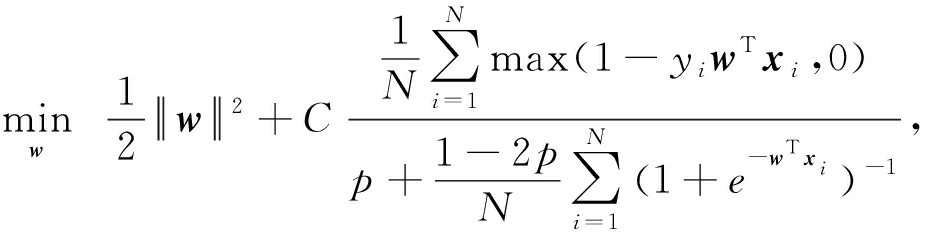
(20)
称之为PASVM模型.
定理1. 表示定理[20].设Ω是一个严格单调递增函数,c是任意损失函数.则每一个正则化风险
![]()
(xN,yN,f(xN)))
(21)
的最优解满足:
(22)
其中,![]() 是f的希尔伯特范数,K(·,·)为核函数,α≥0.
是f的希尔伯特范数,K(·,·)为核函数,α≥0.
易知,PASVM模型满足表示定理.对于PASVM所使用的线性分类器,模型参数w的最优值满足:
(23)
即最优值由训练数据X张成.此时,模型的决策函数为
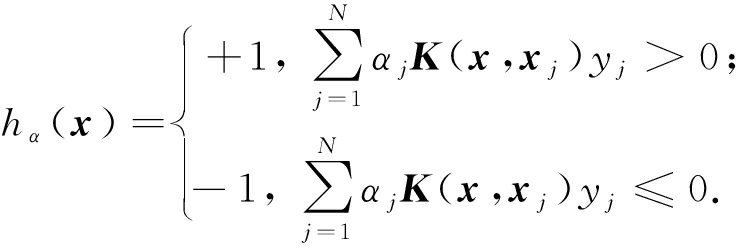
(24)
由表示定理可得,PASVM的核函数形式为
![]()
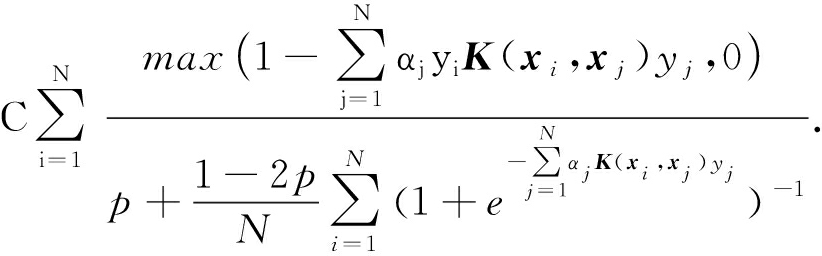
(25)
PASVM的求解问题属于带有正则项的分式规划问题:
![]() (26)
(26)
其中,g2(z)≥0,g3(z)>0.令
![]() (27)
(27)
此类问题的解可以等价转换求解z(r*),其中,
![]()
![]()
(28)
可以看到,上述过程将分式规划问题式(26)转换为一个带有约束的规划问题式(27)和一个一维优化问题式(28)[21].
然而,对于PASVM模型而言,在训练集上,分母的最优值为p+(1-2p)p.因此,可以省去r*的寻找.基于此,PASVM模型的最优解可以通过以下带有约束的规划问题求得:
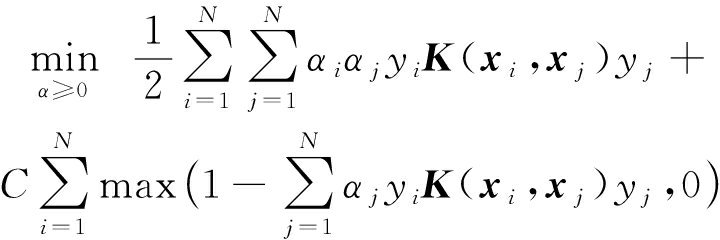 (29)
(29)
(1-2p)p.
与传统SVM模型相比,PASVM模型多了一个约束条件.与SVMperf模型相比,借助分式规划问题,PASVM只需要一个约束条件实现求解,这得益于纯准确度的分母形式可以表示为真实标签和预测标签类别分布的函数.对于F1-measure,Precision而言,使用上述分式规划式(26)求解可能需要寻求最优的r*.
为了进一步提高PASVM模型的泛化能力,我们将半监督学习的思想融入到模型求解过程中.半监督学习使用大量的未标记数据,以及同时使用标记数据进行机器学习.从式(19)中可以看到,q的计算未使用样本的标签.因此,规划问题式(29)约束条件的可以使用未标记数据.具体地,规划问题式(29)可以扩展为
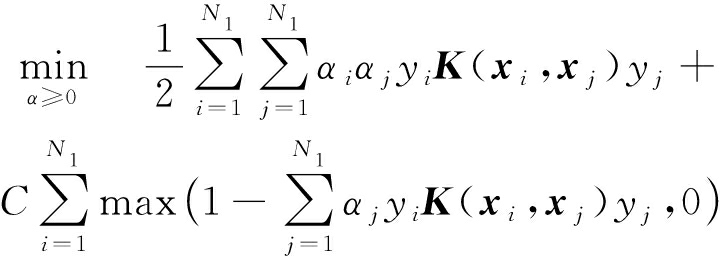 (30)
(30)
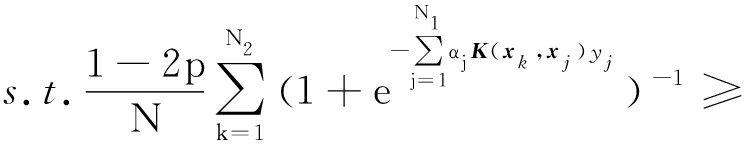
(1-2p)p,
其中,样本xi,xj属于同一集合并且都是标记数据:xi,xj∈D1;xk属于另外一个集合,是标记数据或者未标记数据:xk∈D2.Nt为数据集Dt的样本数量,t=1,2.算法1给出PASVM的分类方法.
算法1. 基于纯准确度的支持向量机PASVM.
输入:标记数据集D1、数据集D2、参数C、待分类样本x;
输出:预测结果.
1) 初始化αj为[0,1]区间的任意值;
2) 计算核相似度矩阵K(xi,xj),xi,xj∈D1,K(xk,xj),xj∈D1,xk∈D2,计算
3) 使用内点法求解问题式(30),得到模型参数αj,j=1,2,…,N1;
4) 预测结果

3 实验分析
为了验证基于纯准确度的SVM方法具有更加优异的性能,本文将PASVM方法与传统的SVM方法、SVMperf[18]、梯度下降法[19]及优化纯准确度的Plug-in[22]和Bisection[22]方法进行比较.
Plug-in方法的决策函数形式为
其中,η(x)=P(Y=1|X=x)为后验类属概率,δ为决策阈值.Plug-in方法是二步法,首先根据已有成熟的概率估计的方法得到后验类属概率,再按照某种搜索方法得到使得目标度量最大的决策阈值.Bisection方法归属于Plug-in这一类方法,不同的是Bisection方法按照二分法搜索δ.
3.1 数据集及设置
本文在KEEL[23]的10种基准数据集上测试PASVM的有效性.10种数据集详细信息描述如表2所示:
Table 2 Description of the Data Set
表2 实验数据集描述
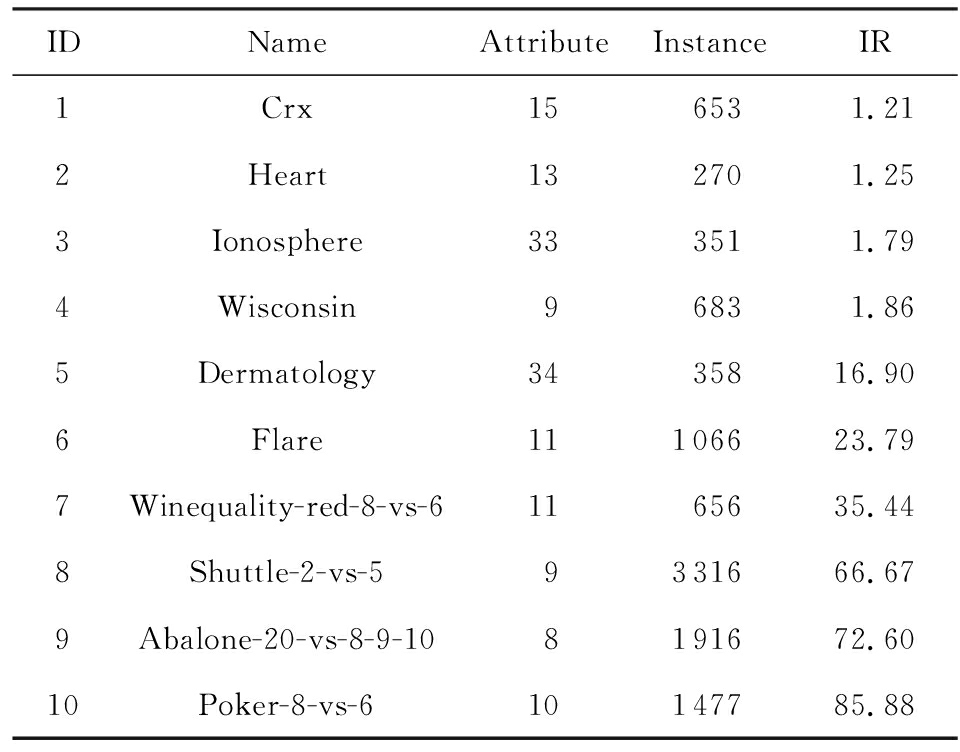
IDNameAttributeInstanceIR1Crx156531.212Heart132701.253Ionosphere333511.794Wisconsin96831.865Dermatology3435816.906Flare11106623.797Winequality-red-8-vs-61165635.448Shuttle-2-vs-59331666.679Abalone-20-vs-8-9-108191672.6010Poker-8-vs-610147785.88
所有数据集按照3∶1∶1的比例随机划分为训练集验证集与测试集.数据集按照训练集的极大极小值进行极差归一化处理.然后,我们选取高斯核函数![]() 对数据集进行核变换,所有方法都在核变换之后运行.通过验证集,核窗宽参数γ在{2-4,2-2,20,22,24,26}中选择,惩罚参数C在{20,22,24,26}中选择.另外,Plug-in方法的后验类属概率通过逻辑斯蒂回归方法得到,切割阈值在验证集的后验概率中选取.
对数据集进行核变换,所有方法都在核变换之后运行.通过验证集,核窗宽参数γ在{2-4,2-2,20,22,24,26}中选择,惩罚参数C在{20,22,24,26}中选择.另外,Plug-in方法的后验类属概率通过逻辑斯蒂回归方法得到,切割阈值在验证集的后验概率中选取.
因对比算法未使用测试集进行学习,为了保证比较的公平性,在实现算法1的过程中,我们不使用测试数据集计算约束条件,而是将训练集的样本按照7∶3的比例划分为D1和D2,p的计算按照D2中属于正类的比例计算.
在每个数据集上,进行50次实验对比,以此考察算法的平均性能.每一次对比在相同的划分下进行.另外,为了创造更加复杂的数据环境,本文对数据集依次加入3%,5%的随机均匀分布的标签噪音.
3.2 实验结果及分析
表3~5分别列出了标签噪音为0%,3%,5%这3种情况时,6种算法在10个数据集上的准确度的平均值和标准差.表6~8分别列出了标签噪音为0%,3%,5%这3种情况时,6种算法在10个数据集上的纯准确度的平均值和标准差.黑体表示算法在该行数据集上取得了最高的性能值.每个数据集上,性能值最高的算法排序为1,性能值第二高的算法排序为2,以此顺推.算法的性能值越高,序值越小.表格最后一行的Average Rank表示每列方法在所有数据集上序值的平均值,越小说明算法取得的性能值越好.表格中的黑色圆点表示PASVM显著好于该方法.显著性检验方法为配对t检验,显著性水平为0.01.
Table 3 Comparison of Accuracy on Data Sets with 0% Noise (Mean±Standard Deviation)
表3 无噪音时不同算法的准确度比较(均值±标准差)

Data IDSVMPlug-inBisectionSVMperfGradientPASVM10.8657±0.02050.8561±0.0201·0.8606±0.02270.8654±0.01400.8657±0.01600.8686±0.016020.8210±0.03220.8017±0.0484·0.8125±0.0320·0.8187±0.0440·0.8272±0.03440.8303±0.032230.9262±0.0272·0.9321±0.03240.9280±0.03430.9244±0.03940.9244±0.03940.9363±0.022740.9617±0.04240.9718±0.01400.9709±0.01310.9703±0.01250.9700±0.01350.9733±0.012250.9947±0.0081·0.9953±0.0080·0.9765±0.0148·0.9988±0.0040·0.9994±0.00291.0000±0.000060.9186±0.05240.9104±0.0488·0.9175±0.0321·0.9286±0.0199·0.9423±0.01330.9378±0.018470.7058±0.24960.9145±0.0636·0.7141±0.0534·0.8737±0.18220.7045±0.2476·0.8591±0.208480.9998±0.0010·0.9990±0.0018·0.9936±0.0038·1.0000±0.00001.0000±0.00001.0000±0.000090.9830±0.00760.9580±0.0323·0.8583±0.1498·0.9832±0.00470.9821±0.00480.9820±0.0056100.9939±0.00850.9902±0.00510.9928±0.0049·0.9945±0.00310.9943±0.00340.9950±0.0028Average Rank3.90004.30004.80002.90003.30001.8000
Note: The best performance is in bold; “·” means the PASVM is significantly better than the corresponding method.
Table 4 Comparison of Accuracy on Data Sets with 3% Noise (Mean±Standard Deviation)
表4 噪音水平为3%时不同算法的准确度比较(均值±标准差)
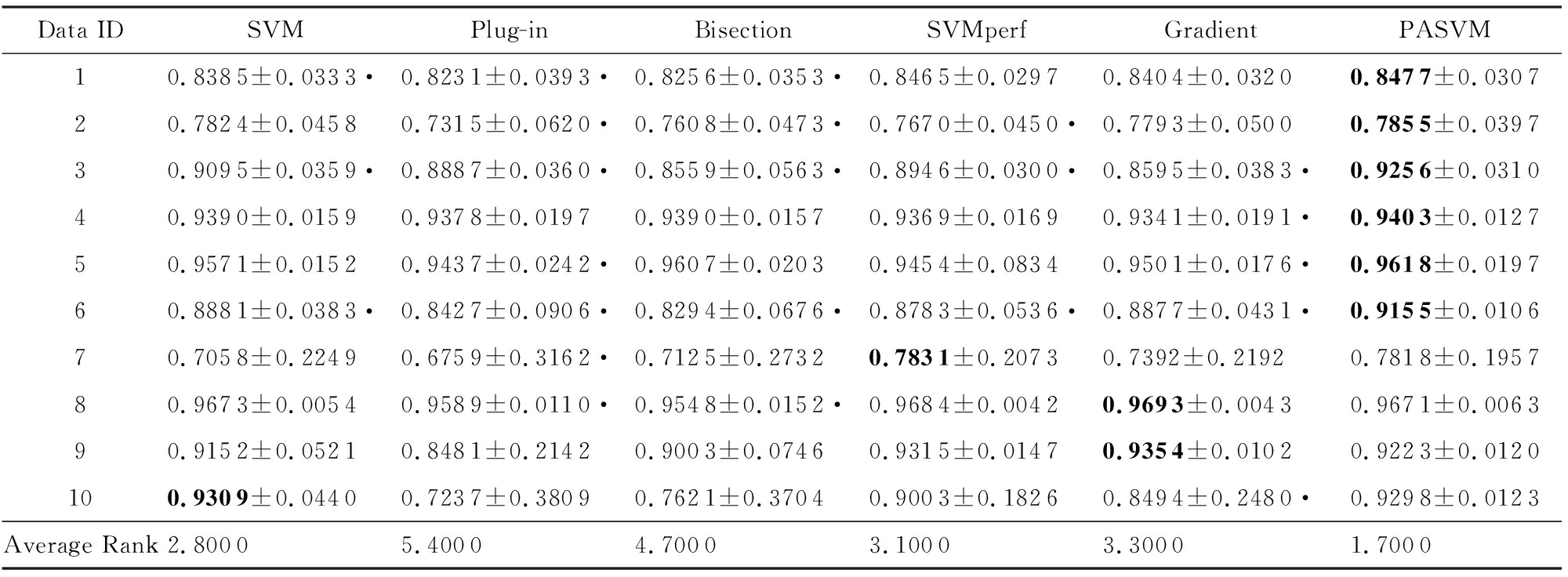
Data IDSVMPlug-inBisectionSVMperfGradientPASVM10.8385±0.0333·0.8231±0.0393·0.8256±0.0353·0.8465±0.02970.8404±0.03200.8477±0.030720.7824±0.04580.7315±0.0620·0.7608±0.0473·0.7670±0.0450·0.7793±0.05000.7855±0.039730.9095±0.0359·0.8887±0.0360·0.8559±0.0563·0.8946±0.0300·0.8595±0.0383·0.9256±0.031040.9390±0.01590.9378±0.01970.9390±0.01570.9369±0.01690.9341±0.0191·0.9403±0.012750.9571±0.01520.9437±0.0242·0.9607±0.02030.9454±0.08340.9501±0.0176·0.9618±0.019760.8881±0.0383·0.8427±0.0906·0.8294±0.0676·0.8783±0.0536·0.8877±0.0431·0.9155±0.010670.7058±0.22490.6759±0.3162·0.7125±0.27320.7831±0.20730.7392±0.21920.7818±0.195780.9673±0.00540.9589±0.0110·0.9548±0.0152·0.9684±0.00420.9693±0.00430.9671±0.006390.9152±0.05210.8481±0.21420.9003±0.07460.9315±0.01470.9354±0.01020.9223±0.0120100.9309±0.04400.7237±0.38090.7621±0.37040.9003±0.18260.8494±0.2480·0.9298±0.0123Average Rank2.80005.40004.70003.10003.30001.7000
Note: The best performance is in bold; “·” means the PASVM is significantly better than the corresponding method.
Table 5 Comparison of Accuracy on Data Sets with 5% Noise (Mean±Standard Deviation)
表5 噪音水平为5%时不同算法的准确度比较(均值±标准差)
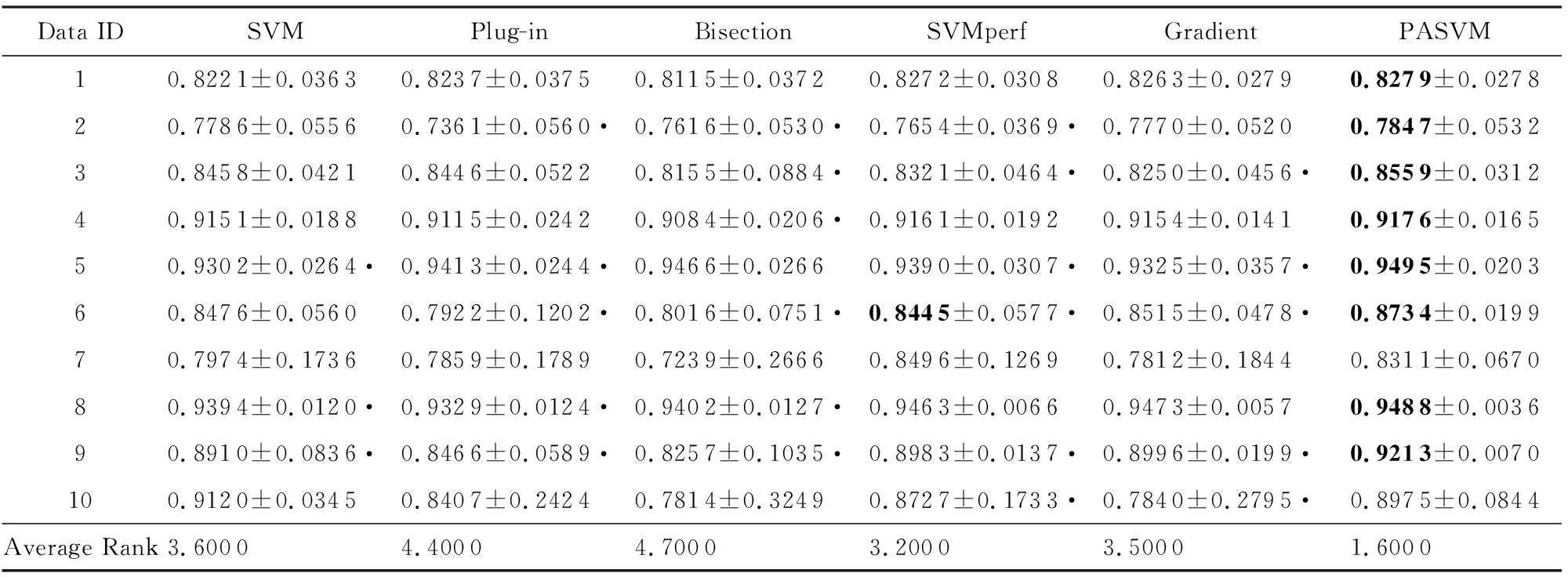
Data IDSVMPlug-inBisectionSVMperfGradientPASVM10.8221±0.03630.8237±0.03750.8115±0.03720.8272±0.03080.8263±0.02790.8279±0.027820.7786±0.05560.7361±0.0560·0.7616±0.0530·0.7654±0.0369·0.7770±0.05200.7847±0.053230.8458±0.04210.8446±0.05220.8155±0.0884·0.8321±0.0464·0.8250±0.0456·0.8559±0.031240.9151±0.01880.9115±0.02420.9084±0.0206·0.9161±0.01920.9154±0.01410.9176±0.016550.9302±0.0264·0.9413±0.0244·0.9466±0.02660.9390±0.0307·0.9325±0.0357·0.9495±0.020360.8476±0.05600.7922±0.1202·0.8016±0.0751·0.8445±0.0577·0.8515±0.0478·0.8734±0.019970.7974±0.17360.7859±0.17890.7239±0.26660.8496±0.12690.7812±0.18440.8311±0.067080.9394±0.0120·0.9329±0.0124·0.9402±0.0127·0.9463±0.00660.9473±0.00570.9488±0.003690.8910±0.0836·0.8466±0.0589·0.8257±0.1035·0.8983±0.0137·0.8996±0.0199·0.9213±0.0070100.9120±0.03450.8407±0.24240.7814±0.32490.8727±0.1733·0.7840±0.2795·0.8975±0.0844Average Rank3.60004.40004.70003.20003.50001.6000
Note: The best performance is in bold; “·” means the PASVM is significantly better than the corresponding method.
Table 6 Comparison of Pure Accuracy on Data Sets with 0% Noise (Mean±Standard Deviation)
表6 无噪音时不同算法的纯准确度比较 (均值±标准差)

Data IDSVMPlug-inBisectionSVMperfGradientPASVM10.7311±0.04120.7120±0.0392·0.7190±0.0465·0.7294±0.0281·0.7310±0.0318·0.7382±0.031620.6339±0.0665·0.5979±0.0959·0.6214±0.0624·0.6306±0.0899·0.6448±0.07210.6545±0.067930.8392±0.05790.8523±0.07160.8414±0.07650.8406±0.08080.8406±0.08080.8583±0.051240.9186±0.08080.9384±0.03040.9363±0.02800.9355±0.02680.9340±0.03010.9414±0.027150.9418±0.0924·0.9480±0.0910·0.6886±0.2576·0.9875±0.0424·0.9937±0.03061.0000±0.000060.1858±0.09720.1823±0.11050.1765±0.10040.1972±0.11240.1939±0.11910.2037±0.137970.0438±0.08790.0636±0.11070.0626±0.05030.0665±0.12050.0541±0.10310.0681±0.154280.9913±0.0337·0.9580±0.0778·0.7729±0.1284·1.0000±0.00001.0000±0.00001.0000±0.000090.1532±0.18370.0972±0.1079·0.1033±0.16220.1651±0.16910.1535±0.17470.1713±0.1877100.6602±0.28110.2970±0.3093·0.5245±0.2865·0.6750±0.19180.6583±0.23070.6276±0.2895Average Rank4.20004.50004.80002.70003.30001.5000
Note: The best performance is in bold; “·” means the PASVM is significantly better than the corresponding method.
Table 7 Comparison of Pure Accuracy on Data Sets with 3% Noise (Mean±Standard Deviation)
表7 噪音水平为3%时不同算法的纯准确度比较(均值±标准差)
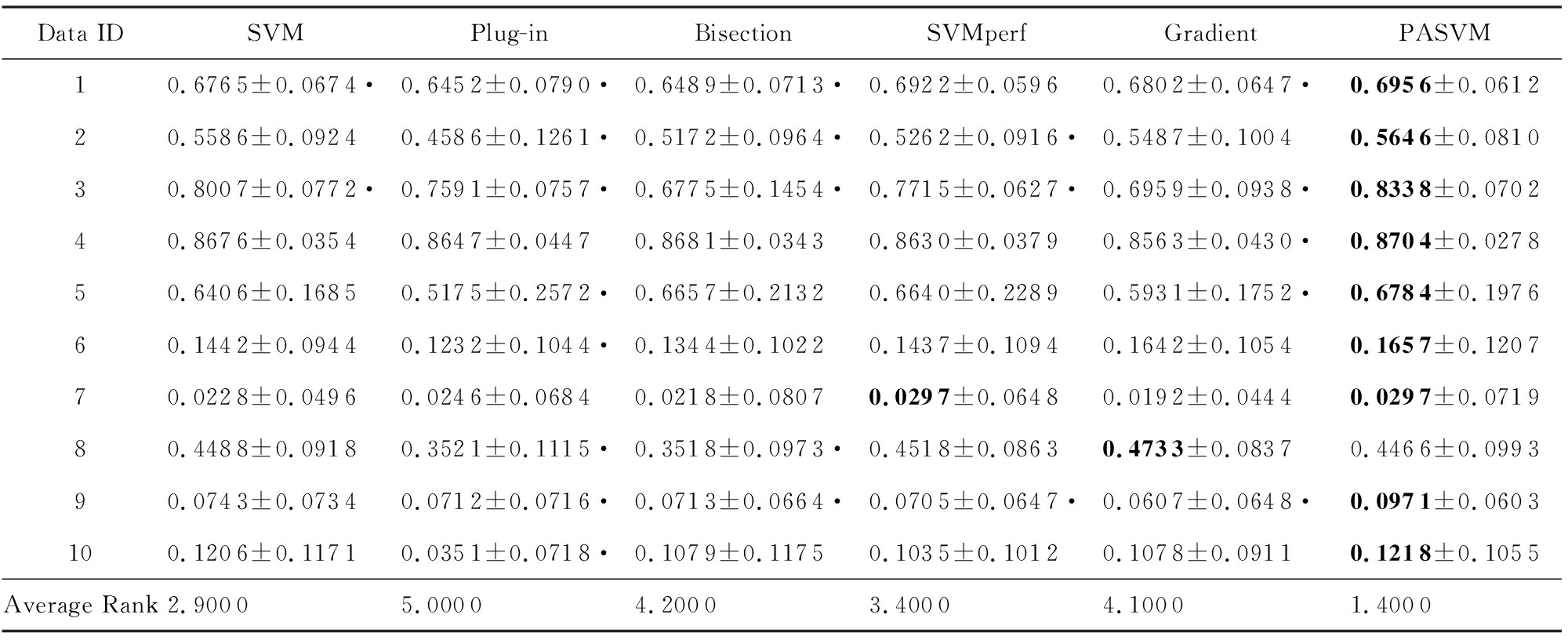
Data IDSVMPlug-inBisectionSVMperfGradientPASVM10.6765±0.0674·0.6452±0.0790·0.6489±0.0713·0.6922±0.05960.6802±0.0647·0.6956±0.061220.5586±0.09240.4586±0.1261·0.5172±0.0964·0.5262±0.0916·0.5487±0.10040.5646±0.081030.8007±0.0772·0.7591±0.0757·0.6775±0.1454·0.7715±0.0627·0.6959±0.0938·0.8338±0.070240.8676±0.03540.8647±0.04470.8681±0.03430.8630±0.03790.8563±0.0430·0.8704±0.027850.6406±0.16850.5175±0.2572·0.6657±0.21320.6640±0.22890.5931±0.1752·0.6784±0.197660.1442±0.09440.1232±0.1044·0.1344±0.10220.1437±0.10940.1642±0.10540.1657±0.120770.0228±0.04960.0246±0.06840.0218±0.08070.0297±0.06480.0192±0.04440.0297±0.071980.4488±0.09180.3521±0.1115·0.3518±0.0973·0.4518±0.08630.4733±0.08370.4466±0.099390.0743±0.07340.0712±0.0716·0.0713±0.0664·0.0705±0.0647·0.0607±0.0648·0.0971±0.0603100.1206±0.11710.0351±0.0718·0.1079±0.11750.1035±0.10120.1078±0.09110.1218±0.1055Average Rank2.90005.00004.20003.40004.10001.4000
Note: The best performance is in bold; “·” means the PASVM is significantly better than the corresponding method.
Table 8 Comparison of Pure Accuracy on Data Sets with 5% Noise (Mean±Standard Deviation)
表8 噪音水平为5%时不同算法的纯准确度比较(均值±标准差)

Data IDSVMPlug-inBisectionSVMperfGradientPASVM10.6429±0.07310.6449±0.07490.6188±0.0776·0.6529±0.06190.6513±0.05620.6555±0.055320.5475±0.11410.4652±0.1131·0.5167±0.1085·0.5247±0.0719·0.5442±0.10420.5611±0.111230.6642±0.09590.6683±0.10950.6025±0.1730·0.6392±0.1056·0.6332±0.1051·0.6908±0.063240.8170±0.04090.8091±0.05480.8023±0.0452·0.8204±0.04050.8173±0.03020.8221±0.035650.5180±0.1547·0.5861±0.18500.6351±0.18560.5997±0.18310.5589±0.1827·0.6376±0.164260.0580±0.0793·0.0359±0.0623·0.0806±0.06490.0446±0.06910.0501±0.0767·0.0837±0.092670.0138±0.0618·0.0650±0.09800.0340±0.0710·0.0261±0.0791·0.0342±0.0775·0.0678±0.088680.2367±0.0561·0.2678±0.0780·0.2825±0.0658·0.2633±0.0678·0.2936±0.0719·0.3226±0.078290.0307±0.04420.0864±0.06110.0813±0.05280.0181±0.0478·0.0274±0.05890.0414±0.0615100.0875±0.07210.0764±0.0860·0.0957±0.07100.0972±0.05380.0833±0.06130.1076±0.0725Average Rank4.10004.00004.30003.80003.60001.2000
Note: The best performance is in bold; “·” means the PASVM is significantly better than the corresponding method.
表3~8的数据表明,整体而言,PASVM取得了较高的准确度和纯准确度值.相较于其他优化准确度的方法,PASVM能够更好地优化纯准确度.
为进一步分析表3~8的实验结果,在95%置信水平下统计每种方法比其他方法统计性好的次数与统计性差的次数之间的差值.具体地,对于数据集的集合S,算法a比算法a′统计性好的次数为
(31)
算法a比算法a′统计性差的次数为
(32)
其中,![]() t为实验次数,μa,s和σa,s分别为算法a在数据集s上评分的平均值和标准差.
t为实验次数,μa,s和σa,s分别为算法a在数据集s上评分的平均值和标准差.
图5与图6展示了在准确度和纯准确度意义下,每种算法的Ba-Wa值.图5与图6显示,在不同噪音水平下,PASVM取得了较高的差值,这说明PASVM算法显著性好于其他算法.
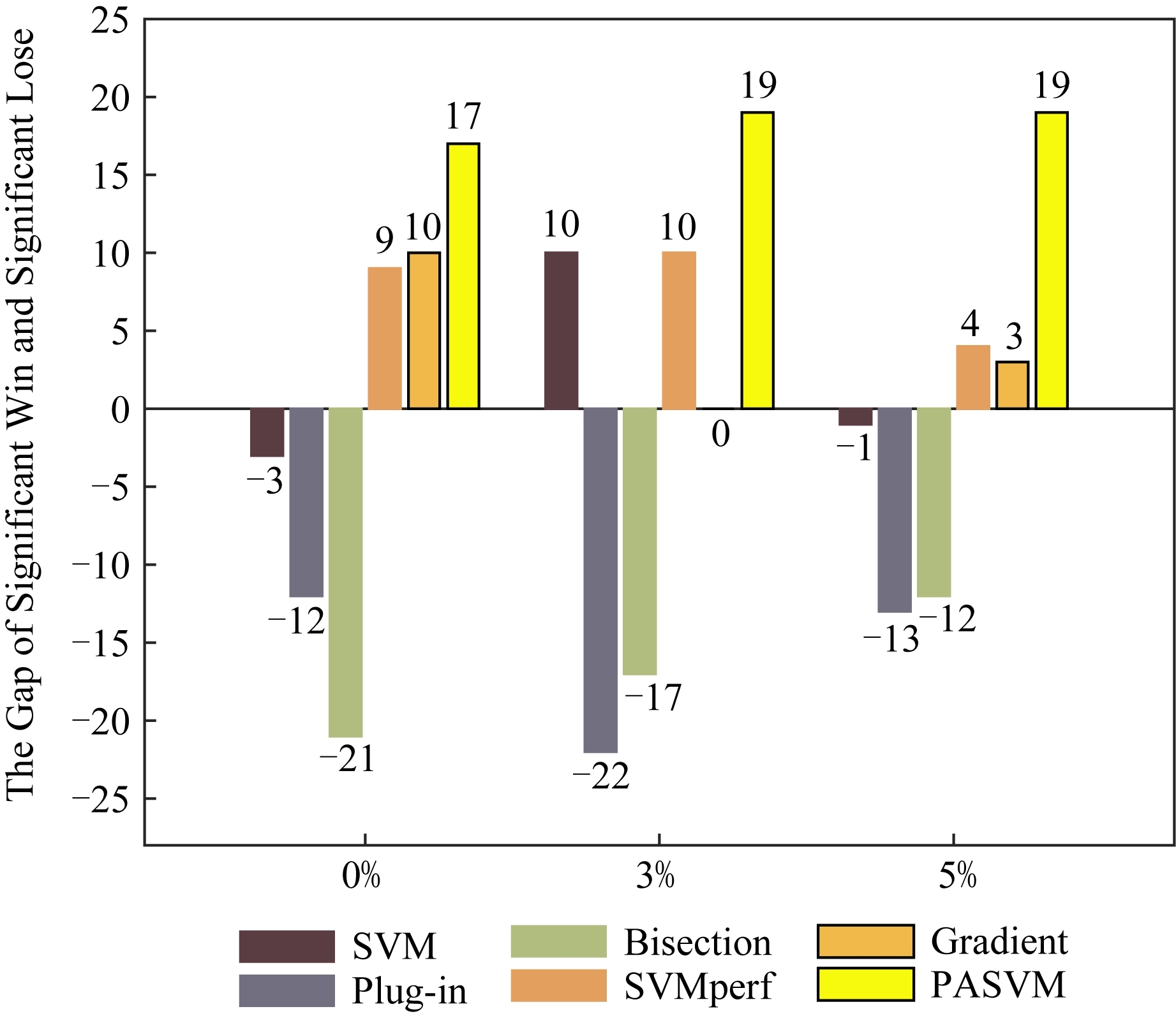
Fig. 5 Significant difference comparison of accuracy
图5 准确度显著性差异比较
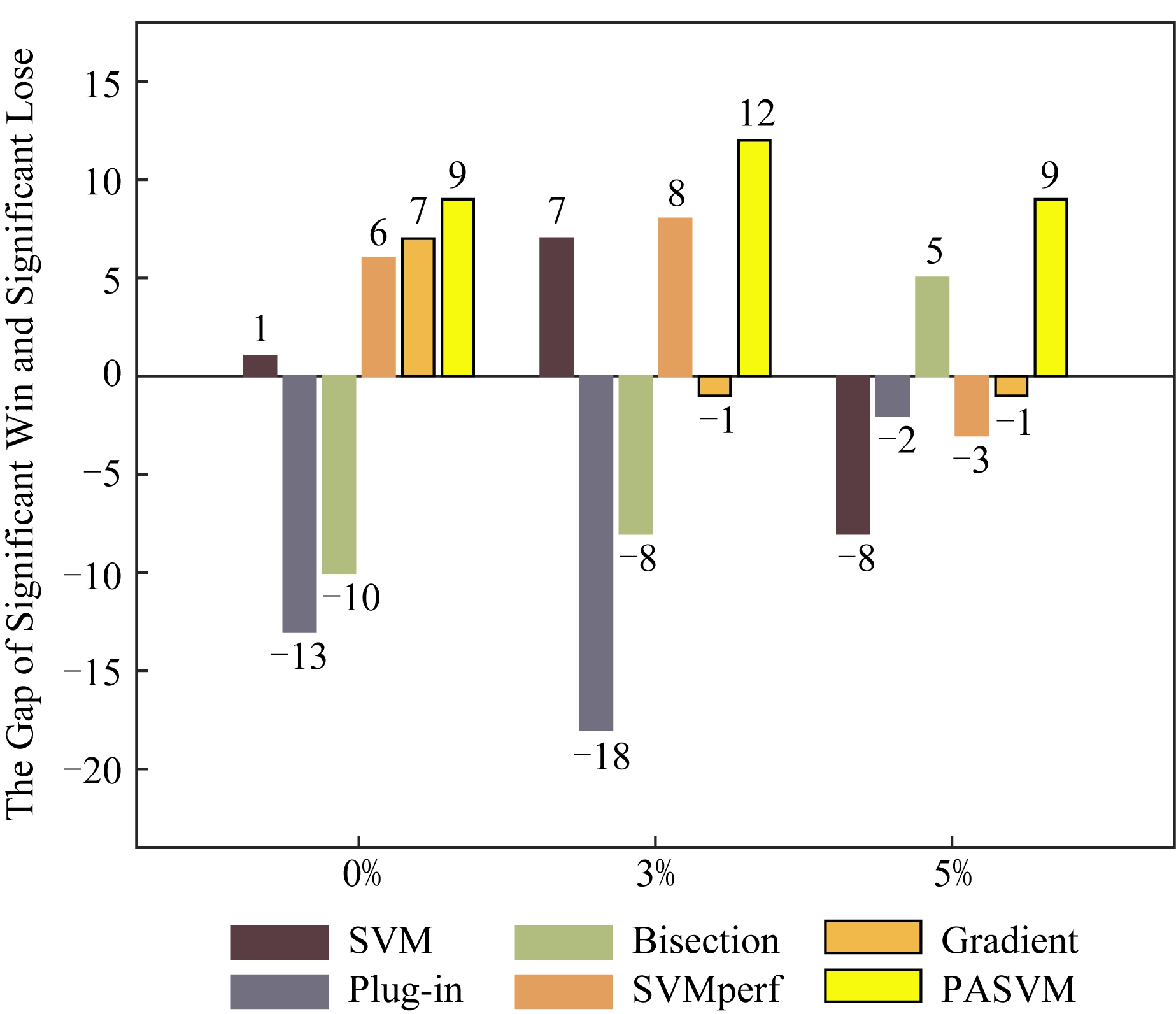
Fig. 6 Significant difference comparison of pure accuracy
图6 纯准确度显著性差异比较
接下来,对PASVM的参数进行分析.图7~9展示了不同噪音水平下,PASVM在验证集上的纯准确度值.可以看到,核函数参数对PASVM的影响比较大,不同数据集上不同核窗宽参数的最优值差异较大.同一核参数下,不同的折中参数得到的验证值基本保持在同一水平.
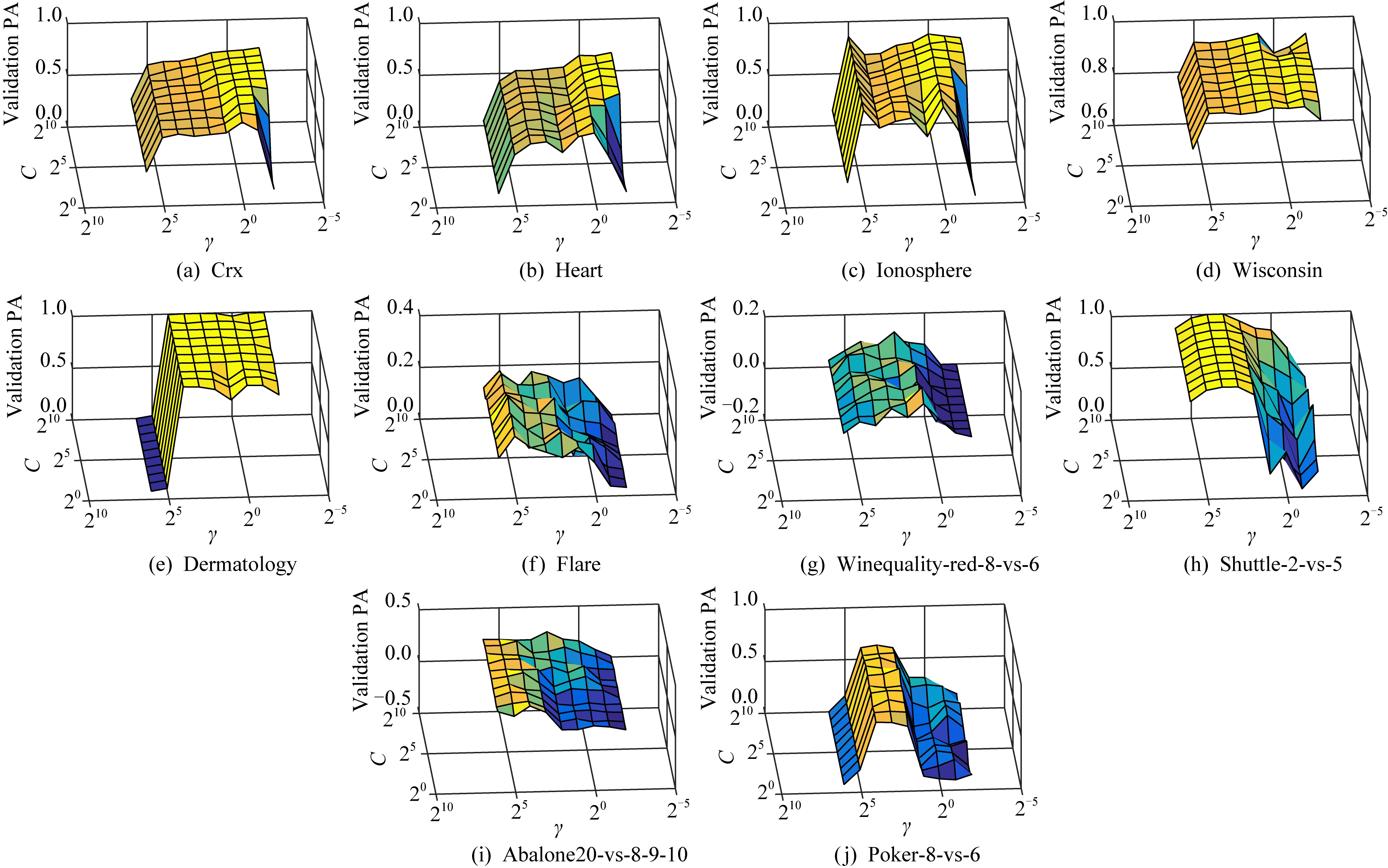
Fig. 7 The impact of parameters on validation sets with 0% noise
图7 无噪音时参数的影响
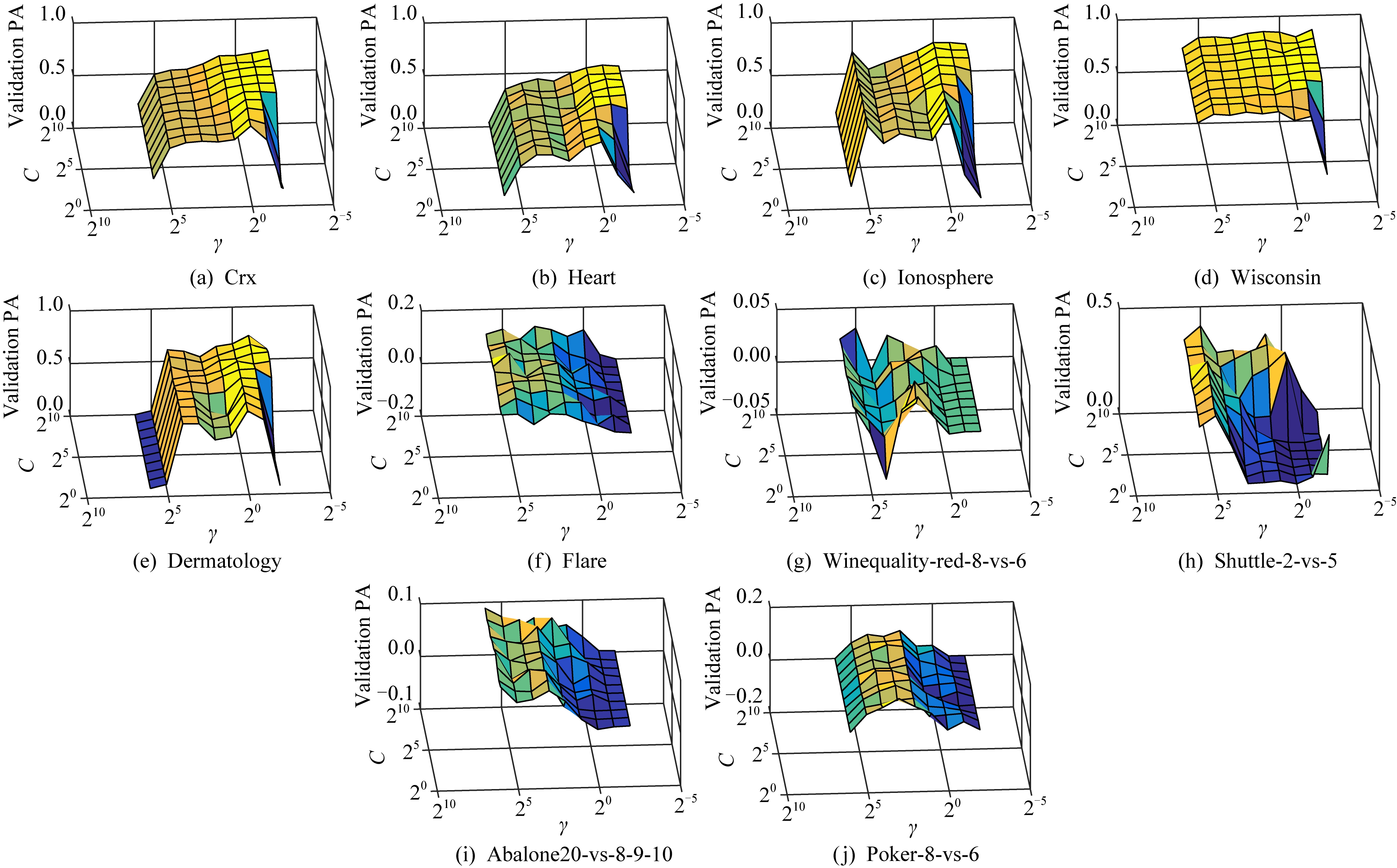
Fig. 8 The impact of parameters on validation sets with 3% noise
图8 噪音含量为3%时参数的影响
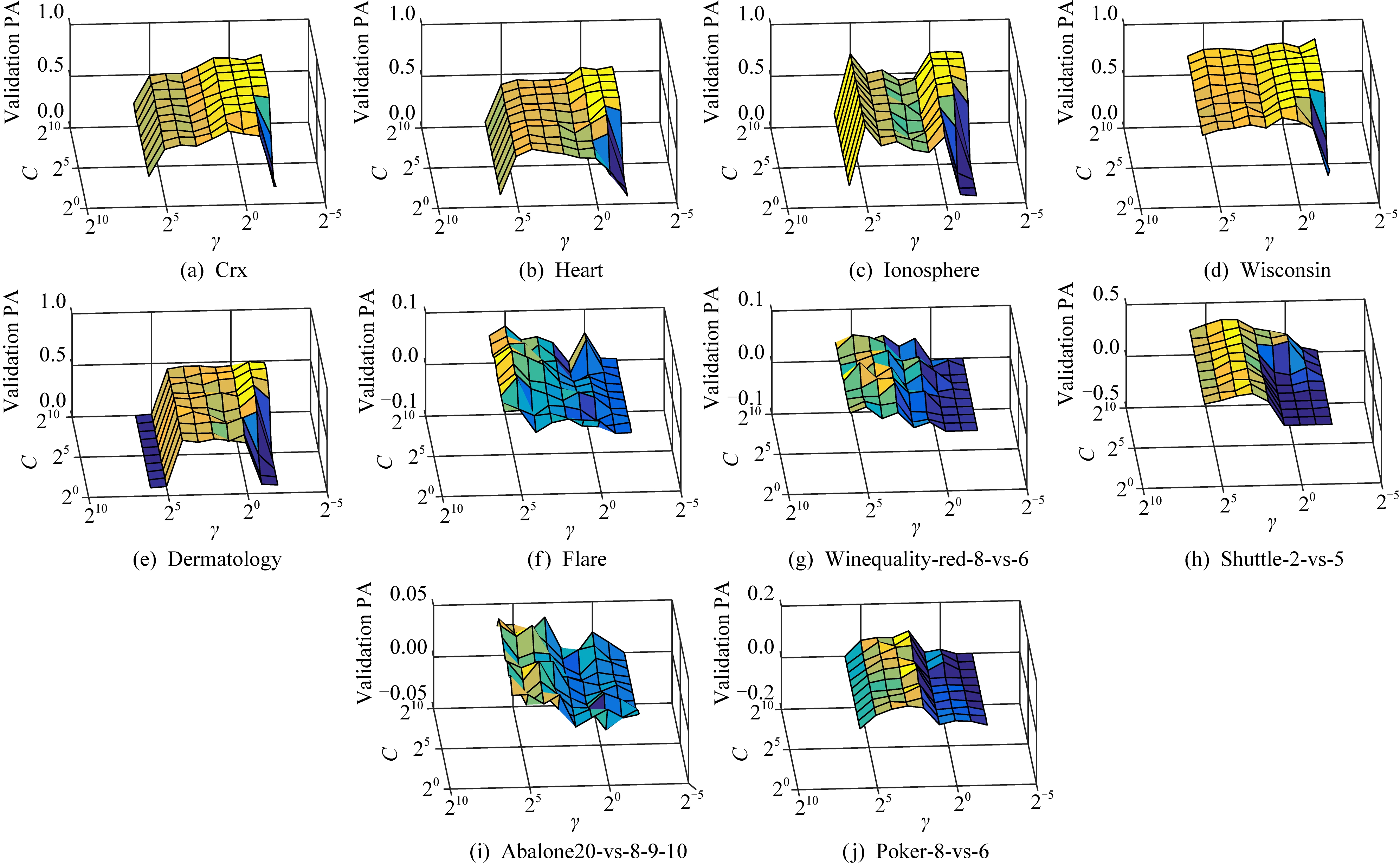
Fig. 9 The impact of parameters on validation sets with 5% noise
图9 噪音含量为5%时参数的影响
4 总 结
为了消除传统支持向量机中的随机一致性,本文给出了纯准确度的定义框架,提出了基于纯准确度的支持向量机模型PASVM.该方法不仅提升了传统SVM的性能,相比于其他优化纯准确度的方法,明显提升了纯准确度值.在未来的工作中,进一步考虑更具与普遍意义的置换划分集的分布来定义其他形式的随机准确度,这将有助于提高分类器对于其他类型的随机性的区分程度.另外,构建消除随机一致性的深度学习模型,以此进一步提高深度学习的性能,也是未来值得关注的研究方向.
[1]Ghahramani Z. Probabilistic machine learning and artificial intelligence[J]. Nature, 2015, 521(7553): 452-459
[2]Zhou Zhihua. Abductive learning: Towards bridging machine learning and logical reasoning[J]. Science China (Information Sciences), 2019, 62(7): No.076101
[3]Budescu D, Bar-Hillel M. To guess or not to guess: A decision-theoretic view of formula scoring[J]. Journal of Educational Measurement, 1993, 30(4): 277-291
[4]Li Feijiang, Qian Yuhua, Wang Jieting, et al. Clustering method based on sample’s stability[J]. Science China: Information Sciences, DOI: 10.1360/SSI-2019-0110 (in Chinese)
(李飞江, 钱宇华, 王婕婷, 等. 基于样本稳定性的聚类方法[J]. 中国科学: 信息科学, DOI: 10.1360/SSI-2019-0110)
[5]Li Feijiang, Qian Yuhua, Wang Jieting, et al. Clustering ensemble based on sample’s stability[J]. Artificial Intelligence, 2019, 273: 37-55
[6]Diamond J, Evans W. The correction for guessing[J]. Review of Educational Research, 1973, 43(2): 181-191
[7]Qian Yuhua, Li Feijiang Liang Jiye, et al. Space structure and clustering of categorical data[J]. IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(10): 2047-2059
[8]Li Feijiang, Qian Yuhua, Wang Jieting, et al. Cluster’s quality evaluation and selective clustering ensemble[J]. ACM Transactions on Knowledge Discovery from Data, 2018, 12(5): 1-27
[9]Zhu Jun, Hu Wenbo. Advances in bayesian machine learning[J]. Journal of Computer Research and Development, 2015, 52(1): 16-26 (in Chinese)
(朱军, 胡文波. 贝叶斯机器学习前沿进展综述[J]. 计算机研究与发展, 2015, 52(1): 16-26)
[10]Wang Jieting, Qian Yuhua, Li Feijiang, et al. Fusing fuzzy monotonic decision trees[J]. IEEE Transactions on Fuzzy Systems, 2020, 28(5): 887-900
[11]Zhang Chunxia, Zhang Jiangshe. A survey of selective ensemble learning algorithms[J]. Chinese Journal of Computers, 2011, 34(8): 1399-1410 (in Chinese)
(张春霞, 张讲社. 选择性集成学习算法综述[J]. 计算机学报, 2011, 34(8): 1399-1410)
[12]Zhou Zhihua. Machine Learning[M]. Beijing: Tsinghua University Press, 2016 (in Chinese)
(周志华. 机器学习[M]. 北京: 清华大学出版社, 2016)
[13]Peter B, Michael J, Jon M. Convexity, classification, and risk bounds[J]. Journal of the American Statistical Association, 2006, 101(473): 138-156
[14]Espinosa M, Gardeazabal J, Optimal correction for guessing in multiple-choice tests[J]. Journal of Mathematical Psychology, 2010, 54(5): 415-425
[15]Vinh N, Epps J, Bailey J. Information theoretic measures for clusterings comparison: Variants, properties, normalization and correction for chance[J]. Journal of Machine Learning Research, 2010, 11(95): 2837-2854
[16]Cohen J, A coefficient of agreement for nominal scales[J]. Educationaland Psychological Measurement, 1960, 20(1): 37-46
[17]Goodman L, Kruskal W. Measures of association for cross classifications[J]. Publications of the American Statistical Association, 1963, 49(268): 732-764
[18]Joachims T. A support vector method for multivariate performance measures[C] //Proc of the Int Conf on Machine learning. New York: ACM, 2005: 377-384
[19]Hazan T, Keshet J, Mcallester D. Direct loss minimization for structured prediction[C] //Proc of Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2010: 1594-1602
[20]Bernhard S, Alexander J. Learning with kernels: Support vector machines, regularization, optimization, and beyond[M]. Cambridge, MA: MIT Press, 2001: 25-60
[21]Freund R, Jarre F. Solving the sum-of-ratios problem by an interior-point method[J]. Journal of Global Optimization, 2001, 19(1): 83-102
[22]Narasimhan H, Ramaswamy H, Saha A, et al. Consistent multiclass algorithms for complex performance measures[C] //Proc of Int Conf on Machine Learning. New York: ACM, 2015: 2398-2407
[23]Alcalafdez J, Sanchez L, Garcia S, et al. KEEL: A software tool to assess evolutionary algorithms for data mining problems[J]. Soft Computing, 2008, 13(3): 307-318



