可达性查询是数据图上的基本操作之一,用于回答有向图中指定的2个顶点间是否存在有向路径,在过去一段时间得到了深入研究[1-16].可达性查询可用于社交网络、生物网络、语义网络、交通网络等检测指定的两点间是否存在某种特定联系,也可作为基本的原子操作,协助回答图上的结构化查询,如XQuery或者SPARQL(SPARQL protocol and RDF query language)表达式.随着实际应用中图规模不断增大和查询约束条件的增加,可达性查询的处理方法也需要支持更多的查询约束条件.例如,在实际的数据图中,每条边除了表示两点之间直接可达的关系外,还常常附带有表示关系特征的文本标签.用户在查询时除了关心两点之间是否可达外,可能想更进一步知道两点之间可达路径上的文本标签是否满足指定的标签约束[17-22].类似的查询有:从哈尔滨出发仅通过高速路是否能到达广州,用户A和用户B的联系是否与工程或者学术相关,用户A和用户B是否存在师生或者血缘上的关联等.这些问题被称为标签约束可达查询的处理问题.
为了回答标签约束的可达性查询,研究者提出了多种索引技术来加速查询响应的速度[17-22],其中最新工作是文献[21]提出的基于地标索引的方法.该方法选择k个地标点,然后建立2种索引:1)每个地标点的可达点及其最小路径标签集;2)非地标点的部分可达点及其路径标签集.查询处理时,如果索引可回答查询,则返回结果;否则需要通过图遍历操作得到结果.实际中,该方法建立的索引的可达信息覆盖率较低,需要执行昂贵的图遍历操作.
针对以上问题,本文首先提出一种基于部分点的双向路径标签索引方法,不仅显著提升可达信息的覆盖率,而且索引规模显著降低.该方法的提出基于以下观察:假设顶点v可达的顶点集是N,M是可达v的顶点集,则基于本文的方法,处理v记录的可达顶点对数量是|M|×|N|+|M|+|N|,而文献[21]构建的是单向索引,仅记录|N|个可达顶点对信息.基于本文的双向索引处理查询可显著减少图遍历的代价,提升系统性能.其次,本文提出一种基于标签集合包含关系的压缩优化策略,进一步减少索引规模.在此基础上,本文提出一种完全索引技术,用以记录所有顶点对的可达信息,从而在查询处理时完全避免图遍历操作.最后,基于真实数据集进行对比实验,实验结果证明了本文所提方法的高效性.
给定有向无环标签图![]() 表示G中的顶点集合,
表示G中的顶点集合,![]() 表示G中有向边的集合,
表示G中有向边的集合,![]() 表示G中边标签的集合,λ函数定义映射
表示G中边标签的集合,λ函数定义映射![]() 从顶点s到顶点t(s,t∈V)存在1条标签为l的有向边,将其记为(s,t,l)∈E.
从顶点s到顶点t(s,t∈V)存在1条标签为l的有向边,将其记为(s,t,l)∈E.
本文处理的是有向无环标签图,对于有环的情况,可通过借鉴文献[20]的方法进行处理,将其转换为无环图.一个有向无环图中的有向边体现了顶点间的可达偏序关系,通过拓扑排序可将顶点的偏序关系全序化,拓扑号即为全序关系的序号.拓扑排序过程中,对于每个被处理顶点s建立1个拓扑号X(s),则对图中任意从s到t的有向边(s,t)来说,有X(s)<X(t).根据可达的传递特性,对s可达的任意顶点t来说,同样存在X(s)<X(t).因此,若X(s)>X(t)成立,则s不可达t.
定义1. 路径标签.给定![]() 中的任意2个顶点(s,t∈V),假设从顶点s到顶点t有1条路径
中的任意2个顶点(s,t∈V),假设从顶点s到顶点t有1条路径![]() 则该路径上的标签可表示为
则该路径上的标签可表示为![]() 到t的路径标签集表示为L(s,t)={Lp|p为从s到t的路径}.
到t的路径标签集表示为L(s,t)={Lp|p为从s到t的路径}.
定义2. 标签约束可达查询.给定图G中的2个顶点s,t以及标签集L,标签约束可达查询就是确定从s到t是否存在有向路径p满足Lp⊆L,用s→Lt表示.如果s到t存在一条满足标签集L的路径,记作s→Lt,查询返回true,否则记作s![]() Lt,查询返回false.
Lt,查询返回false.
假设Lp={a1,a2,…,an},后续讨论中,为了简化表示,在上下文允许的情况下,本文以字符串的形式表示Lp,即Lp=a1a2…an.假设Lpi=a1a2…ai且Lpi⊆Lp,则该关系也可在上下文允许的情况下表示为a1a2…ai⊆a1a2…an.表1列出了本文经常使用的符号及其意义.
Table 1 The Symbols Used in This Paper and Description
表1 本文所用符号及其意义

SymbolsDescriptionG=(V,E,,λ)Labeled directed acyclic graphchildren(v)Outer node set of node vdin(v),dout(v)Indegree and outdegree of node vLpPath label of pL(u,v)Path label set from node u to node vinLabel(v)inLabel(v)={(u,L)|L=L(u,v)}outLabel(v)outLabel(v)={(w,L)|L=L(v,w)}X(v),Y(v)Two topological numbers of node v
1.2.1 无约束的可达性查询
该类查询主要用于判断从源点到目标点是否存在路径.在最新的研究中[14-16],文献[14]讨论了2hop label的并行构建策略,主要用于回答最短路径和一般无约束的可达查询.文献[15]讨论了大图上的近似可达查询处理问题,并提供了近似解决方案.文献[16]改进了2hop label以便加速时态图上的最快路径查询.以上文献均无法用来回答标签约束的可达查询,和本文方法没有可比性.
1.2.2 对点和边都进行标签约束的可达性查询
该类查询对路径上的点和边都进行约束,并且点和边具有多个标签,主要用于判断从源点到目标点是否存在路径,并且路径上所有点和边的标签都满足给定的标签约束.针对该类查询,文献[17]中提出在二级存储框架中开发,将图形拓扑存储在主存储中,标签信息存储在辅助存储中.Yung等人[17]提出一种基于散列映射的算法,其基本思想是利用“完美”散列函数将顶点和边的多个标签映射成散列值,并将散列值存储在主存储器中.查询时,从源点出发进行广度优先遍历(breadth first search, BFS) 深度优先遍历(depth first search, DFS),遍历的过程中验证散列值.对于可能存在散列冲突的顶点或边,则需访问辅助存储器中存储的标签,通过比对标签决定是否继续遍历该分支.最终筛选满足约束的点和边进行遍历,直至到达终点返回可达或者中途就停止了遍历返回不可达.
深度优先遍历(depth first search, DFS),遍历的过程中验证散列值.对于可能存在散列冲突的顶点或边,则需访问辅助存储器中存储的标签,通过比对标签决定是否继续遍历该分支.最终筛选满足约束的点和边进行遍历,直至到达终点返回可达或者中途就停止了遍历返回不可达.
1.2.3 仅对边进行标签约束的可达性查询
该类查询主要用于判断给定2个顶点是否存在有向路径,且路径中每条边的标签仅使用预定义标签集中的标签.针对该类查询,研究者们提出多种不同的解决方法,主要有4种:
1) 基于生成树索引方法
文献[19]提出一个基于树状结构的索引框架.首先定义了2个顶点间的最小路径标签集,然后利用有向最大权生成树算法和采样技术为图G生成一棵有向生成树T,同时对非树边建立一个包含标签集压缩的部分传递闭包NT.基于T,图中的所有路径被划分为3组Ps,Pe,Pn.Ps包含所有成对路径,其中第1条边是T的一部分;Pe包含所有成对路径,其中最后1条边是T的一部分;Pn包含所有成对路径,其中第1条和最后1条边都不在T中.NT(u,v)包含u和v之间的Pn中路径的所有路径标签.实际上,该方法是在无约束可达查询的树状索引基础上,增加了标签集约束实现的,因此该算法存在很多冗余路径并且具有树状索引对稠密图处理效率较低问题.
2) 基于二分图索引方法
文献[20]提出利用强连通分量(strong connected component, SCC)将图转换为二分图来实现标签约束可达性查询.首先将图G分解为强连通分量C1,C2,…,Ck,并计算每个Ci的局部传递闭包,即Ci中每个顶点到其他点的最短路径标签集.其次,用二分图Bi替代每个Ci,将其转化成带有标签的增强有向无环图(augmented directed acyclic graph, ADAG) Ga,d,a,并根据逆拓扑排序的顺序依次计算Ga,d,a中的每个顶点u的最短路径标签集.最后,计算每个u(u∈Ci,u∉Ga,d,a)的最短路径标签集.该方法得到的索引保存了图中每个顶点的完整可达性信息,即标签图的完全传递闭包.因此查询应答相当于索引中的简单查找,但索引构建时间过长,索引规模过大.
3) 基于地标点索引方法
文献[21]提出选择地标点建立索引,并维护其传递闭包中顶点可达信息的地标索引(landmark index, LI+)方法.具体来说,将图中顶点按出度与入度总和降序排列,并选择前k个点作为地标顶点.对于地标点,计算其到其他点的最小路径标签集,并利用辅助索引重新组织部分地标索引;对于非地标点,计算部分路径标签集.查询时,如果该条查询的源点是地标点,则查找地标索引进行回答,否则查找非地标索引.若也不能通过非地标点索引回答,则执行遍历,遍历过程中可以通过辅助索引进行剪枝.该方法的主要缺点是索引的可达信息覆盖率低,图遍历代价高.
4) 基于随机游走的采样算法
文献[22]基于随机游走的采样算法来回答具有全范围正则表达式约束的可达性查询,且可扩展到大图,但该算法提供的是非精确解的近似解决方案,和本文方法不具有可比性.
文献[21]通过构建k个地标点的单向可达索引来回答查询.假设顶点v可达的顶点集是N,则1个地标点对应的索引仅能回答v与|N|个点的可达关系.由于k值与图中顶点数量相比较小,通常情况下文献[21]提出的单向地标索引的可达信息覆盖率低,查询过程中不可避免需要执行大量昂贵的遍历操作.针对该问题,本文提出通过构建v的双向路径标签索引来提升索引的可达信息覆盖率.假设M是可达v的顶点集,则基于本文的方法,处理v记录的可达顶点对数量是|M|×|N|+|M|+|N|,其中M中的顶点通过v可达N中顶点,且可达顶点对数量为|M|×|N|,|M|表示M中顶点和v的可达顶点对数量,|N|表示v和N中顶点的可达顶点对数量.下面具体介绍该索引的构建方法.
2.1.1 基本思想
本文为每个点v设定2个标签,分别是inLabel(v)和outLabel(v).其中,inLabel(v)={(u,L)|L=L(u,v)},用于记录可达v的顶点及该顶点到达v的路径标签;outLabel(v)={(w,L)|L=L(v,w)},用于记录v可达的顶点及v到达该顶点的路径标签.给定查询s![]() Lt,可通过求解outLabel(s)和inLabel(t)的顶点交集来判断s是否可达t.如果交集为空,说明s不可达t;否则,需要进一步检测路径标签是否满足要求,具体检测方法是对于交集中的每个顶点v,将对应的路径标签进行合并,并判断合并的结果是否为L的子集.若是,则说明标签可达,否则还需进一步判断.
Lt,可通过求解outLabel(s)和inLabel(t)的顶点交集来判断s是否可达t.如果交集为空,说明s不可达t;否则,需要进一步检测路径标签是否满足要求,具体检测方法是对于交集中的每个顶点v,将对应的路径标签进行合并,并判断合并的结果是否为L的子集.若是,则说明标签可达,否则还需进一步判断.
例1. 针对图1,假设顶点的处理顺序是v2→v4→v3→v5→v1→v0,根据以上思路建立的索引如表2所示.显然,这种索引虽然可回答所有查询,但存在很多冗余路径,索引规模过大.例如,inLabel(v4)中同时包含(v0,c),(v0,ac),(v0,bc).当给定查询v0→bv5,outLabel(v0)与inLabel(v5)的交集为{v0,v1,v2,v3,v5},将交集顶点对应的标签取并集.对于顶点v0:∅∪ab=ab,∅∪ac=ac,∅∪abc=abc;对于顶点v1:c∪a=ac,c∪ab=abc;对于顶点v2:b∪a=ab,ac∪a=ac;对于顶点v3:ac∪b=abc;对于顶点v5:ab∪∅=ab,ac∪∅=ac,abc∪∅=abc.这些并集标签均不是查询给定约束标签b的子集,因此v0![]() bv5.显然,如果查询不可达,处理效率低.
bv5.显然,如果查询不可达,处理效率低.
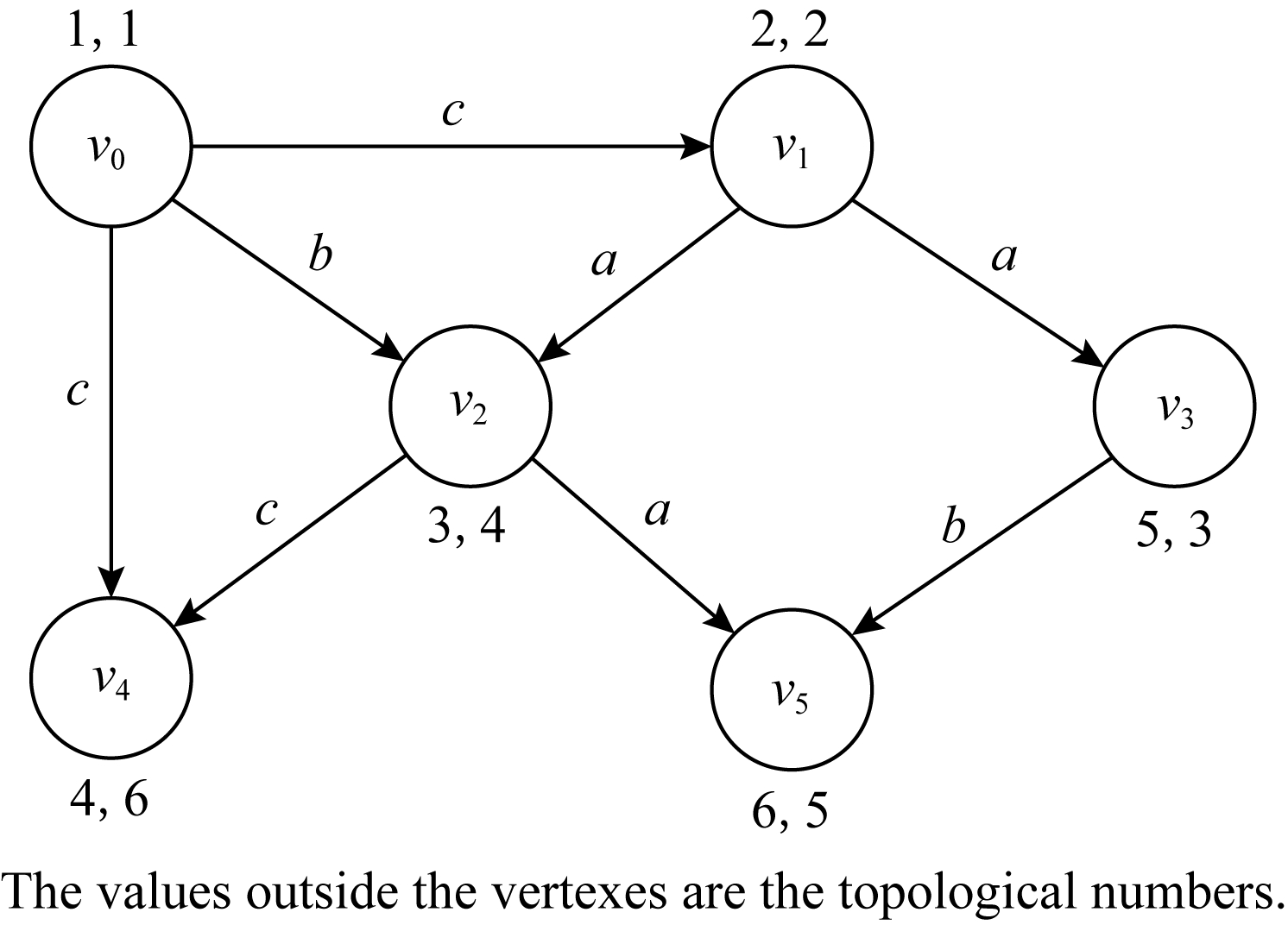
Fig. 1 Labeled DAG G
图1 有向无环标签图G
Table 2 The Initial Path Label Index for Fig. 1
表2 初始路径标签索引

NodeinLabeloutLabelv0{(v0,∅)}{(v0,∅),(v1,c),(v2,b),(v2,ac),(v3,ac),(v4,c),(v4,ac),(v4,bc),(v5,ab),(v5,ac),(v5,abc)}v1{(v0,c),(v1,∅)}{(v1,∅),(v2,a),(v3,a),(v4,ac),(v5,a),(v5,ab)}v2{(v0,b),(v0,ac),(v1,a),(v2,∅)}{(v2,∅),(v4,c),(v5,a)}v3{(v0,ac),(v1,a),(v3,∅)}{(v3,∅),(v5,b)}v4{(v0,c),(v0,ac),(v0,bc),(v1,ac),(v2,c),(v4,∅)}{(v4,∅)}v5{(v0,ab),(v0,ac),(v0,abc),(v1,a),(v1,ab),(v2,a),(v3,b),(v5,∅)}{(v5,∅)}
Note: (v,{Lp1,Lp2,…,Lpn}) is organized into {(v,Lp1),(v,Lp2),…,(v,Lpn)}.
针对以上问题,本文仅构建基于k个顶点的标签索引来减小索引规模,同时提出2种优化方法来降低索引规模.下面具体介绍.
定理1. 给定顶点v,在基于v建立标签索引的过程中,如果遇到已处理过的地标点u,则无需从u继续遍历.
证明. 首先,在处理u的过程中,已经记录了所有u到u可达顶点的路径标签以及可达u的顶点到u之间的路径标签.其次,在处理v时,如果遍历过程中遇到了u,一方面,在处理u时已经得到v和u之间路径的标签,另一方面,如图2所示,对u可达的任意顶点x,处理u时已经得到了两者之间的路径标签.处理v时,如果沿着u继续遍历到x,则得到的标签等价于u到x已经得到的标签与v到u之间路径标签的并集.由于这些信息已经具备,因此无需专门记录v到x的路径标签.
证毕.
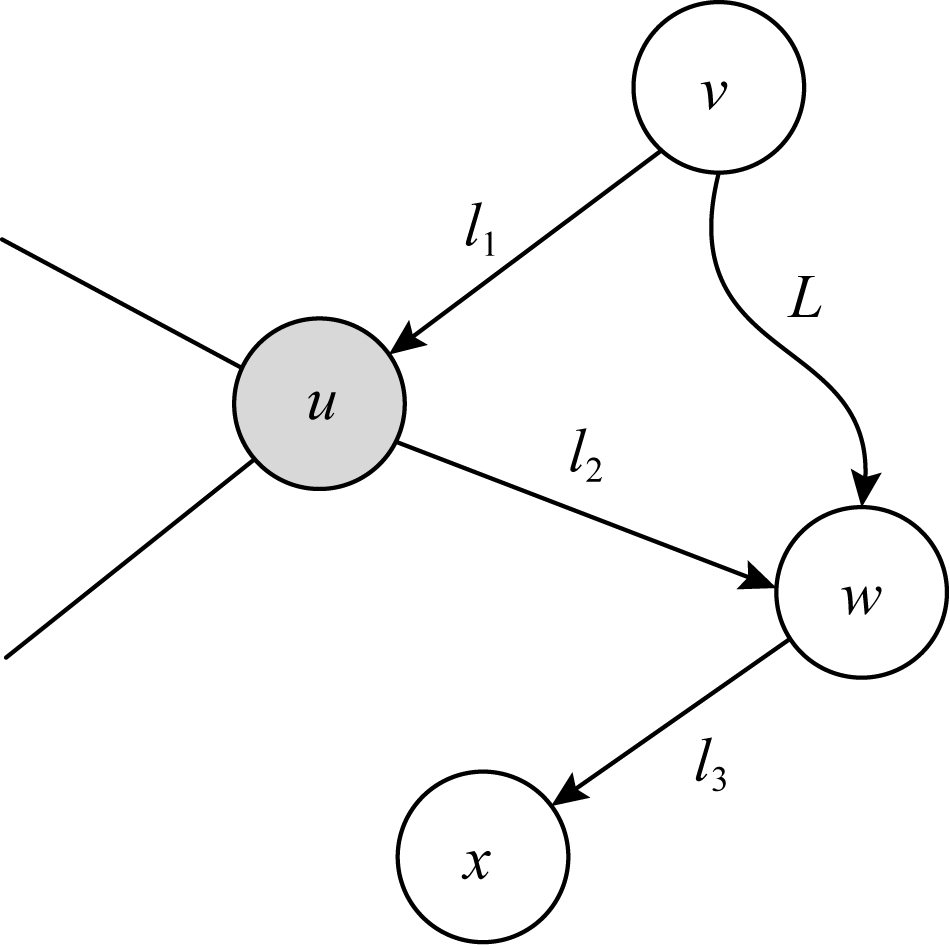
Fig. 2 Illustration of landmark nodes
图2 地标点作用示意图
定理2. 给定顶点v,在基于v建立标签索引的过程中,对于遍历到的顶点w满足:1)v可达w,路径标签是L1;2)v和w之间通过遍历非地标点得到的路径标签是L2.如果L2⊇L1,则无需从w出发继续遍历.
证明. 如图2所示,从v出发建立标签索引.当遍历到w时,发现v可达w,其路径标签是L1=l1∪l2,且v通过非地标点遍历到w的路径标签是L,如果L1⊆L成立,说明对于w之后遍历到的任一点x,v通过直接遍历得到的路径标签是L∪l3,而通过u计算得到的路径标签是L1∪l3,可知通过非地标点得到的标签始终是通过地标点的超集,因此无需从w继续遍历.
证毕.
针对图1,假设选择2个地标点v2和v1,处理顺序是先v2后v1,则基于上述2种优化方法构建的路径标签索引如表3所示.例如,处理完v2再处理v1时,通过BFS遍历到v2,由于v2已被处理过,由定理1可得,不更新索引且停止该条分支的遍历,并开始下一条分支的遍历.当BFS通过路径 v1,v3,v5
v1,v3,v5 遍历到v5时,其路径标签L
遍历到v5时,其路径标签L v1,v3,v5
v1,v3,v5 =ab.由已构建的索引可知,v1通过地标点v2可达v5,对应的路径标签为L
=ab.由已构建的索引可知,v1通过地标点v2可达v5,对应的路径标签为L v1,v2,v5
v1,v2,v5 =a.因为L
=a.因为L v1,v3,v5
v1,v3,v5 ⊇L
⊇L v1,v2,v5
v1,v2,v5 ,由定理2得,不更新索引且无需从v5继续遍历.
,由定理2得,不更新索引且无需从v5继续遍历.
Table 3 Optimized Path Label Index
表3 优化的路径标签索引

NodeinLabeloutLabelv0{(v1,c),(v2,b),(v2,ac)}v1{(v1,∅)}{(v1,∅),(v2,a)}v2{(v2,∅)}{(v2,∅)}v3{(v1,a)}v4{(v2,c)}v5{(v2,a)}
2.1.2 索引构建算法
算法1基于以上2个定理构建双向路径标签索引(bidirectional path label index, BPLI).

本文采用文献[23]中的策略,即按照(dout(v)+1)×(din(v)+1)递减的顺序对图中顶点排序,选择前k个地标点(行①).对每个地标点v,调用BiBFS(v)从正反2个方向进行遍历,分别建立被访问顶点的inLabel和outLabel(行②③).在基于地标点构建路径标签索引的过程中,同时应用定理1和定理2进行剪枝来减小索引规模.对于每个遍历到的点,函数isSuperset(s,t,L)用于根据定理2以及定理1判断是否还继续遍历该分支.
算法1的时间复杂度是O(|V|+|E|),空间复杂度是O(|V|).因为一个顶点进行BFS操作的最坏代价是O(|V|+|E|),而算法1仅仅处理了k个顶点(k是自定义的常数),因此,时间复杂度是O(|V|+|E|).此外,BFS操作需要借助一个辅助队列,总的大小为O(|V|),又每个顶点包含2个拓扑号,因此总的空间复杂度是O(|V|).
例2. 对于图1,根据(dout(v)+1)×(din(v)+1)对图中顶点降序排列,得到的顶点顺序为:v2→v1→v0→v3→v4→v5.假设选择2个地标点,则地标点的处理顺序是v2→v1.
1) 在处理v2时.初始化inLabel(v2)={(v2,∅)}和outLabel(v2)={(v2,∅)}.从v2出发执行BFS遍历到v4和v5,由于marked(v4)=0,需判断outLabel(v2)与inLabel(v4)是否存在顶点交集.发现outLabel(v2)与inLabel(v4)没有交集,因此将(v2,c)插入到inLabel(v4)中.同理,将(v2,a)插入到inLabel(v5)中.此时v2已没有出邻居,从v2出发执行反向BFS遍历到v0和v1.因为v0未被标记且outLabel(v0)与inLabel(v2)没有交集,将(v2,b)插入到outLabel(v0)中.同理,将(v2,a)插入到outLabel(v1)中.继续反向BFS遍历到v0,由已构建的outLabel(v0)和inLabel(v2)可得L v0,v2
v0,v2 =b,而遍历路径
=b,而遍历路径 v2,v1,v0
v2,v1,v0 的标签为L
的标签为L v2,v1,v0
v2,v1,v0 =ac.根据集合关系将(v2,ac)插入到outLabel(v0)中.至此,v2正反2个方向的遍历结束,将其标记为marked(v2)=1.
=ac.根据集合关系将(v2,ac)插入到outLabel(v0)中.至此,v2正反2个方向的遍历结束,将其标记为marked(v2)=1.
2) 在处理v1时.从v1出发执行BFS遍历到v2,由于v2已被标记过,由定理1得,不更新索引并停止该分支的遍历,开始下一分支的遍历,即遍历到v3.因为outLabel(v1)和inLabel(v3)没有交集,将(v1,a)插入到inLabel(v3)中.继续执行BFS遍历,经过路径 v1,v3,v5
v1,v3,v5 遍历到v5,对应的路径标签L
遍历到v5,对应的路径标签L v1,v3,v5
v1,v3,v5 =ab,由已构建的索引知outLabel(v1)与inLabel(v5)的顶点交集为v2,对应的标签取并集可得L
=ab,由已构建的索引知outLabel(v1)与inLabel(v5)的顶点交集为v2,对应的标签取并集可得L v1,v2,v5
v1,v2,v5 =a.又L
=a.又L v1,v3,v5
v1,v3,v5 ⊇L
⊇L v1,v2,v5
v1,v2,v5 ,由定理2得,不更新索引且无需从v5继续遍历.接下来,从v1出发执行反向BFS遍历到v0,因为v0未被标记且outLabel(v0)与inLabel(v1)没有交集,将(v1,c)插入到outLabel(v0)中.至此,v1正反2个方向的遍历结束并标记marked(v1)=1.因此,针对图1建立的索引如表3所示.
,由定理2得,不更新索引且无需从v5继续遍历.接下来,从v1出发执行反向BFS遍历到v0,因为v0未被标记且outLabel(v0)与inLabel(v1)没有交集,将(v1,c)插入到outLabel(v0)中.至此,v1正反2个方向的遍历结束并标记marked(v1)=1.因此,针对图1建立的索引如表3所示.
给定查询s→Lt,可通过求解outLabel(s)和inLabel(t)的交集来判断s是否可达t.如果交集为空,说明s通过地标点不可达t,需要进行遍历判断是否可达;如果交集不为空,说明s可达t,需要进一步检测路径标签是否满足要求,具体检测方法是对于交集中的每个点v,将L(s,v)与L(v,t)进行合并,判断合并的结果是否是L的子集.若是,则说明标签可达,否则需要进行遍历.
例如,当给定查询v1→abcv5时,outLabel(v1)与inLabel(v5)的顶点交集为v2,对应的路径标签L v1,v2,v5
v1,v2,v5 =a⊆abc,所以v1→abcv5.当给定查询v3→acv4时,outLabel(v3)与inLabel(v4)没有交集,不能直接通过索引判断,需要执行遍历得出v3
=a⊆abc,所以v1→abcv5.当给定查询v3→acv4时,outLabel(v3)与inLabel(v4)没有交集,不能直接通过索引判断,需要执行遍历得出v3![]() acv4.
acv4.
可以看出,基于部分地标点构建的路径索引不能高效处理不可达查询,为此本文进一步利用文献[13]中提出的基于栈的互逆拓扑顺序方法来快速处理不可达查询.简而言之,得出拓扑顺序X后,在构建逆序拓扑顺序Y时,始终优先访问拓扑顺序X中拓扑号最大且所有入邻居均被访问的顶点.具体操作步骤见文献[13],此处不再赘述.
由文献[13]可知,求解2个互逆拓扑顺序的时间代价为O(|V|+|E|),且后文中索引大小包含了拓扑号的存储开销.

给定查询s→Lt时,首先利用2个拓扑序号X和Y过滤不可达的查询.如果X(s)>X(t)或Y(s)>Y(t),那么s![]() t(行⑦~⑨);否则,根据双向路径标签索引来判断标签是否满足约束(行⑩~
t(行⑦~⑨);否则,根据双向路径标签索引来判断标签是否满足约束(行⑩~ ).如果不能通过索引判断则需要遍历,并在遍历的过程中根据拓扑序号及标签做进一步判断(行
).如果不能通过索引判断则需要遍历,并在遍历的过程中根据拓扑序号及标签做进一步判断(行 ~
~ ).具体的查询处理过程如算法2所示.
).具体的查询处理过程如算法2所示.
例3. 根据文献[13]中提出的基于栈的互逆拓扑顺序方法,为图1中每个顶点建立2个拓扑序号,如顶点旁的数字所示.其中,左边数字代表X,右边数字代表Y.给定查询v3→bcv2时,X(v3)>X(v2),即v3![]() v2,则v3
v2,则v3![]() bcv2.给定查询v1→acdv5时,X(v1)<X(v5),Y(v1)<Y(v5),则v1不一定可达v5;又因为outLabel(v1)与inLabel(v5)的交集为v2,对应的标签取并集得L
bcv2.给定查询v1→acdv5时,X(v1)<X(v5),Y(v1)<Y(v5),则v1不一定可达v5;又因为outLabel(v1)与inLabel(v5)的交集为v2,对应的标签取并集得L v1,v2,v5
v1,v2,v5 =a⊆acd,所以v1→acdv5.
=a⊆acd,所以v1→acdv5.
由于算法1选择k个顶点建立索引,对某些数据集而言,可能存在索引覆盖率低的问题,并且当索引判断不了时还需要执行遍历操作.基于第2节给出的定理1和定理2,本文进一步提出对所有点建立双向路径标签索引.由于这种索引可用于回答不可达查询,因此基于所有点建立路径标签索引时,不再需要拓扑序号进行过滤,且无需执行图上的遍历操作.
基于第2节构建路径标签的思路为所有点构建的路径标签索引如表4所示.查询算法如算法3所示.
Table 4 Path Label Index for All Nodes
表4 所有点的路径标签索引

NodeinLabeloutLabelv0{(v0,∅)}{(v0,∅),(v1,c)(v2,b),(v2,ac)}v1{(v1,∅)}{(v1,∅),(v2,a)}v2{(v2,∅)}{(v2,∅)}v3{(v1,a),(v3,∅)}{(v3,∅)}v4{(v0,c),(v2,c),(v4,∅)}{(v4,∅)}v5{(v2,a),(v3,b),(v5,∅)}{(v5,∅)}
该方法的时间复杂度为O(|V|×(|V|+|E|)×|Lmax|),空间复杂度为O(|V|×|Lmax|),这里|Lmax|表示所有顶点中最长的标签长度.虽然看起来时间复杂度较高,但实验结果显示,由于剪枝技术的有效性,索引时间比现有方法更快.

本文实验所用机器的基本配置为Intel® CoreTMi5-6600 CPU@3.30 GHz,4 GB内存,1 TB硬盘,操作系统为Linux Ubuntu 16.04.用于比较的算法包括基于遍历的BFS算法、LI+算法[21]以及本文提出的2种算法.所有算法均采用C++语言实现,通过G++7.3.0编译器进行编译.所有算法的源代码由本文作者实现.
本文所用数据集为23个真实数据集,相关统计信息如表5所示.其中,d表示平均出度,约定d≥4时为稠密图,|V|≥100 000时为大图.
Table 5 The Information of Dataset Statistics
表5 数据集统计信息
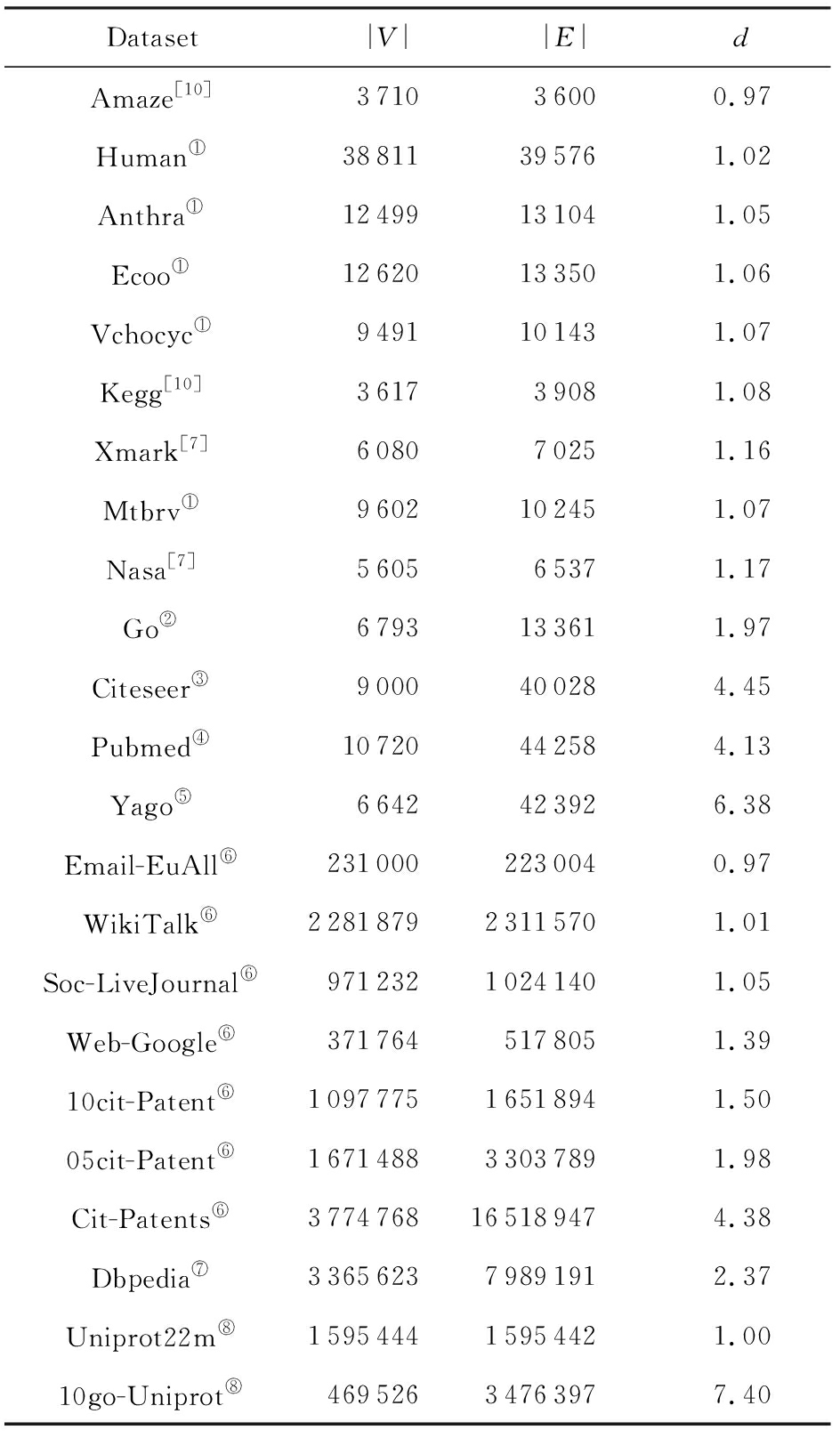
Dataset|V||E|dAmaze[10]371036000.97Human①38811395761.02Anthra①12499131041.05Ecoo①12620133501.06Vchocyc①9491101431.07Kegg[10]361739081.08Xmark[7]608070251.16Mtbrv①9602102451.07Nasa[7]560565371.17Go②6793133611.97Citeseer③9000400284.45Pubmed④10720442584.13Yago⑤6642423926.38Email-EuAll⑥2310002230040.97WikiTalk⑥228187923115701.01Soc-LiveJournal⑥97123210241401.05Web-Google⑥3717645178051.3910cit-Patent⑥109777516518941.5005cit-Patent⑥167148833037891.98Cit-Patents⑥3774768165189474.38Dbpedia⑦336562379891912.37Uniprot22m⑧159544415954421.0010go-Uniprot⑧46952634763977.40
① ecocyc.org ② www.geneontology.org ③ citeseerx.ist.psu.edu ④ pubmedcentral.nih.gov ⑤ mpi-inf.mpg.de/yago-naga/yago ⑥ snap.stanford.edu ⑦ pubmedcentral.nih.gov ⑧ www.uniprot.org
为了比较不同算法对标签可达查询处理的整体性能,本文生成100万个可达查询和100万个不可达查询来进行测试,并且|L|≤8.
针对上述的查询集,所有的运行时间都是执行10次100万个查询的总时间取平均值.所有结果均保留到小数点后2位.本文实验的评估指标包括:
1) 索引构建时间;
2) 索引大小;
3) 查询时间.
实验中,BPLI算法的参数k=32,LI+算法的参数![]() 该值为文献[21]建议的参数值.
该值为文献[21]建议的参数值.
4.4.1 索引构建时间
图3比较了不同规模数据集上的索引构建时间.从图3可以看出,在索引构建时间方面,BPLI和BPLI+优于LI+.对于规模较小的图,如Kegg数据集,BPLI比LI+快1372倍,BPLI+比LI+快891倍.在Pubmed数据集上,BPLI比LI+快21.6倍,BPLI+比LI+快4.4倍.在规模较大的图上,如Email-EuAll数据集,BPLI比LI+快1042倍,BPLI+比LI+快623倍.在Cit-Patents数据集上,BPLI比LI+快111倍,BPLI+比LI+快46倍.原因在于,LI+除了构建地标点的所有单向索引和非地标点的部分单向索引外,还需要根据路径标签对地标点的索引进行重新组织,因此会耗费大量时间.
4.4.2 索引大小
图4展示了不同规模数据集上的索引大小比较.可以看出,由于稀疏小图中LI+索引的地标点个数几乎是顶点个数的一半,构建地标索引的传递闭包较大,如数据集Amaze的索引大小是本文方法的200多倍.对于大图来说,BPLI仅选择了32个顶点建立索引,而LI+中选择了![]() 个地标点建立索引外还建立了非地标点的部分索引,因此,BPLI的索引比LI+小.而BPLI+对图中的每个顶点都进行了剪枝操作,在小图上的索引规模比LI+小.在大图上,BPLI+构建的是所有顶点的路径标签索引,但基于定理1和定理2进行了优化,总的索引规模增长并不明显,甚至在某些数据集上,索引规模远小于LI+.
个地标点建立索引外还建立了非地标点的部分索引,因此,BPLI的索引比LI+小.而BPLI+对图中的每个顶点都进行了剪枝操作,在小图上的索引规模比LI+小.在大图上,BPLI+构建的是所有顶点的路径标签索引,但基于定理1和定理2进行了优化,总的索引规模增长并不明显,甚至在某些数据集上,索引规模远小于LI+.
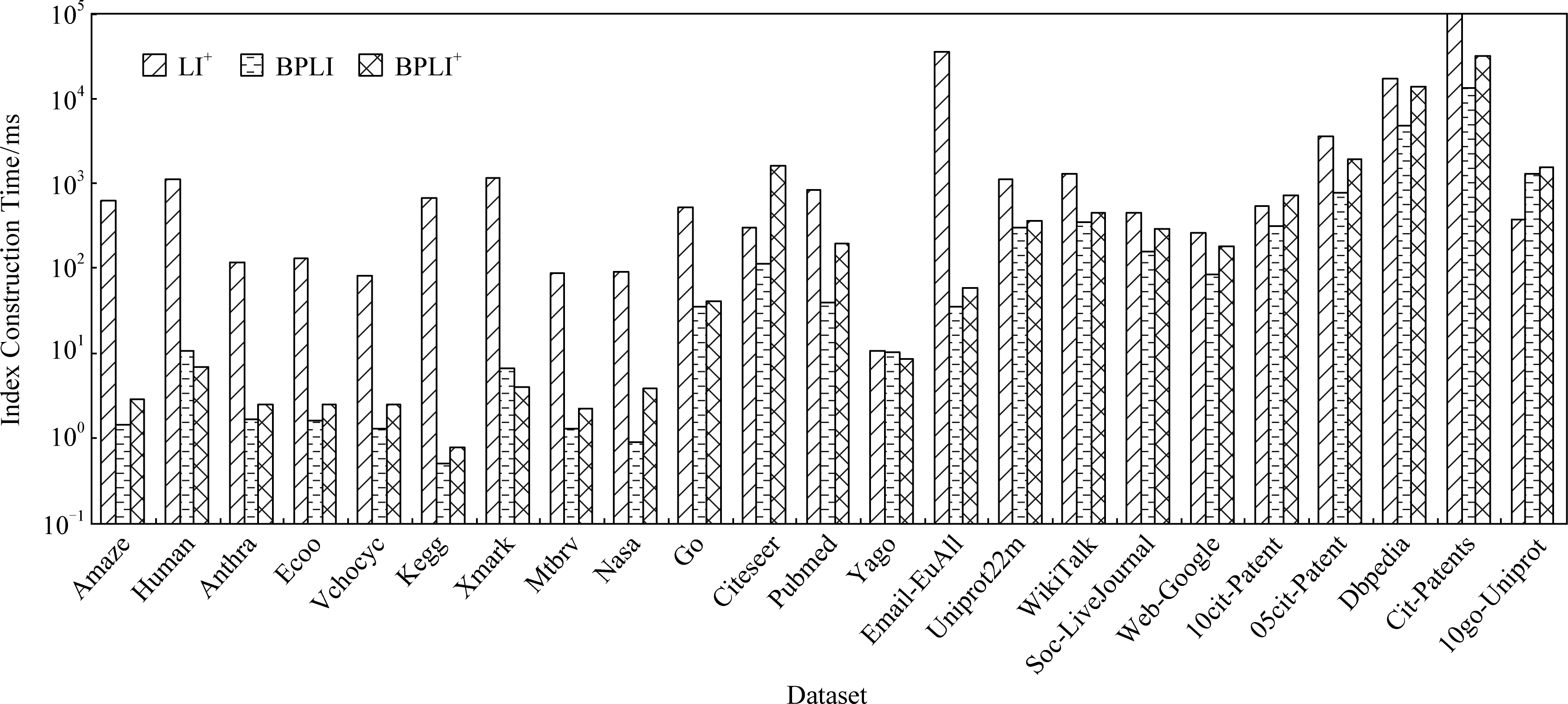
Fig. 3 Comparison of index construction time on different datasets
图3 不同规模数据集上的索引构建时间对比
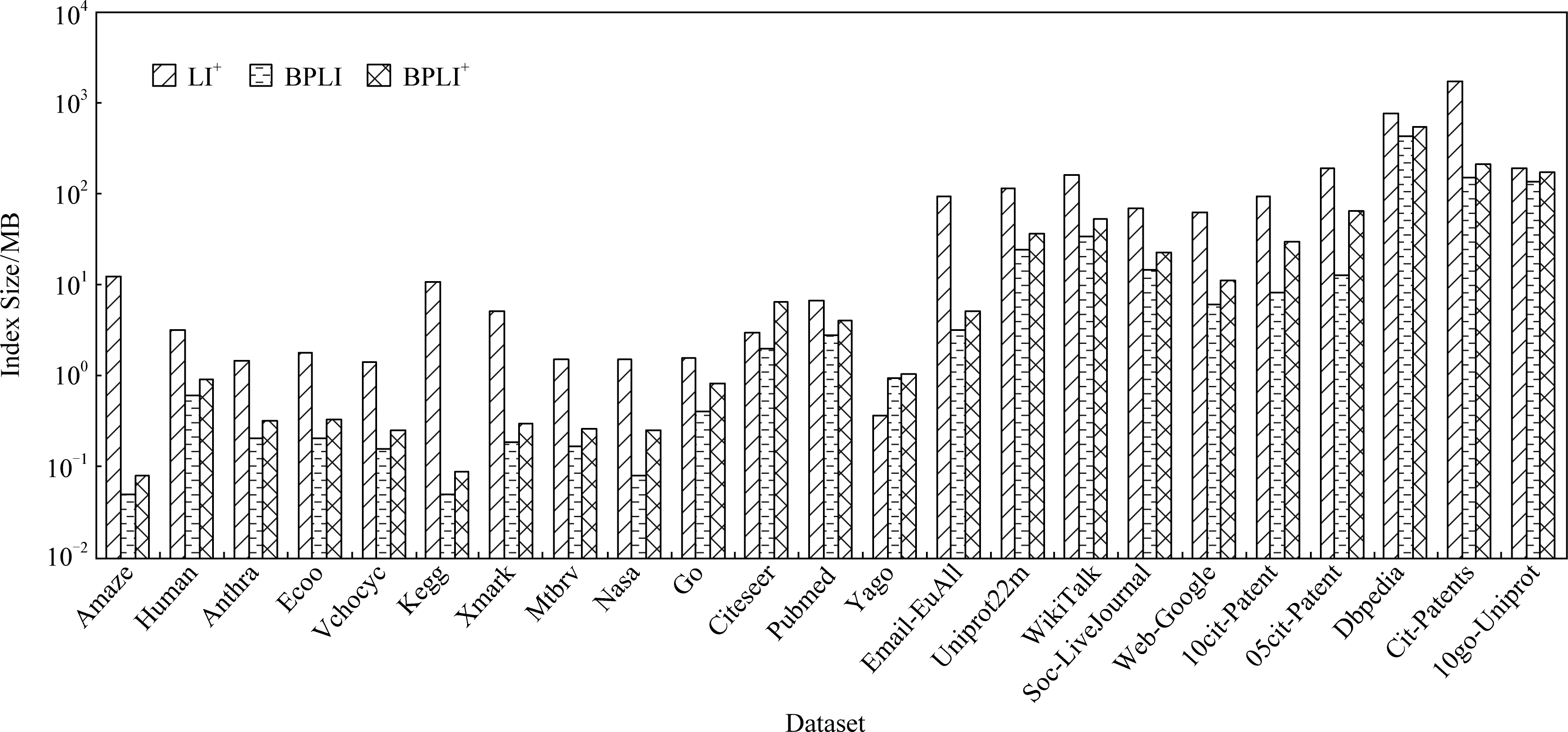
Fig. 4 Comparison of index size on different datasets
图4 不同规模数据集上的索引大小对比
4.4.3 查询时间
图5和图6展示了不同算法分别处理100万不可达查询及100万可达查询的查询时间对比.当查询时间超过10 000 ms时,均显示10 000 ms.本文有如下观察:
1) BPLI方法与BPLI+方法处理可达查询以及不可达查询的效率均高于LI+.原因在于:BPLI使用了拓扑号处理不可达查询,且路径标签索引的可达覆盖率高,因此查询响应时间较短;BPLI+方法无需遍历操作,且索引规模不大,因此查询响应时间最短.
2) BFS没有索引协助,因此查询响应时间最长.
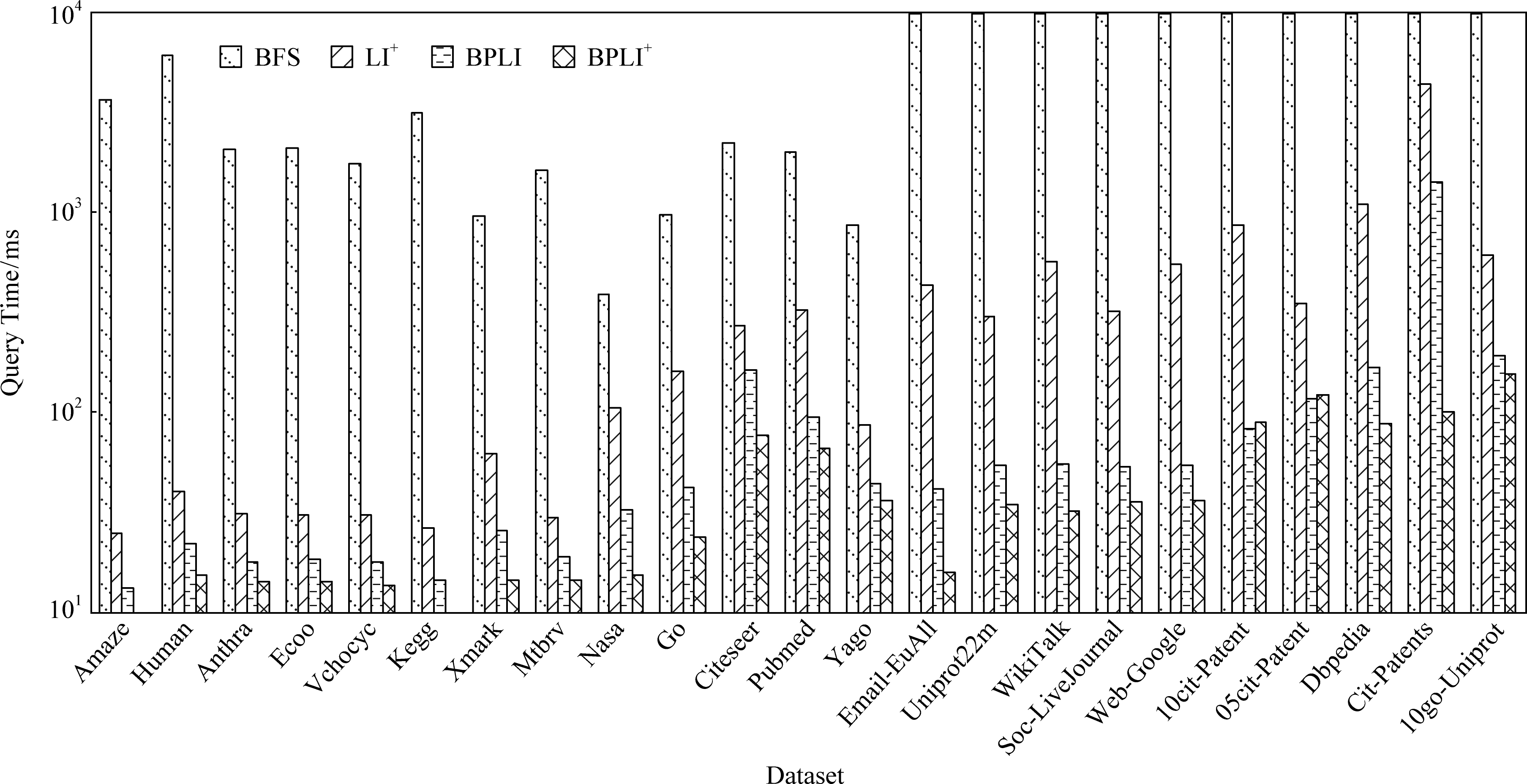
Fig. 5 Comparison of query time on unreachable query workload
图5 不可达查询的查询时间对比
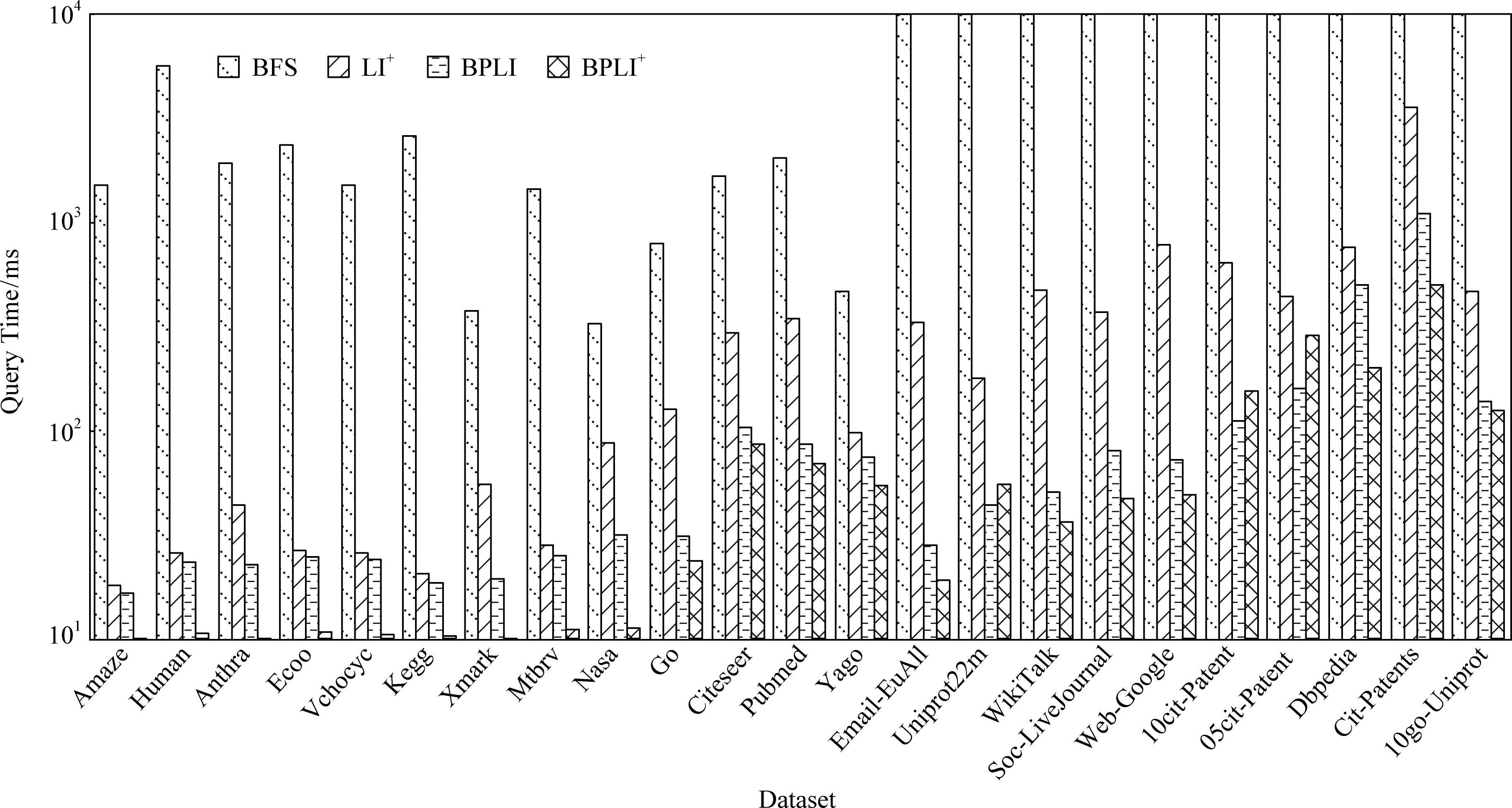
Fig. 6 Comparison of query time on reachable query workload
图6 可达查询的查询时间对比
针对现有方法在处理大图上标签约束可达性查询时索引构建时间长、索引规模大且查询响应慢的问题,本文提出了2种基于地标点的双向路径标签索引,并基于所提出的优化方法来减小索引规模.实验结果从索引构建时间、索引大小以及查询时间3方面验证了本文所提方法的高效性.例如,本文方法在Email-EuAll数据集上的索引规模比LI+降低了96.67%,索引构建时间比LI+降低了99%,可达查询数据集上查询时间比LI+提高了17倍,不可达查询数据集上查询时间比LI+提高了26倍.
[1] Fu Lizhen, Meng Xiaofeng. Reachability indexing for largescale graphs: Studies and forecasts[J]. Journal of Computer Research and Development, 2015, 52(1): 116-129 (in Chinese)
(富丽贞, 孟小峰. 大规模图数据可达性索引技术: 现状与展望[J]. 计算机研究与发展, 2015, 52(1): 116-129)
[2] Cheng James, Huang Silu, Wu Huanhuan, et al. TF-Label: A topological-folding labeling scheme for reachability querying in a large graph[C] //Proc of the 2013 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2013: 193-204
[3] Yildirim H, Chaoji V, Zaki M J. GRAIL: A scalable index for reachability queries in very large graphs[J]. International Journal on Very Large Data Bases, 2012, 21(4): 509-534
[4] Chen Yangjun, Chen Yibin. An efficient algorithm for answering graph reachability queries[C] //Proc of the 24th Int Conf on Data Engineering. Piscataway, NJ: IEEE, 2008: 893-902
[5] Zhu Linhong, Choi B, He Bingsheng, et al. A uniform framework for ad-hoc indexes to answer reachability queries on large graphs[C] //Proc of the 14th Int Conf on Database Systems for Advanced Applications. Berlin: Springer, 2009: 138-152
[6] Yano Y, Akiba T, Iwata Y, et al. Fast and scalable reachability queries on graphs by pruned labeling with landmarks and paths[C] //Proc of the 22nd ACM Int Conf on Information and Knowledge Management. New York: ACM, 2013: 1601-1606
[7] Jin Ruoming, Xiang Yang, Ruan Ning, et al. Efficiently answering reachability queries on very large directed graphs[C] //Proc of the 2008 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2008: 595-608
[8] Chen Yangjun, Chen Yibin. Decomposing DAGs into spanning trees: A new way to compress transitive closures[C] //Proc of the 27th Int Conf on Data Engineering. Piscataway, NJ: IEEE, 2011: 1007-1018
[9] Jin Ruoming, Ruan Ning, Dey S, et al. SCARAB: Scaling reachability computation on large graphs[C] //Proc of the 2012 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2012: 169-180
[10] Trißl S, Leser U. Fast and practical indexing and querying of very large graphs[C] //Proc of the 2007 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2007: 845-856
[11] Yin Dan, Gao Hong, Zou Zhaonian, et al. Reachability query in heterogeneous information networks[J]. Journal of Computer Research and Development, 2016, 53(2): 479-491 (in Chinese)
(尹丹, 高宏, 邹兆年, 等. 异构信息网上的可达性查询[J]. 计算机研究与发展, 2016, 53(2): 479-491)
[12] Van S, Sebastiaan J, Oege D M. A memory efficient reachability data structure through bit vector compression[C] //Proc of the 2011 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2011: 913-924
[13] Chen Ziyang, Chen wei, Li Na, et al. Reachability query processing algorithm for large graphs[J]. Chinese Journal of Computers, 2019, 42(3): 582-595 (in Chinese)
(陈子阳, 陈伟, 李娜, 等. 面向大图的可达性查询处理算法[J]. 计算机学报, 2019, 42(3): 582-595)
[14] Li Wentao, Qiao Miao, Qin Lu, et al. Scaling distance labeling on small-world networks[C] //Proc of the 2019 Int Conf on Management of Data. New York: ACM, 2019: 1060-1077
[15] Sengupta N, Bagchi A, Ramanath M, et al. ARROW: Approximating reachability using random walks over web-scale graphs[C] //Proc of the 35th IEEE Int Conf on Data Engineering(ICDE). Piscataway, NJ: IEEE, 2019: 470-481
[16] Li Lei, Wang Sibo, Zhou Xiaofang. Time-dependent hop labeling on road network[C] //Proc of the 35th IEEE Int Conf on Data Engineering(ICDE). Piscataway, NJ: IEEE, 2019: 902-913
[17] Yung D, Chang Shikuo. Fast reachability query computation on big attributed graphs[C] //Proc of the IEEE Int Conf on Big Data. Los Alamitos, CA: IEEE Computer Society, 2016: 3370-3380
[18] Fan Weifei, Li Jianzhong, Ma Shuai, et al. Adding regular expressions to graph reachability and pattern queries[J]. Frontiers of Computer Science, 2012, 6(3): 313-338
[19] Jin Ruoming, Hong Hui, Wang Haixun, et al. Computing label-constraint reachability in graph databases[C] //Proc of the 2010 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2010: 123-134
[20] Zou Lei, Xu Kun, Yu J X, et al. Efficient processing of label-constraint reachability queries in large graphs[J]. Information Systems, 2014, 40(1): 47-66
[21] Valstar L D J, Fletcher G H L, Yoshida Y. Landmark indexing for evaluation of label-constrained reachability queries[C] //Proc of the 2017 ACM Int Conf on Management of Data. New York: ACM, 2017: 345-358
[22] Wadhwa S, Prasad A, Ranu S, et al. Efficiently answering regular simple path queries on large labeled networks[C] //Proc of the 2019 ACMSIGMOD Int Conf on Management of Data. New York: ACM, 2019: 1463-1480
[23] Akiba T, Iwata Y, Yoshida Y. Fastexact shortest-path distance queries on large networks by pruned landmark labeling[C] //Proc of the 2013 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2013: 349-360
Du Ming, born in 1975. PhD, associate professor. His main research interests include information retrieval techniques, data analysis and mining, and natural language processing.
Yang Yun, born in 1995. Master. Her main research interests include query processing and optimization on graph data.
Zhou Junfeng, born in 1977. PhD, professor. His main research interests include information retrieval techniques, query processing on semi-structured data and graph data, and optimization.
Chen Ziyang, born in 1973. PhD, professor. His main research interests include computation theory, query processing and optimization on graph data.
Yang Anping, born in 1994. Master. His main research interests include query processing and optimization on graph data.