随着传感器和智能设备技术的快速发展以及在实际中的广泛运用,协同收集来自多个信息源的大量数据成为现实.面对具有空间分布的海量数据的处理,作为能够从中提取有价值信息的主要有效工具,机器学习在计算机视觉、医疗保健和金融市场分析等广泛领域的应用取得了巨大成功.其中分布式随机梯度下降算法(stochastic gradient descent, SGD)作为最常用的机器学习方法之一,在每步迭代中只随机训练一个样本数据,大大减少了训练时间,但容易受到Byzantine攻击[1]的影响.由于系统故障、软件bug[2]、数据损坏和通信延迟等原因造成的个体或机器之间共享信息错误[3],统称为Byzantine攻击.所以,在Byzantine环境下研究分布式机器学习如何高效处理共享信息的数据是极为重要的.
目前关于Byzantine攻击的相关研究正如火如荼,上述是几种导致故障的实际原因,体现在算法中又分为Byzantine个体对共享模型参数![]() 和梯度
和梯度![]() 进行更改.文献[1]在假设Byzantine个体数量的上界已知和未知的2种情况下,讨论了Byzantine个体对共享的参数
进行更改.文献[1]在假设Byzantine个体数量的上界已知和未知的2种情况下,讨论了Byzantine个体对共享的参数![]() 进行的更改:
进行的更改:
其中,B表示Byzantine个体,m表示总个体数目,[m]\B表示非Byzantine个体.并且将Byzantine攻击方式分为3种类型:第1种“随机”攻击,输出并共享一个随机向量服从(0,1)的均匀分布,即σ~U[0,1];第2种“反”攻击,共享与模型参数互为相反数的值;第3种“噪声”攻击,给模型参数添加一个高斯噪声服从(0,0.01)的正态分布,即ε~N[0,0.01].文献[2]则假定Byzantine个体对共享的梯度![]() 进行了如下更改:
进行了如下更改:
进而通过在模型参数w上加上一定次数和不同大小的扰动p,即共享模型参数为![]() 能够让随机梯度快速逃离平坦区域,从而逃离了鞍点,这意味着能够有效抵御Byzantine攻击.
能够让随机梯度快速逃离平坦区域,从而逃离了鞍点,这意味着能够有效抵御Byzantine攻击.
Byzantine弹性指的是存在Byzantine攻击的情况下算法仍能正常执行的弹性区间[5].文献[6]分析了经典Byzantine与高维Byzantine的区别与联系,如图1所示.文献[6]也将Byzantine攻击类型分成了3种:高斯攻击、全知型攻击和位翻转型攻击.但仅仅用了SGD去解决上述3种类型的Byzantine攻击的优化问题.

Fig. 1 Two types of Byzantine
图1 Byzantine的2种不同方式
基于梯度的优化算法会因为鞍点处的梯度值为0而易陷入非最优的情形,尤其在高维情况下,包围鞍点的水平或平坦区域范围较大,这导致分布式SGD很难快速逃离该区域,因而长时间陷于鞍点附近.为了有效解决这一重要问题,受文献[4,6]的启发,提出了一种新的Byzantine攻击类型——高维鞍点攻击.虽与文献[4]一样对共享的梯度![]() 进行了更改,但不同之处在于梯度更改的值不同,而且是在高维情况下分析的Byzantine攻击,并结合了文献[6]所提出的动态约束自适应优化算法而非传统的SGD.
进行了更改,但不同之处在于梯度更改的值不同,而且是在高维情况下分析的Byzantine攻击,并结合了文献[6]所提出的动态约束自适应优化算法而非传统的SGD.
文献[7]提出用自适应方法代替传统的SGD来有效解决陷入鞍点而无法达到最优值的困境.通过调整随机梯度噪声的方向,使得噪声能在鞍点处是等方向的,有助于朝正确的方向快速逃离鞍点.但自适应方法则面临两大问题:1)与SGD相比泛化能力差;2)由于不稳定或者极端的学习率会导致算法不收敛.文献[8]不仅验证了极端学习率会导致算法性能差,而且提出了给学习率加上动态约束实现从自适应方法到SGD平缓过渡的方法——具有动态约束的自适应矩估计(adaptive moment estimation with dynamic bound, ADABOUND).结果表明这2种动态约束自适应方法消除了自适应方法和SGD的泛化差异,并且提高了学习速度.
为了解决在分布式高维Byzantine环境下,能最大弹性限度抵御攻击问题,从而高效求解优化问题.仿真分析了当目标函数陷入鞍点时,动态约束自适应相比较于自适应和非自适应方法逃离鞍点要更快,并在数据集分类问题上同样进行了比对实验.其次,提出了一种过滤Byzantine个体的聚合规则Saddle(·),理论证明了它是高维Byzantine弹性的.因此,在分布式高维Byzantine环境下,采用动态约束的自适应优化方法结合聚合规则Saddle(·)能够有效避免鞍点攻击.
定义1. Jensen不等式[9].若对于任意x=(xi),参数λi≥0且![]() 凸函数f(x)满足:
凸函数f(x)满足:![]() 上述公式被称为Jensen不等式.
上述公式被称为Jensen不等式.
定义2. 鞍点.解决非线性规划问题min f(x),s.t. hi(x)≥0,(i=1,2,…,p)的拉格朗日函数,指的是目标函数f(x)和约束函数hi(x)的线性组合,拉格朗日函数为![]() 其中,x∈Rn,拉格朗日系数λ=(λ1,λ2,…,λp)T,λi≥0,L(x*,λ)表示当x为固定值x*时,拉格朗日函数为L(x*,λ);同理,当λ为固定值λ*时,拉格朗日函数为L(x,λ*);当有一组解为(x*,λ*)时,拉格朗日函数的值为L(x*,λ*).若L(x*,λ)≤L(x*,λ*)≤L(x,λ*),则点(x*,λ*)称为鞍点[10].
其中,x∈Rn,拉格朗日系数λ=(λ1,λ2,…,λp)T,λi≥0,L(x*,λ)表示当x为固定值x*时,拉格朗日函数为L(x*,λ);同理,当λ为固定值λ*时,拉格朗日函数为L(x,λ*);当有一组解为(x*,λ*)时,拉格朗日函数的值为L(x*,λ*).若L(x*,λ)≤L(x*,λ*)≤L(x,λ*),则点(x*,λ*)称为鞍点[10].
判断鞍点的一个充分条件是:函数在一阶导数为0处的Hessian矩阵为不定矩阵.
定义3. 严格鞍函数.对于所有的x,满足下列条件:
1) 梯度![]() f(x)很大;
f(x)很大;
2) Hessian矩阵![]() 2f(x)具有负的特征值;
2f(x)具有负的特征值;
3) 点x位于局部极小值附近;
则函数f(x)是严格鞍函数[11-12].
定义4. 高维Byzantine弹性[6].令α是![]() 的任意角,q是[0,m]的任意整数.(gi:i∈[m])是在d维空间上独立同分布的随机向量,梯度G=
的任意角,q是[0,m]的任意整数.(gi:i∈[m])是在d维空间上独立同分布的随机向量,梯度G=![]() f(x)满足E[G]=g,其中E[G]表示G的均值.对于每一维,在这m个值中最高有q个被任意值取代,即对于第j∈[d]维,
f(x)满足E[G]=g,其中E[G]表示G的均值.对于每一维,在这m个值中最高有q个被任意值取代,即对于第j∈[d]维,![]() 有q个元素是Byzantine个体所共享的梯度,其中
有q个元素是Byzantine个体所共享的梯度,其中![]() 表示向量
表示向量![]() 的第j维.高维Byzantine弹性的聚合规则Aggr(·)需满足如下条件:
的第j维.高维Byzantine弹性的聚合规则Aggr(·)需满足如下条件:
![]() 其中
其中 ·
· 表示内积运算.
表示内积运算.
2) 对于指数r=2,3,…,r1+r2+…+rn-q=r,E[Aggr]r≤c1E[G]r1+c2E[G]r2+…+cn-qE[G]rn-q,其中c1,c2,…,cn-q为线性组合的相关系数.
聚合规则Aggr(·)指的是满足规则Aggr(·)的被认为是非Byzantine个体共享的真实信息,相反则被认为是Byzantine个体共享的虚假信息,需要被过滤掉.
Reddi等人[13]提出深度学习[14]优化方法的一般框架(包括自适应和非自适应方法):
① g|t=(g1,g2,…,gn)|t=![]() f(x|t);
f(x|t);
② m|t=φt((g1,g2,…,gn)t)和v|t=Φt((g1,g2,…,gn)t);
③![]()
④![]()
其中,g|t为f(x|t)梯度,α为深度学习步长,t为迭代时间,x|t为第t步迭代的解(x1,x2,…,xn)t,β1和β2分别对应一阶梯度和二阶梯度移动平均的指数,φt和Φt在自适应和非自适应中分别对应如表1所示的值.
Table 1 Adaptive and Non-adaptive Corresponding Values
表1 自适应和非自适应对应值

Gradient FunctionSGDADAGRADRMSPROPADAMφtg|tg|tg|t(1-β1)∑ti=1βt-i1g|iΦtdiag (∑ti=1g|2i)∕t(1-β2) diag (∑ti=1βt-i2g|2i)(1-β2) diag (∑ti=1βt-i2g|2i)
梯度消失或梯度爆炸是深度学习经常会遇到的难题.如果梯度值很小,就会出现梯度消失的情况,从而导致目标函数长时间收敛不到最小值;若梯度值很大,就会出现函数值上下波动,收敛不到最优值.如下列函数,无论步长大小如何,自适应动量估计算法(adaptive moment estimation, ADAM)都无法收敛到最优值.对于函数序列{ft(z)![]() =[-2,2],
=[-2,2],
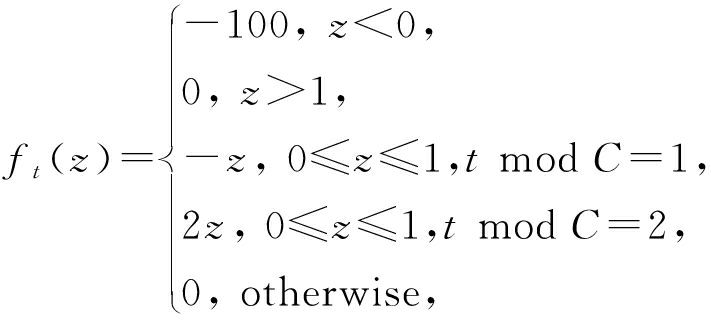
其中C∈N+并满足![]() 这个函数序列:当满足z<0的任一点,能够得到最小的误差界;假设β1=0,当满足z≥0时,ADAM收敛到次优解.因为算法每迭代到第C步,得到一个梯度值为-1,导致算法朝着反方向移动.而且在下一步的时候,即第C+1步,梯度值为2.根据表1的ADAM的梯度更新规则,梯度值越大,对学习率的影响越小.所以第C+1步并不能够缓解上一步的错误.综上所述,自适应方法ADAM由于梯度值大小的问题而导致不收敛[8].
这个函数序列:当满足z<0的任一点,能够得到最小的误差界;假设β1=0,当满足z≥0时,ADAM收敛到次优解.因为算法每迭代到第C步,得到一个梯度值为-1,导致算法朝着反方向移动.而且在下一步的时候,即第C+1步,梯度值为2.根据表1的ADAM的梯度更新规则,梯度值越大,对学习率的影响越小.所以第C+1步并不能够缓解上一步的错误.综上所述,自适应方法ADAM由于梯度值大小的问题而导致不收敛[8].
通过上述分析,自适应方法易受极端学习率影响.为有效克服这一困难,动态约束自适应的算法思想是[8]:通过给梯度加一个阈值区间,并且上下阈值都随时间变化最后收敛到SGD的学习率,从而实现自适应方法向SGD的平缓过渡.
针对梯度消失和梯度爆炸问题,不妨假设![]() 其中
其中![]() 并设定裁剪阈值为ηmax(t)和ηmin(t).
并设定裁剪阈值为ηmax(t)和ηmin(t).
当![]() 时,
时,![]()
当![]() 时,
时,![]()
文献[8]已经证明了动态约束自适应算法收敛,它的遗憾界是![]()
定义5. 鞍点攻击类型为
其中,(gi)j表示第j维第i个个体的梯度值,j∈[d].i∈B时,同时满足Hessian矩阵是不定的.鞍点攻击影响梯度,从而影响学习率,导致目标函数不收敛,所以需要寻求一种聚合规则过滤Byzantine个体.下面提出的聚合规则[15]可以过滤高维鞍点个体,实现抵御攻击的目的.
定义6. 聚合规则Saddle(·)为
其中,对任意维![]() 表示给每个梯度值加噪声扰动p,然后选择最大的m-q个作为非Byzantine梯度集.因为鞍点性质本身具有不稳定性,当给一个处在鞍点位置的球施加一些轻微的扰动,该球可能会从鞍点处滑落,从而实现逃离鞍点找到严格鞍函数的目的.
表示给每个梯度值加噪声扰动p,然后选择最大的m-q个作为非Byzantine梯度集.因为鞍点性质本身具有不稳定性,当给一个处在鞍点位置的球施加一些轻微的扰动,该球可能会从鞍点处滑落,从而实现逃离鞍点找到严格鞍函数的目的.
定理1. 噪声梯度下降法能够在多项式时间内找到严格鞍函数的局部最小值点[10].
定理1验证了聚合规则Saddle(·)是能在有限时间内找到函数最优值,即逃离了鞍点.为了验证聚合规则Saddle(·)更具有一般性,下面证明它是高维Byzantine弹性的.
定理2. 令(gi:i∈[m])是在d维空间上独立同分布的随机向量,其中E[G]=g,假设E[Gi-gi]2=σ2,所以![]() 对于任意维j∈[d],在这m个值中有q个被任意值取代,其中
对于任意维j∈[d],在这m个值中有q个被任意值取代,其中![]() 表示向量
表示向量![]() 的第j维.如果
的第j维.如果![]() 其中
其中![]() 那么聚合规则Saddle(·)是高维Byzantine弹性.
那么聚合规则Saddle(·)是高维Byzantine弹性.
证明.

根据Jensen不等式,
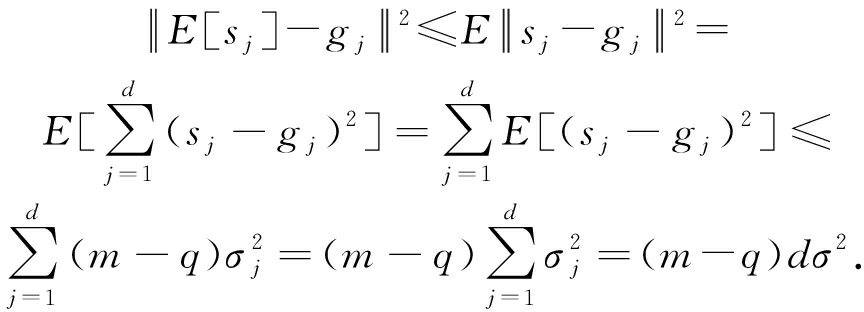
由假设知,![]() 即E[s]在一个以g为中心
即E[s]在一个以g为中心![]() 为半径的圆内.那么
为半径的圆内.那么
其中![]()
以上验证了聚合规则Saddle(·)满足高维Byzantine弹性的条件1).
根据等价范数的定义:有限维空间上的任何2个范数必是等价的.存在常数c1,使得
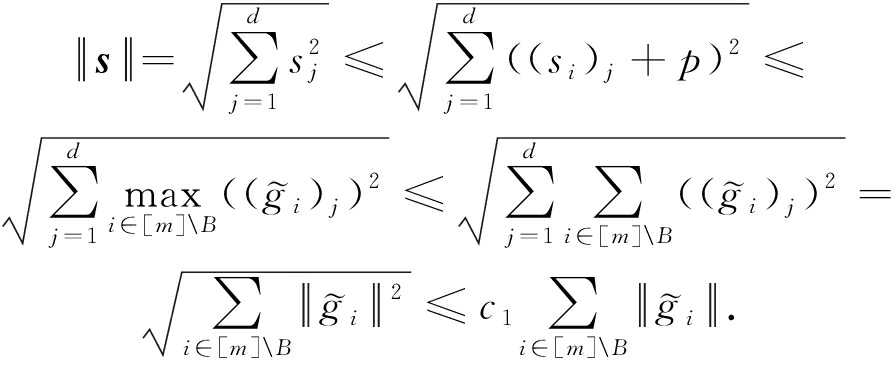
不失一般性,用{g1,g2,…,gm-q}表示![]() 因此,存在常数c2,使得
因此,存在常数c2,使得
![]()
![]()
其中,r1+r2+…+rm-q=r.所以验证了聚合规则Saddle(·)满足高维Byzantine弹性的条件2).
以上证明了聚合规则Saddle(·)是更具有一般性的高维Byzantine弹性,即过滤鞍点的聚合规则是泛化的.
证毕.
以凸函数:
为例,其中b1,b2为随机系数.由鞍点判定条件知,函数ft(x1,x2)的Hessian矩阵是不定的,所以该函数存在鞍点.通过不断对(x1,x2)进行梯度更新,最终找到目标函数的最优值.因为不同的优化方法对梯度更改规则不同(即学习率不同),所以达到目标函数最优值的快慢不同.
如图2(a)所示,动态约束自适应(ADABOUND)方法相比较于自适应梯度算法(adaptive gradient, ADAGRAD)、平方根改进算法(root mean square prop, RMSPROP)、ADAM和SGD逃离鞍点的速度明显比较快.图2(b)表示动态约束自适应的上下阈值随时间变化,最后都收敛到与SGD学习率一致,实现了自适应到非自适应的平缓过渡.
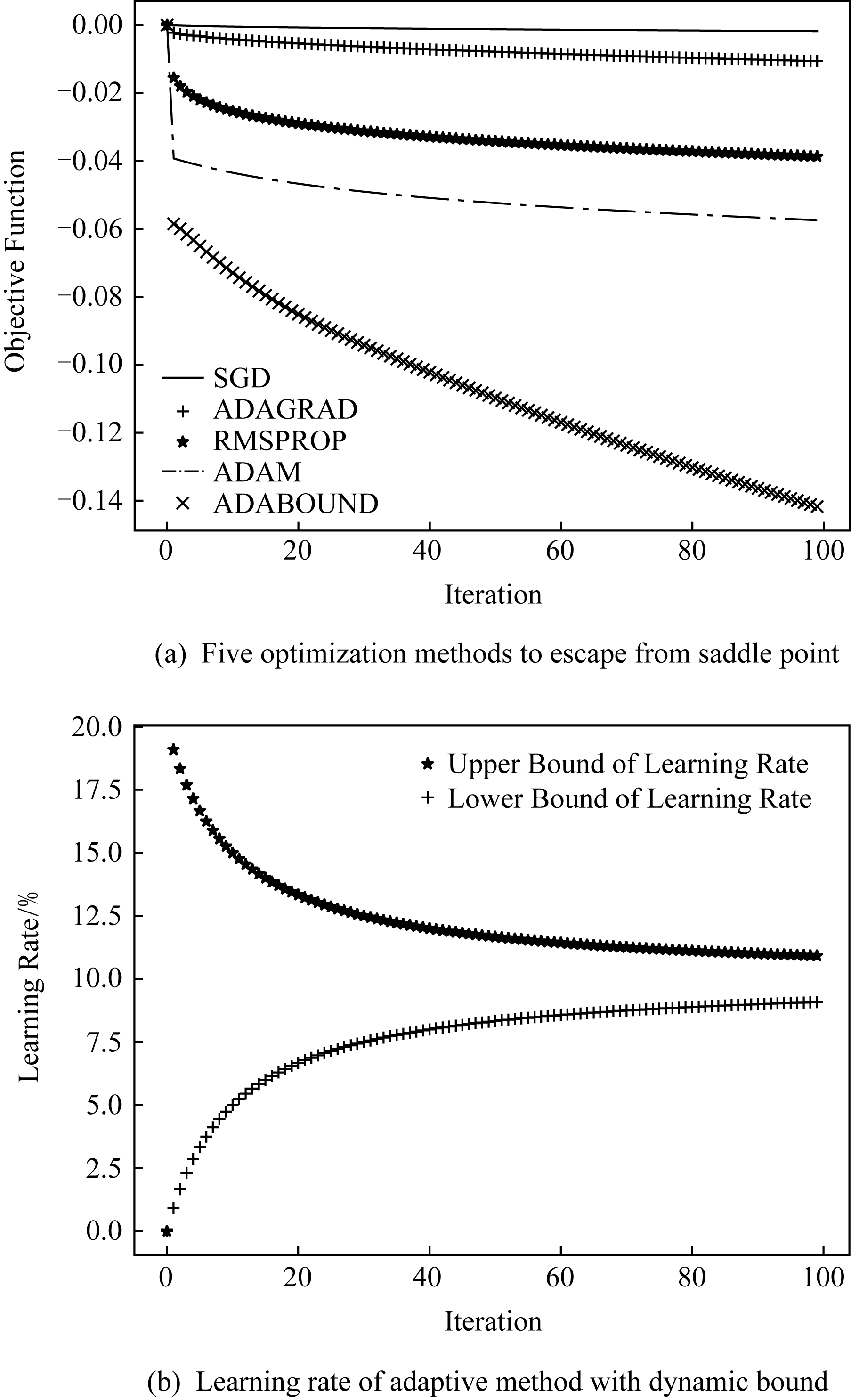
Fig. 2 Comparison of the optimization methods used to escape from saddle point
图2 优化方法用于逃离鞍点的快慢比较
不仅如此,在随机生成的(50 000×30)数据集中,分别用不同的优化方法将该数据集分成10个类.逻辑回归用以解决该分类问题,对于输入的x|t,其对应的类标签为y|t,我们的目标是训练分类模型y|t=wx|t+b的参数w和b,使得属于当前类的概率最大.下面实验通过比较错误率(error rate)与误差(error)来分析方法的优劣.
如图3(a)所示,在数据集分类问题上自适应方法虽然在前期分类的精确度比SGD差一点,但随着训练次数的增加,最后自适应方法明显比SGD的分类错误率要低的多.图3(b)显示,动态约束自适应都比自适应的分类错误率要低。通过图3(c)发现,当前值与真实值的距离测算的误差,动态约束自适应明显比自适应要低.因为错误率![]() 由图3(c)知,ADABOUND比SGD的误差值小,导致误差率却比SGD大的原因是因为在不断训练过程中,训练值越来越接近实际值,并最终趋向一个稳定值.图3(b)表明在10 000次以后,SGD的错误率仍在向下延伸,说明训练值并没有趋于稳定状态.
由图3(c)知,ADABOUND比SGD的误差值小,导致误差率却比SGD大的原因是因为在不断训练过程中,训练值越来越接近实际值,并最终趋向一个稳定值.图3(b)表明在10 000次以后,SGD的错误率仍在向下延伸,说明训练值并没有趋于稳定状态.

Fig. 3 Performance comparison of data set classification by different optimization methods
图3 不同优化方法分类的性能比较
根据2.2节提出的鞍点攻击,该攻击方式会影响梯度,所以对于基于梯度的优化方法就会有一定程度的影响.为了证明动态约束自适应能控制极端梯度的影响,在Byzantine和非Byzantine环境下做了动态约束自适应受环境影响程度的对比实验.并且与文献[6]作比对实验,观察SGD受Byzantine攻击的影响大小.
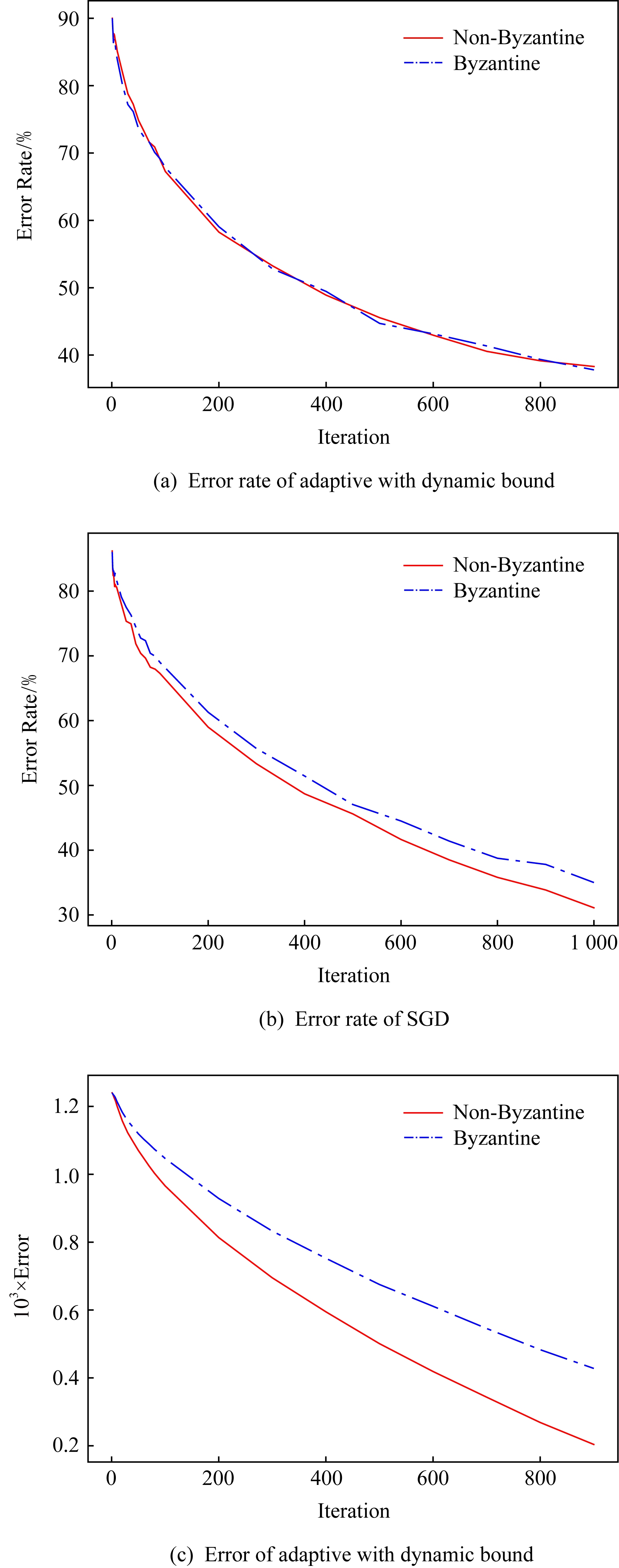
Fig. 4 Performance comparison of optimization methods in Byzantine and non-Byzantine environments
图4 Byzantine和非Byzantine环境下的性能比较
如图4(a)(b),动态约束自适应方法相比较于SGD在Byzantine环境下不会受很大的影响.因为经过梯度裁剪的自适应,不会因为梯度的忽大忽小而导致不收敛.图4(c)表示从误差角度分析,在Byzantine和非Byzantine环境下动态约束自适应受影响的情况.
第3节已经验证了聚合规则Saddle(·)具有高维Byzantine弹性,所以在分布式环境下鞍点攻击的是任意维的个体.不同个体对应不同的工作机器,分布式计算模型参数,然后它们向主机发送局部模型参数[16].所以在分布式环境下研究鞍点攻击,通过观察不同个体总数目的错误率.
如图5所示,不同个体总数目下动态约束自适应方法的分类效果不一样[17].由于高维Byzantine在每一维的随机性较大,所以这也是影响图5结果的直接原因.

Fig. 5 Error rate corresponding to the total number of different individuals
图5 不同个体总数所对应的错误率
结合文献[8]提出的动态约束自适应并应用于分布式Byzantine环境,本文主要提出一种具有高维Byzantine弹性的聚合规则Saddle(·),可有效过滤鞍点攻击的个体,从而实现在确保算法收敛的情况下抵御鞍点攻击的目的.针对数据集分类结果的错误率和误差2个重要指标,通过大量数值仿真比较分析动态约束自适应与自适应和非自适应方法的优劣性.结果表明:结合聚合规则Saddle(·)的动态约束自适应在分布式Byzantine环境下受鞍点攻击的影响较小.
下一步工作希望能够给出不同个体总数所对应不同错误率大小的理论解释,并且能够更大限度地降低错误率.
[1] Jin Richeng, He Xiaofan, Dai Huaiyu. Distributed Byzantine tolerant stochastic gradient descent in the era of big data[EB/OL]. 2019[2019-05-12]. https://arxiv.org/abs/1902.10336v3
[2] Fu Yiqi, Dong Wei, Yin Liangze, et al. Software defect prediction model based on the combination of machine learning algorithms[J]. Journal of Computer Research and Development, 2017, 54(3): 633-641 (in Chinese)(傅艺绮, 董威, 尹良泽, 等. 基于组合机器学习算法的软件缺陷预测模型[J]. 计算机研究与发展, 2017, 54(3): 633-641)
[3] He Yingzhe, Hu Xingbo, He Jinwen, et al. Privacy and security issues in machine learning systems: A survey[J]. Journal of Computer Research and Development, 2019, 56(10): 2049-2070 (in Chinese)(何英哲, 胡兴波, 何锦雯, 等. 机器学习系统的隐私和安全问题综述[J]. 计算机研究与发展, 2019, 56(10): 2049-2070)
[4] Yin Dong, Chen Yudong, Ramchandran K, et al. Defending against saddle point attack in Byzantine-robust distributed learning[EB/OL]. 2018[2018-10-12]. https://arxiv.org/abs/1806.05358
[5] Li Junfei, Hu Yuxiang, Wu Jiangxing. Research on improving the control plane’s reliability in SDN based on Byzantine fault-tolerance[J]. Journal of Computer Research and Development, 2017, 54(5): 952-960 (in Chinese)(李军飞, 胡宇翔, 邬江兴. 基于拜占庭容错提高SDN控制层可靠性的研究[J]. 计算机研究与发展, 2017, 54(5): 952-960)
[6] Xie Cong, Koyejo O, Gupta I. Generalized Byzantine-tolerant SGD[EB/OL]. 2018 [2019-04-15]. https://arxiv.org/abs/1802.10116
[7] Staib M, Reddi S J, Stayen K, et al. Escaping saddle points with adaptive gradient methods[EB/OL]. 2019 [2019-03-12]. https://arxiv.org/abs/1901.09149
[8] Luo Liangchen, Xiong Yuanhao, Liu Yan, et al.Adaptive gradient methods with dynamic bound of learning rate[EB/OL]. 2019 [2019-03-28]. https://arxiv.org/abs/1902.09843
[9] Jensen J. Sur les fonctions convexes et les inégualités entre les valeurs moyennes[J]. Acta Matem, 1906, 30(1): 175-193
[10] Gu Guoli, Liu Qian, Li Min. Augmented Lagrangian saddle point in semi-infinite planning[J]. Journal of Chongqing Normal University: Natural Science, 2016, 33(6): 13-17 (in Chinese)(谷国利, 刘茜, 李敏. 半无限规划中的增广拉格朗日鞍点[J]. 重庆师范大学学报: 自然科学版, 2016, 33(6): 13-17)
[11] Ju Sun, Qing Qu, Wright J. When are nonconvex problems not scary[EB/OL]. 2015 [2019-05-31]. https://arxiv.org/abs/1510.06096
[12] Ge Rong, Huang Furong, Jin Chi, et al.Escaping from saddle points-online stochastic gradient for tensor decomposition[C] //Proc of the 28th Conf on Learning Theory. Piscataway, NJ: IEEE, 2015: 797-842
[13] Sashank J, Reddi S J, Stayen K,et al. On the convergence of ADAM and beyond[C/OL] //Proc of the Int Conf on Learning Representations. Montreal, Canada: MILA, 2018 [2019-05-20]. https://openreview.net/forum?id=ryQu7f-RZ
[14] Georgios D, Mahdi M, Rachid G, et al. Aggregathor: Byzantine machine learning via robust gradient aggregation[C/OL] //Proc of the Conf on Systems and Machine Learning. Romandie,Switzerland: EPFL, 2019 [2019-05-20]. https://www.researchgate.net/publication/332947090_AGGREGATHOR_Byzantine_Machine_Learning_via_Robust_Gradient_Aggregation
[15] Lamport L, Shostak R, Pease M. The Byzantine general’s problem[J]. ACM Transactions on Programming Languages & Systems, 1982, 4(3): 382-401
[16] Li Xiaoling, Wang Huaimin, Guo Changguo, et al. Research and development of distributed constrained optimization problems[J]. Chinese Journal of Computers, 2015, 38(8): 1656-1671 (in Chinese)(李小玲, 王怀民, 郭长国, 等. 分布式约束优化问题研究及其进展[J]. 计算机学报, 2015, 38(8): 1656-1671)
[17] Gong Maoguo, Cheng Gang, Jiao Licheng, et al. Nondominated individual selection strategy based on adaptive partition for evolutionary multi-objective optimization[J]. Journal of Computer Research and Development, 2011, 48(4): 545-557 (in Chinese)(公茂果, 程刚, 焦李成, 等. 基于自适应划分的进化多目标优化非支配个体选择策略[J]. 计算机研究与发展, 2011, 48(4): 545-557)
Li Dequan, born in 1973. PhD, professor. His main research interests include distributed optimization, machine learning and control of sensor network.
Xu Yue, born in 1995. Master candidate. Her main research interests include distributed optimization.
Xue Sheng, born in 1964. Professor, PhD supervisor. His main research interests include coal and gas outburst, gas drainage in goaf and mining area, coal and gas mining and coal spontaneous combustion.