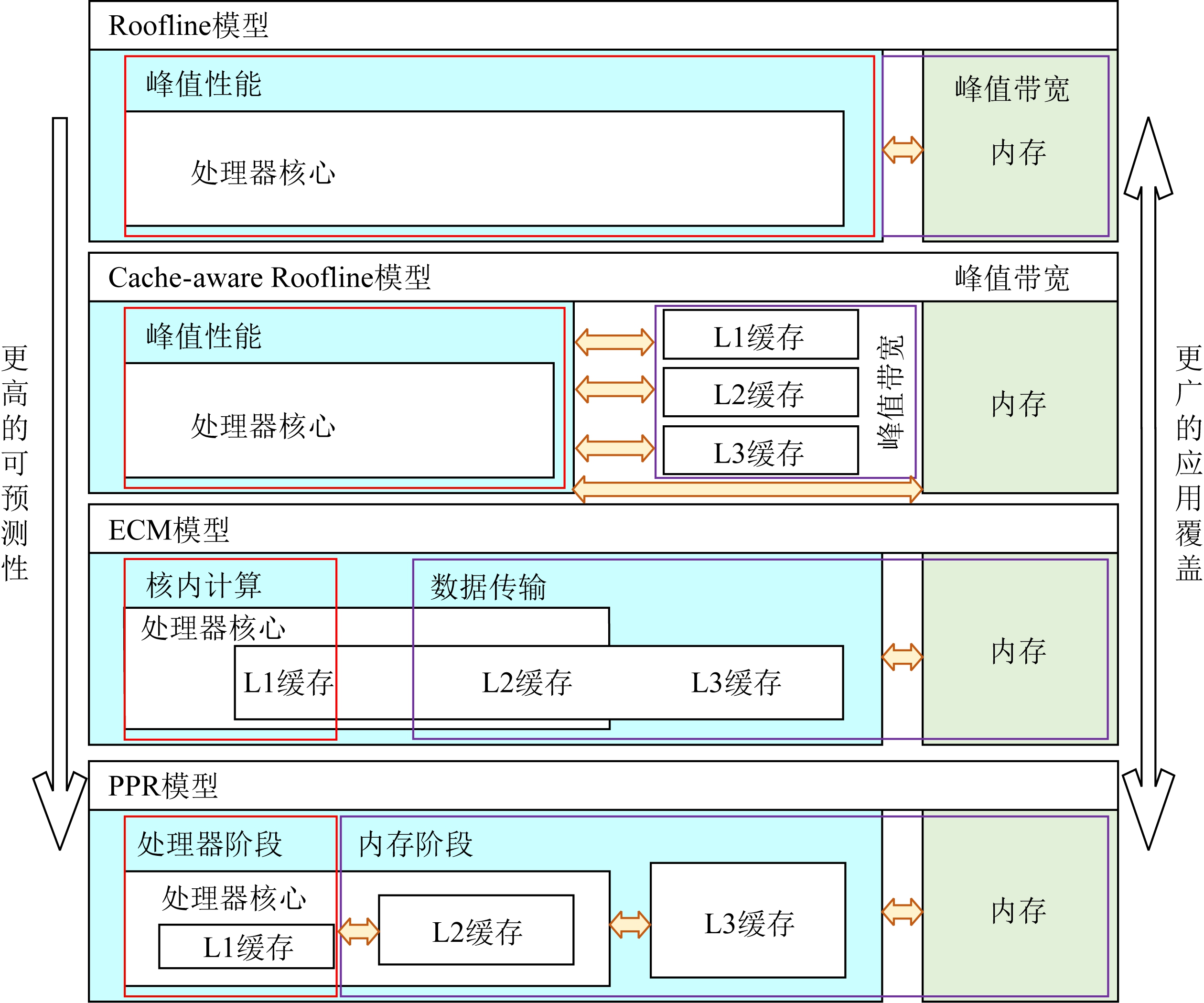
Fig. 1 PPR model and comparison with Roofline, Cache-aware Roofline and ECM
图1 PPR模型和Roofline,Cache-aware Roofline, ECM模型的对比
近些年来,使用性能模型的方法去分析和优化程序已经被广泛地使用.其中以稀疏矩阵向量乘(sparse matrix-vector multiplication, SpMV)y=Ax为例,作为典型的非规则访存的重要计算核心,该算法被广泛应用在信号处理、图像处理和迭代求解器等科学计算和实际应用中[1].但是在现有的多级存储器层次的体系结构上,稀疏矩阵向量乘的效率一般很低,浮点效率往往低于硬件浮点峰值的10%,其主要原因是复杂的存储器层次结构以及应用数据可重用性差的特征导致cache命中率较低,从而凸显了各级存储器之间的访问延迟差异的瓶颈.为了解决这些问题,李肯立等人[2]在GPU上使用概率质量函数模型去选择最佳的稀疏矩阵格式,从而构造不同的访存模式去优化数据重用性问题; Li等人[3]使用建模方法自动调优不同的向量寄存器从而优化矩阵计算开销.但是这些方法都属于粗粒度选择和评判优化方法的优劣,不能细化SpMV在特定平台上具体的执行行为.因此如何建模SpMV的计算过程以及随机的数据传输特性仍然是性能优化的主要挑战.此外,作为规则访存的典型代表,卷积计算在图像分类、目标检测、图像语义分割和神经网络等领域[4]取得了一系列突破性的研究成果,其强大的特征学习与分类能力引起了广泛的关注.之前的研究表明[5-7],卷积操作在不同的数据规模和体系结构下最优的实现方法差异巨大,从而也给性能模型优化提供了发挥的空间.
此外,得益于性能模型包含的分析和优化的特点,近年来已发展出多种建模方法,其中根据模型是否结合体系结构特征大致可以分为2类:
1) 黑盒模型.该方法提取应用特征或者采集运行时数据,拟合或使用机器学习方法对应用程序性能建模.
2) 白盒模型.该方法使用简化的机器模型描述应用程序和硬件的执行关系.
如图1所示,最简化的白盒模型是Konstantinidis等人[8]提出的Roofline模型,该模型描述了应用程序最佳性能与峰值性能、计算访存比和访存带宽之间的关系,预测了不同计算访存比程序可达到的性能上限.同时Cache-aware Roofline模型[9]引入的数据局部性规则扩展了cache在性能模型中的作用.更细粒度的白盒模型由Stengel等人[10]提出的ECM(execution-cache-memory)模型包含了指令执行和内存层次2个部分,该模型把程序运行划分为核内和核外2个阶段,对应于程序在CPU核内的指令执行和数据在内存层次之间的传输2个过程.不过该模型使用Kerncraft工具[11]建模程序的指令开销,导致对指令之间数据依赖的建模准确性较低,而且该模型使用的Pycachesim[11]假定数据在各级cache上的缺失数量相同,该假定对于不存在数据复用或者数据完全被复用的程序来说可以达到比较精确的性能预测,然而对于存在一定比例数据重用的非规则访存应用来说,则无法准确预测出性能,更也无法依据模型的输出结果给出具体的优化方案.

Fig. 1 PPR model and comparison with Roofline, Cache-aware Roofline and ECM
图1 PPR模型和Roofline,Cache-aware Roofline, ECM模型的对比
因此,为了改进指令数据依赖和数据复用的建模问题,我们提出了PPR(probability-process-ram)性能模型,该模型加入了处理器流水线指令建模,也加深了内存层次间数据访存建模能力,以解决预测指令流水线执行和非规则访存中数据传输的建模问题.由此我们的模型扩展了对数据依赖和非规则问题的覆盖范围,同时利用各阶段的建模数据反馈开发者优化性能瓶颈.我们的性能建模由3个步骤组成:
1) 构建平台,检测和提取硬件参数,包括计算单元个数、访存单元个数、流水线长度、指令发射宽度、指令开销以及各级cache大小,cache分组策略和数据传速率延迟等;
2) 对应用程序构建指令执行有向图,预测指令执行开销,并且标记出规则和非规则数据,通过检测到的配置构建一个全新设计的cache模拟器去预测访问数据的传输开销;
3) 分析步骤2得到的时间开销,针对所存在的瓶颈提出反馈的优化方案,并且预测出优化后的性能提升.
本文的主要贡献有3个方面:
1) 提出了PPR性能模型,该模型完整考虑了指令流水、指令执行开销和多级cache数据传输.通过细粒度的性能建模得出更精确的性能预测,并且扩展性能建模范围到数据依赖和非规则应用.
2) 为了精确地模拟多级cache的数据传输开销,我们设计了一个全新的cache模拟器,轻量级地构建于目标机器,并通过模拟应用程序的访存顺序,输出各级cache miss,进而得到数据的传输开销.
3) 通过计算指令执行和数据传输开销预测出程序性能,并分析建模得到的各阶段时间,找出影响性能的关键瓶颈,反馈开发者对应优化.同时我们也对不同的优化方法建模,预测不同优化策略带来的提升效果,最终指导开发者选择最佳的参数或策略.
优化稀疏矩阵向量乘方面,前人已经做了很多的工作[12-13],截至目前,已经大量优化技术被提出,如cache blocking、压缩、重排序以及启发式优化等方法,同时也存在一些问题.具体而言,主要分为3个方面:
1) 改变矩阵存储格式优化访存性能,例如BCSR,ELL,SELL[14]等格式,这些格式存储分块矩阵或对齐数据从而改变访存顺序,减少右端向量的传输次数,优化数据传输开销.所存在的主要问题是格式的选取和转化成本较高,甚至我们也无法准确预测出特定平台上可以获取最佳性能对应的存储格式.
2) 压缩方法,该方法降低矩阵的存储空间,缓解访存带宽的传输压力,但缺点在于压缩和解压的额外开销.
3) 自调优方法,由于不同的矩阵特征往往对应着最佳的矩阵格式和配置参数,通过提取矩阵信息自动选择最优参数以达到最佳性能.但是当前工作[15]提取的矩阵特征有限,主要为行数、列数、非零元个数以及对角数等信息,无法给出十分准确的预测.而所选的格式和参数将决定SpMV性能,就BCSR格式而言,其主要利用分块技术降低右端向量片段的数据传输,不过该格式存在多种分块方法,根据不同矩阵的非零元分布情况,多种分块会导致不同的cache miss次数,从而导致完全不同的性能表现.具体而言,过小的分块对数据的重用不够以至于不能显著提升程序性能,而太大的分块则会填充更多零元而大量增加数据集大小,从而导致访存数据增加和性能降低.因此选取合适的分块对SpMV的性能产生至关重要的影响,参数的选取策略也应该是性能模型的主要目的.所有这些都鼓励我们建立一个针对于非规则访存应用的性能模型.
此外近年来卷积神经网络被广泛应用在各个领域(为了加快训练的速度通常选用单精度浮点计算),并取得了一系列突破性的研究成果.而卷积作为卷积神经网络最大的耗时函数,也成为优化的重点.很多工作[16]也使用向量指令或者特定的硬件结构加速计算部分.但是对于开发者而言,如何在不同的指令集支持和数据规模下选择最佳的优化方案仍然是一个亟待解决的问题,这也是我们提出性能模型的主要动机.
如表1所示,我们的实验基于Haswell微架构的Intel服务器平台,处理器核心支持SSE,AVX,AVX2指令集,每个核心包含一个支持指令乱序执行的端口调度控制器,其中有4个计算端口支持核心每周期2次浮点或者FMA计算,配合使用向量寄存器每个周期最高可达到双精度浮点(DP)16次或单精度浮点(SP)32次的浮点性能,其他4个端口支持访存操作,每个周期支持2个Load和1个Store操作.每个CPU通过4个内存通道与DDR3-1866内存相连.处理器的内存层次由3个片上数据 cache组成(32 KB L1D cache, 256 KB L2 cache和30 MB L3 cache).CPU主频被锁定在2.7 GHz.
Table 1 Special Machine Parameters
表1 实验平台及相关参数
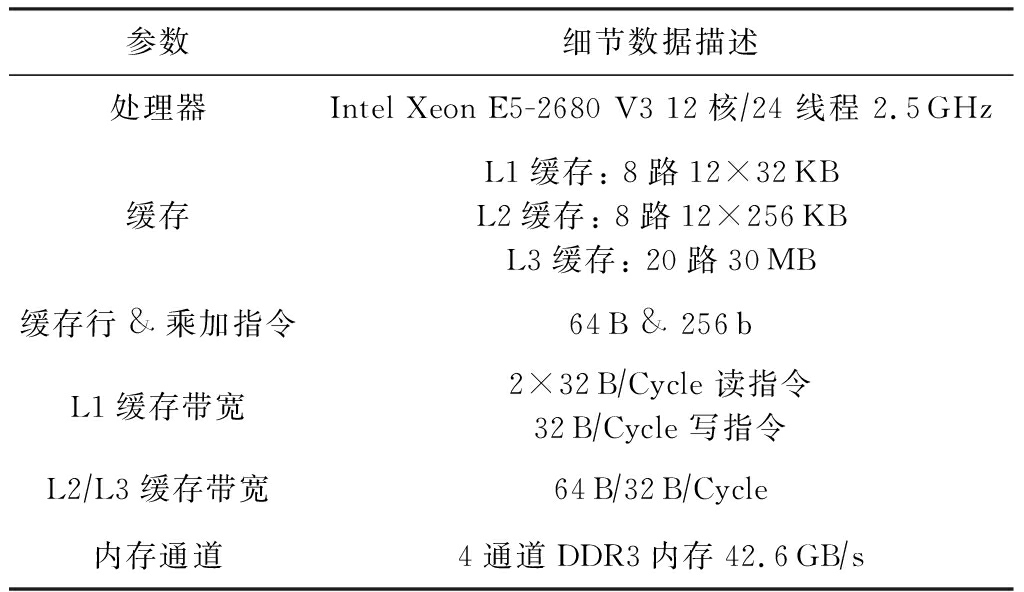
参数细节数据描述处理器Intel Xeon E5-2680 V3 12核∕24 线程 2.5GHz缓存L1缓存: 8路12×32KBL2缓存: 8路12×256KBL3缓存: 20路30MB缓存行&乘加指令64B & 256bL1缓存带宽2×32B∕Cycle 读指令32B∕Cycle 写指令L2∕L3缓存带宽64B∕32B∕Cycle内存通道4通道DDR3内存42.6GB∕s
我们详细介绍PPR性能模型,该模型分为3个阶段:执行阶段、访存阶段和反馈优化阶段.执行阶段预测计算指令和访存指令在核内的执行开销,访存阶段描述了内存层次之间数据的传输开销,反馈优化阶段则汇总和分析建模信息从而指导瓶颈优化.
在高性能领域,大量被使用的指令可以分为2类:计算指令和访存指令,其中计算指令表示计算数值所需要的计算操作,访存指令表示移动数据到寄存器的访存操作.这2种指令在处理器核内部独立端口调度运行.当程序需要的数据全部都缓存在L1 cache时,寄存器访问数据不需要额外的数据传输,那么完成所有的计算和访存指令则代表程序的结束.由于不同处理器指令执行能力差别很大,为了清晰地描述模型的功能,当前我们基于Intel Haswell 微架构E5-2680 V3搭建该模型,该架构1个周期支持2次浮点或者2次FMA计算以及2个Load和一个Store操作.最终2种指令执行所花费的最大时间将会是执行阶段的开销.
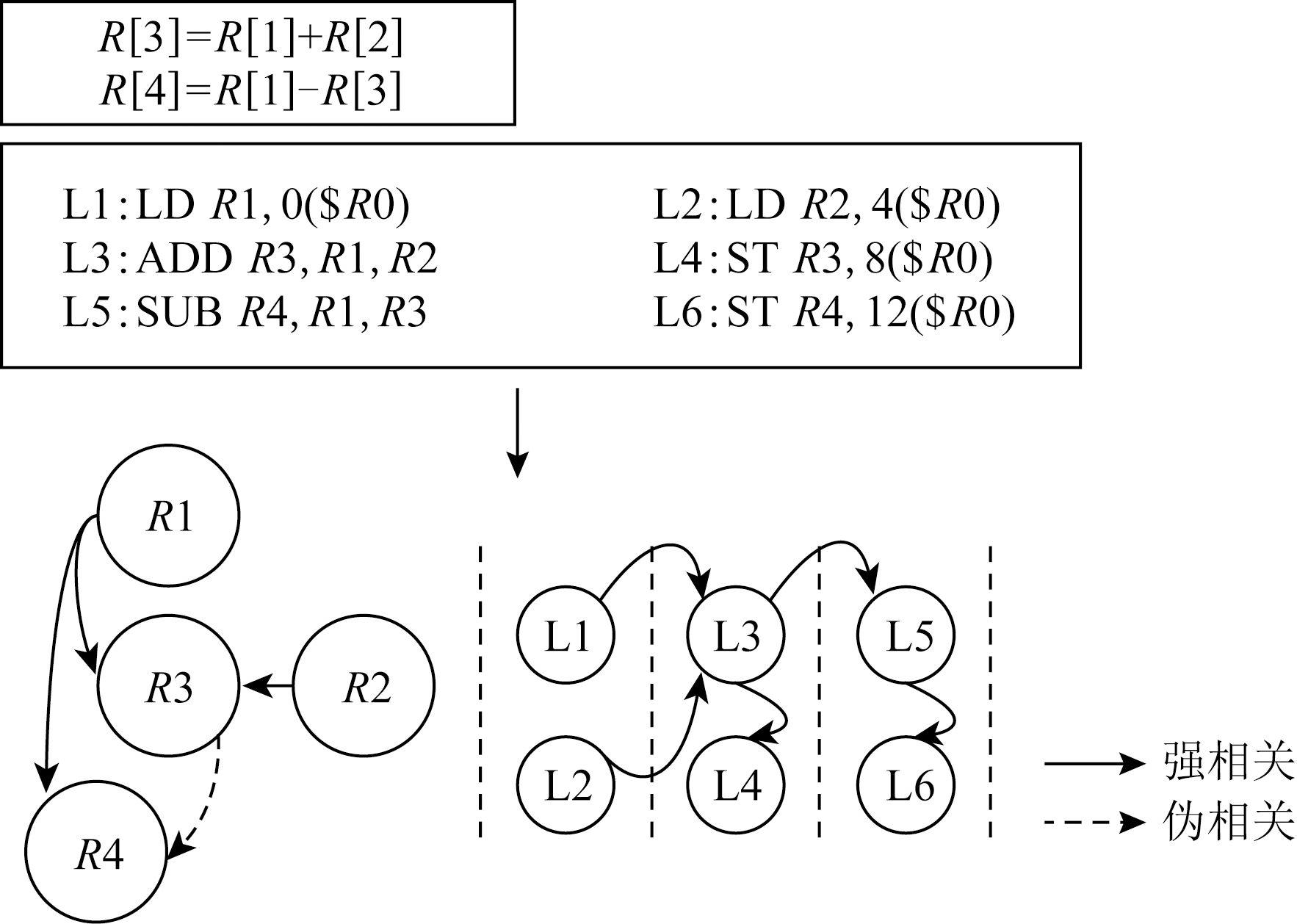
Fig. 2 Schematic for instruction DAG
图2 指令依赖DAG示意图
我们详细描述指令建模流程,在建模特定应用程序时,首先分析汇编后的代码得知程序包含的加法指令、乘法指令、FMA指令、Load指令和Store指令数量分别为:A,M,IFMA,L,S,则A,M,IFMA条计算指令被调度到执行端口执行,而L,S条访存指令被调度到访存端口执行.同时这些指令之间蕴含着先后顺序和数据依赖关系,因此为了充分模拟指令的执行时间,我们构建一个有向图(DAG)分析指令的数据依赖,最终通过模拟DAG在硬件上的执行过程建模指令的执行开销.如图2所示,以一个简单的程序为例,首先代码被编译为汇编指令,其中包含2条浮点计算指令、2条Load指令和2条Store指令,其次通过分析指令间数据依赖关系构建SDAG,并且以处理器双发射和数据forwarding为例,映射出指令执行流水线,最终计算指令花费时间加上等待时间即可得到指令开销.2类指令执行时间最大值即为执行阶段的时间,通过式(1)得出:
Tprocess_phase=max(SDAG(A,M,IFMA),SDAG(L,S)).
(1)
访存阶段主要建模数据在缓存之间以及主存间的传输开销.我们采用的测试平台是3级cache和主存的多级内存层次结构,各级cache的大小、延迟和传输速率都不尽相同,数据可能出现在缓存或者主存的任何一个内存层次中,当访存指令请求数据时会先查找最近的缓存,如在这一级请求失效则会请求更远的数据层次,最终依次把数据从查询到的缓存传到L1 cache.与此同时,cache的数据预取机制可以无阻塞传输可能需要用到的数据到更近的缓存,从而降低数据的访问延迟开销.但是当前cache设计只针对规则访存达到很好的预取,因此为了充分模拟cache的特性,如图3所示,访存阶段首先把数据标记为规则和非规则访存,分2种情况建模数据传输开销.
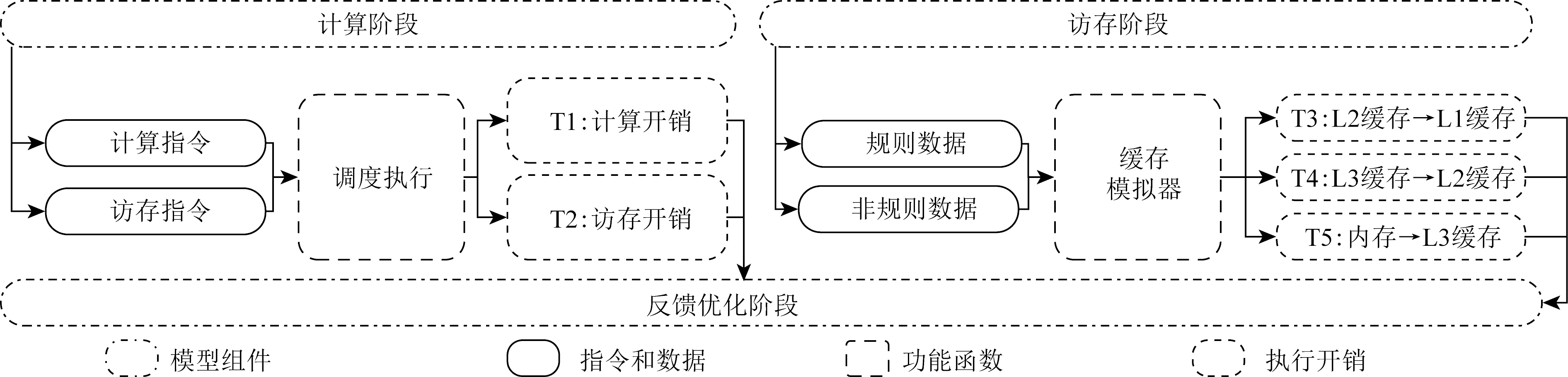
Fig. 3 Three components and execution flow of the PPR model
图3 PPR模型的3个组件和执行流程
1) 规则访存条件.被访问的数据保存在连续的地址空间或者小跨步的地址空间,且小跨步为不超过一个cache line大小的等段式跨越访存.在CPU设计中,数据预取占据了很高的地位,主要原因充分利用无阻塞cache在多级缓存之间同时传输数据,可以最大化cache高带宽特征.为了验证Haswell架构的预取策略,我们设计了大量实验得知 L2 cache和L3 cache对规则访存有很高的预取效率,而L1 cache为了保障受限的空间不被大量未使用的数据占用,以及避免预测机制去竞争有限的带宽,几乎没有使用预取策略.在访问规则数据时,我们可以假设L2 cache 以及之后数据访问延迟被预取机制完全隐藏,数据传输路径上的最小带宽即为传输速度.所需要的数据传输时间为
(2)
其中,Regular_data是规则访存的数据量,Min_Bandwidth为数据所在内存层次传输到L2 cache的最小带宽.
2) 非规则访存条件.被访问的数据保存在超出跨步大小或者随机的地址空间.但是随机的非规则访存数据可能在同一个cache line中,如果假设数据传输大小等于全部访存数据次数个cache line,预测则会大大高于真实的传输次数,此外,非规则访存通常和规则访存在程序中相伴出现,单纯模拟非规则访存也无法精确预估访存开销.因此为了精确预测访存开销,我们设计一个轻量级的cache模拟器建模硬件读取数据时的传输行为.该模拟器的结构如图4所示,构建方法为:
① 读取机器的配置.获取机器上各级cache的大小和组个数,模拟cache间组相联映射构建cache表,组内每个cache line最初赋值为invalid,以表明该cache line没有缓存任何数据.同时,通过使用修改的LRU机制模拟Intel的Smart Cache,并且加入cache替换和预取策略.
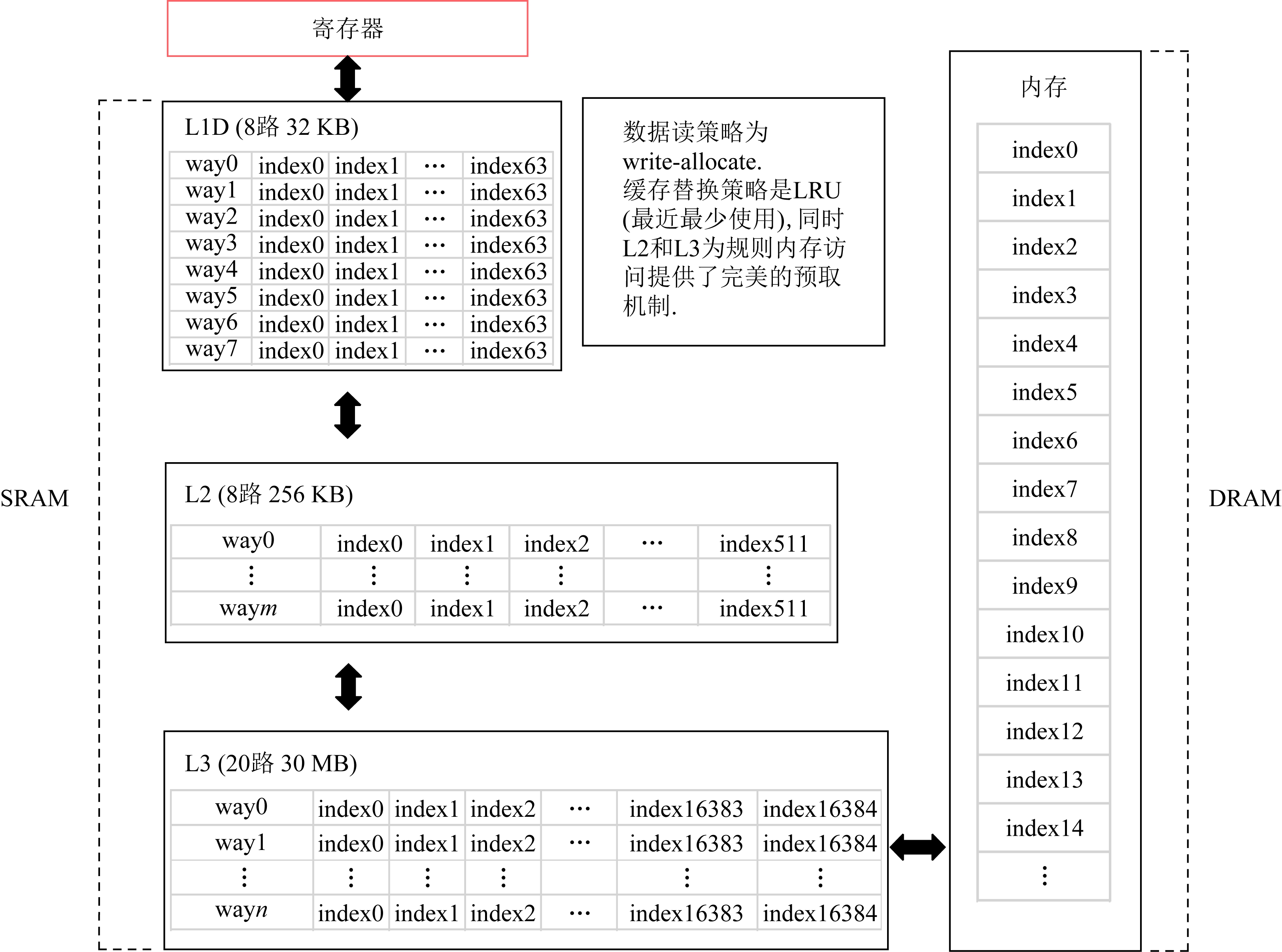
Fig. 4 Multi-level cache simulator
图4 多层次的cache模拟器
② 根据应用访存顺序构建访存序列.首先我们把需要访存的数据按照cache line大小划分和编号,同时标记需要访问的cache line为规则访存或者非规则访存,例如(index1-0,index3-1,index5-1,index2-0)(0代表规则,1代表非规则),该序列主要为了仿真读取cache line的访问顺序.
③ 输入访存序列到cache模拟器.cache模拟器依次读取序列的各个cache块号.我们标记cache miss次数分别是L1_miss,L2_miss和L3_miss, cache line的大小为CL(例如,64 B).模拟器首先如果在L1表查找到该序号则使用LRU策略标记为最新使用过的块,否则先使L1_miss+1,然后去L2表寻找该cache块是否存在,如果存在则把该cache块加入到L1表中,并且判断该序列是否为规则访存,如果是,则预取L3的下一块数据到L2表,如果当前数据L2表不存在则使L2_miss+1,然后进一步寻找L3表,并且重复上述的查找替换操作.访存开销为
TRAM_phase_for_irregular=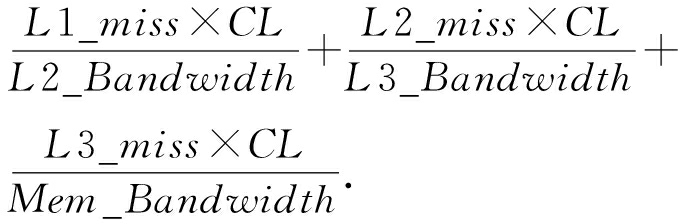
(3)
其中L2_Bandwidth,L3_Bandwidth,Mem_Bandwidth分别为L2到L1,L3到L2和主存到L3的带宽.
由于计算阶段和访存阶段可以并发运行:
PerfPPR=((A+M+2IFMA)×CPU_freq)
(max(SDAG(A,M,IFMA),SDAG(L,S)+
T(Regular_data)+T(IrRegular_data))).
(4)
其中,PerfPPR为基于PPR模型的性能预测,CPU_freq为处理器频率,Regular_data为规则访存数据,IrRegular_data为非规则访存数据.
两者中的最大值即为程序的执行时间,此式(4)则预测出程序的性能.最后通过分析最大时间作为性能瓶颈,反馈开发者优化相应部分.
我们挑选了佛罗里达稀疏矩阵库[17]的部分真实矩阵,借助PPR 模型建模和预测SpMV性能,并且找出性能瓶颈,最终针对瓶颈提出针对性的矩阵优化策略.
本节我们首先使用稀疏矩阵库中13个矩阵来验证PPR模型的正确性,并且与ECM模型对比(使用Kerncraft和Pycachesim工具建模SpMV),进而在建模的基础上找到性能瓶颈并提出优化方案.最后,我们比较了优化后模型预测和实际测量的差异.
用于建模的稀疏矩阵来自于广泛使用的矩阵集如表2所示,这些矩阵具有各种不同的稀疏分布.同时我们的压缩稀疏行(compressed sparse row, CSR)计算内核也使用循环展开和数据对齐等优化, 64 b浮点精度也更符合在实际应用中的效果.
Table 2 Selected 13 Sparse Matrices and Scales
表2 选择的13个稀疏矩阵及其规模
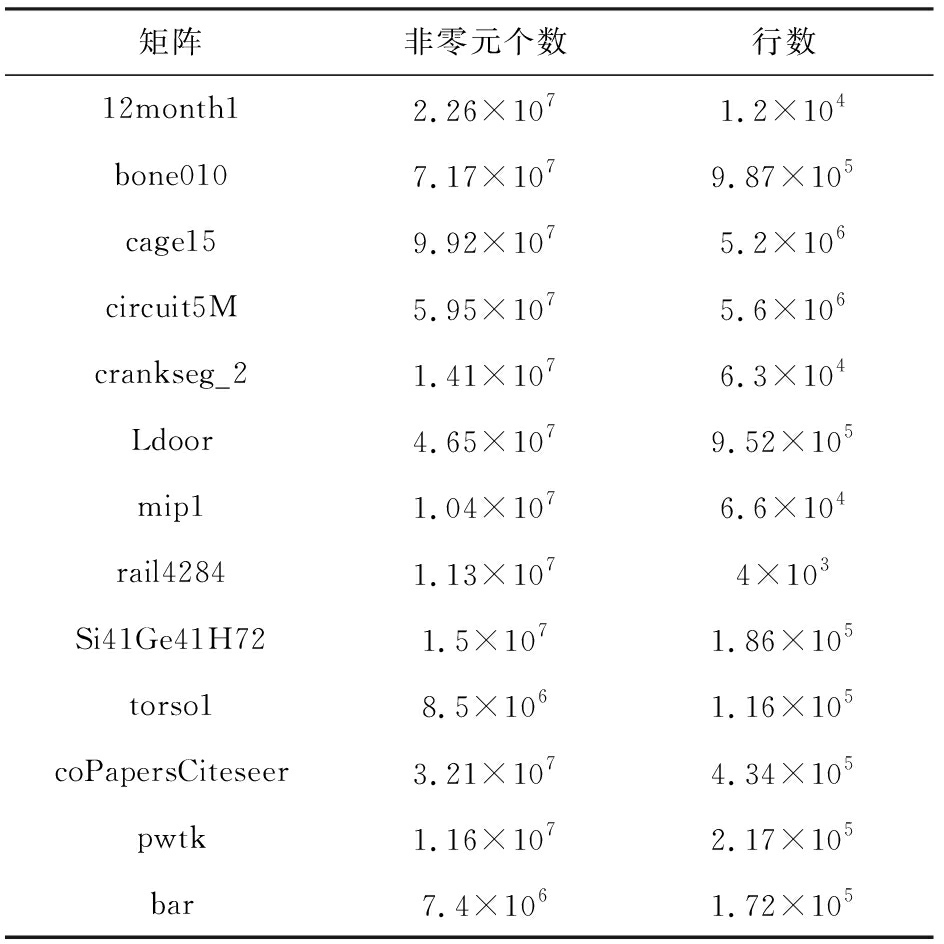
矩阵非零元个数行数12month12.26×1071.2×104bone0107.17×1079.87×105cage159.92×1075.2×106circuit5M5.95×1075.6×106crankseg_21.41×1076.3×104Ldoor4.65×1079.52×105mip11.04×1076.6×104rail42841.13×1074×103Si41Ge41H721.5×1071.86×105torso18.5×1061.16×105coPapersCiteseer3.21×1074.34×105pwtk1.16×1072.17×105bar7.4×1061.72×105
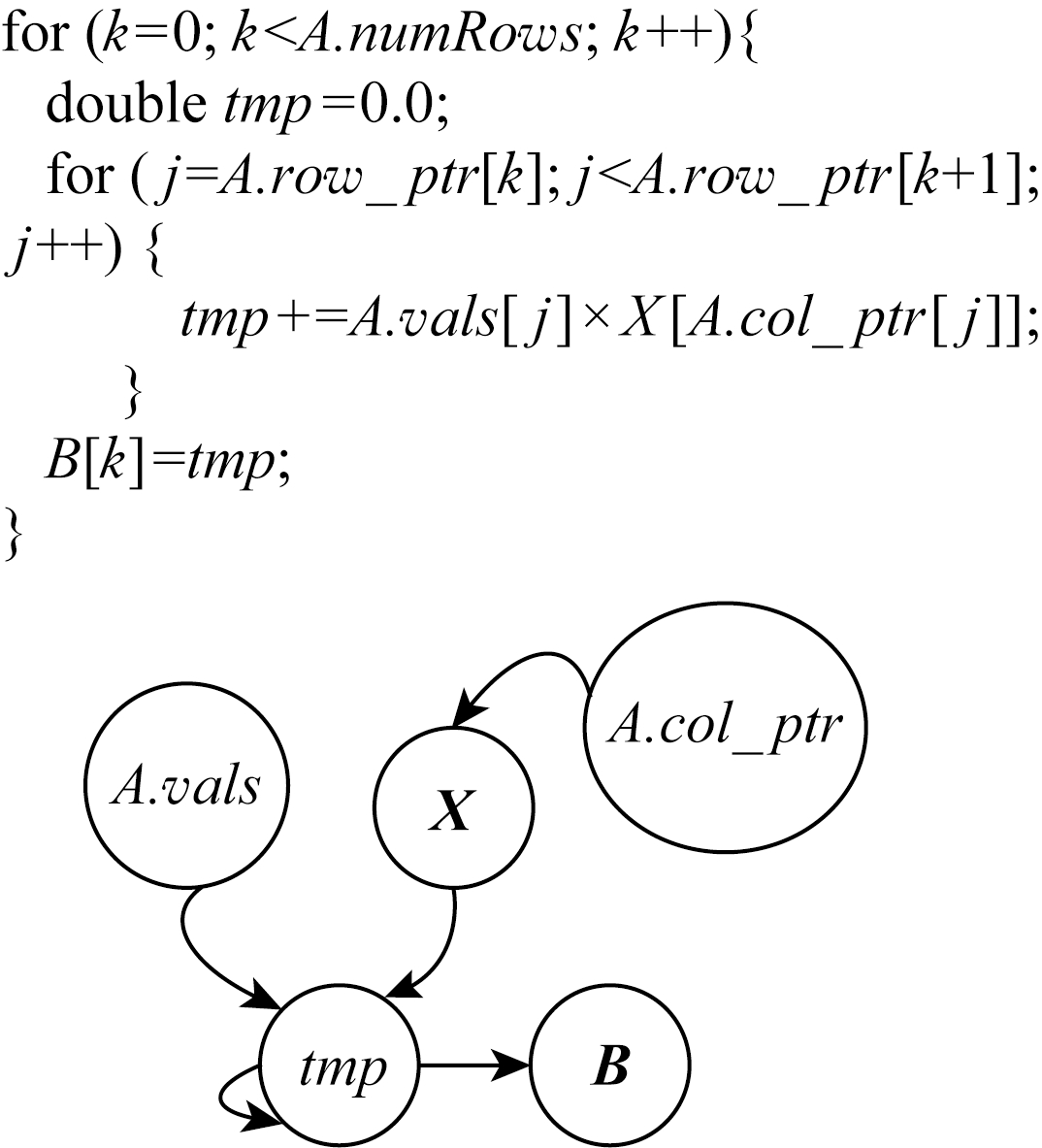
Fig. 5 Pseudo-code for CSR-based SpMV
图5 基于CSR格式的SpMV伪代码
基于CSR格式的SpMV伪代码如图5给出.在“执行阶段”,我们首先基于伪代码上构建指令数据依赖图,其中向量X的数据读入依赖A.col_ptr的结果,累加tmp则依赖于A.vals和X的结果.由于Haswell的1个周期可发射4条指令,编译器通过使用多个寄存器可以生成相互独立的累加指令,但是Load指令需要的数据依赖无法避免.而对于一个稀疏矩阵,令其行、列和非零元分别为R,C,NNZ,则整型数组A.row_ptr的大小为(R+1)×4 B,整型数组A.col_index的大小为NNZ×4 B,双精度数组A.vals的大小为NNZ×8 B,双精度向量X的大小是C×8 B.伪码中的乘法和加法分别含有NNZ条加法和NNZ条乘法指令,此外访问A.row_ptr需要R+1条Load指令,访问A.col_index需要NNZ条Load指令,访问A.value需要NNZ条Load指令,访问向量X需要NNZ条Load指令,输出向量B需要R条Store指令.对于“执行阶段”,通过式(1),在执行计算指令上花费的时间是NNZ个周期,由于访存指令的数据依赖,导致访问X有3个周期的指令延迟,则执行访存指令上花费的时间是5×NNZ个周期.通过循环展开和乱序执行可以使计算指令和访存指令分开执行,则通过式(1),最终花费在执行阶段的时间为5×NNZ个周期.
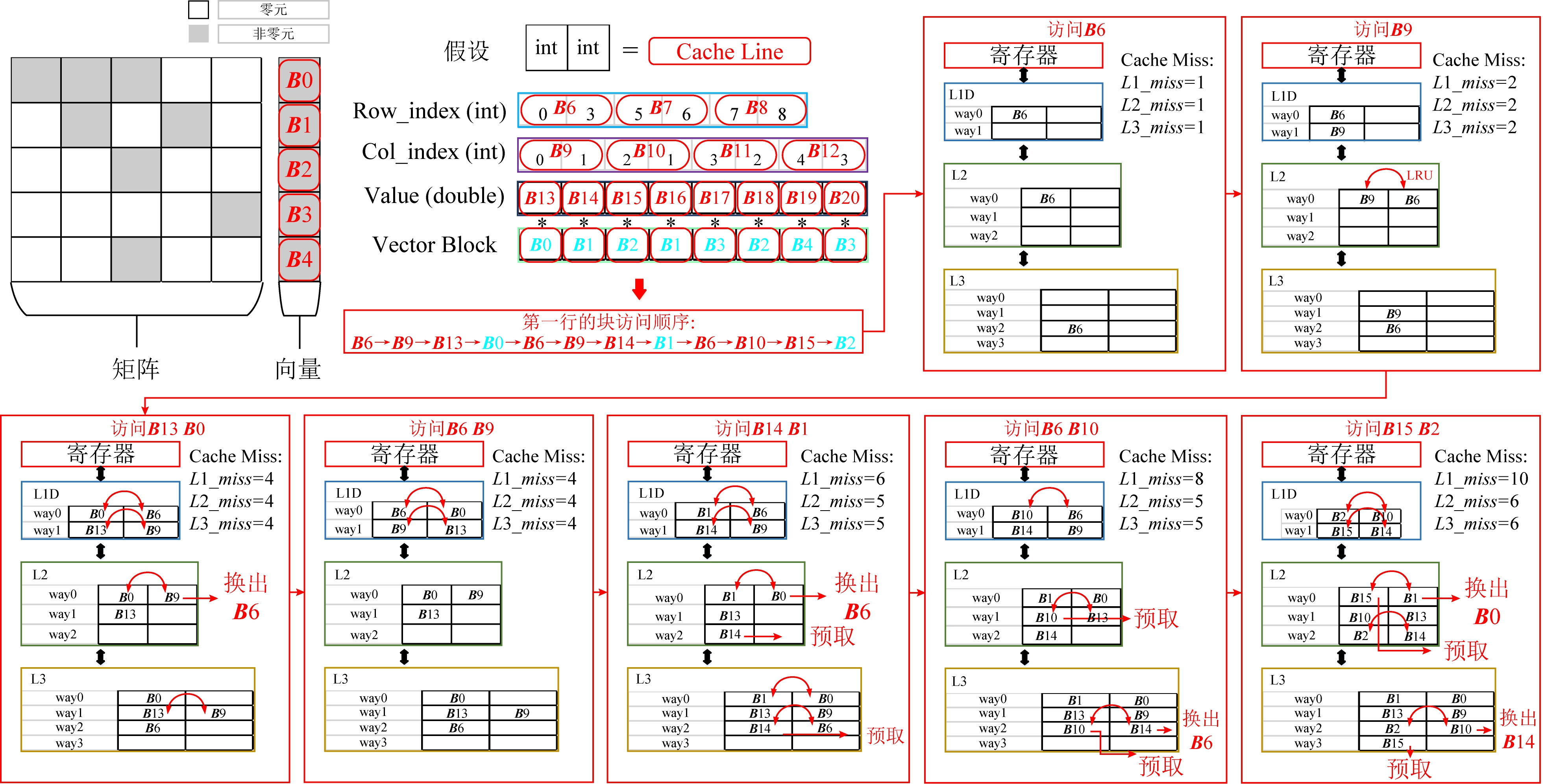
Fig. 6 Schematic work-flow of cache simulator for a fragment of sparse matrix
图6 用于稀疏矩阵片段仿真cache模拟器的执行示意图
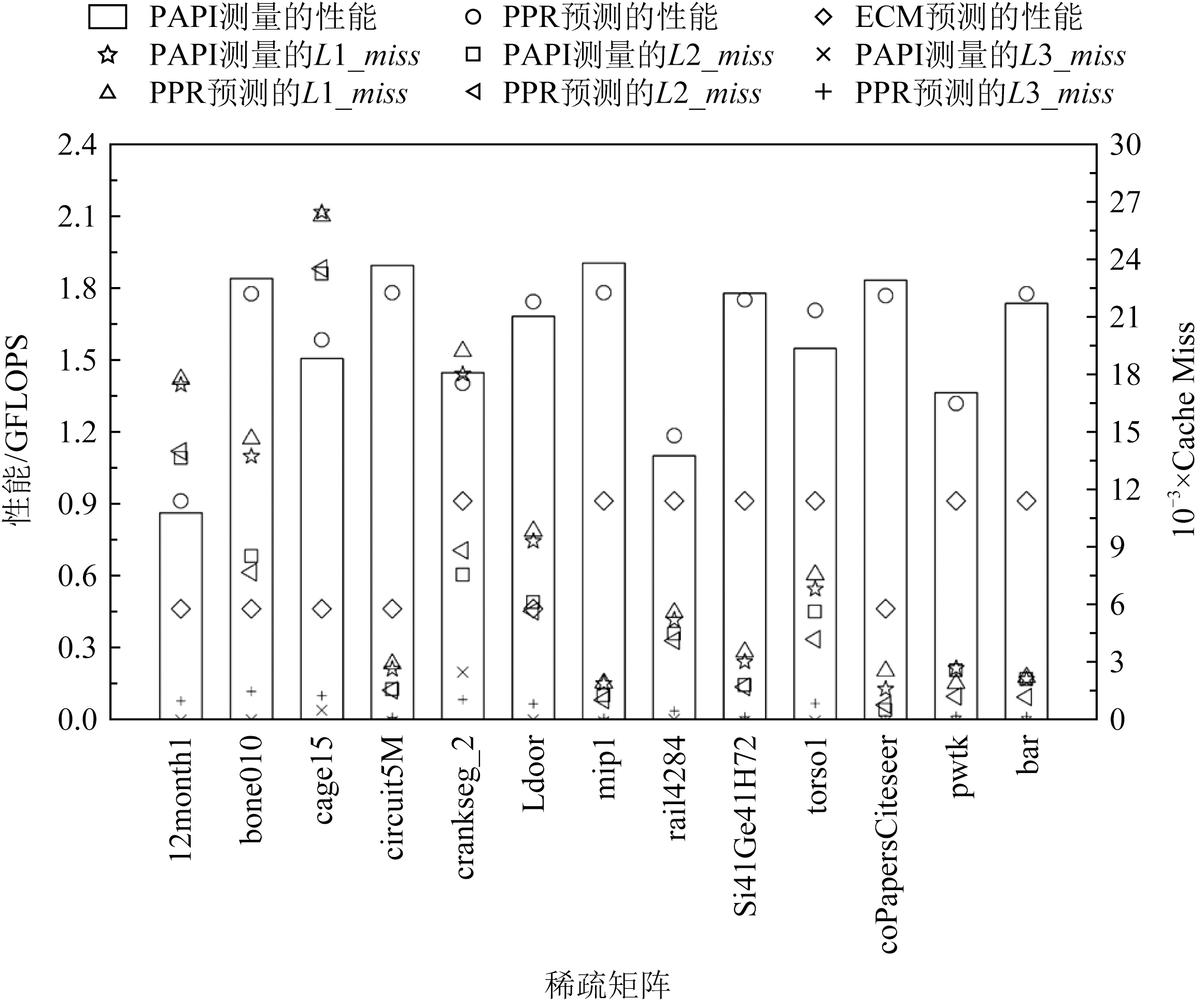
Fig. 7 Comparison of PPR model with actual measurement and ECM model
图7 PPR模型与实际测量和ECM模型的对比
对于“访存阶段”,模型主要建模的非规则访存开销是向量X的数据传输.如图6所示,我们将矩阵和向量的数据以cache line为大小划分为单个小分块,分别标记出规则和非规则访存,并构建访问序列.根据3.2节中提到的建模方法,通过读取目标机器的硬件参数来构建cache模拟器.模拟器依次读取访问序列并记录缓存未命中次数.图6给出了模拟器计算矩阵1行的示意流程图.首先,按照访问的顺序依次读取数据到cache中,其中模拟器对规则访存的数据实现了充分的预取,对非规则访问的数据则逐级读入.具体来说,模拟器标记行偏移、列偏移和值数组为规则访存数据,标记向量为非规则访存数据,在读取规则访存数据1个分片的同时,远端的cache也同时传输需要访问的下一个分片到上一级cache,而对于读取的非规则访存数据,则按照传输顺序,逐步传输到最上层的cache.同时,该模拟器记录了传输所带来的各级cache miss,使用式(3)得出访存时间,最终使用式(4)得到了各个矩阵对应的性能. 如图7所示,横坐标表示我们挑选的13个稀疏矩阵,左侧纵坐标为矩阵的浮点性能,单位GFLOPS.右侧纵坐标表示各级内存层次中的cache miss次数.图7的顶部显示了不同形状代表的不同含义.其中测量的L1,L2,L3缓存未命中使用了PAPI[18]工具统计,以及使用cache模拟器模拟的各级cache miss在图7中用不同形状的图标标记.通过使用PPR模型及式(4)计算的性能用圆圈标记,ECM模型预测的性能则用菱形标记.观察发现,使用cache模拟器模拟的cache miss次数十分接近于PAPI测量的cache miss.相比之下,使用PPR计算出的性能相比ECM模型预测更接近于真实测量,可以大大提升预测精度.结果也间接地反映了模型和cache模拟器的准确性.
从图7中明显看出L2 cache miss在部分矩阵计算时数量较高,原因是访问CSR格式矩阵对应列的向量X导致重复的数据传输,并且结合分析SpMV的建模结果,我们发现主要的时间花费和瓶颈是非规则数据的传输开销.为了解决这个问题,可以通过改变稀疏矩阵访问模式去增加向量X的重用性以及减少数据分片的冗余传输,进而降低数据传输开销,增加浮点运算效率.
对于降低数据传输开销,矩阵分块是一种用于优化数据重用的典型技术.一个m×n的稀疏矩阵可以在逻辑上被划分为r×c块,并且每个块通常包含至少1个非零元素.在处理SpMV计算时,每个块可以把向量的一部分保存在寄存器中,用来重用向量X中相应的元素,以增加向量数据的局部性.这种优化方法叫作分块的CSR,是压缩稀疏行存储格式的一种变种,它也简称为BCSR.该格式连续存储同一块的所有元素,块之间则以行主序存储.BCSR也降低稀疏矩阵的列索引(每个块1个而不是每个非零元1个),也减少了内存传输数量.但是,统一的分块大小需要填充显式的零元素,从而导致额外的计算和数据传输,也成为使用BCSR格式的挑战.
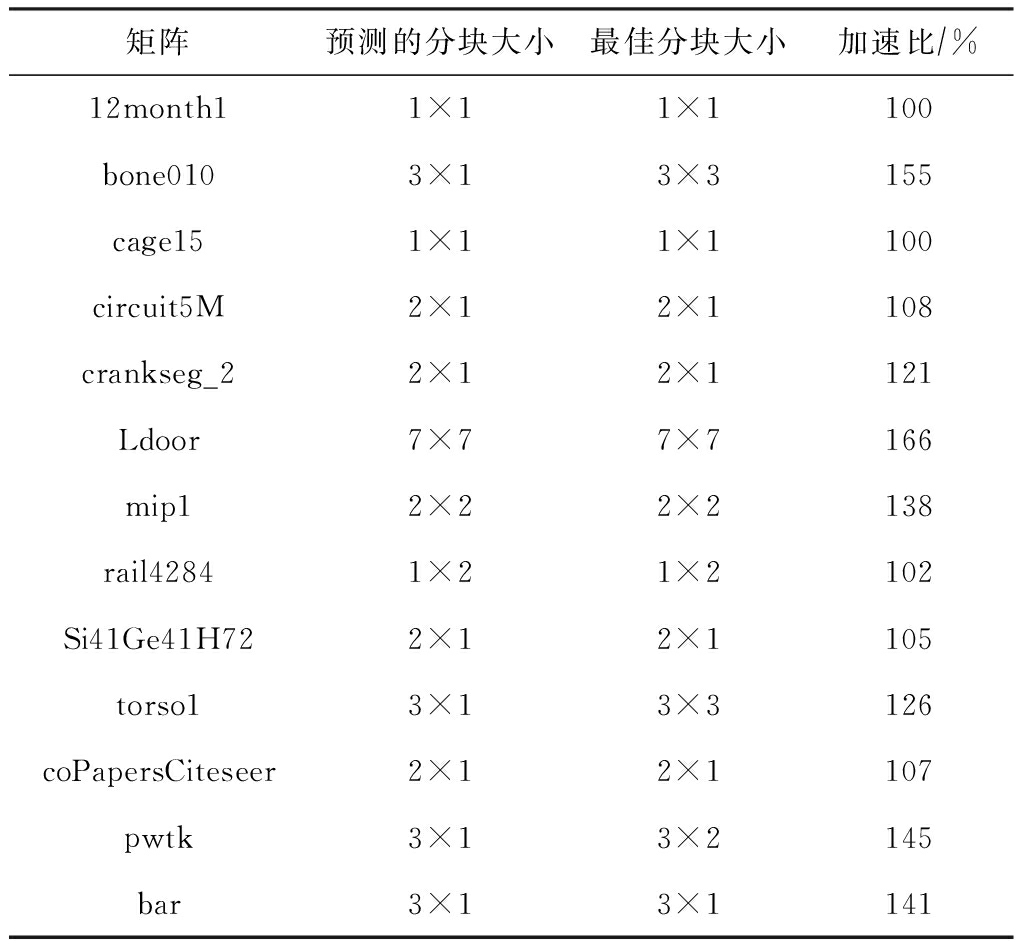
基于以上原理,我们选择BCSR格式并且使用PPR模型解决挑选最优分块问题.传统方法一般采用机器学习或统计方法来预测最优分块形状,其预测在一定条件下是有效的,但预测精度经常不稳定.因此我们使用PPR模型预测计算指令开销并构建访存序列以建模BCSR算法访存开销.通过读取输入矩阵,我们可以得到各种分块下的指令开销和各级cache miss次数,预测出每种分块的性能,最终给出了最优的分块方案.如表3所示,我们为13个矩阵构建BCSR模型并给出预测的最佳分块.通过和实际测量的最佳分块对比,模型的预测十分接近于最佳结果,并且带来了平均124%的性能加速比.同时我们也考虑了建模开销,通过对64种分块大小性能建模和预测,该方法平均花费12个SpMV时间,低于直接执行的64个SpMV时间,相比于直接运行得到的性能,我们的方法大大节约了选择最优参数的开销.
Table 3 Optimal Block Sizes and Speedup
表3 最佳的分块大小及加速比
矩阵预测的分块大小最佳分块大小加速比∕%12month11×11×1100bone0103×13×3155cage151×11×1100circuit5M2×12×1108crankseg_22×12×1121Ldoor7×77×7166mip12×22×2138rail42841×21×2102Si41Ge41H722×12×1105torso13×13×3126coPapersCiteseer2×12×1107pwtk3×13×2145bar3×13×1141
我们使用PPR模型建模规则访存应用-卷积.根据我们的调研发现,直接卷积计算(不变换为矩阵乘法)在不同的数据规模和不同的机器结构下最有效的优化方法差异很大.以一维卷积为例(其他卷积方法都是建立在一维卷积基础上),使用SSE,AVX或者AVX2指令集进行4或者8个单精度浮点计算对程序的影响很大,同时对于当前建模机器中向量寄存器Load指令而言,对齐数据花费时间是非对齐数据时间的一半,但是使用对齐的数据则会增加数据集的大小,而增加数据集大小在不同规模下会影响cache miss数量.所以,我们使用PPR模型定量执行指令、访存指令、cache和内存传输时间,给出模型预期的性能,并且和真实测试到的性能作对比.最后给出在多个指令集支持和不同数据大小上的最佳优化方案.
从算法1可以看出,该卷积1次读取16个kernel数据和16个输入数据去执行16个加法和16个乘法操作.我们可以看出数据具有极好的连续性,第2次卷积操作会重用上一次的15个数据.16次卷积计算则导致16个单精度浮点数传输,占据2个cache line.
算法1. Naïve计算.
输入:输入数据IN、长度length、核数据KERNEL、核长度kernel_length;
输出:输出数据OUT.
① for (i=0;i<(length-kernel_length);
i=i+1) do
② tmp←0;
③ for (k=0,k<kernel_length; i=i+1)
do
④ tmp←tmp+IN[i+k]×
KERNEL[kernel_length-k-1];
⑤ end for
⑥ OUT[i]←tmp;
⑦ end for
在16次卷积操作的过程中,分别读取数据IN中16个元素更新数据OUT的值,其中包含16×16个乘加指令,并且还产生16×16个Load和16个Store指令.通过使用多个寄存器和指令重排,可以完全消除指令之间的数据依赖.对于当前架构,1个周期可以执行2个乘加指令,因此计算指令开销为16×16 2=128个周期,并且1个周期可以执行2个Load指令和1个Store指令,因此访问指令开销为16×16
2=128个周期,并且1个周期可以执行2个Load指令和1个Store指令,因此访问指令开销为16×16 2=128个周期.访存阶段,由于计算的数据都是规则地址空间,访问数据的延迟可以被预取机制覆盖,因此2个cache line需要消耗L2 cache到L1 cache的2个周期,L3 cache到L2 cache的4个周期,主存到L3 cache的10个周期,最后我们可以推断出不同数据大小的GFLOPS性能.当数据都在L1 cache时,CPU主频被锁定在2.7 GHz,通过式(4)可计算出性能为(16×16×2)
2=128个周期.访存阶段,由于计算的数据都是规则地址空间,访问数据的延迟可以被预取机制覆盖,因此2个cache line需要消耗L2 cache到L1 cache的2个周期,L3 cache到L2 cache的4个周期,主存到L3 cache的10个周期,最后我们可以推断出不同数据大小的GFLOPS性能.当数据都在L1 cache时,CPU主频被锁定在2.7 GHz,通过式(4)可计算出性能为(16×16×2) (max(128,128)
(max(128,128) 2.7)=10.8 GFLOPS.当数据在L2 cache时,通过式(4)可计算出性能为(16×16×2)
2.7)=10.8 GFLOPS.当数据在L2 cache时,通过式(4)可计算出性能为(16×16×2) (max(128,128+2)
(max(128,128+2) 2.7)=10.63 GFLOPS.当数据在L3 cache时,通过式(4)可计算出性能为(16×16×2)
2.7)=10.63 GFLOPS.当数据在L3 cache时,通过式(4)可计算出性能为(16×16×2) (max(128,128+4)
(max(128,128+4) 2.7)=10.47 GFLOPS.当数据在主存时,通过式(4)可计算出性能为(16×16×2)
2.7)=10.47 GFLOPS.当数据在主存时,通过式(4)可计算出性能为(16×16×2) (max(128,128+10)
(max(128,128+10) 2.7)=10.02 GFLOPS.具体指令数量和性能如表4所示:
2.7)=10.02 GFLOPS.具体指令数量和性能如表4所示:
Table 4 Measured and Predicted Performance Using Algorithm 1
表4 算法1测量及预测的性能

操作L1容量L2容量L3容量内存容量加法和乘法∕周期128128128128Load指令&Store指令&传输开销∕周期128128+2=130128+4=132128+10=138预测的性能∕GFLOPS10.8010.6310.4710.02测量的性能∕GFLOPS10.5210.3810.179.81
从表4可以看出,无论数据在任何一层的内存层次中,卷积的主要瓶颈为执行计算指令和访存执行的开销.我们将介绍2种不同的优化方法,并分析优化所能带来性能.
SIMD(single instruction multiple data)指单指令多数据技术,从奔腾II处理器系列引入IA-32架构,并且扩展了128 b SSE指令和256 b AVX,AVX2指令的支持.使用SIMD可以向量化计算和访问多个连续数据,从而大大降低指令执行时间.此外,对于向量化Load和Store指令需要确保被访问的首地址按照16 B对齐,访问未对齐数据所花费的时间是对齐数据的2倍.接下来,我们将使用AVX2指令实现数据非对齐和对齐2个版本,最终给出优化建议.
算法2设计了AVX2指令的非对齐算法,一次计算使用AVX2指令同时操作8个单精度浮点数,但是由于数据填充在连续的空间中,访问数据的间隔为4 B,不能保证16 B的访存对齐,因此必须选择_mm256_loadu_ps接口使用非对齐向量访问指令读取非对齐数据.
算法2. AVX展开不对齐计算.
输入:输入数据IN、长度length、核数据KERNEL、核长度kernel_length;
输出:输出数据OUT.
① _m256kernel_reverse[kernel_length];
② for (i=0;i<kernel_length;i=i+1) do
③ kernel_reverse[i] ←_mm256_broadcast_ss
(KERNEL[kernel_length-i-1]);
④ end for
⑤ for (i=0;i<(length-kernel_length 16);
16);
i=i+1) do
⑥ acc0,acc1←_mm256_setzero_ps();
⑦ for (k=0;k<kernel_length 16;k=
16;k=
k+1) do
⑧ data_offset←i×16+k×16;
⑨ for (l=0;l<4;l=l+1) do
⑩ for (m=0;m<4;m=m+1) do
 data_block←_mm256_loadu_ps
data_block←_mm256_loadu_ps
(IN[0]+data_offset+l+
m×4);
 acc0←_mm256_fmadd_ps
acc0←_mm256_fmadd_ps
(kernel_reverse[k×16+l+
m×4],data_block,acc0);
 data_block←_mm256_loadu_ps
data_block←_mm256_loadu_ps
(IN[0]+data_offset+l+
m×4+8);
 acc1←_mm256_fmadd_ps
acc1←_mm256_fmadd_ps
(kernel_reverse[k×16+l+
m×4],data_block,acc1);
 end for
end for
 end for
end for
 end for
end for
 _mm_storeu_ps(OUT[0]+i×16,
_mm_storeu_ps(OUT[0]+i×16,
acc0,acc1);
 end for
end for
由此可以算出,当前架构AVX2指令1个周期可以执行2个乘加指令,每个乘加指令操作8个单精度浮点数,因此计算指令开销为(16×16) (8×2)=16个周期.此外由于使用非对齐的访存指令,1个周期可以执行一个非对齐的Load指令和半个Store指令,因此访问指令开销为(16×16)
(8×2)=16个周期.此外由于使用非对齐的访存指令,1个周期可以执行一个非对齐的Load指令和半个Store指令,因此访问指令开销为(16×16) 8=32个周期.数据在内存层次上的传输和算法1类似.当数据都在L1 cache时,性能则为(16×16×2)
8=32个周期.数据在内存层次上的传输和算法1类似.当数据都在L1 cache时,性能则为(16×16×2) (max(16,32)
(max(16,32) 2.7)=43.2 GFLOPS.当数据在L2 cache时,通过式(4)可计算出性能为(16×16×2)
2.7)=43.2 GFLOPS.当数据在L2 cache时,通过式(4)可计算出性能为(16×16×2) (max(16,32+2)
(max(16,32+2) 2.7)=40.66 GFLOPS.当数据在L3 cache时,通过式(4)可计算出性能为(16×16×2)
2.7)=40.66 GFLOPS.当数据在L3 cache时,通过式(4)可计算出性能为(16×16×2) (max(16,32+4)
(max(16,32+4) 2.7)=38.40 GFLOPS.当数据在主存时,通过式(4)可计算出性能为(16×16×2)
2.7)=38.40 GFLOPS.当数据在主存时,通过式(4)可计算出性能为(16×16×2) (max(16, 32+10)
(max(16, 32+10) 2.7)=32.91 GFLOPS.性能如表5所示:
2.7)=32.91 GFLOPS.性能如表5所示:
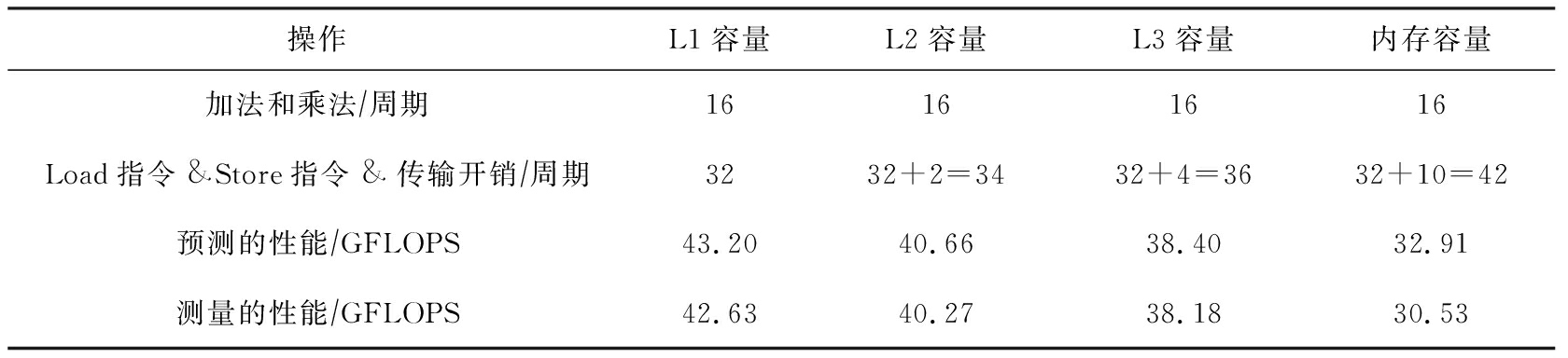
Table 5 Measured and Predicted Performance Using Algorithm 2
表5 算法2测量及预测的性能
操作L1容量L2容量L3容量内存容量加法和乘法∕周期16161616Load指令&Store指令&传输开销∕周期3232+2=3432+4=3632+10=42预测的性能∕GFLOPS43.2040.6638.4032.91测量的性能∕GFLOPS42.6340.2738.1830.53
从表5分析发现,算法2访存指令成为了性能瓶颈,因此我们优化非对齐的访存指令.算法3扩充数据到原有的4倍,使得每一次访存地址都按照16 B地址对齐,不过也带来了额外的数据传输.
算法3. AVX展开对齐计算.
输入:输入数据IN、长度length、核数据KERNEL、核长度kernel_length;
输出:输出数据OUT.
① _m256kernel_reverse[kernel_length];
② for (i=0;i<kernel_length;i=i+1) do
③ kernel_reverse[i]←_mm256_broadcast_ss
(KERNEL[kernel_length-i-1]);
④ end for
⑤ floatin_aligned[4][length];
⑥ for (i=0;i<4;i=i+1) do
⑦ memcpy(in_aligned[i],(IN[0]+i),
(length-i)×sizeof(float));
⑧ end for
⑨ for (i=0;i<(length-kernel_length 16);
16);
i=i+1) do
⑩ acc ← _mm256_setzero_ps();
 for (k=0;k<kernel_length
for (k=0;k<kernel_length 16;k=
16;k=
k+1) do
 data_offset←i×16+k×16;
data_offset←i×16+k×16;
 for (l=0,m=0;l<4&&m<4;l=
for (l=0,m=0;l<4&&m<4;l=
l+1,m=m+1) do
 data_block←_mm256_load_ps
data_block←_mm256_load_ps
(in_aligned[l]+data_offset+
l+m×4);
 acc←_mm256_fmadd_ps (kernel_reverse[k×16+l+m×4],data_block, acc);
acc←_mm256_fmadd_ps (kernel_reverse[k×16+l+m×4],data_block, acc);
 end for
end for
 end for
end for
 _mm_storeu_ps(OUT[0]+i×16,acc);
_mm_storeu_ps(OUT[0]+i×16,acc);
 end for
end for
算法3改进了访存指令开销,1个周期可以执行2个对齐的Load指令和1个Store指令,因此访问指令开销为(16×16) (8×2)=16个周期.为了保证每次访存数据按照16 B对齐,我们扩展数据为原始数据的4倍,使之16次计算数据量增加到了8个cache line.在不同数据规模的性能如表6所示:
(8×2)=16个周期.为了保证每次访存数据按照16 B对齐,我们扩展数据为原始数据的4倍,使之16次计算数据量增加到了8个cache line.在不同数据规模的性能如表6所示:
Table 6 Measured and Predicted Performance Using Algorithm 3
表6 算法3测量及预测的性能
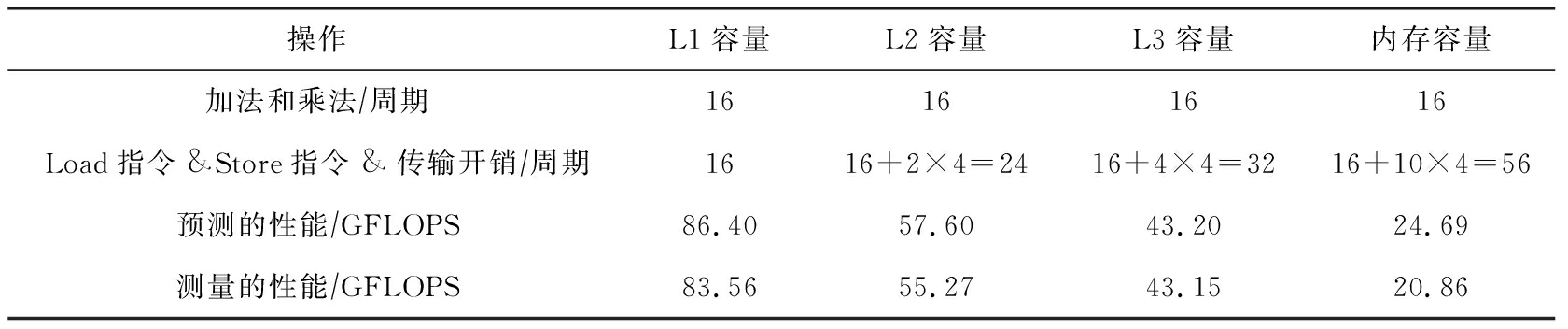
操作L1容量L2容量L3容量内存容量加法和乘法∕周期16161616Load指令&Store指令&传输开销∕周期1616+2×4=2416+4×4=3216+10×4=56预测的性能∕GFLOPS86.4057.6043.2024.69测量的性能∕GFLOPS83.5655.2743.1520.86
对比多种优化方案后,我们发现最佳优化方案取决于数据集的大小.在Haswell架构上,我们发现,当数据小于L3 cache大小时,选择数据对齐的优化算法(算法3)能够得到较高性能,而随着数据逐渐增大.非对齐算法(算法2)则更加合适.
我们详细介绍了PPR性能模型,并且详细描述了执行阶段、访存阶段及反馈优化阶段.然后我们将该模型应用到SpMV和一维卷积上,其中这2种算法是非规则访存和规则访存的典型代表.在建模SpMV时,我们实例化了cache模拟器的工作流程,输出各级cache miss次数,进而帮助反馈优化阶段分析各开销的时间占比.在优化时,我们选择了增加数据重用的BCSR格式,建模目标矩阵在各种分块大小上的指令和数据传输开销,进而得到最优的分块选择.此外,我们针对一维卷积的原始代码和2种优化代码分别建模,详细了解各种优化方法在不同数据量下的性能表现,给出优化建议.该工作现阶段主要是建模单核性能,在此基础上可以进一步提高PPR模型针对多核应用的性能建模和预测能力,揭示出多核的性能瓶颈,最终指导并行程序的性能优化.
[1]Press W H, Teukolsky S A. Biconjugate gradient method for sparse linear systems[J]. Computers in Physics, 1992, 6(4): 400-410
[2]Li Kenli, Yang Wangdong, Li Keqin. Performance analysis and optimization for SpMV on GPU using probabilistic modeling[J]. IEEE Transactions on Parallel and Distributed Systems, 2015, 26(1): 196-205
[3]Li Shigang, Hu Changjun, Zhang Junchao, et al. Automatic tuning of sparse matrix-vector multiplication on multicore clusters[J]. Science China Information Sciences, 2015, 58(9): 1-14
[4]Zitová B, Flusser J. Image registration methods: A survey[J]. Image and Vision Computing, 2003, 21(11): 977-1000
[5]Qadeer W, Hameed R, Shacham O, et al. Convolution engine: Balancing efficiency and flexibility in specialized computing[J]. Communications of the ACM, 2013, 41(3): 24-35
[6]Uhl A. Wavelet packet best basis selection on moderate parallel MIMD architectures[J]. Parallel Computing, 1996, 22(1): 149-158
[7]Chakrabarti C, Vishwanath M. Efficient realizations of the discrete and continuous wavelet transforms: From single chip implementations to mappings on SIMD array computers[J]. IEEE Transactions on Signal Processing, 1995, 43(3): 759-771
[8]Konstantinidis E, Cotronis Y. A quantitative roofline model for GPU kernel performance estimation using micro-benchmarks and hardware metric profiling[J]. Journal of Parallel and Distributed Computing, 2017, 107(1): 37-56
[9]Ilic A, Pratas F, Sousa L. Cache-aware roofline model: Upgrading the loft[J]. IEEE Computer Architecture Letters, 2013, 13(1): 21-24
[10]Stengel H, Treibig J, Hager G, et al. Quantifying performance bottlenecks of stencil computations using the execution-cache-memory model[C] 
 Proc of the 29th ACM on Int Conf on Supercomputing. New York: AMC, 2015: 207-216
Proc of the 29th ACM on Int Conf on Supercomputing. New York: AMC, 2015: 207-216
[11]Hammer J, Eitzinger J, Hager G, et al. Kerncraft: A tool for analytic performance modeling of loop Kernels[J]. Tools for High Performance Computing, 2017, 28(7): 1-22
[12]Buttari A, Eijkhout V, Langou J, et al. Performance optimization and modeling of blocked sparse kernels[J]. International Journal of High Performance Computing Applications, 2007, 21(4): 467-484
[13]Vuduc R, Moon H. Fastsparse matrix-vector multiplication by exploiting variable block structure[J]. High Performance Computing and Communications, 2005, 25(2): 807-816
[14]Kreutzer M, Hager G, Wellein G, et al. A unified sparse matrix data format for efficient general sparse matrix-vector multiply on modern processors with wide SIMD units[J]. SIAM Journal on Scientific Computing, 2014, 36(5): 401-423
[15]Choi J, Singh A, Vuduc R. Model-driven autotuning of sparse matrix-vector multiply on GPUs[J]. ACM SIGPLAN Notices, 2010, 45(5): 115-126
[16]Freeman J, Troyer A. Collaborative textual improvisation in a laptop ensemble[J]. Computer Music Journal, 2011, 35(2): 8-21
[17]Davis T,Hu Yifan. The University of Florida sparse matrix collection[J]. ACM Transactions on Mathematical Software, 2011, 38(1): 1-25
[18]Browne S, Dongarra J, Garner N, et al. A portable programming interface for performance evaluation on modern processors[J]. International Journal of High Performance Computing Applications, 2000, 14(3): 189-204
Xie Zhen, born in 1991. PhD. His main research interests include parallel algorithms, high performance computing and machine learning.
谢 震,1991年生.博士.主要研究方向为并行算法、高性能计算与机器学习.
Tan Guangming, born in 1980. PhD, professor and PhD supervisor. Senior member of CCF. His main research interests include high performance computing and parallel computing.
谭光明,1980年生.博士,教授,博士生导师,CCF高级会员.主要研究方向为高性能计算与并行算法.
Sun Ninghui, born in 1968. PhD, professor and PhD supervisor. Academician of the Chinese Academy of Engineering. His main research interests include high performance computing, parallel algorithm, and file system.
孙凝晖,1968年生.博士,教授,博士生导师,中国工程院院士.主要研究方向为高性能计算、并行算法及文件系统.