图像加密域可逆信息隐藏(reversible data hiding in encrypted image, RDH-EI)是一种对原始图像加密后,在密文图像中可逆地隐藏附加信息,在接收端从含附加信息的密文图像提取信息后,能无损重建原始图像的技术.RDH-EI结合密码学与信息隐藏技术,用来解决云存储场景中用户因图像所有权与管理权分离而产生的安全问题,已成为信息安全与云计算领域的研究热点[1-2].
近10多年发展,RDH-EI在隐藏容量、解密图像质量等方面取得了较好的进展.以隐藏容量为例,从早期算法不足0.01 bpp(bit per pixel)[3],逐步提高至0.3 bpp[4-7]和0.5 bpp[8],最新算法的隐藏容量已接近或超过1 bpp.而对RDH-EI中加密算法的安全性研究才刚刚起步.加密算法的安全性事关图像内容安全保护的成败,对RDH-EI算法至关重要[2].传统图像加密(如像素异或与置乱[9-10]、像素置乱等)方法很难直接用于RDH-EI算法.这是因为加密图像不存在像素间冗余,难以腾出空间用于隐藏附加数据并得到高质量的解密图像.因此,RDH-EI需要设计特殊的图像加密算法.
流密码加密[3-10]和块置乱加密[11-13]是RDH-EI常用的加密算法,流密码和块置乱加密算法具有简单、时间复杂度低的特点.然而,流密码加密方案已被证实无法抵抗唯密文攻击[2],且由于加密图像熵最大化,采用流密码加密的RDH-EI算法往往隐藏容量较低.相比于流密码加密,块置乱加密保留了图像块内像素值相关性,可有效提高RDH-EI算法的隐藏容量,然而,文献[14-16]的研究表明:置乱加密无法抵抗已知明文攻击.2008年Li等人[14]分析并证明了对于已知明文攻击,利用不少于logL(2(MN-1))对明文及其密文能获得较好的攻击效果,其中MN为图像大小,L为最大灰度值;2011年Li等人[15]分析文献[14]的算法时间复杂度,并基于二叉树查找原理降低了攻击算法的时间复杂度;2016年文献[16]基于选择明文攻击,得到了完全正确的置乱序列,正确估计出置乱序列所需要的明文-密文对数为logL(MN);其他针对像素置乱加密的已知明文攻击如文献[17-18].
上述针对置乱加密所提出的已知明文攻击,均是基于置乱加密前后像素值不变的特点来进行攻击.当置乱加密后的图像像素值发生改变,上述已知明文攻击的基本条件将不再满足,生成的加密图像不仅可以抵抗文献[2]中提出的唯密文攻击,同时也可以抵抗上述提到的已知明文攻击.在尽可能多地保留加密图像冗余度的条件下,为了提高加密图像的安全性,2018年Liu等人[19]提出了一种基于冗余信息转移的RDH-EI算法.该算法通过置乱图像的位平面改变原始图像的像素值,并有效提高了RDH-EI的嵌入容量.然而,我们研究发现[20],由于位平面置乱不改变像素位平面比特值,位平面置乱顺序在已知明文攻击下可以被精确估计.攻击者利用位平面置乱序列恢复原始图像的像素值,并估计块置乱序列导致密文图像内容泄露.
为提高安全性,RDH-EI加密算法不仅要改变像素值大小还应进一步改变像素比特值.基于这一观点,研究者提出了块调制-置乱图像加密方案[21-24].块调制-置乱图像加密算法思想如下:首先将图像划分为不重叠的图像块;接着,在同一个图像块内,从[0,255]范围内产生一个随机数对块内像素进行模运算,改变明文图像像素的值,我们称这一过程为“块调制”;最后,将模运算后的图像块根据密钥进行置乱.块调制-置乱加密结合模运算和分块置乱加密,在密文图像块中保留了明文图像块内差值信息,有效提高隐藏容量.同时,由于块调制-置乱加密改变了明文图像的比特值,加密图像可以抵抗文献[20]提出的已知明文攻击.
不过,由于块调制-置乱加密算法在密文图像块中保留了明文图像块内像素间部分相关性,块调制-置乱加密算法在已知明文攻击的条件下仍存在安全隐患.为此,本文提出一种基于图像差值块分类查找的已知明文攻击,可对块调制-置乱加密算法成功实施攻击.本文主要贡献有3个方面:
1) 定义差值直方图距离,通过明-密文差值图像迭代替换构建伪差值图像,明-密文伪差值直方图距离为0,使得在明-密文图像间建立等量关系成为可能.
2) 定义差值块立方均值ρ,将差值块分类并提出一种差值块分类查找的已知明文攻击方法,分析验证了块调制-置乱加密算法存在的安全隐患.
3) 分析已知明文攻击的时间复杂度,在保证加密图像空间冗余的前提下,给出抵抗已知明文攻击的解决方案.
兼顾加密图像的安全性和隐藏容量,最新RDH-EI算法的研究采用块调制-置乱图像加密[21-24]策略生成加密图像.块调制-置乱加密不仅改变了像素值,同时打乱像素位置.用户通过密钥K=(key1 key2)生成的密文图像不仅能抵抗文献[2]提出的唯密文攻击,同时可以抵抗现有的已知明文攻击[17-18,20].另一方面,由于块调制-置乱加密算法保留了原始图像块像素间的部分相关性,有效提高了RDH-EI算法的隐藏容量,如文献[22]中Lena图像的隐藏容量达到2.1 bpp,下面对块调制-置乱图像加密算法进行描述,并对其特性进行分析.
将大小为m×n的原始图像X(以灰度图像为例)分为N个不重叠图像块X={Xi|i=1,2,…,N},每个图像块的像素个数为Nb=(m×n) N.块调制-置乱图像加密可分为2步.
N.块调制-置乱图像加密可分为2步.
Step1. 块调制.由密钥key1生成N个随机正整数集R,R={Ri|Ri∈[0,255],i=1,2,…,N},R即为图像块内像素值的调制密钥.图像块Xi中的像素值按式(1)加密,生成调制加密图像E,E={Ei|i=1,2,…,N}.
Ei=(Xi+Ri) mod 256.
(1)
图像块Xi中所有像素的调制密钥R都相同.这样既改变了图像块中的像素值,又保留了原始图像块像素间的部分相关性.
Step2. 块置乱.由密钥key2生成块置乱序列Π,Π={π(1),…,π(i),…,π(N)},利用置乱序列Π置乱调制加密图像E中图像块,E={Ei|i=1,2,…,N},得到密文图像Y,Y={Yi|i=1,2,…,N},
Yi=Eπ(i).
(2)
因此,块调制-置乱图像加密即改变了像素值,又改变了像素的位置.有效提高了算法抵抗现有唯密文攻击[2]和已知明文攻击[[17-18,20]的能力.同时,密文图像块内还保留了原始图像块内部分像素间的相关性,为提高RDH-EI的隐藏容量提供了可能.文献[22]对密文图像块内像素值求差值,利用差值二叉树编码技术[22]使得RDH-EI算法的隐藏容量达到2 bpp以上.
不过,密文图像块内保留原始块的部分相关性,是否有可能带来新的安全隐患,是一个值得研究的问题.本文研究表明,当攻击者得到1对明-密文图像(X,Y)时,有可能估计出部分密钥,从而导致其他密文图像集的内容信息泄露.
设攻击者得到密文图像Y={Yi|i=1,2,…,N}及其对应的明文图像X={Xi|i=1,2,…,N}.对任一明文块Xi,Xi={xi,j|j=1,2,…,Nb},若能找到与其对应的密文块Yi,Yi={yi,j|j=1,2,…,Nb},则该图像块对应的调制密钥Ri为
![]()
(3)
因此,如何在密文图像中找到明文块Xi对应的密文块Yi,Yi=Eπ(i),即估计块置乱序列Π是已知明文攻击的主要工作.本文利用明-密文图像差值块对块调制-置乱图像加密实施已知明文攻击,估计块置乱序列.本节,给出图像差值块定义,分析并证明了明-密文图像差值块在加密前后有较高概率保持不变的特性,给出具体定义及分析.
定义1. 图像差值块.对任一图像块Xi(以明文图像块为例),Xi={xi,j|j=1,2,…,Nb}.块内所有像素值与第1个像素值的差值,为图像块Xi对应的图像差值块Di,Di={di,j|j=1,2,…,Nb},称差值块.
di,j=xi,j-xi,1, j=1,2,…,Nb.
(4)
相应的密文差值块表示为Dπ(i).明文图像X和密文图像Y中共有N对相互对应的图像块,表示为[Xi Yi]i=1,2,…,N.对明-密文所有图像块分别求差值,得到明文差值图像DX={Di|i=1,2,…,N}和密文差值图像DY={Dπ(i)|i=1,2,…,N},明-密文差值图像中N对相互对应的差值块表示为[Di Dπ(i)]i=1,2,…,N.
对于任意明文块Xi,xi,max和xi,min分别为明文块Xi中的最大值和最小值,块内调制密钥为Ri.根据调制加密前后差值块[Di Dπ(i)]是否发生改变,明文块被分为Case1和Case2这2种类型:
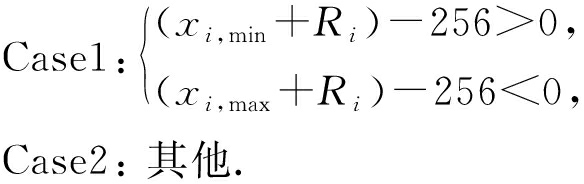
(5)
当明文块Xi满足Case1时,与图像块[Xi Yi]对应的差值块[Di Dπ(i)]满足Di≡Dπ(i),即差值块Di与Dπ(i)中的差值大小相同.当明文块Xi满足Case2时,Di≠Dπ(i),即差值块Di与Dπ(i)中的差值大小不同.
为直观描述Case1与Case2,图1给出一个例子(以2×2图像块为例).对明文块Xi,设调制密钥分别为Ri=96,Ri=91,Ri=94时,生成3组对应的密文块Yi,如图1上方所示.由式(4)分别计算差值块如图1下方所示.
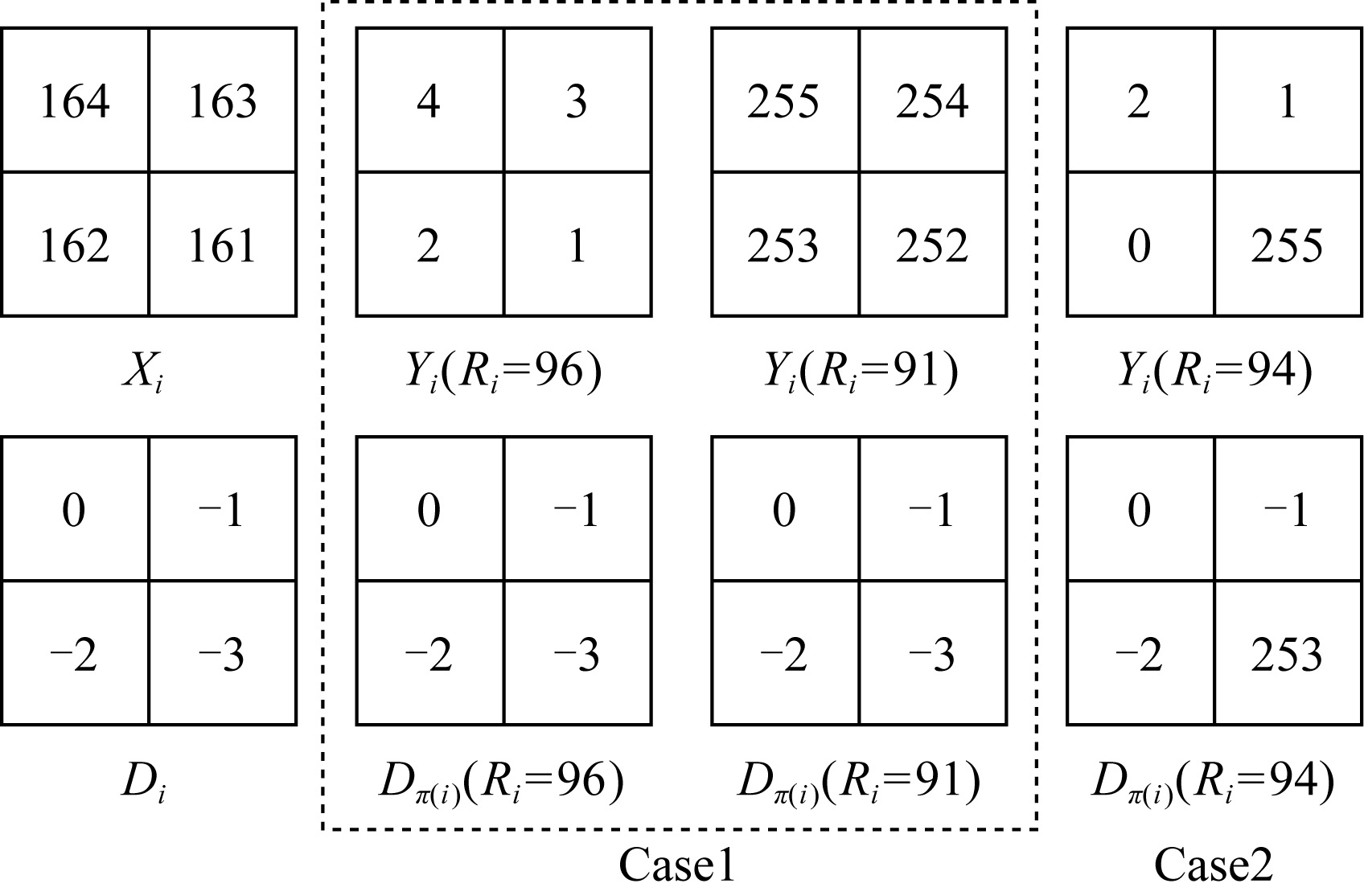
Fig. 1 Plaintext-ciphertext image block and
difference block
图1 明-密文图像块及差值块
由图1可看出,Case2图像块在调制加密后块内差值发生变化,而Case1图像块在调制加密后块内差值不会发生变化,即满足Di≡Dπ(i).明文块是否属于Case1与调制密钥R和明文块Xi中的最大值与最小值有关.
性质1. 块调制-置乱图像加密生成的明-密文差值块[Di Dπ(i)]i=1,2,…,N,满足Di≡Dπ(i)的差值块有较高的出现概率.
证明. 块调制-置乱图像加密同一个图像块中,调制密钥Ri相同,已知调制密钥Ri出现的概率为1 256,对明文图像X中任一明文块Xi,该明文块为Case1图像块,即差值块满足Di≡Dπ(i)的概率为
256,对明文图像X中任一明文块Xi,该明文块为Case1图像块,即差值块满足Di≡Dπ(i)的概率为
![]()
(6)
其中,xi,max和xi,min分别为明文块Xi中的最大值和最小值.自然图像中,由于块内像素间具有较高相关性,明文块Xi中的最大值与最小值差值远小于256,导致差值块满足Di≡Dπ(i)的概率Pi值较高.进一步计算明文图像X中Case1图像块所占比例为
(7)
为验证性质1,以2×2图像块为例,测试不同纹理复杂度的灰度图像Lena和Baboon,在50种不同密钥key1下Q的理论值与实际值,测试结果如图2所示:
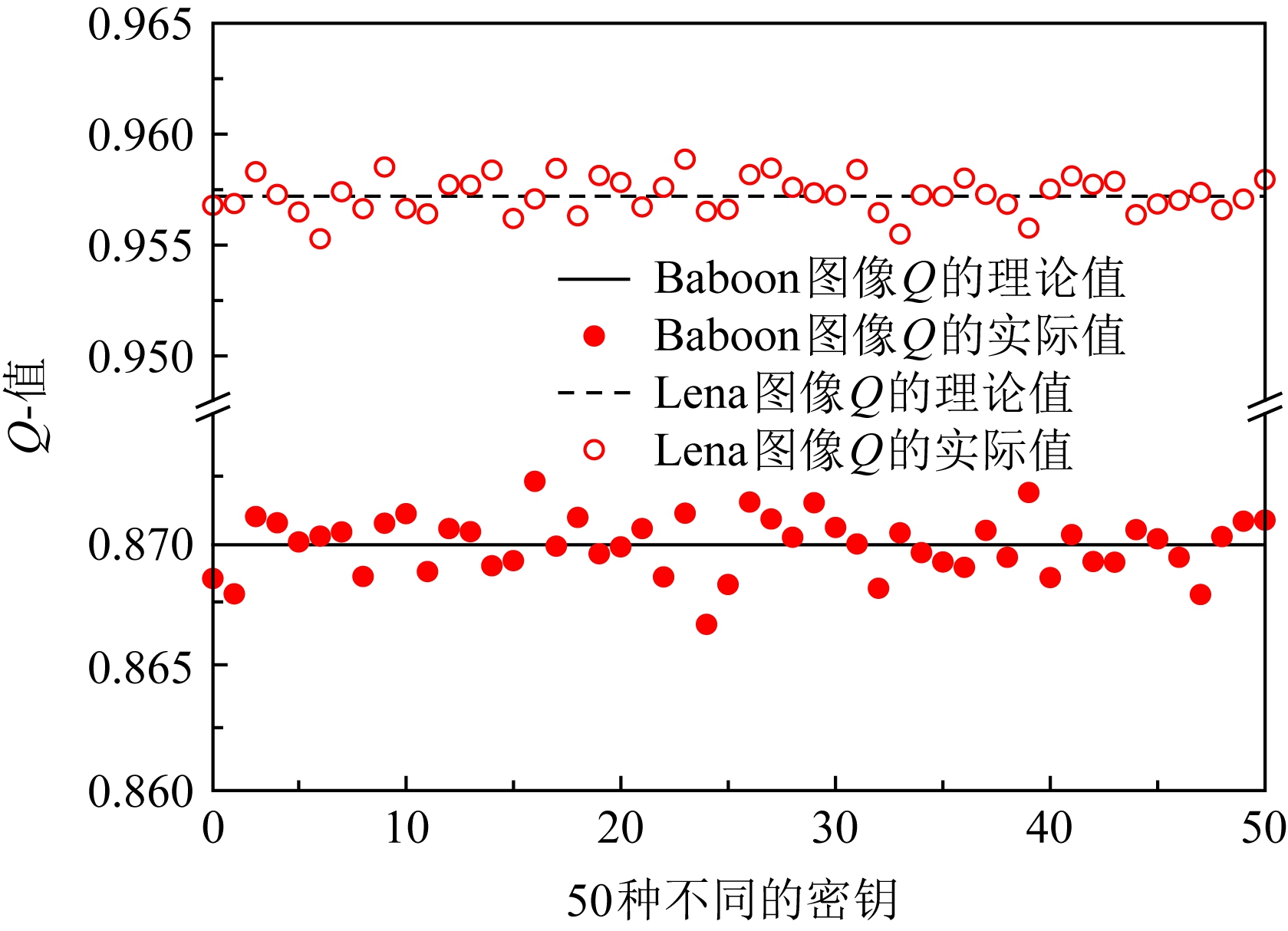
Fig. 2 Theoretical and actual values of Q value for
Lena and Baboon under different secret keys
图2 Lena和Baboon在不同密钥下Q的理论值与实际值
由图2可看出Q的理论值与实际值的误差范围是[-0.2%,+0.2%],对于纹理复杂度较高的Baboon图像,Q值达到87%,对于Lena图像Q值达到95.8%.可见,差值图像中,满足Di≡Dπ(i)的差值块有较高的出现概率.
证毕.
攻击者可利用加密前后保持不变的差值块,在明-密文建立等量关系实施已知明文攻击.然而,由于Case2图像块的存在,明-密文差值图像并不完全一致,因此,已知明文攻击的主要工作包括:1)构建完全一致的明-密文伪差值图像,利用构建的明-密文伪差值图像,在明文和密文建立等量关系进而估计块置乱序列Π;2)块置乱序列Π的快速估计.
由1.2节分析可知,块调制-置乱图像加密在密文图像中保留了原始图像块内差值信息,不过,加密图像的差值直方图和原始图像的差值直方图并不完全相同.而构建完全一致的明密文伪差值图像,是估计块置乱序列Π的前提条件.
在详细描述伪差值图像构建算法之前,为便于描述,先给出相关基本符号与概念的解释和定义.
定义2. 差值直方图距离.明文差值图像为DX,密文差值图像为DY,相应差值直方图分别表示为
![]()
+254,+255},
(8)
![]()
+254,+255},
(9)
其中,hi表示差值元素i出现的频数,差值图像DX和DY的直方图距离dH(H1,H2)定义为
(10)
为降低构建伪差值图像算法时间复杂度,以明文差值块Di={di,j|j=1,2,…,Nb}为例,将明文差值块中的差值求β次方平均值,将差值块Di用α值表示:
![]()
(11)
其中,β=2k+1,k∈N+,k为迭带次数.![]() 表示对第i个差值块中的第j个差值求β次方.对所有明文差值块求α值得到明文α值序列A,A={αi|i=1,2,…,N}.对密文差值块执行同样的操作,得到密文α值序列B.α值序列B中A的相对补集也称为B和A的集合差,表示为B\A,其元素αi属于B,但不属于A,即:
表示对第i个差值块中的第j个差值求β次方.对所有明文差值块求α值得到明文α值序列A,A={αi|i=1,2,…,N}.对密文差值块执行同样的操作,得到密文α值序列B.α值序列B中A的相对补集也称为B和A的集合差,表示为B\A,其元素αi属于B,但不属于A,即:
B\A=B-A={αi|αi∈B,αi∉A}.
(12)
显然,明-密文伪差值图像应满足的条件为:
1) B\A=∅,且A\B=∅;
2) B∩A=A=B.
当明文α值序列A与密文α值序列B满足以上2个条件时,明密文伪差值图像的直方图距离为0.构建伪差值图像的算法如算法1所示:
算法1. 伪差值图像构建算法.
 *由差值图像(DX,DY),构建伪差值图像(D,D′)*
*由差值图像(DX,DY),构建伪差值图像(D,D′)*
输入:明文差值图像DX、密文差值图像DY;
输出:明文伪差值图像D、密文伪差值图像D′.
将明文、密文差值图像DX,DY分解为N个不重叠的图像块;
for k=1,2,…n do
由式(11)分别计算DX,DY所有图像块的α值,得到序列A和B;
求Λ(A\B)和Λ(B\A);
将差值块DΛ(A\B)与Dπ(Λ(A\B))替换为同等大小的全0块;
根据式(10)计算差值直方图距离;
if dH(H1,H2)=0
D=DX;
D′=DY;
break;  *替换成功,退出循环*
*替换成功,退出循环*
else替换失败,继续for循环;
end if
end for
return明密文伪差值图像D,D′.
其中,Λ(A\B)表示取A\B对应差值块的索引地址.
基于2.1节构建的伪差值图像D和D′的基础上,利用分块置乱加密不改变差值的特点,定义差值块立方均值ρ.差值块Di的ρ值为
![]()
(13)
根据差值块的ρ值将差值块分类:ρ值在0附近的图像块为平滑块,反之为纹理块.图3统计了Lena差值图像在2×2分块下的ρ值分布.
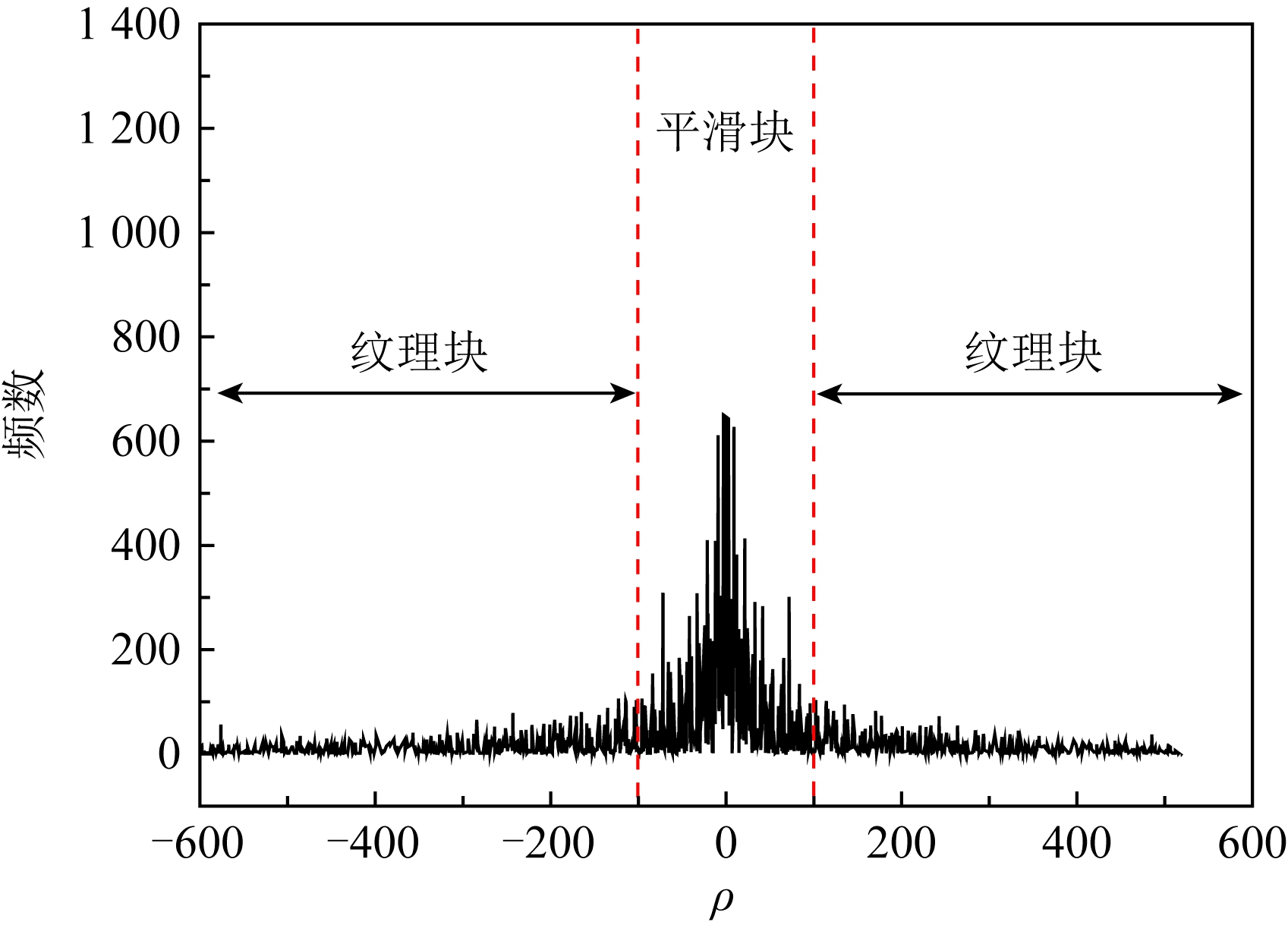
Fig. 3 Distribution of ρ values
图3 ρ值分布图
由图3可看出,大多数差值块的ρ值在0附近.为快速查找密文图像块的置乱坐标,本文提出一种基于差值块ρ值的分类查找算法,描述如Step1~Step3.
Step1. ρ值排序.将明-密文伪差值图像分为N个大小相等、不重叠的差值块.计算明文伪差值图像D与对应密文差值图像D′中所有差值块的ρ值,并按升序排序:
1) 明文伪差值图像D中所有差值块的ρ值排序构成集合J,J={ρ1,…,ρi,…,ρN};
2) 密文伪差值图像D′中所有差值块的ρ值排序构成集合![]()
Step2. 差值块分类.提取D与D′中ρ值相同的差值块,同时保留其原始索引构成的块集合C.伪差值图像D中,所有块集合构成分类集合Ω,Ω={C1,…,Ci,…,CM}.其中,Ci为ρi对应的块集合,![]() 块集合满足4个条件:
块集合满足4个条件:

Fig. 4 Six test images and the corresponding encrypted images
图4 6幅测试图像和对应的加密图像
1) M为块集合的总个数,M≤N;
2) ε为块集合中差值块个数,ε≤N;
3) Ci∩Cj=∅,∀i≠j;
4) C1∪C2∪…∪CM=D.
Step3. 差值块分类查找.明文伪差值图像D中,第i个块集合为![]() 为图像块数.同理,密文伪差值图像D′中,第i个图像块集合为
为图像块数.同理,密文伪差值图像D′中,第i个图像块集合为![]() 令
令![]() 表示块集合Ci中第x个图像块
表示块集合Ci中第x个图像块![]() 的原始索引.则块置乱序列Π={π(1),π(2),…,π(i),π(i+1),…,π(N)}的估计为
的原始索引.则块置乱序列Π={π(1),π(2),…,π(i),π(i+1),…,π(N)}的估计为
![]() 若
若![]()
(14)
其中,![]() 表示差值图像块
表示差值图像块![]() 与
与![]() 块内差值元素值相同.ρi对应的图像块集合查找如算法2所示:
块内差值元素值相同.ρi对应的图像块集合查找如算法2所示:
算法2. 块分类查找过程.
 *由明密文伪差值图像(D,D′),估计Π*
*由明密文伪差值图像(D,D′),估计Π*
输入:明文伪差值图像D、密文伪差值图像D′、差图像块总个数N;
输出:块置乱序列Π.
分别计算D和D′中N个图像块的ρ值,排序并得到集合J与J′;
由图像块ρ值提取明密文差值图像块,构成分类集合Ω;
for Ω中每一个块集合Ci中的图像块do
end if
if任意的![]()
![]()
end if
end for
return块置乱序列Π.
其中,Λ(·)表示取差值块索引,Rand(·)为随机选取函数.
在算法2中,对于仅出现一次的纹理差值块可以精确估计其置乱顺序,而在同一个块集合C中,对重复次数较多的平滑差值块随机且不重复地为其分配坐标.影响置乱序列Π估计正确率的主要因素为纹理块的数量.
差值块分类查找算法对任意差值图像块![]() 攻击者对它的搜索空间从原来的N下降为ε,ε为块集合Ci中差值块个数.从而将N个图像块置乱序列Π的密钥空间从N!降低至M×(ε)!.显著降低了已知明文攻击算法时间复杂度.
攻击者对它的搜索空间从原来的N下降为ε,ε为块集合Ci中差值块个数.从而将N个图像块置乱序列Π的密钥空间从N!降低至M×(ε)!.显著降低了已知明文攻击算法时间复杂度.
选取6幅(512×512)未压缩灰度图像,6幅测试图像按纹理复杂度由低到高顺序排列,它们分别为Airplane,Lena,Woman,Man,Baboon,Camera.测试图像及在2×2分块下的加密图像如图4所示.
在本文提出的已知明文攻击中,攻击者利用块内像素差值在加密前后基本保持不变的特点来估计块置乱序列,对差值图像块采取分类查找的策略实现序列Π的快速估计.本节首先测试了分块大小对加密前后Case1差值块出现比例(Q值)的影响.验证了块调制-置乱加密明-密文差值图像具有较高相似性,这是实施已知明文攻击的前提.然后,对影响块置乱序列Π估计正确率的主要因素进行分析.
在1.2节分析中,块内像素调制加密后,密文块被分为Case1与Case2这2种情况.其中,Case1密文差值块与明文差值块一致,而Case2的密文差值块发生改变.一幅图像的Case1图像块占比越高,其明-密文差值图像直方图距离越小,构建伪差值图像所替换的图像块越少,已知明文攻击的效果越好.反之,已知明文攻击效果越差.
由式(7)可看出,Case1图像块的比例(Q值)与块内最大值xi,max和最小值xi,min的差值有关.随着分块尺寸和图像纹理复杂度的增大,块内像素相关性减弱,xi,max与xi,min的差值增大,从而会导致Case1图像块比例Q值降低.
为验证分块大小对Q值的影响,图5统计了图4(a)~(e)在不同分块大小下的Q值.由图5可看出,在同等分块大小下,随着图像纹理复杂度的增加,Case1图像块占总图像块的比例降低.对于同一幅图像,随着分块尺寸增大,Case1图像块占比有所下降.即使是纹理复杂度较高的Baboon图像在8×8分块下,Q仍在60%以上.可见,分块大小最大、纹理复杂度最高的情况下,1.2节性质1仍然满足.
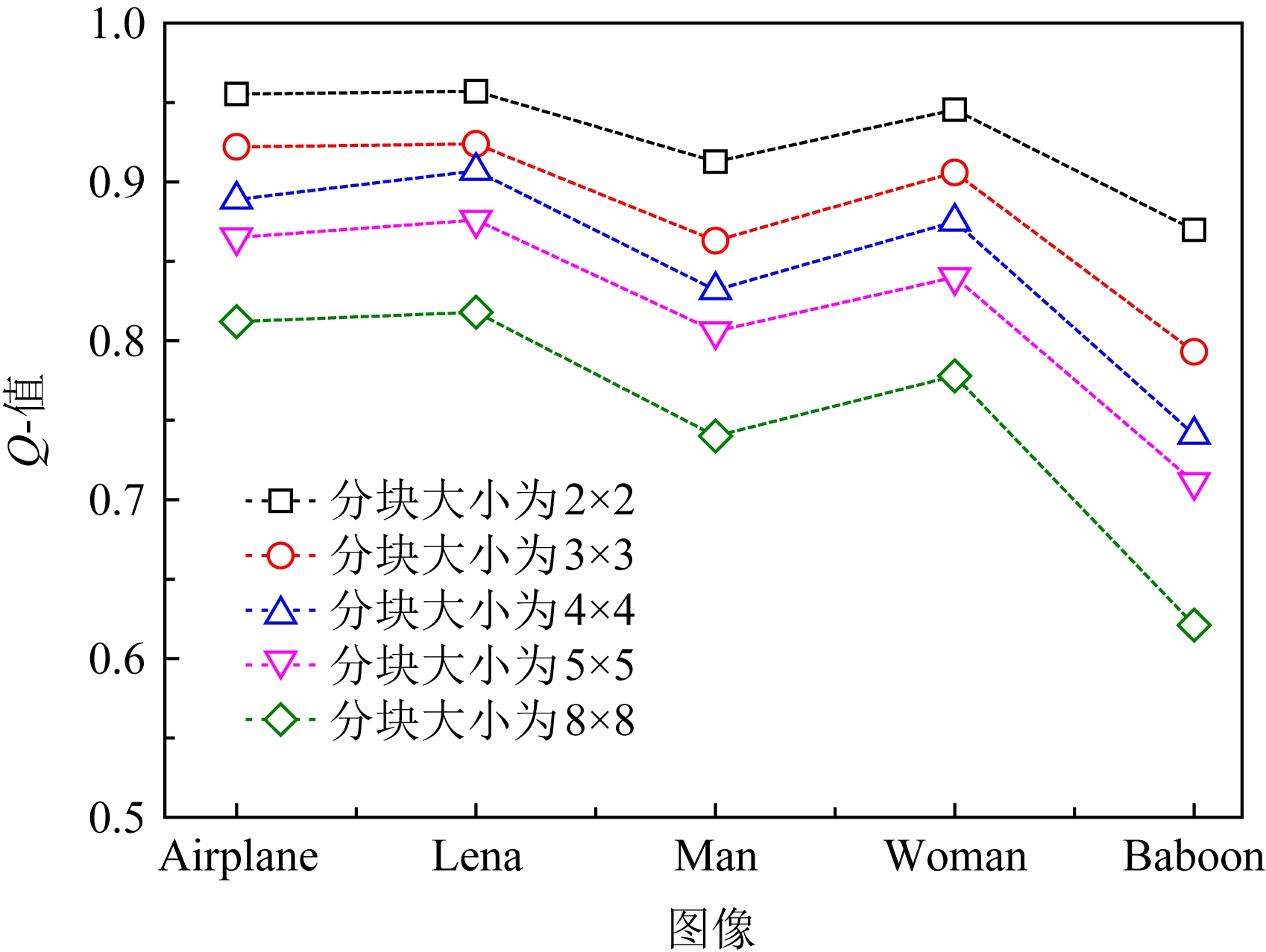
Fig. 5 Q -Value of the test images under different
block sizes
图5 测试图像在不同分块大小下的Q值
在3.1节中,明-密文差值图像直方图距离越大,构建伪差值图像所替换的图像块越多,对块置乱序列Π估计的精确度下降.在2.2节图像块分类查找,将差值块分为纹理块与平滑块,纹理块越多,Π估计精确度越高.可见,影响Π估计精确度的主要因素为图像纹理复杂度与分块大小.本节,首先验证不同纹理复杂度下,现有已知明文攻击[14-18]和本文提出的已知明文攻击在块调制-置乱加密下的有效性,并分析不同纹理复杂度对块置乱序列Π估计精确度的影响.然后,分析不同分块对块置乱序列Π估计精确度的影响.
3.2.1 纹理复杂度对Π的影响
以图4(a)Airplane、图4(b)Lena、图4(e)Baboon为例,这3幅图像中,Airplane图像纹理复杂度最低,Baboon图像纹理复杂度最高.分块大小为2×2下,计算测试图像的ρ值,将ρ值范围在[-150,150]区域的像素置零,范围之外的像素值置为255,生成的纹理分布图如图6(a)所示.图6(a)所示的纹理分布图中,白色为纹理块,黑色为平滑块.
像素置乱加密不改变明文图像的像素值大小,仅改变像素值位置.而块调制-置乱加密在加密过程中改变了像素值大小,因此现有的针对置乱加密的已知明文攻击[14-18]无法破解块调制-置乱加密.为验证现有已知明文攻击与本文提出的已知明文攻击对块调制-置乱加密的有效性,以Li等人[14]提出的针对置乱加密已知明文攻击算法为例,设攻击者分别获取Airplane,Lena,Baboon的明文及对应的密文图像,基于2×2分块,分别用文献[14]的已知明文攻击算法和本文提出的攻击算法估计块置乱序列Π、调制密钥R,进而解密图4(f)的密文图像.解密结果如图6(b)和图6(c)所示.
由图6(b)可知,现有针对仅置乱加密的已知明文攻击算法[14-18]无法破解块调制-置乱加密,这是因为该加密算法改变了明文图像的像素值.对比图6(c)中的攻击结果可以看出,本文提出的已知明文攻击能破解块调制-置乱加密,且对纹理区的图像块攻击效果更好,而信息泄露的部分大多属于纹理区域.对于平滑块,由于差值图像块重复率较高,估计的Π精确度不高.在图6(c)中,利用Airplane明-密文估计Π和R的正确率分别为18.0%和18.1%,利用Lena明-密文估计Π和R的正确率分别为19.0%和19.3%,利用Baboon明-密文估计Π和R的正确率分别为57.0%和57.1%.由图6(c)可看出,虽然密钥估计正确率低于20%,但密文图像仍有信息被泄露,由于Baboon纹理块较多,利用Baboon明-密文图像估计的Π和R去解密图4(f)的密文图像,解密图像视觉效果好于Airplane,Lena.

Fig. 6 Texture distribution map and attack results
under 2×2 block size
图6 纹理分布图及分块大小为2×2的攻击结果
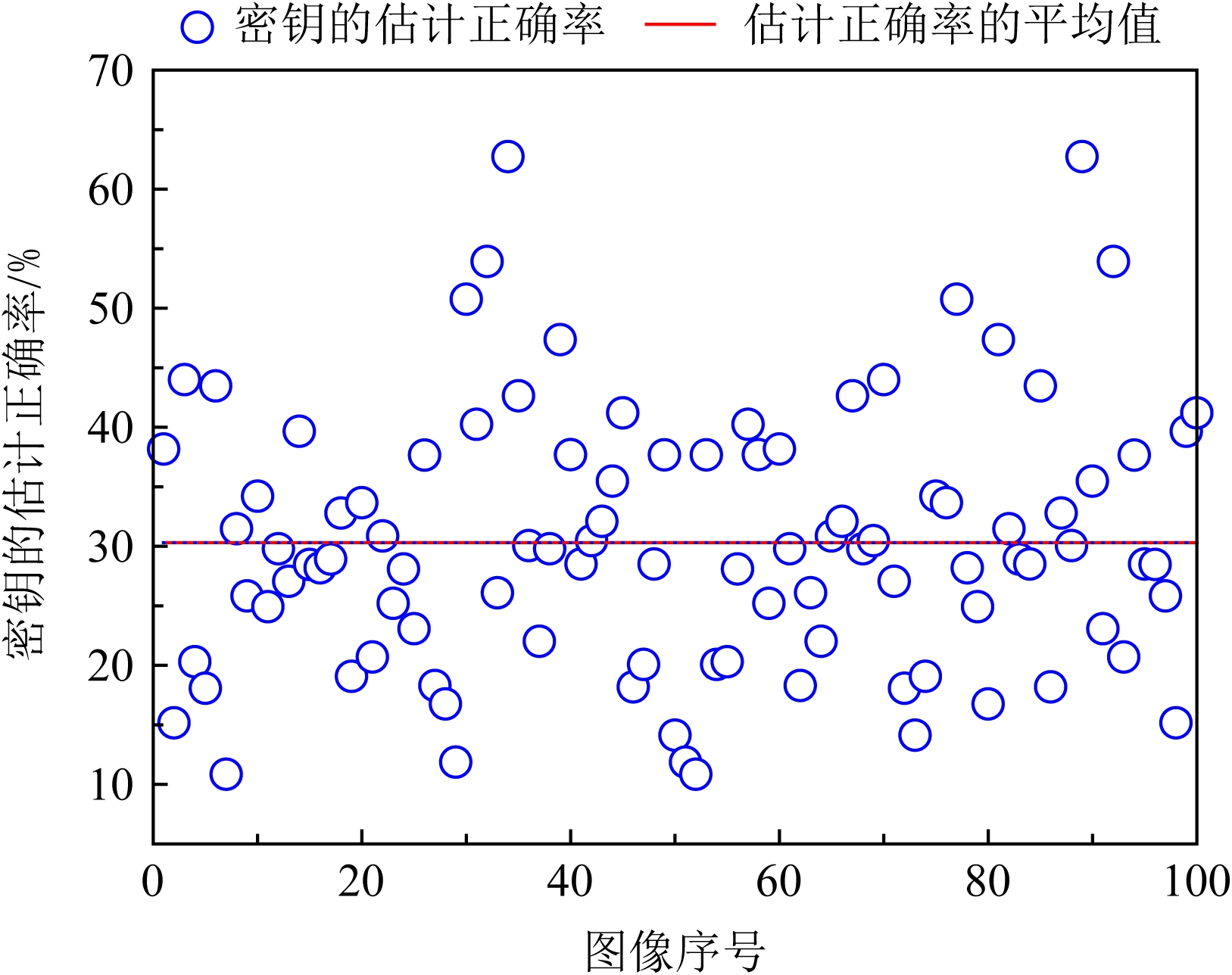
Fig. 7 The estimation accuracy of scrambling sequences
Π estimated by using different images
图7 不同图像内容下块置乱序列Π的估计正确率
用本文提出的已知明文攻击算法测试100张不同纹理复杂度图像(UCID标准图像数据库)在分块2×2下,块置乱序列Π的估计正确率,结果如图7所示.由图7可知,攻击者已知的明文图像内容不同,Π的估计正确率不同.2×2下块置乱序列Π估计正确率平均值为30%.图6(c)的攻击结果可知:当30%块置乱序列被正确估计,密文图像的内容已被严重泄露.
3.2.2 分块大小对Π的影响
分块大小对Π,R的影响主要有2个方面:
1) 分块大小越大,块内像素间的相关性减弱,Case2图像块占比增加,因此,在构建伪差值图像中,被替换的图像块数量增多,这导致Π与R的估计精度降低;
2) 分块大小越小,块内像素间的相关性越高,差值图像块的ρ值集中于0附近,即平滑块的数量提高,平滑块的增多会降低Π与R的估计精度.
由图5可知,对于纹理复杂度较高的图像按8×8分块,明-密文差值图像仍然具有较高的相似度.可见,随着图像块尺寸的增大,Case2图像块占比虽然提高,但是对Π与R的估计精度影响不大.因此,随着分块尺寸的增加,块置乱序列Π与调制密钥R的估计精度呈先升高后逐渐降低的趋势.为分析块大小对密钥估计精度的影响,利用图4(a)~(e)在2×2,3×3,4×4,5×5,8×8不同分块大小下的明-密文图像分别估计密钥Π与R,得到5组密钥,图8统计了5组密钥中块置乱密钥Π的正确率.
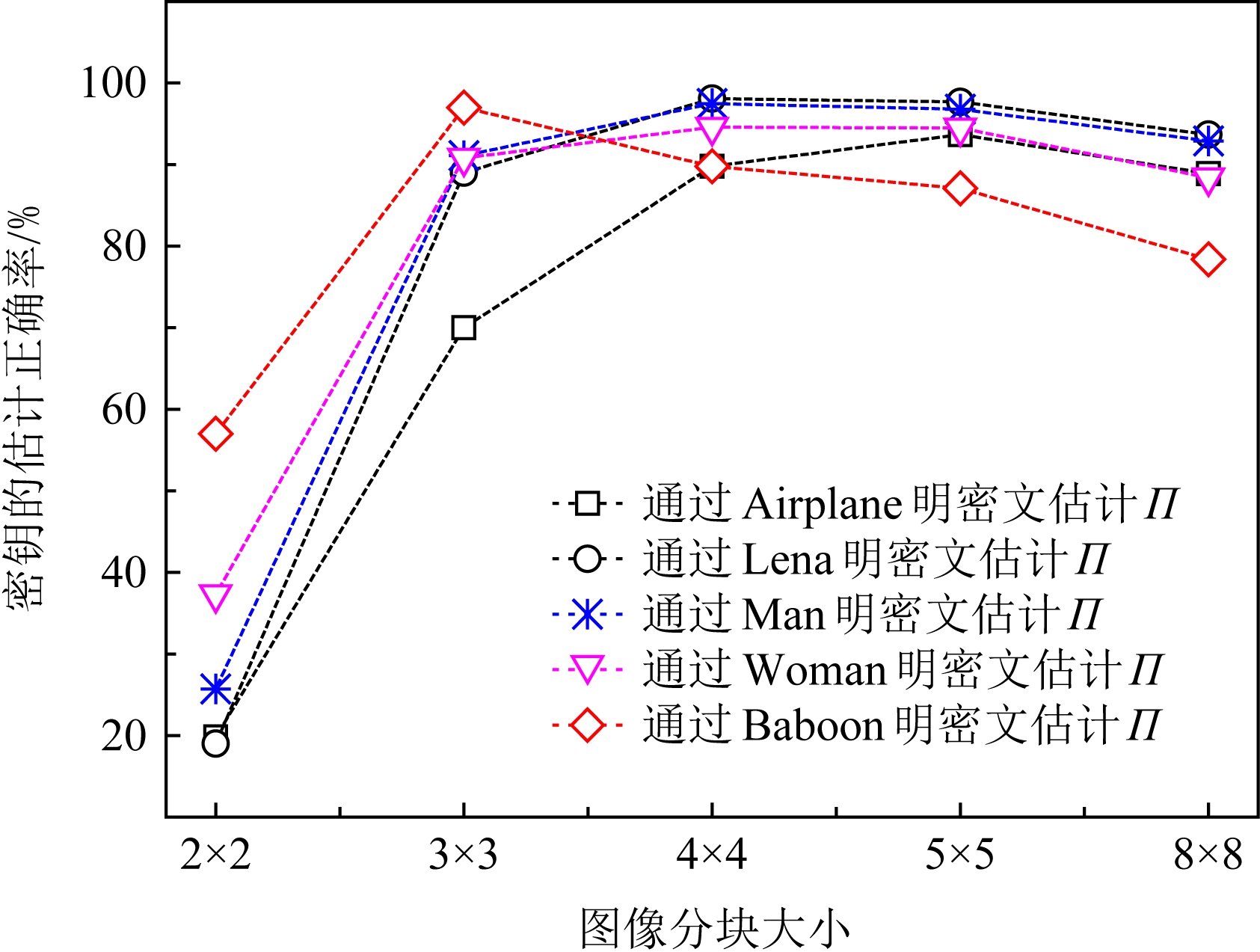
Fig. 8 Estimation accuracy of Π under different
block sizes
图8 置乱序列Π在不同分块大小下的估计正确率
由图8可看出,在分块大小为2×2时,Airplane图像的块置乱序列Π的估计正确率虽然仅有20%,但从图6可以看出,处于纹理块的图像内容仍然被泄露.在分块大小为3×3时,置乱序列Π的估计正确率达到70%以上;当分块大小为4×4时,正确率可以达到90%以上;当分块大小大于5×5时,密钥的估计正确率开始下降.实验结果表明:随着图像分块尺寸的增加,密钥估计正确率先升高后下降.利用5组估计密钥分别解密图4(f)在对应分块大小下的密文图像.解密结果如图9和图10所示:

Fig. 9 The known plaintext attack results under 3×3 block size and 4×4 block size
图9 3×3分块及4×4分块下已知明文攻击结果

Fig. 10 The known plaintext attack results under 5×5 block size and 8×8 block size
图10 5×5及8×8分块大小下的攻击结果
由图9可看出,当分块大小大于2×2时,解密图像的视觉质量整体得到提高,加密图像的大部分原始内容已经泄露.在同样分块大小下,图像纹理复杂度越高,攻击效果可能有所下降,如4×4分块下Man的解密效果好于Baboon的解密效果;而对于纹理复杂度最高的Baboon图像,分块尺寸增加其攻击效果也可能有所降低,如3×3分块大小下Baboon的解密效果好于4×4分块大小下的解密效果.
继续增大分块尺寸,对比图9与图10的实验结果可知,随着分块尺寸的增大,明文图像纹理复杂度越低,攻击效果越好.当已知的明文图像纹理复杂度较高,如Baboon图像,随着分块大小的增加,已知明文攻击效果先提高后逐渐降低,3×3分块下攻击效果最好.解密图像视觉效果降低是因为图像分块大小以及纹理复杂度的增加会导致3.1节中Case1图像块占比的降低,构建伪差值图像所替换的图像块增加,导致块置乱序列Π与调制密钥R的估计正确率降低.
上述实验表明:当分块尺寸大于2×2时攻击者仅需1对明-密文就可以解密得到较好的图像.RDH-EI算法中,分块越小隐藏容量越低,但生成密文图像的安全性越高.为验证更小分块下(1×2和1×3分块)已知明文攻击效果,假设攻击者已知:1对明-密文(Baboon)、2对明-密文(Baboon & Woman)和3对明-密文(Baboon & Woman & Man),分别在1×2和1×3分块大小,用估计的块置乱序列Π解密Camera的密文图像,结果如图11所示:

Fig. 11 Known plaintext attack results for 1 to 3 pairs of plain-ciphertext at
block sizes 1×2 and 1×3
图11 已知1~3对明-密文在分块大小为1×2和1×3下的攻击结果
图11中,在1×2分块下利用1对明-密文估计置乱序列Π的正确率仅为1%,已知明-密文对数增加到2对,Π的估计正确率达到20.3%.当已知明-密文对数增加到3对,Π的估计正确率达到80.2%,如图11(c)密文图像的大部分内容已被泄露(3对明-密文).在1×3分块下利用1对明-密文估计置乱序列Π的正确率为34.6%,密文图像的部分内容被泄露,当已知明-密文对数增加到2对时,Π的估计正确率高达98.8%,密文图像的内容被完全泄露.因此,即使在分块尺寸很小的情况下,块调制-置乱加密仍无法抵抗本文提出的已知明文攻击.
算法时间复杂度是攻击效果的一个重要指标,攻击者的目标是在最短的时间内获得最好的攻击效果.下面对本文提出的已知明文攻击的算法时间复杂度进行分析,本文算法主要有3部分构成,算法每一步的时间复杂度及总的时间复杂度分析为:
Step1. 构建伪差值直方图.设迭代次数k,计算所有图像块α值的时间复杂度为N,N为图像总分块数.利用明文密文差值图像替换B\A与A\B集合图像块的时间复杂度为k×N2.因此,构建伪差值图像的时间复杂度为N+k×N2.图12为测试图像在2×2和3×3下的k值.当分块大小大于等于3×3时k值都为1,在2×2时,图像纹理复杂度越高,k值越低.
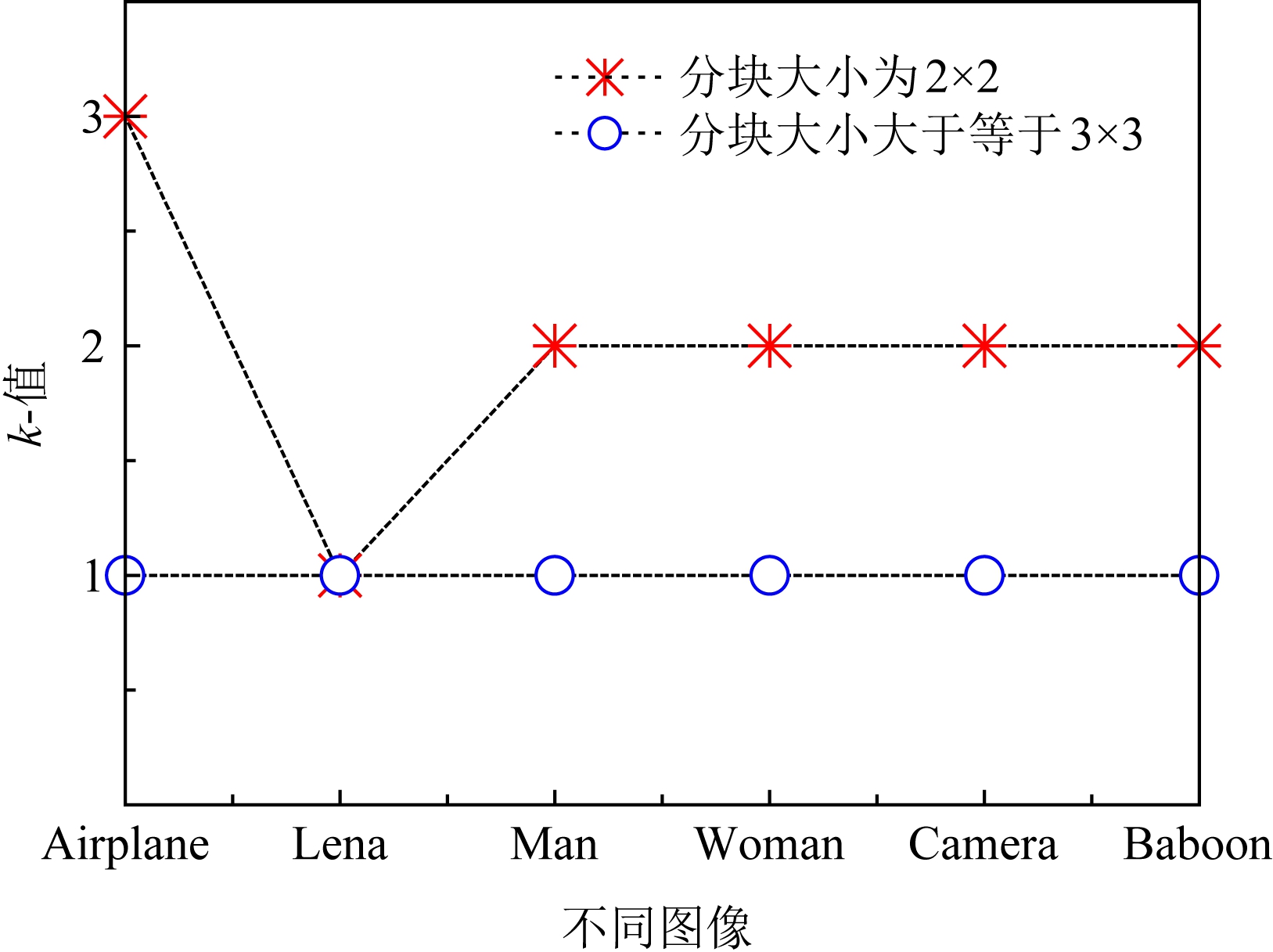
Fig. 12 k-value of different images under different
block sizes
图12 测试图像在不同分块下的k值
Step2. 计算每一图像块的立方均值ρ的算法时间复杂度是N. 排序时间复杂度是N×lb N.
Step3. 图像块分类查找.块集合最好的情况为集合内仅有一个图像块,此时查找的时间复杂度为N.在10 000张图像测试集中发现,自然图像同一个块集合中,块元素个数不超过0.5N,此时图像块分类查找的时间复杂度接近(0.5N)2.查找过程的平均复杂度为![]()
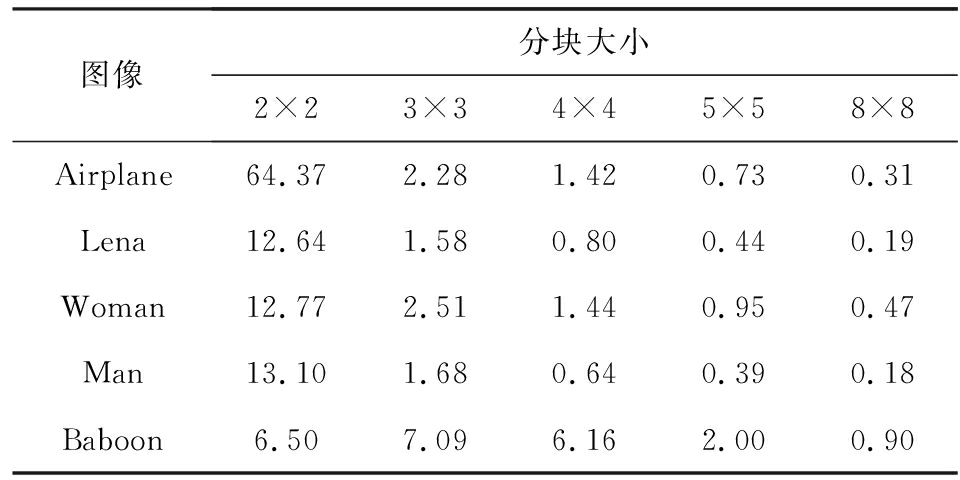
因此,已知明文攻击算法总时间复杂度约为![]() 影响算法时间复杂度的主要因素为分块大小及迭代次数.表1给出已知明文攻击在不同分块大小下实际运行时间.
影响算法时间复杂度的主要因素为分块大小及迭代次数.表1给出已知明文攻击在不同分块大小下实际运行时间.
Table 1 Actual Running Time of the Known-plaintext Attack
表1 已知明文攻击的实际运行时间 s
图像分块大小2×23×34×45×58×8Airplane64.372.281.420.730.31Lena12.641.580.800.440.19Woman12.772.511.440.950.47Man13.101.680.640.390.18Baboon6.507.096.162.000.90
从表1可以看出,已知明文攻击时间复杂度与分块大小和图像的纹理复杂度有关,对于平滑图像Airplane在分块大小为2×2下,估计块置乱密钥耗时最长,耗时约64 s.在分块大小达到8×8时,对于所有测试图像,已知明文攻击估计块置乱序列仅需耗时1 s以内.
为提高块调制-置乱图像加密的安全性能,主要目标是破坏置乱序列Π和调制密钥R的估计条件.在保留密文差值图像冗余度的条件下,给出2种提高加密图像安全性的方案.
策略1. 自适应密钥.已知明文攻击的条件是用户使用相同的密钥加密多张明文图像,即密钥重用.当攻击者通过已知的明-密文对破解用户密钥K,即可解密所有密文图像集.若不同图像内容所用的加密密钥不同时,已知明文攻击的条件无法满足.自适应密钥即用户基于密钥K和图像内容,生成不同的加密密钥![]() 自适应密钥加密过程中,密钥K是用户定义的,而图像加密密钥
自适应密钥加密过程中,密钥K是用户定义的,而图像加密密钥![]() 是由散列函数生成的,从而实现了用户密钥和图像加密密钥的分离.如何生成加密密钥
是由散列函数生成的,从而实现了用户密钥和图像加密密钥的分离.如何生成加密密钥![]() 是自适应密钥策略的关键,文献[25]中,Yi等人提出一种基于SHA的自适应密钥生成方法.该自适应密钥加密算法中,分别输入用户定义的安全密钥K和原始图像X,通过安全的SHA算法生成2个随机SHA序列.将2个SHA序列异或得到随机序列
是自适应密钥策略的关键,文献[25]中,Yi等人提出一种基于SHA的自适应密钥生成方法.该自适应密钥加密算法中,分别输入用户定义的安全密钥K和原始图像X,通过安全的SHA算法生成2个随机SHA序列.将2个SHA序列异或得到随机序列![]() 即为图像的加密密钥.自适应密钥的生成框架如图13所示:
即为图像的加密密钥.自适应密钥的生成框架如图13所示:
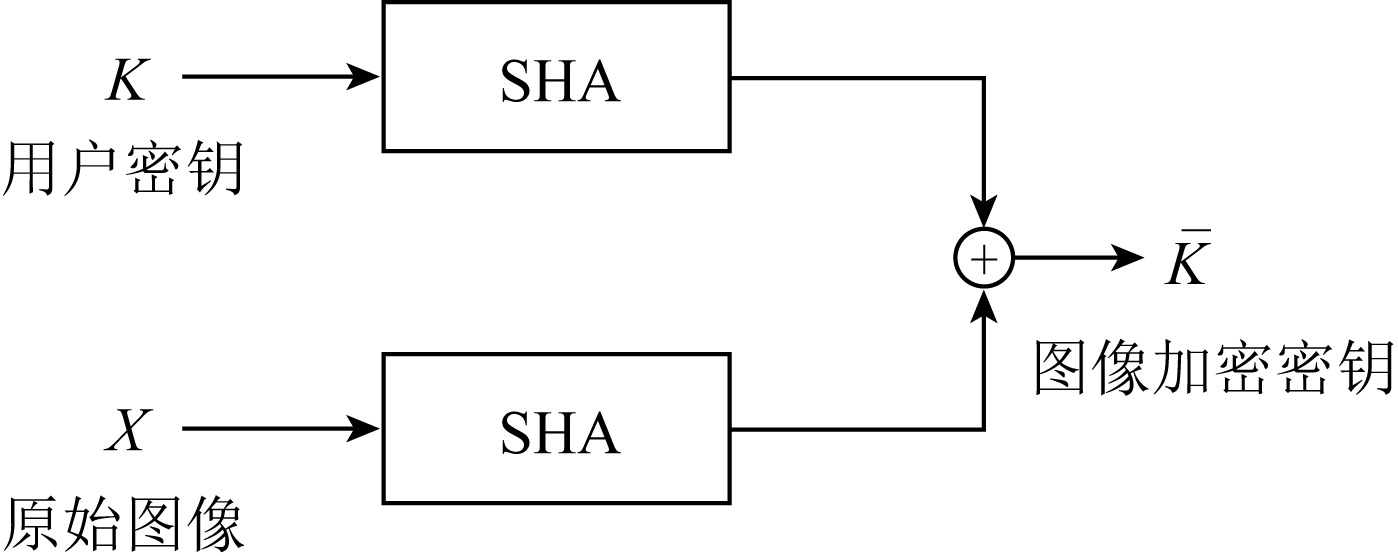
Fig. 13 The generation framework of the adaptive
image encryption key
图13 自适应密钥的生成框架
由于不同密文图像的置乱密钥均不相同,即使攻击者破解某对明-密文图像的置乱密钥,也无法解密其余密文图像.因此,自适应密钥可以抵抗本文提出的已知明文攻击.
策略2. 分类加密.在本文提出的已知明文攻击中,信息泄露的区域主要集中在图像的纹理块区域,而处于纹理块区域的差值块可隐藏的信息量远低于平滑块.因此在加密前可先对图像的纹理块采用安全的图像加密算法加密,以改变纹理区的差值.对平滑块采用调制-置乱加密以保证隐藏容量.
为提高图像加密域可逆信息隐藏算法的隐藏容量,块调制-置乱图像加密算法在RDH-EI中被广泛应用.由于该加密算法结合模运算与分块置乱策略,在密文图像中保留了明文图像块内差值信息,有效地提高了加密图像的隐藏容量及安全性,可有效抵抗唯密文攻击和现有的已知明文攻击.本文分析了块调制-置乱加密算法的安全性,提出了一种基于差值块分类的已知明文攻击方法.首先利用明-密文差值图像迭代替换,构建出直方图距离为零的伪差值图像.在此基础上,利用图像块置乱不改变差值的特点定义差值块立方均值ρ,将差值块分为平滑块与纹理块,并对差值块分类排序查找,实现块置乱序列的快速估计.分析讨论了块大小、图像纹理复杂度与块置乱序列估计正确率之间的关系,给出了在保证图像冗余空间的条件下提高加密图像安全性的策略.实验结果表明,图像分块越大,纹理差值块数量越多,块置乱序列估计正确率越高,块调制-置乱加密难以抵抗本文提出的已知明文攻击.为提高和设计更安全的RDH-EI算法,本文通过对RDH-EI常用的图像加密算法提出一种攻击方案,分析了块调制-置乱图像加密算法的安全性.
[1]Shi Yunqing, Li Xiaolong, Zhang Xinpeng, et al. Reversible data hiding: Advances in the past two decades[J]. IEEE Access, 2016, 4: 3210-3237
[2]Khelifi F. On the security of a stream cipher in reversible data hiding schemes operating in the encrypted domain[J]. Signal Processing, 2018, 143: 336-345
[3]Zhang Xinpeng. Separable reversible data hiding in encrypted image[J]. IEEE Transactions on Information Forensics and Security, 2012, 7(2): 826-832
[4]Ma Kede, Zhang Weiming, Zhao Xianfeng, et al. Reversible data hiding in encrypted images by reserving room before encryption[J], IEEE Transactions on Information Forensics and Security, 2013, 8(3): 553-562
[5]Qian Zhenxing, Zhang Xinpeng. Reversible data hiding in encrypted images with distributed source encoding[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2016, 26(4): 636-646
[6]Hong Wien, Chen Tungshou, Wu Hanyan. An improved reversible data hiding in encrypted images using side match[J]. IEEE Signal Processing Letters, 2012, 19(4): 199-202
[7]Zhang Xinpeng, Qian Zhenxing, Feng Guorui, et al. Efficient reversible data hiding in encrypted images[J]. Journal of Visual Communication and Image Representation, 2014, 25(2): 322-328
[8]Xu Dawen, Wang Rangding. Separable and error-free reversible data hiding in encrypted images[J]. Signal Processing, 2016, 123: 9-21
[9]Yan Shu, Chen Fan, He Hongjie. Reversible data hiding in encrypted image based on neighborhood prediction using XOR-permutation encryption[J].Journal of Computer Research and Development, 2018, 55(6): 97-107 (in Chinese)(鄢舒, 陈帆, 和红杰. 异或-置乱框架下邻域预测加密域可逆信息隐藏[J]. 计算机研究与发展, 2018, 55(6): 97-107)
[10]Qu Lingfeng, He Hongjie, Chen fan. Reversible data hiding in encrypted image based on prediction error and classification scrambling[J]. Journal of Optoelectronics·Laser, 2019, 30(2): 168-174 (in Chinese)(屈凌峰, 和红杰, 陈帆. 基于预测误差分类置乱的图像加密域可逆信息隐藏[J]. 光电子·激光, 2019, 30(2): 168-174)
[11]Yin Zhaoxia, Luo Bin, Hong Wien. Separable and error-free reversible data hiding in encrypted image with high payload[J]. The Scientific World Journal, 2014, 2014: 1-8
[12]Yin Zhaoxia, Abel A, Zhang Xinpeng, et al. Reversible data hiding in encrypted image based on block histogram shifting[C] //Proc of the 2016 IEEE Int Conf on Acoustics, Speech and Signal Processing (ICASSP). Piscataway, NJ: IEEE, 2016: 2129-2133
[13]Yin Zhaoxia, Abel A, Tang Jin, et al. Reversible data hiding in encrypted images based on multi-level encryption and block histogram modification[J]. Multimedia Tools and Applications, 2017, 76(3): 3389-3920
[14]Li Shujun, Li Chengqing, Chen Ghuanrong, et al. A general quantitative cryptanalysis of permutation-only multimedia ciphers against plaintext attacks[J]. Signal Processing: Image Communication, 2008, 23(3): 212-223
[15]Li Chengqing, Lo K. Optimal quantitative cryptanalysis of permutation-only multimedia ciphers against plaintext attacks[J]. Signal Processing, 2011, 91(4): 949-954
[16]Jolfaei A, Wu Xinwen, Muthukkumarasamy V. On the security of permutation-only image encryption schemes[J]. IEEE Transactions on Information Forensics and Security, 2016, 11(2): 235-246
[17]Li Shujun, Li Chengqing, Lo K T, et al. Cryptanalysis of an image scrambling scheme without bandwidth expansion[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2008, 18(3): 338-349
[18]Li Weihai, Yan Yupeng, Yu Nenghai. Breaking row-column shuffle based image cipher[C] //Proc of the 20th ACM Int Conf on Multimedia. New York: ACM, 2012: 1097-1100
[19]Liu Zilong, Pun C. Reversible data-hiding in encrypted images by redundant space transfer[J]. Information Sciences, 2018, 433: 188-203
[20]Qu Lingfeng, Chen Fan, He Hongjie, et al. Security analysis of image encryption algorithm based on bit plane-pixel block scrambling[J]. Journal of Applied Sciences, 2019, 37(5): 631-642 (in Chinese)(屈凌峰, 陈帆, 和红杰, 等. 基于位平面-块置乱的图像加密算法安全性分析[J]. 应用科学学报, 2019, 37(5): 631-642)
[21]Chen Kai, Xu Dawen. An efficient reversible data hiding scheme for encrypted images[J]. International Journal of Digital Crime and Forensics, 2018, 10(2): 1-22
[22]Yi Shuang, Zhou Yicong. Separable and reversible data hiding in encrypted images using parametric binary tree labelings[J].IEEE Transactions on Multimedia, 2019, 21(1): 51-64
[23]Xu Dawen, Su Shubing. Separable reversible data hiding in encrypted images based on difference histogram modification[J]. Security and Communication Networks, 2019, 2019: 1-14
[24]Yi Shuang, Zhou Yicong. Parametric reversible data hiding in encrypted images using adaptive bit-level data embedding and checkerboard based prediction[J]. Signal Processing, 2018, 150: 171-182
[25]Yi Shuang, Zhou Yicong. Binary-block embedding for reversible data hiding in encrypted images[J]. Signal Processing, 2017, 133: 40-51