组合优化问题(combinatorial optimization problem, COP)的求解一直是运筹学领域的一个重要研究方向.典型组合优化问题如旅行商问题(travelling salesman problem, TSP)、车辆路径问题(vehicle routing problem, VRP)、作业车间调度问题(job shop scheduling problem, JSSP)等通常均属于NP-Hard问题.因此，针对组合优化问题设计高效的求解算法一直是该领域的重要研究方向.
目前针对组合优化问题的求解方法一般被分为2种类型：近似算法(approximation algorithm)以及精确算法(exact algorithm).这2类方法面临2个问题的挑战[1-2]：1) 精确算法求解的时间消耗随着问题规模的扩大急遽上升，针对较大规模问题无法在可接受时间内取得最优解；2) 设计有效的启发式算法需要大量针对性的领域知识以及大量的试错(trial-and-error).因此，如何针对组合优化问题设计有效的求解算法，仍然面临重重困难.
近年来，一批深度强化学习方法在组合优化问题的新应用的提出给本问题的解决带来新的思路[3].得益于端到端学习(end-to-end learning)模型[4]的提出，深度强化学习方法能够通过在同一问题分布的不同实例上的训练来提取有关问题实例的深层特征，并基于问题特征对问题实例进行求解.深度强化学习方法在求解组合优化问题时具有如下2个特征：
1) 深度强化学习能够通过训练的方式搜索问题分布的特征并进行求解模型的自完善，且该过程不需要模型设计者掌握问题相关的领域知识；
2) 模型训练结束后，深度强化学习在求解时，能够以O(n)的时间复杂度求解问题实例.
然而，深度强化学习在求解组合优化问题时，仍面临一定的不足：
1) 算法求解表现距离state-of-the-art算法仍有差距；
2) 缺乏解空间的搜索能力，且对输入分布较为敏感.
为解决该问题，本文提出了一种基于蚁群算法和深度学习方法的混合启发式算法框架.该框架采用深度学习方法进行特征提取，然后采用蚁群算法基于问题特征在解空间内进行可行解的搜索.该框架能够有效利用深度学习方法的特征提取能力，以及蚁群算法的解空间搜索能力.
本文的主要贡献有4个方面:
1) 提出了一种基于蚁群算法和深度学习方法的组合优化问题求解方案，并采用该方法对旅行商问题进行了求解.
2) 提出了一种深度学习方法进行旅行商问题特征提取的端到端学习方法，该方法能够将不同规模的旅行商问题实例转化为对应的启发式信息矩阵.
3) 在启发式信息矩阵的基础上，采用蚁群算法对旅行商问题实例进行了求解.
4) 采用TSPLIB中的标准算例对该方法的求解表现和算法稳定性进行了验证.
1 相关工作
本文从蚁群算法和深度学习方法求解组合优化问题2方面分别介绍本文的相关工作.
蚁群算法是一种模拟蚂蚁的觅食行为的仿生算法，该算法由Dorigo于1992年提出[5].在该文中，作者描述了蚁群算法求解旅行商问题的基本流程：首先将人工蚂蚁随机放置于一个开始城市并遵循基于概率的规则逐步构建解.每次产生可行解后，人工蚂蚁会按照解的好坏在路径上留下对应的信息素信息.经过多代迭代后，在信息素的影响下蚁群算法会逐渐收敛到具有较高质量的解.在该工作的基础上，研究者针对蚁群算法进行了大量的改进，主要成果包括[6-9]：精英蚁群算法(elitist ant system, EAS)、最大-最小蚁群算法(max-min ant system, MMAS)、多蚁群系统(ant colony system, ACS)、基于排序的蚁群算法(rank-based ant system, RAS)等.
为改进蚁群算法在旅行商问题上的求解效能，一类典型的解决办法是采用蚁群算法与其他类型启发式算法的混合算法.龚本灿等人[10]采用蚁群算法生成旅行商问题的初始解，并采用3种不同的邻域搜索算子对初始解进行改进.Mavrovouniotis和Yang[11]针对蚁群算法求解旅行商问题中算法收敛速度较慢和容易陷入局部最优的问题设计了多种不同的邻域搜索算子.另一种改进蚁群算法的求解效能的方案是在蚁群算法的求解结构上做改进.Mahi等人[12]提出了一种基于粒子群算法、蚁群算法和3-opt邻域搜索算法的混合启发式算法框架用于求解旅行商问题.该方法被证明具有比当时已有算法更好的算法效能.Pang等人[13]提出了一种基于邻域搜索库的蚁群算法用于求解旅行商问题，计算实验表明采用邻域搜索库能够有效改善算法的求解效能.Manfrin等人[14]将蚁群中的人工蚂蚁分为多个不同的并行运行的蚁群，并采用全局信息素交换的方式在不同的并行蚁群间进行交换，并证明采用并行蚁群的方法能够有效地加速蚁群算法的收敛并提升解的质量.Zhang等人[15]提出了一种改进最大-最小蚁群算法.该算法采用基于最优解的随机采样的方法确定信息素矩阵的最大及最小值，同时确定每次迭代时信息素残留的量.Gan等人[16]将蚁群算法中的人工蚂蚁分为常规蚁和搜索蚁2个不同的族群.其中，常规蚁以传统蚁群算法构建解的方式进行解空间搜索，而搜索蚁则更倾向于在现有最优解的邻域进行可行解的搜索.
近年来，深度强化学习方法在路径规划问题中涌现了大量应用.Vinyals等人[17]提出了一种基于指针网络的旅行商问题求解方式.该方法能够将任意规模的旅行商问题转化为对应规模的向量向量输出，并基于贪婪原则进行求解.Nowak等人[18]提出了一种基于图神经网络(graph neural network, GNN)的旅行商问题求解方法.该方法能够同时接受有监督训练和无监督训练.Prates等人[19]在Nowak[18]的基础上设计了一种基于图卷积网络(graph convolutional network, GCN)的深度学习方法，用于求解TSP问题.该网络能够更好地提取TSP问题中的客户和连边的深层信息.然而，该方法只能通过有监督的方式学习，每次训练需要输入TSP问题实例以及对应的最优解.其中最优解采用Concorde TSP solver产生.Joshi等人[20]则以连边为中心构建了一类新的神经网络结构.在该结构中，连边信息首先输入一个多层卷积神经网络，网络在经过多层卷积后，其输出再经过一个多层感知机(multilayer perceptron, MLP)转化为可能出现在最优解中的概率值.为训练该网络，需要同时向该网络输入3个不同的向量：一个包含全部客户节点位置信息的向量，一个包含全部连边权重的向量，以及一个预期的目标值.其中预期的目标值采用Concorde TSP solver产生.
采用图神经网络方法求解TSP问题目前存在2个主要限制：1)神经网络维度需与问题维度一致；2)图神经网络通常采用有监督学习方式，其学习结果依赖于产生训练实例对应的最优解方法的优劣.Dai等人[21]采用Structure2Vec技术将旅行商问题的图模型以及当前解的状态转换为向量输入，并基于Q学习方法设计了基于该向量输入的求解方式.Bello等人[22]针对文献[17]中训练样本必须带标签(即事先已知最优解和路径)的问题，设计了能够基于经验进行求解的指针网络.Kool等人[23]将深度神经网络和注意力机制进行结合，用于求解旅行商问题.Nazari等人[24]在文献[21]的基础上，考虑到问题求解的动态性因素，提出了基于注意力机制的深度学习方法.该方法将旅行商问题的向量输入和当前部分解通过嵌入层(embeddings)转换为高维向量，并基于该向量进行了问题求解.有关深度学习方法求解旅行商问题的其他方法可见综述文献[25].
本文提出了一种基于深度学习和蚁群算法的组合优化算法混合求解策略.该方法首先使用深度学习方法挖掘问题实例中的特征，并形成对应的特征矩阵.以该矩阵为基础，采用蚁群算法进行解的搜索.该方法能够有效求解不同规模的旅行商问题.
2 旅行商问题模型
旅行商问题是一个经典的组合优化问题.该问题可描述为存在一系列城市和一个商人，商人要按照顺序遍历全部的城市，每个城市只能访问一次.问题优化目标为游历的总路径最短.该问题数学模型如下：旅行商问题可以表示为一个无向图Ts=(S,E)，其中，S为全部城市节点集合，E为城市节点间的连边集合.边eij∈E(i,j∈N,i≠j)有与其相关的成本dij.
该问题的决策变量为
(1)
该问题的优化目标为
(2)
3 深度智慧型蚁群算法框架
深度智慧型蚁群优化算法(deep intelligent ant colony optimization, DIACO)在蚁群算法基础上，通过将蚁群算法中的启发式信息矩阵替换为采用深度强化学习方法提取的问题特征矩阵，对算法的求解效能进行了改进.为介绍智慧型蚁群算法，首先介绍经典蚁群算法框架.
经典蚁群算法在构建旅行商问题的解时采用以下步骤：
1) 随机选择一个城市，并将人工蚂蚁放置于该城市.
2) 人工蚂蚁采用轮盘赌原则选择下一步到达的城市，城市被选择的概率为
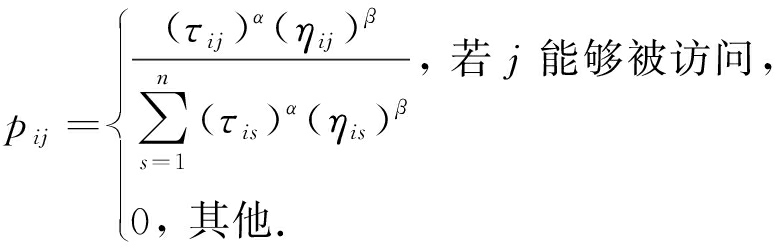
(3)
其中，pij为人工蚂蚁从城市i出发拜访城市j的可能性.τij为人工蚂蚁残留在边ij上的信息素信息，ηij为边ij上的启发式信息.α和β为控制启发式信息和信息素信息重要性的参数.
3) 每当人工蚂蚁访问一个城市时，就将该城市放入当前解，并将该城市加入当前人工蚂蚁的禁止访问列表.
4) 当全部城市都被访问完后，人工蚂蚁返回开始城市，计算当前解的收益，并根据式(4)更新信息素矩阵：
(4)
其中，ρ为信息素蒸发系数，τij(t)为第t代残留在边ij上的信息素信息,
为蚂蚁k在边ij上留下的信息素信息，nA为人工蚂蚁数量.在本文中，采用式(5)设定：
(5)
其中，lk为蚂蚁k求得的当前问题的解的路径长度.
通过以上分析不难看出，蚁群算法求解旅行商问题的效果主要取决于2项信息：信息素信息τij以及启发式信息ηij.目前针对蚁群算法的研究，主要集中在如何通过改进信息素信息τij的更新方式以促进蚁群算法的收敛和改进蚁群算法的效果.而启发式信息则多采用如下方法确定：
(6)
注意到以上问题，在DIACO中，我们设计了基于深度学习方法的问题特征提取方法，并采用该方法获得的问题特征矩阵代替经典蚁群算法中的ηij矩阵，以改进蚁群算法的求解表现.DIACO算法的框架如图1所示：
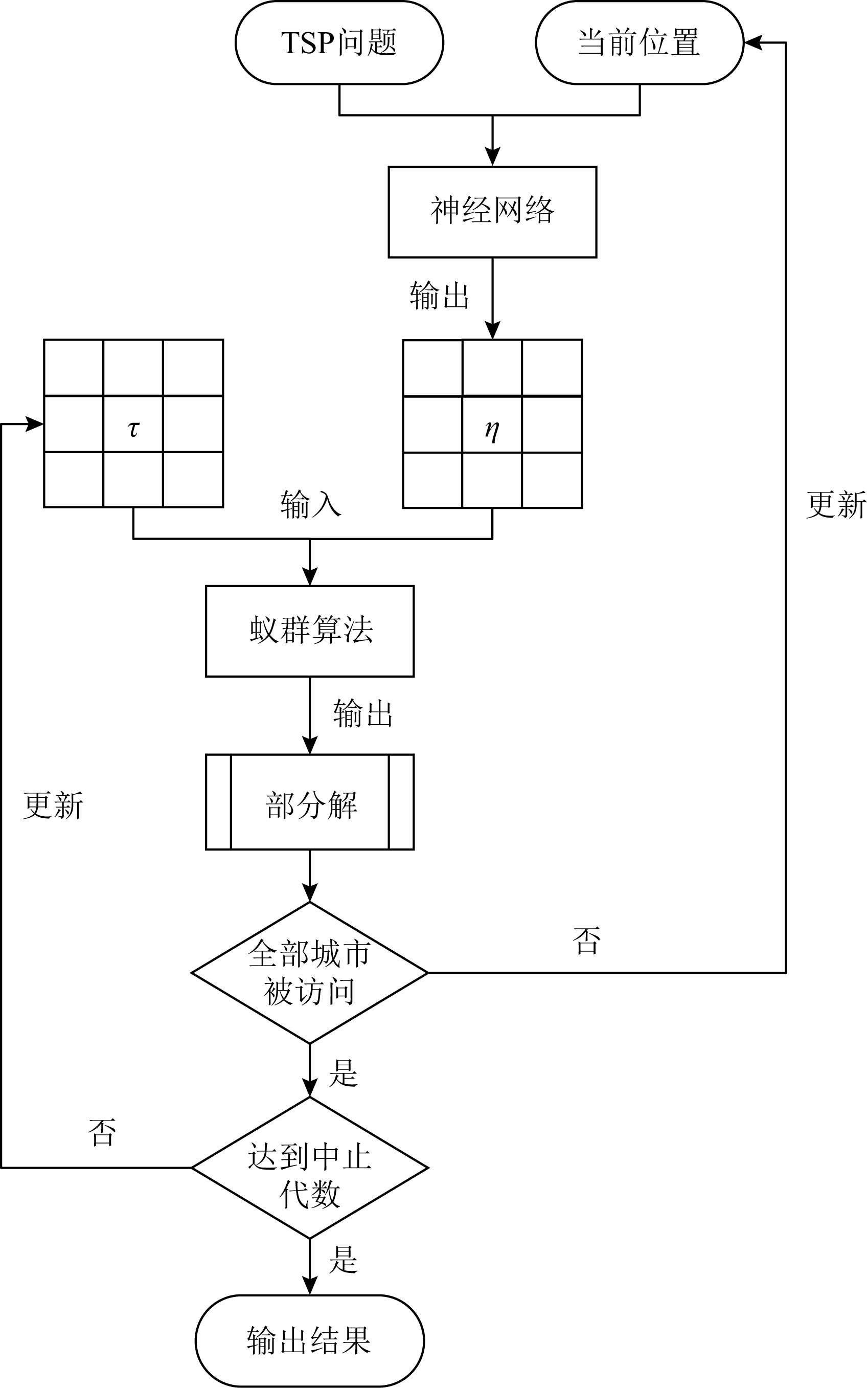
Fig. 1 Algorithm structure of DIACO
图1 DIACO算法结构
在DIACO中，我们首先采用基于注意力机制的神经网络对问题实例进行特征提取，并产生ηij.然后采用蚁群算法对问题实例进行求解.
4 基于注意力机制的神经网络特征提取方法
本文所采用的基于注意力机制的神经网络模型是一种基于策略(policy-based)的深度强化学习方法.该方法不依赖标签信息(ground truth)，而能够通过学习过程中奖励值的反馈进行自完善.以下首先介绍该模型的具体结构.
4.1 模型结构
本文提出的基于注意力机制的神经网络模型(neural networks, NN)由2部分组成:1)编码器-解码器结构.该结构主要负责建立问题输入和特征输出之间的关联.在旅行商问题中，问题输入为全部城市的坐标集合以及当前已构建的部分解的信息.2)注意力模型.该结构综合考虑编码器-解码器中问题输入与输出参数之间的相关性，并给予待访问城市不同程度的关注度.
该模型的具体结构有4个：
1) 编码器.编码器采用一维卷积嵌入层结构，将问题输入转化为高维度向量，以充分利用图Ts中的城市的结构信息.该部分的输入为各个城市的欧氏坐标.
2) 全局变量G.在编码器中，每一个任务对应输出的特征向量是相互独立的，因此这些变量并不能反映出城市之间边的集合E的特征.因此，需要针对边的集合E进行表征.本文采用文献[23]中的多头注意力(multi-head attention, MHA)神经网络结构来进行相关特征的提取，该变量可以被认为是该场景的一个全局变量，它包含了针对边的集合E的相关信息.
3) 解码器.解码器主要用于结合编码器输入、全局变量输入以及当前解的信息，输出针对下一阶段全部可选城市的评价.考虑到旅行商问题求解过程具有一定Markov性，即针对下一阶段可选城市的评价只与初始访问城市和当前所处城市相关，因此，本文将初始访问城市s0、当前所在城市st和当前访问城市同其他待访问城市的距离
作为解码器的输入，并将解码器的结构定义为一个简单的一维嵌入层.
4) 注意力模型.注意力模型用于预测下一步可选择城市中，选择哪个城市获得最优解的可能性更大.采用注意力模型能够给予下一步更可能产生最优解的城市更高的被选择概率.
基于注意力机制的神经网络结构如图2所示.该结构通过嵌入层操作，将城市的坐标特征[xi,yi]、当前访问城市同其他待访问城市的距离
转换成对应维度的特征向量C=(hs1,hs2,…,hsn)和D=(hd1,hd2,…,hdn).之后通过多头注意力模型得到全局变量G.
Fig. 2 Attention based neural network structure
图2 基于注意力机制的神经网络结构
在以上变换的基础上，本文采用文献[22]中的glimpse结构，得到状态变量Z.具体操作如式(7)所示：
Z=glimpse(G;[hs0,hst]),
(7)
其中，s0为初始访问城市，st为当前访问城市，G为全局变量，[hs0,hst]表示对2个向量进行拼接操作.
综上，NN模型的解码由全局变量G、状态变量Z和距离变量D组成.将其输入全连接层进行特征计算，得到各个待访问城市的相关度，最终通过softmax函数对相关度进行归一化，得到针对下一步可选城市的具体评分.具体的计算为
(8)
(9)
其中，Ct和Xt分别表示在第t步已经访问和待访问的城市集合,vT和w表示待学习的神经网络参数，P(ct+1|Ct,Xt)为在时刻t已选城市ct∈Ct，待访问城市Xt的情况下向访问城市ct+1转移的条件概率.该概率越大，代表神经网络认为下一步选择ct+1中的城市可能获得最优解的概率越大.
另外，在NN模型运行过程中，本文采用掩码机制对当前已经被访问过的城市进行屏蔽，使其不会成为模型决策的待选项.掩码机制本身为一串与需访问城市数量等长的一维{0,1}向量.当城市
位于Xt时，该城市对应的掩码mask=1，否则该城市对应的掩码mask=0.
该模型的具体运行流程如图3所示.首先通过随机初始化选择s3作为初始起点，之后基于当前城市s3采用神经网络模型计算下一步可选择的解的特征向量，得到当前状态下待选择城市的匹配度，此时的匹配度s4>s2>s1，因此选择任务s4作为下一访问城市，更新模型各个变量并使用掩码机制对已访城市进行屏蔽，重复上述过程直到模型停止.
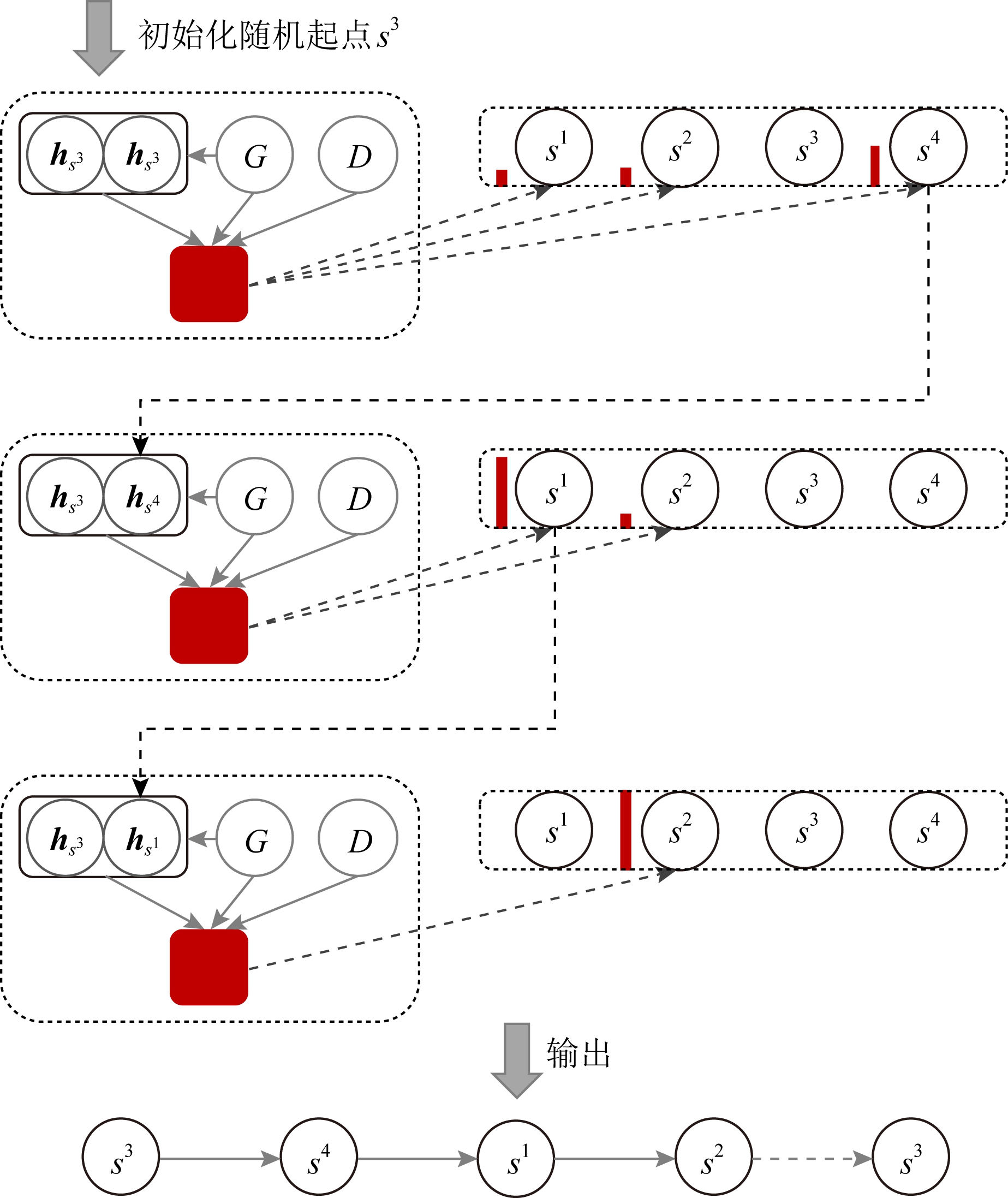
Fig. 3 DIACO workflow
图3 DIACO算法工作流程
4.2 训练方法
为说明NN模型的训练方法，首先需要阐明NN模型的求解过程.
本文所采用的NN模型将旅行商问题的求解看做一个Markov过程.具体而言，在求解旅行商问题时，NN模型首先随机选择一个城市c0∈X0作为初始起点，然后以构建式规则逐步将待访问城市加入当前解.在每步迭代时，NN模型在C0={c0,c1,c2,…,ct}的状态下，通过参数为θ的网络模型选择下一个被访问城市ct+1.采用概率的链式法则，最终生成长度为T′的访问顺序规划C={ct,t=0,1,…,T′}，其中T′为旅行商问题实例的规模.该过程可通过式(10)表示：
(10)
其中，P(C|X0;θ)为在NN的参数组合θ下生成访问序列C的可能性，P(ct+1|Ct,Xt;θ)为在当前状态Ct下基于参数组合θ选择ct+1作为下一步访问城市的概率.因此，存在最优路径集合C*，那么模型的最优参数组合θ*应满足：
(11)
式(11)代表在模型的最优参数组合θ*的条件下，NN模型能够以最大概率求得最优路径集合C*,其中
为在最优路径集合C*条件下，在时刻t被安排访问的城市.这一特性使得当模型的参数组合θ接近于θ*时，由于P(C*|X0,θ)≅1，此时NN模型将能够以较大概率求得最优解且扰动较少.此时的模型较为适合作为DIACO算法的输入.
本文用J(θ)表示在参数组合θ下NN模型批量求解旅行商问题的期望，J(θ)可通过式(12)计算：
(12)
其中，r(C)表示当前路径的目标值.考虑到在式(2)中，旅行商问题的优化目标为最小化总旅行距离，因此NN模型的训练目标可通过式(13)表示：
(13)
其中，π*表示最优策略，该策略包括模型参数及决策策略，π表示NN模型的策略集合.式(13)表示NN模型的训练目标为寻找能够在训练集上取得最小期望路径长度的策略.
为达成该训练目标，本文采用基于策略梯度的强化学习Actor-Critic方法，其伪代码如算法1所示.其中，Actor网络为本文提出的NN模型，Critic网络使用与NN模型相同的特征提取层，而只输入城市的坐标信息，然后2个全连接层将编码器输出的特征信息映射到对应的网络输出.
算法1. Actor-Critic算法.
① 初始化Actor的网络参数θ;
② 初始化Critic的网络参数θc;
③ for 每一代 do
④ 重置梯度:dθ←0,dθc←0;
⑤ N个调度场景;
⑥ for k=1,2,…,N do
⑦ 计步器t←0;
⑧ while 没有达到终止条件 do
⑨ 根据
选择下一个任务
⑩ 更新状态
t←t+1;
end while
计算奖励值Rk;
end for
通过dθ更新θ，通过dθc更新θc;
end for
4.3 启发式矩阵处理
对于训练好的NN模型，本文针对场景中的每个城市，逐一设置为初始起点，并运行一次NN模型，得到剩余城市的特征向量，最终将全部城市的特征向量进行拼接得到启发式矩阵M0，NN模型的简要运行流程如图4所示:
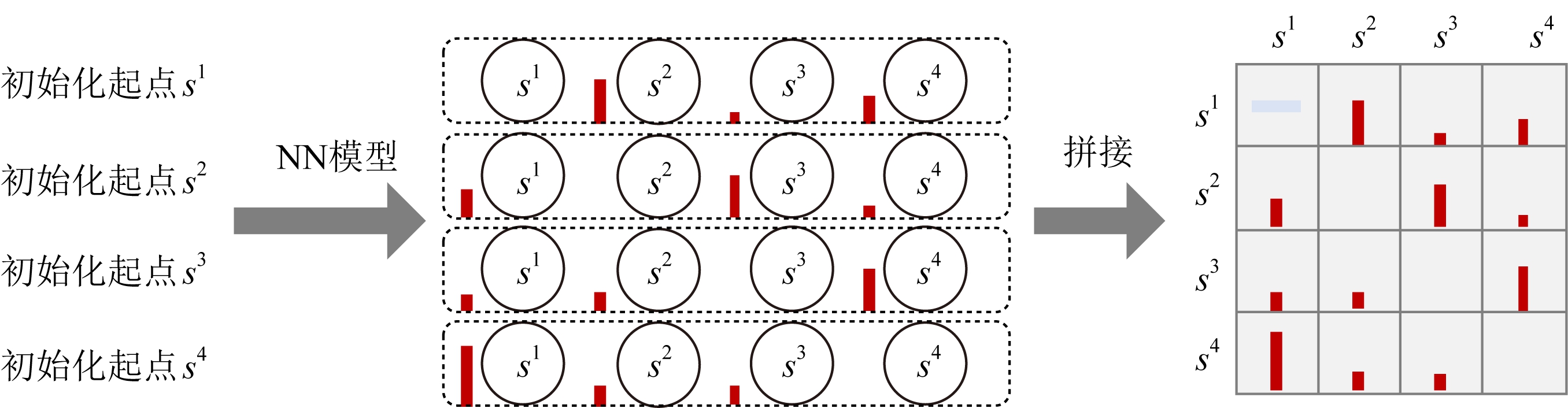
Fig. 4 Characteristic extraction using NN model
图4 采用NN模型进行特征提取
需要额外指出的是，由于NN模型的训练采用构建式规则(本文中为随机贪婪规则)，为了保证求解效能的稳定性，其训练时在不同待选城市间的评分差距较大.图5展示了在29城市规模的算例上的NN模型输出的可视化图像.
Fig. 5 The visualization of the M0 on 29 cities instance
图5 29城市规模算例M0的可视化
考虑到单个城市的特征值与其他城市特征值的差值过大可能导致蚁群算法过早陷入局部最优，从而影响蚁群算法搜索效能的问题，需要对NN模型输出的M0矩阵进行预处理.预处理方法为
(14)
在式(14)中，首先针对输出值
进行等比例缩小，其中n为算例规模.然后采用softmax函数对输出进行处理，缩小不同城市在M0矩阵中的评估值的数量级差距.图6展示了图5中展示的M0矩阵经过预处理后的最终结果.
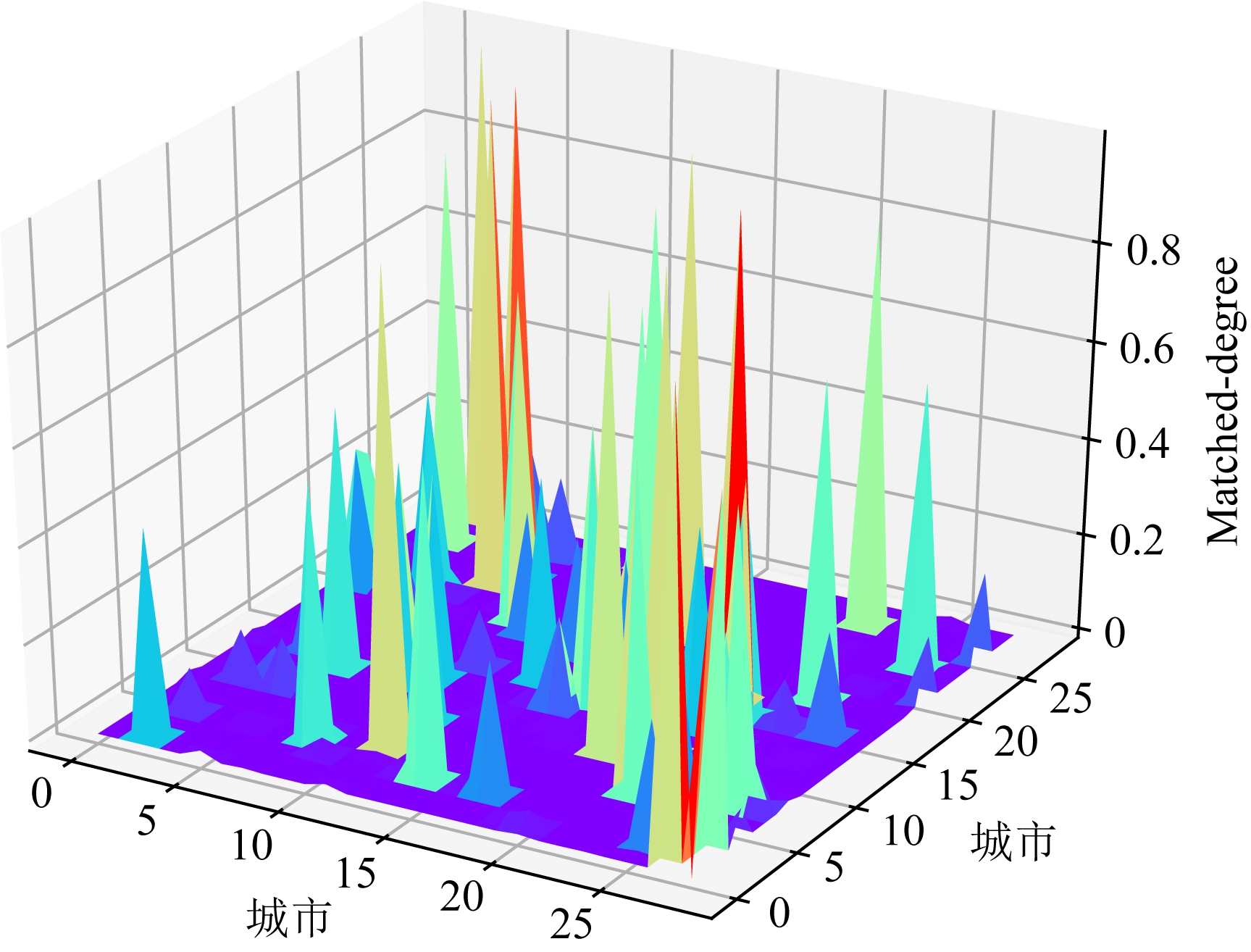
Fig. 6 The visualization of the M0(after pre-processing)
图6 M0的可视化(预处理后)
另外需要指出，本文求解的旅行商问题均为对称旅行商问题，即从城市si旅行到城市sj与从城市sj旅行到城市si应具有相同评价，因此本文采用以下方法对M0进行处理并得到最终的特征矩阵M：
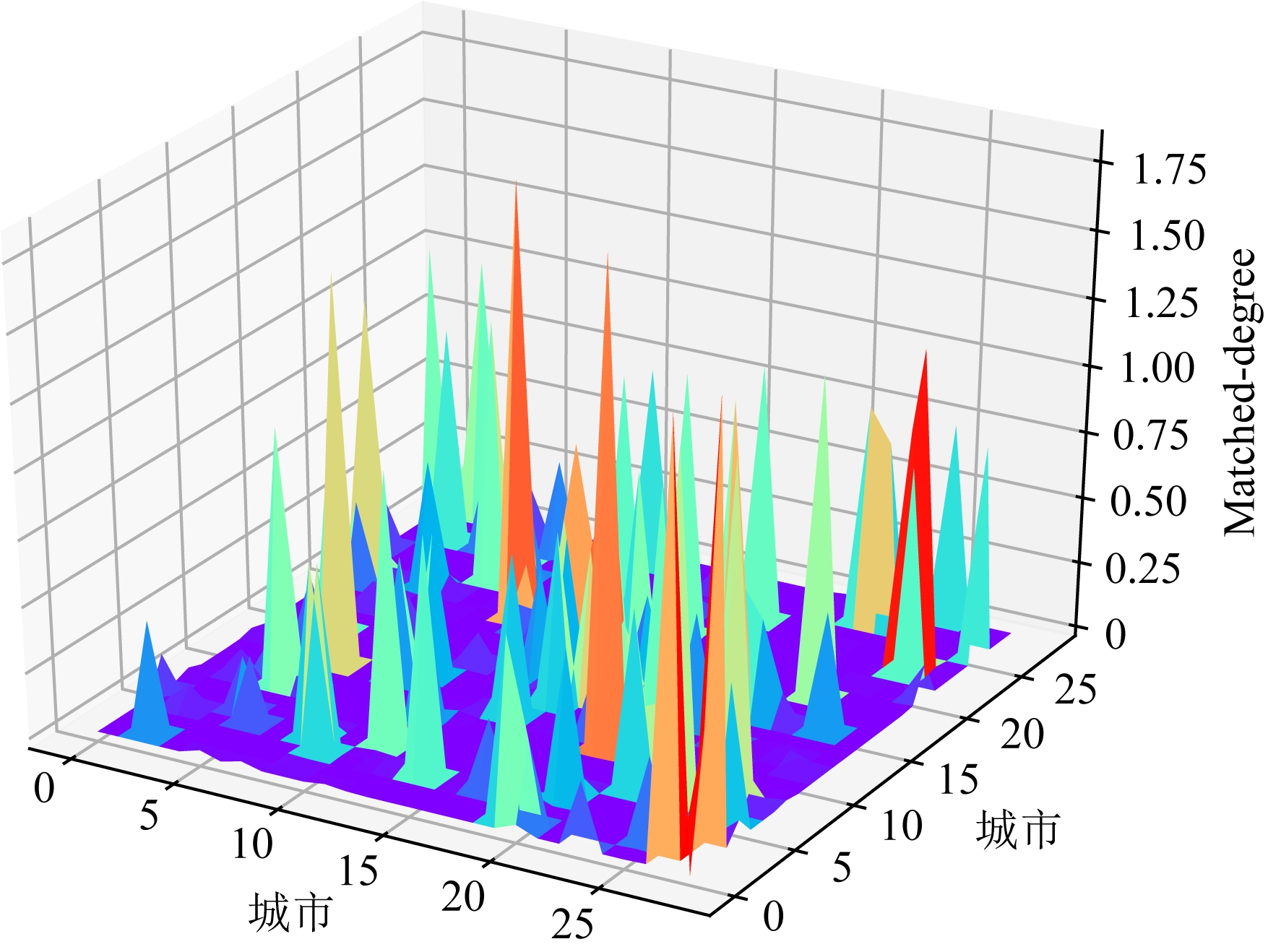
Fig. 7 The visualization of the M
图7 M的可视化
(15)
其中，
为M0的转置，M的可视化结果可见图7.
5 实验与结果
5.1 实验设计
1) 实验参数
NN模型采用(Actor-Cirtic, AC)算法对模型进行训练，为了保证模型在训练过程中的寻优能力以及在测试过程中的稳定性，本文分别采取随机策略和贪婪策略对待访问城市进行选择.AC算法中的Actor即NN模型，参数设置如下：MHA:Q,K,V-dim=128,Head=8,Layer=3,Inner=512；编码器:Conv-1D(Dinput_size=2,Filter=128,kernel_size=1,stride=1)；解码器:Conv-1D(Dinput_size=1,Filter=128,kernel_size=1,stride=1).Critic共包含4层编码器，具体参数设置如下：
编码器1：Conv-1D(Dinput_size=2,Filter=128,kernel_size=1,stride=1)；
编码器2：Conv-1D(256,Filter=20,kernel_size=1,stride=1)；
编码器3：Conv-1D(20,Filter=20,kernel_size=1,stride=1)；
编码器4：Conv-1D(20,Filter=1,kernel_size=1,stride=1).
本文使用Xavier对网络参数进行初始化[26]，并采用Adam优化器[27]对网络参数进行更新，初始学习率η=0.0001，训练的问题规模为20，训练的轮数epoch=100，批训练量为512.
本研究使用的全部蚁群算法中，最大迭代次数为1 000，最大蚂蚁数量为25，ρ=0.9，α=1，β=1.
2) 数据集
本文训练数据[xi,yi]均采用在均匀随机分布Φ下生成，取值范围(0,1)，最终分别得到128万个训练场景，1万个评价场景.
3) 实验设备
模型的训练和测试均运行在一台配置RTX 2080-Ti, i9- 9900k CPU, 64 GB内存的服务器上.编译语言采用Python，编译器采用PyCharm，深度学习框架采用Pytorch 1.02.
4) 对比算法
为了验证DIACO算法的性能，本文采用无NN模型的改进ACO算法作为对比算法，该算法采用城市之间距离矩阵的倒数
作为启发式输入.此外，为了验证随机起点NN模型性能，本文同样采用NN模型对问题进行了求解.
5.2 对比分析
本文选取了任务规模为29,30,48,51,70,76和101的TSPLIB标准测试算例进行测试，每个算法运行20次，算法评价指标选用了求解的平均路径长度(Avg)、解的变异系数(C.V.)和与最优解的差距百分比(Gap)三个指标对全部对比算法的求解效能进行了分析.其中，变异系数的计算方式为CV=Std/Avg，其中，Std为标准差，Avg为均值.显然，变异系数越小代表数据离散程度越低.采用变异系数能够更好地比较多组不同测量尺度的数据间的离散程度的差异.另外需要指出的是，在表1和表2中，理论最优解(OPT)及对比算法找到的最优解用加粗字体标出.bays29的理论最优解用下划线标出，其原因是该理论最优解目前存在一定的争议(其主要原因是不同方法得出的理论最优解在保留不同小数位数时有所不同).
Table 1 Results of DIACO on benchmark Instances
表1 DIACO方法在benchmark算例上的实验结果
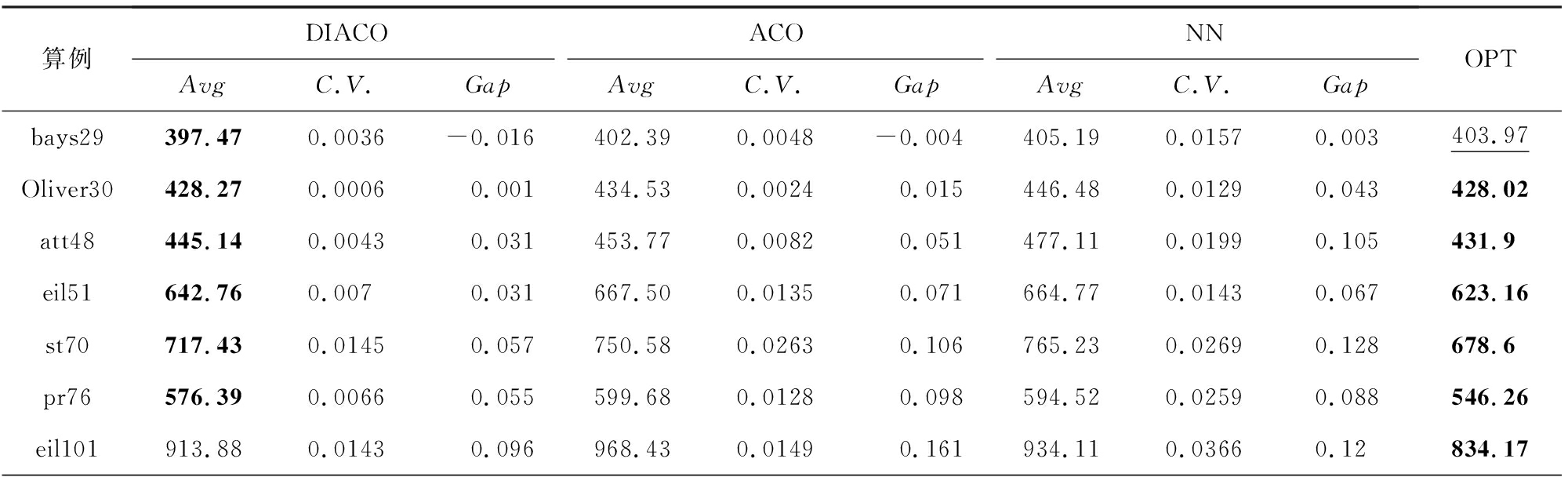
算例DIACOACONNAvgC.V.GapAvgC.V.GapAvgC.V.GapOPTbays29397.470.0036-0.016402.390.0048-0.004405.190.01570.003403.97Oliver30428.270.00060.001434.530.00240.015446.480.01290.043428.02att48445.140.00430.031453.770.00820.051477.110.01990.105431.9eil51642.760.0070.031667.500.01350.071664.770.01430.067623.16st70717.430.01450.057750.580.02630.106765.230.02690.128678.6pr76576.390.00660.055599.680.01280.098594.520.02590.088546.26eil101913.880.01430.096968.430.01490.161934.110.03660.12834.17
续表1
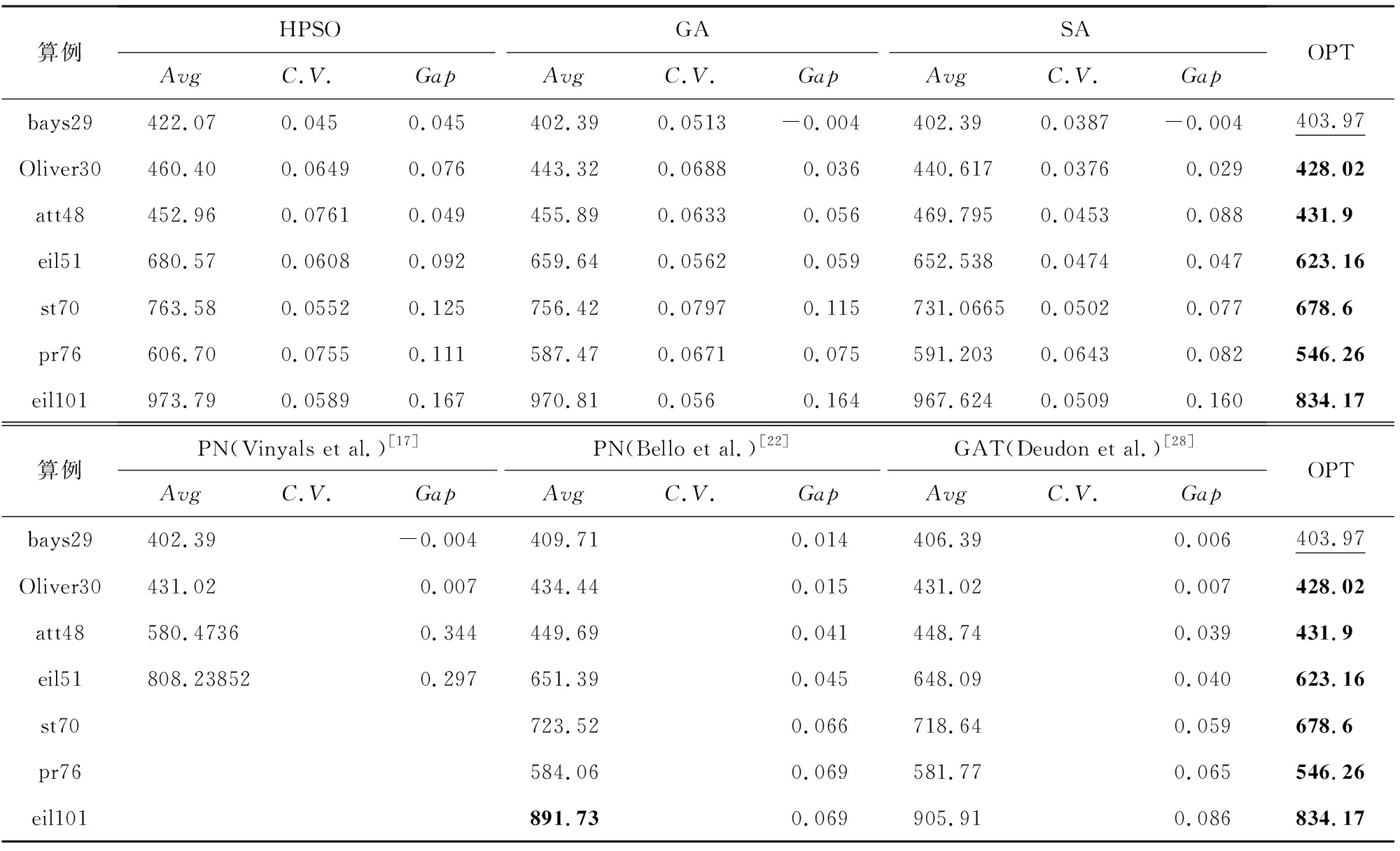
算例HPSOGASAAvgC.V.GapAvgC.V.GapAvgC.V.GapOPTbays29422.070.0450.045402.390.0513-0.004402.390.0387-0.004403.97Oliver30460.400.06490.076443.320.06880.036440.6170.03760.029428.02att48452.960.07610.049455.890.06330.056469.7950.04530.088431.9eil51680.570.06080.092659.640.05620.059652.5380.04740.047623.16st70763.580.05520.125756.420.07970.115731.06650.05020.077678.6pr76606.700.07550.111587.470.06710.075591.2030.06430.082546.26eil101973.790.05890.167970.810.0560.164967.6240.05090.160834.17算例PN(Vinyals et al.)[17]PN(Bello et al.)[22]GAT(Deudon et al.)[28]AvgC.V.GapAvgC.V.GapAvgC.V.GapOPTbays29402.39-0.004409.710.014406.390.006403.97Oliver30431.020.007434.440.015431.020.007428.02att48580.47360.344449.690.041448.740.039431.9eil51808.238520.297651.390.045648.090.040623.16st70723.520.066718.640.059678.6pr76584.060.069581.770.065546.26eil101891.730.069905.910.086834.17
注：黑体数字表示最优解.
Table 2 Results of Different Model Scale DIACO on Benchmark Instances
表2 不同模型规模DIACO方法在benchmark算例上的实验结果
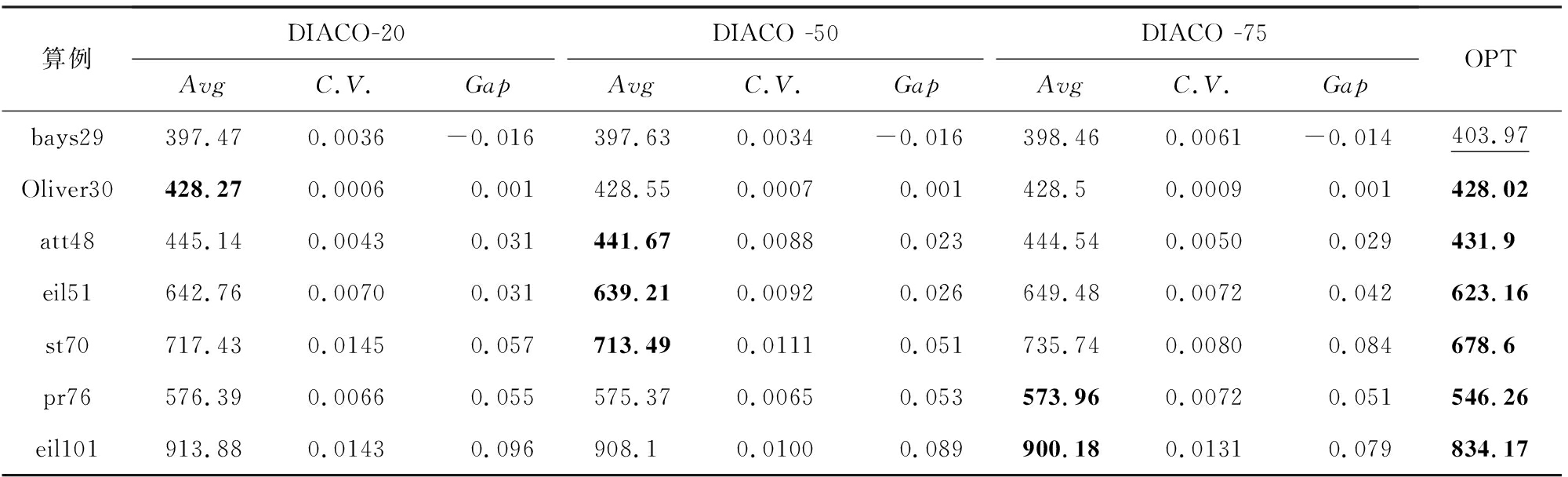
算例DIACO-20DIACO -50DIACO -75AvgC.V.GapAvgC.V.GapAvgC.V.GapOPTbays29397.470.0036-0.016397.630.0034-0.016398.460.0061-0.014403.97Oliver30428.270.00060.001428.550.00070.001428.50.00090.001428.02att48445.140.00430.031441.670.00880.023444.540.00500.029431.9eil51642.760.00700.031639.210.00920.026649.480.00720.042623.16st70717.430.01450.057713.490.01110.051735.740.00800.084678.6pr76576.390.00660.055575.370.00650.053573.960.00720.051546.26eil101913.880.01430.096908.10.01000.089900.180.01310.079834.17
注：黑体数字表示最优解.
表1总结了本文使用的全部算法和理论最优解的对比结果.通过表1可知，DIACO在测试的全部算法中，找到了6个算例的最优值.因此可以认为，相比于其他对比方法，DIACO在较小规模的TSP问题求解上具有一定优势.且相比于其他类型的启发式算法，DIACO具有更好的解的稳定性.另外，在算例bays29中，DIACO取得了比现有的最优解更好的求解结果，其可能原因是在求解过程中距离矩阵的保留位数不同导致的误差.图8总结了不同算法在7组对比算例上的Gap值.
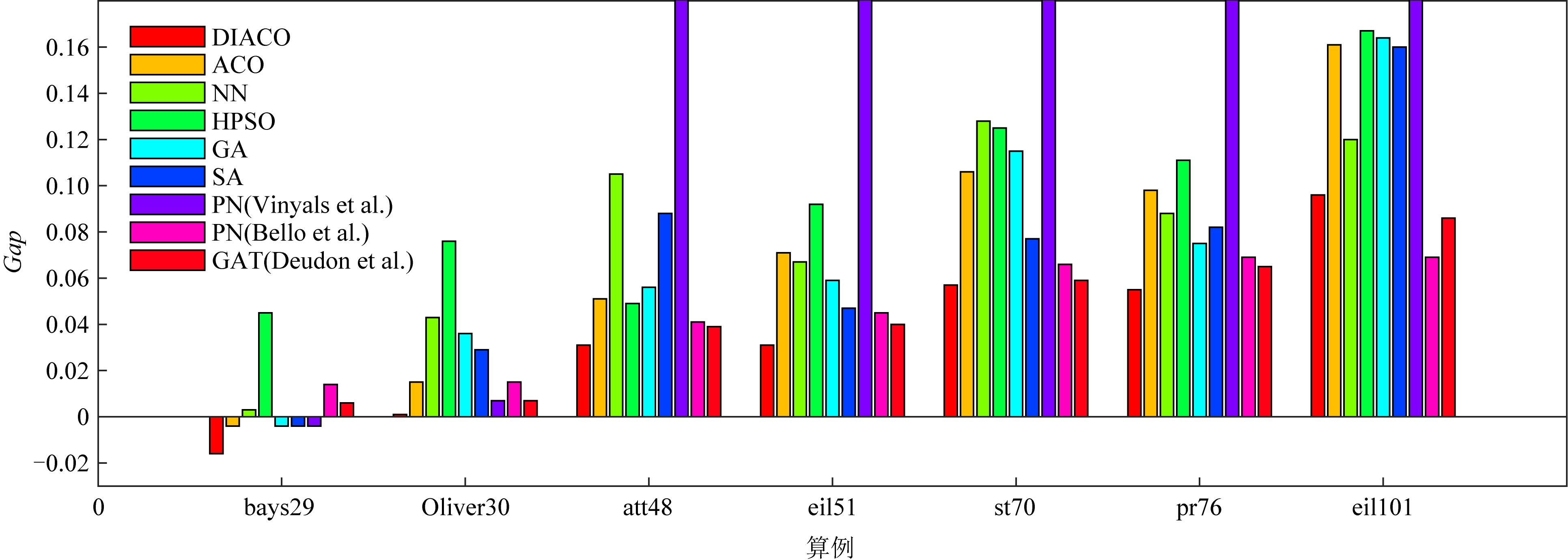
Fig. 8 The Gap of different algorithms
图8 不同算法平均路径长度的Gap图
需要额外指出的是，由于Vinyals等人[17]在较大规模算例上的Gap值太大(超过30%)，因此在此处不再予以列出.
另外，DIACO相比原始的ACO和仅采用NN模型求解的结果而言，算法的求解表现均有提升.其中，相比于原始ACO算法，DIACO的最小平均表现提升约为1.2%.而相对于NN模型，DIACO的最小平均表现提升约为1.9%.若考虑全部7组算例的均值，则DIACO相比于原始ACO的解的表现平均提升约3.47%，DIACO相比于NN模型的解的表现平均提升约4.27%.
另外需要指出，DIACO是一个具有良好的求解稳定性的算法.在7组计算实验中DIACO的最大变异系数约为0.0145.且相比于原始ACO和仅采用NN模型求解的结果，DIACO的变异系数有较大幅度的下降，可以认为DIACO提升了NN模型和ACO算法的计算稳定性.
最后需要说明的是，由于机器学习方法一般采用简单的搜索机制,如贪婪法或者束搜索(beam search, BS)等，因此DIACO相比于一般的机器学习方法具有更大的时间开销.
5.3 模型有效性验证
1) 模型训练过程分析
本节首先给出了NN模型的训练过程分析如图9所示.该图展示了NN模型在平均算例规模为20城市的训练样本上的训练曲线.从图9可以看出，NN模型在训练的前20代平均路径长度快速下降，并在约第60代达到基本稳定状态.从图9可以总结得出，本文所采用的NN模型能够以较快速度达到收敛状态.
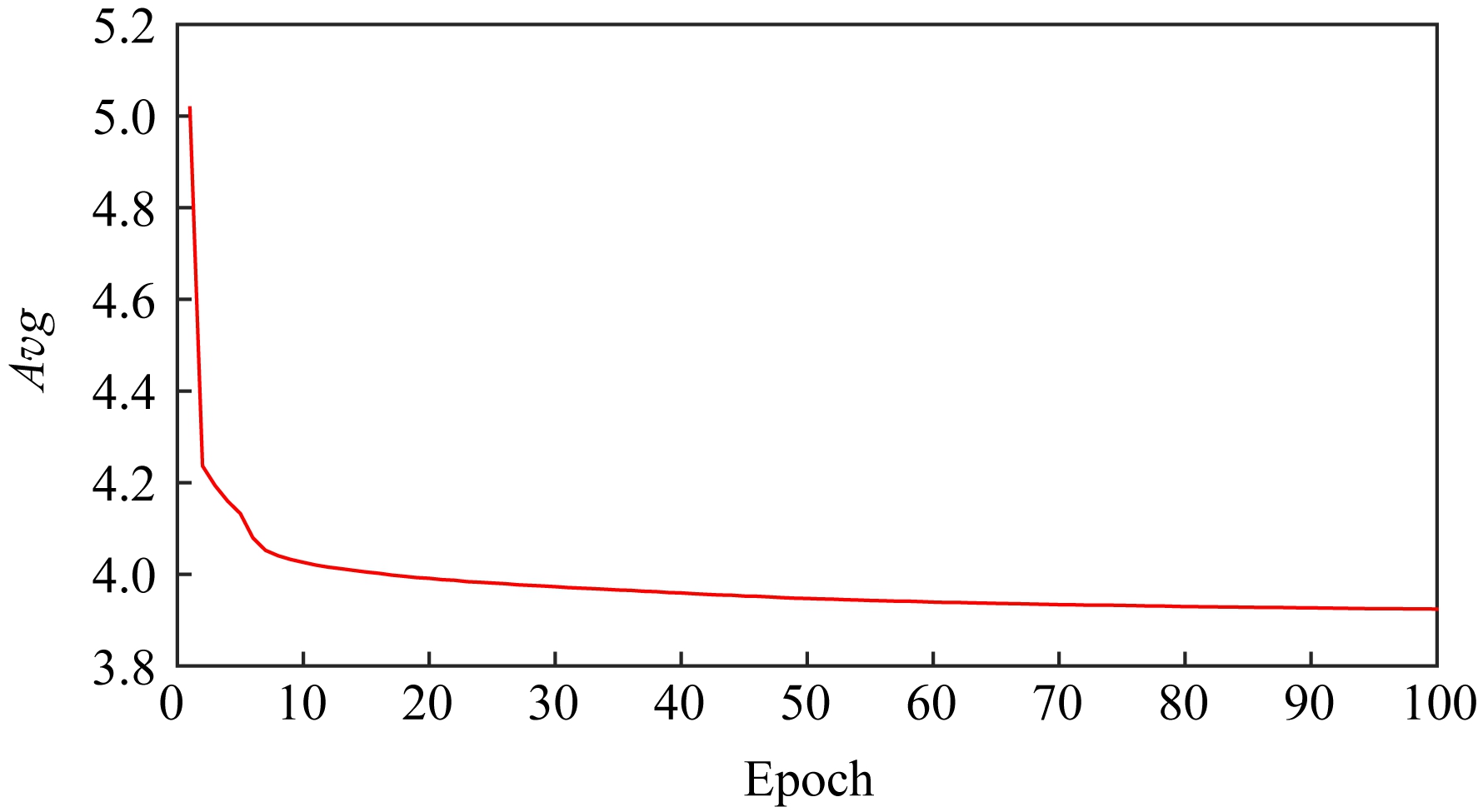
Fig. 9 The training process of NN model at 20 scale instances
图9 NN模型在任务规模20下的训练过程
2) 模型泛化能力验证
为了验证不同规模NN模型下DIACO算法的性能，本文以20-NN模型为基础，采用参数迁移的方式对50和75规模的NN模型进行训练，缩短了模型的训练周期，具体训练128万场景，训练轮次20.模型泛化能力验证的计算结果如图10所示：
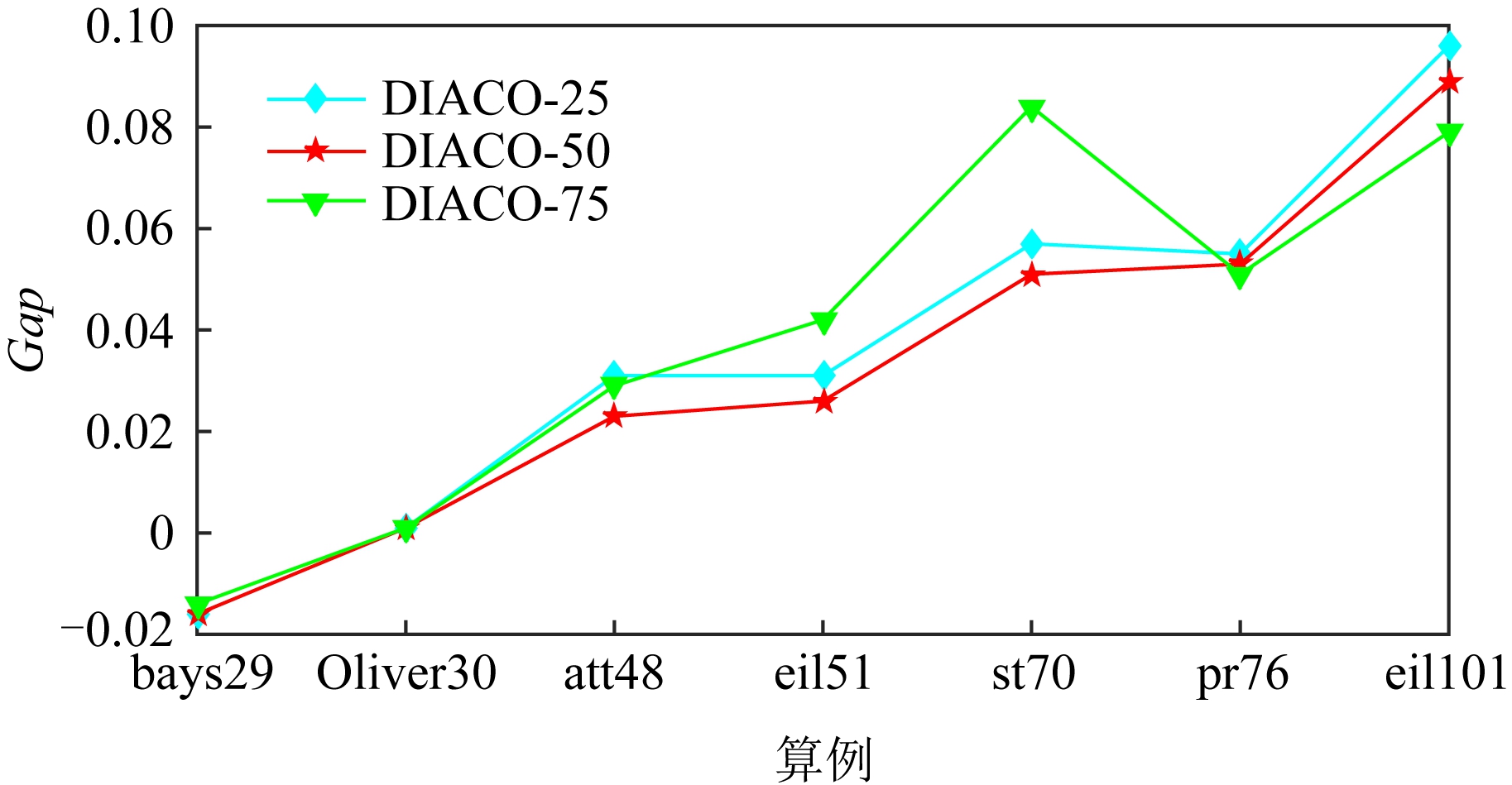
Fig. 10 The Gap of different scale DIACO on 7 instances
图10 不同模型规模DIACO在benchmark算例上的实验结果
由图10可得，在7组测试算例中，50节点规模的DIACO算法获得最好的平均计算表现.且不同规模的DIACO在全部测试场景下的平均Gap均在10%以内，可以认为该方法具有较好的规模泛化性能.
5.4 算法有效性验证
为研究NN模型输出的启发式矩阵的有效性，本文设计一种新的ACO形式.在该ACO中，启发式信息通过式(16)确定：
(16)
在式(16)中，mij为特征矩阵M中的边ij的特征值，ε和δ为控制特征值和基于距离的启发式信息的重要性的参数，且ε和δ满足ε+δ=1.通过调整公式中ε和δ的值，即可控制启发式信息中特征值和基于距离的启发式信息的比例.当ε=1时，该ACO即为DIACO，当δ=1时，该ACO即为经典ACO.我们选取了ε={0,0.1,0.3,0.5,0.7,0.9,1.0}共7种不同的组合进行了验证，其结果如图11所示:
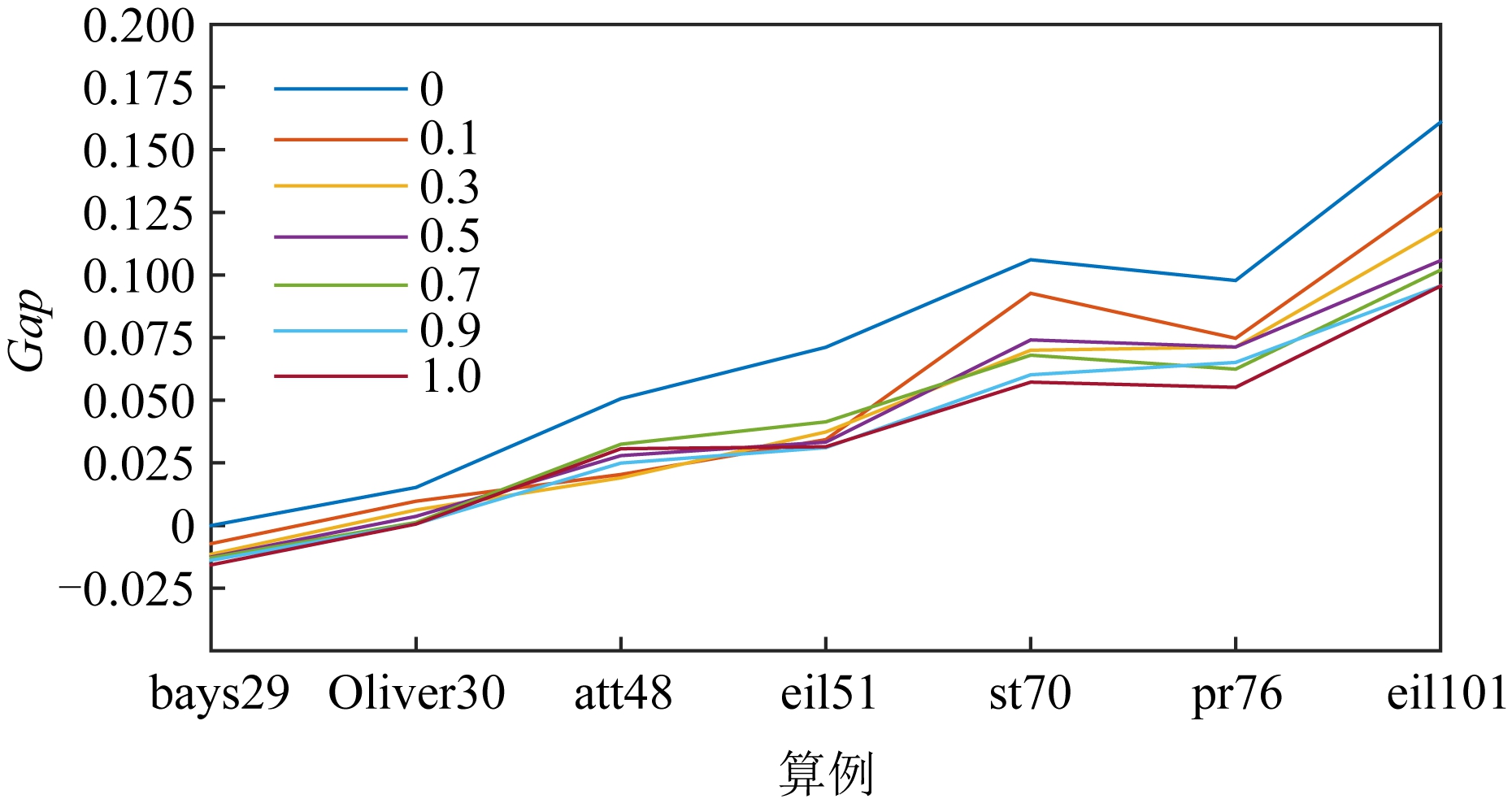
Fig. 11 Algorithm proficiency of NN model
图11 NN模型有效性验证
从图11可知，当ε=1时，即该ACO为DIACO时，该算法能够得到最好的平均表现.因此能够证明使用NN模型替换基于距离的启发式矩阵能够有效提高ACO的求解性能.
6 总 结
有效利用组合优化问题算例提供的启发式信息辅助求解组合优化问题，是改善算法求解组合优化问题效能的重要手段.本文提出了一种基于深度学习和蚁群算法的组合优化问题混合求解策略.该方法首先采用深度学习方法对组合优化问题进行特征提取，在此基础上采用蚁群算法进行搜索求解.为验证该方法的有效性，本文采用旅行商问题标准算例对该求解方法的效能进行了验证.结果表明该方法在旅行商问题上具有良好表现.
本研究可从以下3方面开展后续工作：
1) 深度学习方法对问题的分布具有较强敏感性，问题分布的改变可能导致深度学习方法得到的问题特征矩阵出现较大误差.如何解决问题分布带来的学习误差的问题，是本文后续的重要研究方向之一.
2) 如何有效地提取算例的深层信息，是本文需要解决的另一个问题.由于深度学习方法训练时采用基于平均随机贪婪原则的方式构建解，因此难以避免训练过程的短视问题.因此，如何提高深度学习方法提取特征的深度，是本研究另一个重要的后续工作方向.
3) 在更大规模的问题上开展针对性研究.在本文中，我们发现当问题规模超过100节点时，DIACO算法的表现具有一定程度的下降.其可能原因包括：①网络规模不够导致信息提取不完善；②搜索时间不够导致无法搜索到更好的解.因此，在未来针对DIACO算法的研究中，将着重研究该方法在大规模算例下的表现，以及针对网络在不同规模算例上的泛化性进行研究.
作者贡献声明：王原主要负责论文的思路设计、算法代码编写、实验思路设计、实验数据分析和论文撰写；陈名主要贡献包括深度学习方法设计、算法代码编写、深度学习方法训练、实验数据收集及论文撰写，为本文通信作者；邢立宁主要贡献包括论文思路指导、实验数据分析指导、论文撰写及修改；吴亚辉主要贡献包括优化方法设计、实验数据收集及分析；马武彬主要贡献包括算法代码编写、实验数据采集及分析；赵宏主要贡献包括：对比算法设计、代码编写、实验数据采集.王原和陈名为共同一作.
[1]Kenneth N M, Frank R S, John A B. Job-shop scheduling theory: What is relevant?[J]. Interfaces, 1988, 18(4): 84-90
[2]Lawler E L, Leenstra J K, Kan A H, et al. Sequencing and scheduling: Algorithms and complexity[M] //Handbooks in Operations Research and Management Science, Volume 4: Logistics of Production and Inventory. Amsterdam: Elsevier, 1993: 455-522
[3]Cunha B, Madureira A M, Fonseca B, et al. Deep reinforcement learning as a job shop scheduling solver: A literature review[C] //Proc of the Int Conf on Hybrid Intelligent Systems. Berlin: Springer, 2018: 350-359
[4]Ilya S, Oriol V, and Quoc V L. Sequence to sequence learning with neural networks[C] //Proc of the 27th Int Conf on Neural Information Processing Systems-Volume 2 (NIPS’14). Cambridge, MA: MIT Press, 2014: 3104-3112
[5]Dorigo M. Learning and natural algorithms[D]. Milan: Politecnico di Milan, 1992
[6]Dorigo M, Maniezzo V. Ant system: Optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems, Man, and Cybernetics. Part B, Cybernetics, 1996, 26(1): 29-41
[7]Dorigo M, Gambardella L M. Ant colony system: A cooperative learning approach to the traveling salesman problem[J]. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 53-66
[8]Bullnheimer B, Hartl R F, Strauss C. A new rank based version of the ant system—A computational study[J]. Central European Journal of Operations Research, 1999, 7(1): 25-38
[9]Dorigo M, Birattari M, Stützle T. Ant colony optimization[J]. IEEE Computational Intelligence Magazine, 2006, 1(4): 28-39
[10]Gong Bencan, Li Layuan, Jiang Tingyao, et al. Ant colony algorithm based on local optimization for TSP[J].Application Research of Computers, 2008, 25(7):1974-1976 (in Chinese)(龚本灿, 李腊元, 蒋廷耀, 等. 基于局部优化策略求解TSP的蚁群算法[J]. 计算机应用研究, 2008, 25(7): 1974-1976)
[11]Mavrovouniotis M, Yang Shengxiang. A memetic ant colony optimization algorithm for the dynamic travelling salesman problem[J]. Soft Computing, 2011, 15(7): 1405-1425
[12]Mahi M, Baykan K, Kodaz H. A new hybrid method based on particle swarm optimization, ant colony optimization and 3-opt algorithms for traveling salesman problem[J]. Applied Soft Computing, 2015, 30: 484-490
[13]Pang Shanchen, Ma Tongmao, Liu Ting. An improved ant colony optimization with optimal search library for solving the traveling salesman problem[J]. Journal of Computational & Theoretical Nanoscience, 2015 (12): 1440-1444
[14]Manfrin M, Birattari M, Stützle T, et al. Parallel ant colony optimization for the traveling salesman problem[C] //Proc of Int Workshop on Ant Colony Optimization & Swarm Intelligence. Berlin: Springer, 2006: 224-234
[15]Zhang Zhaojun, Feng Zuren . A novel Max-Min ant system algorithm for traveling salesman problem[C] //Proc of IEEE Int Conf on Intelligent Computing & Intelligent Systems. Piscataway, NJ: IEEE, 2009: 508-511
[16]Gan Rongwei, Guo Qingshun, Chang Huiyou, et al. Improved ant colony optimization algorithm for the traveling salesman problems[J]. Journal of Systems Engineering and Electronics, 2010 (2): 329-333
[17]Vinyals O, Fortunato M, Jaitly M. Pointer networks[C] //Proc of the 28th Int Conf on Advances in Neural Information Processing Systems (NeurIPS). New York: Curran Associates Inc, 2015: 2692-2700
[18]Nowak A, Villar S, Bandeira A S, et al. A note on learning algorithms for quadratic assignment with graph neural networks[C/OL] //Proc of ICML Workshop on Principled Approaches to Deep Learning (PADL). 2017 [2021-03-30]. https://www.padl.ws/papers/Paper%2017.pdf
[19]Prates M, Avelar P, Lemos H, et al. Learning to solve np-complete problems: A graph neural network for decision TSP[C] //Proc of AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI Press, 2019: 4731-4738
[20]Joshi C, Laurent T, Bresson X. An efficient graph convolutional network technique for the travelling salesman problem[J/OL]. CoRR, arXiv:1906.01227, 2019
[21]Dai Hanjun, Khalil E, Zhang Yuyu, et al. Learning combinatorial optimization algorithms over graphs[C] //Proc of Advances in Neural Information Processing Systems (NeurIPS). New York: Curran Associates Inc, 2017: 6348-6358
[22]Bello I, Pham H, Le Q V, et al. Neural combinatorial optimization with reinforcement learning[C/OL] //Proc of Int Conf of Learning Representations (ICLR), 2017 [2021-03-31]. https://openreview.net/forum?id=Bk9mxlSFx
[23]Kool W, Hoof V H, Welling M. Attention, learn to solve routing problems[C/OL] //Proc of Int Conf of Learning Representations (ICLR). 2019 [2021-03-31]. https://openreview.net/forum?id=ByxBFsRqYm
[24]Nazari M, Oroojlooy A, Snyder L, et al. Reinforcement learning for solving the vehicle routing problem[C] //Proc of Advances in Neural Information Processing Systems (NeurIPS). New York: Curran Associates Inc, 2018: 9839-9849
[25]Vesselinova N, Steinert R, Perez-Ramirez D F, et al. Learning combinatorial optimization on graphs: A survey with applications to networking[J]. IEEE Access, 2020 (8): 120388-120416
[26]Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks[C] //Proc of the 13th Int Conf on Artificial Intelligence and Statistic. Breckenridge, CO: PMLR, 2010: 249-256
[27]Kingma D, Ba J. Adam: A method for stochastic optimization[C/OL] //Proc of the 3rd Int Conf on Learning Representations (ICLR). 2015 [2021-03-31]. https://arxiv.org/abs/1412.6980
[28]Deudon M, Cournut P, Lacoste A, et al. Learning heuristics for the TSP by policy gradient[C] //Proc of Int Conf on Integration of Constraint Programming, Artificial Intelligence, and Operations Research. Berlin: Springer 2018: 170-181
