基因组数据是目前最流行的生物信息数据类型之一,自人类基因组计划开始,生物基因序列数据开始呈指数级增长.如何将有效的生物信息特征从海量高维的生物序列数据中提取出来,是目前生物信息领域最重要的问题之一.
近年来,基于基因序列的深度学习模型研究激增,主要原因之一是该类模型可以直接从原始数据进行表示学习或特征学习.深度学习可以自动提取特征,省去了大量手工选择特征的工作量[1].同时,深度学习模型也被证明可以有效识别局部基因序列在特定环境中的作用,并进一步可以用来推断基因的调控规则和表达模式.自编码器[2]、多层感知机(multilayer perception, MLP)[3-4]、玻尔兹曼机(restricted Boltzmann machines, RBMs)[5]、深度信念网络(deep belief networks, DBNs)[6]、卷积神经网络(convolutional neural network, CNN)、循环神经网络(recurrent neural network, RNN)[7]、长短记忆网络(long short-term memory, LSTM)[8]等深度学习方法与基因组研究的结合促进了对基因组学的深刻理解,并为精密医学、药物设计[9]等多个领域提供帮助.
Urda等人[10]使用深度学习方法在分析RNA序列基因表达数据方面优于Lasso(least absolute shrinkage and selection operator).Chen等人[11]提出了一种3层前馈神经网络对基因表达进行预测,其性能优于线性回归.Xie等人[12]的研究表明,他们基于MLP和SDAs的深度模型在SNP基因型预测基因表达量化方面优于Lasso和随机森林.曹明宇等人[13]使用了一种新标注模式,将药物实体及关系的联合抽取转化为端对端的序列标注任务.Karlic等人[14-17]在实验中提出了组蛋白修饰与基因调控之间的相关性,并且在之前的一些机器学习工作中已经进行了研究.Singh等人[18]提出了将MLP叠加在CNN之上的统一判别框架DeepChrome,在预测基因表达水平高低的二元分类任务中,平均AUC(area under curve)为0.8. DeepTarget和deepMirGene分别使用RNN和LSTM模型使用表达数据进行mRNA目标预测,所提方法的一个主要优势是不需要手工制作的特征集[19-20].与此同时,生成模型也被使用来捕捉基因序列中高阶、隐藏的相关性,Way和Greene在癌症基因组RNA序列数据上训练了一个变分自编码模型来捕获生物学相关特征[21-22].
然而,在实际应用中,由于基因组序列之间存在着复杂的相互依赖和长期的相互作用,直接从基因组序列中学习特征非常耗时[23],且成功的预测通常在很大程度上依赖于对生物学知识的正确利用[24].如何在更普遍的无监督环境下构建一个基因序列表示模型,使得模型学习到的基因表示可以更有效地表示基因特征是目前生物信息领域一个主要的研究问题.且目前基因序列的研究大都集中在基因表达、调控等领域上[25],对基因数据进行低维表示也会结合基因交互表达网络的信息[26],直接对病毒基因序列进行表示学习的研究并不多.
因此,本文针对病毒传播网络构建了一种基于传播网络的基因序列表示模型(gene representation based on transmission network, GRTN),将病毒的基因序列信息与传播网络的结构信息相结合,进而得到新的基因序列表示.模型首先把输入序列编码至特定长度的隐藏层以得到降维嵌入,根据网络传播的特点使用正向LSTM和反向LSTM分别对节点的图上下文节点信息进行聚合,然后使用注意力机制对其邻居节点的序列信息进行聚合,进而得到目标节点基因序列的新的表示.依据病毒传播网络中邻居节点的基因序列相似性高于非邻居节点这一特点,对基因序列表示模型进行训练和优化.
该模型学习到的基因序列表示可以作为基因特征或先验信息用于与基因序列相关的任务,为了验证基因序列表示模型的有效性,本文设计一套在病毒传播网络中发现未采样感染者的任务流程.并且通过在模拟的病毒传播网络、真实的澳大利亚新冠病毒传播网络和真实的艾滋病毒传播网络上进行了发现未采样感染者的实验,验证了本文提出的基因序列表示模型的有效性.并通过与各类基因表示方法的对比实验表明模型的高效性.
1 问题描述
病毒传播网络是一种复杂网络,该网络可以表示为G=(V,E,A).其中,V表示网络中节点集合,每个节点表示一个病毒感染者;E表示连边集合,每条边(vi,vj)∈E表示节点vi将疾病传染给节点vj,由于疾病传播是有方向的,故该网络为有向图;A表示节点属性集合,在G中,ai∈A表示节点i的病毒基因序列.
给定一个网络G,基于网络的基因序列表示的核心任务是将网络的特征结合到基因序列中,从而为网络中每一个节点的基因序列学习一个统一的低维度(β)的表示向量,从而将网络中每个节点的属性维度由|A|映射到β(β≪|A|),使其能够捕捉网络中的结构和聚合邻居节点的特征[27-28].
2 模型描述
本节介绍基于传播网络的基因序列表示模型,如图1所示,该模型包括病毒网络中节点病毒序列信息编码、基于网络传播的结构提取、基于图上下文信息的特征表示和基于注意力的节点信息聚合.
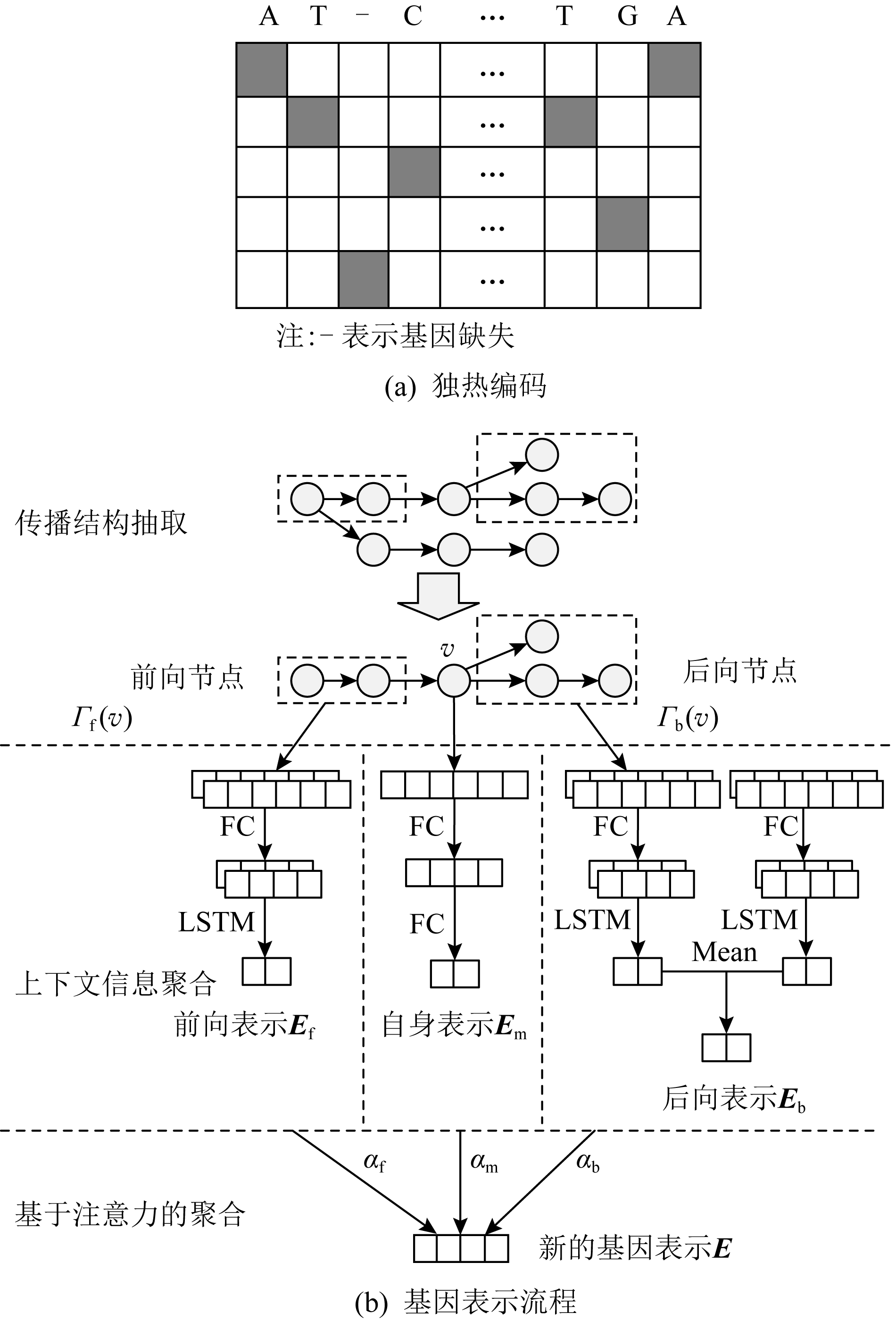
Fig. 1 Gene sequence representation model based on transmission network
图1 基于传播网络的基因序列表示模型
作为病毒传播网络的输入,节点的基因序列首先经过独热编码和维度规约转化为适合模型输入的数据;然后基于网络传播结构对每个节点抽取子图并获得子图中的前向节点信息、后向节点信息和自身表示信息;基于注意力机制,模型将前向信息、后向信息和节点本身的表示信息进行聚合,得到节点的聚合表示;为了能对网络节点的病毒序列信息进行更好的表达,通过设置基于图上下文信息的损失函数,对整个模型经过优化与训练,最终得到节点的表示向量.
2.1 病毒基因序列编码
不同病毒的基因序列长度迥异,但目前已知的大多数病毒序列中,存在着大量的无效基因序列,而且在对基因序列进行测序时,往往也会存在部分序列信息缺失.同时,病毒在传播中会不断发生变异,不同网络节点的病毒基因序列都存在一定差异.但同种病毒传播网络中,所有节点的基因序列大部分是相同的.针对病毒传播网络中基因序列的这种特征,本文采用独热编码,该编码对于不同节点的相同基因片段可以保证其一致性,同时可以有效地表达病毒基因序列的不同.
病毒在特定的传播网络中,存在基因序列相同的片段,本文通过对这些基因片段的删减,对输入数据维度进行了维度归约:若该网络中所有节点的某一位基因值相同,则将该位基因从输入数据中舍弃.通过本节操作,网络中任一节点v的病毒基因序列gv在规约后被编码为相同长度的0/1编码序列xv,作为网络中节点的属性向量.
2.2 网络传播结构抽取
网络传播结构抽取旨在抽取病毒传播网络中与每个节点关联度高的邻居节点集合,从而在保证计算效率的同时,使模型从网络中获取节点的拓扑信息.在该抽取的子图中,目标节点v以外的节点可以划分为2类:前向信息节点集合Γf(v)和后向信息节点集合Γb(v):
Γf(v)=F(v)∪F(i), i∈F(v),
(1)
Γb(v)=S(v)∪S(i), i∈S(v),
(2)
其中,F(v)表示节点v的父节点,S(v)表示节点v的子节点.前向节点是位于病毒传播链中目标节点的祖先节点,即目标节点的父节点及其祖父节点;后向节点是位于病毒传播链中目标节点的子孙节点,即目标节点的子节点和孙子节点.由于病毒基因序列传播变异较快,间隔多代后基因序列之间存在较大差异.此外,研究发现[29-31],网络中距离超过3的节点对之间的互相作用非常小,在本文模型中,选取与目标节点距离小于3的节点,构成目标节点的邻居集合.如图1所示,节点子图抽取得到的网络中,中心节点到所有节点的距离均小于3,由于每个节点只有一个感染源,所以前向信息节点集合的规模较小(0~2个),后向信息节点集合的规模相对更多.通过本节操作,模型中每个节点v的结构信息只和抽取子图中节点Γf(v)和Γb(v)相关.
2.3 基于图上下文的信息表示
基于图上下文的信息表示旨在将每个子图中的信息聚合在一起,子图中的节点称为目标节点的上下文邻居:节点的上文邻居指沿着网络中连边经过一定长度随机游走能到达目标节点的节点集合,节点的下文邻居指从目标节点出发,经过指定长度的随机游走能到达的节点集合.由于节点之间存在传播关系,本文采用LSTM将传播序列信息聚合在一起,对每个节点v,在计算前向表示向量时,直接采用LSTM将前向信息聚合在一起,并用LSTM最后的隐藏层输出为前向表示向量;在计算后向表示时,在每个分支上,采用和前向表示类似的LSTM模型,用LSTM最后的隐藏层作为该分支的表示向量,并用所有分支向量的均值作为后向表示向量.对于自身向量,通过多层全连接层将输入数据转换为需要的维度.通过充分利用子图中所有节点的信息,可以获得前向表示Ef、后向表示Eb和自身表示Em三个表示向量:
Ef(v)=LSTMf(BN(FCf(xi))), i∈Γf(v),
(3)
![]()
|S(v)|, j∈S(i),
(4)
Em(v)=BN(FC(xv)),
(5)
其中,BN表示批标准化操作,FC表示全连接层,3个表示向量的维度相同,记为do.通过该操作,模型获得了每个目标节点在网络子图中抽取的结构信息的表示.
2.4 基于注意力的节点信息聚合
注意力机制已经成为许多序列学习任务中的一项标准配置[32],可以为不同节点分配不同权重,训练时依赖于成对的相邻节点,而不依赖具体的网络结构.本文采用注意力机制学习节点前向、自身和后向向量Ek,k∈{f,m,b}的聚合权重,进而获得每个节点的信息聚合E.
E=AGGREGATE(Ef,Em,Eb),
(6)
其中
AGGREGATE(Ef,Em,Eb)=
αfEf+αmEm+αbEb,
(7)
αk,k∈{f,m,b}为注意力权重系数,本文通过一个共享的注意力向量a∈![]() 2d×1来反映向量Ek对节点自身向量Em的重要性:
2d×1来反映向量Ek对节点自身向量Em的重要性:
emk=aT(Em⊕Ek),
(8)
其中⊕为拼接操作,a为可学习的注意力参数.相应的注意力系数αk可以表示为
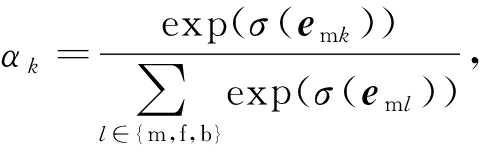
(9)
其中σ为激活函数LeakyRelu.
为了减少数据的方差,提升表示结果的稳定性,将该模式推广到多头注意力形式:注意力机制被独立地重复nh次(每个头的参数初始化不同),并将得到的nh个表示向量拼接作为最终向量:
E=E1⊕E2⊕…⊕Enh,
(10)
2.5 目标优化与模型训练
为了客观衡量病毒传播网络的基因序列表示的效果,本文采用图上下文损失作为损失函数.图上下文损失可以看作交叉熵的一种变形:对每个节点,网络中的所有其他节点,根据距离该节点的距离被划分为正邻居节点和负邻居节点,因此其核心是使目标节点的向量表示与采样正邻居的相似性更高,并与采样负邻居的差异性更大,基于此的优化目标被定义为
![]()
(11)
其中Cv表示从节点v开始的随机游走能到达的节点集合,p(vc|v;Θ)被定义为softmax形式的概率:
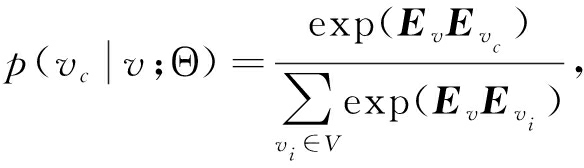
(12)
式(12)通过表示向量内积大小衡量节点对的相似性,通过负采样[33]技术,可以将式(12)中softmax函数进行对数近似为
![]()
![]() vs~P(vc) ln θ(-EvEvs),
vs~P(vc) ln θ(-EvEvs),
(13)
其中,S表示负采样数目,P(vc)表示负采样的概率分布,在本模型中,S=1从而将目标函数简约为交叉熵的形式[34]
ln θ(EvEvc)+ln θ(-EvEvs),
(14)
从而将损失函数转化定义为
![]()
ln θ(-EvEj)]+β![]() ,
,
(15)
其中, v,i,j
v,i,j 是一个三元组,v∈V是目标节点,i∈Cv是其在图G上的上下文邻居,j∈V是负采样节点,θ是sigmoid激活函数,
是一个三元组,v∈V是目标节点,i∈Cv是其在图G上的上下文邻居,j∈V是负采样节点,θ是sigmoid激活函数,![]() 表示L2正则化,β为权重参数.具体而言,首先在每个节点进行重启概率为pr、长度为Lw的随机游走,得到的节点集合即为节点在图中的上下文邻居集合Cv;然后,从图G中随机采样1个负采样节点j∉Cv.为提高计算效率,在每一代训练时,可以按比例选取一定的节点进行采样,从而降低采样和训练节点的数量.
表示L2正则化,β为权重参数.具体而言,首先在每个节点进行重启概率为pr、长度为Lw的随机游走,得到的节点集合即为节点在图中的上下文邻居集合Cv;然后,从图G中随机采样1个负采样节点j∉Cv.为提高计算效率,在每一代训练时,可以按比例选取一定的节点进行采样,从而降低采样和训练节点的数量.
算法1. 基因序列表示算法.
输入:病毒传播网络G=(V,E,A)、节点基因序列g;
输出:网络中每个节点的基因表示E.
① 通过病毒基因序列编码将g转化为x;
② for each v∈V:
③ 分别按照式(1)~(2)抽取节点v的前向信息节点集合Γf(v)和后向信息节点集合Γb(v);
④ 分别按照式(3)~(5)计算前向表示Ef、后向表示Eb和自身表示Em三个表示向量;
⑤ 按照式(8)计算每个节点的注意力系数αk,k∈{f,m,b},并获得每个节点聚合表示E;
⑥ 采样节点的上下文非上下文邻居形成三元组 v,i,j
v,i,j
⑦ end for
⑧ 根据式(14)进行模型训练和优化;
⑨ 循环步骤②~⑧直至到达结束条件.
3 实验设计
本节设计一种病毒传播网络中发现未采样感染者的实验流程,通过在仿真病毒传播网络、真实的新冠病毒传播网络和艾滋病毒传播网络上发现未采样感染者来验证模型的有效性,并对实验结果进行分析.
3.1 未采样感染者发现流程
实际情况下,受限于医疗水平、检测条件、疾病症状的不同,检测到的病毒传播网络往往会存在缺失节点(未采样感染者),其网络规模小于实际的传播网络.如图2所示,虚线节点为未采样感染者,由于这些病患节点在实际网络构建时未被发现,因此网络的实际连边关系存在异常,原本不应有传播关系的父节点和子节点被认为存在直接传播关系(存在连边),如右图虚线所示.
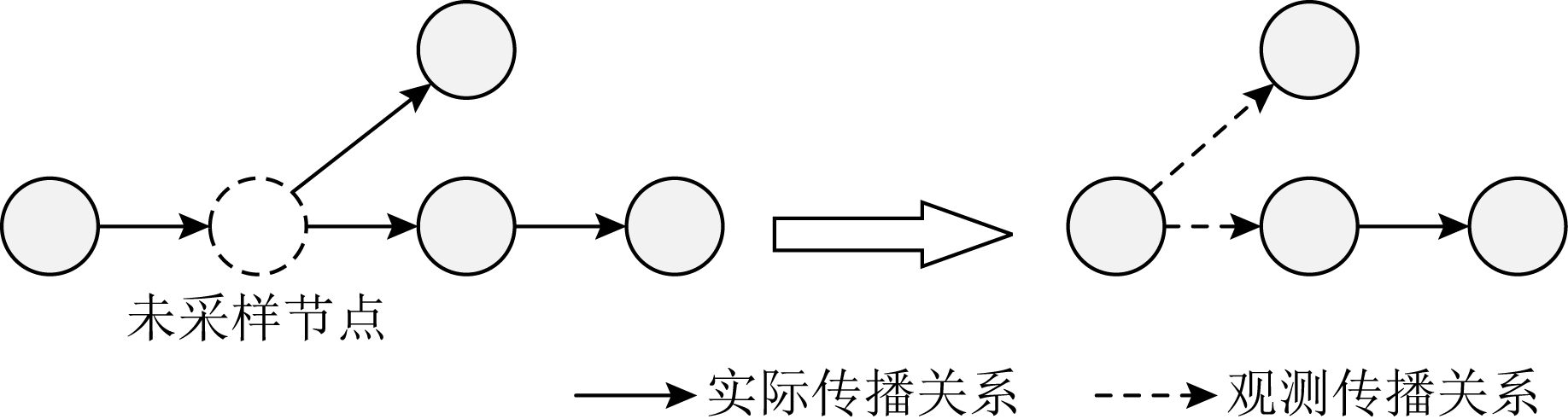
Fig. 2 The un-sampled infections detection
图2 未采样感染者示意图
基于本文基因序列表示模型,我们设计2个未采样感染者发现流程:
① 通过基于病毒传播网络的基因表示模型,获取网络中每个节点的基因表示E;
② 将发现传播网络中未采样节点任务转化为连边得分排序任务,即通过计算两节点的表示的相似度,评价这条连边的稳固性.对于节点对i,j,其连边相似度为
simij=EiEj,
(16)
在所有存在连边的排序中,得分最低的k条连边所对应的节点对被认为是存在未采样感染者的节点组合,进而在实际的医学调查诊断相应环节进行排查.
3.2 数据描述
本文采用仿真和真实的病毒传播网络数据集进行实验.
仿真数据集是根据病毒传播和变异的规律,生成传播网络和网络中每个节点的基因序列,其中,每次仿真基因序列的变异是基于其父节点的基因序列,该网络的生成规则为:
1) 给定病毒基因序列长度L,每位基因取值数量为n,假定每位基因的变异是互相独立的,病毒基因在每一次传播时序列发生变异的概率为p;
2) 给定病毒传播能力值R,每一代传播人数在以R为中心服从泊松分布(为计算方便,模拟生成网络中传染人数在0~6之间对称分布).假定网络中所有节点起始于“零号病人”,即有一个同一父节点,则根据R值,零号病人生成子节点,每个子节点的基因序列的变异是独立的;
3) 重复步骤2),直至传播网络节点数达到给定网络规模N.
基于上述规则,本文生成病毒传播仿真网络,相关参数如表1所示:
Table 1 Parameters of Simulating Network
表1 仿真网络参数设置
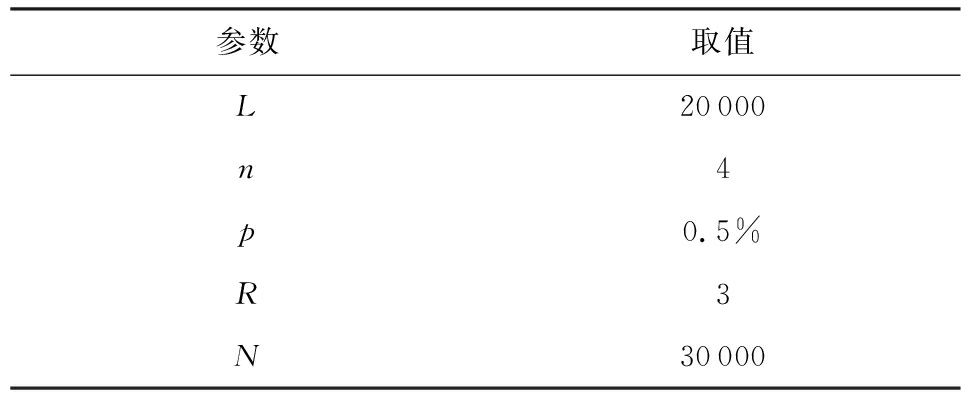
参数取值L20000n4p0.5%R3N30000
真实数据集包括Aussie数据集和HIV数据集.Aussie数据集是部分澳大利亚新型冠状病毒患者地基因序列,病人信息已经匿名化处理,该数据集基因序列数据和标准参考序列比对出现多处缺失,序列质量不高.我们使用TransPhylo对该基因序列集进行分析,TransPhylo是一个可以通过基因数据构建病毒传播网络的工具[35].分析得到病毒传播网络如图3所示,该网络中共有1 032个节点,且约有10%的未采样节点.网络的每个节点代表一名新冠病毒患者,节点的有向连边表示新冠病毒传播关系,每个节点的属性为其感染的新冠病毒的基因序列,基因长度为29 915.基因的每个位置的取值范围为{A,T,C,G,-},其中-表示该位基因缺失.如图3所示,其中节点颜色越深,表示该节点距离零号病人越近.
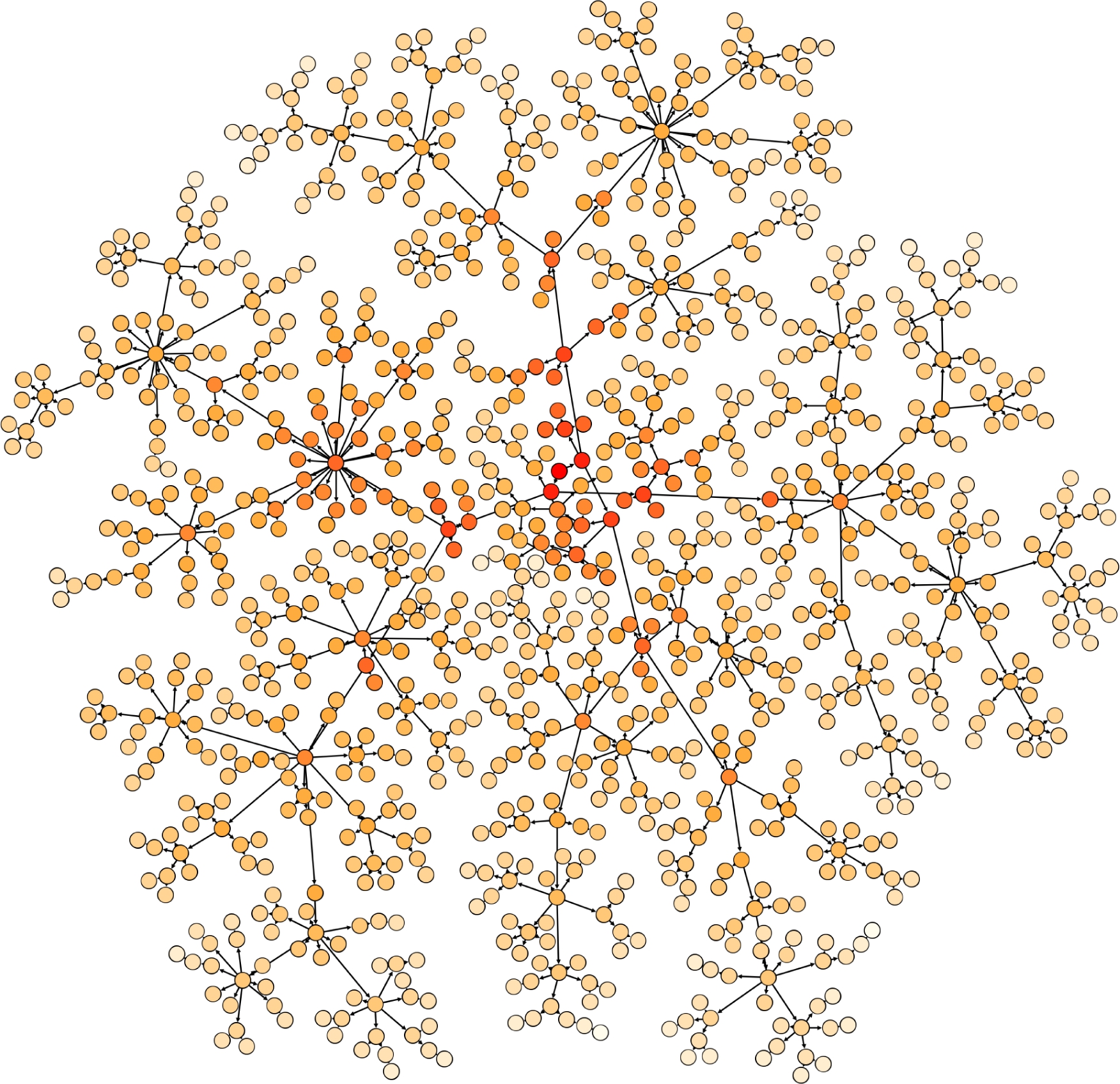
Fig. 3 Aussie: 2019-nCoV transmission network
图3 Aussie新冠病毒传播网络
HIV数据集是加拿大阿尔伯塔省南部部分HIV患者的病毒序列信息,并且包含经TransPhylo分析且经医院验证的病毒传播网络信息.该网络节点数量是140,病毒基因序列长度是1 522,该网络中未采样节点数约为41,即该传播网络包含较多未采样节点,网络如图4所示.病毒传播信息采集中,往往无法获取0号病人的信息,该HIV数据集中同样缺失0号病人基因序列信息.本文参考Lauren等人[36]研究推断与0号病人传播关系最接近的病毒序列,随机改变约30%的序列信息后作为0号病人的病毒序列.

Fig. 4 HIV: HIV transmission network
图4 HIV病毒传播网络
3.3 验证集数据生成
为了验证基因表示模型的有效性,我们会在仿真和真实传播网络中删除一些节点,这些删除的节点即未采样感染者,然后生成一个存在缺失节点的传播网络,存在缺失节点的连边将作为验证集,之后使用模型在该网络上进行缺失节点预测.通过模型预测的结果和验证集的比较,进而计算模型在缺失节点还原结果的准确度.其中缺失网络的生成规则为:
1) 生成指定数目缺失节点,检查缺失节点合理性:若生成节点处于网络两端(没有父节点或没有子节点),移除该节点;
2) 将缺失节点的父节点与子节点连接,生成新的连边;
3) 重复步骤1)~2),直至缺失节点数目达到给定值.
3.4 参数设置
对于基因编码序列属性,模型形式采用独热编码;模型训练代数为1 000,初始学习速率lr=0.01,每进行100代训练,将学习率减半.表示向量维度为do=128,隐藏层维度为dh=1024,L2正则化参数β=0.001,注意力头数nh=4,随机数种子为1,随机游走长度Lw=10,随机游走重启概率pr=20%.
3.5 对比算法
为了验证GRGC模型对基因序列表示的高效性,本文采用5种算法作为基准对比算法,包括不对基因序列降维处理直接用于计算的Direct方法与可以对高维基因序列进行降维及特征提取的PCA和Auto Encoder(AE)方法.此外,由于本文的方法是基于病毒传播网络构建的,因此也选用了GCN和SDNE两种网络表示方法作为对比.
1) Direct方法.直接使用基因序列进行计算,每个节点的基因序列编码后,不对其进行压缩和特征提取,直接将其用于发现缺失节点任务.
2) AE方法.自编码器[37]由编码器和解码器2部分组成,其中编码器能将输入属性压缩成潜在的空间表征,解码器能从潜在空间表征重构数据的输入.自编码器常被用于降维或特征学习,本文首先使用AE模型对基因序列进行训练,然后使用训练好的AE模型的中间层即降维后的序列表示,作为发现缺失节点任务的输入.
3) 主成分分析方法(principal component analysis, PCA)[38].是一种使用最广泛的数据降维算法.PCA的主要思想是通过正交变化将可能存在相关性的N维特征数据映射到线性不相关的k维上,在原有N维特征的基础上重新构造k维特征,进而实现对原始数据的高效和精确的表示,转换后的k维特征则被称为主成分.本文使用基因序列的主成分作为发现缺失节点任务的输入.
4) 图卷积神经网络方法(graph convolutional neural network, GCN)[39].通过低通滤波器产生节点嵌入,将每个节点的信息传递到图中的邻居节点上去,通过卷积运算使得图能够逐层传递信息.本文构建了一个2层GCN模型(隐藏层维度为256,输出层维度为128),并用上下文损失函数训练一个无监督GCN模型,通过输出层的基因表示,计算节点对相似度并发现缺失节点.
5) 结构网络嵌入方法(structural deep network embedding, SDNE)[40].使用深层神经网络对节点表示间的非线性进行建模,整个模型可以被分为2个部分:一个是由Laplace矩阵监督的建模第1级相似度的模块,另一个是由无监督的深层自编码器对第2级相似度关系进行建模.本文采用3层神经网络结构(2层隐藏层维度分别为500和300,输出层维度为128).
3.6 评价指标
对所有对比算法和本文方法,本文通过AUC,RS和k-RS三个指标评价其效果.
链路预测中常用AUC指标[41]衡量算法的效果:每次随机地从验证集中选取1条存在的边和1条不存在的边并比较这2条边的指标值,如果存在的边的分值大于不存在的边的分值,则记为1分;如果2个边的分数值相等,则记为0.5分;若存在边的分值小于不存在边的分值,则记为0分.独立重复地比较N次,如果有n′次验证集中的边的分数值大于不存在的边,有n″次验证集中边分数值等于不存在边的分数,则AUC指标计算结果为
![]()
(17)
AUC的指标值越接近1,说明获得的表示向量在连边预测上的能力越强.
RS即排序分(ranking score),考虑了验证集中的边在模型预测结果中排序的位置.令H=U-ET为未知边的集合(相当于验证集中的边和不存在的边的集合),re表示e∈EP在排序中的排名.那么这条验证边的排序分为
![]()
(18)
该数据集上的总的排序分为
(19)
根据目标,本文希望存在未采样感染者的连边对的排名更靠后,因此,RS指标越大,表明该表示向量在预测任务中表现越好.
k-RS统计RS得分前k条边中验证集边所占的比例.如果模型预测结果中有m条边在验证集中,k-RS定义为
![]()
(20)
k-RS指标侧重于评价验证集中特征最明显的那部分边,在实际应用时,我们只会关心排名特征最明显的部分(排名最靠前的部分),从而在准确率和覆盖率中进行权衡,k-RS指标不再关注本身特征就不明显的边,从而更好地反映和评价算法在真实使用时的效用.
4 实验分析
本文分别在仿真病毒传播网络和Aussie新冠病毒传播网络、HIV病毒传播网络进行实验.为了使实验更符合真实场景,即现实中获取的病毒传播网络往往存在未采样感染者,因此我们首先在仿真或者真实数据集的基础上生成存在一定节点缺失的网络,然后在该存在缺失节点的网络上训练基因表示模型.
在仿真数据实验中,我们首先将模型在生成的病毒传播网络上进行训练,然后使用节点缺失比例为10%和20%的传播网络对模型进行测试.节点缺失网络按照3.3节缺失网络生成规则生成,即选取未采样节点并将其在数据集中删除.然后通过分析模型成功找出缺失节点的正确率来评价算法的表现.在Aussie数据上,测试网络的缺失节点比例分别为10%和20%.在HIV传播网络实验中,由于病毒传播网络规模较小,10%的节点缺失总数是14,较小的验证集会导致测试结果波动较大,因此在HIV实验中我们使用全网络进行模型训练,在30%节点缺失的网络上进行测试.
4.1 结果分析
本节实验提到的k-RS指标中,百分数值表示排名靠前相应比例的连边数(25%表示RS得分排名前25%的连边),Top 20表示最可能包含缺失节点的20条连边.表中实验结果均是10次生成缺失节点实验的平均值,分值越高代表算法预测存在缺失节点的正确率越高.
从表2和表3可以看出,在仿真数据中,采用Direct方法的基因表示在进行缺失节点发现任务中的表现最好,这是因为仿真数据的基因序列生成及变异是严格按照规则生成,因此仿真基因序列中无效序列较少,对基因序列进行降维特征提取反而丢失了重要的特征.但由实验结果可见,GRTN方法在仿真数据集上的表现依然优于Direct以外的对比方法.
Table 2 Results on Simulating Network with 10% Nodes Missing
表2 缺失10%节点仿真数据中各指标表现 %
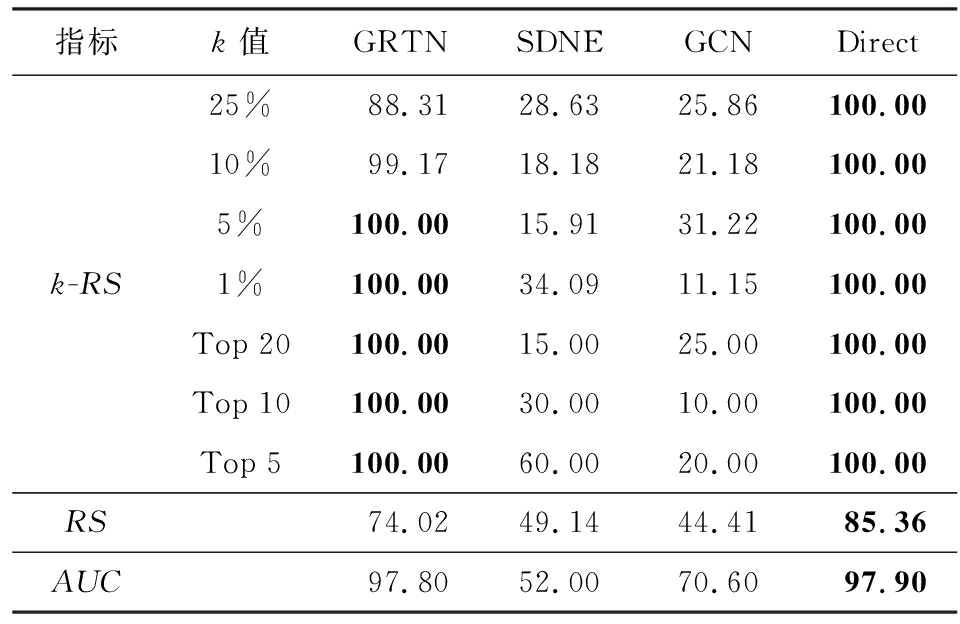
指标k值GRTNSDNEGCNDirect25%88.3128.6325.86100.0010%99.1718.1821.18100.005%100.0015.9131.22100.00k-RS1%100.0034.0911.15100.00Top 20100.0015.0025.00100.00Top 10100.0030.0010.00100.00Top 5100.0060.0020.00100.00RS74.0249.1444.4185.36AUC97.8052.0070.6097.90
注:黑体数字表示该行最优结果.
Table 3 Results on Simulating Network with 20% Nodes Missing
表3 缺失20%节点仿真数据中各指标表现 %
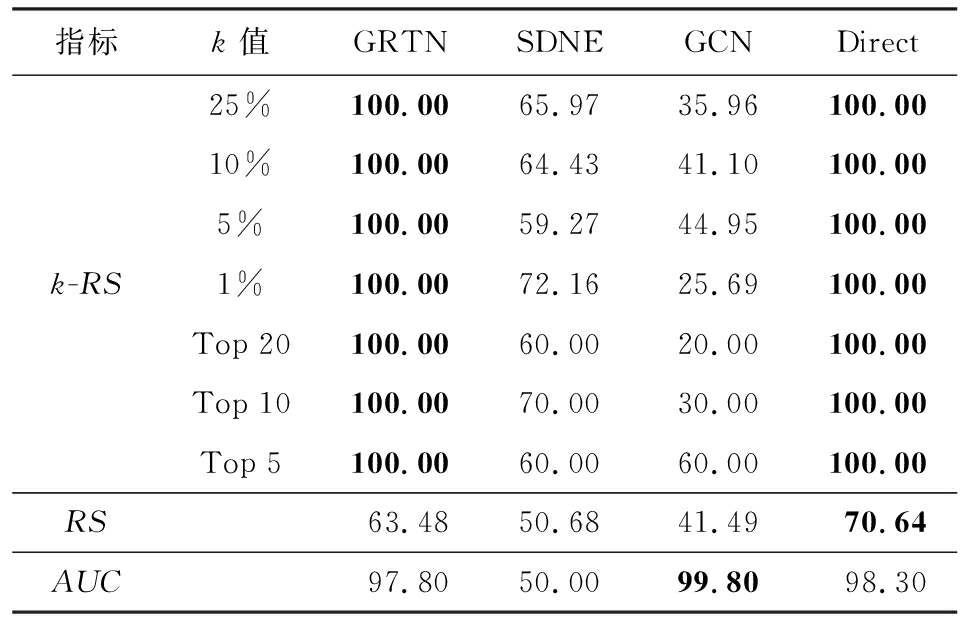
指标k值GRTNSDNEGCNDirect25%100.0065.9735.96100.0010%100.0064.4341.10100.005%100.0059.2744.95100.00k-RS1%100.0072.1625.69100.00Top 20100.0060.0020.00100.00Top 10100.0070.0030.00100.00Top 5100.0060.0060.00100.00RS63.4850.6841.4970.64AUC97.8050.0099.8098.30
注:黑体数字表示该行最优结果.
为探究本文方法在实际应用中的价值,我们也在真实新冠病毒网络中进行了实验.分析表4和表5可得,在真实的新冠病毒病毒基因序列数据集中,采用Direct进行基因表示的实验结果要远低于本文提出的GRTN方法.而GRTN方法通过聚合节点本身的基因序列信息和传播网络的特征信息,在多数验证指标上取得了最优的成绩,在Top-5和RS等指标上结果略差于GCN方法,但其综合表现在所有方法中最好.
Table 4 Results on Aussie with 10% Nodes Missing
表4 缺失10%节点Aussie中各指标表现 %

指标k值GRTNSDNEGCNDirectAEPCA25%45.7831.913.8427.4719.6430.2910%53.1513.8210.0036.4220.0222.965%56.3115.7120.0038.4724.7830.48k-RS1%60.2910.6333.3342.3335.0042.05Top 2051.5040.005.0036.0020.5023.00Top 1055.0060.0010.0038.0025.0030.00Top 562.0060.0020.0046.0036.0048.00RS55.6949.7033.3254.1155.6955.62AUC96.2212.7099.6031.6496.2256.14
注:黑体数字表示该行最优结果.
Table 5 Results on Aussie with 20% Nodes Missing
表5 缺失20%节点Aussie中各指标表现 %
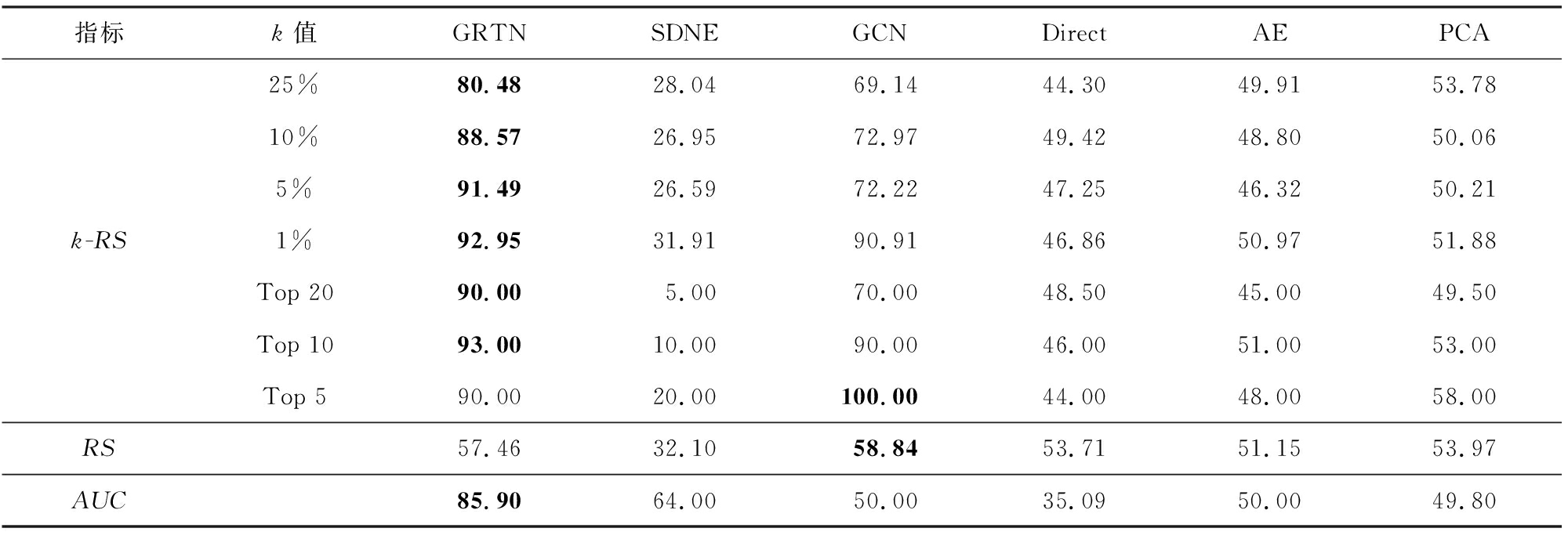
指标k值GRTNSDNEGCNDirectAEPCA25%80.4828.0469.1444.3049.9153.7810%88.5726.9572.9749.4248.8050.065%91.4926.5972.2247.2546.3250.21k-RS1%92.9531.9190.9146.8650.9751.88Top 2090.005.0070.0048.5045.0049.50Top 1093.0010.0090.0046.0051.0053.00Top 590.0020.00100.0044.0048.0058.00RS57.4632.1058.8453.7151.1553.97AUC85.9064.0050.0035.0950.0049.80
注:黑体数字表示该行最优结果.
为探究本文模型的适用性,本文选取HIV病毒传播网络进行试验.因为HIV病毒基因网络节点数目相对较少,只关注排名靠前的节点的指标时(比如k-RS指标的前3%),实验结果波动极大,由表6中结果可得,虽然HIV的病毒序列特征与COVID-19病毒的极为不同,即HIV的序列长度要远远小于COVID-19,且该网络本身即包含大量缺失节点,但从实验结果可以看出,基于病毒传播网络的基因表示模型(GRTN)在处理缺失节点发现的任务上,表现要远远好于其他对比方法.
Table 6 Results on HIV with 30% Nodes Missing
表6 缺失30%节点HIV数据集中各指标表现 %

指标k值GRTNSDNEGCNDirectAEPCAk-RS100%74.6258.3354.9062.2946.9558.3575%89.8246.6747.3757.4147.2050.2250%96.8736.6740.0055.6546.4443.7825%97.9046.6758.3368.6355.2460.2710%100.0050.0080.0054.5077.5077.00Top 2097.0050.0040.0055.5050.0049.50Top 10100.0060.0060.0067.0056.0065.00Top 5100.0060.0080.0054.0074.0076.00RS63.7754.4953.4353.1545.6350.91AUC85.1423.7077.6043.2376.1254.36
注:黑体数字表示该行最优结果.
4.2 模型分析
4.1节实验验证了GRTN模型的有效性,本节从表示聚合分模块能力和注意力使用等多个方面分析模型的表现效果.
4.2.1 表示聚合分析
在GRTN模型中,节点的基因表示由Ef,Eb和Em经过注意力聚合得到,在本节,用GRTN-f表示去掉目标节点上文节点信息聚合的模型,GRTN-b表示去掉下文节点信息聚合的模型,用GRTN-cut表示对输入基因序列不进行维度约减的操作,用GRTN-2n表示不考虑目标节点距离为2的邻居信息的模型.综合上述多个角度,对方法进行消融实验.
从表7结果可知,本文模型通过结合前向、后向和自身的表示信息表现效果最佳,缺失前向表示的信息对模型的效果影响更大,后向节点表示信息对模型表现也有较大影响,单纯使用节点自身表示的退化模型,效果较差.当只聚合目标节点的子节点和父节点信息时,模型效果较差,这说明只使用一阶邻居的信息进行基因表示是不充分的.当不对输入数据维度进行约减时,模型效果有明显的下降,这说明模型对基因序列降维后进行了有效特征提取,相比不降维的全序列数据,可以去掉基因序列数据中无用的干扰信息.而对比同样是对数据进行降维提取特征的PCA和AE,说明基于传播网络上下文的基因表示模型效果更优.
Table 7 Ablationstudy on Aussie with 20% Nodes Missing
表7 缺失20%节点Aussie中各模块消融实验 %
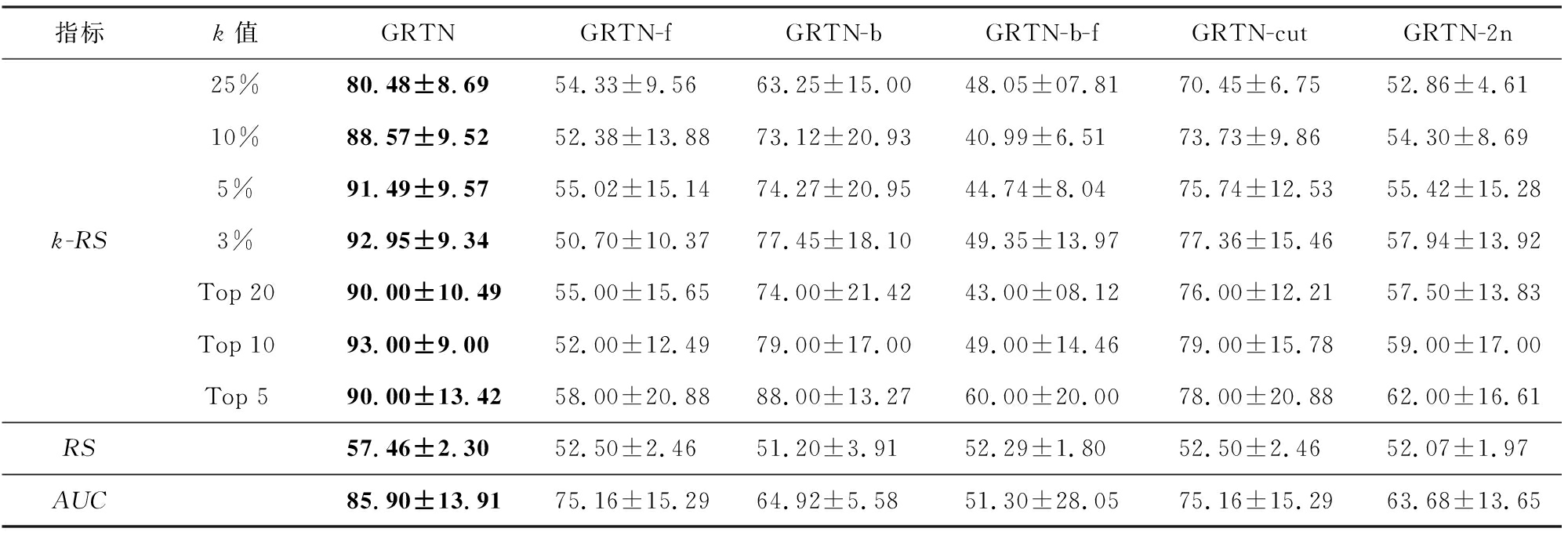
指标k值GRTNGRTN-fGRTN-bGRTN-b-fGRTN-cutGRTN-2n25%80.48±8.6954.33±9.5663.25±15.0048.05±07.8170.45±6.7552.86±4.6110%88.57±9.5252.38±13.8873.12±20.9340.99±6.5173.73±9.8654.30±8.695%91.49±9.5755.02±15.1474.27±20.9544.74±8.0475.74±12.5355.42±15.28k-RS3%92.95±9.3450.70±10.3777.45±18.1049.35±13.9777.36±15.4657.94±13.92Top 2090.00±10.4955.00±15.6574.00±21.4243.00±08.1276.00±12.2157.50±13.83Top 1093.00±9.0052.00±12.4979.00±17.0049.00±14.4679.00±15.7859.00±17.00Top 590.00±13.4258.00±20.8888.00±13.2760.00±20.0078.00±20.8862.00±16.61RS57.46±2.3052.50±2.4651.20±3.9152.29±1.8052.50±2.4652.07±1.97AUC85.90±13.9175.16±15.2964.92±5.5851.30±28.0575.16±15.2963.68±13.65
注:黑体数字表示该行最优结果.
4.2.2 注意力权重分析
在Aussie中,本文提取节点的Ef、Eb和Em向量的注意力权重,统计如表8所示.对于处于网络不同位置、属性信息不同的节点,其注意力系数有明显差异.从整体影响力来说,前向注意力的系数权重比较高,这和4.2.1节中前向节点影响大的结论一致.图5展示了网络中节点7和节点621的局部结构,以节点7为例,该节点处于网络中的末端位置,没有后向节点,其属性结果很大程度上和其父节点相关,故αf高,虽然模型给出了αb的系数,但是该节点的Eb为0;节点621同时存在子节点和父节点,注意力系数和三者皆有关系.
Table 8 Values of Forward, Backward and Self Attention
表8 前向、后向和自身注意力系数
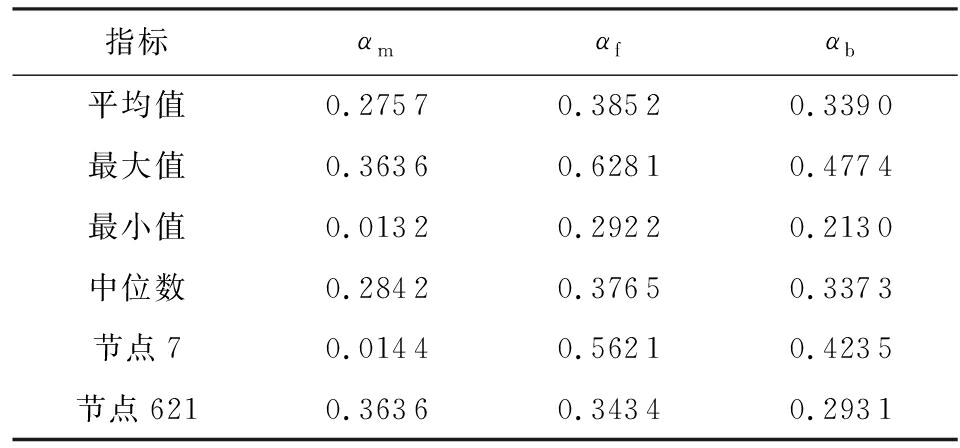
指标αmαfαb平均值0.27570.38520.3390最大值0.36360.62810.4774最小值0.01320.29220.2130中位数0.28420.37650.3373节点70.01440.56210.4235节点6210.36360.34340.2931

Fig. 5 Nodes attention analysis
图5 节点注意力分析
4.2.3 多头注意力分析
为了探讨不同注意力机制使用对模型效果的影响,列出采用不同注意力机制的模型在Aussie中的表现结果,如图6所示.本节使用的不同注意力机制有:
1) average-4.采用4头注意力机制,每个注意力的表示维度为128,将4个注意力的表示向量输出在每个维度上取平均值.
2) concat-2.采用2头注意力机制,每个注意力的表示维度为128,将2个注意力的表示向量输出拼接在一起.
3) concat-4.采用4头注意力机制,每个注意力的表示维度为128,将4个注意力的表示向量输出拼接在一起.
4) single.单头注意力表示,输出的表示向量维度为128.

Fig. 6 Model performances with different attention
mechanisms on Aussie with 20% nodes missing
图6 采用不同注意力机制的算法在Aussie上预测准确率表现(20%节点缺失)
从图6分析可知,采用单头注意力的模型表示结果的随机性较大,采用拼接操作和取均值操作均可以提高模型的效果,其中采用拼接操作的效果更优,并且随着拼接的注意力模块的增加,模型表现有一定提高.
5 结 论
本文基于病毒传播网络构建了一种新的基因序列表示方法,在对节点病毒序列进行编码后,使用注意力机制对节点及其邻居节点的序列信息进行聚合,进而得到目标节点病毒基因序列的表示.为了验证基因序列表示模型的有效性,本文设计一套在病毒传播网络中发现未采样感染者的任务流程,可以在实际的医学调查诊断的相应环节进行辅助排查.本文用网络缺失点发现任务对得到的基因序列表示进行评估,模型在模拟病毒传播网络、真实的澳大利亚新冠病毒传播网络和艾滋病毒网络上的实验结果验证了模型的有效性.
作者贡献声明:马扬和刘泽一提出论文理论方法、思路,进行实验及论文撰写,为本文同等贡献第一作者;程光权和刘忠指导论文思路与撰写,为本文共同通信作者;梁星星、阳方杰、成清对论文提出修改建议.
[1]Torng W, Altman R B. 3D deep convolutional neural networks for amino acid environment similarity analysis[J]. BMC Bioinformatics, 2017, 18(1): 1-23
[2]Fukushima K. Cognitron: A self-organizing multilayered neural network[J]. Biological Cybernetics, 1975, 20(3): 121-136
[3]Rumelhart D E, Hinton G E, Williams R J. Learning internal representations by error propagation[R]. California Univ San Diego La Jolla Inst for Cognitive Science, 1985
[4]Svozil D, Kvasnicka V, Pospichal J. Introduction to multi-layer feed-forward neural networks[J]. Chemometrics and Intelligent Laboratory Systems, 1997, 39(1): 43-62
[5]Rumelhart D, Hinton G, Williams R. Parallel distributed processing: Explorations in the microstructure of cognition, vol. 1[J]. Language, 1986, 63(4): 45-76
[6]Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507
[7]Elman J L. Finding structure in time[J]. Cognitive Science, 1990, 14(2): 179-211
[8]Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780
[9]Leung M K K, Xiong Huiyuan, Lee L J, et al. Deep learning of the tissue-regulated splicing code[J]. Bioinformatics, 2014, 30(12): i121. doi:10.1093/bioinformations/btu277
[10]Urda D, Montes-Torres J, Moreno F, et al. Deep learning to analyze RNA-seq gene expression data[C] //Proc of the Int Work-Conf on Artificial Neural Networks. Berlin: Springer, 2017: 50-59
[11]Chen Yifei, Li Yi, Narayan R, et al. Gene expression inference with deep learning[J]. Bioinformatics, 2016, 32(12): 1832-1839
[12]Xie Rui, Wen Jia, Quitadamo A, et al. A deep auto-encoder model for gene expression prediction[J]. BMC Genomics, 2017, 18(9): 39-49
[13]Cao Mingyu, Yang Zhihao, Luo Ling, et al. Joint drug entities and relations extraction based on neural networks[J]. Journal of Computer Research and Development, 2019, 56(7): 1432-1440 (in Chinese)(曹明宇, 杨志豪, 罗凌, 等. 基于神经网络的药物实体与关系联合抽取[J]. 计算机研究与发展, 2019, 56(7): 1432-1440)
[14]Karli![]() R, Chung H R, Lasserre J, et al. Histone modification levels are predictive for gene expression[J]. Proceedings of the National Academy of Sciences, 2010, 107(7): 2926-2931
R, Chung H R, Lasserre J, et al. Histone modification levels are predictive for gene expression[J]. Proceedings of the National Academy of Sciences, 2010, 107(7): 2926-2931
[15]Cheng Chao, Yan K K, Yip K Y, et al. A statistical framework for modeling gene expression using chromatin features and application to mod ENCODE datasets[J]. Genome Biology, 2011, 12(2): 1-18
[16]Dong Xianjun, Greven M C, Kundaje A, et al. Modeling gene expression using chromatin features in various cellular contexts[J]. Genome Biology, 2012, 13(9): 1-17
[17]Ho B H, Hassen R M K, Le N T. Combinatorial roles of dna methylation and histone modifications on gene expression[C] //Proc of the National Foundation for Science and Technology Development Conf on Information and Computer Science. Berlin: Springer, 2014: 123-135
[18]Singh S, Yang Yang, Poczos B, et al. Predicting enhancer-promoter interaction from genomic sequence with deep neural networks[J]. Quantitative Biology, 2019, 7(2): 122-137
[19]Lee B, Baek J, Park S, et al. deepTarget: End-to-end learning framework for microRNA target prediction using deep recurrent neural networks[C] //Proc of the 7th ACM Int Conf on Bioinformatics, Computational Biology, and Health Informatics. New York: ACM, 2016: 434-442
[20]Park S, Min S, Choi H, et al. deepMiRGene: Deep neural network based precursor microrna prediction[J]. arXiv preprint, arXiv:1605.00017, 2016
[21]Way G P, Greene C S. Extracting a biologically relevant latent space from cancer transcriptomes with variational autoencoders[J]. Pacific Symposium on Biocomputing, 2018, 23: 80-91
[22]Weinstein J N, Collisson E A, Mills G B, et al. The cancer genome atlas pan-cancer analysis project[J]. Nature Genetics, 2013, 45(10): 1113-1120
[23]Yue Tianwei, Wang Haohan. Deep learning for genomics: A concise overview[J]. arXiv preprint, arXiv: 802. 0810, 2018
[24]Beer M A, Tavazoie S. Predicting gene expression from sequence[J]. Cell, 2004, 117(2): 185-198
[25]Du Jingcheng, Jia Peilin, Dai Yulin, et al. Gene2vec: Distributed representation of genes based on co-expression[J/OL]. BMC Genomics, 2019, 80(1): 7-15. [2021-04-01]. https://doi.org/10.1186/s12864-018-5370-x
[26]Jan H, Teresa M P. Embedding gene sets in low-dimensional space[J/OL]. Nature Machine Intelligence, 2020, 2(7): 367-368. [2021-04-01]. https://doi.org/10.1038/s42256-020-0204-3
[27]Ye Zhonglin, Zhao Haixing, Zhang Ke, et al. Network representation learning using the optimizations of neighboring vertices and relation model[J]. Journal of Computer Research and Development, 2019, 56(12): 46-61 (in Chinese)(冶忠林, 赵海兴, 张科, 等. 基于邻节点和关系模型优化的网络表示学习[J]. 计算机研究与发展, 2019, 56(12): 46-61)
[28]Wu Yao, Shen Derong, Kou Yue, et al. Heterogeneous information networks embedding based on multiple meta-graph fusion[J]. Journal of Computer Research and Development, 2020, 57(9): 1928-1938 (in Chinese)(吴瑶, 申德荣, 寇月, 等. 多元图融合的异构信息网嵌入[J]. 计算机研究与发展, 2020, 57(9): 1928-1938)
[29]Sun Yizhou, Norick B, Han Jiawei, et al. Pathselclus: Integrating meta-path selection with user-guided object clustering in heterogeneous information networks[J]. ACM Transactions on Knowledge Discovery From Data, 2013, 7(3): 1-23
[30]Dong Yuxiao, Chawla N V, Swami A. metapath2vec: Scalable representation learning for heterogeneous networks[C] //Proc of the 23rd ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2017: 135-144
[31]Sun Yizhou, Han Jiawei. Mining heterogeneous information networks: Principles and methodologies[J]. Synthesis Lectures on Data Mining and Knowledge Discovery, 2012, 3(2): 1-159
[32]Velikovi P, Cucurull G, Casanova A, et al.Graph attention networks[J]. arXiv preprint, arXiv:1710.10903, 2017
[33]Mikolov T, Sutskever I, Chen Kai, et al. Distributed representations of words and phrases and their compositionality[J]. arXiv preprint, arXiv:1310.4546, 2013
[34]Zhang Chuxu, Song Dongjin, Huang Chao, et al. Hetero-geneous graph neural network[C] //Proc of the 25th ACM SIGKDD Int Conf on Knowledge Discovery & Data Mining. New York: ACM, 2019: 793-803
[35]Didelot X, Fraser C, Gardy J, et al. Genomic infectious disease epidemiology in partially sampled and ongoing outbreaks[J]. Molecular Biology and Evolution, 2017, 34: 997-1007
[36]Lauren M, Deshan P, Raynell L, et al. Evaluation of a phylogenetic pipeline to examine transmission networks in a canadian HIV cohort[J]. Microorganisms, 2020, 8(2): 196-196
[37]Gehring J, Auli M, Grangier D, et al. A convolutional encoder model for neural machine translation[J]. arXiv preprint, arXiv:1611.02344, 2016
[38]Tharwat A. Principal component analysis-a tutorial[J]. International Journal of Applied Pattern Recognition, 2016, 3(3): 197-240
[39]Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint, arXiv:1609.02907, 2016
[40]Wang Daixin, Cui Peng, Zhu Wenwu. Structural deep network embedding[C] //Proc of the 22nd ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2016: 1225-1234
[41]Japkowicz N, Shah M. Evaluating Learning Algorithms: A Classification Perspective[M]. Cambridge, UK: Cambridge University Press, 2011: 193-214






