量子游走是经典随机游走在量子世界的对应物，它描述了微观世界中粒子的随机演化过程.经典随机游走本身应用十分广泛，比如k-SAT问题[1]、图像分割问题[2]、图匹配算法[3-4]等.量子游走也有广泛的用途：实现通用量子计算[5-8]；完成量子通讯协议[9-11]；制备纠缠量子态[12]等.另外，由于量子纠缠、量子干涉和量子非定域性，量子游走可以更快地搜索目标标记点，因此量子游走可以用来设计量子算法，像搜索标记点问题[13-16]、元素区分问题[17]、搜索三角形问题[18]等.当前基于量子游走的量子模拟或展示各种量子游走模型自身性质的实验已经在许多不同的物理系统上进行了实施，比如光子[19]、离子阱[20]、超导处理器[21]等.量子游走包含离散时间量子游走[22]和连续时间量子游走[23]，这里我们主要研究离散时间量子游走.

量子游走可以定义在任意给定的图上，其中一维圆是一种最为基础且常见的图，它可以作为实现大规模量子网络的一个基本模块.对于圆上的量子游走，许多学者也已经进行了广泛研究[24-26].

量子相干起源于量子叠加原理，它不仅可以描述量子信息处理的状态演变过程，而且可以反映和解释量子力学中的许多关键核心问题.因此，量子相干被应用到量子计算和量子信息的许多方面，比如量子搜索算法[27]、量子密钥分发[28]、量子计量学[29]等.量子相干的量化方式[30]有很多种，像基于相对熵的、基于skew信息的以及l1范数相干等.由于量子态的l1范数相干[31]形式简单、便于计算，我们这里将采用l1范数相干.

由于两硬币量子游走模型近年来在量子通讯协议中的突出表现[9-12]，本文主要讨论了在一维圆上两硬币量子游走过程中量子相干的动力学行为，并基于此考虑了其在完美状态转移等量子通讯协议中的演变规律.

1 预备知识

量子游走是经典随机游走在量子世界的对应物.由于硬币已经变成了系统的内部自由度，游走者依据硬币状态来决定在给定的图上如何行走，而硬币的状态是由硬币算子来调节控制的.因此，整个演化是发生在位置空间和硬币空间的复合希尔伯特空间上.我们将含有N个点的一维圆记作N-circle.下面，我们将主要讨论在N-circle上的量子游走.

1.1 在圆上的两硬币量子游走模型

多硬币量子游走是由Brun等人于2003年首次提出[32].我们这里主要考虑两硬币量子游走模型.对于两硬币游走模型，粒子是按顺时针行走还是逆时针行走,是通过交替地使用2枚硬币算子来决定的.也就是说，在奇数步，它由第1个硬币操作C1决定;在偶数步，它由第2个硬币操作C2决定.因此，N-circle上的两硬币量子游走在奇数步(翻转第1枚硬币的结果)的酉变换可以写成:

(IN⊗C1⊗I2),

在偶数步(翻转第2枚硬币的结果)的酉变换可以写成:

(IN⊗I2⊗C2),

其中,I2是2×2的单位矩阵，IN是N×N的单位矩阵.

如果我们总共走t步，那么相应的酉算子可以表示为(k=1,2,…):

经过t步量子游走之后，游走者的量子态可以写为

其中振幅fx,c1,c2(t)满足：

1.2 在圆上的两纠缠硬币量子游走模型

对于单硬币量子游走最直接的一种推广就是对硬币空间进行高维推广，另外可以结合量子纠缠这一典型的量子资源来扩展量子游走的演化并发掘它的非经典性.两纠缠硬币量子游走模型于2005年首次被提出[33],并在后来得到在数值[34-35]和理论[36-37]等方面的更深入研究.

区别于1.1节所介绍的两硬币量子游走模型，该模型中的2枚硬币在每一步游走时均会作用而非轮流交替作用，另外游走者每一步游走均有3种类型的移动，向前、向后和保持不动.具体地，在N-circle上的一步两纠缠硬币量子游走的酉变换可以写成:

(IN⊗C1⊗C2).

1.3 量子游走的l1范数相干

量子相干可以衡量量子态具有的量子关联，并可以刻画其更具一般意义的性质，甚至反过来也能够启发更丰富的物理意义.量子相干的度量有很多种，鉴于l1范数相干形式的简便性，我们主要考虑在量子游走中的l1范数相干.

对于给定的密度算子ρ，它的l1范数相干[31]定义为

从而，对于经过t步量子游走之后的量子态|ψ(t)〉，它相应的密度矩阵ρt，即|ψ(t)〉〈ψ(t)|为

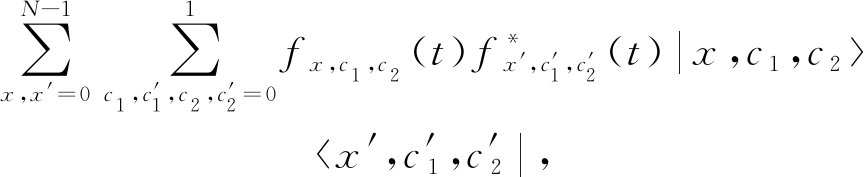
其中f*表示f的复共轭.当然，位置子空间的密度矩阵即

trC(|ψ(t)〉〈ψ(t)|)=

根据l1范数相干的定义，我们可以直接知道:经过t步量子游走之后的量子态|ψ(t)〉在整个空间的量子相干和在位置子空间的量子相干分别为

下面我们将主要依据这2个公式对两硬币量子游走和其实现完美状态转移这一过程进行量子相干的相关分析.

2 主要结果

在本节中，我们将给出主要结果，即初始量子态和不同的硬币算子的选择对在一维圆上两硬币量子游走过程中量子相干的影响，并基于此来考虑它在完美状态转移这一量子通讯协议中的演变规律.

2.1 硬币算子为Hadamard算子的相干性定理

对于在N-circle上的两硬币量子游走，我们选取2个硬币算子均为无偏的Hadamard算子H，即C1=H且C2=H.我们发现对于初态，只要位置空间的量子态是均衡叠加态(硬币状态可以是任意的)，整个量子相干演化就极其有规律，具体如下：

定理1.如果量子游走的初态为其中a,b,c,d均为复数且|a|2+|b|2+|c|2+|d|2=1，那么整个演化过程是以4为周期，且

1)在任一时刻t，粒子处于位置x的概率P(x,t)均为其中,t=0,1,…；x=0,1,…,N-1.

2)经过t步量子游走之后的量子态|φ(t)〉在整个空间的量子相干为(k=0,1,…):

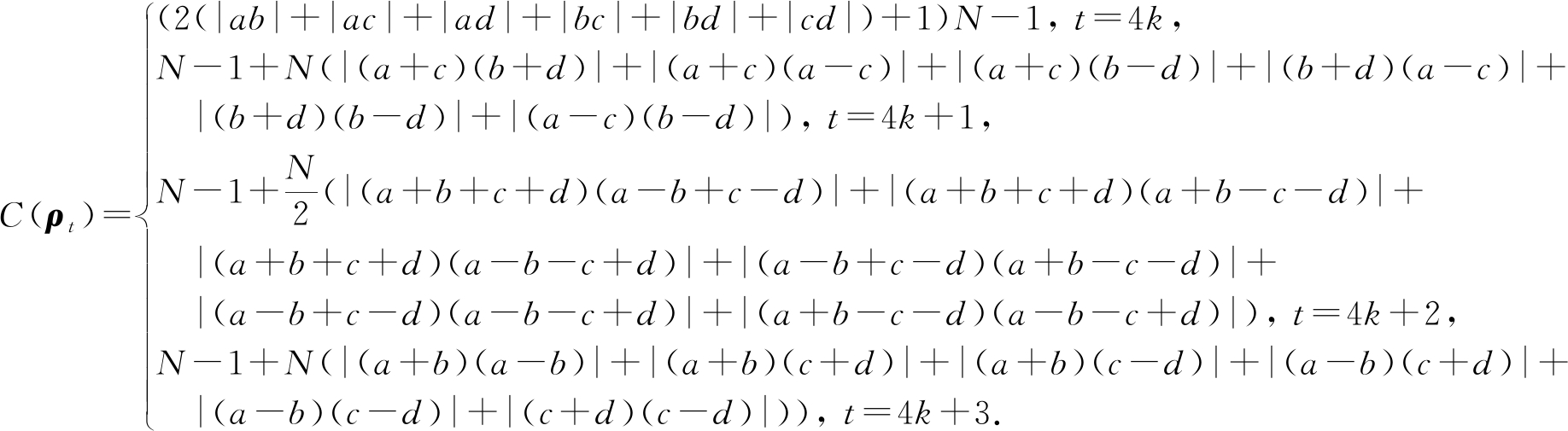
(1)

3)经过t步量子游走之后的量子态|φ(t)〉在位置子空间的量子相干为N-1.

证明. 根据两硬币量子游走模型知，对于量子初态

c|10〉+d|11〉)，

经过4步量子游走该量子态会依次演化为

(b+d)|01〉+(a-c)|10〉+(b-d)|11〉),

(a-b+c-d)|01〉+(a+b-c-d)|10〉+
(a-b-c+d)|11〉),

(a-b)|01〉+(c+d)|10〉+(c-d)|11〉),

c|10〉+d|11〉).

由以上具体的演化过程，我们可以直接发现量子游走是具有周期性的且周期是4.

同时对于圆上的任意一点x，根据初态的归一性，即|a|2+|b|2+|c|2+|d|2=1，我们可以直接计算得出P(x,0)=P(x,1)=P(x,2)=P(x,3)=结合该量子游走演化过程是以4为周期的这一性质，我们可以知道在任一时刻t，粒子处于位置x的概率P(x,t)均为其中,t=0,1,…；x=0,1,…,N-1.

根据量子相干的定义，通过计算可知量子游走之后的量子态在整个空间的量子相干依次为

|c|+|d|)+|c|(|a|+|b|+|d|)+
|d|(|a|+|b|+|c|))=N-1+
2N(|ab|+|ac|+|ad|+|bc|+
|bd|+|cd|)=(2(|ab|+|ac|+|ad|+
|bc|+|bd|+|cd|)+1)N-1,

)+

|b-d|)+|b+d|(|a+c|+|a-c|+
|b-d|)+|a-c|(|a+c|+|b+d|+
|b-d|)+|b-d|(|a+c|+|b+d|+
|a-c|))=N(1+|(a+c)(b+d)|+
|(a+c)(a-c)|+|(a+c)(b-d)|+
|(b+d)(a-c)|+|(b+d)(b-d)|+
|(a-c)(b-d)|)-1,

+
)+

|(a+b+c+d)(a+b-c-d)|+
|(a+b+c+d)(a-b-c+d)|+
|(a-b+c-d)(a+b-c-d)|+
|(a-b+c-d)(a-b-c+d)|+
|(a+b-c-d)(a-b-c+d)|)=N-1+

|(a+b+c+d)(a+b-c-d)|+
|(a+b+c+d)(a-b-c+d)|+
|(a-b+c-d)(a+b-c-d)|+
|(a-b+c-d)(a-b-c+d)|+
|(a+b-c-d)(a-b-c+d)|),

)+

|c-d|)+|a-b|(|a+b|+|c+d|+
|c-d|)+|c+d|(|a+b|+|a-b|+
|c-d|)+|c-d|(|a+b|+|a-b|+
|c+d|))=N-1+N(|(a+b)(a-b)|+
|(a+b)(c+d)|+|(a+b)(c-d)|+
|(a-b)(c+d)|+|(a-b)(c-d)|+
|(c+d)(c-d)|).

结合周期性可知，该定理的结论(2)成立.

量子游走之后的量子态在位置空间的量子相干为

)=N-1,

)=N-1,

+
)=N-1,

)=N-1.

结合周期性可知，经过t步量子游走之后的量子态|φ(t)〉在位置子空间的量子相干为N-1.

证毕.

注1.定理1中初态的选择只要求位置子空间上是均衡叠加态，而对两硬币态并没有任何限制，可以是可分态也可以是纠缠态.即两硬币量子态的选取对于量子游走演化的周期和概率分布并没有影响.其中，由于均衡叠加状态本身体现的无偏性，在量子游走搜索问题中它经常被选为量子游走的初态.特别地，当量子游走的初态为全空间的均衡叠加态，即

整个演化过程的周期为4，且在任一时刻t，粒子处于位置x的概率P(x,t)均为其中，t=0,1,…；x=0,1,…,N-1.经过t步量子游走之后的量子态|φ(t)〉在整个空间的量子相干为

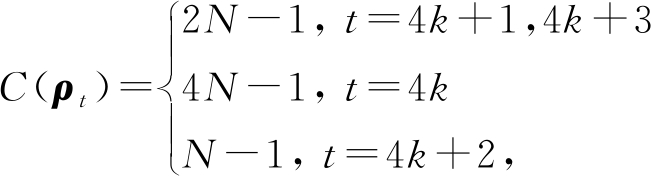
其中k=0,1,…,在位置子空间的量子相干为N-1.

注2.事实上，关于在一维N-circle上单硬币量子游走的量子相干演化[38]，若硬币算子选为Hadamard算子且初态为均衡叠加量子态时，整个演化过程也是具有周期性的且周期为2，位置空间的量子相干一直恒为N-1.结合注1的分析，我们可知对于在圆上的量子游走，只要使用Hadamard算子为硬币算子且选取全空间的均衡叠加态为初态，那么整个演化过程就会具有周期性，这并不依赖于硬币的个数；但是周期会依赖于硬币个数，即在一维圆上的k硬币量子游走的周期为2k.

2.2 含参coin的量子相干性

在2.1节，我们讨论了当2个硬币算子均为固定的Hadamard阵时，两硬币子空间的初态的任意选择在演化过程中对量子相干的影响.这里，我们假定量子初态为均衡叠加态

下面来考虑硬币算子的选取对量子相干性带来的影响.为书写简便，我们假定硬币算子这里的参数是满足矩阵为酉阵这一条件的任一复数.那么，在两硬币量子游走下量子态演化为

(a+c)|01〉+(b+d)|10〉+(b+d)|11〉),

(a+c)(n+t)|01〉+(b+d)(m+s)|10〉+
(b+d)(n+t)|11〉),

(b+d)c)(m+s)|00〉+((a+c)a+
(b+d)c)(n+t)|01〉+((a+c)b+
(b+d)d)(m+s)|10〉+((a+c)b+
(b+d)d)(n+t)|11〉),

可以发现该演化过程是十分有规律的.我们记：

其中

且

T为转置符号，另记

|e1〉=(a,c)T，|e2〉=(b,d)T，|g〉=(1,1)T，
|f1〉=(m,s)T，|f2〉=(n,t)T，

并规定(a,c)T∘(b,d)T=ab+cd，不难通过数学归纳法得知(k=1,2,…)：

|p2k-1〉⊗|q2k-1〉=(|e1〉∘|p2k-2〉，|e2〉∘
|p2k-2〉)T⊗|q2k-2〉|p2k〉⊗|q2k〉=
|p2k-1〉⊗(|f1〉∘|q2k-1〉，|f2〉∘|q2k-1)T.

根据1.3节给出的量子相干公式，可以计算出该演化过程中时刻t全空间和位置子空间的量子相干分别为

N2()]=

特别地，若硬币算子为行和相同的二阶酉矩阵，像形如的酉算子，其中r∈[0,1]且θ∈[0,2π]，不妨记2个硬币算子C1和C2的行和分别为复数i和j，则同样利用数学归纳法可知：对于k=1,2,…，有

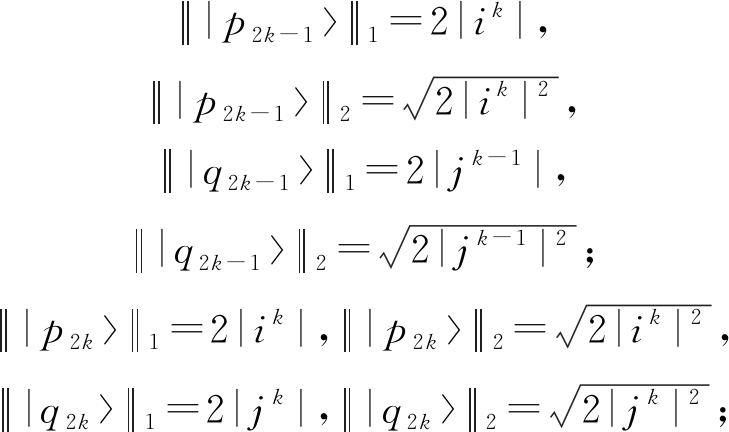
从而，时刻t全空间和位置子空间的量子相干分别为

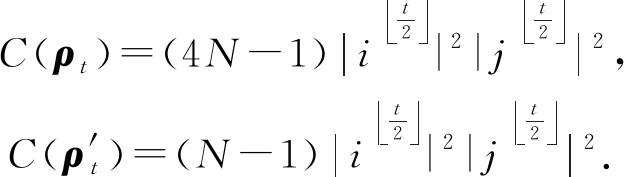
此时量子相干仅依赖于2个硬币算子的行和，且呈正相关的关系.此外，全空间的量子相干和位置子空间的量子相干这二者的比值固定，严格取决于一维圆的顶点个数.

2.3 完美状态转移协议中的量子相干

量子游走可以用来实现量子通讯，比如完美状态转移，即将量子态从一点转移至另一点且保真度为1.文献[39]提出了用单硬币量子游走模型实现在含偶数个点的一维圆上将量子态从一点完美传输到对点的通讯协议.基于此，我们利用两硬币量子游走模型在任意N-circle上可完美传输量子态至圆上的任意位置[10]，这大大改善了文献[39]中完美状态转移协议的局限性.下面我们来分析这2种方案里状态完美转移过程中量子相干的变化.假定要传输的量子态为α|0〉+β|1〉，其中复数α和β满足|α|2+|β|2=1.

文献[10]提出的在N-circle上完美状态转移的方案所用的硬币算子依赖于步数，其中至多有2步会用到Pauli阵X，其余步数均选取单位阵I为硬币算子.由1.3节中量子相干的式(1)可知，用来实现完美状态转移的t步量子游走内，全空间的量子相干一直恒为2|αβ|，在位置空间的量子相干为0.

文献[39]使用单硬币量子游走来实现完美状态转移，该模型的量子相干演化在文献[38]中已经有所探讨.文献[39]具体是从硬币算子的角度出发研究了2种情况，其中任意二阶酉算子可以写为

第1种情况是研究了λ≠1的硬币算子在特定圆上的完美状态转移，比如在4-circle上进行4步硬币算子为的单硬币量子游走，只需一个简单的矫正算子就可以使得量子态α|0〉+β|1〉从位置x=1传到目标位置x=3.那么根据量子相干的定义可知，在这4步量子游走中，全空间的量子相干具体演化为

C(ρ0)=2|αβ|，
C(ρ1)=|α+β|×|α-β|，

C(ρ3)=4|αβ|+1，
C(ρ4)=C(ρ0)=2|αβ|.

在位置空间的量子相干为

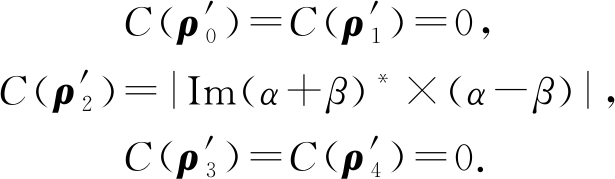
第2种情况研究了使用λ=1的硬币算子进行步量子游走来实现在N-circle上的完美状态转移，其中N为偶数且θ，φ≠0.同样地，根据量子相干的定义可知在这步量子游走过程中，全空间的量子相干一直恒为2|α β|，在位置空间的量子相干为0.这与我们文献[10]使用两硬币量子游走来实现完美状态转移过程中量子相干的演变规律是相同的.

根据以上情形的量子相干对比分析，我们可以看出在利用量子游走来实现完美状态转移的过程中，硬币算子的选取是会直接影响到量子相干的.具体来说，如果硬币算子是对角或反对角形式的，即将一个基态映射到另一个基态上去的(计算基)，那么量子相干在演化过程中会保持不变，恒为定值.否则，若硬币算子将一个基态映射到一些基态的叠加态上(计算基)，比如无偏的Hadamard算子等，此时量子相干在量子游走过程中不会保持不变，而是会依赖于量子游走的步数，随时间变化而变化.

3 模型等价性及在隐形传输上的应用

对于由2枚硬币控制的量子游走，我们在1.1节和1.2节分别介绍了2种模型.这里不考虑初态的选取，二者最主要的区别就是硬币算子的作用方式.模型1是通过2枚硬币交替作用，每一步仅有一枚硬币算子在起作用，经过这枚硬币的翻转作用后游走者依据硬币的当前状态进行移动(向前或向后移动一个单位)；模型2是2枚硬币在每一步游走中均起作用，基于此，游走者向前移动、向后移动一个单位或者保持不动.在本节中，我们将说明这2种模型在一定意义下是等价的，并给出量子相干的比较和具体的应用来详细说明这一点.

对于两硬币量子游走，在奇数步和偶数步量子游走的酉算子分别是U1和U2，因此每2步量子游走对应的演化为

N〉〈x|⊗|11〉〈11|)·(IN⊗C1⊗C2),

即每2步量子游走，2枚硬币均起作用，且游走者依据经硬币翻转操作之后的量子态向前、向后移动2个单位或者保持不动.而对于两纠缠硬币量子游走具体形式已在1.2节由酉算子V给出，可以直接看出，每2步两硬币量子游走相当于一步两纠缠硬币量子游走，差别仅仅是在游走者发生移动的前提下二者相差一个单位.在这个意义下，从量子游走酉算子的角度来看，这2个模型是等价的.

下面，我们从量子相干的角度与注1中的结果进行对比来说明2种模型就上面指出的不同之处所造成的影响.同样地，当量子游走的初态为全空间的均衡叠加态时，即

在两纠缠硬币量子游走下(C1=C2=H)，量子态演化依次为

从而，整个演化过程的周期为2，且在任一时刻t，粒子处于位置x的概率P(x,t)均为其中,t=0,1,…；x=0,1,…,N-1.经过t步量子游走之后的量子态|φ(t)〉在整个空间的量子相干为

其中k=0,1,….在位置子空间的量子相干为N-1.事实上，该演化过程的周期性和全空间量子相干与注1结果的区别是因为这2种量子游走模型和V)移动时相差一个单位.

我们接下来通过量子游走实现隐形状态传输[9]这一应用来说明二者的这种等价性.我们以在4-circle上对单量子比特隐形传输为例.在该协议中，量子初态为|φ(0)〉=|0〉(a|0〉+b|1〉)|0〉，经过2步量子游走，分别选取C1=I和C2=H，量子态演化为

|0〉|-〉(a|1〉-b|0〉)+|2〉|+〉(a|0〉+b|1〉)+
|2〉|-〉(a|0〉-b|1〉)],

其中且接下来只需对位置空间和第1个硬币空间分别选取测量基{|0〉，|1〉，|2〉，|3〉}和{|+〉,|-〉}来测量，再根据测量结果用相应的矫正算子来矫正就可以完成状态的隐形传输.

事实上，基于2种量子游走模型的等价性，对于同样的初态，利用两纠缠硬币量子游走模型同样可以实现隐形状态传输.具体如下：选取硬币算子为C=C1⊗C2=I⊗H，只需一步量子游走(V)，就可以得到量子态：

|0〉|-〉(a|1〉-b|0〉)],

其中且然后对位置空间和第1个硬币空间分别选取测量基和{|+〉,|-〉}来进行测量，再通过合适的矫正算子进行矫正即可.因此，基于量子游走模型的等价性，可以启发我们设计出更加简单高效的量子通讯协议.

4 结 论

量子游走是经典随机游走的量子对应物，由于它在量子计算领域的广泛应用，其本身的性质研究也备受关注.本文针对一维圆上的两硬币量子游走的量子相干进行了分析.我们具体地讨论了初始量子态和硬币算子的选取对量子相干的影响，以及它在量子通讯协议——完美状态转移——中的演变.另外，我们也探讨了2种两硬币量子游走模型之间的等价性，并基于此阐述了其在量子隐形传输中的作用.我们这里仅探讨了量子游走过程中量子相干性质的变化如何受影响，反之，量子相干的变化如何影响量子游走的各种性质是未来值得探索的问题.进一步，它在量子计算或量子密码中的作用也值得探索[40].

参考文献

[1]Wei Wei,Erenrich J,Selman B.Towards efficient sampling:Exploiting random walk strategies[C] //Proc of the 19th National Conf on Artificial Intelligence.Palo Alto,CA:AAAI,2004:670-676

[2]Grady L.Random walks for image segmentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2006,28(11):1768-1783

[3]Cho M,Lee J,Lee K M.Reweighted random walks for graph matching[C] //Proc of European Conf on Computer Vision.Berlin:Springer,2010:492-505

[4]Lee J,Cho M,Lee K M.Hyper-graph matching via reweighted random walks[C] //Proc of CVPR 2011.Piscataway,NJ:IEEE,2011:1633-1640

[5]Childs A M.Universal computation by quantum walk[J].Physical Review Letters,2009,102(18):180501

[6]Childs A M,Gosset D,Webb Z.Universal computation by multiparticle quantum walk[J].Science,2013,339(6121):791-794

[7]Lovett N B,Cooper S,Everitt M,et al.Universal quantum computation using the discrete-time quantum walk[J].Physical Review A,2010,81(4):042330

[8]Underwood M S,Feder D L.Universal quantum computation by discontinuous quantum walk[J].Physical Review A,2010,82(4):042304

[9]Wang Yu,Shang Yun,Xue Peng.Generalized teleportation by quantum walks[J].Quantum Information Processing,2017,16(9):1-13

[10]Shang Yun,Wang Yu,Li Meng,et al.Quantum communication protocols by quantum walks with two coins[J].EPL (Europhysics Letters),2019,124(6):60009

[11]Shang Yun,Li Meng.Experimental realization of state transfer by quantum walks with two coins[J].Quantum Science and Technology,2019,5(1):015005

[12]Li Meng,Shang Yun.Entangled state generation via quantum walks with multiple coins[J].npj Quantum Information,2021,7(1):1-8

[13]Shenvi N,Kempe J,Whaley K B.Quantum random-walk search algorithm[J].Physical Review A,2003,67(5):052307

[14]Santha M.Quantum walk based search algorithms[C] //Proc of Int Conf on Theory and Applications of Models of Computation.Berlin:Springer,2008:31-46

[15]Portugal R.Quantum Walks and Search Algorithms[M].Berlin:Springer,2018

[16]Li Meng,Shang Yun.Generalized exceptional quantum walk search[J].New Journal of Physics,2020,22(12):123030

[17]Ambainis A.Quantum walk algorithm for element distinctness[J].SIAM Journal on Computing,2007,37(1):210-239

[18]Magniez F,Santha M,Szegedy M.Quantum algorithms for the triangle problem[J].SIAM Journal on Computing,2007,37(2):413-424

[19]Schreiber A,Cassemiro K N,Potoek V,et al.Photons walking the line:A quantum walk with adjustable coin operations[J].Physical Review Letters,2010,104(5):050502

[20]Zähringer F,Kirchmair G,Gerritsma R,et al.Realization of a quantum walk with one and two trapped ions[J].Physical Review Letters,2010,104(10):100503

[21]Yan Zhiguang,Zhang Yuran,Gong Ming,et al.Strongly correlated quantum walks with a 12-qubit superconducting processor[J].Science,2019,364(6442):753-756

[22]Aharonov Y,Davidovich L,Zagury N.Quantum random walks[J].Physical Review A,1993,48(2):1687

[23]Farhi E,Gutmann S.Quantum computation and decision trees[J].Physical Review A,1998,58(2):915

[24]Bednarska M,Grudka A,Kurzyński P,et al.Quantum walks on cycles[J].Physics Letters A,2003,317(1-2):21-25

[25]Solenov D,Fedichkin L.Continuous-time quantum walks on a cycle graph[J].Physical Review A,2006,73(1):012313

[26]Sadowski P,Miszczak J A,Ostaszewski M.Lively quantum walks on cycles[J].Journal of Physics A:Mathematical and Theoretical,2016,49(37):375302

[27]Shi Hailong,Liu Siyuan,Wang Xiaohui,et al.Coherence depletion in the Grover quantum search algorithm[J].Physical Review A,2017,95(3):032307

[28]Ma Jiajun,Zhou You,Yuan Xiao,et al.Operational interpretation of coherence in quantum key distribution[J].Physical Review A,2019,99(6):062325

[29]Pires D P,Silva I A,deAzevedo E R,et al.Coherence orders,decoherence,and quantum metrology[J].Physical Review A,2018,98(3):032101

[30]Streltsov A,Adesso G,Plenio M B.Colloquium:Quantum coherence as a resource[J].Reviews of Modern Physics,2017,89(4):041003

[31]Baumgratz T,Cramer M,Plenio M B.Quantifying coherence[J].Physical Review Letters,2014,113(14):140401

[32]Brun T A,Carteret H A,Ambainis A.Quantum walks driven by many coins[J].Physical Review A,2003,67(5):052317

[33]Venegas-Andraca S E,Ball J L,Burnett K,et al.Quantum walks with entangled coins[J].New Journal of Physics,2005,7(1):221

[34]Panahiyan S,Fritzsche S.One-dimensional quantum walks driven by two-entangled-qubit coins[J].Physics Letters A,2020,384(26):126673

[35]Panahiyan S,Fritzsche S.Increasing the efficiency of quantum walk with entangled qubits[J].arXiv preprint arXiv:1905.11076,2019

[36]Liu Chaobin,Petulante N.One-dimensional quantum random walks with two entangled coins[J].Physical Review A,2009,79(3):032312

[37]Liu Chaobin.Asymptotic distributions of quantum walks on the line with two entangled coins[J].Quantum Information Processing,2012,11(5):1193-1205

[38]He Zhimin,Huang Zhiming,Li Lüzhou,et al.Coherence of one-dimensional quantum walk on cycles[J].Quantum Information Processing,2017,16(11):1-14

[39]Yalçnkaya ,Gedik Z.Qubit state transfer via discrete-time quantum walks[J].Journal of Physics A:Mathematical and Theoretical,2015,48(22):225302

[40]Wang Yongli,Xu Qiuliang.Principle and research progress of quantum computation and quantum cryptography[J].Journal of Computer Research and Development,2020,57(10):2015-2026 (in Chinese)(王永利,徐秋亮.量子计算与量子密码的原理及研究进展综述[J].计算机研究与发展,2020,57(10):2015-2026)

Dynamics of Coherence in Quantum Walk with Two Coins

Li Meng1,2 and Shang Yun1,3,4

1(Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190) 2(School of Mathematical Sciences,University of Chinese Academy of Sciences,Beijing 100049) 3(NCMIS,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190) 4(MDIS,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190)

Abstract Quantum walk is an important model of quantum computing,and quantum walk with multiple coins has attracted more and more attention due to its outstanding performance in quantum communication protocols.Quantum coherence can not only describe the characteristics of quantum states,but also reflect the properties of quantum evolution process.In this paper,we analyze quantum coherence for the model of quantum walk with two coins on the one dimensional circle.On the one hand,we discuss the influence of the choice of initial quantum state and coin operators on quantum coherence.When the coin operator is Hadamard operator,as long as the initial state in subspace is equal superposition,the whole evolutionary process of quantum walk is periodic,and quantum coherence only depends on the number of vertexes of the circle and steps;When the initial state is equal superposition and there are no limits on the coin operators,the evolution of the quantum state is also extremely regular.On the other hand,we find that in the process of perfect state transfer by quantum walk,the coin operator will determine the quantum coherence directly.In addition,we also discuss the equivalence between the two quantum walk models,and based on this,we point out the possibility of application and improvement in quantum teleportation.

Key words quantum walk;two coins;quantum coherence;state transfer;quantum teleportation

中图法分类号 TP38

DOI:10.7544/issn1000-1239.2021.20210266

收稿日期：2021-03-29； 修回日期：2021-05-14

基金项目：国家重点研发计划项目(2016YFB1000902);国家自然科学基金项目(61872352,61472412);国家自然科学基金创新群体项目(61621003)

This work was supported by the National Key Research and Development Program of China (2016YFB1000902),the National Natural Science Foundation of China (61872352,61472412),and the Program for Creative Research Group of the National Natural Science Foundation of China (61621003).

通信作者:尚云(shangyun@amss.ac.cn)

Li Meng,born in 1995.PhD.Her main research interests include quantum computing and quantum walks.

李 萌，1995年生.博士.主要研究方向为量子计算与量子游走.

Shang Yun,born in 1972.Professor and PhD supervisor.Senior member of CCF.Her main research interests include quantum computing and its fundamental theory,quantum logic,quantum dot cellular automata and complex network.

尚 云，1972年生.研究员，博士生导师.CCF高级会员.主要研究方向为量子计算及其基础理论、量子逻辑、量子点元胞自动机和复杂网络等.