区块链本质上是一种去中心化、不可更改、可追溯的分布式数据库.近十几年来,区块链技术迅速发展,从区块链1.0(从以比特币为代表)开始,经历区块链2.0(到以太坊为代表的智能合约),进入区块链3.0(以去中心化应用Dapp为代表),应用领域不断扩大,被认为是引发下一代产业革命的核心要素,是助推未来数字化经济发展、支撑社会各界数字化转型的国家战略技术[1].
在区块链发展过程中,去中心化和不可算改性往往被认为是区块链构建信任的关键性质.区块链借此实现数据共享、共治,进而共建安全可信的生态系统.然而,随着区块链的发展,人们逐渐对其不可更改性有了更全面、更深刻的辩证性认识.事实上,区块链的不可更改性也带来诸多不利的方面[2-5].例如,在以太坊2016年的The DAO事件中,已经上链的合约中存在漏洞,导致了大规模的以太币非法转移,由于缺乏相应的区块链修正机制,官方只得通过硬分叉来勉强解决问题,而之后爆发的ATN事件也面临区块链修改机制的需求.现有公开运行的诸多区块链上,如比特币系统,存在一些负面的、恶意的违法信息,而且受制于不可更改性、同时借助区块链的公开性而广泛传播,既危害了广大用户,也危害了区块链本身,甚至可能危害社会、国家安全.特别是在区块链日益广泛、深刻地融入到金融、保险、司法、社会治理等诸多领域的背景下,区块链技术迫切需要安全、便捷、可控的技术手段来更新链上关键数据并清除有害数据,进而实现区块链的有效合法监管,保障区块链的健康发展.
2017年,著名密码学家Atenise等人[2]首次提出了可修正区块链的概念,并给出了较为系统的解决方案,所依赖的关键密码学工具是变色龙哈希函数.可修正(redactable,editable)区块链的研究逐渐在区块链研究领域引起关注.2020年5月,袁勇等人发表了关于可修正区块链的综述文章[3],较为系统性地梳理和研究其现实需求及工作框架,从数据修改、删除、插入、过滤和隐藏等环节详细阐述了可修正区块链的技术与方法,并讨论了该领域亟需解决的若干关键问题.
本文以变色龙哈希函数为主要工具研究了可修正区块链的构造问题,主要贡献包括3个方面:
1) 提出了称作一次变色龙哈希函数的新型密码原语:当每个标签下的碰撞都不超过一个时,敌手计算任何新碰撞都是不可行的,相当于碰撞陷门未暴露任何信息;而存在某个标签下的碰撞超过一个时,则所有标签下的二对一碰撞都可以扩展为任意的三对一碰撞,相当于碰撞陷门部分暴露.
2) 基于RSA假设构造了在随机预言模型下可证明安全的一次变色龙哈希函数,其效率与基于RSA的最经典高效的普通变色龙哈希函数相当[6].
3) 基于一次变色龙哈希函数概念实现了区块链的(至多)一次修正机制,并基于RSA问题给出该机制的高效构造.对于新提出的可修正区块链,每个区块所允许的修改次数不得超过一次,否则任何修改过的区块内容都可以被任何人修改成任何内容.之前的可修订区块链对修订次数不做限定,既赋予了合法修改者过高修改权限,也导致了现有可修改区块链难以高效实现的后果.
1 相关工作
本节主要介绍以变色龙哈希函数为构件的可修正区块链相关工作,可修正区块链的其他构造方法可参见文献[3].
变色龙哈希函数是一种带陷门的特殊抗碰撞哈希函数[7].陷门持有者可轻易地计算任意输入数据的哈希碰撞,从而可以在不改变哈希函数输出的情况下,任意地改变哈希函数的输入.对于未知陷门者,变色龙哈希函数与传统的哈希函数一样具有抗碰撞性.作为一种基础的密码学原语,变色龙哈希函数是构造变色龙哈希签名、紧致安全签名、同态签名、可净化签名、身份认证、可验证计算、可证明安全公钥加密等各类密码学方案的重要工具.关于变色龙哈希函数较为系统的研究,可参阅文献[6].
可修正区块链的概念是由Atenise等人在2017年正式提出[2].其核心思想是用变色龙哈希函数代替普通抗碰撞哈希函数(内层哈希)来计算区块所有交易的摘要,而此哈希值又被普通哈希函数链(外层哈希)固定在区块链上.这一方法是目前最成熟的可修正区块链技术,已作为专利授权给了埃森哲公司.其优点在于,在拥有密钥的用户利用变色龙哈希特性修改历史数据时,操作简单,且对前后区块没有影响,可以避免硬分叉.文献[2]指出,为了适应可修正区块链的应用需求,变色龙哈希函数需要满足加强的抗碰撞性质,即在修改块引起了多个变色龙哈希碰撞暴露的情况下,计算新的哈希碰撞(意味着非法的区块修改操作)仍然是不可行的.然而具有增强抗碰撞性的变色龙哈希的构造面临较高技术难题.文献[2]所给出的构造方法不得不依赖公钥加密、零知识证明等复杂密码原语.可修正机制自然对不可更改性和去中心化两大特性带来不利影响,对修正特权进行最大程度的限制是必要的设计准则.为此,文献[2]将门限密码方法引入了变色龙哈希函数,用以实现修正陷门及操作在多个主体间的分享.本文则注意到限制修改权限的其他维度,即陷门持有者对一个区块的修改次数.特别是从区块链用户角度看,区块链理应最大限度地保证不可更改性.因此,为了增加很少动用的可更改性质而引入“无限次”修改权限是不合理的.
为了实现细粒度更高的修改机制,Derler等人于2019年将变色龙哈希函数改进为基于策略变色龙哈希函数[8].对于基于策略变色龙哈希函数,只要某主体所拥有的角色属性满足指定策略,该主体私钥就可以用来计算碰撞.通过引入基于策略变色龙哈希函数,文献[8]实现了从区块层面到交易层面的细粒度的可控修正机制.Derler等人也给出基于策略变色龙哈希函数的构造框架,其可看做是基于属性加密和附带临时陷门变色龙哈希函数的组合,而这2个组件构造的复杂性也造成了此方案实现的复杂程度.作为进一步的功能扩展,Tian等人[9]于2020年提出了带黑盒审计的基于策略变色龙哈希函数,并将其应用于可修正区块链,为所有的区块修改操作提供了事后审计监督机制,在一定程度上达到预防修改特权滥用的效果.
变色龙哈希函数主要是为了丰富区块链修正机制的功能,其运行效率却受制于底层复杂构件的限制.文献[10]则构造了更高效率的具有加强抗碰撞性的变色龙哈希函数,但仍然需要依赖双线性对、零知识证明、公钥加密等密码构件.Wu等人[11]基于格上困难问题构造了具有加强抗碰撞性的变色龙哈希函数,并借助格工具避免了公钥加密和零知识证明等复杂构件,同时也因格工具而带有格密码本身的局限性.由此可见,高效率的加强抗碰撞性变色龙哈希函数仍然是实现高效可修正区块链的关键技术环节.李佩丽等人[4]针对联盟链改进了可修改区块链技术,结合秘密共享方案设计了新的变色龙哈希函数,使得在共同决策结果满足修改触发条件情况下,联盟链中的每个用户都有修改历史记录的权利.
2 预备知识
2.1 RSA假设
定义1. 设KRSA(1λ)是一个概率多项式时间算法,输入安全参数1λ,输出一个RSA模N和2个大素数p,q,使得N=pq,还输出e,d使得ed=1 mod (p-1)(q-1),称敌手A(t,ε)解决RSA问题,如果其运行时间不超过t,其成功概率:
![]() x←R
x←R![]() N,X←xemod N)≥ε .
N,X←xemod N)≥ε .
如果不存在算法能够(t,ε)解决RSA问题,则称RSA问题是(t,ε)困难的.RSA假设是指,任何概率多项式时间的敌手![]() 解决RSA问题的概率都是关于λ的可忽略函数.
解决RSA问题的概率都是关于λ的可忽略函数.
2.2 一次变色龙哈希函数
定义2. 一次变色龙哈希函数由4个多项式时间算法组成:
CH=(ChGen,ChHash,ChVer,ChCld).
1) ChGen(1λ)→(hk,tk)
此密钥生成算法输入为安全参数1λ,输出是哈希公钥hk和碰撞私钥tk.
2) ChHash(hk,τ,m)→(h,r)
此哈希计算算法输入哈希公钥hk、标签τ、消息![]() 然后选择随机种子c,最后输出哈希值及相应的认证值h,r.如果r=c,则称此哈希函数为公开掷币型,否则称为秘密掷币型.本文考虑前者,方便起见将该算法表示为
然后选择随机种子c,最后输出哈希值及相应的认证值h,r.如果r=c,则称此哈希函数为公开掷币型,否则称为秘密掷币型.本文考虑前者,方便起见将该算法表示为
ChHash(hk,τ,m,r)→h或 h=Hash(hk,τ,m,r).
3) ChVer(hk,τ,h,m,r)→b
此哈希验证算法输出b,表示h是否为合法的哈希函数值.本文考虑公开掷币型变色龙哈希函数,此算法也就是判定等式ChHash(hk,τ,m,r)=h是否成立.
4) ChCld(hk,tk,τ,m,r,m′)→r′
此碰撞算法输出r′使得:
ChHash(hk,τ,m,r)= ChHash(hk,τ,m′,r′),m≠m′
5) 抗一次碰撞性
称CH=(ChGen,ChHash,ChVer,ChCld)为安全的一次变色龙哈希哈数,若:
性质1. 对于任何敌手![]() 其成功概率
其成功概率
都是可忽略的,其中集合![]() 由碰撞预言机
由碰撞预言机![]() 维护:对于每次询问(hk,τ,m,r,m′),若ChVer(hk,τ,h,m,r)=1且
维护:对于每次询问(hk,τ,m,r,m′),若ChVer(hk,τ,h,m,r)=1且![]() 中不存在形如(τ,*,*)的数组,则将(τ,m,m′),(τ,m′,m)添加到
中不存在形如(τ,*,*)的数组,则将(τ,m,m′),(τ,m′,m)添加到![]() 中,同时返回r′使得ChVer(hk,τ,h,m′,r′)=1,此时我们称(hk,τ,m,r,m′,r′)为二重碰撞.否则,返回“非法询问”.
中,同时返回r′使得ChVer(hk,τ,h,m′,r′)=1,此时我们称(hk,τ,m,r,m′,r′)为二重碰撞.否则,返回“非法询问”.

Fig. 1 Redactable blockchain structure diagram
图1 可修订区块链结构图
性质2. 存在概率多项式时间的敌手![]() 输入包括一个三重碰撞,即
输入包括一个三重碰撞,即
(τ1,h1,m1,1,r1,1,m1,2,r1,2,m1,3,r1,3)
满足m1,1,m1,2,m1,3两两不同且:
ChVer(hk,τ1,h1,m1,j,r1,j)=1,j=1,2,3,
一个二重碰撞,即(τ2,h2,m2,1,r2,1,m2,2,r2,2)满足m2,1≠m2,2且:
ChVer(hk,τ2,h2,m2,j,r2,j)=1,j=1,2,
及目标消息m2,3(与m2,1,m2,2不同![]() 成功输出r2,3的概率:
成功输出r2,3的概率:
Pr(ChVer(hk,τ2,h2,m2,3,r2,3)=1),
即(τ2,h2,m2,1,r2,1,m2,2,r2,2,m2,3,r2,3)是三重碰撞的概率不可忽略.
注1. 抗一次碰撞性的形式化定义所给出的安全概念涵盖了2种情形:
1) 性质1保证.对于碰撞达到一次的任何标签,算出新碰撞是不可行的;
2) 性质2保证.一旦某个标签下的3个消息碰撞到一个哈希值(该标签下的碰撞超过了一次),则对于碰撞达到一次的任何标签,算出新碰撞变得可行.后面将结合可修正区块链环境,进一步讨论抗一次碰撞性的应用意义.
2.3 区块链及可修正性
沿用文献[2],先给出普通区块链的形式化描述.首先,一个区块就是一个三元组
B= s,x,ctr
s,x,ctr ,s∈{0,1}κ,x∈{0,1}*,ctr∈
,s∈{0,1}κ,x∈{0,1}*,ctr∈![]() .
.
称上述区块B有效,如果:
![]()
 (H(ctr,G(s,x))<D)∧ (ctr<q)=1,
(H(ctr,G(s,x))<D)∧ (ctr<q)=1,
(1)
此处,
H:{0,1}*→{0,1}κ,G:{0,1}*→{0,1}κ
是抗碰撞哈希函数,分别称作外层哈希和内层哈希,而参数D∈![]() 和q∈
和q∈![]() 分别是一个用户在指定时间内被限定的区块困难层次和最大哈希次数.区块链
分别是一个用户在指定时间内被限定的区块困难层次和最大哈希次数.区块链![]() 就是区块链接而成的序列.最右边的区块称作链头
就是区块链接而成的序列.最右边的区块称作链头![]() 当链头
当链头![]() 时,可通过添加新区块B′=
时,可通过添加新区块B′= s′,x′,ctr′
s′,x′,ctr′ 扩展为更长新链
扩展为更长新链![]() 而B′满足s′=H(ctr,G(s,x)).
而B′满足s′=H(ctr,G(s,x)).
沿用文献[2],再给出可修正(Redactable)区块链的形式化描述,其区块为四元组B= s,x,ctr,r
s,x,ctr,r ,其中s,x,ctr如前所述,而新增r则是对应的变色龙哈希函数中的随机值.称(可修正)区块B有效,如果
,其中s,x,ctr如前所述,而新增r则是对应的变色龙哈希函数中的随机值.称(可修正)区块B有效,如果
![]()
 (H(ctr,ChHash(hk, (s,x),r))<D)∧(ctr<q)=1,
(H(ctr,ChHash(hk, (s,x),r))<D)∧(ctr<q)=1,
(2)
即相比于普通区块链,内层哈希函数G不再是普通哈希函数,而是变色龙哈希函数.对于链头Head(C)= s,x,ctr,r
s,x,ctr,r 的可修正区块链
的可修正区块链![]() 可通过添加新区块B′=
可通过添加新区块B′= s′,x′,ctr′,r′
s′,x′,ctr′,r′ 扩展为更长的新链C′=C‖B′,B′满足
扩展为更长的新链C′=C‖B′,B′满足
s′=H(ctr,ChHash(hk,(s,x),r))
为了便于理解,图1给出可修正区块链模型的图示(内层的变色龙哈希函数表示为G(hk,(s,x),r)):
对于可修正区块链及其对内层变色龙哈希函数性质要求的详细阐述,请参阅文献[2].
3 基于RSA的一次变色龙哈希函数构造及安全性证明
本节先给出基于RSA的一次变色龙哈希函数的构造,然后在随机预言模型下证明其安全性.鉴于本方案可看做基于RSA的经典变色龙哈希函数的扩展[6],且关键运算仅由模指数构成,此节对效率分析不做赘述.
3.1 具体方案
本节构造一个基于RSA难题的一次变色龙哈希函数
CH=(ChGen,ChHash,ChVer,ChCld).
1) ChGen(1λ)→(hk,tk)
根据输入的安全参数1λ,选择同样长度的2个不同的大素数p,q,并计算N=pq.然后,选择足够大的素数e>2l,此处l是保证e足够大的一个参数.接着,计算d使得ed=1 mod (p-1)(q-1).然后,随机选择x0←R![]() N,并计算
N,并计算![]() 最后,选定2个密码学意义下安全的哈希函数:
最后,选定2个密码学意义下安全的哈希函数:
He:{0,1}→![]()
![]()
![]()
![]()
相应的哈希公钥和碰撞私钥为
hk=(N,e,X0,He,HN),tk=d.
2) ChHash(hk,τ,m)→(h,r),
给定哈希公钥hk,标签τ和消息m∈![]() e,计算
e,计算
此处
![]()
![]()
![]()
然后,输出h,r.方便起见,将本过程表示
h=Hash(hk,τ,m,r).
3) ChVer(hk,τ,h,m,r)→b
对于输入的标签τ,哈希值h,消息![]() 及随机值r,如果h=Hash(hk,τ,m,r),该算法返回b=1.否则,返回b=0.
及随机值r,如果h=Hash(hk,τ,m,r),该算法返回b=1.否则,返回b=0.
4) ChCld(hk,tk,τ,m,r,m′)→r′
对于标签τ,消息![]() 及随机值
及随机值![]()
![]() N×{0,1}k,待碰撞消息
N×{0,1}k,待碰撞消息![]() 该算法先随机选择
该算法先随机选择![]() 然后计算:
然后计算:

对以上计算结果,易知:
Hash(hk,τ,m,r)=Hash(hk,τ,m′,r′), ![]()
![]()
因此,![]() 可以看做对应标签τ的子碰撞私钥,而私钥d则是针对所有标签的主碰撞私钥.
可以看做对应标签τ的子碰撞私钥,而私钥d则是针对所有标签的主碰撞私钥.
3.2 安全性证明
首先,证明引理1,其对应定义2中抗一次碰撞性的性质1;然后,证明引理2,其对应定义2中抗一次碰撞性的性质2;最后,综合2个引理,证明上述构造方案在RSA假设下是安全的一次变色龙哈希函数.
引理1. 在随机预言模型下,对于上述变色龙哈希函数方案CH,如果存在运行时间不超过t、成功概率不低于ε的攻击算法![]() (参见定义2),那么存在运行时间不超过t′、成功概率不低于ε′的RSA问题攻击算法:
(参见定义2),那么存在运行时间不超过t′、成功概率不低于ε′的RSA问题攻击算法:
其中,e是自然底数,qN和qC分别是![]() 访问随机预言机(对应哈希函数HN(·))和碰撞预言机的次数,TME表示模N的指数运算时间.
访问随机预言机(对应哈希函数HN(·))和碰撞预言机的次数,TME表示模N的指数运算时间.
证明. 设![]() 是攻击上述一次变色龙哈希函数的敌手,可适应性访问随机预言机
是攻击上述一次变色龙哈希函数的敌手,可适应性访问随机预言机![]() 次
次![]() 次)和碰撞预言机
次)和碰撞预言机![]() 次),其具体行为如定义2所述.本证明则是调用
次),其具体行为如定义2所述.本证明则是调用![]() 构造攻击RSA难题的有效算法
构造攻击RSA难题的有效算法![]() (如定义1所示).
(如定义1所示).
1) 首先,![]() 获得RSA挑战实例(N,e,X),其攻击目标则是算得x使得xe=X mod N,即x=Xdmod N.
获得RSA挑战实例(N,e,X),其攻击目标则是算得x使得xe=X mod N,即x=Xdmod N.
![]() 取哈希公钥hk=(N,e,X0,He,HN),其中X0=X,在随机预言模型下,哈希函数He(·)和HN(·)被看作随机预言机,由
取哈希公钥hk=(N,e,X0,He,HN),其中X0=X,在随机预言模型下,哈希函数He(·)和HN(·)被看作随机预言机,由![]() 模拟.
模拟.
![]() 通过操作来模拟预言机
通过操作来模拟预言机![]() 和
和![]()
① 当![]() 收到针对预言机
收到针对预言机![]() 的询问值时,若此询问值未曾出现过,
的询问值时,若此询问值未曾出现过,![]() 则选择并返回上次的哈希值,否则
则选择并返回上次的哈希值,否则![]() 选择并返回介于1,e之间的一个随机数.
选择并返回介于1,e之间的一个随机数.
② 当![]() 收到针对预言机
收到针对预言机![]() 的询问值τj,1≤j≤qN时,其应答值HN(τj)随机选定,其概率分布满足:
的询问值τj,1≤j≤qN时,其应答值HN(τj)随机选定,其概率分布满足:
![]()
![]()
![]()
![]() e,
e,
(3)
此处,j0是由![]() 事先随机选定的介于1与qN的整数.
事先随机选定的介于1与qN的整数.
③ 当![]() 收到针对预言机
收到针对预言机![]() 的询问值
的询问值![]() 时,若
时,若![]() 返回“失败”;若τj曾在以前的询问中出现过,则返回“无效询问”;否则
返回“失败”;若τj曾在以前的询问中出现过,则返回“无效询问”;否则![]() 通过随机预言机
通过随机预言机![]() 的模拟获得
的模拟获得![]() 使得
使得![]() 参见式(3),然后随机选取
参见式(3),然后随机选取![]() 并计算:
并计算:
![]()
(4)
通过计算模拟:
![]()
(5)
等式![]() 的成立来自推导:
的成立来自推导:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Hash(τj,mj,rj).
Hash(τj,mj,rj).
4) 最后![]() 返回
返回![]() 如果
如果![]() 且
且![]() 从未出现在碰撞预言机
从未出现在碰撞预言机![]() 的询问值中,则
的询问值中,则![]() 可通过计算得出x=Xd.否则,
可通过计算得出x=Xd.否则,![]() 返回“失败”.由
返回“失败”.由![]() 依次可得:
依次可得:
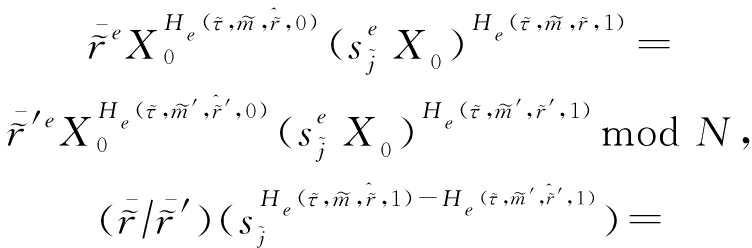
再由扩展的欧几里得算法可得:
此处的s,t满足:
下面再来分析![]() 的成功概率.在
的成功概率.在![]() 的运行中,只要条件1,即在步骤③中,对所有的qC次碰撞询问,都有
的运行中,只要条件1,即在步骤③中,对所有的qC次碰撞询问,都有![]() 和条件2,即在步骤④中,
和条件2,即在步骤④中,![]() 都成立时,
都成立时,![]() 为
为![]() 所模拟的环境就完全符合定义2.由HN(·)模拟值的概率分布,2个条件同时成立的概率是
所模拟的环境就完全符合定义2.由HN(·)模拟值的概率分布,2个条件同时成立的概率是![]() 因此有:
因此有:
![]() 成功
成功![]() 成功)≈
成功)≈ ![]() 成功).
成功).
最后简要分析![]() 的运行时间.
的运行时间.![]() 的运行时间
的运行时间![]() 的主要构成是
的主要构成是![]() 的运行时间,qN次随机预言机
的运行时间,qN次随机预言机![]() 的模拟和qC次碰撞预言机
的模拟和qC次碰撞预言机![]() 的模拟,而每次模拟不超过3个模指数运算TME.因此,在考虑运行时间主要构成的条件下可得:
的模拟,而每次模拟不超过3个模指数运算TME.因此,在考虑运行时间主要构成的条件下可得:
证毕.
引理2. 对于变色龙哈希函数方案,存在针对三重碰撞的概率多项式时间攻击算法![]() 见定义2,即对于任意给定的一组三重碰撞(τ1,h1,m1,1,r1,1,m1,2,r1,2,m1,3,r1,3)满足:
见定义2,即对于任意给定的一组三重碰撞(τ1,h1,m1,1,r1,1,m1,2,r1,2,m1,3,r1,3)满足:
![]() for j=1,2,3,X1,1=HN(τ1),
for j=1,2,3,X1,1=HN(τ1),
(6)
一组二重碰撞(τ2,h2,m2,1,r2,1,m2,2,r2,2)满足:
![]() for j=1,2,X1,2=HN(τ2)
for j=1,2,X1,2=HN(τ2)
(7)
和目标消息m2,3,总能输出r2,3满足:
此处,当i分别1,2时,mi,1,mi,2,mi,3各不相同.
证明. 算法![]() 可如下构造.由式(6)可得:
可如下构造.由式(6)可得:
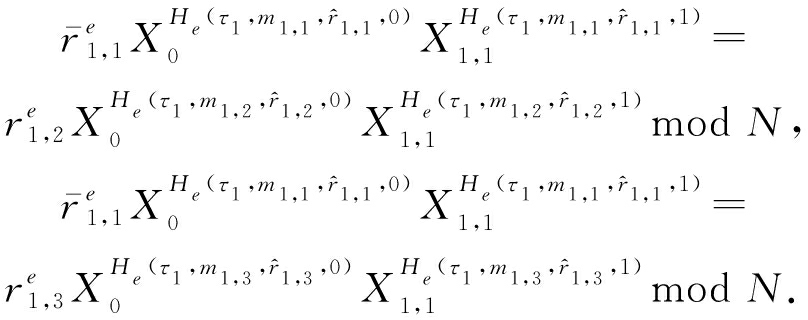
取![]() 则进一步得
则进一步得
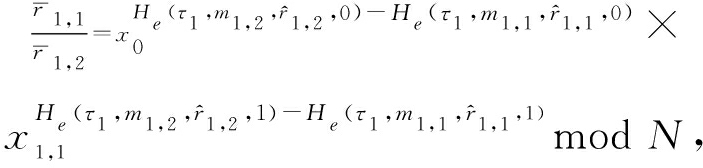
(8)
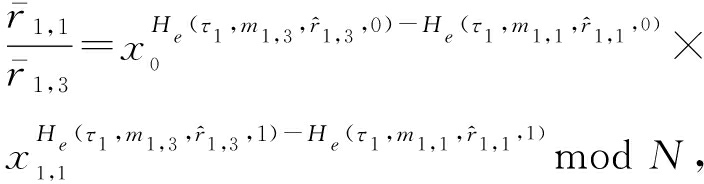
(9)
由哈希函数(理想化为随机预言机)的随机性知,式(8)(9)中指数部分为零的概率可忽略,从而利用扩展的欧几里得算法知,存在s′,t′,s″,t″使得:
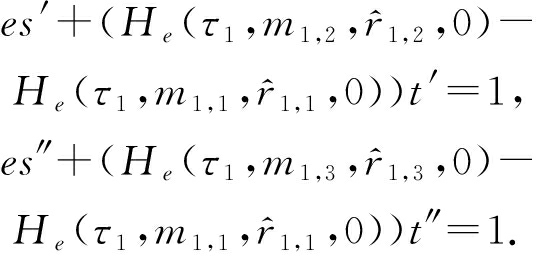
对于等式(8)两边同时先取t′次方再乘以![]() 记
记![]() 可得:
可得:
![]()
![]() =x0
=x0![]() mod N.
mod N.
(10)
同理,由式(9)可得:
![]()
(11)
对于式(10)(11),两边分别相除得:
再由扩展欧几里得算法,可得s‴,t‴使得:
es‴+h21t′-h31t″t‴=1.
从而可得:
结合式(11),进一步得到:
由式(7)得:
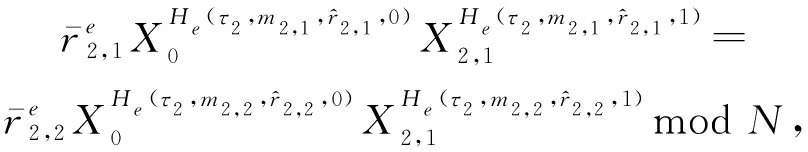
取![]() 从而可得:
从而可得:
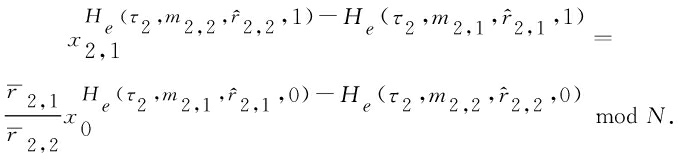
再由扩展欧几里得算法,可得:
![]() mod N,
mod N,
此处
由(x0,x2,1),根据所构造的一次变色龙哈希函数的求碰撞算法ChCld,可得:
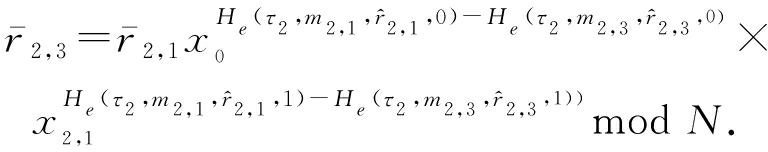
证毕.
综合引理1,2得:
定理1. 变色龙哈希函数
CH=(ChGen,ChHash,ChVer,ChCld)
是安全的一次变色龙哈希函数.
4 基于一次变色龙哈希函数的可修正区块链
4.1 方案描述
如第2.3节所述,在文献[2]中,由普通区块链到可修正区块链的本质改动是把内层的普通抗碰撞哈希函数替换为具有增强抗碰撞性的变色龙哈希函数,参见第2.3节中式(1)(2),与此类似,本节所考虑的可修正区块链则是进一步将内层哈希替换为一次变色龙哈希函数.
首先,给出本文所构造可修正区块链的结构描述.具体来讲,沿用文献[2]相关符号,给出可修正(Redactable)区块链的形式化描述,其区块为四元组 s,x,ctr,r
s,x,ctr,r ,其中B=
,其中B= s,x,ctr,r
s,x,ctr,r 参见第2.3节,而区块标识符τ可根据具体应用而约定选取,不显式地体现为区块元素.称(可修正)区块B有效,如果
参见第2.3节,而区块标识符τ可根据具体应用而约定选取,不显式地体现为区块元素.称(可修正)区块B有效,如果
![]()
 (H(ctr,Hash(hk, τ,(s,x),r))<D)∧(ctr<q)=1,
(H(ctr,Hash(hk, τ,(s,x),r))<D)∧(ctr<q)=1,
即相比于普通区块链,内层哈希函数G不再是普通哈希函数,而是一次变色龙哈希函数.对于链头![]() 的可修正区块链
的可修正区块链![]() 可通过添加新区块B′=
可通过添加新区块B′= s′,x′,ctr′,r′
s′,x′,ctr′,r′ 扩展为更长的新链
扩展为更长的新链![]() 满足:
满足:
s′=H(ctr,Hash(hk,τ,(s,x),r)).
4.2 方案分析
首先,分析合法(对任何区块至多修改一次)修改区块信息的操作过程.由一次变色龙哈希函数性质,可对该区块链进行修正操作:设区块B= s,x,ctr,r
s,x,ctr,r 和区块B′=
和区块B′= s′,x′,ctr′,r′
s′,x′,ctr′,r′ 前后相连,区块标识符分别为τ和τ′,故满足关系:
前后相连,区块标识符分别为τ和τ′,故满足关系:
s′=H(ctr,Hash(hk,τ,(s,x),r)),
对于修改区块B中的内容x修正为![]() 的请求,利用碰撞私钥tk可算得
的请求,利用碰撞私钥tk可算得![]() 使得:
使得:
根据定义2中抗一次碰撞性中性质1,在修改者未曾二次修改任何区块时(即对于变色龙哈希函数,每个标签所对应的碰撞不超过一次),任何人没有能力可将做过修改过一次的区块进行第二次修改,当然也就更没有能力去修改未曾修改过的区块.
然后,分析非法(对某区块至少修改过二次)修改区块信息的操作过程.对于某个标识符为τ的区块B,假设修正者先后将内容x修正为![]() 同时计算
同时计算![]() 使得:
使得:
则得到针对一次变色龙哈希函数的三重碰撞.而根据定义2中的性质2,基于一个三重碰撞,任何二重碰撞可以扩展成为三重碰撞.对应到可修正区块链环境下,出现二次修改区块后,任何人都有能力将修改过一次的区块中内容变为任何内容.简言之,修改权限的违规(指某个区块的修改过2次),则“可修改”功能崩溃,当然也就意味着整个区块链的崩溃.
4.3 同类比较及分析
据第1节所述,文献[2]中的可修正区块链方案(称作方案B)最为典型.本节选择该方案与本文所提可修正区块链方案(称作方案A)进行比较.
从功能角度比较,普通区块链是0次可修正区块链,体现了区块链不可更改性;方案B是∞-次可修正型区块链,即修改特权者可对任何区块进行任意多次修改;而方案A是一次可修正型区块链,即修改特权者可修改每个区块的次数至多一次.1)由于区块链是由诚实者占多数的矿工群体维护、存在较多待修正内容的区块链会被广泛抵制等客观原因,实际运行的区块链中需要修正内容的区块占比非常少,即需要动用修正特权的场合并不多,而需要对一个区块反复修正的场景更是极少;2)不可更改性是区块链的关键特性,可修正性从某种程度上伤害了这一特性.因此,在引入可修正性时,最大程度地限制修正特权是设计可修正区块链的重要准则.事实上,文献[2]非常重视可修正权的限制,主要是通过在多个用户间分享修正权来避免特权滥用.相比之下,方案A则从修改次数的维度上,对修改特权进行了最大程度限制,从而更好地提升可修正区块链的用户信任度.另外,方案A也可以引入方案B的特权分享机制,从而可在2个维度上限制修正特权.
从构造模块的密码学性质看,方案B要求底层的变色龙哈希函数具有所谓的增强的抗碰撞性,可简单表述为敌手在获得同一哈希值的n个原像后,也不能得到算出第n+1个原像;而方案A要求底层的变色龙哈希函数具有相对弱一些的抗碰撞性,可简单表述为敌手获得同一哈希值的2个原像后,也不能得到算出第3个原像.
从算法复杂度来看,为了实现增强的抗碰撞性,文献[2]提出的构造方案需要借助公钥加密、零知识证明等复杂的密码原型;而本文所构造的一次变色龙哈希函数方案,则是对基于RSA的经典变色龙哈希方案的简单推广[6],就哈希计算而言只是将原本的2个模幂的模乘变成了3个模幂的模乘.
因此,相比于文献[2]的可修正区块链方案,本文所提可修正区块链方案在功能上可实现更严格、更合理、更全面地修正特权的管控机制,同时在实现途径上可提供更简单高效的构造方法.
5 结束语
区块链以其不可更改、去中心化、可追溯等特点迅速发展为学术界、工业界乃至全社会的热点技术,应用场景快速扩展和渗透,成为支撑社会数字化转型和数字化经济发展的基础.然而,区块链的不可更性也面临越来越多的现实挑战,区块链上不可避免地会存在各类有害信息,给区块链的健康发展带来巨大障碍.在司法、经济、金融、社会治理等关键领域引入区块链的前提是监管已经成为业界共识,但作为监管机制基础的可修正区块链研究才刚刚起步.本文从可修正区块链实际需求分析的入手,发现现有可修正区块链对于可修正次数没有任何限制.这既给底层变色龙哈希函数的高效构造设置了更高的技术难度,也因过高的修改权限降低了普通用户对可修正区块链的接受度,而无限多的修改次数对于区块链的修正者并不必要.为此,本文以区块链的一次修正机制为目标,将上层区块链修正需求转化为底层的变色龙哈希函数的安全性质需求,继而抽象出与之契合的一次变色龙哈希函数的新型密码学原语,并基于经典的RSA问题给出了高效的实现方案,借此进一步实现了高效的可修正区块链方案.
[1]Zeng Shiqin, Hu Ru, Huang Tao, et al. Survey of blockchain: Principle, progress and application[J]. Journal of Communications, 2020, 41(1): 134-151 (in Chinese)(曾诗钦, 霍如, 黄韬, 等. 区块链技术研究综述: 原理, 进展与应用[J]. 通信学报, 2020, 41(1): 134-151)
[2]Ateniese G, Magri B, Venturi D, et al. Redactable blockchain-or-rewriting history in bitcoin and friend[C] //Proc of the 2017 IEEE European Symp on Security and Privacy(EuroS&P). Piscataway, NJ: IEEE, 2017: 111-126
[3]Yuan Yong, Wang Feiyue. Editable Blockchain: Models, Techniques and Methods[J]. ACTA Automatica Sinica, 2020, 46(5):831-846 (in Chinese)(袁勇, 王飞跃. 可编辑区块链:模型,技术与方法[J]. 自动化学报, 2020, 46(5): 831-846)
[4]Li Peili, Xu Haixia, Ma Tianjun, et al. Research on fault-correcting blockchain technology[J]. Journal of Cryptologic Research, 2018, 5(5): 501-509 (in Chinese)(李佩丽, 徐海霞, 马添军, 等. 可更改区块链技术研究[J]. 密码学报, 2018, 5(5): 501-509)
[5]Hong Xuehai, Wang Yang, Liao Fangyu. Review on the technology research of blockchain security supervision[J]. Bulletin of National Natural Science Foundation of China, 2020, 34(1): 22-28 (in Chinese)(洪学海, 汪洋, 廖方宇. 区块链安全监管技术研究综述[J]. 中国科学基金, 2020, 34(1): 22-28)
[6]Bellare M, Ristov T. A characterization of chameleon Hash functions and new, efficient designs[J]. Journal of Cryptology, 2014, 27(4): 799-823
[7]Krawczyk H, Rabin T. Chameleon signatures[C] //Proc of the Network and Distributed System Security Symp(NDSS 2000). Reston, VA, USA: The Internet Society, 2000: 143-154
[8]Derler D, Samelin K, Slamanig D, et al. Fine-grained and controlled rewriting in blockchains:chameleon-hashing gone attribute-based[C] //Proc of the Network and Distributed System Security Symp(NDSS 2019). Reston, VA: The Internet Society, 2019: 1-15
[9]Tian Yangguang, Li Nan, Li Yingjiu, et al. Policy-based chameleon Hash for blockchain rewriting with black-box accountability[C] //Proc of Annual Computer Security Applications Conf (ACSAC’20). New York: ACM, 2020: 813-828
[10]Khalili M, Dakhilalian M, Susilo W. Efficient chameleon Hash functions in the enhanced collision resistant model[J]. Information Sciences, 2020, 510: 155-164
[11]Wu Chunhui, Ke Lishan, Du Yusong. Quantum resistant key-exposure free chameleon Hash and applications in redactable blockchain[J]. Information Sciences, 2021, 548(1): 438-449




