为了满足应用对于不同资源以及性能的需求,现在大家越来越趋向于将它们部署在数据中心上[1].但是,数据中心中的资源竞争也随着任务数目的增加变得更加激烈,并且会导致任务完成时间(job completion time,JCT)的增加以及整个数据中心效率的降低.在应用竞争的资源中,网络资源往往是最为关键的一种.有调研报告称,在数据中心中,网络传输时间占到了任务完成时间的50%[2].这种情况就对数据中心的网络资源调度提出了要求,需要尽量通过调度来提升网络的效率,从而加速分布式任务.
基于此,过去数十年来研究者们提出了很多网络调度的技术.传统的网络调度算法大多聚焦在减少流完成时间[3-4]或者提升流之间的公平性[5-6]等方面;由于它们往往不考虑任务的具体网络需求,所以无法捕捉到每个应用网络需求的详细特征.因此,它们在减少JCT以及提升网络效率上的表现无法令人满意.
意识到这个缺陷之后,研究者们开始针对具体的应用来设计网络调度的算法.其中,coflow[7]的提出是向着任务感知的网络调度迈出的关键一步.研究者发现,许多分布式任务是由一定数目的处理阶段按照某种顺序组织而成的,而这一类任务重要的一个性质就是2个连续阶段中的后一个,无法在前一个向它传输的所有网络流完成之前开始.基于这个特征,coflow被定义为2个计算阶段之间所有网络流的总和.相比于优化传统的流传输指标,优化coflow的完成时间更接近于我们加速任务执行的目的.
然而,伴随着现在的分布式任务越来越复杂,简单的coflow抽象已经无法完全表达任务的网络需求.比如,分布式计算框架TensorFlow[8],PyTorch[9],MxNet[10]都采用了一种基于有向无环图(directed acyclic graph, DAG)的运行方式.在这一类任务的执行过程中,只要某一个计算任务需要的网络传输完成,那么这个计算任务就可以立即开始计算.因此,从整个任务执行的角度来说,并不是所有的网络传输都是完全等同的.所以,如果我们能更加精细地利用任务的这种需求来指导网络调度,应当能够取得更好的加速效果.
与此同时,我们也应当注意数据中心中任务的多样性.并不是所有的任务都是基于计算图或者可以将计算图提供给网络管理者的.比如说那些运行在Spark[11]框架上的任务、视频、音频以及文件传输任务等.这些任务的性能同样也受到网络资源的制约,因此如果我们仅仅关注那些提供了DAG的任务,其他任务的性能就会受到很大的负面影响.
综合以上2点考虑,我们开始思考这个问题:鉴于不同任务对于网络需求的差异性,我们能否设计一种任务感知的网络调度器,可以通过减少任务的完成时间从而提升整个数据中心的工作效率.
为了探索这个问题,我们提出了一种基于DAG的网络调度器JIT(just in time).JIT利用部分任务提供的DAG来针对性地需求分析与网络调度,从而加速这些任务的执行;与此同时,对于其他的任务,JIT也会尽量满足它们的网络需求,从而达到提升数据中心整体性能的目的.本文的主要贡献总结为3点:
1)通过对任务执行过程的细致分析,我们发现一些网络传输可以在被推迟的同时不影响任务的整体完成时间.因此,我们提出最晚到达时间(latest arrival time, LAT)来描述这种特征.更进一步地,我们提出了一种协同考虑DAG与网络资源状况的启发式算法来计算网络传输的LAT.
2)首先构建了一个整数线性规划模型(integer linear programming, ILP)来描述基于LAT的网络调度问题.然后,我们通过数学分析发现这个模型可以通过变换成为一个同解的线性规划模型(linear programming, LP).通过这个转化,就可以采用数学求解器对调度问题进行快速求解.
3)通过基于真实任务的模拟验证了JIT的确能够提升数据中心的整体效率.实验结果显示,JIT可以将提供计算图的应用加速1.55倍,同时减少对于其他任务的影响,从而提升数据中心的整体效率.
1 研究动机与JIT结构设计
1.1 研究动机
越来越多的分布式计算框架选择采用DAG来驱动任务的执行.在这些框架里,一个任务会被分解为许多子任务,包括计算与网络传输子任务.每个子任务就是任务DAG中的一个节点,而子任务之间的依赖关系就用节点之间的边来表示.如果从节点j到节点i的边存在,那么节点j就是节点i的一个前驱节点.一个子任务节点在它所有的前驱节点完成之前,是无法开始执行的.由于本文的关注点在网络调度,所以从我们的角度来看网络传输子任务是没有前驱节点的.以图1中的简单任务为例,在这个任务中,T1,T2是2个网络传输子任务,C1,C2是2个计算子任务.T1完成之后,C1就可以开始;类似地,C2需要等待C1和T2这2个任务的完成.
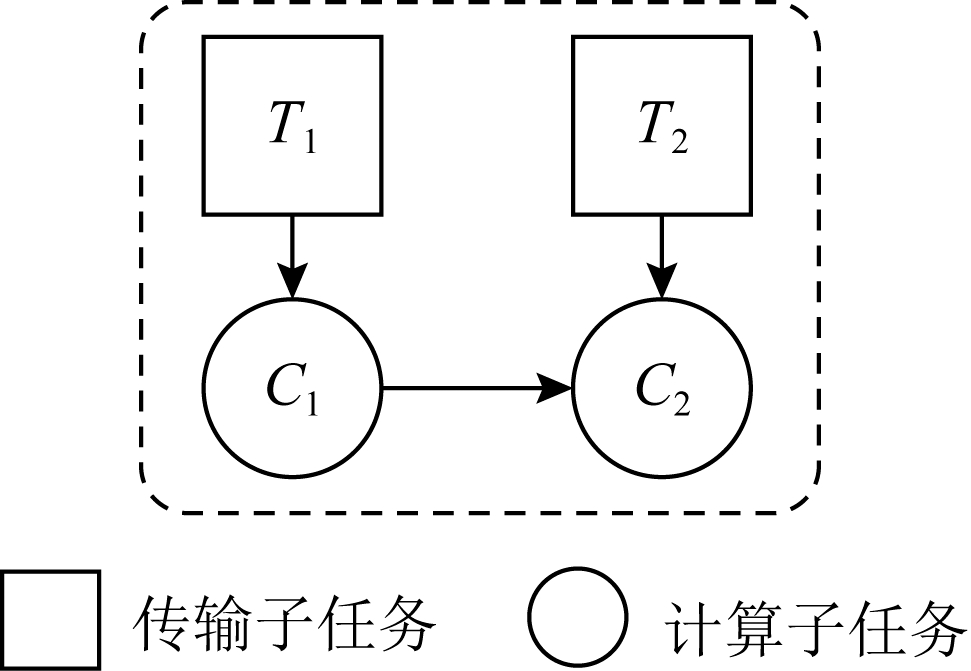
Fig.1 DAG of an example job
图1 示例任务的DAG
为了更加细致地研究这一类基于DAG的任务,我们利用TensorFlow 1.13运行了一系列典型的任务,观察它们网络传输的情况.图2中以Inception任务(包含190个网络传输)为例,展示出了我们的分析结果.在图2中,2条曲线分别表示网络数据传输完成与网络数据被后续计算使用的时间.我们发现这2个时间之间存在一个很大的差值,这意味着即使网络传输完成了,但是后续的计算仍然需要等待一段时间才能开始.我们在基于TensorFlow运行的其他任务以及其他基于DAG的框架中也观察到了类似的结果.
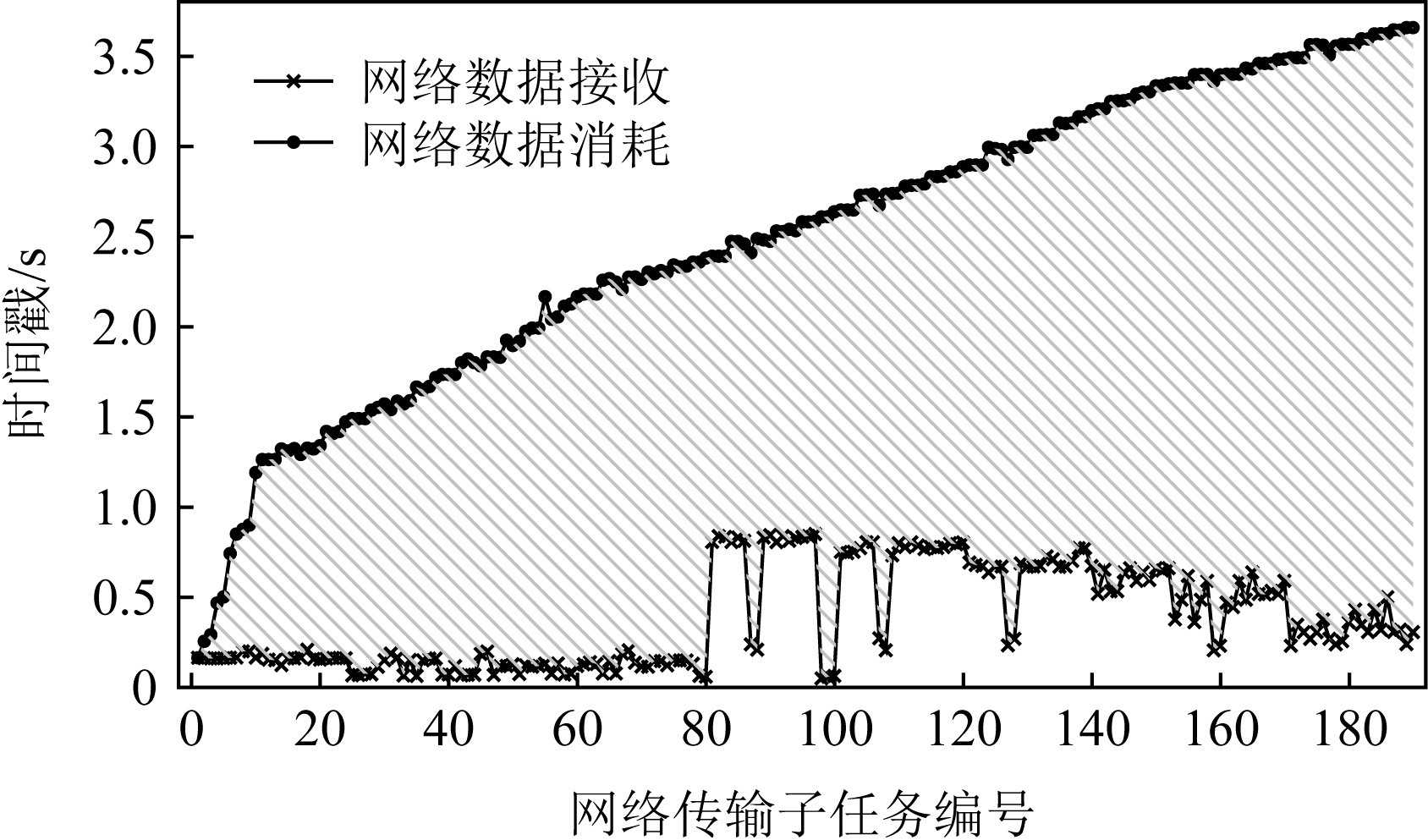
Fig.2 Data waiting in TensorFlow
图2 TensorFlow中的等待现象
造成这一现象的原因是计算任务不仅仅需要等待它所需的网络传输数据,也需要等待它所依赖的计算节点执行完成.我们以图1为例:假设T1,T2均在时刻0完成了传输,那么C1可以立即开始执行;然而,C2由于需要等待C1完成,不能立刻开始执行.因此,T2仍需要等待C1的完成,才能被C2使用,这也就产生了图2中的时间差值.基于此,我们发现一个计算任务所依赖的传输任务的完成时间,只要不晚于它所依赖的前驱计算任务的完成时间,那么就不会对这个计算任务的开始时间造成延迟.
1.2 最晚到达时间
为了描述我们在1.1节中发现的这种数据等待现象,我们提出了LAT的定义.LAT表示一个网络传输在不会对它后续计算造成延迟的情况下的最晚到达时间.换句话说,如果一个网络传输在它的LAT之前到达,那么它的后续计算任务需要等待它的前驱计算任务完成;反之,就需要等待这个网络传输的到达.
根据LAT的定义,只要满足网络传输的LAT就足够保证任务的完成时间不被推迟.基于LAT,我们可以将一部分网络传输延迟,使得它们恰好在LAT之前到达.此时,就能够减少这些传输的网络资源占用,从而可以把释放出来的网络资源分配给其他的任务,达到提升数据中心整体效率的目的.
同以往研究者们提出的流最终期限相比[12-14],本文提出的LAT有2个独特的特征:1)流的最终期限通常是由用户指定的,用来表示它们所必需满足的完成时间.然而,LAT是与任务的具体特征以及集群资源状况密切相关的.因此,我们需要在任务执行的同时完成对LAT的估计.2)最终期限通常用来表示一个流必需在某个时刻之前完成.未能满足最终期限要求的流,就会被丢弃.但是,对于LAT来说,为了满足任务的网络要求,即使一个网络传输未能满足LAT要求,也需要继续完成.
1.3 JIT设计
实现一个基于LAT的网络调度器是充满挑战的,我们主要需要解决3个问题:
1)LAT的不准确估计会导致调度问题不可解或者JCT增加,因此,我们需要设计算法尽量准确地估计网络传输的JCT;
2)如引言所述,考虑到JIT调度器有2个调度的目标,我们需要为JIT的调度问题建立一个统一的模型;
3)考虑到JIT的实用性需求,我们需要在很短的时间内给出调度方案,同时保证方案的调度效果.
我们将在第2,3节中详细介绍JIT是如何处理这些挑战的.在图3中,我们首先展示了JIT调度器的整体结构.

Fig.3 Architecture of JIT network scheduler
图3 JIT网络调度器的结构
我们采用了中心式的架构来实现JIT.在求解调度策略之前,JIT从集群管理器与任务处获取相关信息.在最开始,JIT需要获取集群的基本信息,包含带宽信息与网络拓扑结构等.对于一个具体的任务,它需要将自己的DAG信息提供给JIT,包含网络传输与计算任务的大小.相比于之前的工作[15],JIT并不要求获得额外更多的信息.JIT首先收集这些信息,然后基于DAG使用一个启发式算法来计算LAT.具体的网络调度策略则通过一个LP模型求解.JIT同时也针对实际应用场景对于求解速度的要求还进行了一些合理的简化.最后,JIT将调度方案发送给各个机器.对于那些没有提供DAG信息的任务,它们将占用剩余的网络资源进行传输.这样可以避免这些任务由于带宽饥饿而无法正常完成.数据中心管理员可以选择这一过程中具体使用的调度算法,来适应不同的场景需求.
2 LAT的估计
我们提出了一个启发式算法来计算LAT,如算法1所示.这个算法的主要特点是同时考虑了DAG与网络状态,从而更准确地估计LAT.
算法1.LAT估计算法.
输入:完成集合DoneSet=∅,就绪集合ReadySet=∅,待求集合TodoSet={所有网络传输子任务};
输出:网络传输i的预计LAT li.
① while(TodoSet≠∅或ReadySet≠∅)do
② for网络传输i in TodoSet do
③ if for all j∈pred(i)and j∈DoneSet then
④ ReadySet←i;
/*将i放入ReadySet中*/
⑤ end if
⑥ end for
⑦ for网络传输i in ReadySet do
⑧ li=0
⑨ for网络传输j in pred(i)do
⑩![]()
 if temp>li
if temp>li
 li=temp;
li=temp;
 end if
end if
 end for
end for
 end for
end for
 end while
end while
我们在图4中展示了一个示例任务的LAT计算过程.为了简洁,我们这里只展示了一个任务的计算过程(多个任务的处理情况是完全一样的).5个计算任务(圆形)的计算负载分别是L1=1,L2=2,L3=1,L4=2,L5=1. 4个网络传输任务(方形)的大小为S1=1,S2=2,S3=2,S4=1.假设任务部署在机器3上,T1与T2是由机器1发送至机器3的,T3与T4是从机器2发送到机器3的.这里所有机器的入口与出口带宽均设为单位1.

Fig.4 An example of LAT calculation
图4 LAT计算示例
结合算法1来讲,我们使用了3个集合来存储网络传输.DoneSet(存储已经计算完毕LAT的传输)、ReadySet(存储接下来准备进行计算的传输)以及TodoSet(存储还没有纳入考虑范围的传输).如果从一个网络传输j所连接的计算任务到另一个网络传输i所连接的计算任务之间有至少1条路径,我们就称j是i的一个前驱传输.传输i的所有前驱传输的集合我们记作pred(i).例如,在图4中,pred(T1)=∅,而pred(T4)={T1,T2,T3}.在最初,所有的传输都会被放入TodoSet,而其他2个集合此时均为空集.整个算法只有在所有传输计算完毕,也就是所有传输移动到DoneSet时才会终止.
算法1的第1步是将所有就绪的传输挑选出来.如果一个传输所有的前驱传输都已经完成了LAT的计算,那么它就进入了就绪状态,也会从TodoSet移动到ReadySet.实质上,这个计算的顺序就是网络传输的一个拓扑排序.第2步,我们计算ReadySet中每一个传输的LAT,计算过程如算法1的行⑦~ 所示.传输i的任何一个前驱传输j,都会确定一个li的下界:lj,从j到i所需要的计算时间
所示.传输i的任何一个前驱传输j,都会确定一个li的下界:lj,从j到i所需要的计算时间![]() 以及预计i的传输时间trans(i)之和.
以及预计i的传输时间trans(i)之和.
![]() 是完成从与j相连的计算任务到与i相连的计算任务之间所有计算所需要的时间.例如,在图4中,
是完成从与j相连的计算任务到与i相连的计算任务之间所有计算所需要的时间.例如,在图4中,![]() =1+2=3.受到Varys[15]中计算流完成时间的启发,我们计算i的传输时间为
=1+2=3.受到Varys[15]中计算流完成时间的启发,我们计算i的传输时间为
(1)
其中,size(i)是网络传输i的大小,![]() 与
与![]() 分别表示传输i的发送机器a的出口带宽以及接收机器b的入口带宽,num(a)与num(b)分别表示从机器a发出与进入机器b的网络传输的数目.我们应当注意到LAT的计算过程并不需要与任务的复杂交互,所需要的DAG信息在任务开始执行时就已经提交给JIT了.
分别表示传输i的发送机器a的出口带宽以及接收机器b的入口带宽,num(a)与num(b)分别表示从机器a发出与进入机器b的网络传输的数目.我们应当注意到LAT的计算过程并不需要与任务的复杂交互,所需要的DAG信息在任务开始执行时就已经提交给JIT了.
3 调度问题建模与分析
本节首先将JIT的调度问题建模为一个ILP问题;然后,为了快速求解这个问题,我们介绍了如何将这个初始ILP模型转化为一个等价的LP模型.此外,我们还介绍了为了加速JIT的求解速度所采用的一些简化措施.
3.1 问题建模
与许多之前的网络调度工作[13,15]所采用的假设相同,我们将整个数据中心网络抽象为一个巨大的连接着所有机器的无阻塞交换机.所有机器的集合为M,任务集合为J.我们使用一种时间槽的方式考虑时间,即将时间划分为具有相同间隔的连续时间槽,其集合为T.在每个时间槽t内,每个机器可以分别从它的出端口以及入端口传输C个单位的网络数据.任务n中包含nf个传输子任务,其中从机器i发送到机器j的第k个网络传输记作![]() 它的数据大小记作
它的数据大小记作![]() 开始时间记作
开始时间记作![]() 以及最晚到达时间记作
以及最晚到达时间记作![]() 我们将任务n中从机器i到机器j的网络传输的总数记作U(i,j,n).调度决策使用
我们将任务n中从机器i到机器j的网络传输的总数记作U(i,j,n).调度决策使用![]() 来表示,代表在时间槽t内分配给传输
来表示,代表在时间槽t内分配给传输![]() 的带宽.因为JIT的调度粒度为最小的物理带宽分配单元,所以所有的决策变量
的带宽.因为JIT的调度粒度为最小的物理带宽分配单元,所以所有的决策变量![]() 均为整数,即:
均为整数,即:
![]()
![]() ,∀i,j∈M,k∈U(i,j,n),n∈J,t∈T.
,∀i,j∈M,k∈U(i,j,n),n∈J,t∈T.
(2)
特别地,![]() 代表网络传输
代表网络传输![]() 在时间槽t内没有分配任何网络带宽资源.
在时间槽t内没有分配任何网络带宽资源.
由于JIT的目标是提升整个数据中心的效率,所以我们不能忽视那些没有提供DAG的任务.考虑到这个问题,我们将JIT中的调度问题建模,记为P1:
(3)
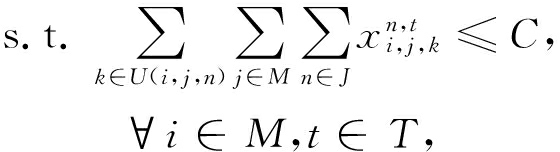
(4)
(5)
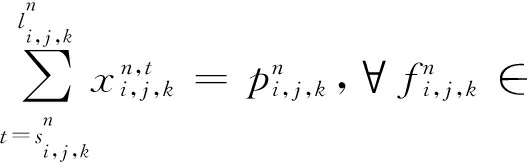 任务n,
任务n,
(6)
(7)
在P1中,式(3)旨在最小化所有链路在整个时间范围内的最大带宽占用.通过实现这个目标,JIT可以避免提供DAG的任务占用过多的网络带宽,从而将省下来的带宽分配给未调度的任务.这样,JIT不仅可以加速提供那些具有DAG的任务,还可以为那些没有DAG的任务争取更多的网络资源.
伴随着这个优化目标,JIT需要满足4个限制条件.式(4)与式(5)表示的是每个机器上入端口和出端口的总带宽使用不能超过链路最大带宽C.式(6)限制了网络传输必需在它的开始时间与LAT之间完成,同时通过满足LAT要求保证了任务的性能.最后一个条件式(7),限制了一个网络传输在开始时间之前与LAT之后的传输速率为0.
3.2 向非线性模型转换
模型P1很显然是一个ILP模型,而ILP作为NP问题通常是很难求解的[16].但是,有一类特殊的ILP可以转换为等价的LP问题.这一类ILP需要满足2个条件:1)目标函数是可分离的凸目标函数;2)限制条件系数构成的矩阵形成一个全幺模矩阵[17].接下来我们将证明P1模型恰好满足这2个条件.
3.2.1 可分离凸目标函数
如果一个函数可以记为用一个单变量表示的一组凸函数的和,那么它就是一个可分离的凸函数.为了将我们P1模型中的目标函数重建为可分离的凸函数,我们使用了Flutter[18]中定义的字典序以及字典序最小化问题2个概念,介绍如下:
定义1.对于一个包含K个元素的向量,用v表示这个向量的一个非增序排列,也就是说v1≥v2≥…≥vK.
定义2.对任意2个具有K个元素的向量p,q∈![]() K,如果p1<q1或者∃k∈{2,3,…,K}使得pk<qk并且pi=qi,∀i∈{1,2,…,k-1}成立,那么我们就称p是比q字典序小的,用p
K,如果p1<q1或者∃k∈{2,3,…,K}使得pk<qk并且pi=qi,∀i∈{1,2,…,k-1}成立,那么我们就称p是比q字典序小的,用p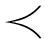 q来表示.类似地,如果pk=qk,∀k∈{1,2,…,K}或者p
q来表示.类似地,如果pk=qk,∀k∈{1,2,…,K}或者p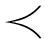 q,那么就称p是字典序不大于q的,用p≼q表示.
q,那么就称p是字典序不大于q的,用p≼q表示.
定义3.字典序最小化问题lexminxh(x)表示求解向量h∈![]() K的问题,其中h是由K个关于x的目标函数组成.更加具体一点,最优解h*在x*处取得,满足h*=h(x*)≼h(x),∀x∈
K的问题,其中h是由K个关于x的目标函数组成.更加具体一点,最优解h*在x*处取得,满足h*=h(x*)≼h(x),∀x∈![]() K.
K.
借由定义1~3,我们可以将模型P1转换成为等价的字典序最小化问题的模型P2:
(8)
同时满足式(4)~(7).其中,![]() 实际意义是在时间槽t内从机器i到机器j的总带宽占用.通过转换,我们发现δ是一个包含|T||M||J|个元素的向量.P1模型的优化目标是最小化各个链路上的最大带宽占用,也就是寻求δ中的最小值.因此,初始的P1模型可以通过等价的P2模型来求解.
实际意义是在时间槽t内从机器i到机器j的总带宽占用.通过转换,我们发现δ是一个包含|T||M||J|个元素的向量.P1模型的优化目标是最小化各个链路上的最大带宽占用,也就是寻求δ中的最小值.因此,初始的P1模型可以通过等价的P2模型来求解.
为了求解P2模型中的字典序最小化问题,我们构造了一个关于δ的函数,定义为
(9)
其中δu是δ中第u个元素.
关于构造的函数g(δ),我们有2个引理:
引理1.g(δ)是一个凸函数.
证明. 根据式(9),g(δ)是一系列|δ|δu的求和,而其中每一个|δ|δu显然是凸函数.所以,g(δ)也是一个凸函数.
证毕.
引理2.∀p,q∈![]() K,p≼q⟺g(p)≤g(q).
K,p≼q⟺g(p)≤g(q).
证明. 假设q-p中第1个正元素的索引为r,由于p,q中的元素均为整数,也就是说qr≥pr+1.
我们首先来证明p≼q⟹g(p)≤g(q).我们可以将左侧作差:
![]()
![]()
![]() -(|δ|-r+1)
-(|δ|-r+1)![]() ≥
≥
![]() ≥0.
≥0.
(10)
然后,对于g(p)≤g(q)⟹p≼q,我们通过它的逆否命题 (p≼q)⟹
(p≼q)⟹ (g(p)≤g(q))来证明,该逆否命题也等价于p≻q⟹g(p)>g(q).这个等价形式可以通过将式(10)中的p,q交换而获得简单的证明.
(g(p)≤g(q))来证明,该逆否命题也等价于p≻q⟹g(p)>g(q).这个等价形式可以通过将式(10)中的p,q交换而获得简单的证明.
证毕.
基于引理1和引理2,我们将原模型P2转换为等价的P3模型:
(11)
同时满足式(4)~(7).
3.2.2 全幺模矩阵
现在我们来检查模型是否满足第2个条件:模型限制条件所构成的系数矩阵是一个全幺模矩阵.如果一个线性模型的系数矩阵满足全幺模的条件,那么就会确定一个极点为整数点的多面体,也就是说如果这个LP模型有最优解,那么一定是整数解.
引理3.式(4)~(7)的系数构成一个全幺模矩阵.
证明.如果一个l×n的矩阵A满足:1)所有的元素都是从{-1,0,1}中选取;2)任何行索引的子集(例如I⊆{1,2,…,l})可以被分为2个不相交的集合I1与I2,使得![]() 对于任意的j∈{1,2,…,n}成立,那么这个矩阵A就是一个全幺模矩阵.
对于任意的j∈{1,2,…,n}成立,那么这个矩阵A就是一个全幺模矩阵.
首先,很容易确认我们模型的系数矩阵中所有元素不是0就是1,所以满足第1个条件.
现在来检查第2个条件.在我们的模型中,式(4)和式(5)都包含|M||T|个不等式.同时,式(6)和式(7)分别包含![]() 与
与![]() 个等式.因此,对于我们l×n的系数矩阵A,可得
个等式.因此,对于我们l×n的系数矩阵A,可得![]() 对于第2个条件,我们可以将任意子集I⊆{1,2,…,l}分为2个集合,其中所有索引在{1,2,…,2|M||T|}中的为I1,其他的为I2.我们可以发现,I1中所有行任意一列相加的和为2;对于I2,所有行任意一列相加的和为1.因此,我们有
对于第2个条件,我们可以将任意子集I⊆{1,2,…,l}分为2个集合,其中所有索引在{1,2,…,2|M||T|}中的为I1,其他的为I2.我们可以发现,I1中所有行任意一列相加的和为2;对于I2,所有行任意一列相加的和为1.因此,我们有![]() 并且
并且![]() 恰好满足第2个条件.
恰好满足第2个条件.
证毕.
3.3 等价LP的转换
我们通过使用λ表示(λ-representation)技术[17]来获得等价的LP模型.对于一个单变量w∈[0,C]∩![]() ,一个整数凸函数f:[0,C]∩
,一个整数凸函数f:[0,C]∩![]() →
→![]() 可以通过以下的方法进行线性化:
可以通过以下的方法进行线性化:
(12)
(13)
(14)
λs∈![]() 且λs>0,∀s∈P,
且λs>0,∀s∈P,
(15)
其中,P为w所有取值的集合,在我们的问题中,P=[0,C]∩![]() .显然这会引入|P|个正实数变量λs并且利用这些新的变量定义了一个关于w的新组合.
.显然这会引入|P|个正实数变量λs并且利用这些新的变量定义了一个关于w的新组合.
我们利用这种表示,并将其应用到式(9)的每一个凸函数![]() 中,最终获得了LP模型P4:
中,最终获得了LP模型P4:
![]()
![]()
∀i,j∈M,∀t∈T,
![]()
![]()
![]() 且
且![]()
(16)
同时满足式(4)~(7).
至此,原ILP模型P1转化为等价的LP模型P4.我们可以使用LP求解器(比如Gurobi[19])来求解P4.为了表述的简洁,我们默认JIT就是指一个采用类似求解器的调度器.
3.4 其他简化措施
由于网络传输的时间无法提前预知,因此JIT需要进行动态的求解;除此之外,一个分布式任务往往包含数百个网络传输,求解一个这样的LP模型往往需要数十秒的时间.这个时间量级对于实际场景中的网络调度是难以接受的.基于此,我们做了2方面的针对性简化使得JIT更加实用.
1)在LP模型中,一个任务的所有传输只有一部分会被纳入计算.我们的建模揭示了具有较小LAT的网络传输应该有更高的优先级,因此,我们可以将那些具有较大LAT的网络传输看做背景流量,使用剩余带宽进行传输.从DAG的角度来看,那些具有较小LAT的网络传输正是在拓扑排序中比较靠前的部分.因此,我们引入了一个参数α,表示被纳入LP模型中的网络传输的比例(默认α=0.4,即选取拓扑排序中前40%的网络传输).在4.2节中,对于α的影响也进行了讨论.
2)调度器只有在某一个新的分布式任务提交第1个网络传输时进行1次求解.基于对TensorFlow的运行测试,我们发现同一个任务的网络传输几乎都是同时开始的,这也支撑了我们的简化.对于实际场景中其他没有这种特征的任务,我们也可以采用其他的措施来降低调度开销(比如每隔固定时间调度1次等).
结合这2种简化机制,我们使JIT更加适合实际场景.
4 实验分析
4.1 实验设置
1)任务集.由于没有公开权威的数据中心任务记录,我们沿袭相关工作中采用已久的假设[20-21],基于泊松分布来构建我们的任务队列.我们选取了5种经典的深度学习任务来作为基于DAG的任务,它们分别是LeNet,AlexNet,VGG16,Inception,ResNet152.在我们的测试中,每一次的训练迭代被视为一个任务.这些任务的相关信息总结在表1中.每一种任务的比例都是统一的25%.此外,为了验证JIT提升数据中心性能的有效性,我们还在任务队列中加入了一些文件传输的任务.这些任务的网络传输大小是从{5 Gb,10 Gb,20 Gb,30 Gb,40 Gb}中选取的.所有网络任务的发送和传输机器都是随机指定的.
Table 1 Specifications of Evaluated Jobs
表1 评测任务相关参数
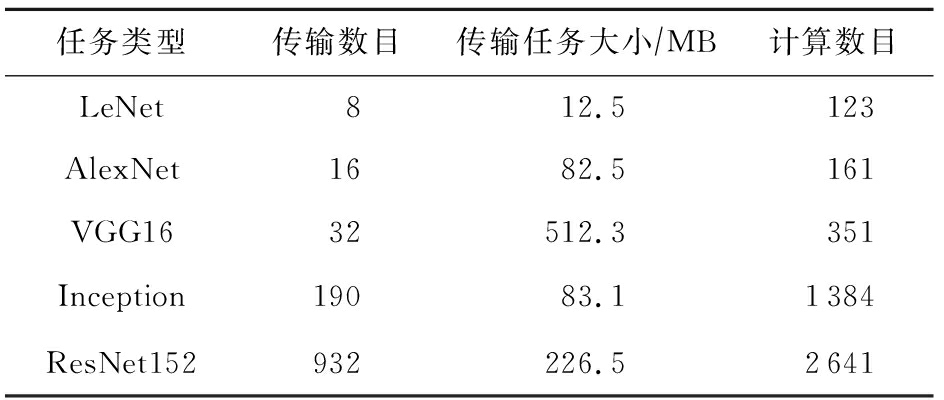
任务类型传输数目传输任务大小∕MB计算数目LeNet812.5123AlexNet1682.5161VGG1632512.3351Inception19083.11384ResNet152932226.52641
2)评判基准.作为比较,在实验中我们选取了3种调度器与JIT进行比较.
① TensorFlow(v1.13).TensorFlow是一个具有代表性的基于DAG的计算框架.在它的实现中,如果一个网络传输被接收机器请求,同时在发送机器上准备就绪,就会开始传输.在有多个网络传输的情况下,它们的发送是按照随机的顺序完成的[22].
② Sincronia[23].这是一种基于coflow概念的网络调度器.它证明了只要按照某种“正确”的顺序发送coflow,不用管理coflow内部的网络传输细节,就可以保证达到不超过理想时间4倍的平均coflow完成时间.它采用一种贪心策略来预测未完成coflow的传输顺序.我们在模拟器中,按照相关的文献说明,实现了这个调度策略.
③ TicTac[22].在这个网络调度算法中,所有的网络传输按照一个算法给定的顺序依次进行传输.这个算法是依据任务的DAG图来确定顺序的.与JIT不同,TicTac没有考虑多个任务的场景,它关注找到单个任务条件下的最优解.因此,在实际场景下,它的性能会受到影响.因此,我们采用了先入先出(first in first out, FIFO)+TicTac来处理多任务的情况.
3)实验设置.我们模拟了一个包含100个机器额数据中心网络,参照数据中心的普遍配置,机器的入端口和出端口带宽都设为1 Gbps.我们采用了与TicTac[22]中类似的办法,通过在TensorFlow v1.13中运行任务获取相关的信息.此外,使用Gurobi v7.5.2作为我们的数学求解器.我们使用Python 3.6实现了一个基于流的模拟器来检验不同的调度策略对于任务性能的影响.
4)指标.本文旨在加速这些DAG任务的同时,降低它们的带宽使用.因此,我们使用的评测指标主要是2个,加速比(speedup, S)以及剩余带宽的比例(ratio of remaining bandwidth, H).
调度策略1相比于调度策略2的加速比为
(17)
剩余带宽的比例为
(18)
其中![]() 表示机器i出端口分配给DAG任务后的剩余带宽.由于对于集群来说出端口与入端口总的带宽使用量相等,因此在这里我们只考虑出端口.
表示机器i出端口分配给DAG任务后的剩余带宽.由于对于集群来说出端口与入端口总的带宽使用量相等,因此在这里我们只考虑出端口.
4.2 实验结果
在图5中我们展示出了DAG任务在不同调度器下的加速比情况.可以发现,所有5种任务都在JIT的调度下取得了显著的加速效果.总的来说,与初始的TensorFlow相比,这些任务的平均加速比为1.55;而对应到每一类任务,所取得的加速比则分别为1.34,1.53,1.70,1.81,1.39.这些任务获取的加速效果不同的原因是传输的平均等待时间不同.如图6所示,初始等待时间较长的任务,例如VGG16,就会获得相对更好的加速效果.
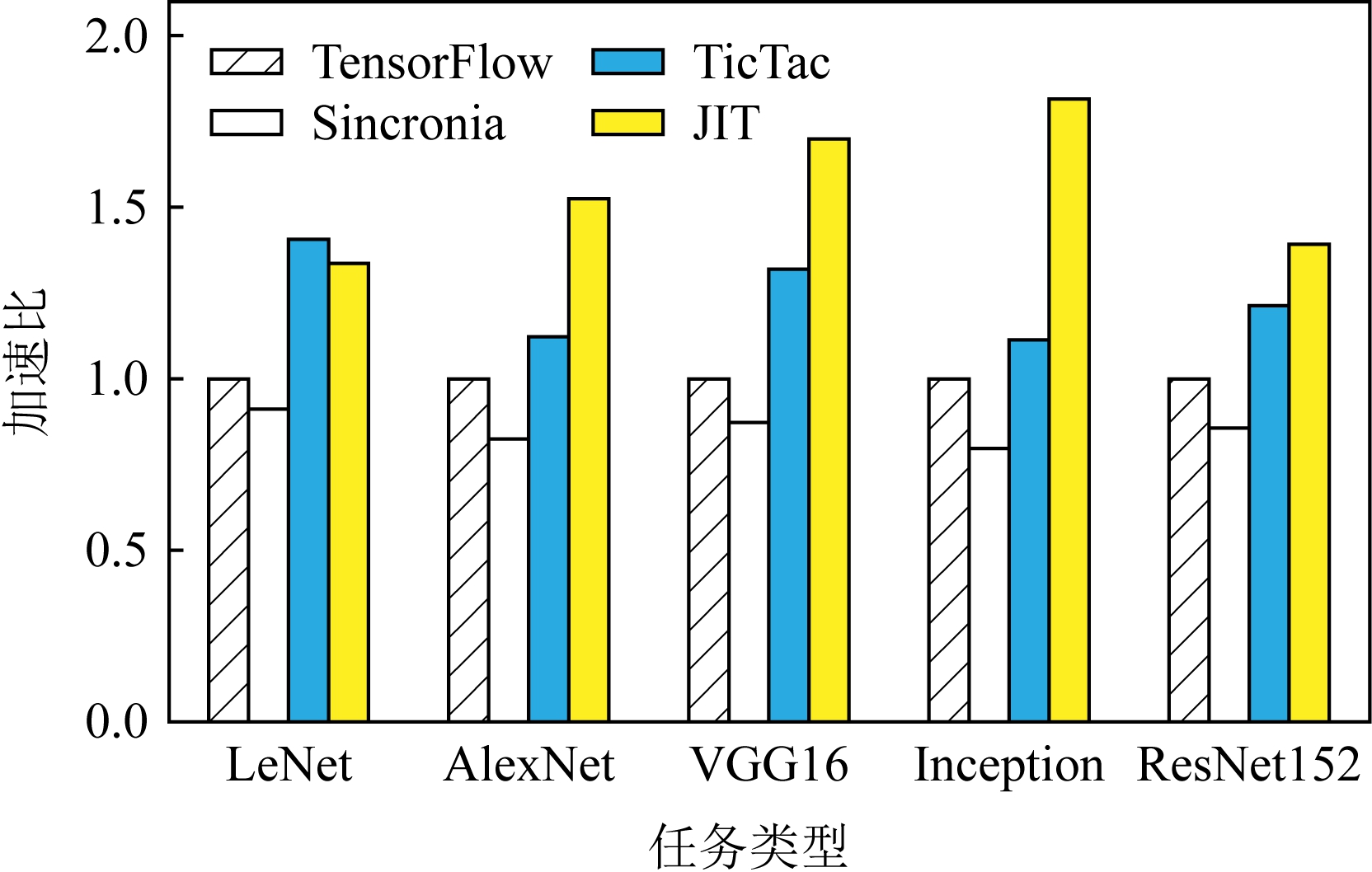
Fig.5 Comparison of speedup
图5 加速比比较

Fig.6 Comparison of data waiting time
图6 不同调度策略网络传输等待时间比较
至于使用coflow抽象进行调度的Sincronia,所取得的性能甚至要比初始的TensorFlow更差.这是因为coflow的抽象旨在使得coflow内部的传输都尽量同时完成,但是显然基于DAG的任务中,网络传输有明显的优先级.与之对比的就是TicTac调度算法,它专注于使每一类任务都使用理想优先级进行传输.所以,在某些任务上,它甚至取得了比JIT更好的效果(比如LeNet,两种调度器的加速比分别为1.40与1.34);但是,5种任务的平均加速比却只有JIT的81.4%(1.23相比于1.55).鉴于数据中心中往往有许多的任务并行执行,因此在实际应用场景中JIT就会更加实用.
图6中比较了不同调度策略下的网络传输等待时间.可以发现JIT可以显著缩短网络传输的等待时间.例如Inception中网络传输在使用默认TensorFlow调度时,平均等待时间高达2.1 s;但是通过JIT的调度,这个时间减少了94.3%,只需要0.12 s.这个等待时间的大幅减少正好符合了我们让网络传输在正好的时间到达的初始目标.作为对比,Sincronia却会使得这个等待时间增加,因为它会让同一个任务的传输尽可能同时到达;这样索引值比较大的传输甚至会等待整个任务的执行时间才会被使用.至于TicTac,在缩短等待时间上的效果远不如JIT.作为一个考虑多任务的调度器,JIT可以更好地处理不同任务之间的网络竞争.
为了能够更加细致地分析JIT的性能,我们也在图7中绘制了在Inception任务中每个网络传输的具体情况.我们可以将其与图2对比,网络传输接收与使用时间之间的差异显著缩小;这就意味着通过JIT的调度,网络传输在完成后不需要等很久就会被使用,也会减少网络资源的浪费情况.除此之外,这个结果也验证了我们LAT计算算法的准确性以及JIT调度的有效性.
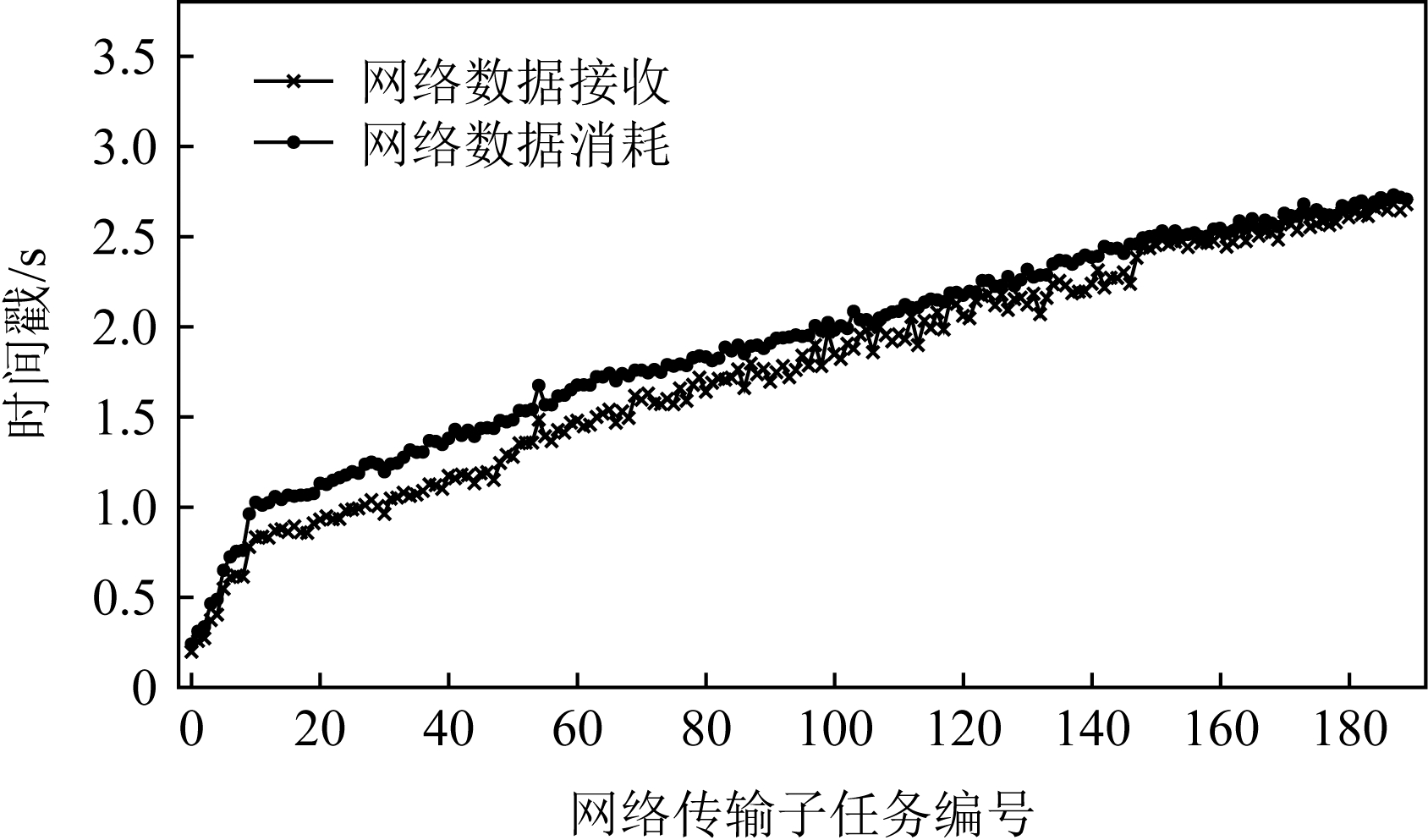
Fig.7 Data waiting time in Inception after optimization
图7 优化后Inception中等待时间
为了评估另一个指标剩余带宽,我们在图8中绘制了每个调度器在将DAG任务的资源分配结束后剩余网络带宽的CDF图.从图8中,我们观察到2方面内容:1)4种调度器剩余带宽的最小值分别为0.173,0.175,0.173,0.334.显然JIT的调度策略使用了更少的网络资源,也减少了对于数据中心网络的压力;2)相比于其他3种调度器,JIT的剩余带宽更加均衡,大致都在0.334~0.793.而初始TensorFlow调度下的剩余带宽就不均衡得多,从0.173到几乎为1的情况都有.考虑占比50%的情况,JIT与TensorFlow的剩余带宽分别为0.665与0.556.这也意味着JIT调度之后的剩余带宽更有利于其他的任务使用.
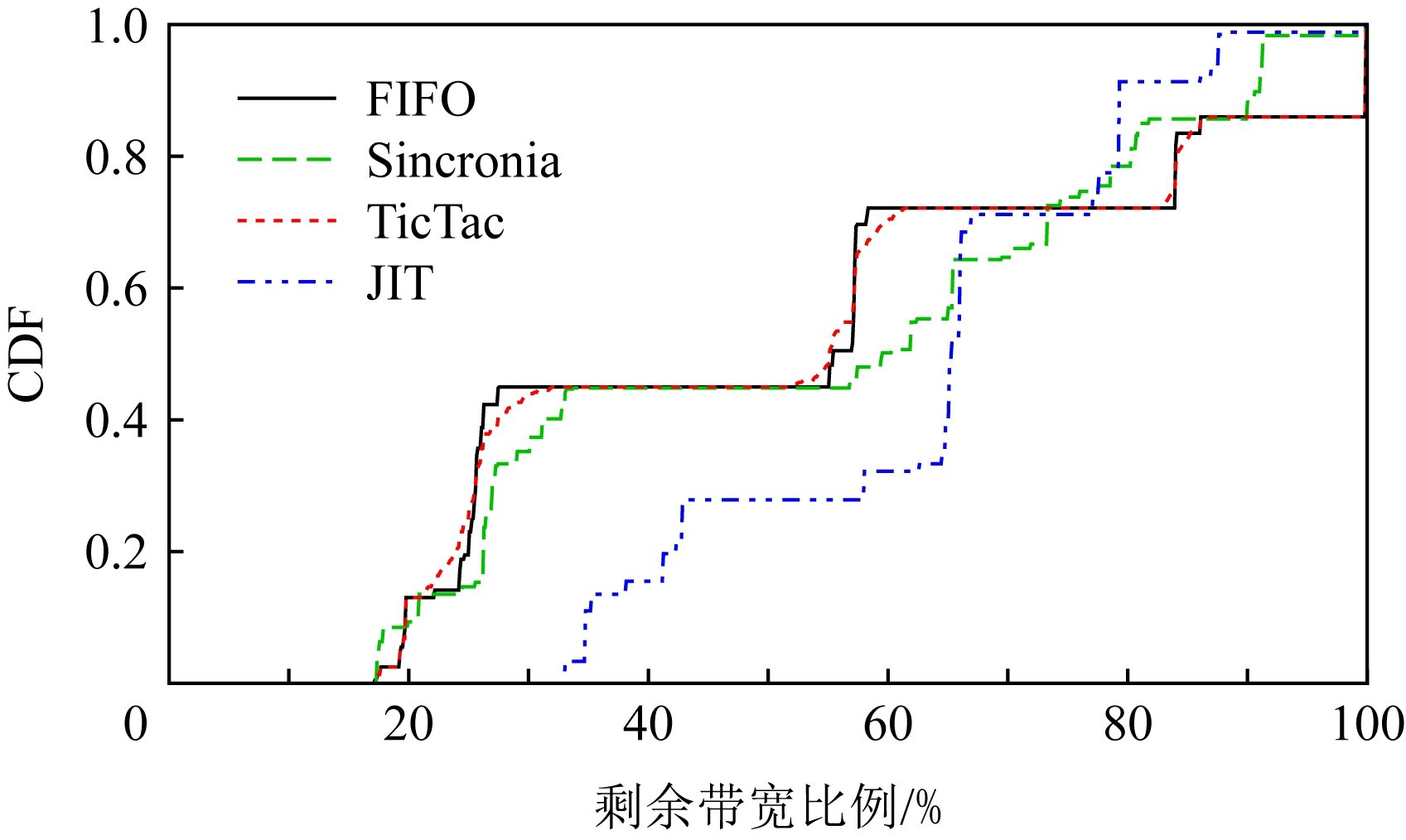
Fig.8 CDF of remaining bandwidth with different schedulers
图8 不同调度器下剩余带宽的CDF
为了更加直接地检验JIT在缓解网络压力上的效果,我们在图9中展示了作为背景文件传输任务的完成时间.相比于在一个空的数据中心中的运行时间,这些任务在JIT下完成时间分别增加了1.20,1.30,1.45,1.75,2.10倍.而这些任务在4种调度器下的平均完成时间增加为2.23,2.05,2.23,1.56倍.Sincronia同样可以减少任务时间的增加幅度,但是效果没有JIT明显.我们同样也注意到JIT在缓解时长增加上的效果伴随着文件大小的增加而减少.这是因为相比于较大的文件传输任务,小的任务可以更加有效地利用JIT的剩余带宽.图9的结果确认了JIT在缓解网络压力、提升数据中心整体效率的效果.
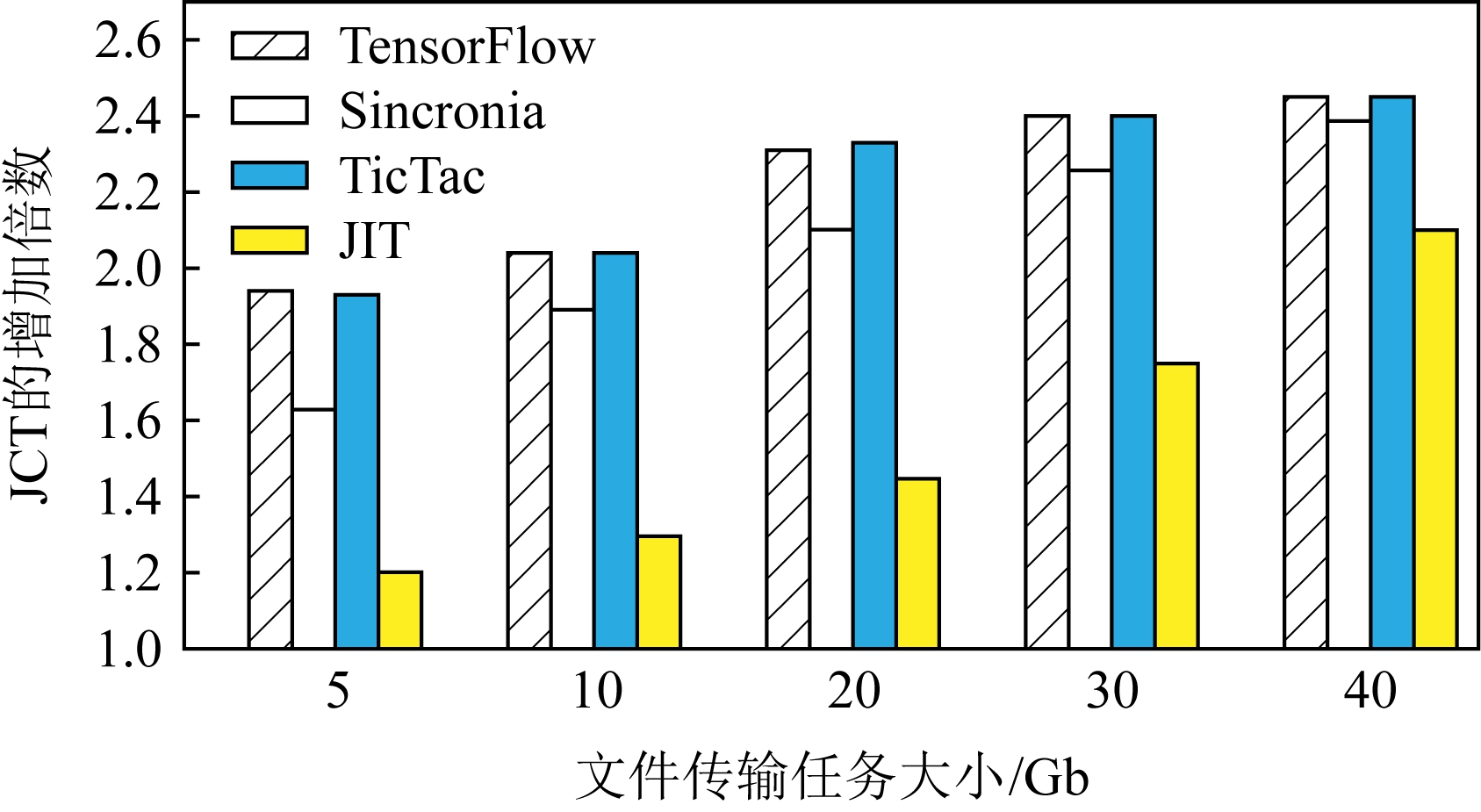
Fig.9 JCT of background jobs
图9 背景文件传输任务的JCT
如3.4节中所述,我们通过只选取一定比例(默认α=0.4)的网络传输来优化JIT的计算速度.因此,我们在这里重点分析α的取值对于JIT调度性能的影响.α的取值分别为0.1,0.2,0.3,0.4,0.5,0.6,对应的测试结果展示在图10中.当α从0.1增加到0.6,我们可以清楚地观察到加速效果获得了提升(加速比从1.09增加到1.62);同时,剩余带宽从48.2%减少到32.4%.这是因为一个较大的α值会将更多的网络传输纳入LP模型之中,相应的JIT就可以更加准确精细地控制网络传输,但是会消耗更多的网络资源.通过测试,我们选择了0.4作为默认的α值.这是因为当α>0.4时,加速效果的提升并没有之前那么明显,但是求解复杂性会继续上升.因此,我们为了性能以及效率的平衡选取了这个取值.
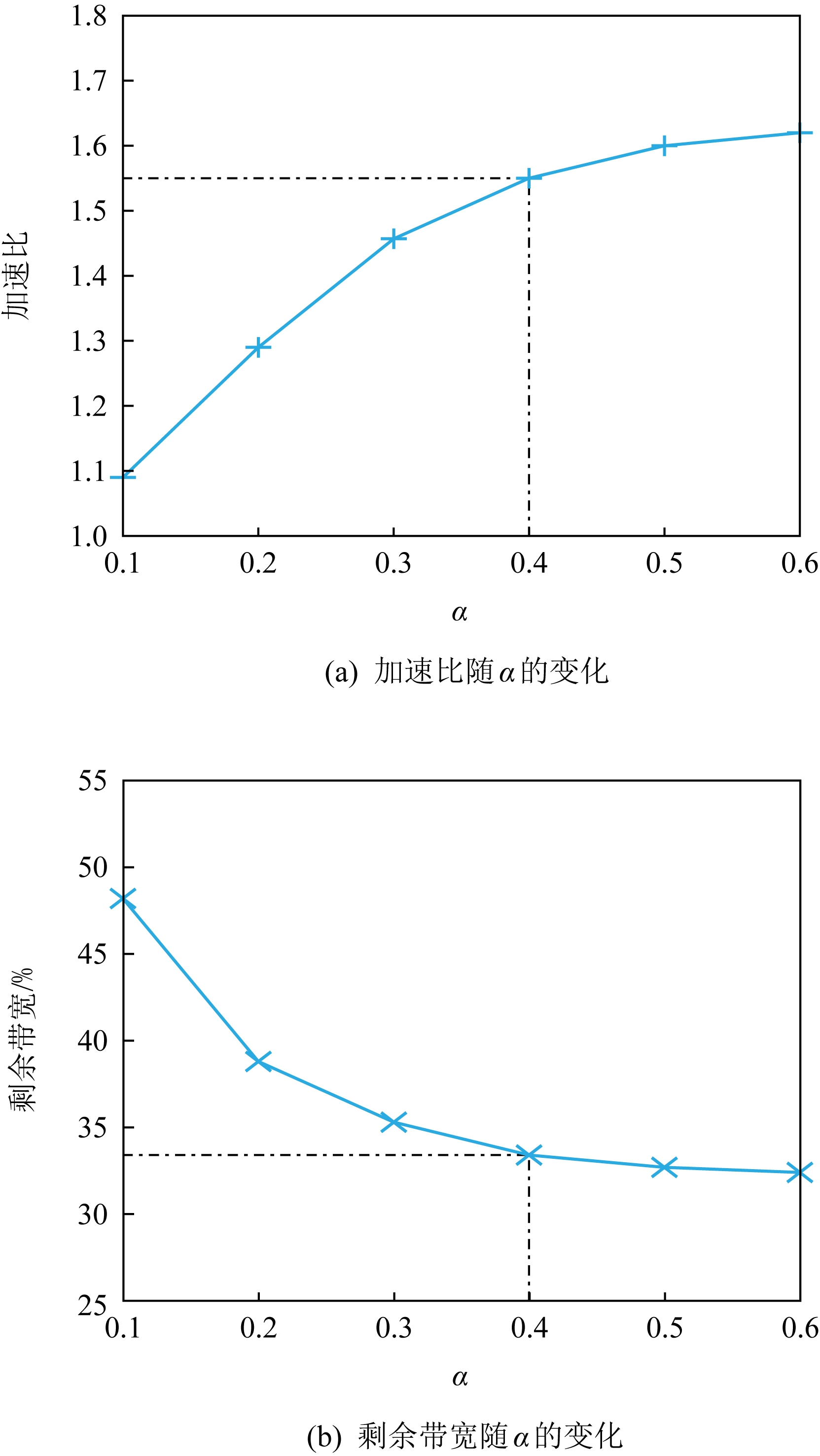
Fig.10 Scheduling effect of different α
图10 α对于JIT调度效果的影响
在设计JIT的过程中,实用性一直是我们关注的一个重点,也就是说JIT应该有较短的求解时间.因此,我们在图11中记录了求解LP问题的耗时.在图11中,任务的数目(我们选取的是VGG16)从10增加到80,运行时间通过多次测试求得平均值.从图11中看出JIT的求解过程是相当高效的:甚至在任务数目增加到70时,求解时间依然小于1 s.这个时间在实际应用场景下是可以接受的,也支持了JIT扩展到更大规模的可能性.JIT的可扩展性主要来自2个方面的原因:1)我们将其建模成为了一个高效的LP模型;2)我们对其进行了针对性的求解时间优化.
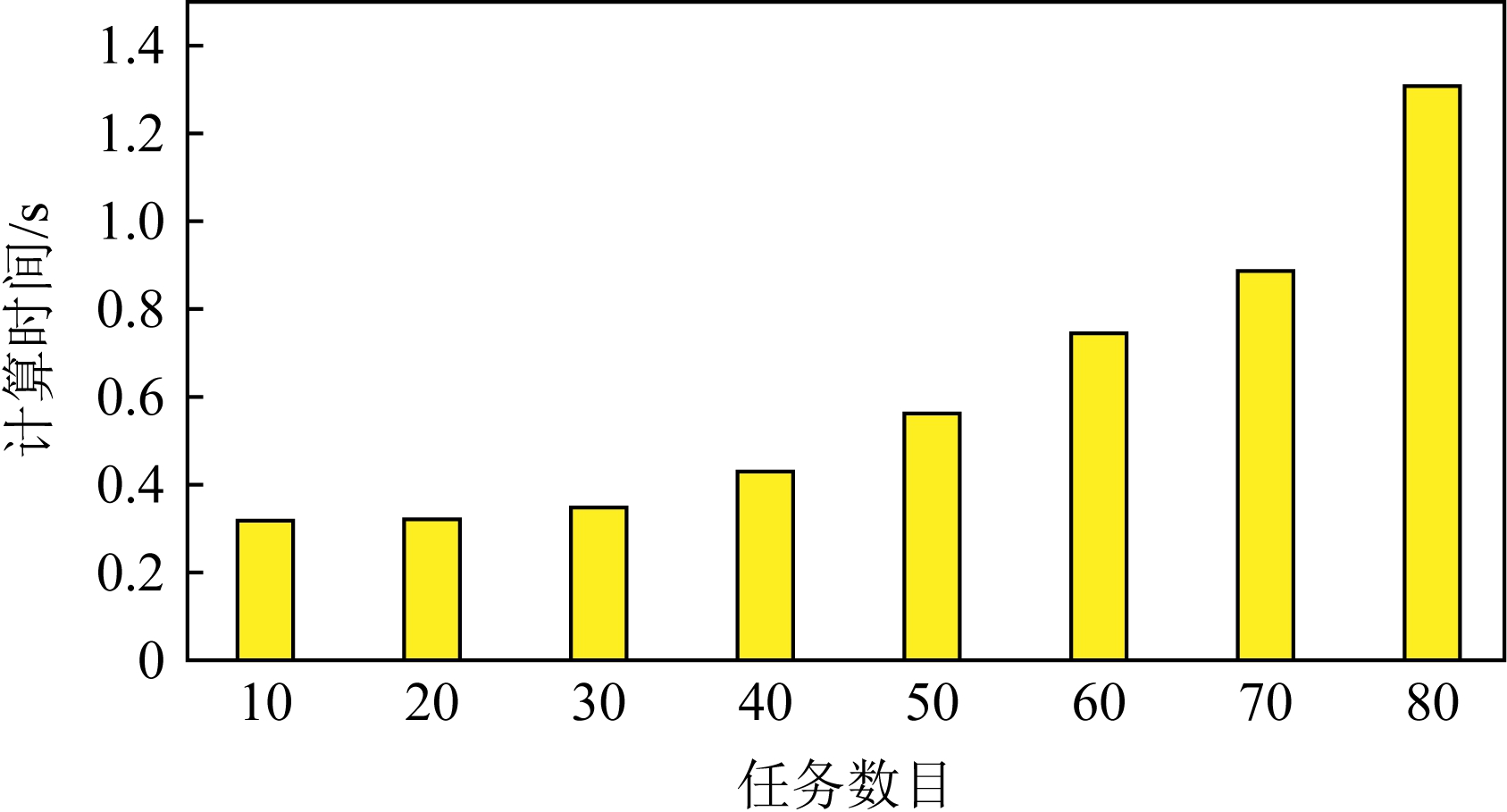
Fig.11 Computation time of JIT linear program at different scales
图11 问题规模对JIT线性模型求解计算时间的影响
5 相关工作
由于JIT的目标是在加速基于计算图的任务,同时也减少对于其他任务的影响,它就与流调度和基于计算图的优化技术有重叠的部分.在这2方面都已经有许多研究工作,本节介绍一些与JIT最为相关的工作.
1)流调度技术.传统的流调度技术目标往往是减少流完成时间[3-4]、提升流之间的公平性或者维持整个网络的负载均衡[5-6].但是,这些工作都忽视了任务级别的网络需求,因此难以提升任务的性能.意识到这个缺陷之后,Varys[15]意图通过减少一个任务中2个计算阶段之间所有流(也就是coflow)的最大完成时间来加速任务的执行.在这之后,如何基于任务的具体特征来进行网络调度的工作也逐渐增多.Tian等人[24]提出在多阶段的任务中,coflow之间也是存在依赖关系的,并为此提出了一个近似调度算法;Im等人[25]发现在某些任务中,即使一个coflow只完成了一部分,对于任务来说也是有意义的,所以他们的目标是寻求最大化coflow的部分吞吐量;此外,Tian等人[26]还提出了一种新的流量抽象MacroFlow,用来定义coflow传输到同一个机器的流的集合,并通过这个抽象来加速每一个机器上的任务执行;Xu等人[13]研究了有deadline和没有deadline的coflow在一起的混合调度问题.与以往这些工作不同,JIT通过对于任务网络需求更加细致的分析,从而提供更高效的调度方案.
2)基于计算图的任务的优化.伴随着集群规模的增加,网络越来越容易成为性能的瓶颈,这对于现在很多基于计算图的框架来说尤为突出.为此,研究者们提出了很多优化手段,大致可以分为2类:数据压缩[27-29]与网络调度[22,30-35].其中,第2种的目标是通过网络调度来提升性能,因此也与我们的工作更加相关.在TicTac[22]中,作者依据DAG图指定每一个任务中网络传输的严格顺序.但是,对于多任务场景下存在的网络竞争没有考虑.Wei等人[32]通过优先传输对于模型收敛更加重要的网络传输来加快任务执行,但是他们没有充分挖掘DAG所提供的信息.BytePS[34]在多种不同框架中实现了它们提出的单任务调度策略,但是它与TicTac一样没有考虑多任务的处理.MLNet[35]则旨在通过控制流量来缓解网络拥塞.与以上的调度技术相比,JIT更深层次地挖掘了DAG所提供的网络需求信息,并且基于此,提出了LAT来指导网络调度.
6 讨 论
我们针对实际应用中JIT可能遇到的问题进行2点讨论.
1)LAT估计准确性对于JIT性能的影响.由于网络的动态性以及复杂性,很难达到对于LAT的准确估计.在我们的实验中(图7),可以看出在JIT调度之后,网络传输的完成时间与使用时间也是不完全相等的.但是相比于其他调度手段,JIT已经大大减少了它们之间的差异,从而缩短了任务的完成时间.此外,在实际的使用中,我们还可以通过周期性地计算LAT来进行调度、提升对于网络资源情况的掌握程度等来提高LAT预测的准确率以及提升JIT的调度效果.这也是我们未来工作的一个方向.
2)JIT对于极短流的处理.由于JIT是一个集中式的网络调度器,因此对于那些传播时间很短的网络流,也称为极短流,并不是很适用.相比于很短的传输时间,计算以及调度的开销就显得更加突出.但是我们注意到,JIT在满足DAG任务网络传输需求的同时最小化了它们的带宽占用,以期将更多的带宽分配给其他的网络流,从而提升数据中心的整体性能.因此,我们可以换一个角度,将这些极短流作为背景流量处理,通过JIT的调度,提升它们的网络资源分配,从而达到整体调度的目的.
7 结 论
在数据中心中,网络带宽通常都是稀缺资源.目前我们大多通过减少传输数据的大小或者流完成时间进行优化.但是由于缺少对于网络传输与计算之间关系的清晰认识,这些手段往往难以有效提升网络资源的利用效率.比如,实际情况下网络传输完成之后甚至还需要继续等待一段时间才会被后续的计算使用.基于我们对于DAG任务的观察,在本文中提出了一个新的JIT调度器.JIT的目标是通过减少传输完毕后的等待时间来加速任务的执行.为了达到这个目标,我们提出了LAT缩短传输的等待时间,同时减少任务的网络资源占用.我们设计了一个同时考虑网络状况以及DAG信息的启发式算法来计算LAT.基于LAT,将整个调度问题建模为一个ILP模型,目标是在满足LAT的同时减少网络占用.通过数学分析,我们成功地将初始的ILP模型转化为了等价的LP模型,并且还针对性地利用合理简化将JIT的运行时间减少至不到1 s.通过详实的实验分析,我们展示了JIT可以提供1.55的加速比,同时有效减少它们的网络占用,从而成功提升数据中心的整体效率.
[1]Barroso L, ClidarasJ, Hoelzle U.The datacenter as a computer: An introduction to the design of warehouse-scale machines[J].Synthesis Lectures on Computer Architecture, 2009, 4(1): 1-108
[2]Chowdhury M, Zaharia M, Ma J, et al.Managing data transfers in computer clusters with orchestra[J].ACM SIGCOMM Computer Communication Review, 2011, 41(4): 98-109
[3]Xu Hong, Li Baochun.RepFlow: Minimizing flow completion times with replicated flows in data centers[C]//Proc of INFOCOM’14.Piscataway, NJ: IEEE, 2014: 1581-1589
[4]Al-Fares M, Radhakrishnan S, Raghavan B, et al.Hedera: Dynamic flow scheduling for data center networks[C]//Proc of NSDI’10.Berkeley, CA: USENIX Association, 2010: 89-92
[5]Alizadeh M, Edsall T, Dharmapurikar S, et al.CONGA: Distributed congestion-aware load balancing for datacenters[C]//Proc of ACM SIGCOMM’14.New York: ACM, 2014: 503-514
[6]Chen Yi, Wang Xuan, Cai Lin.On achieving fair and throughput-optimal scheduling for TCP flows in wireless networks[J].IEEE Transactions on Wireless Communications, 2016, 15(12): 7996-8008
[7]Chowdhury M, Stoica I.Coflow: A networking abstraction for cluster applications[C]//Proc of ACM HotNets’12.New York: ACM, 2012: 31-36
[8]Abadi M, Barham P, Chen Jianmin, et al.TensorFlow: A system for large-scale machine learning[C]//Proc of OSDI’16.Berkeley, CA: USENIX Association, 2016: 265-283
[9]Paszke A, Gross S, Massa F, et al.PyTorch: An imperative style, high-performance deep learning library[C]//Proc of NIPS’19.Cambridge, MA: MIT Press, 2019: 8026-8037
[10]Chen Tianqi, Li Mu, Li Yutian, et al.MxNet: A flexible and efficient machine learning library for heterogeneous distributed systems[EB/OL].(2015-12-03)[2020-07-01].https://arxiv.org/abs/1512.01274
[11]Zaharia M, Chowdhury M, Franklin M J, et al.Spark: Cluster computing with working sets[J].HotCloud, 2010, 10(10): 95-101
[12]Gushchin A, Tseng H, Tang Ao.Optimization-based network flow deadline scheduling[C]//Proc of ICNP’16.Piscataway, NJ: IEEE, 2016: 1-10
[13]Xu Renhai, Li Wenxin, Li Keqiu, et al.Shaping deadline coflows to accelerate non-deadline coflows[C]//Proc of IWQOS’18.Piscataway, NJ: IEEE, 2018: 1-6
[14]Lucier B, Menache I, Naor J, et al.Efficient online scheduling for deadline-sensitive jobs[C]//Proc of SPAA’13.New York: ACM, 2013: 305-314
[15]Chowdhury M, Zhong Yuan, Stoica I.Efficient coflow scheduling with varys[C]//Proc of ACM SIGCOMM’14.New York: ACM, 2014: 443-454
[16]Sierksma G.Linear and Integer Programming: Theory and Practice[M].Boca Raton, FL: CRC, 2001
[17]Meyer R.A class of nonlinear integer programs solvable by a single linear program[J].SIAM Journal on Control and Optimization, 1977, 15(6): 935-946
[18]Hu Zhiming, Li Baochun, Luo Jun.Flutter: Scheduling tasks closer to data across geo-distributed datacenters[C]//Proc of IEEE INFOCOM’16.Piscataway, NJ: IEEE, 2016: 1-9
[19]Bixby B.The Gurobi Optimizer[CP].[2020-07-01].https://www.gurobi.com/
[20]Amaral M, Polo J, Carrera D, et al.Topology-aware GPU scheduling for learning workloads in cloud environments[C]//Proc of ACM SC’17.New York: ACM, 2017: 1-12
[21]Yan Feng, Ruwase O, He Yuxiong, et al.SERF: Efficient scheduling for fast deep neural network serving via judicious parallelism[C]//Proc of IEEE SC’16.Piscataway, NJ: IEEE, 2016: 300-311
[22]Hashemi S, Jyothi S, Campbell R.TicTac: Accelerating distributed deep learning with communication scheduling[EB/OL].(2018-03-08)[2020-07-01].https://arxiv.org/abs/1803.03288
[23]Agarwal S, Rajakrishnan S, Narayan A, et al.Sincronia: Near-optimal network design for coflows[C]//Proc of ACM SIGCOMM’18.New York: ACM, 2018: 16-29
[24]Tian Bingchuan, Tian Chen, Dai Haipeng, et al.Scheduling coflows of multi-stage jobs to minimize the total weighted job completion time[C]//Proc of IEEE INFOCOM’18.Piscataway, NJ: IEEE, 2018: 864-872
[25]Im S, Shadloo M, Zheng Zizhan.Online partial throughput maximization for multidimensional coflow[C]//Proc of IEEE INFOCOM’18.Piscataway, NJ: IEEE, 2018: 2042-2050
[26]Tian Bingchuan, Tian Chen, Sun Jiajun, et al.Using the macroflow abstraction to minimize machine slot-time spent on networking in Hadoop[C]//Proc of ACM APNET’18.New York: ACM, 2018: 36-42
[27]Courbariaux M, Bengio Y, David J.Binaryconnect: Training deep neural networks with binary weights during propagations[C]//Proc of NIPS’15.Cambridge, MA: MIT Press, 2015: 3123-3131
[28]Gupta S, Agrawal A, Gopalakrishnan K, et al.Deep learning with limited numerical precision[C]//Proc of ICML’15.Cambridge, MA: MIT Press, 2015: 1737-1746
[29]Lin Yujun, Han Song, Mao Huizi, et al.Deep gradient compression: Reducing the communication bandwidth for distributed training[EB/OL].(2017-12-05)[2020-07-01].https://arxiv.org/abs/1712.01887
[30]Zhang Hao, Zheng Zeyu, Xu Shizhen, et al.Poseidon: An efficient communication architecture for distributed deep learning on GPU clusters[C]//Proc of ATC’17.Cambridge, MA: MIT Press, 2017: 181-193
[31]Li Mu, Andersen D, Park J, et al.Scaling distributed machine learning with the parameter server[C]//Proc of OSDI’14.Cambridge, MA: MIT Press, 2014: 583-598
[32]Wei Jinliang, Dai Wei, Qiao A, et al.Managed communication and consistency for fast data-parallel iterative analytics[C]//Proc of ACM SOCC’15.New York: ACM, 2015: 381-394
[33]Hu Zhiyao, Li Dongsheng, Li Ziyang.Recent advances in datacenter flow scheduling[J].Journal of Computer Research and Development, 2018, 55(9): 1920-1930(in chinese)(胡智尧, 李东升, 李紫阳.数据中心网络流调度技术前沿进展[J].计算机研究与发展, 2018, 55(9): 1920-1930)
[34]Peng Yanghua, Zhu Yibo, Chen Yangrui, et al.A generic communication scheduler for distributed DNN training acceleration[C]//Proc of ACM SOSP’19.New York: ACM, 2019: 16-29
[35]Mai Luo, Hong Chuntao, Costa P.Optimizing network performance in distributed machine learning[C]//Proc of HOTCLOUD’15.Cambridge, MA: MIT Press, 2015: 1-7



