量子计算机的发展及量子算法的应用对密码算法的设计和分析产生了巨大而深远的影响[1],在量子环境下对对称密码的安全性评估已成为密码学研究中的一个热点问题.已有的量子算法中针对对称密码的分析方法主要有Grover量子算法[2]、Simon量子算法[3]以及Grover和Simon量子算法相结合的量子攻击[4]等.已有的公开文献中基于上述量子算法的加速优势,对各类对称密码结构进行了基于不同模型、不同条件下的量子分析.
Kuwakado等人[5]对3轮Feistel结构进行了量子条件下的区分攻击,3轮Feistel结构与随机置换可以在多项式时间内区分,而在经典条件下,已证明3轮Feistel结构与随机置换不能在多项式时间内区分.Kuwakado等人[6]对EM(Even,Mansour)结构[7]进行了基于Simon量子算法的量子分析,在量子条件下,单轮EM结构是不安全的,量子敌手可以在多项式时间内找到密钥.Kaplan等人[8]利用Simon量子算法在多项式时间内破解了一系列广泛使用的基于分组密码的认证和认证加密工作模式.Kaplan等人[9]基于Grover量子算法提出了量子差分和线性分析.
Leander等人[4]利用Grover量子算法和Simon量子算法的结合,对分组密码DESX(extension of DES)所采用的FX(extension of block cipher F)结构[10-11]进行了量子攻击,FX结构的安全强度和其底层分组密码的安全强度一致,前后白化密钥没有提高算法的安全强度.此后,结合Grover和Simon量子算法,基于不同的量子设置条件,更多的密码结构(Feistel结构,Type-1型、Type-2型、Type-3型广义Feistel结构)被分析研究,经典条件下已证明多个在多项式时间内不可区分的结构在量子条件下可以区分[12-19].
基于Grover量子算法和Simon量子算法的密码结构安全性评估的文献较为常见,但作为生日碰撞攻击量子化的BHT(Brassard,Høyer,Tapp)量子算法[20],还没有公开文献研究其针对对称密码的安全性评估,仅有对算法本身的研究[21-23].由于经典条件下,生日碰撞攻击在对密码算法安全性评估中的广泛应用,研究量子条件下碰撞算法对密码算法的安全性评估和BHT量子算法在密码算法上的具体应用具有重要的意义.
本文通过对多轮EM结构进行分析,研究了经典条件和量子条件下的碰撞算法与差分密钥恢复攻击的结合,从BHT量子算法的角度对差分密钥恢复攻击进行量子化.本文的主要贡献有2个方面:
1)研究了经典条件下多轮EM结构的差分碰撞密钥恢复攻击.针对多轮EM分组密码结构,结合经典条件下的生日碰撞,我们对其进行了差分碰撞密钥恢复攻击,当差分传递概率2-p≥2-n /2时,r轮EM结构的密钥恢复时间复杂度为O(2p+n /2),比穷举最后轮密钥的时间复杂度O(2p+n)快了2n /2倍.
2)基于BHT量子算法对多轮EM结构的差分碰撞密钥恢复攻击进行量子化.通过研究BHT量子算法和差分密钥恢复攻击的结合,对多轮EM结构的差分碰撞密钥恢复攻击进行量子化,当差分传递概率2-p>2-n /3时,结合BHT量子算法的量子差分碰撞密钥恢复时间复杂度要优于Grover搜索的直接二次加速,显示了BHT量子算法在密码分析中的有效性.
1 量子算法与量子分析模型
本文主要研究生日碰撞和BHT量子算法与差分密钥恢复攻击的结合,从而对经典密码分析方法进行量子化,本文的关注重点是差分密码分析的密钥恢复阶段,不从差分链的选取进行研究.
1.1 Grover量子算法
Grover量子算法[2]由Grover在1996年提出,对于1个拥有N个数据的无序数据库,用Grover量子算法只需搜索O(N1/2)次,而经典算法需要O(N)次.Grover量子算法加快了对经典条件下密钥的搜索,对经典安全通信构成了威胁.
Grover量子算法使用1个n量子比特寄存器Oracle,包括可能需要的附加工作量子比特,算法的目的是用最少的Oracle应用次数求出搜索问题的1个解.
算法从n量子比特初态|0 ⊗n开始,用Hadamard变换使计算机处于叠加态
⊗n开始,用Hadamard变换使计算机处于叠加态![]() 量子搜索算法由反复应用Grover迭代的量子子程序组成.通过进行
量子搜索算法由反复应用Grover迭代的量子子程序组成.通过进行![]() 次Grover迭代,就能以概率O(1)得到搜索问题的1个解(M为解的个数),这是在量子条件下对经典算法要求的O(N/M)次Oracle调用的二次加速.
次Grover迭代,就能以概率O(1)得到搜索问题的1个解(M为解的个数),这是在量子条件下对经典算法要求的O(N/M)次Oracle调用的二次加速.
1.2 BHT量子算法
BHT量子算法[20]由Brassard,Høyer,Tapp在1998年提出,BHT量子算法被设计为针对2-to-1目标函数F求解碰撞,即对于函数:
F:X→Y,
其中,|X|=2|Y|,|Y|=2n.
BHT量子算法以Grover量子算法为基础,以O(2n /3)的量子查询复杂度、量子时间复杂度、量子存储复杂度找到函数F的1个碰撞,算法过程为:
Step1.从集合X中随机挑选2n /3个元素,放入集合X′.
Step2.询问函数F,构造列表L={(x,F(x))},其中x∈X′,|L|=2n /3,并将列表L存于量子存储单元中.
Step3.检查L中是否存在碰撞.
Step3.1.若L中存在碰撞,即有(x,F(x)),(y,F(y))∈L,满足x≠y且F(x)=F(y),则输出碰撞.
Step3.2.若L中不存在碰撞,构造分类函数:

应用Grover量子算法对F1(x)求解.
BHT量子算法的量子查询复杂度、量子时间复杂度、量子存储复杂度均为O(2n /3).
1.3 量子分析模型
依据Zhandry[24]给出的量子设置中伪随机函数(pseudo-random function, PRF)和伪随机置换(pseudo-random permutation,PRP)安全性的概念,Kaplan等人[9]根据收集数据方式的不同,在对密码进行量子分析时,提出标准安全和量子安全2种不同的量子分析模型.
如果没有有效的量子算法能够通过只进行经典查询区分分组密码与PRP(或PRF),那么分组密码就是针对量子分析的标准安全,简称Q1模型,该模型中,分析者用经典方式收集数据,用量子计算处理数据;如果即使能进行量子查询,也没有有效的量子算法能够区分分组密码与PRP(或PRF),则分组密码对量子分析是量子安全,简称Q2模型,该模型中,分析者可以直接用经典输入的量子叠加来查询密码oracle,并接收相应输出的叠加.
由于Q2模型的强大的量子查询能力,现有公开的量子密码分析文献中大都采用Q2模型.Q2模型中,对手的攻击能力非常强,但有可能设计安全的协议来抵抗这种攻击.很多在经典模型中安全的消息鉴别码(message authentication codes, MAC)和认证加密算法(authenticated encryption, AE)被Q2攻击[8]破解.另一方面,在量子模型中,假设标准安全PRF或量子安全PRF,常见的加密模式已经被证明是安全的[25].
2 差分碰撞密钥恢复攻击
EM密码结构是Even和Mansour[6]提出的分组密码结构,可认为是高级加密标准(Advanced Encryption Standard, AES)的简约形式.已经证明,任何经典算法都需要密钥长度的子指数时间来破译EM密码,在这个意义上,EM密码结构对任何经典对手都是安全的.
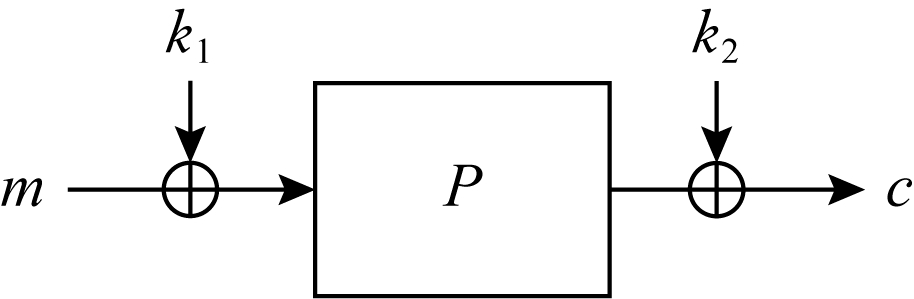
Fig.1 One round EM structure
图1 单轮EM结构
单轮EM结构如图1所示,P是{0,1}n上的公开随机置换,密钥k=k1‖k2长度为2n(单位为b),其中k1,k2∈{0,1}n.加密算法为c=Ek(m)=P(k1⊕m)⊕k2,其中m,c∈{0,1}n分别是明文及其密文,解密以m=Dk(c)=P-1(k2⊕c)⊕k1进行.
通过迭代置换P并在其中插入密钥k1,k2,…,kr+1的方式,可以获得r轮EM结构:
EMk1,k2,…,kr+1(m)=
P(P(P(m⊕k1)⊕k2)⊕…)⊕kr+1,
其中,r+1个轮子密钥可以相互独立,也可以由主密钥一并生成,本文假设r+1个轮子密钥k1,k2,…,kr+1相互独立.
根据差分密码分析的概念,多轮EM密码一般意义上的差分密码分析如图2所示:

Fig.2 Differential cryptanalysis of r-round EM structure
图2 r轮EM结构的差分密码分析
本文不考虑差分链的搜寻,关注的重点是恢复密钥kr+1阶段的复杂度.
令EK表示完整r轮EM密码加密算法,DK表示完整r轮EM密码解密算法,m和m⊕α表示差为α的输入明文对,P为最后密钥恢复轮的轮函数,P-1为最后轮函数的逆,分组长度和密钥长度用n表示,前r-1轮差分区分器用![]() 表示,输入输出差为(α,β)时的差分概率为2-p,则
表示,输入输出差为(α,β)时的差分概率为2-p,则
![]()
![]()
P(y⊕β)⊕kr+1=c′,
DK(c)=m,
DK(c′)=m⊕α,
成立.
在经典条件中,一般利用
P-1(c⊕kr+1)⊕P-1(c′⊕kr+1)=β
对密钥kr+1进行测试,直接穷举或通过分析具体算法先求出部分值,再通过穷举剩余密钥的方式求解密钥kr+1,计算复杂度为O(2p+n),密钥恢复过程如图3所示:

Fig.3 Key recovery of differential cryptanalysis
图3 差分密码分析的密钥恢复
将c′表示为以c和β为输入的函数:
c′=EK(m⊕α)=P(P-1(c⊕kr+1)⊕β)⊕kr+1.
P和β的值已知,可以构造函数c″:
c″=P(P-1(c)⊕β).
如图4所示,进而构造f函数:
f=c′⊕c″=
P(P-1(c⊕kr+1)⊕β)⊕P(P-1(c)⊕β)⊕kr+1=
EK(m⊕α)⊕P(P-1(c)⊕β)=
EK(DK(c)⊕α)⊕P(P-1(c)⊕β).
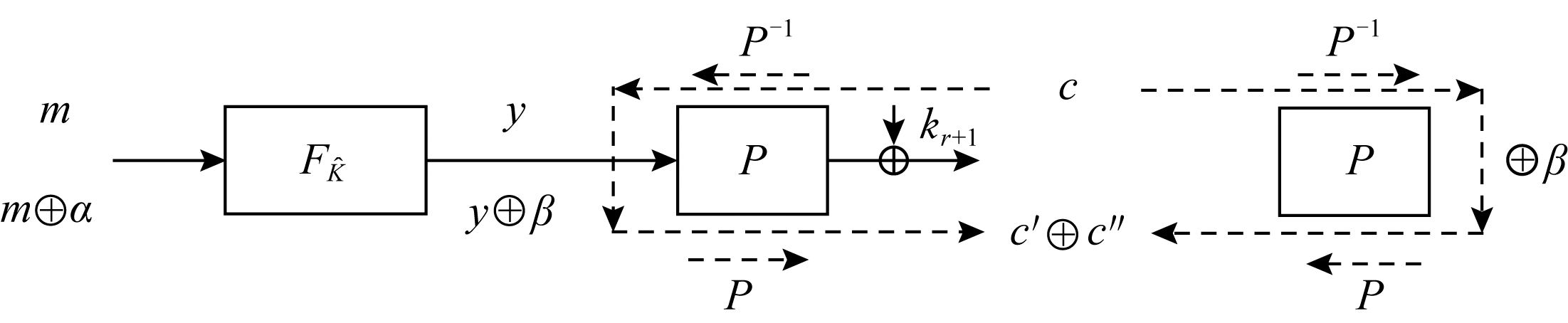
Fig.4 Construction of f=c′⊕ c″ function
图4 f=c′⊕ c″函数的构造
也即,当差分传递链成立时,f函数可以写为
f=P(P-1(c⊕kr+1)⊕β)⊕P(P-1(c)⊕β)⊕kr+1.
对于f函数,当差分传递概率不同时,有2种情况:
1)差分传递概率为1
即无论变量c如何变化,β总是以概率1出现,也即f函数以概率1成立.
当f函数输入为c和c⊕kr+1时,有
f(c)=P(P-1(c⊕kr+1)⊕β)⊕P(P-1(c)⊕β)⊕kr+1,
f(c⊕kr+1)=P(P-1(c⊕kr+1⊕kr+1)⊕β)⊕
P(P-1(c⊕kr+1)⊕β)⊕kr+1=
P(P-1(c)⊕β)⊕P(P-1(c⊕kr+1)⊕β)⊕
kr+1=f(c),
即函数值保持不变,函数f(c)存在周期s=kr+1.
在经典条件下,由生日碰撞攻击可知,当任意选取2n /2个输入c时,可以高概率求出1对碰撞(c,c⊕kr+1),使得f(c)=f(c⊕kr+1),从而轻易求出密钥kr+1,时间复杂度和数据复杂度为O(2n /2).
2)差分传递概率2-p<1
当输入2p个差为α的对时,存在1个输入对的输出差为β,出现2n /2个符合输出差的输入对时,根据生日攻击,即可以高概率求出1对碰撞(c,c⊕kr+1),使得f(c)=f(c⊕kr+1),也即可高概率求出密钥kr+1.那么在计算2n /2×2p个输入c的函数值f(c)后,存在1对碰撞(c,c⊕kr+1),时间复杂度和数据复杂度为
O(2n /2×2p)=O(2n /2+p).
由于对输入c的形式不做限制,可以在选择明文攻击的条件下对多轮EM结构进行差分密钥恢复攻击.
算法1.基于生日碰撞的多轮EM结构差分密钥恢复攻击.
输入:明文m集合M(|M|=2n /2+p);
输出:密钥kr+1.
Step1. 任选1个包含2n /2+p个m元素的集合M.
Step2. 对于每一个m,分别计算:
c=EK(m),
c′=EK(m⊕α),
c″=P(P-1(c)⊕β),
g(m)=c′⊕c″=
EK(m⊕α)⊕P(P-1(EK(m))⊕β).
Step3. 检查是否存在不同的m值(m0,m1),使得g(m0)=g(m1)成立.
Step4. 对于每1对碰撞,计算:
kr+1=EK(m0)⊕EK(m1).
Step5. 将m0或m1对应的c和c′,以及kr+1代入式:
P-1(c⊕kr+1)⊕P-1(c′⊕kr+1)=β,
验证该式是否成立,如果成立则输出密钥kr+1.
复杂度分析:
EM结构分组和密钥长度以及随机置换P的输入均为n位,生日碰撞攻击下,对于g(m)函数,2n /2+p个输入值约有2p个碰撞出现,共得到2p个候选密钥.在随机假设的条件下,错误密钥通过公式P-1(c⊕kr+1)⊕P-1(c′⊕kr+1)=β测试的概率为2-n,则通过测试的错误密钥数为2p-n.
1)p>n /2时,集合M中元素个数2n /2+p>2n,超过数据总长度,攻击失败.
2)p≤n /2时,集合M中元素个数2n /2+p≤2n,通过测试的错误密钥数为2p-n≤2-n /2<1.2n /2+p个明文中共有2n /2个明文及其构成的差为α的明文对,r-1轮后输出差为β .即在生日碰撞攻击下,有2n /2个输入值符合f函数,则可以高概率求出1对所需碰撞,进而求出正确密钥,时间复杂度和数据复杂度均为
O(2n /2×2p)=O(2n /2+p).
当p≤n /2时,对比经典条件下的r轮EM结构的差分密钥恢复的时间复杂度O(2p+n),我们对r轮EM结构的差分碰撞密钥恢复攻击速度提高了2n /2倍,时间复杂度明显降低.
3 量子差分碰撞密钥恢复攻击
本节基于BHT量子算法对多轮EM结构差分密钥恢复攻击进行量子化.由第2节分析可知,g(m)函数成立的概率为前r-1轮输入输出差(α,β)的差分传递概率2-p,当1对m值(m0,m1)同时满足g(m)函数时,概率为2-p×2-p=2-2p,那么g(m)函数为2-to-1函数的概率也为2-2p,此时g(m)函数以概率2-2p符合BHT量子算法的适应条件.
可以在量子Q2模型下,以量子选择明文的攻击条件,通过BHT量子算法对多轮EM结构差分碰撞密钥恢复攻击进行量子化.
算法2.基于BHT量子算法的多轮EM结构差分密钥恢复攻击.
输入:明文m集合M′(|M′|=l);
输出:密钥kr+1.
Step1.从明文m集合中随机挑选l个元素,放入集合M′.
Step2.询问函数g(m),构造列表L={(m,g(m))},其中m∈M′,|L|=l,将列表L存于量子存储单元中.
Step3.检查L中是否存在不同的m值(m0,m1),使得g(m0)=g(m1)成立.
Step3.1.对于每1对碰撞,计算:
kr+1=EK(m0)⊕EK(m1).
Step3.2.将m0或m1对应的c和c′,以及kr+1代入式:
P-1(c⊕kr+1)⊕P-1(c′⊕kr+1)=β.
验证该式是否成立,如果成立则输出密钥kr+1.
Step4.若L中不存在碰撞或无法解出正确密钥kr+1,构造分类函数:

Step5.应用Grover量子算法对g1(m)求解,计算并输出kr+1=EK(m0)⊕EK(m).
复杂度分析:
Step3前需要计算g(m)函数的l个输出值,并都存在量子存储空间中,此步骤需要l的量子存储复杂度、量子查询复杂度与量子时间复杂度.
已知g(m)函数成立的概率为前r-1轮的差分传递概率2-p,出现(m0,m1)同时符合g(m)函数的概率为2-2p,由于列表L中的元素个数为l,因此在Step4中调用Grover量子算法对g1(m)求解时对应解的个数是l×2-2p.
L中所有数据都存在量子空间中,因此Grover量子算法每次查询都能以量子叠加态访问所有l个数据,依据Grover量子算法,有
再由![]() 易得
易得![]() 则Grover量子算法迭代查询G操作
则Grover量子算法迭代查询G操作![]() 次,量子查询复杂度:
次,量子查询复杂度:
则设量子时间复杂度:
其中,TO为以量子叠加态访问Oracle的时间,T|ψ 为Hadamard变换的时间.算法将L的元素都存在量子寄存器里,依据量子时间复杂度约定,若能以量子叠加态访问Oracle,则只需要O(1)的时间,即TO=O(1).
为Hadamard变换的时间.算法将L的元素都存在量子寄存器里,依据量子时间复杂度约定,若能以量子叠加态访问Oracle,则只需要O(1)的时间,即TO=O(1).
此外![]() 可以由Hadamard矩阵对|0
可以由Hadamard矩阵对|0 变换得到,也是O(1)时间,因此算法对应的量子时间复杂度为t×(O(1))=O(2n /2+p×l-1/2).
变换得到,也是O(1)时间,因此算法对应的量子时间复杂度为t×(O(1))=O(2n /2+p×l-1/2).
由于Step3前需要计算函数g(m)的l个输出值,总的量子时间复杂度为
max{l,2n /2+p×l-1/2}.
当l=2n /2+p×l-1/2,即l=2n /3+2p/3时,可得max{l,2n /2+p×l-1/2}最小值为O(2n /3+2p/3).
另外,当l×2-2p≥1,即l≥22p时Grover搜索才能有解,即上述复杂度成立的条件为
l=2n /3+2p/3≥22p,即p≤n /4.
当p≤n /4时,有最小复杂度O(2n /3+2p/3),否则,量子时间复杂度为max{l,2n /2+p×l-1/2},其中l≥22p,考虑2个可变参数l和p.
1)参数l
① 当l=2n /3+2p/3时,有最小值2n /3+2p/3;
② 当l<2n /3+2p/3时,max{l,2n /2+p×l-1/2}=2n /2+p×l-1/2;
③ 当l>2n /3+2p/3时,max{l,2n /2+p×l-1/2}=l.
2)参数p
① p≤n /4时,取l=2n /3+2p/3≥22p,max{l,2n /2+p×l-1/2}有最小值2n /3+2p/3;
② n /4<p≤n /2时,2n /3+2p/3<22p,取l=2n /3+2p/3时,Grover搜索无解,取l>2n /3+2p/3,max{l,2n /2+p×l-1/2}=l,且需l≥22p,取l=22p,则有max{l,2n /2+p×l-1/2}=l=22p;
③p>n /2时,由于l×2-2p<2n×2-2p<1,Grover搜索无解,量子碰撞算法不能对该差分分析量子化,此时,和经典生日攻击一致,p>n /2时,2n /2+p>2n,所需数据量超过所有明密文对个数,无法求出正确密钥.
有关文献中的量子差分攻击只用Grover搜索进行量子化,当只用Grover量子搜索对本文所述差分分析进行量子化时,其分类函数为
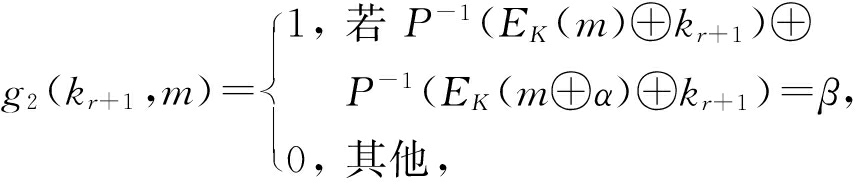
该分类函数取1的概率为2-n-p,根据Grover量子算法,找到密钥kr+1的时间复杂度为O(2n /2+p/2).
1)p≤n /4时,有
O(2n /3+2p/3)<O(2n /2+p/2).
2)n /4<p<n /3时,有
max{l,2n /2+p×l-1/2}=l=22p<2n /2+p/2,
也即有:
O(22p)<O(2n /2+p/2).
上述2种情况下,基于BHT量子算法的差分密钥恢复结果优于直接利用Grover搜索.
3)n /3≤p<n /2时,有
max{l,2n /2+p×l-1/2}=l=22p≥2n /2+p/2,
也即有
O(22p)≥O(2n /2+p/2).
此种情况下,Grover搜索结果更优.
经典条件和量子条件下的对比结果汇总在表1中,结果显示,当p<n /3,即差分传递概率2-p>2-n /3时,基于BHT碰撞搜索算法的量子差分碰撞密钥恢复攻击要优于基于Grover搜索的量子差分的直接二次加速.
Table 1 Time Complexity of Key Recovery Under Classical and Quantum Conditions
表1 经典和量子条件下的密钥恢复时间复杂度

攻击条件差分密钥恢复差分碰撞密钥恢复经典O(2n+p)p≤n∕2,O(2n∕2+p)量子O(2n∕2+p∕2)p≤n∕4,O(2n∕3+2p∕3)
4 总 结
本文通过对多轮EM分组密码结构进行分析,研究了经典条件生日碰撞、BHT量子算法和差分密钥恢复攻击的结合方法,对多轮EM结构进行了差分碰撞密钥恢复攻击,并从量子碰撞算法的角度对其进行量子化.
研究结果表明:经典条件下,当差分传递概率2-p≥2-n /2时,r轮EM结构的差分碰撞密钥恢复攻击快了2n /2倍;量子条件下,当2-p>2-n /3时,基于BHT碰撞搜索算法的量子差分碰撞密钥恢复攻击时间复杂度要优于基于Grover搜索的差分攻击.结果同时表明,当2-p≤2-n /3时,基于Grover搜索的差分密钥恢复攻击的二次加速仍然是最优选择.
[1]Wang Yongli, Xu Qiuliang.Principle and research progress of quantum computation and quantum cryptography[J].Journal of Computer Research and Development, 2020, 57(10): 2015-2026(in Chinese)(王永利, 徐秋亮.量子计算与量子密码的原理及研究进展综述[J].计算机研究与发展, 2020, 57(10): 2015-2026)
[2]Grover L K.A fast quantum mechanical algorithm for database search[C]//Proc of the 28 Annual ACM Symp on the Theory of Computing.New York: ACM, 1996: 212-219
[3]Simon D R.On the power of quantum computation[C]//Proc of the 35th IEEE Symp on the Foundations of Computer Science.Piscataway, NJ: IEEE, 1994: 116-123
[4]Leander G, May A.Grover meets Simon-Quantumly attacking the FX-construction[G]//LNCS 10625: Proc of the 23rd Int Conf on the Theory and Applications of Cryptology and Information Security.Berlin: Springer, 2017: 161-178
[5]Kuwakado H, Morii M.Quantum distinguisher between the 3-round Feistel cipher and the random permutation[C]//Proc of the 2010 IEEE Int Symp on Information Theory.Piscataway, NJ: IEEE, 2010: 2682-2685
[6]Kuwakado H, Morii M.Security on the quantum-type Even-Mansour cipher[C]//Proc of the 2012 Int Symp on Information Theory and Its Applications.Piscataway, NJ: IEEE, 2012: 312-316
[7]Even S, Mansour Y.A construction of a cipher from a single pseudorandom permutation[J].Journal of Cryptology, 1997, 10(3): 151-161
[8]Kaplan M, Leurent G, Leverrier A, et al.Breaking symmetric cryptosystems using quantum period finding[G]//LNCS 9815: Proc of the 36th Annual Int Cryptology Conf.Berlin: Springer, 2016: 207-237
[9]Kaplan M, Leurent G, Leverrier A, et al.Quantum differential and linear cryptanalysis[J].Transactions on Symmetric Cryptology, 2016(1): 71-94
[10]Kilian J, Rogaway P.How to protect DES against exhaustive key search[G]//LNCS 1109: Proc of the 16th Annual Int Cryptology Conf.Berlin: Springer, 1996: 252-267
[11]Kilian J, Rogaway P.How to protect DES against exhaustive key search(an analysis of DESX)[J].Journal of Cryptology, 2001, 14(1): 17-35
[12]Dong Xiaoyang, Dong Bingyou, Wang Xiaoyun.Quantum attacks on some Feistel block ciphers[J].Designs Codes and Cryptography, 2020, 88(1): 1179-1203
[13]Dong Xiaoyang, Wang Xiaoyun.Quantum key-recovery attack on Feistel structures[J].Science China:Information Sciences, 2018, 61(10): 240-246
[14]Ito G, Hosoyamada A, Matsumoto R, et al.Quantum chosen-ciphertext attacks against Feistel ciphers[G]//LNCS 11405: Proc of the the Cryptographers' Track at the RSA Conf.Berlin: Springer, 2019: 391-411
[15]Dong Xiaoyang, Li Zheng, Wang Xiaoyun.Quantum cryptanalysis on some generalized Feistel schemes[J].Science China:Information Sciences, 2019, 62(2): 180-191
[16]Ito G, Iwata T.Quantum distinguishing attacks against type-1 generalized Feistel ciphers[EB/OL].[2020-01-15].https://eprint.iacr.org/2019/327
[17]Ni Boyu, Dong Xiaoyang.Improved quantum attack on type-1 generalized Feistel schemes and its application to CAST-256[J].Journal of Electronics and Information Technology, 2020, 42(2): 295-306(in Chinese)(倪博煜, 董晓阳.改进的Type-1型广义Feistel结构的量子攻击及其在分组密码CAST-256上的应用[J].电子与信息学报, 2020, 42(2): 295-306)
[18]Ni Boyu, Ito G, Dong Xiaoyang, et al.Quantum attacks against type-1 generalized Feistel ciphers and applications to CAST-256[G]//LNCS 11898: Proc of the 20th Int Conf on Cryptology in India.Berlin: Springer, 2019: 433-455
[19]Hodi S, Ramkilde L K, Kidmose A B.On quantum distinguishers for type-3 generalized Feistel network based on separability[G]//LNCS 12100: Proc of the Int Conf on Post-Quantum Cryptography.Berlin: Springer, 2010: 461-480
[20]Brassard G, Høyer P, Tapp A.Quantum cryptanalysis of Hash and claw-free functions[G]//LNCS 1380: Proc of the Latin American Symp on Theoretical Informatics.Berlin: Springer, 1998: 163-169
[21]Hosoyamada A, Sasaki Y, Xagawa K.Quantum multi collision-finding algorithm[G]//LNCS 10625: Proc of the 23rd Int Conf on the Theory and Applications of Cryptology and Information Security.Berlin: Springer, 2017: 179-210
[22]Liu Qipeng, Zhandry M.On finding quantum multicollisions[EB/OL].[2020-01-15].https://eprint.iacr.org/2018/1096
[23]Hosoyamada A, Sasaki Y, Tani S, et al.Improved quantum multicollision-finding algorithm[G]//LNCS 11505: Proc of the Int Conf on Post-Quantum Cryptography.Berlin: Springer, 2019: 350-367
[24]Zhandry M.How to construct quantum random functions[C]//Proc of the 53rd Annual IEEE Symp on Foundations of Computer Science.Piscataway, NJ: IEEE, 2012: 679-687
[25]Mayuresh V A, Ehsan E T, Gelo N T, et al.Post-quantum security of the CBC, CFB, OFB, CTR, and XTS modes of operation[G]//LNCS 9606: Proc of the Post-Quantum Cryptography.Berlin: Springer, 2016: 44-63


