在过去几年,深度学习已经在人工智能和机器学习上取得了成功,给社会带来了巨大的进步.深度学习的特点是堆积多层的神经网络层,从而具有更好的学习表示能力.卷积神经网络(convolutional neural network, CNN)的飞速发展更是将深度学习带上了一个新的台阶[1-2].CNN的平移不变性、局部性和组合性使其天然适用于处理像图像这样的欧氏结构数据的任务中[3-4],同时也可以应用于机器学习的其他各个领域[5-7].深度学习的成功一部分源自于可以从欧氏数据中提取出有效的数据表示,从而对其进行高效的处理.另一个原因则是得益于GPU的快速发展,使得计算机具有强大的计算和存储能力,能够在大规模的数据集中训练和学习深度学习模型.这使得深度学习在自然语言处理[8]、机器视觉[9]和推荐系统[10]等领域都表现出了良好的性能.
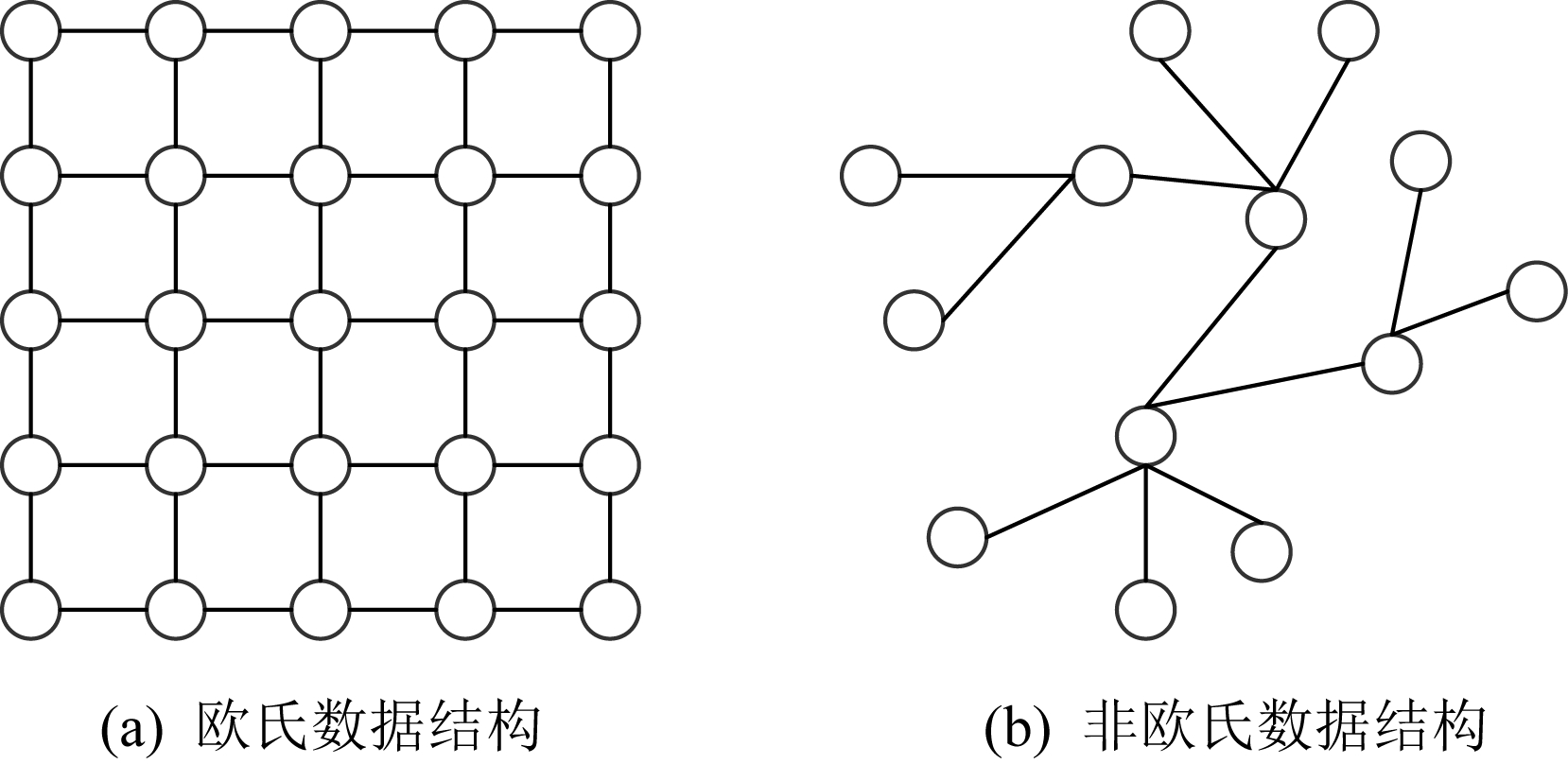
Fig. 1 Two data structures
图1 2种数据结构
但是,现有的神经网络只能对常规的欧氏结构数据进行处理.如图1(a)欧氏数据结构,其特点就是节点有固定的排列规则和顺序,如2维网格和1维序列.而当前越来越多的实际应用问题必须要考虑非欧氏数据,如图1(b)非欧氏数据结构中节点没有固定的排列规则和顺序,这就使得不能直接将传统的深度学习模型迁移到处理非欧氏结构数据的任务中.如若直接将CNN应用到其中,由于非欧氏数据中心节点的邻居节点数量和排列顺序不固定,不满足平移不变性,这就很难在非欧氏数据中定义卷积核.针对图神经网络(graph neural network, GNN)的研究工作,最开始就是在如何固定邻居节点数量以及如何给邻居节点排序展开的,比如PATCHY-SAN[11],LGCN[12],DCNN[13]方法等.完成上述2项工作之后,非欧氏结构数据就转化为欧氏结构数据,然后就可以利用CNN处理.图是具有点和边的典型非欧氏数据,在实际中可以将各种非欧氏数据问题抽象为图结构.比如在交通系统中,利用基于图的学习模型可以对路况信息进行有效的预测[14].在计算机视觉中,将人与物的交互看作一种图结构,可以对其进行有效地识别[15].
近期已有一些学者对图神经网络及其图卷积神经网络分支进行了综述[16-19].本文的不同之处在于,首先由于经典模型是很多变体模型的基石,所以给出了经典模型的理论基础以及详细推理步骤.在1.2节基于空间方法的图卷积神经网络中,多用图的形式列出模型的实现过程,使模型更加通俗易懂.文献[16-19]并未对目前广大学者热点讨论的问题进行总结,所以在第5节针对图神经网络的讨论部分,首次列出了目前研究学者对GNN的热点关注问题,比如其表达能力、过平滑问题等.然后,在第6节中总结了图神经网络新框架.同时,针对图神经网络的应用,在第7节中较全面地介绍了GNN的应用场景.最后,列出了图神经网络未来的研究方向.在图2中列出了本文的主体结构.
研究图神经网络对推动深度学习的发展以及人类的进步具有重大意义.首先,现实中越来越多的问题可以抽象成非欧氏结构数据,由于图数据的不规则性,传统的深度学习模型已经不能处理这种数据,这就亟需研究设计一种新的深度神经网络.而GNN所处理的数据对象就是具有不规则结构的图数据,GNN便在这种大背景下应运而生[20-21].然后,图数据的结构和任务是十分丰富的.这种丰富的结构和任务也正是和人们生活中要处理的实际问题相贴合的.比如,图数据有异质性以及边的有向连接特性,这和推荐系统中的场景完全类似.图数据处理任务中节点级别、边级别以及整图级别也同样可以应用到深度学习的各个应用场景中.所以,GNN的研究为解决生活中的实际问题找到了一种新的方法和途径.最后,GNN的应用领域是十分广泛的,能够处理各种能抽象成图数据的任务.不管是在传统的自然语言处理领域[22-24]或者图像领域[25-26],还是在新兴的生化领域[27-28],GNN都能表现出强大的性能.
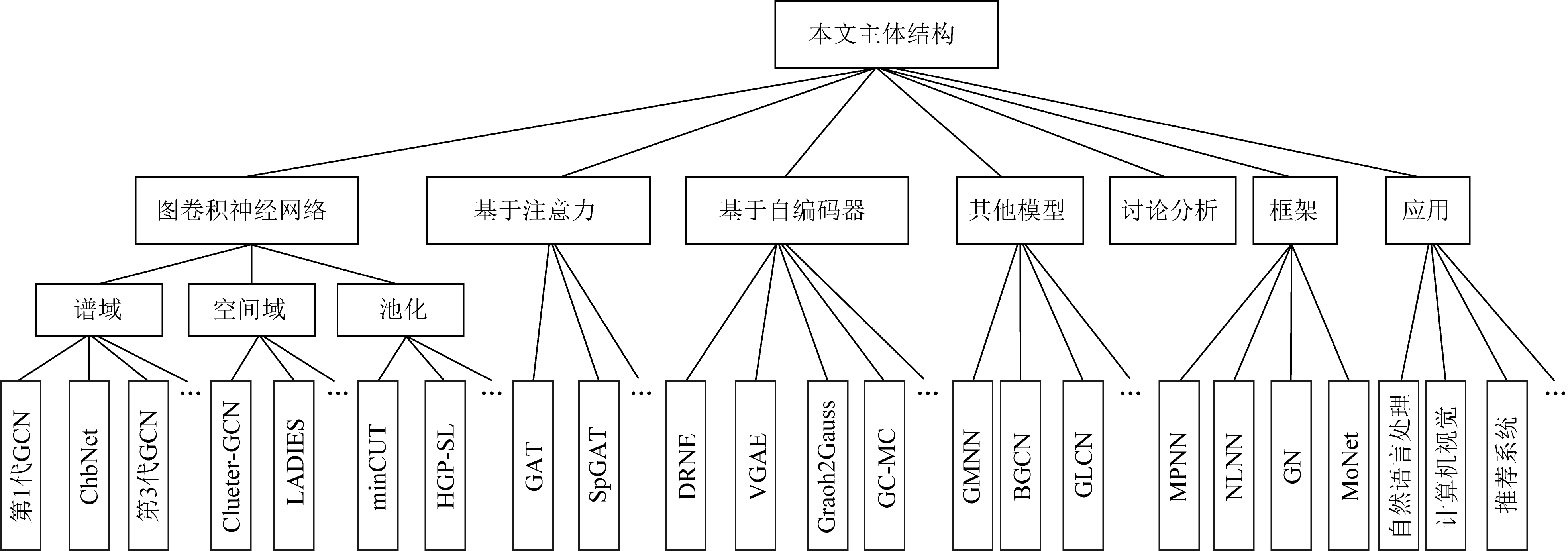
Fig. 2 The main structure
图2 主体结构
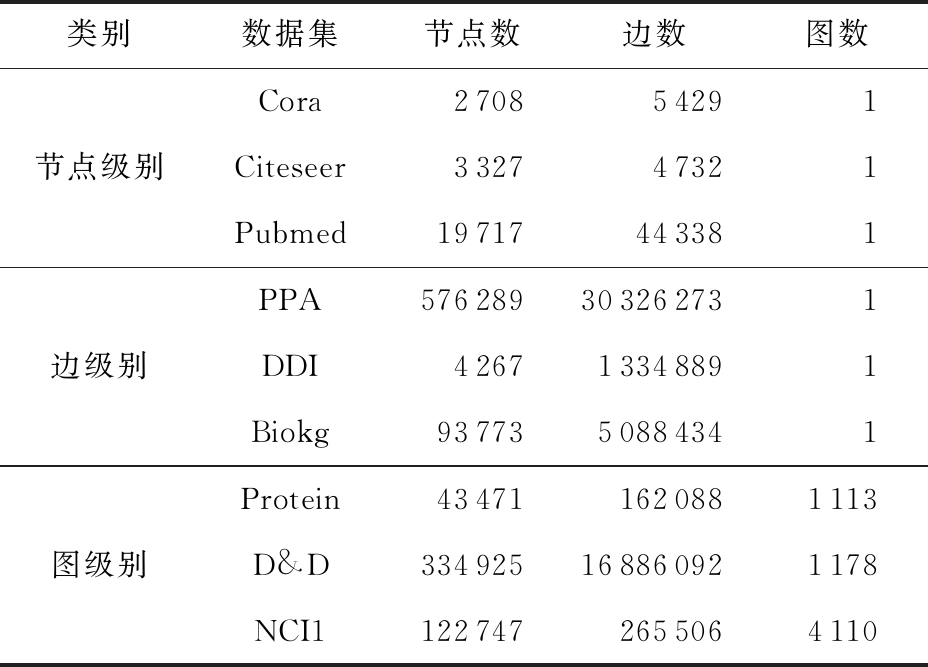
现实生活中越来越多的实际处理任务都可以抽象成图结构数据,应用场景是非常多的.图中包含节点、边和整个图结构.GNN的处理任务也主要从节点级别、边级别和整个图级别出发.在节点级别可以完成针对节点的分类,比如在引文数据集中,可以完成对相似论文的分类任务[29].边级别可以完成链路预测任务,比如推荐系统中用户对电影是否感兴趣等[30].而图级别则可以完成对整个图属性的预测,比如在生化预测任务中,可以实现对某个分子是否产生变异进行预判[31].针对不同的处理任务,常用的数据集如表1所示:
Table 1 Common Datasets
表1 常用数据集
类别数据集节点数边数图数Cora 2708 5429 1节点级别Citeseer332747321Pubmed19717443381PPA576289303262731边级别DDI426713348891Biokg9377350884341Protein434711620881113图级别D&D334925168860921178NCI11227472655064110
1 图卷积神经网络
CNN已经在图像识别、自然语言处理等多个领域取得了不俗的成绩,但其只能高效地处理网格和序列等这样规则的欧氏数据.不能有效地处理像社交多媒体网络数据、化学成分结构数据、生物蛋白数据以及知识图谱数据等图结构的非欧氏数据.为此,无数学者经过不懈努力,成功地将CNN应用到图结构的非欧氏数据上,提出了图卷积神经网络(graph convolutional network, GCN).GCN是GNN中一个重要分支,现有的大多数模型基本上都是在此基础上变化推导而来.下面我们将按照从基于谱方法、空间方法和池化3方面对GCN进行总结和概括.
1.1 基于谱域的图卷积神经网络
基于谱域的GCN是利用图信号理论,以傅里叶变换为桥梁,成功地将CNN迁移到图上.该方法从谱域出发,应用拉普拉斯矩阵来处理图这种非欧氏结构数据,整个数学推导非常巧妙,值得我们学习研究.本节首先介绍谱理论知识,解释说明怎样利用图信号理论将传统的CNN迁移到图上,然后列举了在基于谱域GCN这一小类中的典型模型.
1.1.1 谱理论知识
首先给出归一化拉普拉斯矩阵L的定义:
![]()
(1)
其中,D表示图G的度矩阵,A表示图G的邻接矩阵,In为一个n阶的单位阵.
信号f(x)的傅里叶变换及其逆变换为
F(w)=φ(w)=![]() f(x) exp (-iwx)dx,
f(x) exp (-iwx)dx,
(2)
f(x)=φ-1(F(w)),
(3)
其中,φ表示傅里叶变换.可以发现,将时域变到谱域的傅里叶变换实质上是求f(x)和以exp(-iwx)为基向量的积分.然后我们对拉普拉斯矩阵进行特征值分解:L=UΛU-1,其中Λ为各个特征值为对角元素的矩阵,U为各个特征值对应的特征向量组成的向量矩阵.由于U是正交矩阵,所以L=UΛU-1=UΛUT.再将传统傅里叶变换的基底exp(-iwx)用UT替换,并用矩阵的形式表示出来,得到图上y的傅里叶变换为![]() 同理,可以得到逆变换
同理,可以得到逆变换![]()
由卷积定理,任意函数的傅里叶变换是函数傅里叶变换的乘积,将其用逆变换的形式表示为
f*g=φ-1(φ(f)·φ(g)).
(4)
然后利用上面得到的图上傅里叶变换及其逆变换,便可以得到最终图上的卷积形式:
f*g=U(UTf·UTg),
(5)
其中,f和g分别表示图上的信号.我们把UTg写作gθ,看作一个以θ为参数的卷积核:
f*g=UgθUTf.
(6)
对于式(6),可以将其分解开来理解,其中UTf为图上信号的傅里叶变换,gθUTf为在谱域傅里叶变换之后的卷积,UgθUTf是卷积之后的逆变换,便得到图上的卷积形式.
1.1.2 模 型
文献[32]是将CNN泛化到非欧氏空间的论文,称之为“第1代GCN”,其主要的贡献是设计了在不规则网格上CNN的应用.为了更新节点特征,其定义的第k层输出为
(7)
其中,j=1,2,…,fk,Fk,i,j为卷积核,含有可学习的参数,xk,i为第k层第i个节点的特征,fk为更新后节点输出特征的维度,fk-1为聚集节点输入特征的维度,h为非线性激活函数.这样就输出了聚集后新的节点特征,并且完成了降维的操作.同时,加入了一个可学习的卷积核.非常巧妙地将传统的CNN迁移到了图上,这就不再要求待处理数据具有平移不变性.完美地适应于图结构数据的节点无序、邻居个数不确定的特性.
该方法虽然在图上实现了卷积运算,利用邻居节点特征表征了中心节点特征,实现了GCN一个质的飞跃,为谱域GCN的发展奠定了基石.但第1代GCN的缺点也是非常明显的.首先,在更新中心节点特征时利用上一层的节点特征不一定是该中心节点的邻居节点.谱域的GCN是基于拉普拉斯矩阵的,没有利用含有邻居信息的邻接矩阵,所以不具有局部性.其次,该方法的计算复杂度为O(n2),计算开销非常大,每次都需要对拉普拉斯矩阵进行特征分解.
针对第1代GCN的局限性,文献[33]利用切比雪夫多项式去近似卷积核,设计了一种新的卷积核,提出了切比雪夫网络(Chebyshev network, ChebNet).ChebNet大大降低了计算复杂度,提高了计算效率.ChebNet利用迭代K次的切比雪夫多项式Tk(x)对式(4)中的gθ进行替换拟合:
(8)
其中,![]() 为以拉普拉斯矩阵L特征值为对角元素的矩阵,λmax为其最大特征值.θ为切比雪夫系数,并且切比雪夫多项式的递推关系为Tk(x)=2xTk-1(x)-Tk-2(x),T0=1,T1=x.将式(8)利用切比雪夫多项式拟合的gθ替换式(5)中的卷积核Fk,i,j:
为以拉普拉斯矩阵L特征值为对角元素的矩阵,λmax为其最大特征值.θ为切比雪夫系数,并且切比雪夫多项式的递推关系为Tk(x)=2xTk-1(x)-Tk-2(x),T0=1,T1=x.将式(8)利用切比雪夫多项式拟合的gθ替换式(5)中的卷积核Fk,i,j:
![]()
![]()
![]()
(9)
其中,![]()
ChebNet相较于第1代GCN,在计算效率上有了明显的提升.比较式(7)(9),不难看出式(7)中没有了拉普拉斯矩阵L的特征向量U,而是变换为了![]() 这就不需要再对L进行耗时的特征分解操作,将会使计算效率大大提高.但在替换拟合过程中采用了K次迭代的切比雪夫多项式,这也使得ChebNet具有一定的局部性.在文献[33]中作者同时还给出了图卷积的结构形式,如图3所示.图卷积包含4部分:1)输入的图信号,图3中以词袋为例;2)特征提取,也就是卷积层,在该卷积层中通过卷积和非线性激活函数,最后再由下采样和池化完成图上的特征提取;3)通过一个全连接层完成对图的分类;4)输出信号,输出各个节点的标签实现整个分类任务.
这就不需要再对L进行耗时的特征分解操作,将会使计算效率大大提高.但在替换拟合过程中采用了K次迭代的切比雪夫多项式,这也使得ChebNet具有一定的局部性.在文献[33]中作者同时还给出了图卷积的结构形式,如图3所示.图卷积包含4部分:1)输入的图信号,图3中以词袋为例;2)特征提取,也就是卷积层,在该卷积层中通过卷积和非线性激活函数,最后再由下采样和池化完成图上的特征提取;3)通过一个全连接层完成对图的分类;4)输出信号,输出各个节点的标签实现整个分类任务.
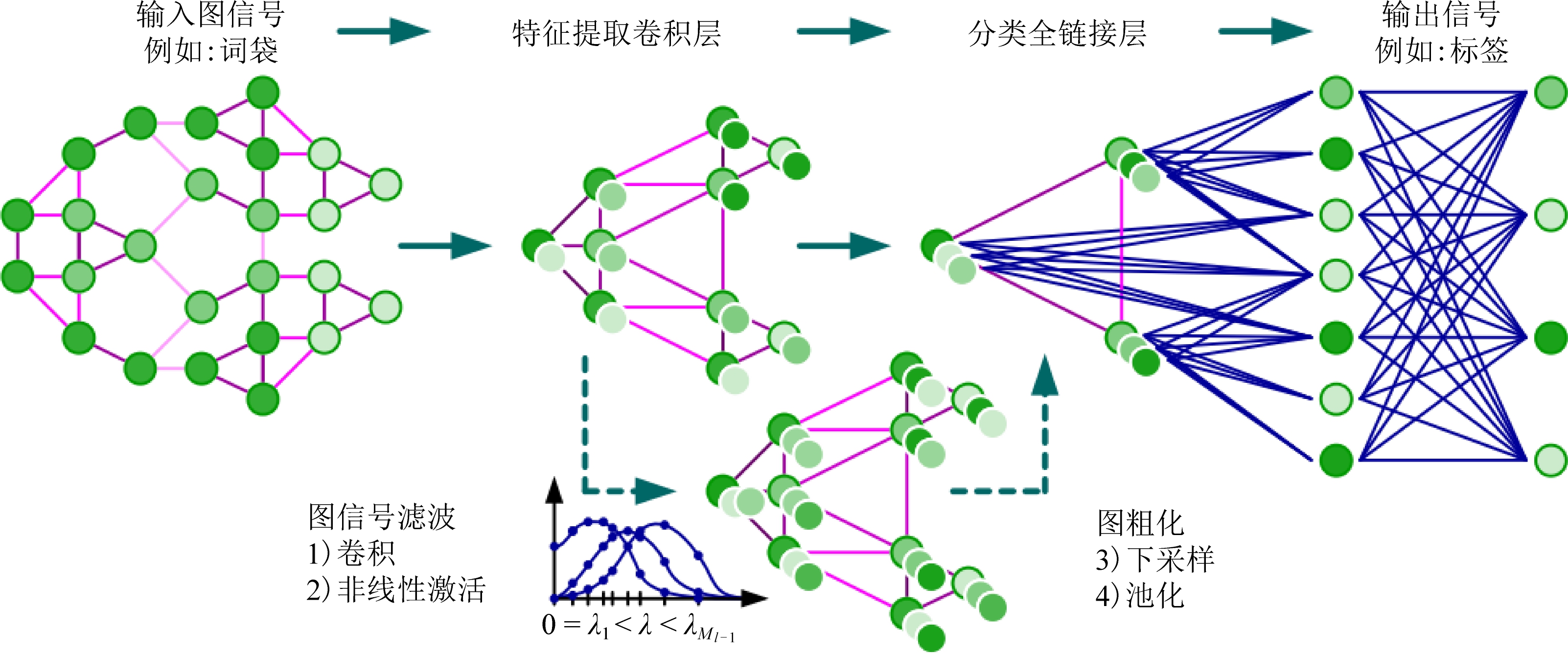
Fig. 3 The structure of graph convolution[33]
图3 图卷积的结构[33]
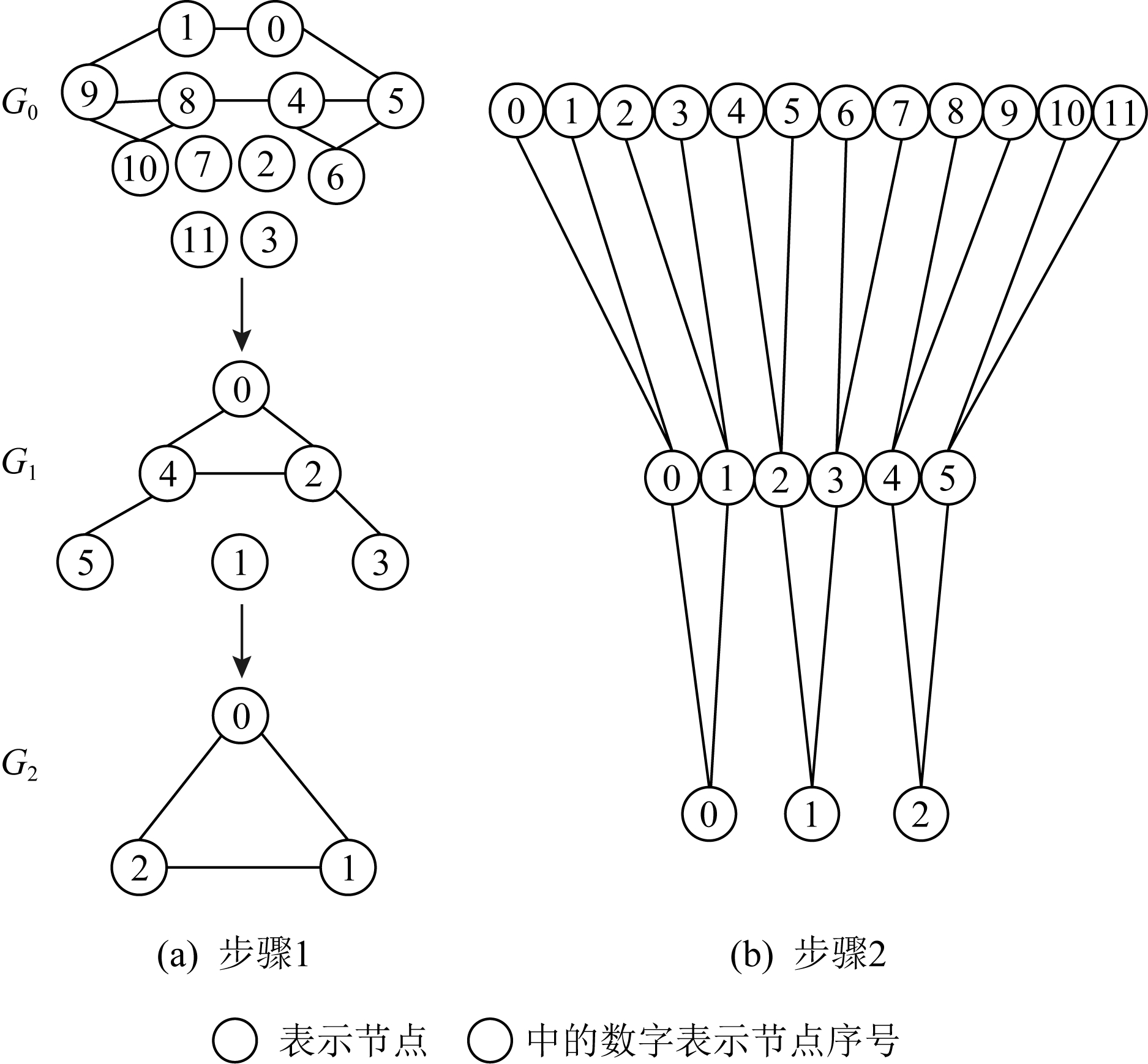
Fig. 4 Pooling process
图4 池化过程
文献[33]还提出了一种针对图信号的快速池化过程,该方法采用了一种二叉树的方式,包含创建一个平衡的二叉树和重新排列顶点2个步骤.在池化之后,每个节点要么有2个子节点,要么有1个子节点.将只有1个子节点的父节点图中添加一些辅助节点,使图中的每个顶点都有2个子节点,从而构成一个二叉树.然后将该二叉树平摊构成1维信号,最后对该信号采样即可表示为一次图池化过程.图4为将含有任意排序的8个顶点的图进行池化示例图,选择大小为4的算子对其进行池化操作可以看作是操作2次大小为2的池化算子.为使图4中的每个顶点都有2个孩子,从而可以构成一个二叉树.在G0中增加4个辅助节点,在G1中增加1个辅助节点.经过2次池化可以得到含有3个顶点的G0图.将该过程中的二叉树摊平为如图4右侧1维信号,对其进行采样即表示每一次的池化过程.
第3代GCN[34]考虑将谱域图卷积神经网络应用在实际的半监督场景中,比如引文网络的图结构数据,一些节点的标签未知,需要对节点完成分类的任务.Kipf等人[34]为了使ChebNet有更好的局部连接特性,使用一阶的切比雪夫多项式对其进行简化,令K=1,并令λmax=2,则将式(7)简化为
![]()
![]()
(10)
其中,j=1,2,…,fk.
在该实际应用中,为了进一步限制参数的个数来解决过拟合问题.最小化每层运算复杂性(例如矩阵乘法),于是令θ=θ0=-θ1:
(11)
其中,![]() 即在原来的邻接矩阵上加入了自循环(在聚合邻接节点特征时也考虑了自己的特征),
即在原来的邻接矩阵上加入了自循环(在聚合邻接节点特征时也考虑了自己的特征),![]() 为学习的参数.
为学习的参数.
在该半监督节点分类的问题中,引入了一个简单而灵活的f(X,A)模型,在图上进行有效的消息传播.在数据X和邻接矩阵A上调节模型f(X,A),这是由于邻接矩阵A包含数据X中不存在的信息,如在引文网络中文档之间的引文链接或知识图中的关系情况.
在实验部分的实际分类任务中,首先在预处理阶段得到邻接矩阵![]() 然后,前项传播模型采用2层的GCN网络:
然后,前项传播模型采用2层的GCN网络:
Z=f(X,A)=![]()
(12)
其中,θ为可学习参数,最后通过一个非线性激活函数就可得到每个标签的预测结果.损失函数采用交叉熵表示,评估预测结果为
(13)
其中,yL是所有标签的集合.
为了解决依赖于图傅里叶变换的GCN计算量大的缺点,Xu等人[35]提出了利用图小波变换的图小波神经网络(graph wavelet neural network, GWNN),GWNN通过快速算法获得图小波变换,而无需采用计算量巨大的矩阵分解,从而大大提高了计算效率.不难看出基于谱域的GCN具有一定的局限性.首先是其网络结构不能太大太深,谱域的GCN不适用于大规模图数据上的建模.由于在前向传播过程中,需要用到所有节点的拉普拉斯矩阵.现在实际工业中面临的图结构数据基本上都是成千万上亿的节点,如若用该类方法将所有节点的拉普拉斯矩阵输入,是非常不现实的,计算代价非常大甚至根本无法运行起来.并且在文献[34]中仅仅只采用2层神经网络,当增加层数的时候基于谱域的GCN性能并没有提高,2层的神经网络不能发挥深度学习的优势,所以不能构建更多的隐层也是该类方法的局限之一.能不能构造更大更深的GNN是当前学者研究的热点问题之一,已有不少文献对其进行了分析研究,我们将会在第5节的讨论部分进行详细的探讨.最后,该类方法不能处理有向图结构数据.因为在应用谱理论推导时必须保证拉普拉斯矩阵的对称性才能进行谱分解,进而完成整个数学推导过程.
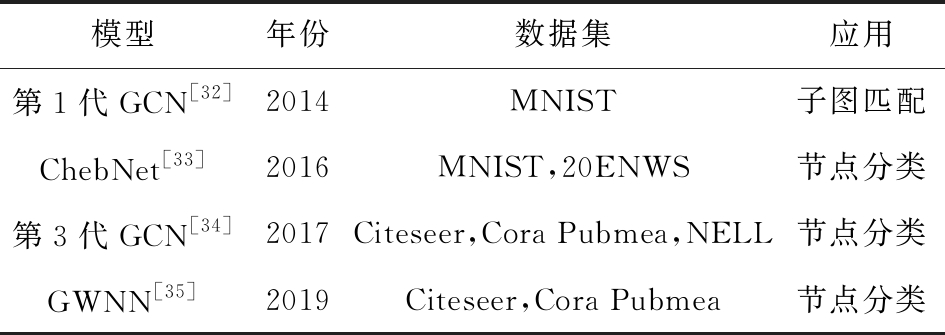
表2对基于谱域的图卷积神经网络模型进行了汇总.但从研究趋势来看,GCN发展方向较倾向于基于空间域的图卷积神经网络,下面将对其进行详细的介绍.
Table 2 Graph Convolutional Neural Network Models Based on Spectral Domain
表2 基于谱域的图卷积神经网络模型
模型年份数据集应用第1代GCN[32]2014MNIST子图匹配ChebNet[33]2016MNIST,20ENWS节点分类第3代GCN[34]2017Citeseer,Cora Pubmea,NELL节点分类GWNN[35]2019Citeseer,Cora Pubmea节点分类
1.2 基于空间域的图卷积神经网络
基于空间域的图卷积神经网络不同于从信号处理理论出发的谱域图卷积神经网络,空间域图卷积神经网络是从图中的节点出发,设计聚集邻居节点特征的聚合函数,采用消息传播机制,思考怎样准确高效地利用中心节点的邻居节点特征来更新表示中心节点特征.CNN的本质是加权求和,空间域的图卷积神经网络正是从CNN的基本构造过程出发,从求和的角度来完成GNN聚合邻居节点的目的.由于图中的节点无序且邻居节点个数不确定,所以空间域的图卷积神经网络的一种思想的2个步骤是:1)固定邻居节点个数;2)给邻居节点排序.如果完成了上述2个步骤,非欧氏结构数据就变成了普通的欧氏结构数据,自然地传统的算法也就可以完全迁移到图上来.其中,步骤1也是便于将GNN应用于节点数量巨大的图上.下面我们首先介绍2个典型的空间域图卷积神经网络模型,然后总结了针对其效率低的改进模型.
1.2.1 模 型
早在2009年文献[36]第1次提出了空间域的图卷积神经网络——NN4G(neural network for graphs),但当时没有引起人们的注意.直到2016年文献[11]提出了一种新的思路来解决如何使CNN能够高效地处理图结构数据,设计了对任意的图卷积神经网络的方法,作者称之为PATCHY-SAN(select-assemble-normalize).该方法首先从图中选择一个固定长度的节点序列;然后对序列中的每个节点,收集固定大小的邻居集合;最后,对由当前节点及其对应的邻居构成的子图进行规范化.通过以上3个步骤来构建卷积,这样就把原来无序且数量不定的节点变成了有序数量固定的节点,下面将对每一个步骤进行详细的介绍,为了方便理解每一步均配有对应的图示说明:
1) 节点序列选择.对于输入的图,首先定义一个要选择的中心节点个数的w.在节点序列选择时主要采用中心化的方法进行选取,越和中心节点关系密切的节点越重要,图5为节点序列选择示意图(w=5).
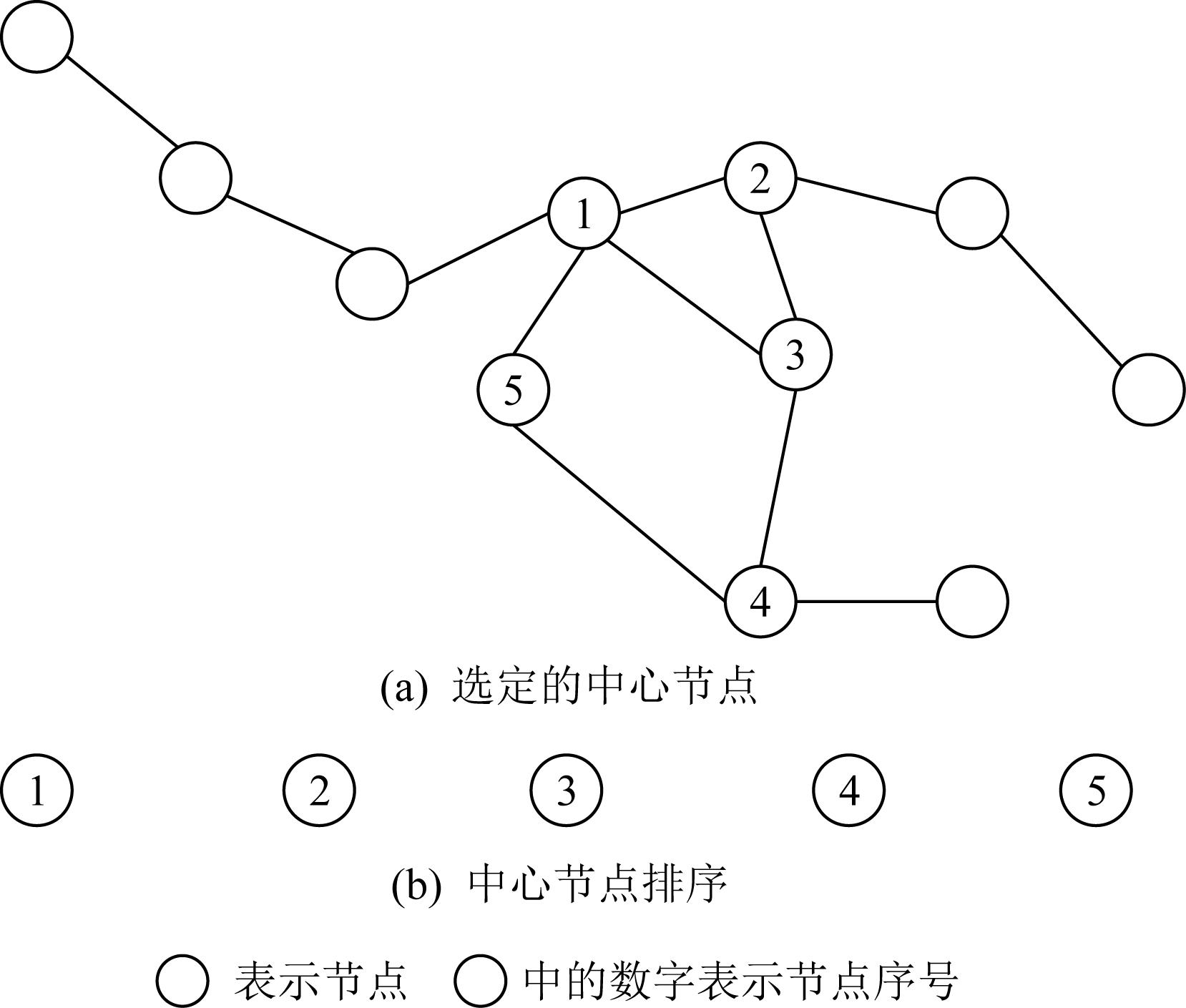
Fig. 5 Node sequence selection(w=5)
图5 节点序列选择(w=5)
2) 收集每个节点固定大小的邻居集合.找到每一个中心节点的邻域,构建一个候选域.然后再从当中选择感知野中的节点,找到中心节点最直接相邻的节点,如果数量不够再从间接相邻的节点中候选,如图6所示:
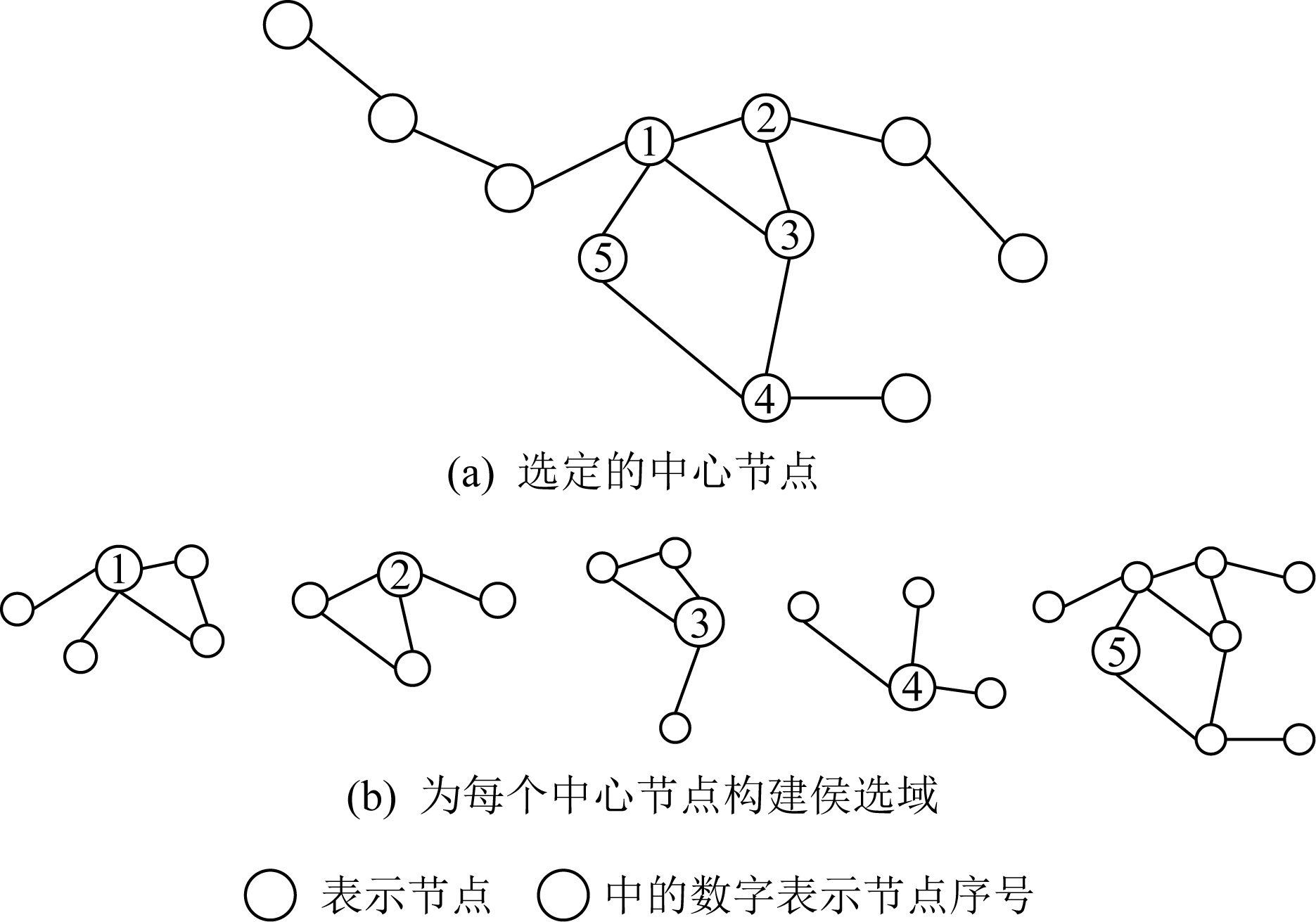
Fig. 6 Select at least 4 nodes(including yourself) for each central node
图6 为中心节点至少选择4个节点(包括自己)
3) 邻域节点规范化.在上一步得到的每一个中心节点的近邻节点个数N可能和设定的个数k不相等.所以,在规范化的过程中就是要为它们标注顺序并进行选择,并且按照该顺序映射到向量空间当中.如果N<k,补上哑节点(人为增加的邻居节点,以满足预设邻居节点个数);如果N>k,则需要进行排序之后去掉后面的节点.所以对中心节点的近邻节点进行排序是这一步的关键.如图7所示卷积核为4,要选出4个节点,并给每个节点标注顺序标签的实例图.
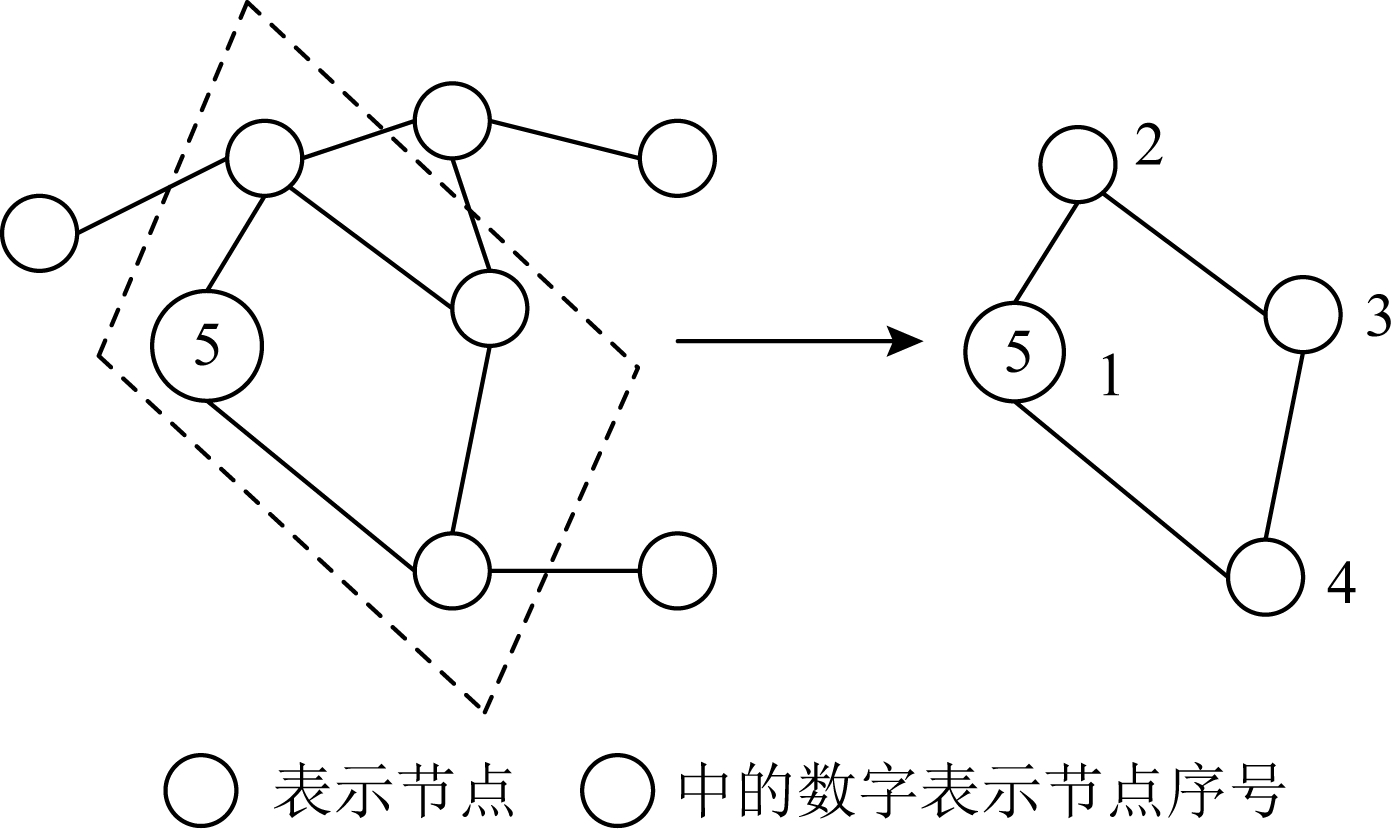
Fig. 7 Neighborhood nodes normalization
图7 邻域节点规范化
Niepert等人[11]定义了数学期望值的大小来衡量标签的好坏,以此来给近邻节点排序.在总的集合当中随机抽取出2个图,计算它们在矢量空间中图的距离和在图空间中的距离差异的期望,期望值越小则表明该近邻节点越好,排在首位.具体的表示形式为
![]()
![]() g[dS(Al(G),Al(G′))-dG(G,G′)],
g[dS(Al(G),Al(G′))-dG(G,G′)],
(14)
其中,l是给标签排序的过程,g是未标记的图的集合,dS是矩阵中的距离函数,dG是图空间中的距离函数,Al是标签的邻接矩阵.
同样为了给中心节点的邻居节点固定数量和排序,文献[12]设计了一个可学习的卷积层,能够根据邻居节点的排列顺序选择固定数量的节点个数,从而完成图结构数据向欧氏结构数据的转化.可学习的卷积层包含将图结构数据转化为欧氏结构数据和进行卷积运算2个部分,逐层传播规则公式为
![]()
(15)
其中,Xl为输入矩阵,K为预设要选择的邻居节点最大个数,g(·)为将图结构数据转换为欧氏结构数据的函数.在完成上述映射之后,数据结构已经变为我们经常处理的标准欧氏数据结构,函数c(·)可选用标准的一阶卷积算子,完成聚合节点特征的操作.这里只介绍函数g(·)的实现过程,这也是实现空间卷积的核心操作.我们以一个具体的实例来说明函数g(·)的实现过程,如图8所示,然后再将其一般化.
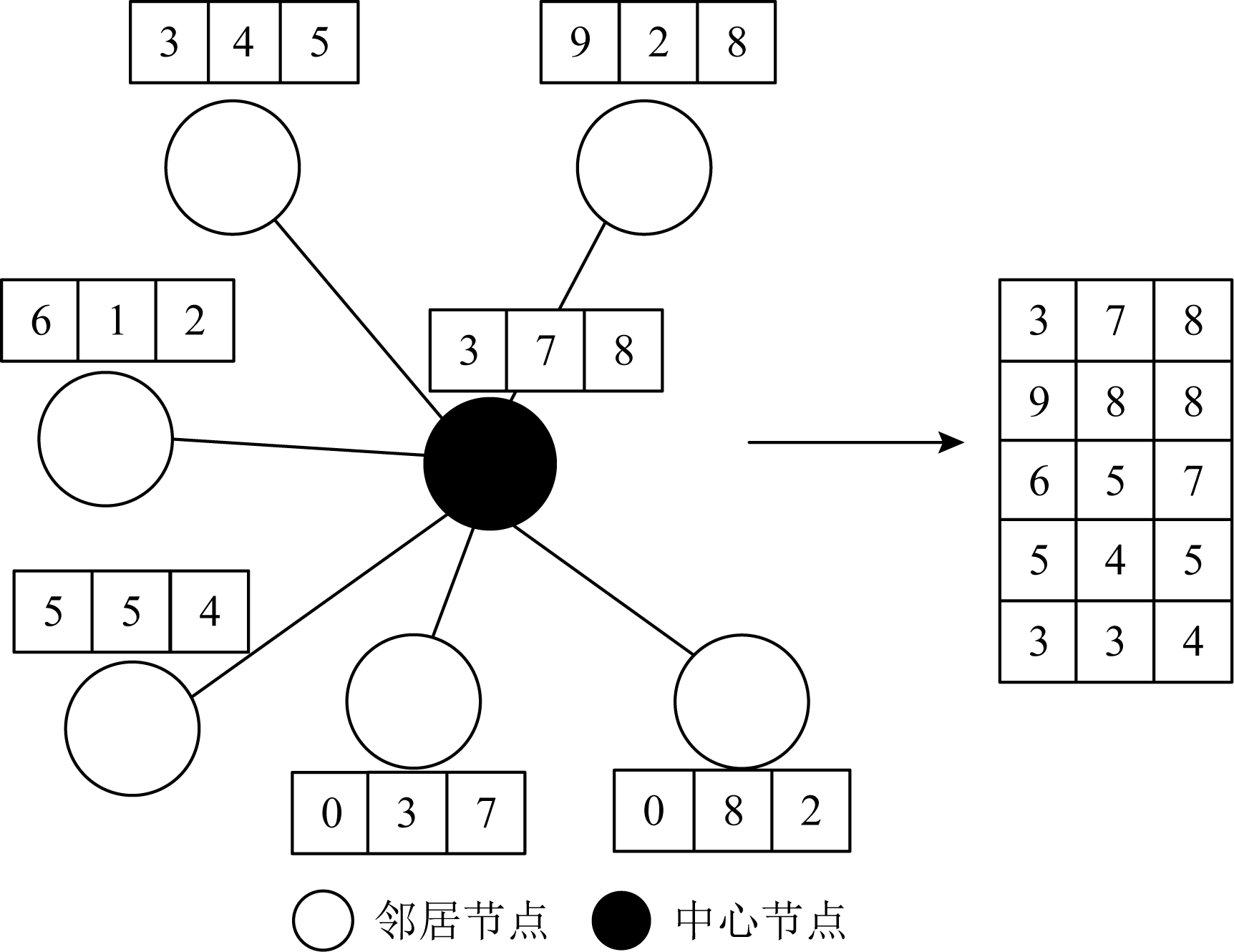
Fig. 8 The realization process[12]
图8 实现过程[12]
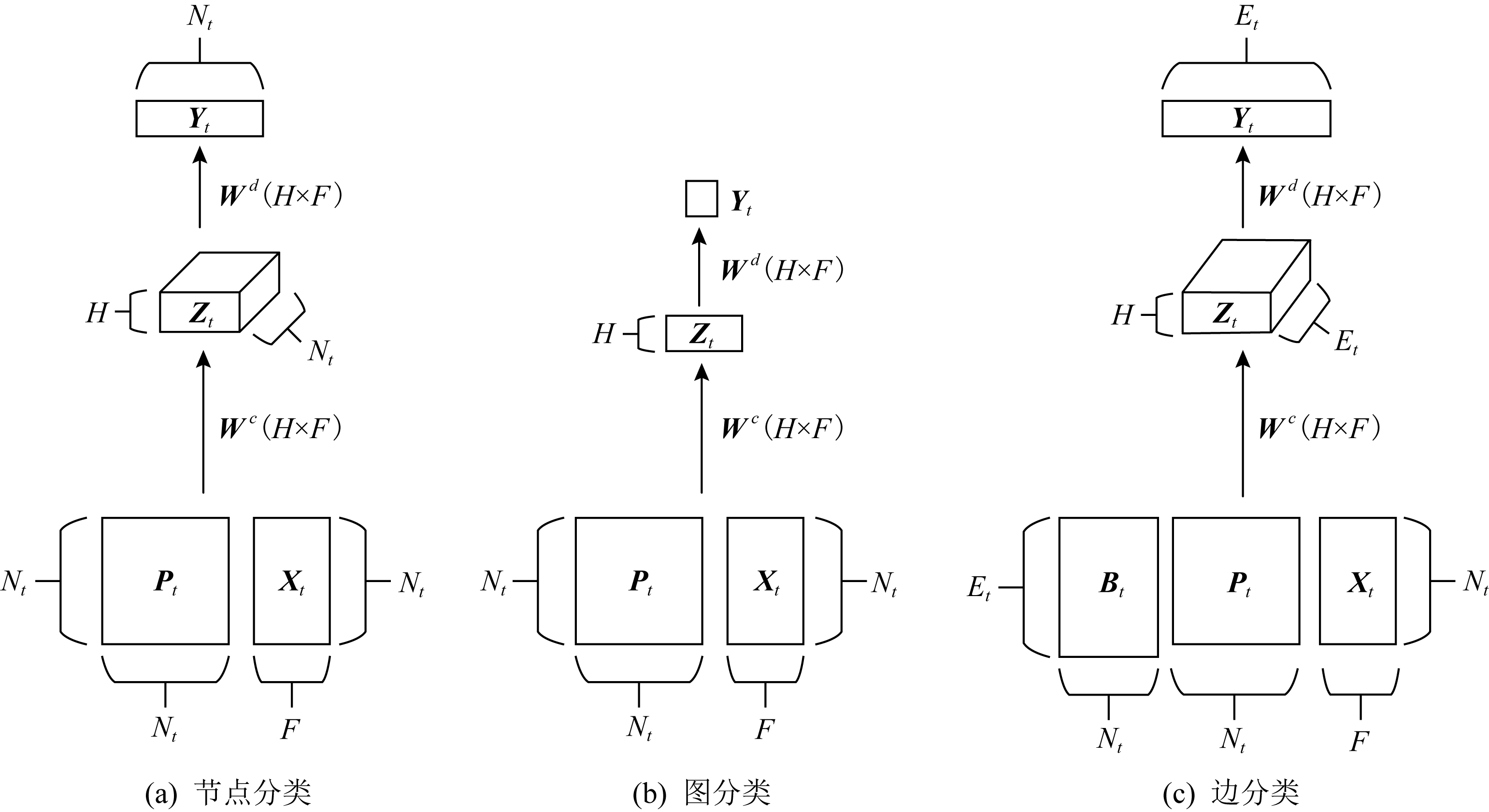
Fig. 9 Different classification tasks[13]
图9 不同分类任务[13]
图8为k=4的实例图,即选择中心节点(实心圆)的4个邻居节点来表征中心节点.该中心节点有6个邻居节点,每个节点特征的维度是3.首先将6个邻居节点的第1维特征从大到小排序,然后选择前4个作为4个邻居节点的第1维特征,第2维和第3维特征按此方法依此类推,便可以得到4个邻居的特征.这样将图结构数据转化为了标准的欧氏结构数据.将其一般化,首先明确需要固定邻居节点的个数为k.假设N个节点的特征向量为![]() 其中xl∈
其中xl∈![]() N×C,即每个节点有C个特征.通过查找邻接矩阵A可以计算出中心节点i有n个邻居节点,用{i1,i2,…,in}表示,将其连接起来可以表示为
N×C,即每个节点有C个特征.通过查找邻接矩阵A可以计算出中心节点i有n个邻居节点,用{i1,i2,…,in}表示,将其连接起来可以表示为![]() 得到矩阵
得到矩阵![]() 如果n<k,则用0补全矩阵.然后对
如果n<k,则用0补全矩阵.然后对![]() 中的第1列从大到小排序,选取前k个值.执行此操作直到第C列.最后再将中心节点自己的特征
中的第1列从大到小排序,选取前k个值.执行此操作直到第C列.最后再将中心节点自己的特征![]() 放在第1行,就可以得到处理完成之后的矩阵
放在第1行,就可以得到处理完成之后的矩阵![]()
![]() (k+1)×C.
(k+1)×C.
不同于对邻居节点排序和确定数量,文献[13]通过对图结构输入中的每个节点扫描其扩散过程来构造隐表示,提出了扩散卷积神经网络(diffusion-convolutional neural networks, DCNN).DCNN认为封装图扩散的表示比图本身可以提供更好的预测基础,利用了节点、边或者图的邻接矩阵来考虑各个处理对象的不同深度邻居的特征信息,所谓的深度就是中心节点的不同阶邻居.并探讨了在图结构数据上各种分类任务中的性能,该模型具有精度高、灵活性强和速度快的优点.如图9为不同分类任务的示意图,其中Nt表示图G的节点个数,F表示节点特征维度,H为各个处理对象的不同深度邻居,Wc为权重张量,Pt为节点度的转移概率矩阵,Xt为所有节点的特征矩阵.DCNN的主要任务是将图G作为输入,输出分类任务的类标签预测值Y或者其概率分布的估计值P(Y|X).将其对应于各个层级的分类任务中,也就是预测每个图形中各个节点的标签,或者每个图形中各个边的标签,或者每个图本身的标签.在图9中假定不同分类任务的扩散卷积表示为Zt.在图9(a)中,节点分类任务返回一个Nt×H×F的张量.在图9(c)中,边分类任务返回Mt×H×F的矩阵.而图9(b)图分类任务中返回一个H×F的矩阵.
1) 在图9(a)中,节点分类任务表示为
(16)
其中,t,i,j,k分别代表图、节点、深度和特征.![]() 为包含能量序列Pt的Nt×H×Nt张量.式(16)写成矩阵的形式为
为包含能量序列Pt的Nt×H×Nt张量.式(16)写成矩阵的形式为
![]()
(17)
最后,通过一个全连接层得到对Y的预测(表示为![]() 并通过最大软函数找到条件概率分布P(Y|X):
并通过最大软函数找到条件概率分布P(Y|X):
![]()
(18)
P(Y|X)=softmax(f(Wd⊙Z)).
(19)
2) 通过对上述节点分类任务取均值,便可以将DCNN扩展到图分类任务上,如图9(b)所示,其数学公式形式为
![]()
(20)
其中,![]() 是1个Nt×1的向量.
是1个Nt×1的向量.
3) 通过1)和2)已经完成了图和节点层面的分类任务,边分类任务是对与该边首尾连接的节点进行转化,将边分类任务同样转化到节点的分类任务中.新的邻接矩阵![]() 通过在原来的邻接矩阵At上增加一个关联矩阵得到:
通过在原来的邻接矩阵At上增加一个关联矩阵得到:
![]()
(21)
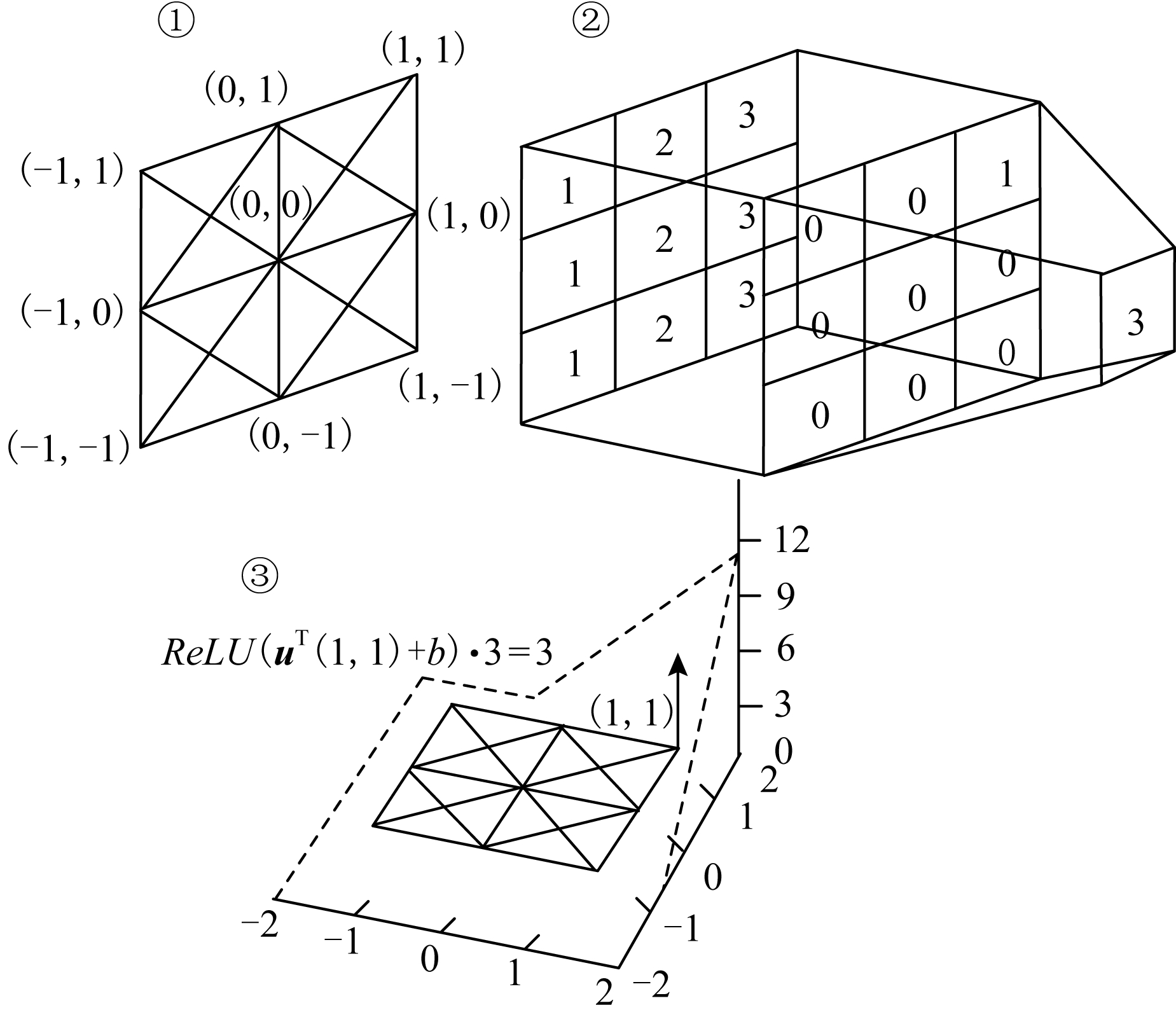
Fig. 10 The motivation of method[37]
图10 方法动机[37]
![]() 可以被用于计算
可以被用于计算![]() 然后替换Pt,如图9(c),以此来完成对边的分类任务.通过分析上述的空间GCN模型不难发现,它们都没有考虑节点空间位置的结构信息,而是仅仅借助邻接矩阵来利用邻居节点信息.但在处理如化学合成物等3维空间信息时,邻接矩阵往往不能完全保留图结构的全部信息.Spurek等人[37]为了解决这个问题,提出了几何图卷积网络(geometric graph convolutional neural networks, geo-GCN),该网络利用节点的空间特征来聚合邻居节点的信息,使用空间特征有效地学习位于空间中的图.试图在传统的GCN中加入空间信息来构造更加一般化的图卷积网络.我们首先介绍该方法的动机,如图10所示.图10中①②为了将卷积算子应用到图中,提取出右上角元素的结果.图10中①表示像素的空间坐标关系,各个邻居节点通过边进行连接.图10中③为将类似卷积运算应用于几何图表示上,最后利用线性修正单元函数进行线性变换(u=(2,2)T,b=-3).然后将其一般化到图结构数据上.
然后替换Pt,如图9(c),以此来完成对边的分类任务.通过分析上述的空间GCN模型不难发现,它们都没有考虑节点空间位置的结构信息,而是仅仅借助邻接矩阵来利用邻居节点信息.但在处理如化学合成物等3维空间信息时,邻接矩阵往往不能完全保留图结构的全部信息.Spurek等人[37]为了解决这个问题,提出了几何图卷积网络(geometric graph convolutional neural networks, geo-GCN),该网络利用节点的空间特征来聚合邻居节点的信息,使用空间特征有效地学习位于空间中的图.试图在传统的GCN中加入空间信息来构造更加一般化的图卷积网络.我们首先介绍该方法的动机,如图10所示.图10中①②为了将卷积算子应用到图中,提取出右上角元素的结果.图10中①表示像素的空间坐标关系,各个邻居节点通过边进行连接.图10中③为将类似卷积运算应用于几何图表示上,最后利用线性修正单元函数进行线性变换(u=(2,2)T,b=-3).然后将其一般化到图结构数据上.
图10的计算过程为:利用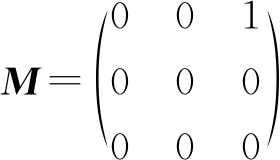 考虑线性卷积,将右上角的元素3提取出来.这样图10中每个点的坐标q-p∈{-1,0,1}2,其中像素的邻域坐标p=(px,py)T可以通过像素坐标q=(qx,qy)T来确定.然后通过向量u∈
考虑线性卷积,将右上角的元素3提取出来.这样图10中每个点的坐标q-p∈{-1,0,1}2,其中像素的邻域坐标p=(px,py)T可以通过像素坐标q=(qx,qy)T来确定.然后通过向量u∈![]() 2和偏差b∈
2和偏差b∈![]() 来定义图算子:
来定义图算子:
![]()
![]()
(22)
在图10中,u=2η,b=-3,其中η=(1,1)T,很容易观测到:
![]()
(23)
其中,z=q-p∈{-1,0,1}2,结果可以等价于利用矩阵M将右上角中的元素3提取出来.
将上述过程一般化,则可以定义geo-GCN公式.首先定义每个节点vi的坐标pi∈![]() t.为了更好地进行图表示,将一般化的卷积转换为
t.为了更好地进行图表示,将一般化的卷积转换为
![]()
(24)
其中,u∈![]() t,b∈
t,b∈![]() 是可学习参数,它们是相当于对邻居节点vi操作的卷积滤波器.类似于传统的卷积,这个变换可以扩展到多重的滤波器.使用U=(u1,u2,…,uk)和b′=(b1,b2,…,bk)来定义k个滤波器,中间的向量表示
是可学习参数,它们是相当于对邻居节点vi操作的卷积滤波器.类似于传统的卷积,这个变换可以扩展到多重的滤波器.使用U=(u1,u2,…,uk)和b′=(b1,b2,…,bk)来定义k个滤波器,中间的向量表示![]() 定义为
定义为![]() 最后对这些向量应用多层感知机就可以得到将节点位置信息考虑在内的最终结果.
最后对这些向量应用多层感知机就可以得到将节点位置信息考虑在内的最终结果.
除了上述经典的模型之外,学者对图卷积神经网络进行了更一步的研究.比如,Jiang等人[38]针对现有的GCN通常使用固定图的弊端,提出了一种通过将图学习和图卷积集成在一个统一的网络体系结构中的图学习卷积网络(graph learning convolution neural network, GLCN),用于图数据表示和半监督学习,在半监督学习场景下学习一种最适合GCN的最优图结构.Brockschmidt[39]提出了关系图动态卷积网络(relational graph dynamic convolutional networks, RGDCN)和一种新的基于特征的线性调制模型 GNN-FiLM(GNN type using feature-wise linear modulation)探索利用超参数网络对图进行学习.Jiang等人[40]提出了一个高斯诱导卷积(Gaussian induced convolution, GIC)框架来对不规则图进行局部卷积滤波.Zhou等人[41]提出了一种通用弧形结构的高阶图卷积网络和自适应图卷积网络(high-order and adaptive graph convolutional network, HA-GCN),其中高阶算子为了保障在实现卷积时能够到达k跳邻居,自适应滤波模块根据局部图连接和节点特征动态调整卷积运算符的权重.Chami等人[42]提出了一个归纳式双曲图卷积神经网络(hyperbolic graph convolutional neural network, HGCN),利用GCN的表达能力和双曲几何来学习分层的无标度图的归纳节点表示,来解决GCN在处理双曲几何结构时存在难以定义卷积算子和不清楚如何将特征转移为具有适当曲率的双曲线的困难.
同时,Zhang等人[43]提出了通过参数随机图模型合并不确定图信息方法的贝叶斯图卷积神经网络(Bayesian graph convolutional neural networks, BGCN),将观察到的图视为来自随机图的参数族的实现,解决了GCN在处理图结构的相关不确定性方面存在的问题.Pal等人[44]提出了一种BGCN处理节点分类任务的非参数生成模型,并将其整合到BGCN框架中,同时,作者又在文献[45]中介绍了基于复制节点的选择生成式模型,同样将其整合到了BGCN框架中.这种改进的最大优点在于使用了图拓扑推断中节点特征和训练标签提供的信息,结果表明该方法在处理节点分类任务时也有着不俗的表现.
1.2.2 针对计算效率低的改进模型
1.2.1节模型虽然在空间域上实现了将传统的卷积算子转移到图结构数据上,有效地聚集了邻居节点的信息.但当利用神经网络对各个模型进行训练时,却发现每个模型的训练效率是非常低的.这是由于在每一轮训练中都需要将整个图的节点作为输入,但在实际的处理任务中,一般需要处理的图节点数量是非常多的,这就需要占用较大的计算资源和内存,使1.2.1节模型无法应用于大图.针对训练效率低的问题,很多学者进行了研究探索.来源于深度模型在处理大图片时采用随机切片的灵感,LGCN[12]提出了一种子图训练的方法.由于该方法简单有效,我们以一个实际的具体例子进行阐述,如图11所示:
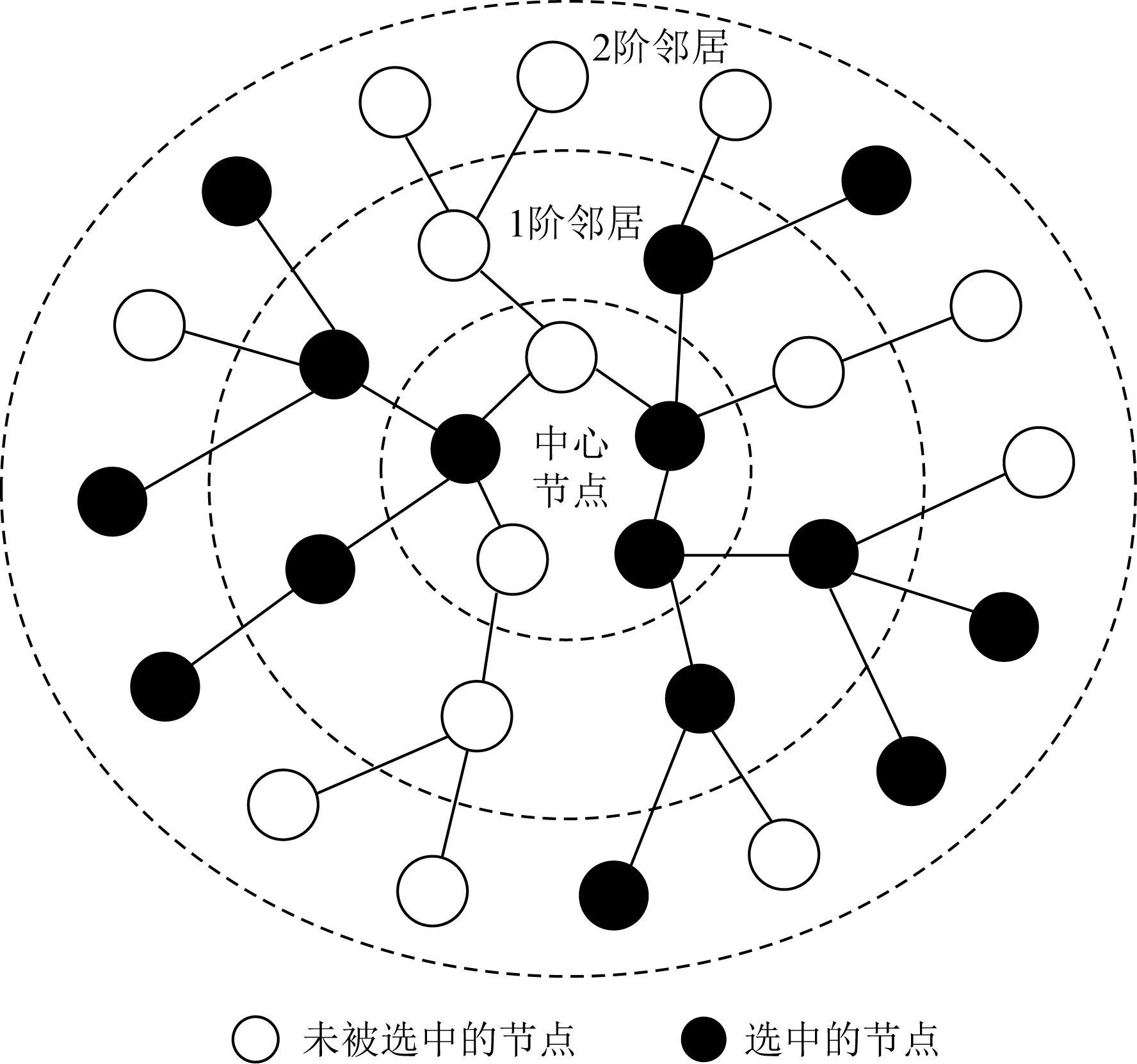
Fig. 11 Method of subgraph training[12]
图11 子图训练方法[12]
在图11中,我们的目标子图是要包含15个节点,首先对中心节点初始化选择3个节点,然后对初始化的3个节点的一阶邻居采用深度第一的搜索方法随机选择5个节点,完成第1次迭代.在下一次迭代中,在二阶邻居节点随机选择7个节点.通过2次迭代便完成了子图的构造,简单有效地解决了训练效率低的问题.这其中的迭代次数可以根据自己需要进行配置.
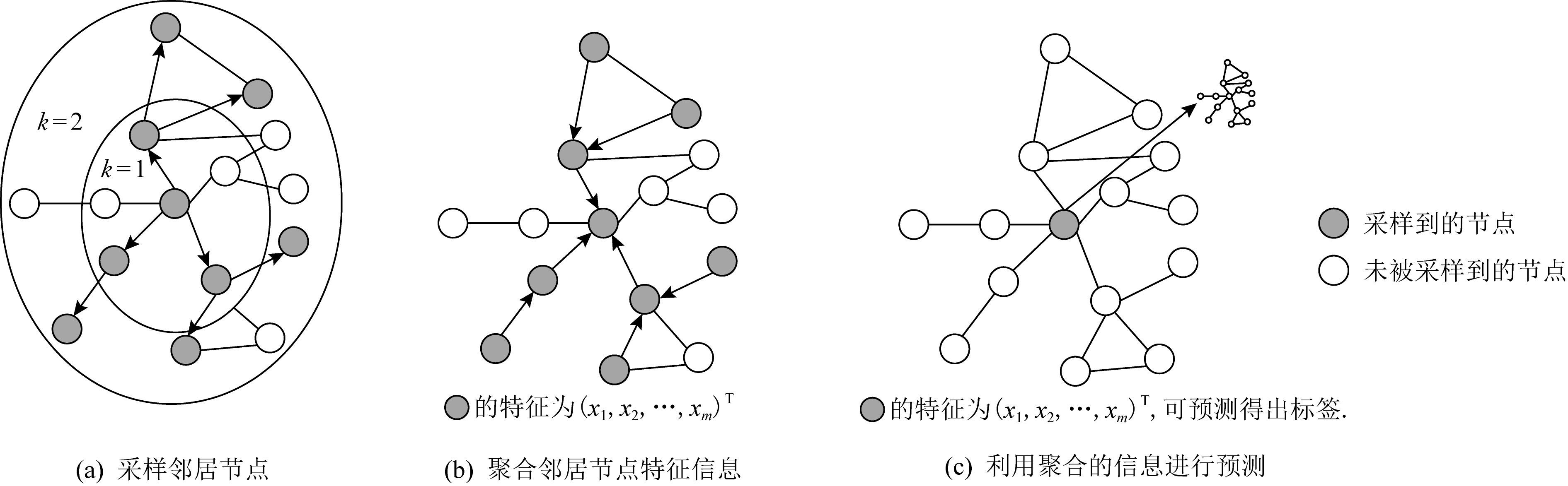
Fig. 12 The overall idea of the GraphSAGE algorithm[46]
图12 GraphSAGE算法的整体思路[46]
同样,为了使图卷积神经网络能够应用于大规模的图上,文献[46]提出了一种针对图结构数据的归纳式的学习方法——图采样和聚集方法(graph sample and aggregate, GraphSAGE).GraphSAGE不是学习某个具体节点的嵌入表示,而是学习用于采样和聚集邻居节点来生成节点新的嵌入表示的聚合函数.它不像先前直推式的方法针对固定的图结构,在训练时所有节点的信息必须事先知道.由于现实中很多图是不断变化,一些节点信息是未知的.所以要对将要出现的看不见的节点进行嵌入,或者是对完全新的子图进行嵌入表示.通过GraphSAGE方法学习到的聚合函数可以应用于当图动态增加节点的情景,这就使得GraphSAGE能够应用于大规模的图结构数据上.该方法总共包含3个步骤,如图12所示:1)采样邻居节点,采样中心节点的一阶和二阶邻居节点;2)设计聚合函数,利用邻居节点来表征中心节点;3)将聚集的邻居节点信息利用多层神经网路对中心节点进行预测.GraphSAGE的核心思想是学习聚集邻居节点特征的聚合函数,分别给出了均值聚集、长短时间记忆聚集(long short term memory, LSTM)和池化聚集3个候选聚合函数.
1) 均值聚集.该方法通过求各个邻居节点向量![]() 的均值,和直推式图卷积神经网络的方法基本类似:
的均值,和直推式图卷积神经网络的方法基本类似:
![]()
(25)
![]() 表示节点v在步骤k的嵌入向量.该聚合函数和其他聚合最大的区别是它不执行聚集邻居向量
表示节点v在步骤k的嵌入向量.该聚合函数和其他聚合最大的区别是它不执行聚集邻居向量![]() 连接当前节点的前一层
连接当前节点的前一层![]() 联级操作,而是采用了一种可以被看作跳跃连接的执行方式.
联级操作,而是采用了一种可以被看作跳跃连接的执行方式.
2) 基于LSTM聚集.该方法比均值聚集有更强大的表达能力.由于LSTM以顺序方式处理输入数据,所以LSTM不是置换不变的.若要使LSTM适应图结构数据的无序集合,只需对邻居节点进行随机排列即可.
3) 池化聚集.在这种聚集方法中,每个邻居的向量都通过全连接的神经网络独立反馈.在完成此转换之后,将最大池化聚集应用于聚合各个邻居信息的聚合操作中:
![]() ∀ui∈N(v)},
∀ui∈N(v)},
(26)
其中,max代表取各个元素的最大值.
GraphSAGE的采样体现在上述3个聚合函数中,它不是聚合中心节点的所有邻居节点,而是首先采样一定数量的邻居节点再进行处理.这样就把要处理的节点数量限制在某个区间之内,不再需要输入整个图,从而提高了计算效率.从采样角度来说,也同样为GraphSAGE能够处理大图提供了保障.
不同于GraphSAGE采样邻居节点的方法,文献[47]提出了一种针对当前节点所在卷积层的采样方法,称之为快速图卷积网络算法(fast learning with graph convolutional networks, FastGCN).FastGCN是一种结合了重要性采样的批量训练算法,不仅避免了对测试数据的依赖,还为每个批量操作产生了可控的计算消耗.该方法将图的顶点解释为某种概率分布下的独立同分布的样本,并将损失和每个卷积层作为顶点嵌入函数的积分.然后,通过定义样本的损失和样本梯度的蒙特卡罗近似计算积分,可以进一步改变采样分布,以减小近似方差.
GraphSAGE和FastGCN都是固定采样节点个数进行的采样,文献[48]提出了一种能适用于拥有众多节点大图的自适应采样方法.该方法通过在自上而下的网络中逐层构建网络,依据概率的大小对顶层的下层进行采样,其中采样的邻域由不同的父节点共享,并且由于采用固定大小的采样方法而避免了过度扩展.同时该采样器是自适应的,能够明显减少采样方差,从而提高了GCN的计算效率.实验表明该方法相比于GraphSAGE和FastGCN在计算效率上都有明显的提升.在逐层采样中,依据概率的大小定义了前向传播的模型:
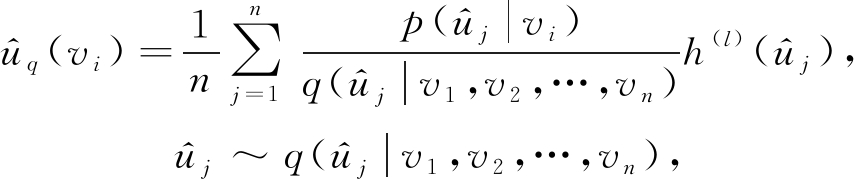
(27)
其中,p(uj|vi)表示在以vi为采样条件下采样uj的概率大小,q(uj|v1,v2,…,vn)表示在当前层所有节点的采样条件下采样uj的概率大小,![]() 为了增加式(27)的计算速度,采用蒙特卡罗均值的近似期望值来计算
为了增加式(27)的计算速度,采用蒙特卡罗均值的近似期望值来计算![]() 便得到逐层采样方法:
便得到逐层采样方法:
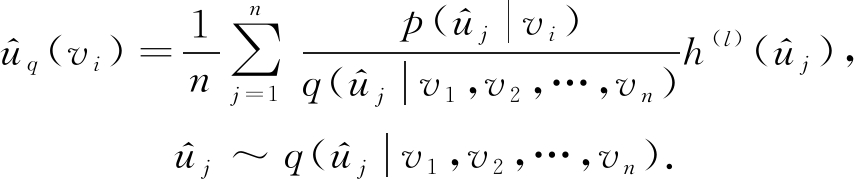
(28)
在该逐层采样策略中采样节点![]() 是被当前层的所有节点所共享的,并且是被父节点可见的,这种共享机制可以加强节点间的消息传播.n表示每一层的固定个数大小,这样总的采样节点个数便会随着网络层数线性增加.
是被当前层的所有节点所共享的,并且是被父节点可见的,这种共享机制可以加强节点间的消息传播.n表示每一层的固定个数大小,这样总的采样节点个数便会随着网络层数线性增加.
文献[49]提出了一种针对图卷积神经网络的随机训练方法.传统的GCN采用从其邻居节点递归计算中心节点的表示方法,导致了感受野大小随层数呈指数增长,致使在计算时占用非常大的内存.该方法是一种基于控制变量的算法,允许对任意邻居大小进行采样,从而控制感受野的大小,减小计算负担.文献[50]提出了一种聚类图卷积的方法(cluster-graph convolutional network, Cluster-GCN),利用图的聚类结构,基于高效的图聚类算法来设计批次,在计算时只需要将节点嵌入存储在当前批处理中.在每个步骤中,Cluster-GCN对与图聚类算法识别的密集子图相关联的节点块进行采样,并将搜索范围限制在该子图的邻域中.这种方法虽然简单但能够有效地减小内存占用率和计算时间,同时能够达到与以前的算法相当的测试精度.Cluster-GCN还可以在不需要太多时间和内存开销的情况下训练更深层的GCN,从而提高了预测精度.这样Cluster-GCN使GNN向做大做深的方向迈进了一大步.文献[51]提出了一种分层的重要性采样方法(layer-dependent importance sampling, LADIES)来解决传统GCN方法在计算时带来的计算时间长和内存消耗大的问题.在当前层的前一层采样节点的基础上,LADIES选择中心节点的邻域节点构造一个二部图,并据此计算重要概率.然后,根据计算的概率对一定数量的节点进行抽样,每层递归地进行这样的过程,构建整个计算图.结果证明,该方法比GraphSAGE占用更小的内存,并且还可以得到较FastGCN更小的方差.文献[52]则提出了一个针对图自编码和变分自编码的通用框架,该方法仅选择节点的子集来训练模型,而不是采用整个图.并且应用了简单有效的消息传播机制,从而提高了图神经网络的计算速度.
表3对基于空间域的图卷积神经网络进行了汇总,分别比较了它们的测试数据集和应用等方面的差异.
Table 3 Graph Convolutional Neural Network Models Based on Spatial Domain
表3 基于空间域的图卷积神经网络模型
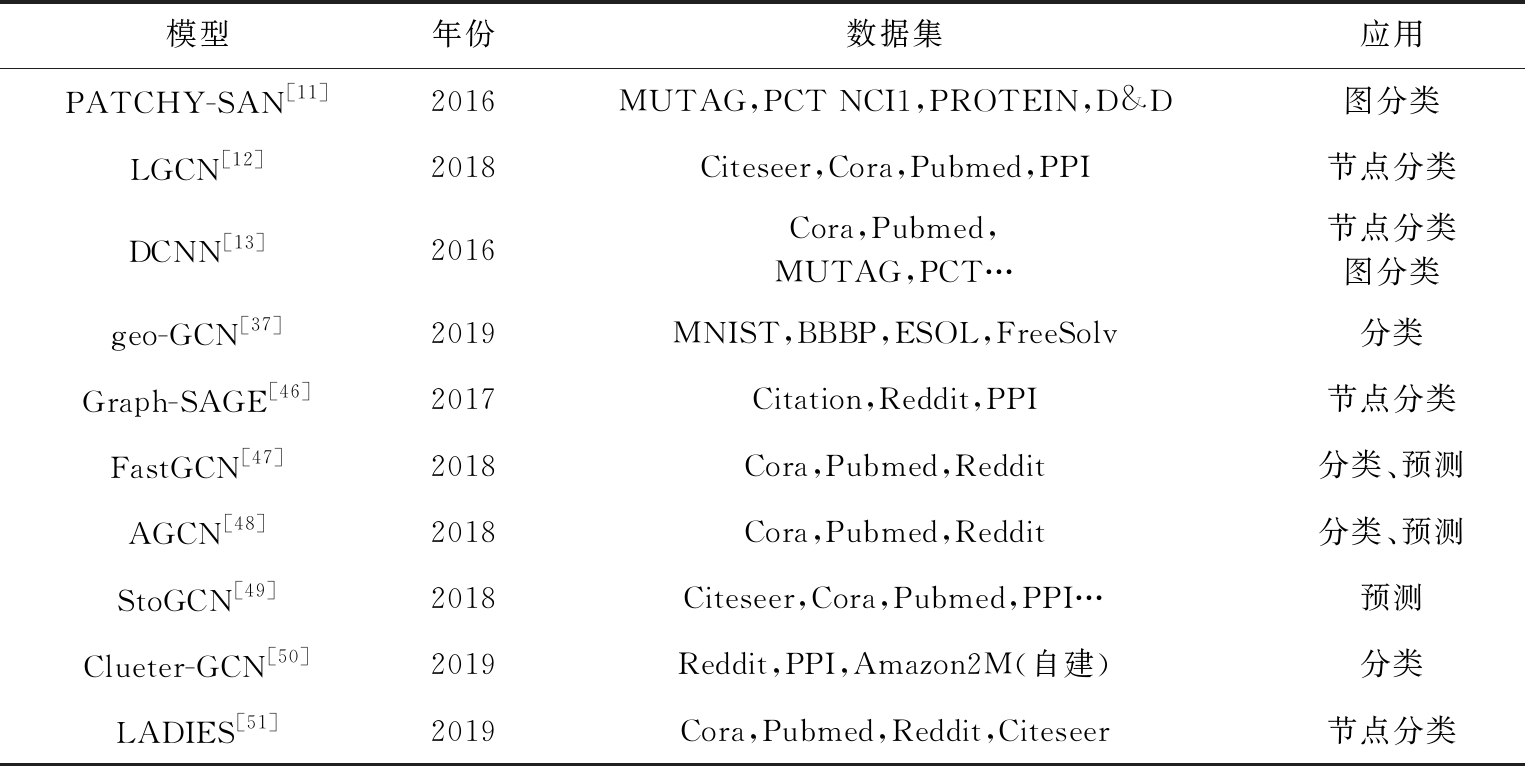
模型年份数据集应用PATCHY-SAN[11]2016MUTAG,PCT NCI1,PROTEIN,D&D图分类LGCN[12]2018Citeseer,Cora,Pubmed,PPI节点分类DCNN[13]2016Cora,Pubmed,MUTAG,PCT…节点分类图分类geo-GCN[37]2019MNIST,BBBP,ESOL,FreeSolv分类Graph-SAGE[46]2017Citation,Reddit,PPI节点分类FastGCN[47]2018Cora,Pubmed,Reddit分类、预测AGCN[48]2018Cora,Pubmed,Reddit分类、预测StoGCN[49]2018Citeseer,Cora,Pubmed,PPI…预测Clueter-GCN[50]2019Reddit,PPI,Amazon2M(自建)分类LADIES[51]2019Cora,Pubmed,Reddit,Citeseer节点分类
1.3 从池化考虑的图卷积神经网络
当前针对图卷积神经网络的研究大多集中在怎样使卷积算子更加适应于图结构数据上,如何设计有效的聚合函数,从而实现对中心节点特征的有效表示.池化操作在传统的卷积操作中扮演着重要的角色,所以在图卷积中的作用也是巨大的,但很多人却忽视了对图池化算子的研究.这是由于很难在图上定义一个统一标准的图池化算子,具有一定的难度,所以对于图池化算子的研究远远落后于其他方面的研究.图池化算子同样在设计深度学习结构时扮演着重要的角色,它能够学习出图的层次结构表示.而当需要处理整个图层面的问题时,图池化算子又是必须要考虑的.所以也有一些学者对图卷积神经网络当中的池化算子进行了研究.
Bianchi等人[53]设计了一种基于minCUT最优化利用可微无监督损失的池化算子,可以和消息传播层混合在一起作为一个单独的神经网络层,如图13所示,为在消息传递层加入minCUT池化层的深度GNN结构.minCUT池化策略通过取多层传播的均值来计算聚类分配矩阵S∈![]() N×K,把每个节点特征xi映射为S的第i行,S=softmax(ReLU(XW1)W2),其中Θpool=W1∈
N×K,把每个节点特征xi映射为S的第i行,S=softmax(ReLU(XW1)W2),其中Θpool=W1∈![]() F×H,W2∈
F×H,W2∈![]() H×K是可训练的参数.通过最小化一般特定任务的损失和无监督损失Lu,可以优化参数ΘMP和Θpool.无监督损失Lu由Lc和Lo两部分组成,其中用于估计指定聚类S的Lc称为切割损失项,正交损失项Lo用于去除产生具有相似大小的聚类簇,避免Lc损失函数产生的正交解.
H×K是可训练的参数.通过最小化一般特定任务的损失和无监督损失Lu,可以优化参数ΘMP和Θpool.无监督损失Lu由Lc和Lo两部分组成,其中用于估计指定聚类S的Lc称为切割损失项,正交损失项Lo用于去除产生具有相似大小的聚类簇,避免Lc损失函数产生的正交解.
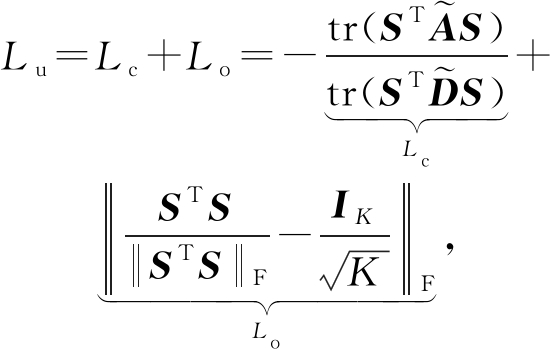
(29)
其中,![]() 表示Frobenius范数.邻接矩阵和图信号的粗化计算公式为
表示Frobenius范数.邻接矩阵和图信号的粗化计算公式为
![]()
(30)
其中,Xpool∈![]() K×F中的元素
K×F中的元素![]() 是第i组中第j个特征的平均权重.
是第i组中第j个特征的平均权重.![]() 是对称矩阵Apool∈
是对称矩阵Apool∈![]() K×K的元素,同时也是第i个族和j个族的边的数量.由于自循环会阻碍处在池化层后的消息传播操作向其邻接节点传播,通过将对角线置0重新计算邻接矩阵:
K×K的元素,同时也是第i个族和j个族的边的数量.由于自循环会阻碍处在池化层后的消息传播操作向其邻接节点传播,通过将对角线置0重新计算邻接矩阵:
![]()
(31)
其中,diag(·)返回对角矩阵.
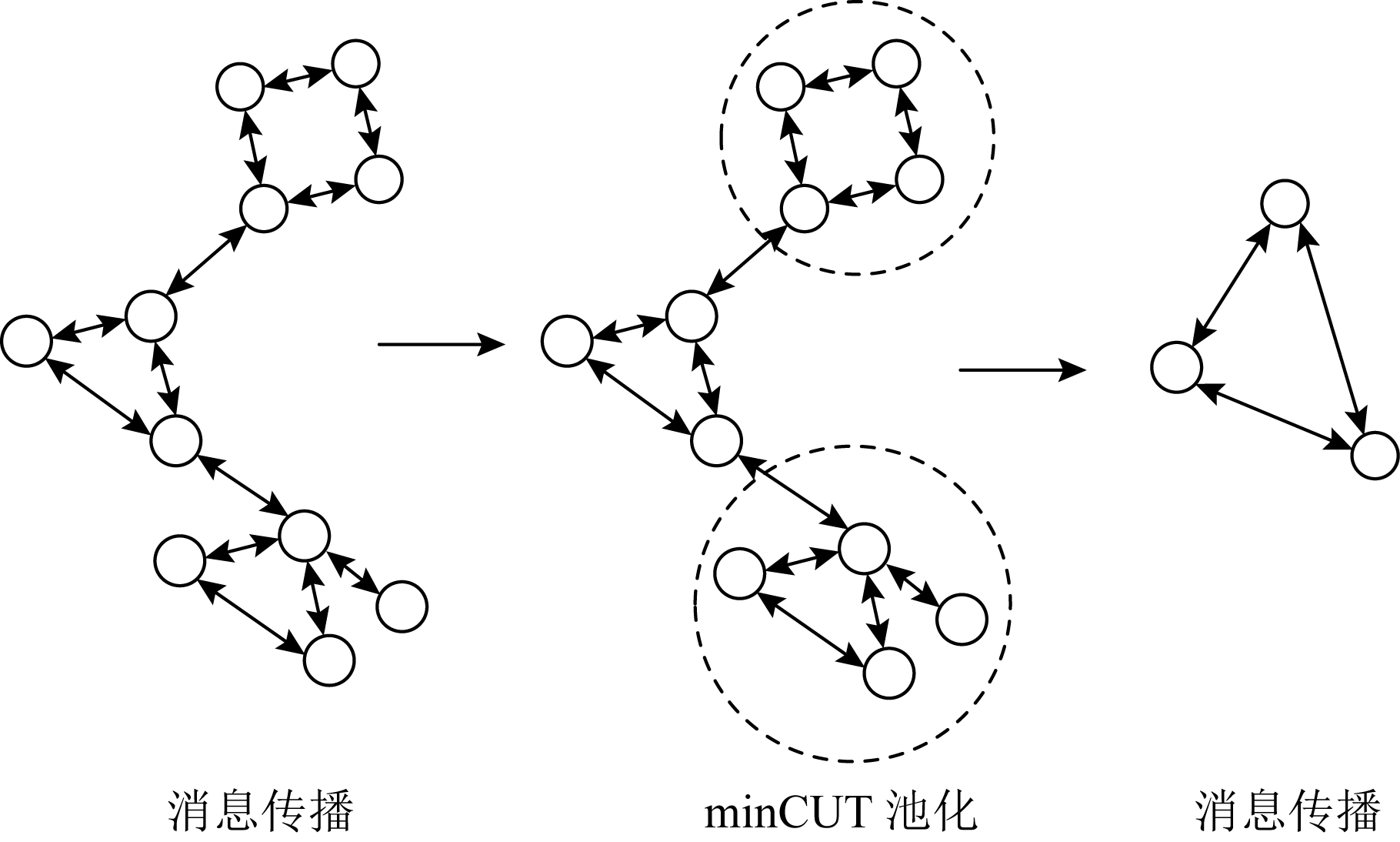
Fig. 13 The deep GNN structure
图13 深度GNN结构
文献[54]提出了带结构学习的层次图池化算子(hierarchical graph pooling with structure learning, HGP-SL).HGP-SL是非参数的,可以充分利用节点特征和图形结构信息,并且自适应地选择节点子集以形成后续层的诱导子图.该方法很容易实现,能够很方便地集成到各种图神经网络结构中.并且可以将图池化算子和结构学习结合到一个统一的模块中,生成图的层次表示.由于1个节点的表示可以通过它的邻域表示来重构,这意味着这个节点可能在池化操作中被删除而几乎没有信息丢失.基于该原因,HGP-SL首先利用曼哈顿距离定义了节点信息的得分:
![]()
(32)
其中,p∈![]() ni表示图中每个节点的得分,
ni表示图中每个节点的得分,![]() 表示L1范数.在获得节点信息得分之后,对图中的节点进行重新排序.为了逼近图的信息,然后选择节点信息得分相对较大的节点.这是由于它们可以提供更多的信息,所以在构造合集图时会保留这些节点.从而完成对图的池化操作,节点选择规则为:
表示L1范数.在获得节点信息得分之后,对图中的节点进行重新排序.为了逼近图的信息,然后选择节点信息得分相对较大的节点.这是由于它们可以提供更多的信息,所以在构造合集图时会保留这些节点.从而完成对图的池化操作,节点选择规则为:
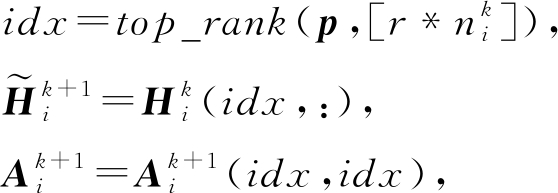
(33)
其中,r表示池化速率,top_rank(·)表示返回前![]() 的值索引的函数.
的值索引的函数.![]() 和
和![]() 分别表示从节点表示矩阵和邻接矩阵提取选择出来的行或者列.在下一层中,利用处理后的节点表示矩阵和邻接矩阵就可以完成针对图的池化操作.
分别表示从节点表示矩阵和邻接矩阵提取选择出来的行或者列.在下一层中,利用处理后的节点表示矩阵和邻接矩阵就可以完成针对图的池化操作.
文献[55]认为图中节点之间空间位置信息非常重要,提出了在图池化中将图的结构信息考虑其中的STRUCTPOOL方法.图池化的目的是为了减少图中的节点数目并学习新的表示.假设将有n个节点的原始图G池化成有k个节点的新图![]() 方法将图池化看作一个节点聚类问题,其目的是学习出一个簇分配矩阵M∈
方法将图池化看作一个节点聚类问题,其目的是学习出一个簇分配矩阵M∈![]() n×k.在池化时将n个节点分配给k个不同的簇,然后将每个簇转化为新图
n×k.在池化时将n个节点分配给k个不同的簇,然后将每个簇转化为新图![]() 中的一个新节点,则新图
中的一个新节点,则新图![]() 可表示为
可表示为
![]()
(34)
其中,X是整个图的特征矩阵.函数g(·)的计算为:如果![]() 其他,
其他,![]() 最后,利用了条件随机场的方法来捕捉不同节点之间的分配关系.
最后,利用了条件随机场的方法来捕捉不同节点之间的分配关系.
文献[56]提出了一种可微的图池化方法(differentiable pooling, DIFFPOOL),它以端到端的方式学习分配矩阵,并且可以把图的层次结构展示出来.在l层中学习到的分配矩阵S(l)∈![]() nl×nl+1含有l层节点被分配聚类到l+1层中的概率:
nl×nl+1含有l层节点被分配聚类到l+1层中的概率:
![]()
(35)
其中,X表示特征矩阵.
文献[57]则针对图池化算子提出了一种在任意图中保留丰富信息特征的无参数池化算子iPool.该算子的特点是复杂度低并且能够自适应图结构,从而可以提高GNN在提取网络数据和层次表示方面的能力.iPool的另一个优势是基于局部运算,所以能够产生同构图下的不变性.注意力机制在被提出来之后,在深度学习的各个领域得到了非常好的应用,文献[58]将自注意力机制应用到图池化过程中(self-attention graph pooling, SAGPool).SAGPool方法同样将图本身的特征信息和图空间位置结构信息考虑在内,利用自注意力机制决定应该取舍的节点.虽然上述一些方法对未利用图的结构信息这一缺陷进行了改进,但图局部的结构信息仍未被考虑在内.文献[59]提出了一种基于图傅里叶变换的特征池化算子,将局部信息和全局信息考虑在内,在池过程中充分利用节点特征和局部结构,采用合并全局节点的方法来输出整个图表示的方式.并设计了基于该池化算子的池化层,与传统的图卷积层进一步结合,形成了一个用于图分类的图卷积神经网络框架.
为了给读者一个直观的认识,我们将从池化考虑的图卷积神经网络模型总结归纳于表4中:
Table 4 Graph Convolutional Neural Network Models Considered from Pooling
表4 从池化考虑的图卷积神经网络模型
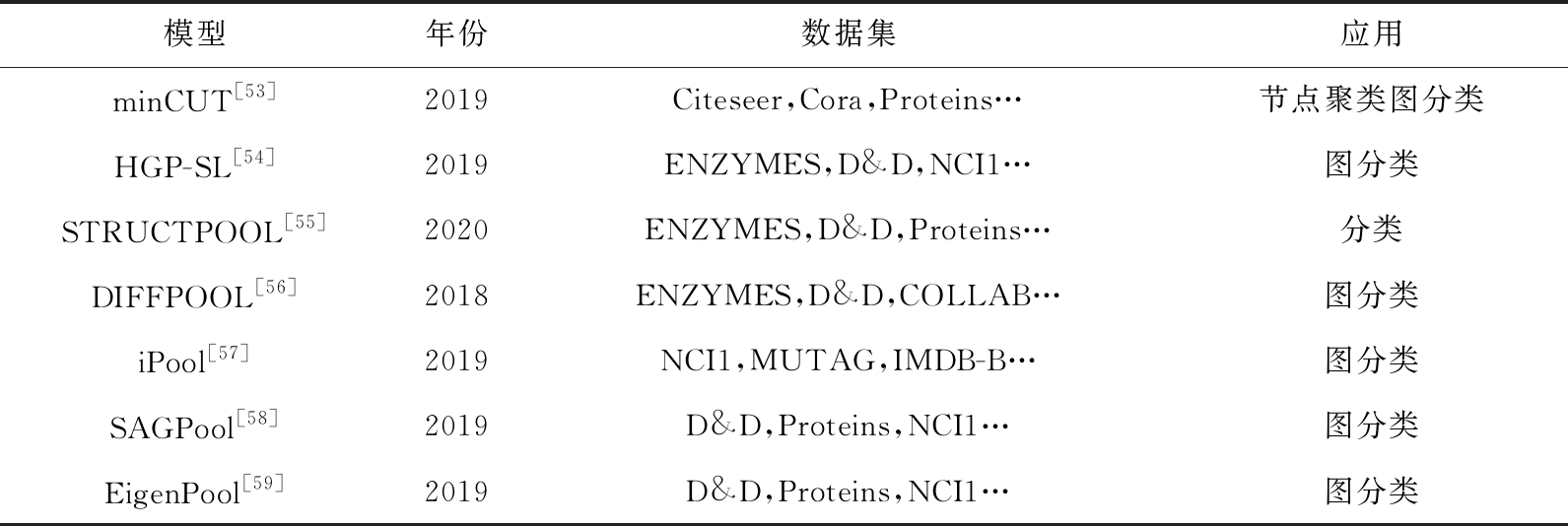
模型年份数据集应用minCUT[53]2019Citeseer,Cora,Proteins…节点聚类图分类HGP-SL[54]2019ENZYMES,D&D,NCI1…图分类STRUCTPOOL[55]2020ENZYMES,D&D,Proteins…分类DIFFPOOL[56]2018ENZYMES,D&D,COLLAB…图分类iPool[57]2019NCI1,MUTAG,IMDB-B…图分类SAGPool[58]2019D&D,Proteins,NCI1…图分类EigenPool[59]2019D&D,Proteins,NCI1…图分类
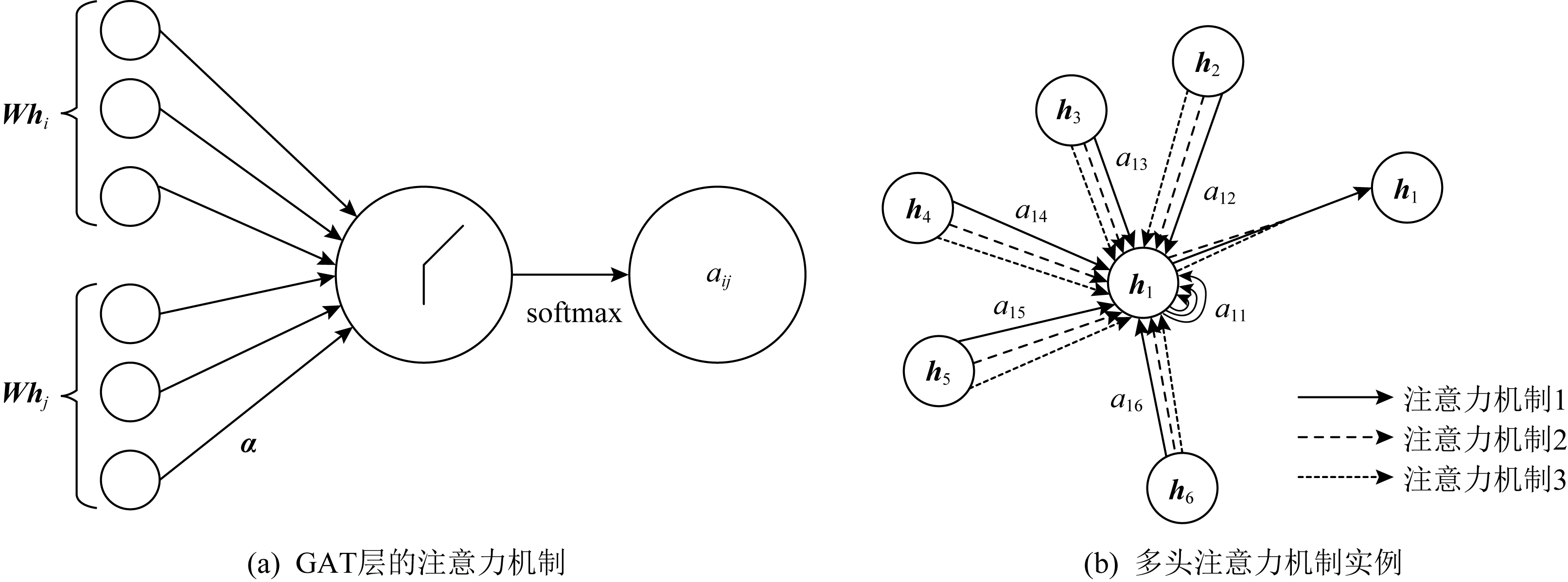
Fig. 14 The structure of GAT layer
图14 GAT层的结构
2 基于注意力实现的图神经网络
注意力机制在处理序列任务已经表现出强大的能力[60],比如在机器阅读和学习句子表征的任务中.其强大的优势在于允许可变大小的输入,然后利用注意力机制只关心最重要的部分,最后做出决策处理.一些研究发现,注意力机制可以改进卷积方法,从而可以构建一个强大的模型,在处理一些任务时能够取得更好的性能.为此,文献[61]将注意力机制引入到了图神经网络中对邻居节点聚合的过程中,提出了图注意力网络(graph attention networks, GAT).在传统的GNN框架中,加入了注意力层,从而可以学习出各个邻居节点的不同权重,将其区别对待.进而在聚合邻居节点的过程中只关注那些作用比较大的节点,而忽视一些作用较小的节点.GAT的核心思想是利用神经网络学习出各个邻居节点的权重,然后利用不同权重的邻居节点更新出中心节点的表示,如图14为GAT层的结构示意图.图14(a)表示节点i和节点j间权重的计算,图14(b)表示某一节点在其邻域内采用了多头的注意力机制来更新自身表示.
节点j相对于节点i的注意力因子求解为
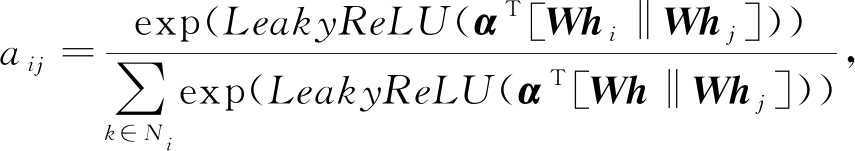
(36)
其中,aij表示节点j相对于节点i的注意力因子,W是一个用于降维的仿射变换,αT表示权重向量参数,‖表示向量的拼接操作,![]() 为泄露修正线性单元.然后加上非线性激活函数δ,利用学习到的注意力因子aij就可以实现对中心节点i的更新:
为泄露修正线性单元.然后加上非线性激活函数δ,利用学习到的注意力因子aij就可以实现对中心节点i的更新:
(37)
为了使模型更加稳定,作者还应用了多头注意力机制.把原来只利用一个函数计算注意力因子改为设置K个不同的函数来共同计算注意力因子,每个函数的结果都可以得到一组注意力参数,并且还能为下一层的加权求和提供一组参数.在各个卷积层中,K个不同注意力机制互不影响,独立工作.最后把每个注意力机制得到的结果拼接或求均值,即可得到最后的结果.若同时计算K个不同的注意力机制,则可得到:
(38)
其中,‖表示拼接操作,![]() 是第k个注意力参数函数求得的注意力因子.对于最后一个卷积层,如果利用多头注意力机制进行求解,则要利用求平均的方式来求解:
是第k个注意力参数函数求得的注意力因子.对于最后一个卷积层,如果利用多头注意力机制进行求解,则要利用求平均的方式来求解:
(39)
文献[62]同样将多头注意力机制引入到对邻居节点的聚合过程中,提出了门控注意力网络(gated attention networks, GAAN).但不同于GAT采用求平均或拼接的方式来确定最后的注意力因子.GAAN认为采用多头注意力机制虽然能够聚集中心节点的多个邻居节点信息,但并非每头注意力机制的贡献都是相同的,某一头注意力可能会捕获到无用的信息.于是GAAN为多头注意力中的每头注意力机制分别赋予了不同的权重,以此来聚合邻居节点信息,完成对中心节点的更新.因此,GAAN首先计算一个介于0(低重要性)和1(高重要性)之间的附加软门,为每头注意力分配不同的权重.然后结合多头注意力聚合器,便可以得到门控注意力聚合器:
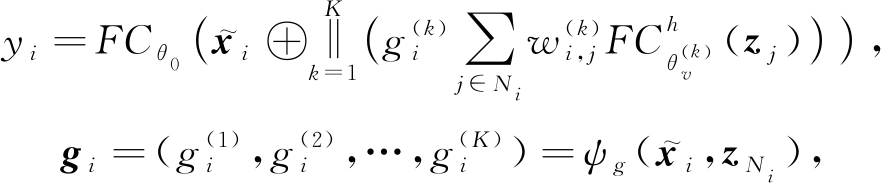
(40)
其中,FCθ0(·)表示线性变换后不应用激活函数,⊕是连接操作,K是注意力机制的数量,![]() 是节点i和节点j间的第k头注意力权重,
是节点i和节点j间的第k头注意力权重,![]() 是第k头用于查询向量的参数.
是第k头用于查询向量的参数.![]() 是节点i第k头的门控值,应用卷积网络ψg并取中心节点特征
是节点i第k头的门控值,应用卷积网络ψg并取中心节点特征![]() 和邻居节点特征zNi来计算gi.卷积网络ψg可根据自己的实际需要来进行设计,文献[62]采用了平均池化和最大池化进行构造:
和邻居节点特征zNi来计算gi.卷积网络ψg可根据自己的实际需要来进行设计,文献[62]采用了平均池化和最大池化进行构造:
![]()
![]()
(41)
其中,θm表示将邻居节点的特征向量映射到dm维,θg表示拼接好的特征向量映射到第k个门.最后,文献[62]的作者利用GGAN构造了门控递归单元,成功应用到交通速度预测问题上.
文献[63]中提出,尽管GAT在多项任务中取得了很好的效果,但目前仍缺乏对其判别能力的清晰理解.所以该文作者对利用注意力机制作为聚合器的图神经网络的表示特性进行了理论分析,分析了该类图神经网络始终无法区分不同结构的所有情况.结果表明,现有的基于注意力的聚合器无法在聚合时保留节点特征向量的多集合的基数从而限制了它们的判别能力.该文提出的方法对基数进行了修改,并且可以将其应用于任何类型的注意力机制中.Zhang等人[64]则开发了一种适用于超图基于注意力机制的图神经网络——自注意力图神经网络(self-attention graph neural networks, SAGNN).SAGNN能够处理不同类型的超图,并且可以适用于各种学习任务和具有变量的同构和异构超图.该方法能够改善或匹配超图学习的最新性能,解决了先前方法的缺点,例如无法预测非k均匀异构超图的超边.U2GNN[65]模型则通过引入通用的自注意力网络提出了一种新颖的图嵌入模型,它可以学习出能够用于图分类的低维嵌入向量.在实现时,U2GNN首先利用注意力层进行计算,然后进行递归转换以迭代地记住每次迭代中每个节点及其邻居节点的向量表示的权重大小,最后输出的总和即为整个图的最终嵌入表示.该方法可以解决现有模型中的弱点,以产生合理的节点嵌入向量.
上述模型都是将注意力机制应用到空间域的图神经网络中.为了更好地利用图的局部和全局结构信息,文献[66]首次尝试将注意力机制从空间域转移到谱域,提出了谱域图注意力网络(spectral graph attention network, SpGAT).在SpGAT中,选择图小波作为谱基,并根据指标将其分解为低频和高频分量.然后根据低频分量和高频分量构造2个不同的卷积核,将注意力机制应用于这2个核上,分别捕捉它们的重要性.通过对低频分量和高频分量引入不同的可训练注意力权重,可以有效地捕捉图中局部和全局信息,并且相对于空间域的注意力SpGAT大大减少了学习参数,从而提高了GNN的性能.
为了更好地理解注意力机制在图神经网络中的应用,以及识别出影响注意力机制的因素.文献[67]设计了一系列实验和模型对其进行了深入研究分析.首先利用图同构网络(graph isomorphism network, GIN)模型[68]在数据集上进行实验,却发现其表现非常差,并且很难学习注意力子图网络.于是作者将GIN和ChebyNet网络结合在一起提出了ChebyGIN网络模型,然后加上注意力因子从而形成注意力模型,并且采用了一种弱监督的训练方法来改善模型的性能,将模型分别在颜色计数和三角形计数任务中进行实验.最后得出4个结论:1)图神经网络中注意力机制对于节点的注意力主要贡献是可以推广到更复杂或者有噪声的图上,这种能力可以将一个无法推广的模型转换为一个非常健壮的模型;2)影响注意力机制在GNN中性能的因素有注意力模型的初始化、GNN模型的选择和注意力机制及GNN模型的超参数;3)弱监督的训练方法可以使注意力机制在GNN模型中表现出更好的性能;4)注意力机制可以使GNN对较大且有噪声的图更具鲁棒性.
我们将上述基于注意力的图卷积神经网络模型总结于表5中:
Table 5 Attention-Based Graph Neural Network Models
表5 基于注意力的图神经网络模型
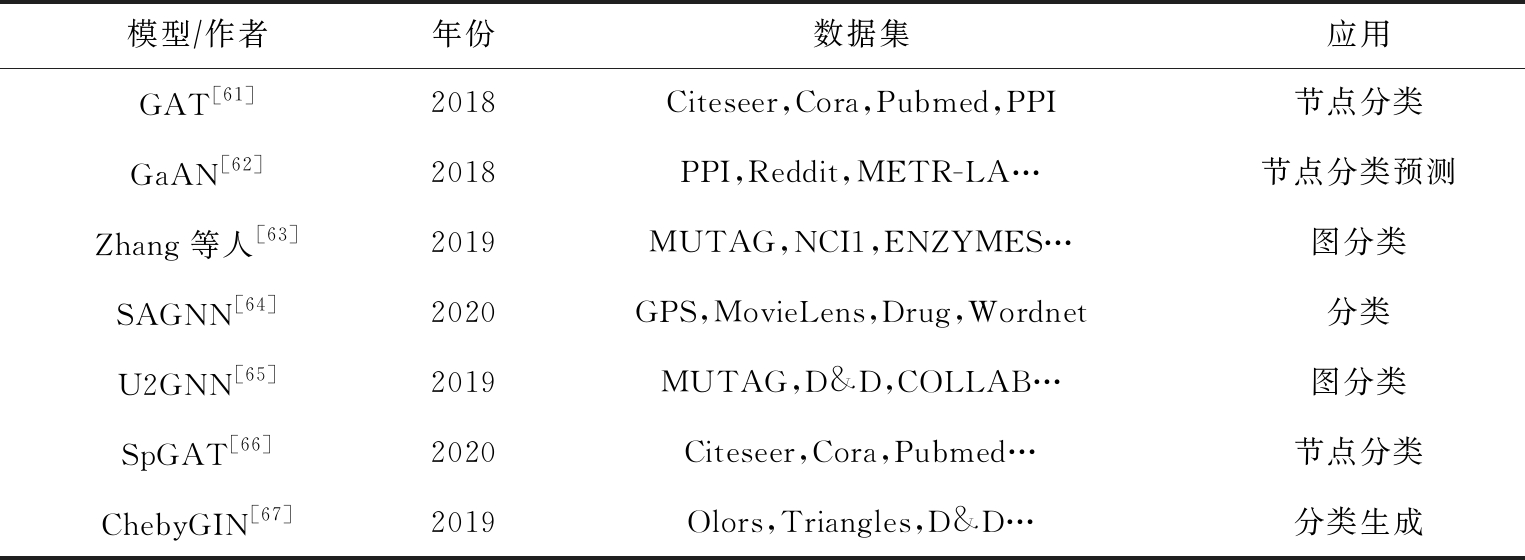
模型∕作者年份数据集应用GAT[61]2018Citeseer,Cora,Pubmed,PPI节点分类GaAN[62]2018PPI,Reddit,METR-LA…节点分类预测Zhang等人[63]2019MUTAG,NCI1,ENZYMES…图分类SAGNN[64]2020GPS,MovieLens,Drug,Wordnet分类U2GNN[65]2019MUTAG,D&D,COLLAB…图分类SpGAT[66]2020Citeseer,Cora,Pubmed…节点分类ChebyGIN[67]2019Olors,Triangles,D&D…分类生成
3 基于自编码器实现的图神经网络
在无监督学习任务中,自编码器(autoencoder, AE)及其变体扮演者非常重要的角色,它借助于神经网络模型实现隐表示学习,具有强大的数据特征提取能力.AE通过编码器和解码器实现对输入数据的有效表示学习,并且学习到的隐表示的维数可以远远小于输入数据的维数,实现降维的目的.AE是目前隐表示学习的首选深度学习技术,当我们把具有某些联系的原始数据(X1,X2,…,Xn)输入到AE中进行重构学习时,可以完成特征提取的任务.自编码器的应用场景是非常广泛的,经常被用于数据去噪、图像重构以及异常检测等任务中.除此之外,当AE被用于生成与训练数据类似的数据时,称之为生成式模型.由于AE具有上述优点,一些学者便将AE及其变体模型应用到图神经网络当中来.文献[69]第1个提出了基于变分自编码器(variational autoencoder, VAE)的变分图自编码器模型(variational graph autoencoder, VGAE),将VAE应用到对图结构数据的处理上.VGAE利用隐变量学习出无向图的可解释隐表示,使用了图卷积网络编码器和一个简单的内积解码器来实现这个模型.在该模型中,其编码器借助于2层GCN来实现:
(42)
其中,![]() 节点的平均值矩阵为μ=GCNμ(I,A),节点的方差为log σ=GCNσ(I,A).2层GCN为
节点的平均值矩阵为μ=GCNμ(I,A),节点的方差为log σ=GCNσ(I,A).2层GCN为
![]()
(43)
其中,![]() 是对称规范的邻接矩阵.用于将图重建出来的生成模型则是利用隐变量的内积计算得来:
是对称规范的邻接矩阵.用于将图重建出来的生成模型则是利用隐变量的内积计算得来:![]() 其中
其中![]() 为矩阵A中的各个元素.最后,将损失函数定义为
为矩阵A中的各个元素.最后,将损失函数定义为
L=Eq(H|I,A)[log p(A|H)]-KL[q(H|I,A)‖P(H)],
(44)
其中,等式右边第1项表示交叉熵函数,第2项表示解码器生成的图和输入图之间的KL距离.
现有的网络嵌入方法大多是通过低维向量空间中的一个点来表示每个节点.这样,整个网络结构的形成是确定性的.然而,现实中网络在形成和演化过程中充满了不确定性,这就使得这些方法存在一些弊端.针对以上弊端,文献[70]提出了一种嵌入到Wasserstein空间中的深度变分图嵌入方法(deep variational network embedding, DVNE).由于高斯分布本质上代表了不确定性性质,DVNE利用深度变分模型学习Wasserstein空间中每个节点的高斯嵌入,而不再是用一个点向量来表示节点.这样可以在保持网络结构的前提下,对节点的不确定性进行建模.DVNE方法中利用第二Wasserstein距离(W2)来衡量分布之间的相似性.用一个深度变分模型来最小化模型分布和数据分布之间的Wasserstein距离,从而提取出均值向量和方差项之间的内在关系.
在DVNE的实现过程中,2个高斯分布函数的W2距离定义为
W2(N(μ1,Σ1);N(μ2,Σ2))2=![]()
(45)
其中,N(μ,Σ)表示高斯分布.DVNE的损失函数L由2部分组成:一是保持一阶近似L1范数基于排序的损失;二是保持二阶近似L2范数重构损失.
L=L1+αL2,![]()
![]()
(46)
其中D={(i,j,k)|j∈N(i),k∉N(j)}是一个三元组集合,Eij是节点i和节点j的W2距离.C是输入特征,Q是编码器,C~PC,⊙表示哈达玛积,G是解码器,Z表示随机变量.最后通过最小化损失函数来学习模型中的参数.
文献[71]将AE引入到对顶点的学习表示当中,提出了一种结构化的深度网络嵌入(structural deep network embedding, SDNE)方法.现有的网络嵌入方法大多采用浅层模型,无法捕捉高度非线性的网络结构,导致网络表现不够好.SDNE方法利用二阶近似来捕获全局网络结构,导致网络表现不够好.同时利用一阶近似来保持局部网络结构.最后通过在半监督的深度模型联合利用一阶和二阶邻近度来保持网络结构,这样就能够有效地捕获高度非线性网络结构并保持全局和局部结构.则该模型的损失函数为
Lmin=L2nd+αL1st+vLreg,
(47)
其中,L2nd为二阶近似的损失函数,L1st为一阶近似的损失函数,Lreg则是为了防止过拟合的正则化项.各个损失函数的定义为
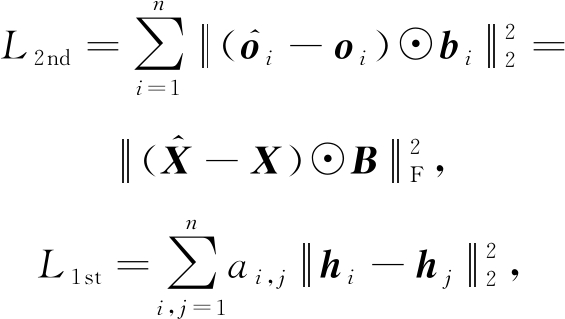
(48)
其中,![]() 如果ai,j=0,bi,j=1,否则bi,j=β>1,b和β均为参数.ai,j是邻接矩阵A中的元素.
如果ai,j=0,bi,j=1,否则bi,j=β>1,b和β均为参数.ai,j是邻接矩阵A中的元素.
规则等价即位于网络不同部分的顶点可能具有相似的角色或位置,在网络嵌入的研究中很容易被忽略.文献[72]则提出了一种深度递归网络嵌入(deep recursive network embedding, DRNE)来学习具有规则等价性的网络嵌入,将节点的邻域转化为有序序列,用一个规范化的LSTM层来表示每个节点,通过递归来聚合它们的邻居特征,DRNE的损失函数为
![]()
(49)
其中,Xv和Xu表示节点v和节点u的嵌入向量表示,Agg是利用LSTM实现的聚合函数.在一个递归步骤中,节点的嵌入表示可以保持其邻域的局部结构.通过迭代更新学习到的表示,学习到的节点嵌入向量可以在全局意义上整合它们的结构信息,从而实现规则等价.在对邻域节点序列化时,采用最有效的邻域排序度量——度的大小——对其进行排序.最后加上正则化项作为整个模型的损失函数来更新参数.图15为DRNE框架,其中图步骤1为邻居节点采样;步骤2为按邻居节点的度对节点进行排序;步骤3为归一化LSTM层,将邻居节点的嵌入表示聚合到目标节点的嵌入表示中,Xi是节点i的嵌入向量,LN表示层归一化;步骤4为正则化器.
文献[73]将AE应用在推荐系统的矩阵补全上,提出了图卷积矩阵补全方法(graph convolution matrix completion, GC-MC).GC-MC将矩阵补全看作是图上的一个链接预测问题,设计了一种基于二部交互图的可微信息传递的图自编码框架.其编码器借助于图卷积实现,解码器则利用一个双线性函数完成.文献[74]针对图数据的对抗图嵌入提出了一个新的框架.为了学习鲁棒嵌入,提出了对抗正则化图自动编码器(adversarially regularized graph autoencoder, ARGA)和对抗正则化变分图自动编码器(adversarially regularized variational graph autoencoder, ARVGA)两种对抗方法.除了上述方法外,基于自编码器的图神经网络还有能够有效学习大规模图上节点嵌入的Graph2Gauss[75]方法.表6对基于自编码器的图神经网络模型进行了总结.
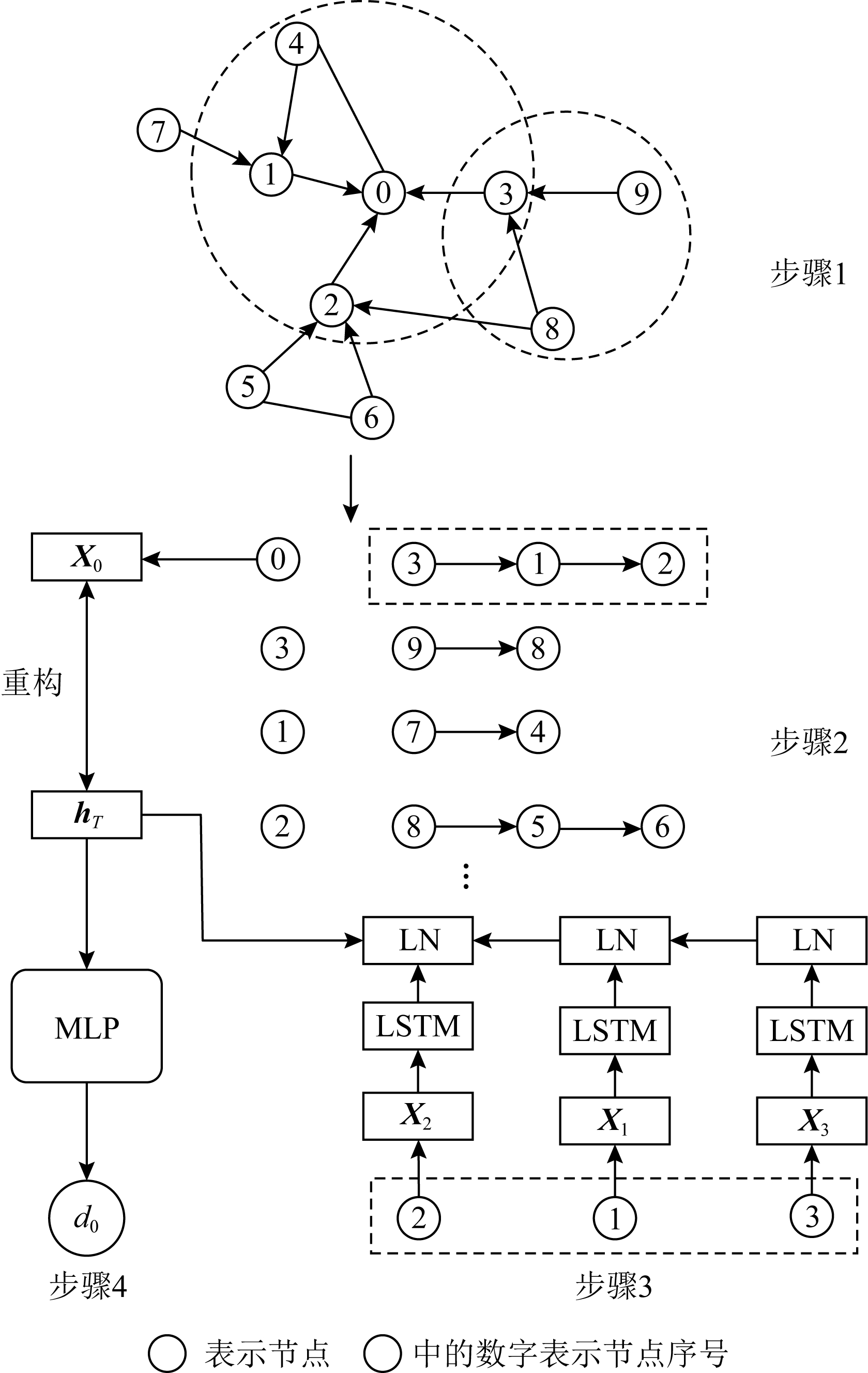
Fig. 15 DRNE framework
图15 DRNE框架
Table 6 Autoencoder-Based Graph Neural Network Models
表6 基于自编码器的图神经网络模型
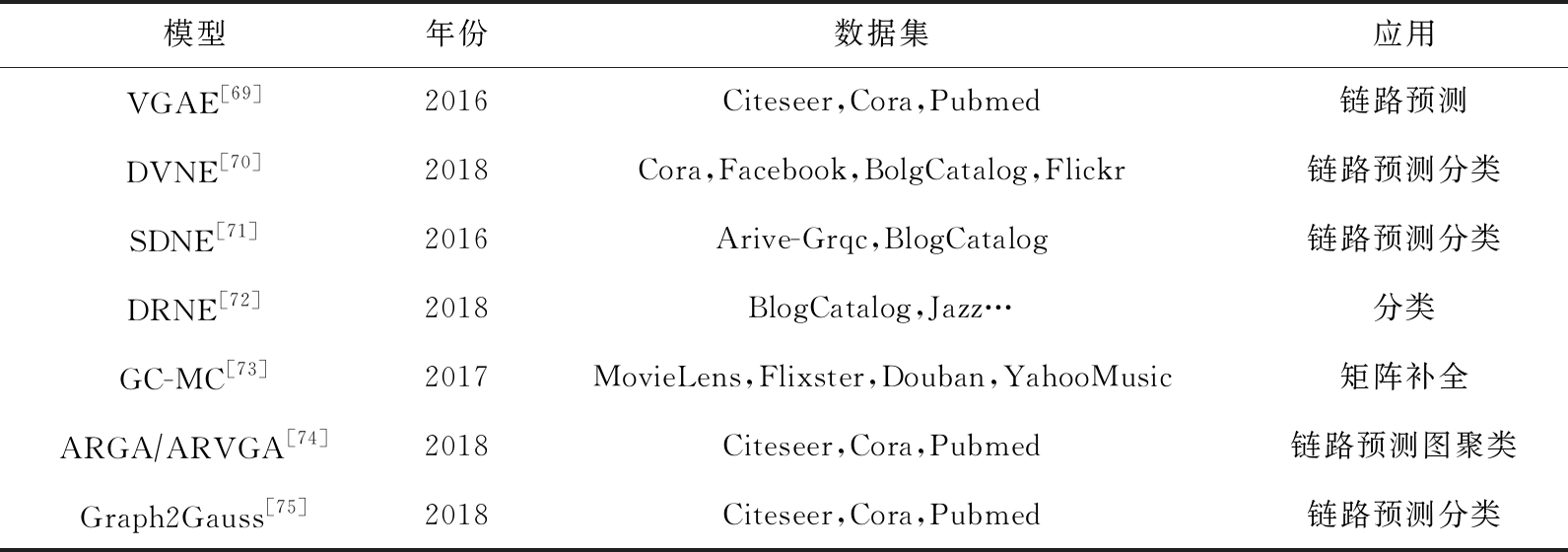
模型年份数据集应用VGAE[69]2016Citeseer,Cora,Pubmed链路预测DVNE[70]2018Cora,Facebook,BolgCatalog,Flickr链路预测分类SDNE[71]2016Arive-Grqc,BlogCatalog链路预测分类DRNE[72]2018BlogCatalog,Jazz…分类GC-MC[73]2017MovieLens,Flixster,Douban,YahooMusic矩阵补全ARGA∕ARVGA[74]2018Citeseer,Cora,Pubmed链路预测图聚类Graph2Gauss[75]2018Citeseer,Cora,Pubmed链路预测分类
4 其他模型
除图卷积神经网络、基于注意力和自编码的图神经网络外,还有很多学者致力于图神经网络的发展,提出了众多模型.由于图神经网络模型具有巨大潜力,在各个方向上都有很大的研究价值.在此,对基于高斯过程、时空领域、Markov模型、交叉领域等多个方向的模型进行了总结概括,供广大学者借鉴从而进行更深一步的研究,以起到抛砖引玉的作用.
在处理节点分类任务时,Qu等人[76]针对半监督目标分类问题提出了图Markov神经网络(graph Markov neural network, GMNN),GMNN集成了统计关系学习和GNN的优点,GMNN使用条件随机场对象标签的联合分布进行建模,使用变分最大期望算法进行有效训练.图16所示为GMNN框架,其中实线和虚线正方形分别是已标记和未标记的对象,黑色/白色正方形是属性,直方图是对象的标签分布,实心圆圈是对象表示.GMNN通过在E步和M步之间交替进行训练.针对半监督学习问题,Ng等人[77]提出了一种通过使用经验核均值嵌入分布回归构建的基于高斯过程的贝叶斯方法.特别是在标签稀缺的主动学习实验中,该模型不需要验证数据集就可以尽早停止以防止过拟合.在机器学习中,时空领域的学习仍然是一个具有挑战性的问题.文献[78]提出了一种适用于捕获在不断变化场景中不同实体的局部特征和复杂高层交互的循环时空图神经网络(recurrent space-time graph, RSTG).RSTG的实现通过计算从特定位置提取的要素并在每个时刻进行缩放来考虑局部信息,再通过迭代在空间域的信息传递整合大范围的时间和空间信息.Ouyang等人[79]针对现有的GNN在交叉领域信息传播遇到的挑战提出了一种新的变种模型深度多图嵌入(deep multi-graph embedding, DMGE)模型用于交叉领域的表示学习.
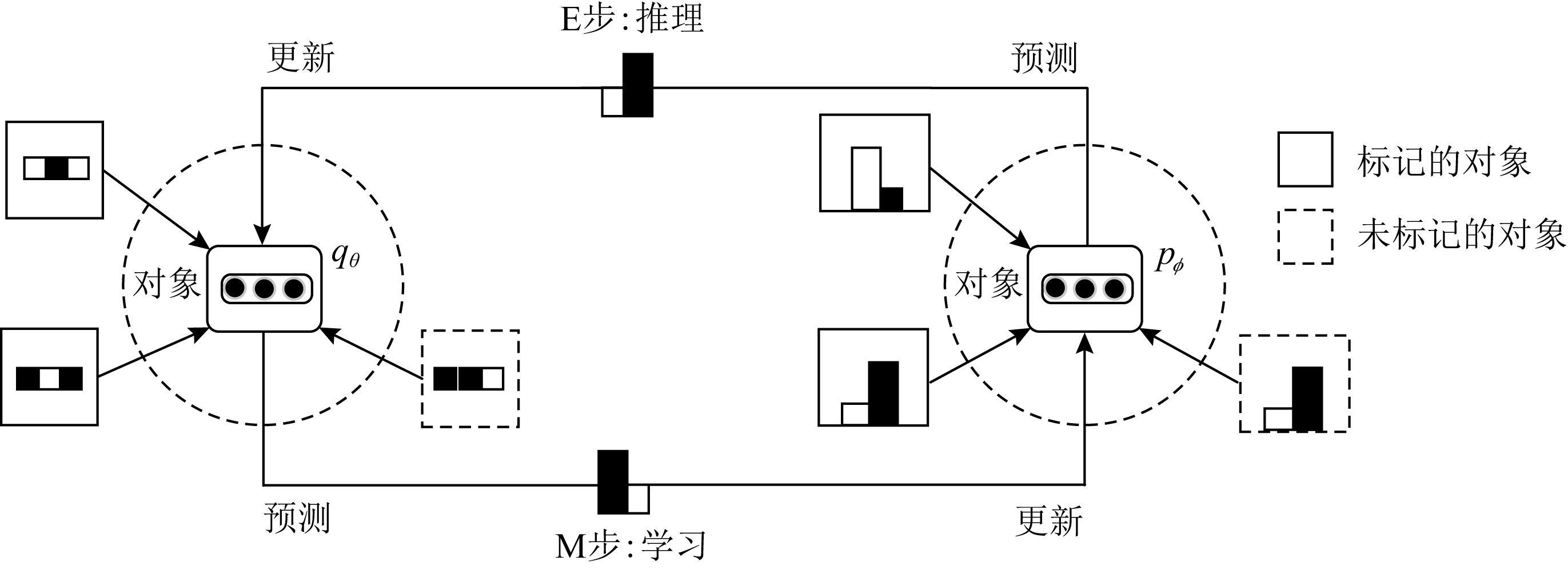
Fig. 16 GMNN framework[76]
图16 GMNN框架[76]
Zhang等人[80]针对GNN在对图结构进行处理时,大多是考虑成对的依赖关系的弊端,提出了能够捕获更高阶的依赖关系的因子图神经网络(factor graph neural network, FGNN)模型.Chen等人[81]提出了可以捕获对话框中的对话流的GraphFlow模型,该模型是为了解决在处理对话式阅读理解问题时,现有的方法不能有效捕获对话历史这一缺陷.Cao等人[82]提出的多频道图神经网络(multi-channel graph neural network, MuGNN)是用于解决在实体校准时受限于结构异质性的问题.文献[83]提出二分图神经网络(bipartite graph neural network, BGNN)用来处理特殊的二分图结构.Verma等人[84]针对GCN中卷积运算会带来信息损失这一缺陷,提出了能够在局部节点池中捕获更多信息的图胶囊网络(graph capsule network, GCAPS-CNN)模型,而不是通过聚合(标准GCN模型中使用的图卷积运算)捕获信息.Du等人[85]提出了通过梯度下降训练的无限宽的多层GNN,并且享有GNN的全部表达能力的图神经正切核(graph neural tangent kernels, GNTKs).Xu等人[86]认为现在图上表示学习方法采用的邻居聚合方式是一种不完美的策略,于是该文作者探索了一种新的架构——跳跃知识网络,灵活地为每个节点利用不同的邻居范围来实现更好的结构表示.Su等人[87]提出了一种用于图生成的概率自回归模型——图变分循环神经网络(graph variational recurrent neural network, GraphVRNN).该模型通过对图数据的隐变量进行建模,从而可以捕获图结构基础节点属性的联合分布.Sato等人[88]提出了第1个具有理论保障的GNN恒定时间近似算法,分析邻居采样以获得针对GraphSAGE和GCN的恒定时间近似算法.Carr等人[89]介绍了可以对任意图数据进行操作,以稀疏上下文点为特征,并输出目标点分布的图神经过程(graph neural processes, GNP).
5 针对图神经网络的讨论分析
虽然图神经网络近几年发展迅猛,各种模型层出不穷.但图神经网络也同样存在一些局限性,对其理论研究不足,为此一些学者便从整体宏观的角度对图神经网络进行了分析讨论.到目前为止,对GNN的评价还只是经验上的,文献[90]便从理论的角度研究了图神经网络,将其与1维Weisfeiler-Leman图同构启发式方法(1-dimensional Weisfeiler-Leman, 1-WL)联系起来.证明了图神经网络在区分非同构(子)图方面具有与1-WL相同的表现力,则图神经网络在处理任务上和1-WL存在着相同的缺点.为此,作者提出了一个可以考虑多尺度上的高阶图结构的广义图神经网络.文献[91]也同样证明了图神经网络的表达力上限是WL测试结果.并提出了将残差/稠密连接和扩张卷积应用于GCN体系结构上,从而成功地训练出一个56层的GCN网络.并将其应用到点云语义分割的流形任务中,在S3DIS数据集上实现近4%的性能提升,证明了该深层GCN的有效性.上述方法虽然用检测图同构的方法证明图神经网络在识别图中节点的能力上限,但并没有解决节点分类器是布尔类型时的情况.文献[92]则从该角度研究了图神经网络的逻辑表达能力.图神经网络在处理非欧氏数据时已经表现出了强大的能力,但目前的模型大多都局限于非常浅的模型,图神经网络能不能做深一直是一个研究的热点.文献[93]则对GCN处理半监督分类任务进行了深入研究,证明了GCN其实是拉普拉斯平滑的特殊形式.详细说明了中心节点的特征更新是靠不断聚合邻居节点特征实现的,这就使得相邻节点的相似性增强,从而使分类能力大大增强.但如果堆积多层GCN,则输出特征可能过度平滑,使来自不同簇的顶点可能变得不可区分,从而不能完成分类任务.为了解决上述问题,文献[93]作者提出了联合训练和自训练的方法.文献[94]同样对当堆积更多的层数时,GCN在处理分类任务时,其性能不会提高进行了理论分析.通过(增广的)正规化拉普拉斯的谱分布,将图神经网络的渐近行为与图的拓扑信息联系起来.从而证明了如果GCN的权重满足由图谱确定的条件,则当层大小变为无穷大时,GCN的输出除了用于判别节点的节点度和连接分量外,不携带任何信息.为此作者为图神经网络的权值规范化提供了一个原则性的指导,提出的权值缩放方法提高了GCN在真实数据中的性能.文献[95]发现图神经网络在学习图的节点距方面有很大的限制,如果不认真设计模型,即使有多层和非线性激活函数,GCN在学习图的节点距时仍会发生严重的故障.为此采用了模块化的GCN设计,使用不同的传播规则和剩余连接,可以显著提高GCN的性能.最后发现深度在对图的节点距学习过程中比宽度影响更大,较深的GCN更能学习高阶图的节点距.文献[96]用数学知识证明节点嵌入和结构图表示的关系.最后利用不变量理论和因果关系提出了一个统一的理论框架.通过大量的数学推导,证明了结构表示与节点嵌入之间的关系类似于分布及其样本之间的关系,所有可以由节点嵌入执行的任务也可以由结构表示执行,反之亦然.文献[97]则研究了图神经网络在信息传递框架下的表达能力.发现当图神经网络中的宽度和深度受到限制时,其表达能力也会进一步受到限制.图神经网络中的宽度和深度大小设计,应适配于输入图的大小,并且图神经网络可以计算其输入上的任何函数.
6 框 架
第1~5节介绍了图神经网络模型及其变种,不难看出图神经网络模型众多,所以一些学者试图将各种图神经网络模型统一到一个标准的框架中.文献[98]提出了消息传播神经网络(message passing neural networks, MPNNs)的通用框架,概括基于空间的图神经网络的一般形式.文献[99]提出了统一的基于自注意力机制图神经网络框架,并且提出了能够捕获深度神经网络中大范围依赖关系的非局部神经网络(non-local neural network, NLNN)方法.文献[100]提出了可以将各种图神经网络模型推广统一的图网络(graph network, GN).文献[101]则提出了能够学习局部、平稳和组合的特定任务特征的混合模型网络(mixture model networks, MoNet)统一框架.
6.1 消息传播神经网络
文献[98]提出了GNN的一种通用框架,概括了基于空间的GNN一般形式,取名为消息传播神经网络.这个框架抽象出GNN的一些共性,把基于空间的GNN看作是一个消息传播过程,信息可以沿着边从一个节点传递到另一个节点.并且举例说明将门图神经网络、交互式神经网络、分子图神经网络、深度张量神经网络和基于拉普拉斯矩阵方法的神经网络等8个典型的GNN模型一般化到其提出的MPNN框架中.
在MPNN框架中,定义了消息传递阶段和读出阶段2个步骤.所谓的消息就是邻居节点状态,在消息传递阶段完成的工作是利用消息函数Mt聚合中心节点状态![]() 邻居节点状态
邻居节点状态![]() 及其相连边的信息特征evw,得到聚合后的状态
及其相连边的信息特征evw,得到聚合后的状态![]() 然后借助中心节点的更新函数Ut完成对中心节点v的状态更新,其中t为时间步长:
然后借助中心节点的更新函数Ut完成对中心节点v的状态更新,其中t为时间步长:
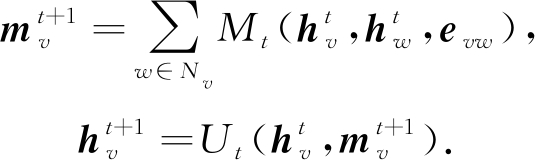
(50)
如果只是在图上做节点层面的任务,只需要完成上面的2个步骤就可以实现.由于文献[98]的作者提出的MPNN是一个通用的GNN框架,作者还必须考虑处理整个图的任务.所以作者还归纳了读出函数,在读出阶段利用读出函数R,以得到的各个更新后的节点状态为输入,计算出整个图的特征向量:
![]()
(51)
当前基于图结构数据的神经网络都可以归纳成包含消息函数Mt、更新函数Ut和读出函数R的设计形式.当然,读出函数R的有无根据实际的处理任务取舍.不同GNN只是对MPNN框架中的函数Mt,Ut,R进行了不同的配置和更改.为了说明该框架的通用性,对8个典型的GNN模型进行了详细分析.分别讨论了各个模型的函数Mt,Ut,R.在深度张量神经网络中,对以上3个函数的配置为:
![]()
(52)
其中,Wfc,Wcf,Wdf为矩阵,![]() 为偏置向量.读出函数通过单个隐层神经网络独立地传递每个节点状态,并对输出求和,最后输出整个图的特征向量.
为偏置向量.读出函数通过单个隐层神经网络独立地传递每个节点状态,并对输出求和,最后输出整个图的特征向量.
6.2 非局部神经网络
文献[99]提出了一种可以捕获深度神经网络中大范围依赖关系的非局部神经网络.NLNN最初的应用领域是在计算机视觉当中,受启发于非局部均值滤波方法[102].NLNN可以对所有位置的特征加权计算,聚合更多的信息,可以应用于时间和空间上,所以它可以被看作是不同自注意力机制方法的统一.在很多处理任务中,都需要捕获大范围依赖关系.比如,在时序任务中,RNN操作是一种主要的捕获大范围依赖关系手段.而在CNN中则是通过堆叠多个卷积模块来形成大感受野.目前的卷积和循环算子都是在空间和时间上的局部操作,大范围依赖关系捕获是通过重复堆叠和反向传播得到,这些方法存在很多不足之处.和传统的方法相比,NLNN具有3个优点:1)与卷积运算和递归运算相比,非局部运算通过计算任意2个位置之间的交互直接捕获长依赖;2)即使神经网络的层数不多也能达到最佳效果;3)非局部运算支持可变的输入大小,并且可以轻松地与其他运算相结合.下面我们将会介绍NLNN的通用公式以及具体实现的实例.
受启发于非局部均值滤波方法,通用的NLNN一般化公式为
(53)
其中,x是输入信号,i是输出特征图的某一位置索引,j是该图中所有可能位置的索引,函数f用于计算i和其他位置的相关性,函数g是进行信息变换的一元输入函数,C是一个归一化函数,保证变换前后整体信息不变.
由于式(53)中的函数g和f都是一般化的通式,在具体的神经网络中,需要给予具体的函数形式实现.因为线性嵌入的一元输出函数g比较简单,故可以采用卷积形式实现g(xi)=Wgxi,其中Wg是一个可学习的参数矩阵.接下来讨论函数f的不同实现形式.
从非均值滤波和双边滤波的角度看,首先利用高斯函数实现f:
![]()
(54)
其中,![]() 是点乘相似度,归一化因子
是点乘相似度,归一化因子![]()
在嵌入的向量空间中,有高斯滤波的变种:
f(xi,xj)=exp(θ(xi)Tφ(xj)),
(55)
其中,![]() 前面的高斯函数形式是在当前空间中直接计算,此公式更加通用,在嵌入的空间中计算高斯距离.对于所有i,把
前面的高斯函数形式是在当前空间中直接计算,此公式更加通用,在嵌入的空间中计算高斯距离.对于所有i,把![]() 变成计算所有j的softmax便可以得到:
变成计算所有j的softmax便可以得到:
![]()
(56)
对应文献[103]中自注意力机制的表达式.
函数f还可以考虑点乘相似度实现:
f(xi,xj)=θ(xi)TΦ(xj),
(57)
其中,C(x)=N,N为输入x的数量.利用连接运算同样也可以实现:
![]()
(58)
其中,[,]表示连接运算,Wf为将连接向量转化为标量的权重向量,C(x)=N.
最后,为了使其具有更好的灵活性,能够任意地插入到现有的神经网络结构中,将式(53)的非局部运算变成了一个非局部模块:
Zi=Wzyi+xi,
(59)
其中,yi已在式(53)中给出,“+xi”表示残差连接.如图17为一个非局部模块实例,图17中特征图以其张量的形状显示,例如,对于1 024个通道,T×H×W×1024.“⊗”表示矩阵的倍增,“⊕”表示元素求和.对每行执行softmax运算.矩形方框表示1×1×1卷积,此处显示的是嵌入向量的高斯变换,瓶颈为512个通道.可以通过去除θ和φ来完成原始向量的高斯变换,并且可以通过将softmax替换为1/N来实现点积变换.
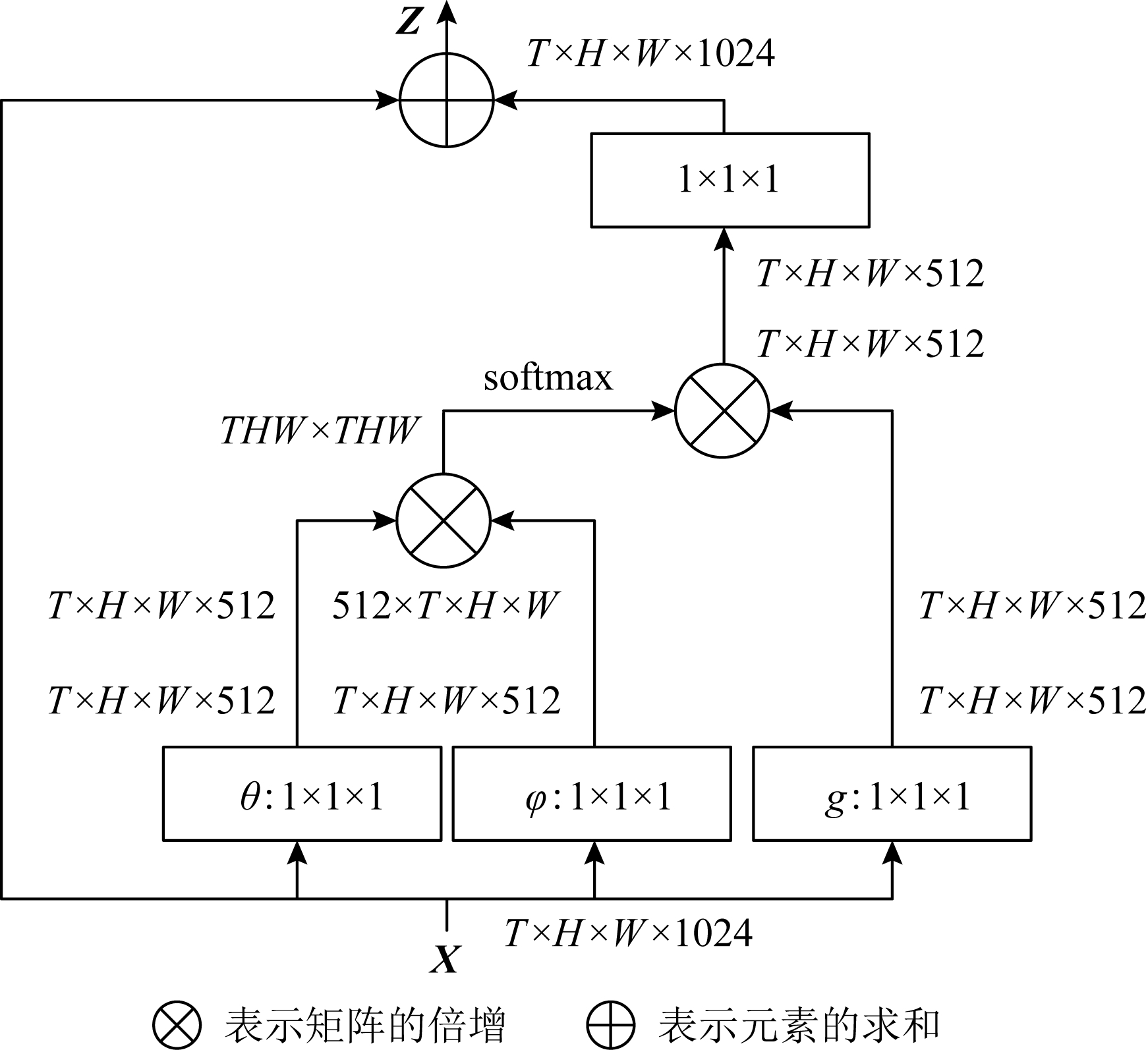
Fig. 17 Non-local module instance[99]
图17 非局部模块实例[99]
6.3 图网络
文献[100]从组合泛化入手,探讨了如何在深度学习结构中使用关系归纳偏置,促进对实体、关系,以及对组成它们的规则进行学习.并且提出了一种具有强相关性归纳偏AI框架——图网络(GN),GN泛化并扩展了各提到的MPNN和NLNN方法.之所以取名叫图网络是因为除了利用神经网络的方法实现它之外还可以利用其他方法实现.我们首先给出了图的定义,然后介绍了GN中的核心单元GN块的内部结构以及其计算步骤,最后说明了设计GN结构的基本原则.
1) 图的定义.在该GN框架中,一个图被定义为一个三元组G=(u,V,E).其中,u表示一个全局属性;V={Vi}i=1:Nv是节点集合,其中每个Vi表示节点的属性;E={(ek,rk,sk)}k=1:Ne是边的集合,其中每个ek表示边的属性,rk是接收节点,sk是发送节点.
2) GN块.每个GN块包含3个针对节点、边和全局属性的更新函数φ和3个从边到节点、从边到全局属性和从节点到全局属性的聚合函数ρ:
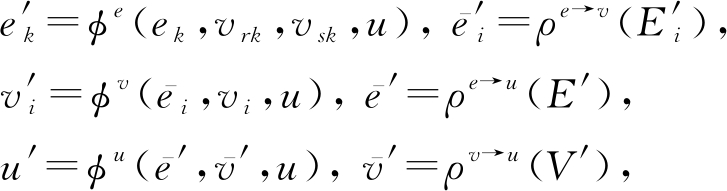
(60)
其中,![]()
3) GN块的计算步骤.当GN块的输入为图G时,计算从边开始,然后到节点层面,最后到全局级别.总共包含6个步骤,但这个执行顺序不是固定不变的,可以改变函数的顺序.同样,每一个步骤也不是必需的,根据自己实际处理的任务进行取舍:
① φe作用于每一条边,参数为(ek,vrk,vsk,u),返回![]() 每个节点i的每条边输出的结果集和每条边输出的结果集分别为
每个节点i的每条边输出的结果集和每条边输出的结果集分别为
![]()
(61)
(62)
② ρe→v作用于![]() 将投影到顶点i的边的所有边更新聚集到
将投影到顶点i的边的所有边更新聚集到![]() 用于下一步的节点更新.
用于下一步的节点更新.
③ φv应用于每个节点i,计算更新后的节点属性![]() 每个节点输出的结果集为
每个节点输出的结果集为![]()
④ ρe→u作用于E′,将所有边的更新聚合到![]() 将用于下一步的全局更新.
将用于下一步的全局更新.
⑤ ρv→u作用于V′,聚合所有节点的更新![]() 将用于下一步的全局更新.
将用于下一步的全局更新.
⑥ φu作用于每个图,计算全局属性的一次更新u′.
4) 设计原则.GN块包含灵活的表示、可配置的GN块内部结构和可组合的多个GN块结构.
① 灵活的表示.该灵活性主要体现在属性和图结构本身的表示上.GN块的全局属性、节点属性和边属性可以使用任意的表示格式.在深度学习实现中,实值向量和张量是最常见的.同时还可以使用其他结构数据,如序列、集合,甚至图.GN块的输出也可以根据任务的需求进行定制:比如文献[104]聚焦于边作为输出,文献[105]聚焦于节点输出,文献[106]聚焦于整个图的输出.至于图结构本身的灵活性表示,定义输入数据表示为图时,通常有2种情况:首先,有些已经显式地指定了实体和关系,就输入显式地指定了关系结构;其次,有些数据表示中,关系结构并不明确,必须经过推断或假设.
② 可配置的GN块内部结构.GN块中的结构和功能可以以不同的方式进行配置,可以灵活配置将哪些信息作为其函数的输入,以及如何产生输出边、节点和全局更新等.通过这样不同的配置,就可以得到不同的GNN模型.比如文献[107]使用全连接的GN块,它们的聚合函数采用神经网络实现,更新函数则利用逐元素求和的方法实现.
③ 可组合的多个GN块结构.图网络可以通过GN块来构造复杂的模型结构,一个GN块的输出可以作为另一个GN块的输入,组成大的GN块.任意数量的GN块也可以相互组合.其中最常见的结构设计就是编码-解码和基于循环的配置.其他的一些技术例如跳跃连接、LSTM和门控循环单元等也可以被应用于GN组合结构的构造中.
6.4 混合模型网络
6.1~6.3节所述的3个框架在文献[16]同样也有总结概括,除此之外,Monti等人[101]还提出了混合模型网络(MoNet)的统一框架,将图卷积神经网络体系结构推广到图和流形等非欧几里德域结构数据上,该框架并能够学习局部、平稳和组合的特定任务特征.MoNet遵循空间域方法的一般原理,将卷积类操作作为模板与图或流形上的局部内在“图小块”匹配.其创新之处在于提取图小块的方法:以前的方法使用固定图小块,MoNet使用参数构造.文献[101]中表明GCNN[108],ACNN[109],GCN[34],DCNN[13]等各种处理非欧氏结构数据的方法都可以看作是MoNet的特殊实例.文中定义了流型上图小块算子的一般形式为
(63)
其中,![]() 为图上或流形上的点,
为图上或流形上的点,![]() 每个
每个![]() 关联一个伪坐标为
关联一个伪坐标为![]() 的d维向量,在这些坐标中并定义了含有可学习参数Θ的加权函数WΘ(u)=(w1(u),w2(u),…,wJ(u)).J表示从流形提取的维度.则其卷积形式可以写成:
的d维向量,在这些坐标中并定义了含有可学习参数Θ的加权函数WΘ(u)=(w1(u),w2(u),…,wJ(u)).J表示从流形提取的维度.则其卷积形式可以写成:
(64)
该过程的构造关键是伪坐标u和加权函数w(u)的选择.在流形和图上的一些典型的神经网络都可以看作是对其进行的特定设置.GCNN,ACNN则可以看作在流形上的局部极坐标上使用高斯核,GCN可以解释为在由图顶点的度数给定的伪坐标上应用三角形核.作者在加权函数选择方面考虑了一个具有可学习参数的参数核:
![]()
(65)
其中,Σj是d×d和d×1的协方差矩阵,μj是高斯核的平均向量.最后从图像、图形3维形状分析的角度对所提出的方法在标准任务上进行了测试,结果表明该方法始终优于先前提出的非欧氏深度学习方法.
7 图神经网络的应用
由于非欧氏结构数据出现在越来越多的实际场景中,所以将GNN应用到传统机器学习场景中,会带来不小的惊喜.比如将其应用到自然语言处理上可以解决跨句的多元关系语义提取,在推荐系统方面可以有效地完成矩阵补全问题.本节将从自然语言处理、计算机视觉、推荐系统、预测问题等领域对GNN的应用进行详细阐述.
7.1 在自然语言处理方面的应用
长期以来,人们一直认为语义表示对于强制意义保留和提高机器翻译方法的泛化性能很有用.Marcheggiani等人[22]第1个将有关源语句的谓词参数结构的信息(即语义角色表示)整合到基于标准的注意力神经机器翻译模型中,填补了这一方面的空白.该模型主要包括编码-译码模型和利用图卷积网络将语义偏差注入句子的编码器.实验结果表明该模型表现良好.先前大多数自然语言处理多采用的是基于语法的方法,依靠于线性启发法或者标准的递归网络,还有树变换器和超边替换语法.Beck等人[23]提出了一个图到序列的神经网络模型,利用编码器-解码器架构,采用基于门控图神经网络的编码器,可以在不丢失信息的情况下整合完整的图结构.同时为了解决小规模标签词汇表的问题,引入了图转换,将边更改为其他的节点.这样既确保了边具有特定于图的隐向量,同时也解决了参数爆炸问题.
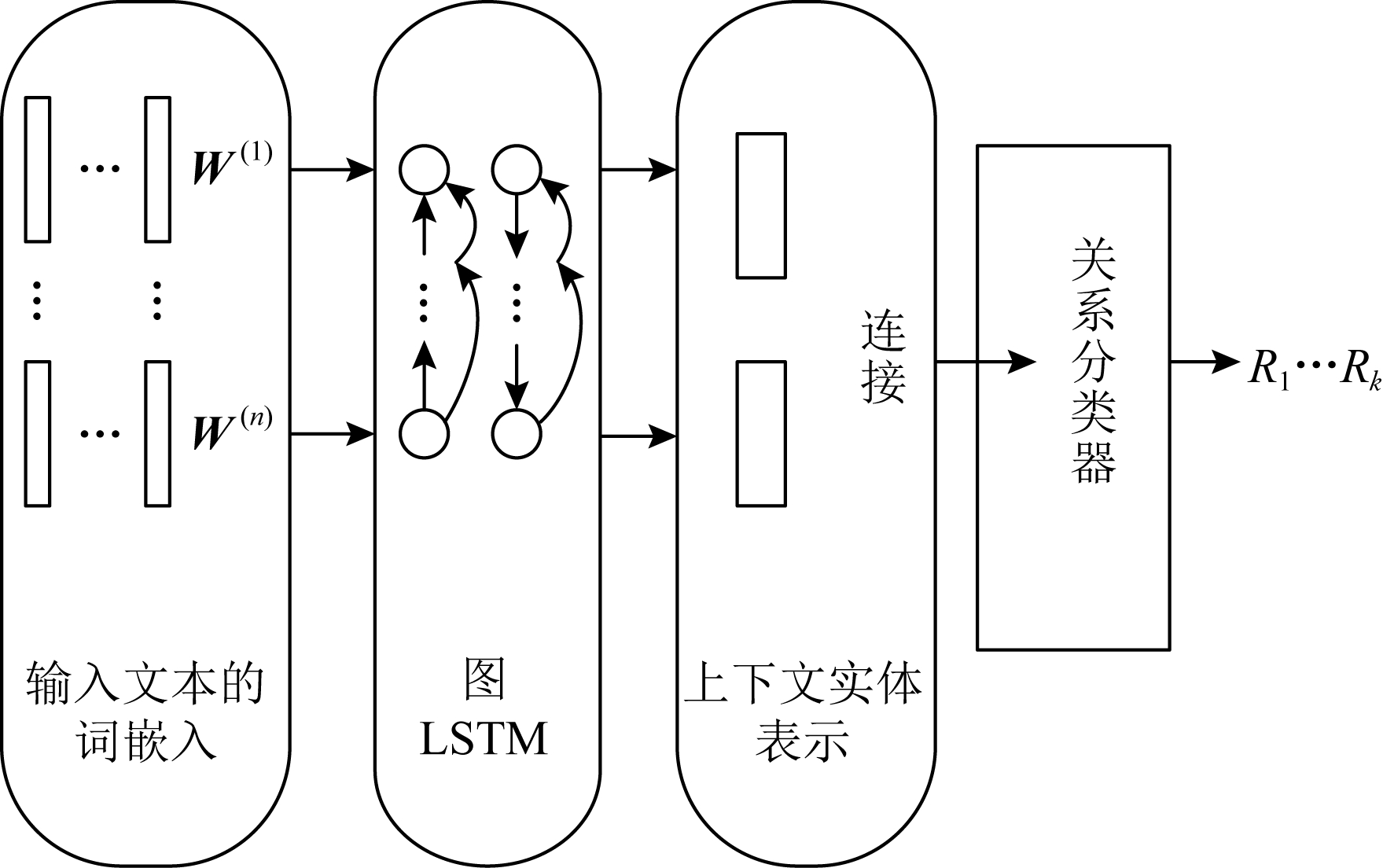
Fig. 18 The general structure of LSTMs
图18 LSTMs通用结构
传统的关系抽取主要关注在一个句子中的二分类相关性问题,这种方法并不适应于多个句子和多元关系.最近,自然语言处理研究学者对在高值域提取跨语句的n元关系问题产生了很大的兴趣.为此,Peng等人[24]提出了基于图长短期记忆网络的通用关系提取框架,其可以轻松扩展到跨语句n元关系提取.该模型的整体结构如图18所示,主要包括输入层,图中输入层是输入文本的词嵌入向量;接下来是图LSTM层,图LSTM层学习每个单词的上下文表示;对于所讨论的实体,它们的上下文表示被连接起来并成为关系分类器的输入;最后关系分类器利用这种表示产生最终的预测结果.
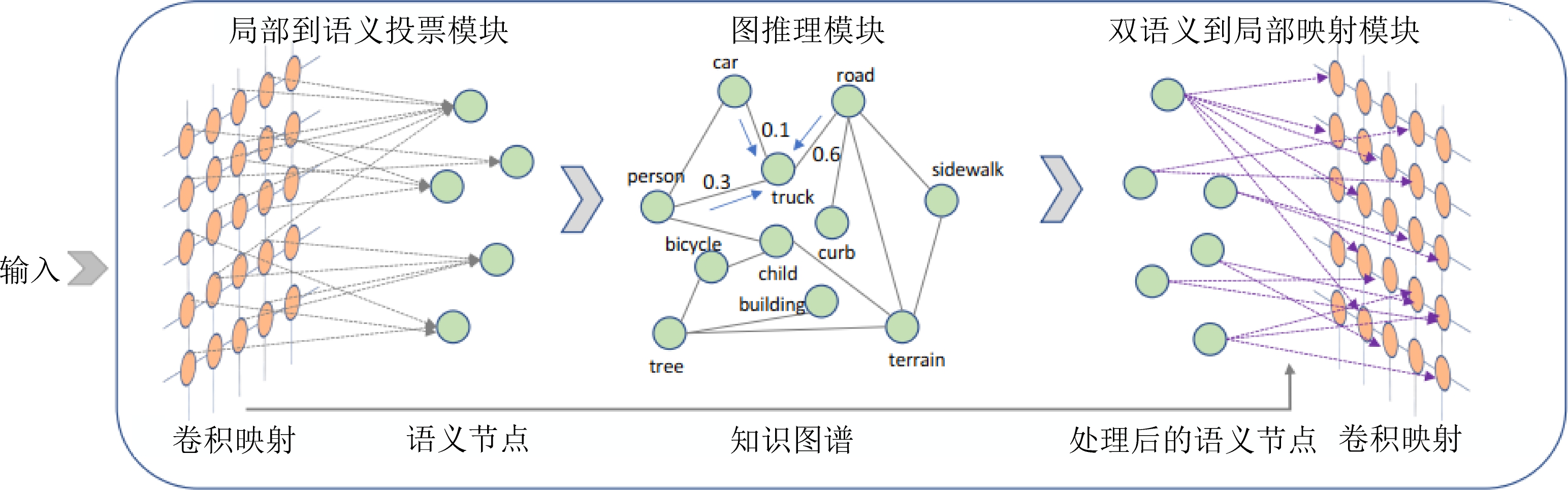
Fig. 19 The structure of SGR[26]
图19 SGR结构[26]
传统的社交媒体定位常常依赖于IP地址和GPS信息等,但这些信息不仅有噪声并且是很难拿到的.Rahimi等人[110]利用用户地理位置的公共信息,采用GCN将用户文本和网络结构信息整合,达到获取更加准确的社交媒体位置定位的目的.在文中主要采用了GCN并配上“highway gates”机制来进行信息过滤,提取出有明确的地理位置信息的监督样本.Sahu等人[111]在句间关系提取方面也提出了一个基于图的新模型,该图以单词为节点,而单词之间的多个句子间和句子依存关系作为边来构造,以捕获局部和非局部依赖性信息.从而改善了现有方法在处理句间关系提取时没有完全利用局部和非局部特性,以及语法和语义的依赖关系.Zhu等人[112]同样也在关系推理和关系提取方面做了一些研究.在许多自然语言处理任务(例如关系提取)中,多跳关系推理是必不可少的,GNN是进行多跳关系推理的最有效方法之一.作者提出了根据自然语言句子生成图神经网络参数的方法(graph neural networks with generated parameters, GP-GNN),从而使GNN能够处理非结构化文本输入上的关系推理.在GP-GNN中通过将自然语言编码为参数并执行层与层之间的传播来解决关系消息传递任务.在自然语言处理中,可以通过识别句子的语法和语义来预测句中事件的事实性(event factuality prediction, EFP),它用来评估句子中提到的事件发生程度的概率大小.在先前的一些工作中,只是简单地组合了句子语意和语法信息,没有深入去探索和了解二者的关系和协调性.Veyseh等人[113]提出了一种基于GCN能够整合语义和语法结构的新方法.在该方法中包含亲和度矩阵,以量化单词之间的连接强度,从而促进了语法和语义信息的集成.该语义亲和度矩阵利用长短期记忆网络生成,然后将其与依赖树的语法亲和度矩阵线性集成,生成EFP中GCN丰富的亲和度矩阵.
7.2 在计算机视觉方面的应用
图神经网络在计算机视觉中也有着巨大的应用潜力.Simonovsky等人[25]发现当前的图卷积神经网络未利用边缘标签,会导致局部邻域的视图过于同质.为此引入了边缘条件卷积(edge-conditioned convolution, ECC),这是一种在空间域中对图信号执行的操作,其中滤波器权重取决于边缘标签,并针对每个特定输入样本动态生成.对原始点云数据进行构图和采样之后,并将ECC成功应用到点云上.
Qi等人[15]为了能够实现检测和识别图像和视频中的人与物交互作用(human-object interactions, HOI)的目的,提出了图解析神经网络(graph parsing neural network, GPNN),它是以端到端的方式推断解析图.可以实现对空间、时间(视频)等人与物交互的检测和识别.首先检测出所有的人和物,以人和物作为节点,任意2个节点之间都有边,表示人与物交互关系,构造一个全连接图.HOI主要面临的问题是如何预测出人与物之间的关系,预测关系其实就是预测出一个动作.然后通过不断地迭代优化,更新节点和边的特征.相当于不断学习人与物之间的关系,最后迭代至收敛后给每个节点预测一个动作,得到HOI关系.在GPNN的实现过程中借助于图神经网络框架中的连接函数、消息函数、更新函数和读出函数完成.
Liang等人[26]为了探索如何利用外部人类知识为网络赋予全局语义推理能力,提出了一个新的符号图推理层(symbolic graph reasoning, SGR)并且为了能够和局部卷积配合使用.如图19所示为SGR的整体结构图,每个SGR层由原始的局部到语义投票模块、图推理模块和双语义到局部映射模块这3个模块构成.其中,在局部到语义投票模块中,每个符号节点的个性化可视化证据可以通过从所有局部表示形式进行投票得出.图推理模块被实例化为在该图上传播信息以用于所有符号节点的等距特征的演化.最后,对局部语义的双重对偶学习了进化的符号节点与局部特征.图19中,每个符号节点都通过局部到语义的投票模块从所有局部特征接收投票,然后通过语义到局部的映射模块将其演变后的特征印后推理推回到每个位置.为简单起见,在知识图中省略了更多的边和符号节点.SGR层可以添加到任何卷积层之间,并将不同的先验映射实例化.
从人体骨架来识别人的动作是计算机视觉中的一个重要研究领域,文献[114]提出了时空图卷积网络ST-GCN,这是第1个将图神经网络用于动态骨骼建模任务中的文献,对人的行为动作进行识别.该模型可以自动从数据中学习空间和时间模式,将人体关节看作图中的节点.而图中的边则是由骨骼中关节自然连接的空间边和在连续时间步骤中连接相同关节的时间边2种边类型构成.同时,ST-GCN能够在动态骨骼序列中捕获动态信息,这对于RGB模态是很必要的.在2个具有挑战性的公开数据集上的实验结果显示,该模型优于先前的骨骼识别模型.ST-GCN还为解决其他类似的任务开辟了新的研究方向.文献[115]发现现有的方法丢失了隐式的联合关系,于是提出了一个自动设计的基于骨架动作识别图卷积神经网络.该网络充分挖掘节点间的时空相关性,并通过提供多个动态图模块来丰富搜索空间.最后还提出了一种有效的取样与记忆进化策略,以寻找该任务的最佳架构.文献[116]对计算机视觉中的定位进行了研究.提出了一种语言引导的图表示方法,能够对短语和视觉对象的全局上下文进行编码,并提出了一种全局优化的图匹配策略.作者还开发了一个模块化的图神经网络来实现基于图的视觉定位,以及一个2阶段的学习策略来共同训练整个模型.图像或视频始终包含多个对象或动作,多标签识别技术在计算机视觉中得到了急速的发展.文献[117]对传统的利用图卷积的多标签识别框架进行了改进,提出了一种标签图叠加框架.首先,将统计信息生成的标签图叠加到由标签的知识先验构造的图中,建立标签相关性模型,然后对最终的叠加图进行多层图卷积,实现标签嵌入抽象,从而使识别性能大大提高.文献[118]则针对现有的目标检测方法对每个数据集分别进行处理,只适合于特定的领域,如果不进行大量的再训练,则无法适应其他领域.提出了一种新的通用对象检测器,它结合了图迁移学习,在多个数据集上传播相关的语义信息,以达到语义一致性.大量实验表明,该方法在多目标检测基准上取得了最新的结果.识别特定菜肴图像的成分是自动膳食评估的核心.由于在食品加工过程中,配料的外观呈现出巨大的视觉变化,需要采集不同烹调和切割方法下的训练样本进行鲁棒识别,但获得足够的完全带标签的训练数据并不容易.文献[119]则将多关系图卷积神经网络引入进来,为零样本和小样本处理菜肴成分识别提供了依据.
7.3 在推荐系统方面的应用
推荐系统一般包含监督学习和无监督学习两大类模型,在无监督学习中推荐系统的目标就是矩阵补全,以此来对用户进行更好的推荐.荷兰阿姆斯特丹大学的Berg等人[73]基于user-item的二分图,提出了一种图卷积矩阵补全(GC-MC)和图自编码框架,其中观测到的评分用连接边来表示,最终的预测评分就相当于预测在这个user-item二分图中的连接边.把矩阵补全视为在图上的链路预测任务,以此来解决推荐系统中的评分预测问题.此外,Monti等人[120]使用图神经网络和循环神经网络结合的方式实现了推荐系统中矩阵的补全.
图神经网络在推荐系统上虽然表现很好,但把这些算法应用到数百亿的用户上仍然很困难.为此,Ying等人[121]提出了一种在Pinterest上的大规模深度推荐引擎,开发了一种高效的图卷积算法PinSage,该算法融合了随机游走和图卷积,生成顶点的表示,并整合了顶点信息和图结构.同时作者还介绍了PinSage相较于传统图卷积网络的优势以及一些新的训练技术:1)通过对节点周围的邻域进行采样并从该采样的邻域动态构造计算图来执行高效的局部卷积;2)开发了一种生产者-消费者体系结构,用于构建小批次训练,以确保在模型训练期间最大限度地利用GPU;3)设计了一个分发经过训练的模型策略以生成数十亿个节点的MapReduce管道;4)使用短随机游走技术对计算图进行采样;5)基于随机游走相似性衡量结点特征重要性;6)设计了新的训练方法,在训练过程中给予难以训练的实例更高的抽样机会.最后,PinSage算法利用Pinterest上的75亿样本进行训练,生成了相比其他深度学习和基于图的方法更高质量的推荐结果,为新一代基于图卷积结构的大规模推荐系统奠定了基础.
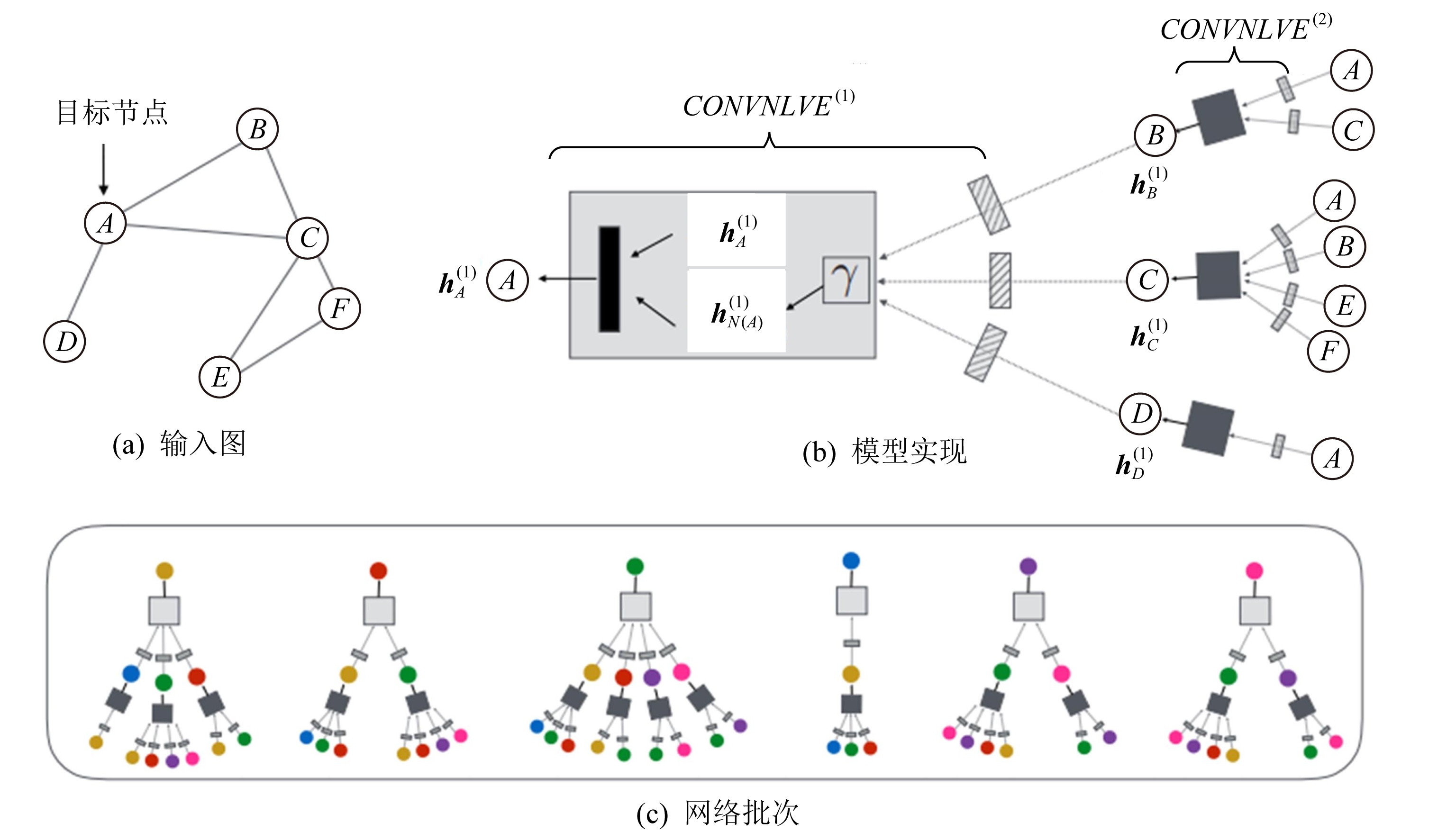
Fig. 20 The structure of PinSage model[121]
图20 PinSage模型结构[121]
图20为深度为2的PinSage模型结构图.图20(a)为一个小的示例输入图.图20(b)为利用2层神经网络实现的模型,节点A的隐表示为![]() 由其前一层的隐表示
由其前一层的隐表示![]() 及其邻域N(A)的隐表示
及其邻域N(A)的隐表示![]() 计算得到.图20(c)为计算输入图中每个节点的嵌入表示的神经网络.当神经网络从一个节点到另一个节点时,它们都共享相同的参数集(函数CONVNLVE(1)和CONVNLVE(2)的参数)中具有相同阴影图案的框共享参数,γ表示池化函数,细矩形框表示多层神经网络.虽然每个节点的神经网络不同,但它们都共享相同的参数集.
计算得到.图20(c)为计算输入图中每个节点的嵌入表示的神经网络.当神经网络从一个节点到另一个节点时,它们都共享相同的参数集(函数CONVNLVE(1)和CONVNLVE(2)的参数)中具有相同阴影图案的框共享参数,γ表示池化函数,细矩形框表示多层神经网络.虽然每个节点的神经网络不同,但它们都共享相同的参数集.
知识图谱(knowledge graph, KG)能够捕获结构化信息以及实体之间的关系,提供很好的信息描述方法.将其应用到推荐系统中,可以大大提高推荐系统的性能.但是,该领域中的现有方法大多依赖人工特征选取过程.为了解决这个弊端,Wang等人[122]提出了带有标签平滑度正则化的知识感知图神经网络(knowledge-aware graph neural networks with label smoothness regularization, KGNN-LS).KGNN-LS通过使用用户特定的关系评分功能并聚合具有不同权重的邻居信息,将GNN体系结构应用于KG上.该方法首先通过应用可训练的函数计算特定用户的嵌入,该函数可以为给定的用户标识出带有重要性的知识图关系.这样,就可以将知识图转换为特定用户的加权图,然后将图神经网络应用于计算个性化的嵌入表示.为了提供更好的归纳偏置,需要依靠标签平滑度假设.该假设假定知识图中的相邻节点可能具有相似的用户相关标签/分数.基于会话的个性化推荐问题旨在根据用户的连续行为来预测用户的下次点击.现有的基于会话的推荐方法仅将用户的所有会话视为单个序列,而忽略了会话之间的关系.带有注意力机制的个性化图神经网络(personalizing graph neural networks with attention mechanism, A-PGNN)为了解决现有的基于会话的个性化推荐问题[123].在A-PGNN中主要包括2个组件:1)个性化图神经网络,用于捕获用户会话序列中的复杂转换.与传统的GNN模型相比,它还考虑了用户在序列中的角色.2)变换模型中的点生成注意力机制,它利用机器翻译中的注意力机制来显式地模拟历史会话对当前会话的影响.这2部分使以用户特定的方式学习项目和会话之间的多级过渡关系成为可能.文献[30]则提出了一种与评级相关的局部图模式方法,称之为基于图的归纳矩阵补全(inductive graph-based matrix completion, IGMC).它是一个不使用边信息,并且不依赖于用户/项目内容的归纳矩阵完成模型.实验表明,一个从MovieLens数据集训练出来的模型可以直接用于预测豆瓣电影的收视率,其性能出奇的好.一些学者也同样将图卷积神经网络应用在基于协同过滤的推荐系统中,但是图卷积神经网络存在过平滑效应,大多数基于GCN的模型无法进行较深层的建模.文献[124]提出了一种基于用户交互建模的残差网络结构,解决了在稀疏用户交互数据图中进行卷积运算的过平滑问题.
7.4 在预测问题方面的应用
由于GNN的结构和化学分子结构类似,所以在分子预测问题上有着广泛的应用.在文献[125]中,作者针对目前分子预测方法不能随网络的复杂性很好地扩展问题,提出了一个可以附加到GNN上以提高模型表示能力的辅助模块,但又不会妨碍原始的GNN架构,该辅助模块可以连接到各种生化应用中常用的GNN中.借助该辅助架构,在实践中应用的许多GNN性能得到了更一致的改善,并且在流形的分子图数据集上实现了最先进的性能.分子的几何形状(也称构象)是分子最重要的特征之一,传统的构象生成方法将人工设计的分子力场能量函数减至最小,而该分子力场能量函数与自然界中观察到的分子的真实能量函数没有很好地关联.Mansimov等人[126]提出了一个条件深度生成图神经网络,该网络通过直接学习在给定分子图的情况下生成分子构象,从数据中学习能量函数.生成彼此不太相似的构象来保持几何多样性,并且计算速度也很快.机器学习通常用于虚拟筛选中,来预测发现对目标蛋白质具有药理活性的化合物.编制模块是GCN的一种形式,它可以关注单原子特征和成对的原子特征,但是原子间距离的相关性是不确定的.于是,Ohue等人[127]对编制模块进行了3点改进:1)修改图上环原子之间的距离,使图上的距离更接近坐标距离;2)根据特征的卷积层中图上的距离大小,使用不同的权重矩阵;3)再将特征转换为原子特征时,使用了距离的加权和.结果表明,改进后的编制模块比改进前的性能要好很多.此外,Capela等人[31]提出了一种基于GNN的多任务预测方法,用于预测分子的属性.同样,针对分子属性预测问题,Shindo等人[128]提出了一种简单而强大的GNN模型,引入具有门控功能的递归神经网络,实现了对分子属性的有效预测.
随着机器学习的兴起,人们对使用机器学习准确预测金融市场走势产生了越来越大的兴趣.尽管人工智能在金融领域取得了一些成就,但当前许多方法仅限于使用技术分析来捕获每个股价的历史趋势,只能依靠某些实验装置以获得良好的预测结果.Matsunaga等人[129]研究了金融市场预测和GNN交叉领域的工作效率问题,认为GNN有潜力通过将公司知识图直接纳入到预测模型来模拟投资者的决策方式.在其研究中主要使用滚动窗口分析法在不同市场和更长的时间范围内测试该方法的有效性.
社交平台领域中预测在线内容的流行度是一项很重要的任务,如何捕捉级联效应是准确预测未来受欢迎程度并解决此问题的关键之一.受到图神经网络成功应用于各种非欧氏结构数据上的启发,Cao等人[130]研究了沿着网络结构的关键级联效应.作者通过2个耦合的GNN对级联效应中的2个关键组件进行建模,即节点激活状态和影响范围之间的迭代相互作用.一个GNN通过用户的激活状态对人际影响进行建模.另一个GNN通过来自邻居的人际关系影响来模拟用户的激活状态.GNN中邻居聚合的迭代更新机制,有效地捕获了沿基础网络的级联效应.结果表明,该方法大大优于最新的一些预测方法.
GNN在疾病预测方面也扮演着重要的角色.Li等人[27]将图结构循环神经网络(graph-structured recurrent neural network, GSRNN)应用到了流行疾病预测上.为了提高模型效率,作者通过变换后的L1范数稀疏网络权重,但不会降低预测精度.疾病基因预测是指预测基因和疾病之间的关联,其有可能通过对各种疾病的候选基因进行优先排序来有效优化早期治疗的开发流程.Singh等人[28]将变分图自动编码器应用到疾病基因预测问题中.于此同时,作者还提出了一种扩展方法——受约束的图自编码器,用于异构图中2个不同节点类型之间的连接预测问题.
7.5 其他领域的应用
Luceri等人[131]利用基于图神经网络架构,解决了仅考虑在线社交网络中其他社交联系人的可用信息来推断用户当前位置的问题.该方法依靠小部分可用信息就可以将近50%的Tweets定位到1km以下的精度.随着智能设备的普及,通过传感器收集的数据量也在增加.生命日志是一种大数据,用于分析从各种智能设备收集的个人日常生活中的行为模式.Shin等人[132]提出了一种定义带有结点和边的图结构并从生成的生活日志图中提取日常行为模式的方法.在图像去噪方面,Valsesia等人[133]提出了一种含有图卷积层的神经网络,以利用局部和非局部相似性.图卷积层在特征空间中动态构造邻域,以检测由隐层产生的特征图中的潜在相关性.实验结果表明,该结构在处理去噪任务方面优于经典的卷积神经网络.Guo等人[134]提出了一种用于图像理解的基于多线索的图神经网络.与传统的特征和决策融合方法相比,该方法忽略了特征可以交换信息这一事实,所提出的GNN能够在从不同模型中提取的特征之间传递信息.Zhong等人[135]发现现有的许多基于脑电信号的情绪识别研究都没有利用脑电信号的拓扑结构,于是提出了用于基于脑电信号的情绪识别正则化图神经网络(regularized graph neural network, RGNN),该网络得到了生物学支持并捕获了本地和全局通道间关系,实现了对情绪的有效识别.Jin等人[136]将GNN应用到分子优化方面,他们将分子优化视为图到图的翻译问题,目的是学习到根据可用的成对分子语料库从一个分子图映射到具有更好性能的另一个分子图.为此对图到图的神经网络进行改进,提出了连接树编码器-解码器,可对具有神经注意力的分子图进行解码.并且还提出了一种新的对抗训练方法,将连接树编码器-解码器与对抗训练相结合.在最后的实验结果中表明该模型具有非常好的效果.在对舆情事件演化趋势评估任务中,且训练样本含有少量标签的情况下.秦涛等人[137]利用图卷积神经网络构建了一个舆情演化趋势评估模型,为社交网络中的舆情管控提供了一个强有力的决策支撑算法.
8 未来研究展望
GNN虽然起步较晚,但由于其强大的性能,已经取得了不俗的表现,并且也在例如计算机视觉和推荐系统等实际应用中发挥着巨大的作用.不难发现,GNN确实更符合当前实际应用的发展趋势,所以在近几年才会得到越来越多人的关注.但是,GNN毕竟起步较晚,还没有时间积累,研究的深度和领域还不够宽广.目前来看,它依然面临着许多亟待解决的问题,本节总结了GNN以后的研究趋势.
1) 动态图.目前,GNN处理的图结构基本上都是静态图,涉及动态图结构的模型较少[138-139],处理动态图对GNN来说是一个不小的挑战.静态图的图结构是静态不变的,而动态图的顶点和边是随机变化的,甚至会消失,并且有时还没有任何规律可循.目前针对GNN处理动态图结构的研究还是比较少的,还不够成熟.如果GNN能够成功应用于动态图结构上,相信这会使GNN的应用领域更加宽广.将GNN模型成功地推广到动态图模型是一个热点研究方向.
2) 异质图.同质图是指节点和边只有一种类型,这种数据处理起来较容易.而异质图则是指节点和边的类型不只一种,同一个节点和不同的节点连接会表现出不同的属性,同一条边和不同的节点连接也会表现出不同的关系,这种异质图结构处理起来就相对复杂.但异质图却是和实际问题最为贴切的场景,比如在社交网络中,同一个人在不同的社交圈中可能扮演着父亲、老师等不同的角色.对于异质图的研究还处在刚起步的阶段[140-141],模型方法还不够完善.所以,处理异质图也是将来研究的一个热点.
3) 构建更深的图神经网络模型.深度学习的强大优势在于能够形成多层的不同抽象层次的隐表示,从而才能表现出优于浅层机器学习的强大优势.但对于图深度学习来说,现有的图神经网络模型大多还是只限于浅层的结构.通过实验发现,当构造多层的神经网络时,实验结果反而变差.这是由过平滑现象造成的,GNN的本质是通过聚合邻居节点信息来表征中心节点.当构造多层的神经网络之后,中心节点和邻居节点的差异就会变得微乎其微,从而会导致分类结果变差.如何解决过平滑现象,使图神经网络能够应用于更多层的结构,从而发挥出深度学习的强大优势.虽然已有文献对其进行了讨论[91],但构建更深的图神经网络模型仍是值得深入研究的问题.
4) 将图神经网络应用到大图上.随着互联网的普及,图神经网络处理的数据也变得越来越大,致使图中的节点数量变得巨大,这就给图神经网络的计算带来了不小的挑战.虽然一些学者对该问题进行了研究改进[142],但针对将图神经网络应用到大图上的研究同样是将来研究的热点问题,在这方面,引入摘要数据结构,构造局部图数据,并能适当地融合局部图结构,形成整体图神经网络的表示是可能的思路.
5) 探索图中更多有用的信息.在当前诸多学者对于图神经网络模型的研究中,仅仅利用了图中节点之间有无连接这一拓扑结构信息.但是,图是一个非常复杂的数据结构,里面还有很多有用的信息未被人们发现利用.比如,图中节点的位置信息.中心节点的同阶邻居节点处于不同位置,距离中心节点的远近不同应该会对中心节点产生的影响程度不同.如果能够探索出图中更多的有用信息,必会将图神经网络的性能提升一个层次,这是一个非常值得探讨的问题.
6) 设计图神经网络的数学理论保障体系.任何神经网络模型必须有强大的数学理论支撑才能发展得更快,走得更远.现在对于图神经网络模型的设计,大多还只是依靠研究者的经验和基于机理逻辑设计出来的,并且对于图神经网络模型的性能分析仅仅是从实验结果中得来,并没有从数学理论层面给出一个合理的解释.目前,该领域已有一些研究[90-91],但为图神经网络设计出强大的数学理论,指导图神经网络的构造、学习和推理过程.能够给出图神经网络学习结果正确性的数学理论保障,仍是未来发展的一个重要方向.
7) 图神经网络的工业落地.当前对于图神经网络的研究大多还只是停留在理论层面,首先设计出模型,然后在公开数据集上进行测试验证,鲜有把工业的实际情况考虑在内.虽然图神经网络在工业上已有一小部分的实际应用,但还远没有达到大规模应用的程度.任何研究只有真正地在工业界落地,才能发挥它的应用价值,反之也会促进其进一步的研究发展.尽快将图神经网络应用到实际的工业场景中,是一个亟需解决的问题.
9 总 结
GNN作为近几年火热的神经网络,受到越来越多人的关注研究.由于传统的神经网络只能处理结构化的数据,面对非欧几里德数据就显得无能无力.GNN依靠其强大的点和边来对非欧几里德数据建模,高效地解决了在实际应用中遇到的图结构数据问题.和传统的神经网络相比,GNN对输入节点的顺序没有要求,并且在各个顶点之间的边中存储着相邻顶点的依赖关系,通过对中心节点的邻居节点加权求和来更新中心节点的隐状态.同时,GNN对图结构也没有要求,可以是环形图,也可以是有向图或者无向图.通过阅读近几年来大部分有关GNN模型和应用的文章,本文对GNN进行了系统的综述,阐述了GNN的各类模型以及一些典型的应用.
本文对GNN的研究现状进行了深入的综述和分析讨论,并对GNN的未来研究趋势进行了展望和总结.在第1节中,首先详细介绍了GNN模型的一个重要分支图卷积神经网络,分别从基于谱域、空间域以及池化进行了阐述,详细说明了ChebNet,GCN,PATCHY-SAN,LGCN等模型.在第2,3节中,介绍了GAT,SAGNN,SpGAT等基于注意力机制的图神经网络和DVNE,SDNE,DRNE等基于自编码器的图神经网络.第4节则补充了一些基于其他方法实现的图神经网络.第5节总结了一些学者针对图神经网络的平滑性、表现能力、到底能做多深等问题的分析讨论.第6,7节则概括了图神经网络的4个框架以及在自然语言处理、计算机视觉、推荐系统、预测问题等领域的应用.最后描述了GNN未来的研究趋势.
GNN是一个功能非常强大的神经网络,能够应用在相较于一般数据更加复杂的图结构数据上.综上所述,各种实现GNN的模型已经很丰富并且得到了迅速的发展,并且在各个领域得到了很好的应用.虽然有些模型存在自身的缺陷和局限性,但随着更多科研人员的学习研究,相信这些缺陷在不久的将来会得到解决.可以预见,GNN一定能使人工智能的发展迈向一个新的台阶.
作者贡献声明:马帅收集参考文献,负责实际调查研究,构思论文架构,负责论文撰写;刘建伟提出写作命题,收集参考文献,指导论文撰写,提供基金支持;左信负责研究项目管理,参与论文监管.
[1]Lecun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324
[2]Gu Jiuxiang, Wang Zhenhua, Kuen J, et al. Recent advances in convolutional neural networks[J]. Pattern Recognition, 2018, 77: 354-377
[3]Lawrence S, Giles C L, Tsoi A C, et al. Face recognition: A convolutional neural-network approach[J]. IEEE Transactions on Neural Networks, 1997, 8(1): 98-113
[4]Ciresan D C, Meier U, Masci J, et al. Flexible,high performance convolutional neural networks for image classification[C] //Proc of the 22nd Int Joint Conf on Artificial Intelligence. San Francisco, CA: Morgan Kaufmann, 2011: 1237-1242
[5]Dalal N, Triggs B. Histograms of oriented gradients for humandetection[C] //Proc of the IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2005: 886-893
[6]Fan Jialue, Xu Wei, Wu Ying, et al. Human tracking using convolutional neural networks[J]. IEEE Transactions on Neural Networks, 2010, 21(10): 1610-1623
[7]Huang Weilin, Qiao Yu, Tang Xiao’ou. Robust scene text detection with convolution neural network induced MSER trees[C] //Proc of the European Conf on Computer Vision. Berlin: Springer, 2014: 497-511
[8]Kim Y. Convolutional neural networks for sentence classification[J]. arXiv preprint, arXiv:1408.5882, 2014.
[9]Donahue J, Jia Yangqing, Vinyals O, et al. DeCAF: A deep convolutional activation feature for generic visual recognition[C] //Proc of the Int Conf on Machine Learning. New York: ACM, 2014: 647-655
[10]Zhu Han, Li Xiang, Zhang Pengye, et al. Learning tree-based deep model for recommender systems[C] //Proc of the 24th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2018: 1079-1088
[11]Niepert M, Ahmed M H, Kutzkov K, et al. Learning convolutional neural networks for graphs[C] //Proc of the 33rd Int Conf on Machine Learning. New York: ACM, 2016: 2014-2023
[12]Gao Hongyang, Wang Zhengyang, Ji Shuiwang. Large-scale learnable graph convolutional networks[C] //Proc of the 24th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2018: 1416-1424
[13]Atwood J, Towsley D. Diffusion-convolutionalneural networks[C] //Proc of the Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2016: 1993-2001
[14]Diao Zulong, Wang Xin, Zhang Dafang, et al. Dynamic spatial-temporal graph convolutional neural networks for traffic forecasting[C] //Proc of the AAAI Conf on Artificial Intelligence. Menlo Park: AAAI, 2019: 890-897
[15]Qi Siyuan, Wang Wenguan, Jia Baoxiong, et al. Learning human-object interactions by graph parsing neural networks[C] //Proc of the European Conf on Computer Vision. Berlin: Springer, 2018: 401-417
[16]Zhou Jie, Cui Ganqu, Zhang Zhengyan, et al. Graph neural networks: A review of methods and applications[J]. arXiv preprint, arXiv:1812.08434, 2018
[17]Wu Zonghan, Pan Shirui, Chen Fengwen, et al. A comprehensive survey on graph neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(1): 4-24
[18]Zhang Ziwei, Cui Peng, Zhu Wenwu. Deep learning on graphs: A survey[J/OL]. IEEE Transactions on Knowledge and Data Engineering. 2020[2020-07-09]. https://ieeexplore. ieee.org/abstract/document/9039675
[19]Xu Bingbing, Cen Keting, Huang Junjie, et al. A survey on graph convolutional neural network[J]. Chinese Journal of Computers, 2020, 43(5): 755-780 (in Chinese)(徐冰冰, 岑科廷, 黄俊杰, 等. 图卷积神经网络综述[J]. 计算机学报, 2020, 43(5): 755-780)
[20]Gori M, Monfardini G, Scarselli F. A new model for learning in graph domains[C] //Proc of the IEEE Int Joint Conf on Neural Networks. Piscataway, NJ: IEEE, 2005:729-734
[21]Scarselli F, Gori M, Tsoi A C, et al. The graph neural network model[J]. IEEE Transactions on Neural Networks, 2009, 20(1): 61-80
[22]Marcheggiani D, Bastings J, Titov I. Exploiting semantics in neural machine translation with graph convolutional networks[C] //Proc of the North American Chapter of the Association for Computational Linguistics. Stroudsburg, PA: ACL, 2018: 486-492
[23]Beck D, Haffari G, Cohn T. Graph-to-sequence learning using gated graph neural networks[J]. arXiv preprint, arXiv:1806.09835, 2018
[24]Peng Nanyun, Poon H, Quirk C, et al. Cross-sentence n-ary relation extraction with graph LSTMs[J]. Transactions of the Association for Computational Linguistics, 2017, 5(1): 101-115
[25]Simonovsky M, Komodakis N. Dynamic edge-conditioned filters in convolutional neural networks on graphs[C] //Proc of the IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2017: 3693-3702
[26]Liang Xiaodan, Hu Zhiting, Zhang Hao, et al. Symbolic graph reasoning meets convolutions[C] //Proc of the 32nd Advances in Neural Information Processing Systems.Cambridge, MA: MIT Press, 2018: 1858-1868
[27]Li Zhijian, Luo Xiyang, Wang Bao, et al. A study on graph-structured recurrent neural networks and sparsification with application to epidemic forecasting[C] //Proc of the World Congress on Global Optimization. Berlin: Springer, 2019: 730-739
[28]Singh V, Lio P. Towards probabilistic generative models harnessing graph neural networks for disease-gene prediction[J]. arXiv preprint, arXiv:1907.05628, 2019
[29]Liao Renjie, Brockschmidt M, Tarlow D, et al. Graph partition neural networks for semi-supervised classification[J]. arXiv preprint, arXiv:1803.06272, 2018
[30]Zhang Muhan, Chen Yixin. Inductive matrix completion based on graph neural networks[C/OL] //Proc of the Int Conf on Learning Representations. 2020 [2020-08-13]. https://arxiv.org/abs/1904.12058
[31]Capela F, Nouchi V, Van Deursen R, et al. Multitask learning on graph neural networks applied to molecular property predictions[J]. arXiv preprint, arXiv: 1910.13124, 2019
[32]Bruna J, Zaremba W, Szlam A, et al. Spectral networks and deep locally connected networks on graphs[C/OL] //Proc of the Int Conf on Learning Representations. 2014 [2020-08-21]. https://arxiv.org/abs/1312.6203
[33]Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering[C] //Proc of the Advances in Neural Information Processing Systems.Cambridge, MA: MIT Press, 2016: 3844-3852
[34]Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[C/OL] //Proc of the Int Conf on Learning Representations. 2017 [2020-09-11]. https://arxiv.org/abs/1609.02907
[35]Xu Bingbing, Shen Huawei, Cao Qi, et al. Graph wavelet neural network[C/OL] //Proc of the Int Conf on Learning Representations. 2019 [2020-09-18]. https://arxiv.org/abs/1904.07785
[36]Micheli A. Neural network for graphs: A contextual constructive approach[J]. IEEE Transactions on Neural Networks, 2009, 20(3): 498-511
[37]Spurek P, Danel T, Tabor J, et al. Geometric graph convolutional neural networks[J]. arXiv preprint, arXiv: 1909.05310, 2019
[38]Jiang Bo, Zhang Ziyan, Lin Doudou, et al. Graph learning-convolutional networks[J]. arXiv preprint, arXiv: 1811.09971, 2018
[39]Brockschmidt M. GNN-Film: Graph neural networks with feature-wise linear modulation[C] //Proc of the 37th Int Conf on Machine Learning. New York: ACM, 2020: 1144-1152
[40]Jiang Jiatao, Cui Zhen, Xu Chunyan, et al. Gaussian-induced convolution for graphs[C] //Proc of the AAAI Conf on Artificial Intelligence.Palo Alto, CA: AAAI, 2019: 4007-4014
[41]Zhou Zhenpeng, Li Xiaocheng. Convolution on graph: A high-order and adaptive approach[J]. arXiv preprint, arXiv: 1706.09916, 2017
[42]Chami I, Ying R, Re C, et al. Hyperbolic graph convolutional neural networks[C] //Proc of the Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2019: 4869-4880
[43]Zhang Yingxue, Pal S, Coates M, et al. Bayesian graph convolutional neural networks for semi-supervised classification[C] //Proc of the AAAI Conf on Artificial Intelligence. Menlo Park: AAAI, 2019: 5829-5836
[44]Pal S, Rego F, Coates M. Bayesal graph convolutional neural networks using non-parametric graph learning[J]. arXiv preprint, arXiv: 1910.12132, 2019
[45]Pal S, Rego F, Coates M. Bayesian graph convolutional neural networks using node copying[J]. arXiv preprint, arXiv: 1911.04965, 2019
[46]Hamilton W L, Ying R, Leskovec J. Inductive representation learning on large graphs[C] //Proc of the Advances in Neural Information Processing Systems.Cambridge, MA: MIT Press, 2017: 1024-1034
[47]Chen Jie, Ma Tengfei, Xiao Cao. FastGCN: Fast learning with graph convolutional networks via importance sampling[C/OL] //Proc of the Int Conf on Learning Representations. 2018[2020-08-21]. https://arxiv.org/abs/1801.10247
[48]Huang Wenbing, Zhang Tong, Rong Yu, et al. Adaptive sampling towards fast graph representation learning[C] //Proc of the Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2018: 4558-4567
[49]Chen Jianfei, Zhu Jun, Song Le. Stochastic training of graph convolutional networks with variance reduction[C] //Proc of the Int Conf on Machine Learning. New York: ACM, 2018: 941-949
[50]Chiang Weilin, Liu Xuanqing, Si si, et al. Cluster-GCN: An efficient algorithm for training deep and large graph convolutional networks[C] //Proc of the ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2019: 257-266
[51]Zou Difan, Hu Ziniu, Wang Yewen, et al. Layer-dependent importance sampling for training deep and large graph convolutional networks[C] //Proc of the Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2019: 11249-11259
[52]Salha G, Hennequin R, Tran V A, et al. A degeneracy framework for scalable graph autoencoders[C] //Proc of the Int Joint Conf on Artificial Intelligence.San Francisco, CA: Morgan Kaufmann, 2019: 3353-3359
[53]Bianchi F M, Grattarola D, Alippi C. minCUT pooling in graph neural networks[J]. arXiv preprint, arXiv: 1907.00481, 2019
[54]Zhang Zhen, Bu Jiajun, Ester M, et al. Hierarchical graph pooling with structure learning[J]. arXiv preprint, arXiv: 1911.05954, 2019
[55]Yuan Hao, Ji Shuiwang. Structpool: Structured graph pooling via conditional random fields[C/OL] //Proc of the Int Conf on Learning Representations. 2020[2020-09-28]. https://par.nsf.gov/servlets/purl/10159731
[56]Ying Rex, You Jiaxuan, Morris C, et al. Hierarchical graph representation learning with differentiable pooling[C] //Proc of the Advances in Neural Information Processing Systems.Cambridge, MA: MIT Press, 2018: 4805-4815
[57]Gao Xing, Xiong Hongkai, Frossard P. iPool-information-based pooling in hierarchical graph neural networks[J]. arXiv preprint, arXiv: 1907.00832, 2019
[58]Lee J, Lee I, Kang J. Self-attention graph pooling[C] //Proc of the Int Conf on Machine Learning. New York: ACM, 2019: 3734-3743
[59]Ma Yao, Wang Suhang, Aggarwal C C, et al. Graph convolutional networks with eigenpooling[C] //Proc of the ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2019: 723-731
[60]Bahdanau D, Cho K, Bengio Y. Neural machine translation by jointly learning to align and translate[C/OL] //Proc of the Int Conf on Learning Representations. 2015[2020-07-21]. https://arxiv.org/abs/1409.0473
[61]Velickovic P, Cucurull G, Casanova A, et al. Graph attention networks[C/OL] //Proc of the Int Conf on Learning Representations. 2018[2020-07-01]. https://arxiv.org/abs/1710.10903
[62]Zhang Jiani, Shi Xingjian, Xie Junyuan, et al. GaAN: Gated attention networks for learning on large and spatiotemporal graphs[C] //Proc of the Uncertainty in Artificial Intelligence. Arlington, VA: AUAI Press, 2018: 339-349
[63]Zhang Shuo, Xie Lei. Improving attention mechanism in graph neural networks via cardinality preservation[J]. arXiv preprint, arXiv:1907.02204, 2019
[64]Zhang Ruochi, Zou Yuesong, Ma Jian. Hyper-SAGNN:A self-attention based graph neural network for hypergraphs[C/OL] //Proc of the Int Conf on Learning Representations. 2020[2020-09-28]. https://arxiv.org/abs/1911.02613
[65]Nguyen D Q, Nguyen T D, Phung D. A universal self-attention graph neural network[J]. arXiv preprint, arXiv:1909.11855, 2019
[66]Chang Heng, Rong Yu, Xu Tingyang, et al. Spectral graph attention network[J]. arXiv preprint, arXiv:2003.07450, 2020
[67]Knyazev B, Taylor G W, Amer M R. Understanding attention and generalization in graph neural networks[C] //Proc of the Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2019: 4204-4214
[68]Xu Keyulu, Hu Weihua, Leskovec J, et al. How powerful are graph neural networks[C/OL] //Proc of the Int Conf on Learning Representations. 2019[2020-08-09]. https://arxiv.org/abs/1810.00826
[69]Kipf T N, Welling M. Variational graph auto-encoders[J]. arXiv preprint, arXiv:1611.07308, 2016
[70]Zhu Dingyuan, Cui Peng, Wang Daixin, et al. Deep variational network embedding in wasserstein space[C] //Proc of the ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2018: 2827-2836
[71]Wang Daixin, Cui Peng, Zhu Wenwu. Structural deep network embedding[C] //Proc of the ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2016: 1225-1234
[72]Tu Ke, Cui Peng, Wang Xiao, et al. Deep recursive network embedding with regular equivalence[C] //Proc of the ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2018: 2357-2366
[73]Berg R, Kipf T N, Welling M. Graph convolutional matrix completion[J]. arXiv preprint, arXiv:1706.02263, 2017
[74]Pan Shirui, Hu Ruiqi, Long Guodong, et al. Adversarially regularized graph autoencoder for graph embedding[C] //Proc of the Int Joint Conf on Artificial Intelligence. San Francisco, CA: Morgan Kaufmann, 2018: 2609-2615
[75]Bojchevski A, Gunnemann S. Deep Gaussian embedding of graphs: Unsupervised inductive learning via ranking[C/OL] //Proc of the Int Conf on Learning Representations. 2018[2020-07-24]. https://arxiv.org/abs/1707.03815
[76]Qu Meng, Bengio Y, Tang Jian. GMNN: Graph Markov neural networks[C] //Proc of the Int Conf on Machine Learning. New York: ACM, 2019: 5241-5250
[77]Ng Y C, Colombo N, Silva R. Bayesian semi-supervised learning with graph Gaussian Processes[C] //Proc of the Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2018: 1690-1701
[78]Nicolicioiu A, Duta I, Leordeanu M. Recurrent space-time graph neural networks[C] //Proc of the Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2019: 12818-12830
[79]Ouyang Yi, Guo Bin, Tang Xing, et al. Learning cross-domain representation with multi-graph neural network[J]. arXiv preprint, arXiv: 1905.10095, 2019
[80]Zhang Zhen, Wu Fan, Lee W S. Factor graph neural network[J]. arXiv preprint, arXiv: 1906.00554, 2019
[81]Chen Yu, Wu Lingfei, Zaki M J. GraphFlow: Exploiting conversation flow with graph neural networks for conversational machine comprehension[J]. arXiv preprint, arXiv: 1908.00059, 2019
[82]Cao Yixin, Liu Zhiyuan, Li Chenjiang, et al. Multi-channel graph neural network for entity alignment[C] //Proc of the Annual Meeting of the ACL. Stroudsburg, PA: ACL, 2019: 1421-1461
[83]He Chaoyang, Xie Tian, Rong Yu, et al. Bipartite graph neural networks for efficient node representation learning[J]. arXiv preprint, arXiv: 1906.11994, 2019
[84]Verma S, Zhang Zhili. Graph capsule convolutional neural networks[J]. arXiv preprint, arXiv: 1805.08090, 2018
[85]Du S S, Hou Kangcheng, Poczos B, et al. Graph neural tangent kernel: Fusing graph neural networks with graph kernels[J]. arXiv preprint, arXiv: 1905.13192, 2019
[86]Xu Keyulu, Li Chengtao, Tian Yonglong, et al. Representation learning on graphs with jumping knowledge networks[C] //Proc of the Int Conf on Machine Learning. New York: ACM, 2018: 5449-5458
[87]Su Shihyang, Hajimirsadeghi H, Mori G. Graph generation with variational recurrent neural network[J]. arXiv preprint, arXiv: 1910.01743, 2019
[88]Sato R, Yamada M, Kashima H, et al. Constant time graph neural networks[J]. arXiv preprint, arXiv: 1901.07868, 2019
[89]Carr A, Wingate D. Graph neural processes towards Bayesian graph neural networks[J]. arXiv preprint, arXiv: 1902.10042, 2019
[90]Morris C, Ritzert M, Fey M, et al. Weisfeiler and Leman go neural: Higher-order graph neural networks[C] //Proc of the AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2019: 4602-4609
[91]Li Guohao, Muller M, Thabet A, et al. DeepGCNs: Can GCNs go as deep as CNNs?[C] //Proc of the IEEE Int Conf on Computer Vision. Piscataway, NJ: IEEE, 2019: 9267-9276
[92]Barcelo P, Kostylev E V, Monet M, et al. The logical expressiveness of graph neural networks[C/OL] //Proc of the Int Conf on Learning Representations. 2020[2020-10-03]. https://openreview.net/forum?id=r1lZ7AEKvB
[93]Li Qimai, Han Zhichao, Wu Xiaoming. Deeper insights into graph convolutional networks for semi-supervised learning[C] //Proc of the AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2018: 3538-3545
[94]Oono K, Suzuki T. Graph neural networks exponentially lose expressive power for node classification[C/OL] //Proc of the Int Conf on Learning Representations. 2020[2020-10-12]. https://arxiv.org/abs/1905.10947
[95]Dehmamy N, Barabasi A L, Yu R. Understanding the representation power of graph neural networks in learning graph topology[C] //Proc of the Advances in Neural Information Processing Systems.Cambridge, MA: MIT Press, 2019: 15413-15423
[96]Srinivasan B, Ribeiro B. On the equivalence between positional node embeddings and structural graph representations[C/OL] //Proc of the Int Conf on Learning Representations. 2019[2020-06-11]. https://arxiv.org/abs/1910.00452
[97]Loukas A. What graph neural networks cannot learn: Depth vs width[C/OL] //Proc of the Int Conf on Learning Representations. 2020[2020-09-19]. https://arxiv.org/abs/1907.03199
[98]Gilmer J, Schoenholz S S, Riley P F, et al. Neural message passing for quantum chemistry[C] //Proc of the Int Conf on Machine Learning. New York: ACM, 2017: 1263-1272
[99]Wang Xiaolong, Girshick R, Gupta A, et al. Non-local neural networks[C] //Proc of the IEEE Conf on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE, 2018: 7794-7803
[100]Battaglia P W, Hamrick J B, Bapst V, et al. Relational inductive biases, deep learning, and graph networks[J]. arXiv preprint, arXiv:1806.01261, 2018
[101]Monti F, Boscaini D, Masci J, et al. Geometric deep learning on graphs and manifolds using mixture model CNNs[C] //Proc of the IEEE Conf on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE, 2017: 5425-5434
[102]Buades A, Coll B, Morel J M. A non-local algorithm for image denoising[C] //Proc of the IEEE Conf on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE, 2005: 60-65
[103]Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[C] //Proc of the Advances in Neural Information Processing Systems.Cambridge, MA: MIT Press, 2017: 6000-6010
[104]Kipf T, Fetaya E, Wang K C, et al. Neural relational inference for interacting systems[C] //Proc of the Int Conf on Machine Learning. New York: ACM, 2018: 2688-2697
[105]Wang Tingwu, Liao Renjie, Ba J, et al. NerveNet: Learning structured policy with graph neural networks[C/OL] //Proc of the Int Conf on Learning Representations. 2018[2020-06-26]. https://openreview.net/forum?id=S1sqHMZCb
[106]Gilmer J, Schoenholz S S, Riley P F, et al. Neural message passing for quantum chemistry[C] //Proc of the Int Conf on Machine Learning. New York: ACM, 2017: 1263-1272
[107]Hamrick J B, Allen K R, Bapst V, et al. Relational inductive bias for physical construction in humans and machines[J]. arXiv preprint, arXiv:1806.01203, 2018
[108]Masci J, Boscaini D, Bronstein M M, et al. Geodesic convolutional neural networks on Riemannian manifolds[C] //Proc of the IEEE Int Conf on Computer Vision Workshops. Piscataway, NJ: IEEE, 2015: 37-45
[109]Boscaini D, Masci J, Rodola E, et al. Learning shape correspondence with anisotropic convolutional neural networks[C] //Proc of the Advances in Neural Information Processing Systems.Cambridge, MA: MIT Press, 2016: 3197-3205
[110]Rahimi A, Cohn T, Baldwin T. Semi-supervised user geolocation via graph convolutional networks[C] //Proc of the Meeting of the ACL. Stroudsburg, PA: ACL, 2018: 2009-2019
[111]Sahu S K, Christopoulou F, Miwa M, et al. Inter-sentence relation extraction with document-level graph convolutional neural network[C] //Proc of the Meeting of the ACL. Stroudsburg, PA: ACL, 2019: 4309-4316
[112]Zhu Hao, Lin Yankai, Liu Zhiyuan, et al. Graph neural networks with generated parameters for relation extraction[C] //Proc of the Meeting of the ACL. Stroudsburg, PA: ACL, 2019: 1331-1339
[113]Veyseh A P B, Nguyen T H, Dou Dejing. Graph based neural networks for event factuality prediction using syntactic and semantic structures[C] //Proc of the Meeting of the ACL. Stroudsburg, PA: ACL, 2019: 4393-4399
[114]Yan Sijie, Xiong Yuanjun, Lin Dahua. Spatial temporal graph convolutional networks for skeleton-based action recognition[C] //Proc of the 32nd AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2018: 7444-7452
[115]Peng Wei, Hong Xiaopeng, Chen Haoyu, et al. Learning graph convolutional network for skeleton-based human action recognition by neural searching[C] //Proc of the AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2020: 2669-2676
[116]Liu Yongfei, Wan Bo, Zhu Xiaodan, et al. Learning cross-modal context graph networks for visual grounding[C] //Proc of the AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2020: 11645-11652
[117]Wang Ya, He Dongliang, Li Fu, et al. Multi-label classification with label graph superimposing[C] //Proc of the AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2020: 12265-12272
[118]Xu Hang, Fang Linpu, Liang Xiaodan, et al. Universal-RCNN: Universal object detector via transferable graph R-CNN[C] //Proc of the AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2020: 12492-12499
[119]Chen Jingjing, Pan Liangming, Wei Zhipeng, et al. Zero-shot ingredient recognition bymulti-relational graph convolutional network[C] //Proc of the AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2020: 10542-10550
[120]Monti F, Bronstein M M, Bresson X. Geometric matrix completion with recurrent multi-graph neural networks[C] //Proc of the Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2017: 3697-3707
[121]Ying Rex, He Ruining, Chen Kaifeng, et al. Graph convolutional neural networks for web-scale recommender systems[C] //Proc of the ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2018: 974-983
[122]Wang Hongwei, Zhang Fuzheng, Zhang Mengdi, et al. Knowledge-aware graph neural networks with label smoothness regularization for recommender systems[C] //Proc of the ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2019: 968-977
[123]Zhang Mengqi, Wu Shu, Gao Meng, et al. Personalized graph neural networks with attention mechanism for session-aware recommendation[J/OL]. IEEE Transactions on Knowledge and Data Engineering. 2020[2020-10-25]. https://ieeexplore. ieee. org/abstract/document/9226110
[124]Chen Lei, Wu Le, Hong Richang, et al. Revisiting graph based collaborative filtering: A linear residual graph convolutional network approach[C] //Proc of the AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2020: 27-34
[125]Ishiguro K, Maeda S, Koyama M, et al. Graph warp module: An auxiliary module for boosting the power of graph neural networks in molecular graph analysis[J]. arXiv preprint, arXiv:1902.01020, 2019
[126]Mansimov E, Mahmood O, Kang S, et al. Molecular geometry prediction using a deep generative graph neural network[J]. Scientific Reports, 2019, 9(1): 1-13
[127]Ohue M, Ii R, Yanagisawa K, et al. Molecular activity prediction using graph convolutional deep neural network considering distance on a molecular graph[J]. arXiv preprint, arXiv:1907.01103, 2019
[128]Shindo H, Matsumoto Y. Gated graph recursive neural networks for molecular property prediction[J]. arXiv preprint, arXiv:1909.00259, 2019
[129]Matsunaga D, Suzumura T, Takahashi T. Exploring graph neural networks for stock market predictions with rolling window analysis[J]. arXiv preprint, arXiv:1909.106602, 2019
[130]Cao Qi, Shen Huawei, Gao Jinhua, et al. Popularity prediction on social platforms with coupled graph neural networks[C] //Proc of the 13th Int Conf on Web Search and Data Mining. New York: ACM, 2020: 70-78
[131]Luceri L, Andreoletti D, Giordano S. Infringement of tweets geo-location privacy: An approach based on graph convolutional neural networks[J]. arXiv preprint, arXiv:1903.11206, 2019
[132]Shin W, Kim T, Cho S B. Lifelog patterns analyzation using graph embedding based on deep neural network[J]. arXiv preprint, arXiv:1909.04252, 2019
[133]Valsesia D, Fracastoro G, Magli E, et al. Image denoising with graph-convolutional neural networks[C] //Proc of the IEEE Int Conf on Image Processing. Piscataway, NJ: IEEE, 2019: 2399-2403
[134]Guo Xin, Polania L, Zhu Bin, et al. Graph neural networks for image understanding based on multiple cues: Group emotion recognition and event recognition as use cases[C] //Proc of the IEEE Winter Conf on Applications of Computer Vision. Piscataway, NJ: IEEE, 2020: 2921-2930
[135]Zhong Peixiang, Wang Di, Miao C. EEG-based emotion recognition using regularized graph neural networks[J/OL]. IEEE Transactions on Affective Computing. 2020[2020-08-21]. https://ieeexplore. ieee.org/abstract/d ocument/9091308
[136]Jin Wengong, Yang Kevin, Barzilay R, et al. Learning multimodal graph-to-graph translation for molecular optimization[J]. arXiv preprint, arXiv:1812.01070, 2018
[137]Qin Tao, Shen Zhuang, Liu Huan, et al. Learning torank for evolution trend evaluation of online public opinion events[J]. Journal of Computer Research and Development, 2020, 57(12): 2490-2500 (in Chinese)(秦涛, 沈壮, 刘欢, 等. 基于排序学习的网络舆情演化趋势评估方法研究[J]. 计算机研究与发展, 2020, 57(12): 2490-2500)
[138]Li Jiachen, Yang Fan, Tomizuka M, et al. Evolvegraph: Multi-agent trajectory prediction with dynamic relational reasoning[C/OL] //Proc of the Advances in Neural Information Processing Systems.Cambridge, MA: MIT Press, 2020 [2020-07-19]. https://www. researchgate.net/publication/344454811_EvolveGraph_Multi-Agent_Trajectory_ Prediction_ with_Dynamic_Relational_Reasoning
[139]Huang Jialei, Zhan Guanqi, Fan Qingnan, et al. Generative 3D part assembly via dynamic graph learning[J]. arXiv preprint, arXiv:2006.07793, 2020
[140]Fu Xinyu, Zhang Jiani, Meng Ziqiao, et al. MAGNN: Metapath aggregated graph neural network for heterogeneous graph embedding[C] //Proc of the World Wide Web Conf. New York: ACM, 2020: 2331-2341
[141]Wang Xiao, Ji Houye, Shi Chuan, et al. Heterogeneous graph attention network[C] //Proc of the World Wide Web Conf. New York: ACM, 2019, 2022-2032
[142]Lee J B, Rossi R A, Kong Xiangnan, et al. Higher-order graph convolutional networks[J]. arXiv preprint, arXiv:1809.07697, 2018


