随着地理定位技术与移动社交服务的发展，融合位置信息的地理社交网络(如Foursquare、Gowalla、美团网、街旁网等)成为广受用户欢迎的一类社交媒体平台.据统计，截至2020年，美团平台上的活跃商家个数以及年度交易用户总量已分别增长至680万和5.1亿[1]；与此同时，2020年度Foursquare通过旗下的签到业务已在全球190个国家与地区累计收集了9 500万个不同类别的兴趣点信息[2].地理社交网络有效地连接了用户的线上信息与线下行为，便捷的线下服务与相对低廉的线上广告成本，也使得更多商家将地理社交网络作为一类有效的市场推广途径.
面向社交网络“病毒式”营销(viral marketing)[3-4]，影响力最大化(influence maximization, IM)问题旨在从社交网络中寻找并激活k个具有高影响力的用户节点(影响力种子)，利用社交用户间“口口相传”(word of mouth, WOM)[5-6]的特性，触发影响力在用户间的连锁式传播，从而使影响力传播最大化.近年来，得益于5G与物联网技术的发展，基于位置的广告营销呈现出极大的商业潜力.据权威部门预测，2021年位置营销服务将在北美市场创造约1 375亿美元的收益[7].对应基于位置的营销研究，地理社交网络中的空间感知影响力最大化问题已成为IM领域一个重要的研究分支.区别于传统IM问题在社交网络全图中实现最大化传播，空间感知IM问题考虑了用户在物理世界中的空间属性，使影响力在一部分位置相关的用户群体中达到最佳的传播效果.
Li等人[8]最早在基于位置的社交网络中研究了位置感知影响力最大化(location-aware influence maximization, LAIM)问题，给定一个查询范围，LAIM问题尝试从社交网络中寻找k个种子节点，使影响力在查询范围内的用户中达到最大传播规模.然而，在LAIM问题中，用户如何设定合理的查询范围是一个潜在的难题.具体而言，假如用户设定的查询范围过小，大量空间邻近用户将因在查询范围之外而无法成为营销推广对象；若查询范围设定过大，则相当一部分被激活的用户将处于查询范围的边缘区域，受空间移动的限制，这部分用户无法真正成为线下活跃用户.为解决此问题，Wang等人[9]提出距离感知影响力最大化(distance-aware influence maximization, DAIM)问题，认为距离查询位置更近的用户将更有可能被营销活动所吸引，因而具有更高的推广价值.基于此，DAIM对各用户分配了不同的价值权重，以指导空间距离加权下的影响力种子选择.
值得注意的是，当前有关空间感知IM问题的研究，都只将固定位置处的单一空间对象作为推广目标.这一设定仅能在有限的空间范围内吸引较少的客户，故不利于商家最大化地拓展其市场潜力.为实现利益最大化，商家需要有多个营销目标，如连锁店公司对旗下的多家门店进行联合推广.考虑到大型连锁公司旗下庞大的门店规模(如星巴克在中国大陆的门店规模总计约为5 000家，2020年新增门店259家[10])，受广告篇幅与费用的限制，商家将无法在单条广告中穷尽所有门店信息.如何从所有门店中优先推选出一部分最具潜力的门店作为线上推广主体，并搭配有效的社交营销策略以实现商家利益的最大化是本文研究的重点.图1进一步展示本文的研究动机.
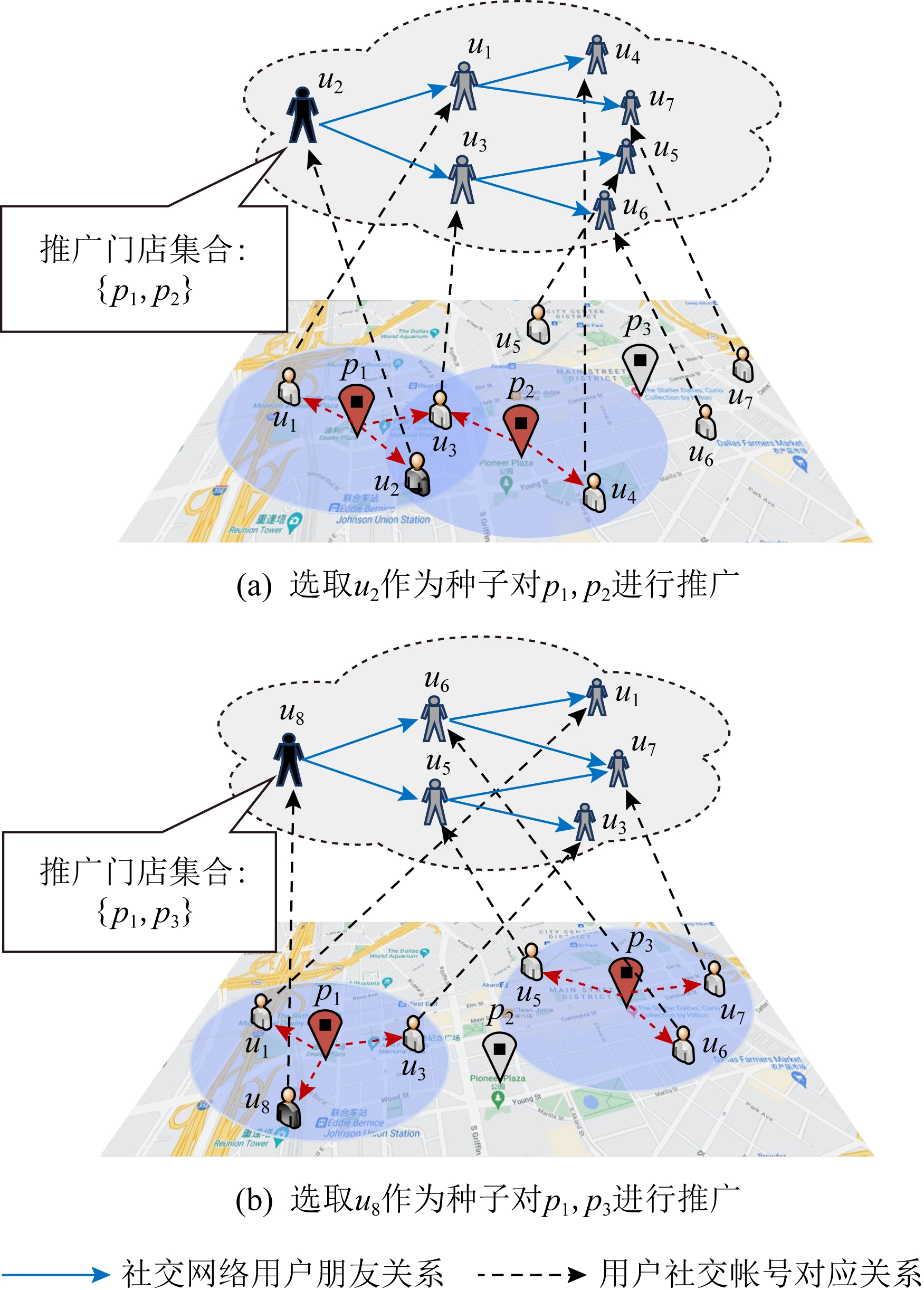
Fig. 1 An example of location based social advertising for multiple promotion targets
图1 基于位置的多目标营销场景示例
图1展示了某城市中心新开设的3家星巴克门店(p1,p2,p3).为方便统计，规定单一的某家门店仅能对其附近3 km范围内(图中兴趣点图标周围圆形阴影区域)的用户产生影响，同时商家发布广告的内容篇幅最多容纳2家门店信息，且营销的费用预算为1(影响力种子个数为1).在此条件下，若选择门店p1,p2作为营销推广目标，用户u2作为发起线上影响力传播的种子，则影响力传播过程将激活7名用户，其中4名(u1,u2,u3,u4)位于推广位置的邻近区域，故此次营销的实际收益为4；若选择门店p1,p3作为推广目标，并改变影响力种子为用户u8，则影响力传播的总体规模为6，但由于传播过程中所有用户均与推广门店位置邻近，故该策略下商家营销的实际收益将上升为6.
在图1示例中，本质是求解一组推广目标与影响力种子集合的最优搭配，从而使商家在基于位置的营销中获得最大化的收益.本文将该问题称为基于多目标组合优化的空间感知影响力联合推广(location-aware joint influence promotion, LA-JIP)问题.相比于传统IM问题以及空间感知的IM问题变种，LA-JIP问题的求解有着更多的挑战：1)在不同位置组合下，用户权重的衡量将更为复杂，且评估影响力传播过程中所获得的收益本身是一个#P难题，如何对影响力传播收益进行高效而准确的评估是解决LA-JIP问题的关键；2)LA-JIP问题涉及对推广目标的位置与影响力种子的联合选取，该问题本身为一个NP难问题，且目标函数不满足子模特性，故传统的贪心策略将无法直接对该问题实现理论精度保障下的求解；3)LA-JIP是一个多目标组合优化问题，由于不同优化目标间彼此关联性强，故难以针对某一目标设计有效的剪枝方式以加速问题的精确求解.综上所述，本文工作的主要贡献有4个方面：
1) 面向真实应用，首次研究了地理社交网络中基于多目标组合优化的空间感知影响力联合推广问题LA-JIP，通过发现门店推广位置与影响力种子的最优组合搭配，以实现商家利益最大化的营销推广；
2) 基于反向影响力采样技术，提出了在用户影响力加权条件下的影响力传播收益上下界推导方法，以有效地评估多目标组合下的营销推广效益；
3) 提出了满足结果精度收敛的迭代处理算法，通过多轮的结果迭代优化，该算法能够在一定的理论精度保障下对LA-JIP问题进行高效的近似求解；
4) 在多个真实数据集上对所提问题及技术方法的有效性进行了验证.实验结果表明相比传统IM或DAIM问题，LA-JIP能够有效地提升空间感知影响力推广收益；此外，所提出的迭代处理算法相比传统贪心策略下的基准算法，结果质量提高10%～50%、算法运行效率快1～2个数量级.
1 相关工作
影响力最大化问题最早可追溯至对“病毒式营销[3-4]”和“口碑效应[5-6]”的研究.Domingo和Richardson首次将影响力最大化分析引入社交领域[6,11]，并指出了该问题在舆情预警与市场营销中的重要性.随后，Kempe等人[12]首次从算法角度将影响力最大化定义为一个组合优化问题，在独立级联(independent cascade, IC)模型与线性阈值(linear threshold, LT)模型下证明了该问题的NP难复杂性，并基于问题的子模特性在贪心策略下提出了精度为(1-1/e)的近似算法，但该算法需涉及大量耗时的蒙特卡罗模拟来对节点影响力进行评估，因而算法时间复杂度极高，不适用于大规模社交网络.此后，一些研究者提出了启发式方法以识别高影响力的用户节点[13-16]，这类方法尽管在效率上有较大提升，但其求得结果的精度缺乏理论保证.后续大量研究工作致力于提出满足理论精度保证的高效近似算法[17-22]，以支持大规模社交网络图下的IM问题求解.针对这一目标，大量高效的影响力采样策略被提出.其中基于反向影响力采样技术的算法被证明不仅具有理论精度保障，而且满足渐线性的时间复杂度，因而成为当下最为有效的一类IM问题处理方法.这类算法的核心是采样足够规模的随机反向影响力可达集，从而对高影响力节点展开有效的分析与选择.后续基于该方向的一系列拓展工作[18-22]，集中解决了如何在不改变结果精度的前提下尽可能地减少随机反向可达集的采样规模，以最大化地提升算法的处理效率.
近年来随着移动社交服务的兴起，地理社交网络中的空间感知影响力最大化问题引起了学术界的广泛关注.Li等人[8]最先研究了空间感知影响力最大化的问题原型，该工作借鉴了“口碑营销”的思想，通过从全局社交网络中寻找k个种子节点，以触发影响力在给定空间查询范围内的最优传播效果.进一步地，Wang等人在文献[9]中提出了距离感知的影响力最大化(distance-aware influence maximization, DAIM)问题，给定一个地理位置坐标，DAIM根据用户与查询位置间距离的远近，对不同位置处的用户推广效益进行加权处理，最终使所选种子的影响力能够在邻近用户群体中产生最优的推广效果.类似DAIM，文献[23]综合考虑了社交影响力传播过程中的时间有效性，研究了目标用户影响力最大化问题，该工作基于反向影响力采样的思想提出了基于加权反向可达采样树的近似算法，实现了理论精度保障下的问题求解.受LAIM启发，文献[24]研究了地理社交影响力最大化拓展(geo-social influence spanning maximization, GISM)问题,给定查询区域R,GISM综合考虑区域R中用户的总体激活情况以及R中各个子区域内部用户的激活比率，使影响力能够在尽可能多的子区域间有更均衡的传播效果，GISM在区域性的政客竞选中有着重要的应用价值.此外，Zhong等人面向DAIM问题探讨了高效的锚点采样技术[25].Wang等人在社交媒体数据流上对LAIM问题展开了探索[26].Shi等人在文献[27]中通过对地理社交网络中兴趣点签到数据的分析，探索了地理位置驱动下影响力最大化问题.于亚新等人[28]在考虑竞争的地理社交网络中研究了避免种子重叠的多方影响力博弈问题.面向多标准决策优化，Wang等人[29]探讨了不同种子选取策略下的Pareto结果集高效求解方法，通过权衡营销过程中的代价与收益，为商家提供全面的营销决策支持.值得注意的是，上述的所有工作仅局限于通过改变影响力种子的选取策略来实现空间感知的影响力推广，而忽略了推广目标本身在空间属性方面所具有的优化潜能，这也是本文研究工作与现有工作的最大不同之处.
2 问题定义
本节首先介绍问题的相关预备知识，其次对问题进行形式化定义与难度分析，最后基于贪心策略提出一种启发式方法作为求解问题的基准算法.表1列出了文中常用的符号及其含义.
Table 1 Symbols and Description
表1 符号及含义
符号含义 =(V,E)地理社交网络
2.1 预备知识
地理社交网络可被抽象成一张带有空间信息的有向图
其中V代表社交网络图的节点集合(社交用户)，E代表社交网络图的边集合(社交关系).图中每个节点都关联了一个空间坐标(x,y)，其中x与y分别表示用户所在位置的经度和纬度.在社交网络图中，每条边〈u,v〉∈E上带有一个影响权重值p(u,v)，表示节点v受u影响而被激活的概率，此处定义节点v(u)是节点u(v)的出边(入边)邻居.
对社交网络中影响力传播过程的分析需借助特定的传播模型.目前学术界对影响力传播模型的研究主要集中于：独立级联(independent cascade, IC)模型、线性阈值(linear threshold, LT)模型以及触发模型，读者可查阅文献[30]对各模型的相关细节进行深入的了解.本文使用IC模型来对社交网络上影响力传播过程进行建模.
IC模型是一种概率模型.在IC模型中，社交网络中的每个节点仅能有2种状态：激活状态(active)或者未激活状态(inactive).只有处于激活状态的节点才会对其邻居节点产生影响.基于此，独立级联模型将影响力的传播过程抽象为以下多个轮次的随机过程：
1) 在初始时刻t0，种子集S中的用户被激活，社交网络中其他节点为未激活状态，影响力从S出发向周边节点进行传播；
2) 在时刻ti，上轮中被新激活的用户u以概率p(u,v)对所有未激活的出边邻居v进行激活尝试，用户间的激活尝试仅进行一次，且不同用户间的激活尝试彼此独立(u对v的激活不受其他节点的影响).若v被成功激活，则v将保持激活状态直至传播结束.令Si表示时刻ti新激活的用户集；
3) 在时刻ti+1，Si中用户(上轮中新激活的用户)继续执行2)中步骤.
上述过程重复执行，直到社交网络中不存在可被激活的节点时，影响力传播过程结束.假设传播结束的时刻为tm,则此时Sm=∅.
定义1. 影响力规模.考虑到影响力传播过程的随机性，种子的影响力规模 
(S)定义为传播结束时社交网络中被激活用户个数的期望，即 
令社交网络中某用户u受S影响而激活的概率为p(S
u)，则对 (S)的计算可进一步转化为 
(S
u).
定义2. 影响力收益.给定一个地理社交网络
一组空间对象的位置集合
若将L中对象的组合作为推广目标，通过种子S发起线上的影响力传播推广，则当影响传播结束时，在用户中获得的推广收益 L(S)可表示为
(Su)×w(u,L),
(1)
其中，w(u,L)代表用户u相对
的推广价值(用户权重).借鉴文献[9]对用户权重的度量方式，本文认为用户的权重与用户u距离L中最近位置的距离成反比，具体为
(2)
其中，c表示最大用户权重，β表示权重随距离增大而衰减的速率，
表示u到
中最近位置的欧氏距离.值得注意的是，式(2)同样支持其他距离度量方式，如：曼哈顿距离、路网距离等.
2.2 问题定义与复杂度分析
给定一个地理社交网络一组带有地理位置标签的空间对象候选集合
一个整数k,以及一个整数m(m<i)；LA-JIP问题旨在从
中选择m个空间对象的组合作为推广目标集L，同时从
中选取k个用户作为影响力种子集S，并要求从所有潜在的种子集与推广目标集中求得一组最优的集合搭配情况〈S*,L*〉，使在所有可能的集合搭配中，S*与L*组合能够在社交网络用户中产生最大的影响力收益，形式化表述为
(3)
定理1. LA-JIP问题为NP难问题.
证明. 考虑一个LA-JIP问题的特例：当m=1时，LA-JIP问题可转化为求解
中拥有最大影响力收益的单个位置及其对应的种子集.此时只需对中各位置分别进行DAIM求解，即可获得LA-JIP问题的最优解.因此，LA-JIP问题的求解难度必定难于DAIM问题.由于DAIM问题已在文献[9]中被证明为NP难问题，故LA-JIP问题同样为NP难问题.
证毕.
定理2. 在多目标组合推广场景中，计算种子在特定推广对象下的影响力收益为#P难问题.
证明.当式(2)中权重衰减速率参数β=0时，社交网络中所有用户权重将统一为1，此时影响力收益将转化为传统IM问题中的影响力规模.由于计算影响力规模为#P难问题，故计算影响力收益同样为#P难问题.
证毕.
2.3 基准算法
考虑到当前有关IM问题的大多数工作倾向于使用贪婪策略来实现对问题的近似最优求解[17-22]，为此本文继承这一思想，提出一类启发式算法对LA-JIP问题进行直观的求解.基准算法的基本思路在于使用贪婪策略，通过一轮循环来选取指定个数的种子与位置目标的集合配对，具体流程如算法1所示.该算法根据种子与推广位置的个数进行循环计算.在每次循环中，对不同用户(位置)在当前S*,L*组合下的影响力收益增幅进行计算(行③⑤)，并选取当前拥有最大影响力收益增幅的用户(位置)加入集合S*(L*)中(行④⑥).由于LA-JIP问题需要对2组集合的搭配进行优化，且集合内部与集合间元素都存在相关性，故算法1循环内部需交替地执行当前最优种子与位置的选取，以实现对2组集合元素的同步优化.值得注意的是，由于首次循环中算法考察当前最优的位置需借助已有种子的影响力传播情况，因此我们规定种子的选择步骤应优先于位置的选择.
算法1. 基准算法(Baseline).
输入：地理社交网络
候选对象位置集合
整数k、整数m(m<i)；
输出：推广位置集L*、影响力种子集S*.
① S*←∅,L*←∅；
② while |L*|<m且|S*|<k
③ 
L*(S*∪{u})-L*(S*)；
/*选择当前影响力收益增幅最大的用户*/
④ if |S*|<k then S*←S*∪{u*}；
⑤
L*∪l(S*)-L*(S*)；
/*选择当前影响力收益增幅最大的位置*/
⑥ if |L*|<m then L*←L*∪{l*}；
⑦ end while
⑧ return L*，S*.
算法1以一种较为直观的方式对LA-JIP进行了求解，但由于LA-JIP的非子模特性，该方法无法保证其返回的结果在严格意义下拥有(1-1/e)的近似度.
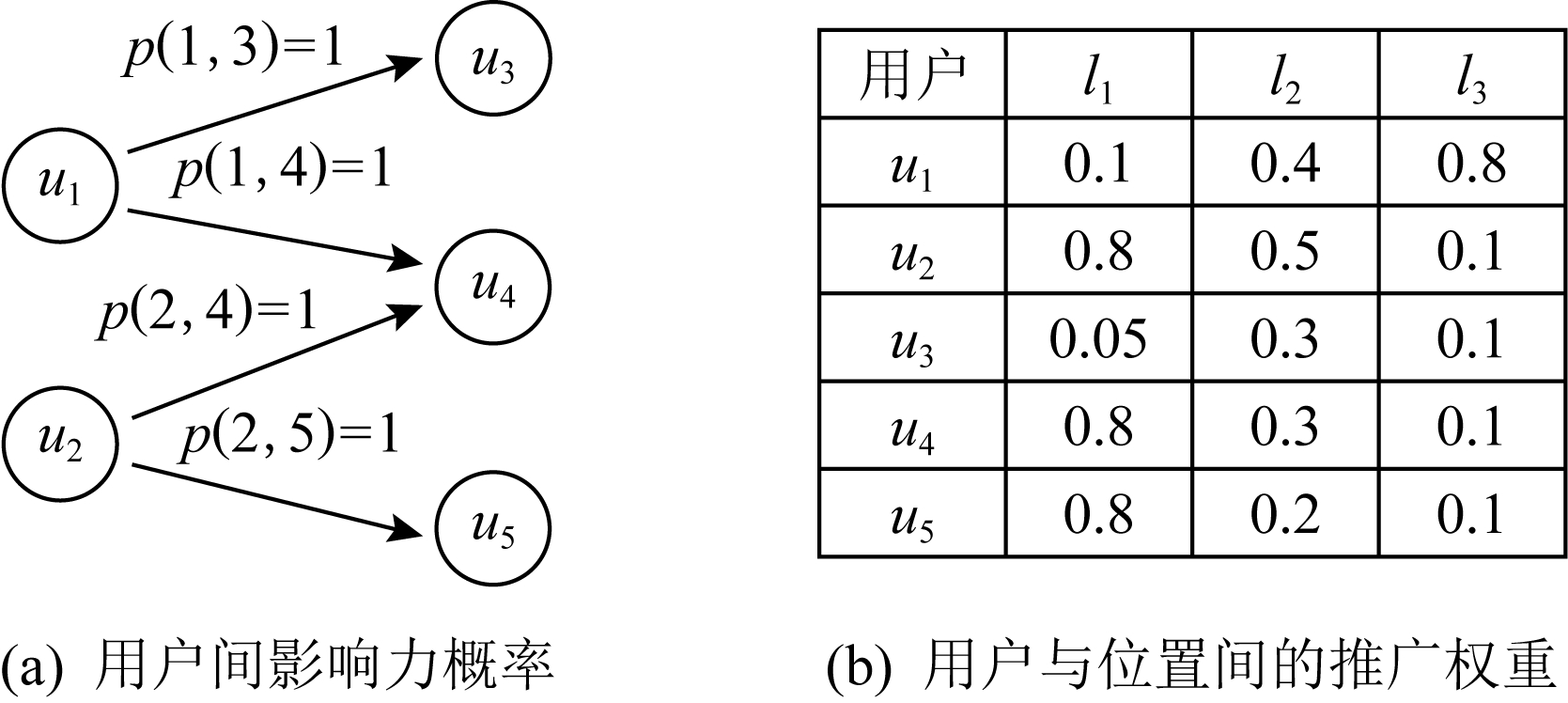
Fig. 2 The example of non-submodularity in LA-JIP
图2 LA-JIP问题非子模特性证明示例
定理3. LA-JIP问题的目标函数不满足子模特性.
证明. 给定目标函数f,称函数f满足子模特性，当且仅当f(A∪{x})-f(A)≥f(B∪{x})-f(B)成立，其中，A⊆B,x∉B.以图2中的示例证明 L(S)的非子模特性.图2(a)为一组用户影响力的传播情况，图2(b)为用户在不同推广位置下具有的权重值，令S=∅,L=∅,S′={u1},L′={l1}，有(S∪L)⊆(S′∪L′)，由于 L∪{l3}(S∪{u2})-L(S)=0.1×3-0=0.3，L′∪{l3}(S′∪{u2})-L′(S′)=(0.8×4+0.1)-0.95=2.35，因而 L′∪{l3}(S′∪{u2})-L′(S′)>L∪{l3}(S∪{u2})-L(S)，故 L(S)不满足子模特性的成立条件.
证毕.
3 多轮次迭代算法
由于基准算法无法提供明确的理论精度保证，故本节提出一套基于迭代的处理框架以支持精度收敛的LA-JIP问题求解.首先介绍反向影响力采样技术及影响力无偏估计策略的原理；其次基于鞅不等式(martingale inquality)设计针对影响力传播收益的上下界评估方法；最后基于上述技术对迭代算法的运行流程展开介绍，并给出结果置信度分析.
3.1 反向影响力采样技术
对影响力传播的评估涉及期望的求解，该问题实际为#P难问题，在大规模社交网络图中将产生巨大的计算开销.为了解决这一挑战，反向影响力采样(reverse influence sampling, RIS)是一类加速影响力评估的有效方法.RIS技术的核心在于构建一组采样结果集，即随机“反向可达集合”(random reverse reachable set, RR set)，并基于RR set对种子的影响力进行无偏估计(unbiased estimation).随机反向可达集合(RR set)可通过以下步骤生成：
1) 在社交网络图
中随机均匀地选择一个用户ui作为采样源点；
2) 从ui出发，在
上执行随机化的反向广度优先拓展，在此过程中以概率p(u,v)对每条被访问的边〈u,v〉进行激活尝试，并将所有被激活边上的节点加入反向可达集合Ri；
3) 上述步骤重复执行，直至采样到一定规模的RR set集合
RR set的构建细节与优化技术可查看文献[17-19,22].
当采样的RR set集合达到一定规模后，具有高影响力的用户节点将频繁出现在当前采样到的RR set集合中.因此，种子S的影响力规模与S在
中覆盖到的RR set数量呈线性相关，故可将S对中RR set的覆盖频率作为影响力规模的无偏估计[17]：
(4)
其中，(S)表示影响力规模的无偏估计值，|Cover(S,
表示种子S在
中覆盖到的RR set集合.
受上述基于RR set的影响力规模评估策略的启发，我们考虑用户权重差异，进一步对种子的影响力收益进行无偏估计：L(S)，具体为
(5)
其中
表示当推广目标为L时，与种子集S相交的部分RR set对应的采样源点(用户)的权重之和(即S在中的加权覆盖值)，具体为
(6)
3.2 影响力收益上下界评估方法
本节利用一类有效的概率统计方法：鞅不等式(martingale inquality)来量化影响力收益无偏估计值与影响力收益真实值之间的差异.
定义3[19]. 给定一组随机变量序列M1,M2,…,Mθ，若E[|Mi|]<+∞，E[Mi|M1,M2,…,Mi-1]=Mi-1，则称该随机变量序列为鞅.
定理4[19]. 给定一组伯努利分布下的随机变量序列X1,X2,…,Xθ，其中随机变量的期望为E(Xi)、方差为Var(Xi)，则统计量
满足鞅的特性[19]，且有如下不等式成立:
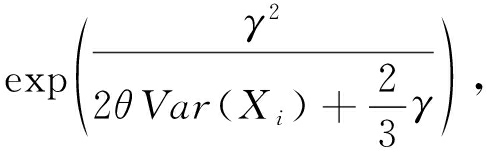
(7)
(8)
基于不等式(7)和(8)，可通过RR set集合来构建无偏估计值
与真实影响力收益值 L(S)间的误差关系.令
为当前采样的RR set集合、S为种子，则随机变量Zi为
假设在所有用户中最大的用户权重值为
对随机变量Zi进行标准化，进一步构建随机变量
将Yi代入不等式(7)，可得：
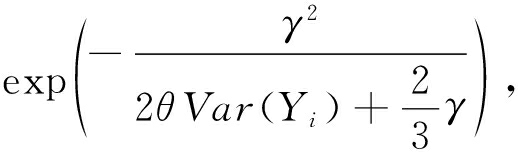
(9)
由于
且
为期望E[Yi]的伯努利变量)，则不等式(9)可进一步转化为
(10)
同理将变量
代入式(8),经转化可得：
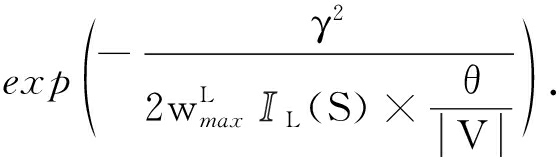
(11)
式(10)(11)在一定置信度下提供了量化
与
间误差的方法.基于此，提出定理5对种子影响力收益的上下边界进行理论推导.
定理5. 给定一组RR set集合
推广目标位置集L，令用户最大权重为给定概率参数δ∈(0,1)，则种子S的影响力收益满足如下推导关系：
其中
证明：
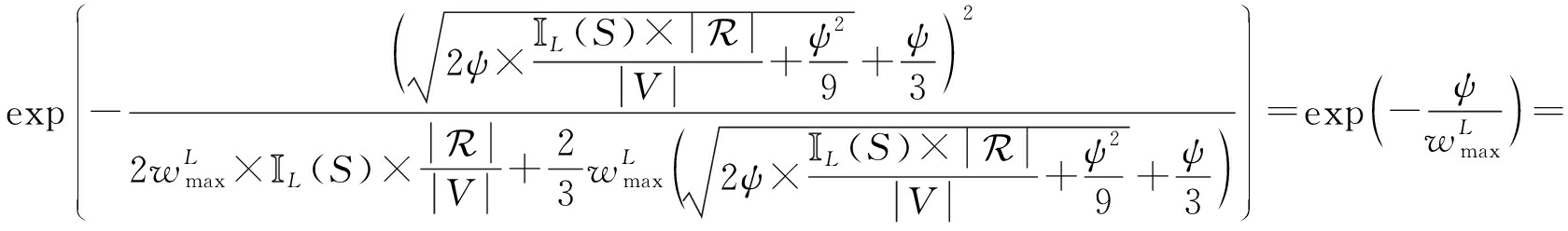
exp(-ln(1/δ))=δ，
因此，
成立.
证毕.
定理6. 给定一组RR set集合推广目标位置集L，设用户最大权重为在概率参数δ∈(0,1)下，种子S的影响力收益有如下推导关系：
1-δ,
其中
证明:
因此，
成立.
证毕.
3.2.1 位置集与种子集明确时影响力收益上下界评估
1) 影响力收益下界.根据定理5，给定推广位置集L，可在1-δ的概率下推导出种子S的影响力收益下界：
具体为
(12)
2) 影响力收益上界.根据定理6，给定推广位置集L，可在1-δ的概率下推导出种子S的影响力收益上界：
具体为
(13)
式(12)和(13)在推广位置与影响力种子组合内容已知的情况下对影响力收益上下界进行评估.以下将在位置集与种子集组合不确定的情况下，推导出所有潜在组合可获得的最大影响力收益上界.
3.2.2 潜在位置与种子组合下的影响力收益上界推导
假设LA-JIP问题中满足最大影响力收益的位置集为Lopt，种子集为Sopt.由于无法提前获取Lopt与Sopt中的内容，故无法直接利用式(13)对Lopt(Sopt)的上界进行评估.一种直观的上界评估方式可以为
(14)
其中,
表示
中所有位置都成为推广目标时对应有最大影响力收益的种子集，
表示贪婪策略下选出的种子集.然而，当
时，使用式(14)将导致
使上界评估过松.为此，本文提出定理7对
进行最优化的评估.
定理7. 给定一组RR set集合
一组当前选择的推广位置集
及种子集S(|S|=k)，根据L与S组合中内容，如下不等式成立：
(15)
其中
表示仅考虑单个位置时未被选择的位置集中有最大加权覆盖值的m个位置，S*L为推广目标为L时在贪心策略下获得的种子集.S*li为当推广目标仅包含位置li时在贪心策略下获得的种子集.
证明. 根据影响力收益的定义(定义2)，有
其中,
表示当种子为Sopt、推广位置集为L时，额外增加位置li可在上获得的加权覆盖值增量，
表示在未选择的位置中下有最大加权覆盖值增量的m个位置的权重增量之和.根据子模不等式有
其中，
表示当推广目标为L时有最大加权覆盖值(通过贪心策略获得)的种子集.记
则有
令
最终可得：
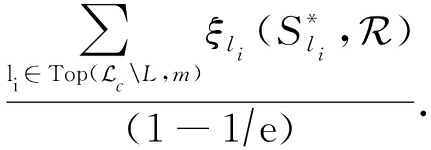
证毕.
将式(15)中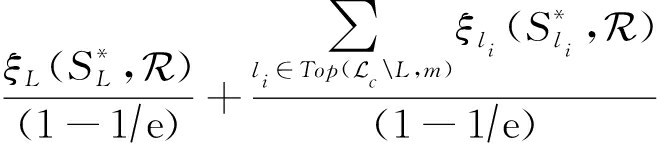
表示为
综合式(14)和(15)，则LA-JIP问题最优解对应的影响力收益上界推导可修改为
(16)
3.3 LA-JIP多轮迭代处理算法
基于3.2节中影响力收益上下界评估方法，迭代算法的执行流程如算法2所示.
算法2. 迭代算法.
输入：地理社交网络
候选位置集合整数k、整数m(m<i)、精度误差ε、概率参数δ；
输出：推广目标位置集L*、影响力种子集S*.
① S*←∅，L*←∅，ratio←0；
② 初始化2组RR set集合
③ while ratio<1-1/e-ε
④ if (Round=1)
⑤ S*
使用IM处理算法[21]求得的种子集初始化S**/；
⑥ else
⑦ 根据位置集
更新用户权重向量
⑧ S*
/*使用基于权重的贪婪算法在
中选取k个种子[21]*/
⑨ end if
⑩ L*
利用贪心策略优化L*中位置布局以进一步提升
在
上根据式(12)计算影响力收益下界
在
上根据式(16)对最大影响力收益上界
进行推导；
if (ratio>1-1/e-ε)
break;
else
加倍
中的RR set规模；
end if
Round++；
end while
return L*,S*.
算法2总体上利用2组不同的RR set集合来获取问题的可行解，并在多轮验证中对结果展开迭代优化.在首轮计算中，算法2先使用传统的IM处理算法：OPIM-C[21]初始化影响力种子集S*(行④⑤)，进而根据当前获得的S*调用算法Greedy_MultiLoc对推广位置集L*进行选择(行⑩，具体细节见算法3).此后算法2在另一组RR set集合上根据式(12)对当前S*与L*组合下的影响力收益下界
进行评估(行)，并在
上根据式(16)对LA-JIP问题最优结果对应的影响力传播收益
进行推导(行).若当前结果精度：
满足用户设定的精度阈值：1-1/e-ε，则跳出迭代循环.否则，加倍中RR set的采样个数并进入下一轮迭代.在下一轮迭代中，根据上轮中获得的位置集L*来更新用户权重，并基于更新的权重信息在中使用贪心策略选取新的种子集S*(行⑧)，Greedy_MultiSeed同文献[31-32]中算法2，故此处不做详细赘述.在后续过程中，继续交替地执行对位置集L*与种子集S*的迭代优化与更新操作，直到所求结果的精度满足用户预期的阈值.
Greedy_MultiLoc为算法2中重要功能函数，其被算法2反复调用以实现不同轮次下对当前最优位置集的更新，其伪代码如算法3所示.
算法3. Greedy_MultiLoc算法.
输入：种子S*相交的RR set集合
候选位置集整数m；
输出：推广目标位置集L*.
① L*←∅；
② while |L*|<m
③ l*
选择当前有最大加权覆盖值增量的位置*/
④ L*←L*∪{l*}；
⑤ end while
⑥ return L*.
在执行过程中，Greedy_MultiLoc根据上轮迭代获得的影响力种子集S*更新当前的位置选择策略，具体为通过贪婪策略从候选位置集中重新评估并选择m个当前最优的位置并更新L*(行③④).在算法3中，贪婪策略的最优化目标函数为：给定种子集S*下，当前位置集L*在RR set集合中产生的加权覆盖值.
接下来进行结果置信度分析.假设算法2中while循环的最大迭代次数为rmax.由于每轮迭代中，影响力收益上下界评估将产生2δ的出错概率，故算法在所有轮次下累计出错的概率为2δ×rmax.因此，将以1-2δ×rmax的置信概率获得指定精度下的近似结果.通常情况下，设定参数δ=1/|V|[18-22]，由于算法2在实际执行过程中的迭代次数远小于|V|，因而1-2δ×rmax≈1，即算法能够以较高的置信度获得(1-1/e-ε)下的近似求解.
4 实验评估
4.1 数据集与测试环境
为验证本文研究内容及所提技术方法的有效性，本节使用2组真实的地理社交网络数据集：Brightkite和Gowalla进行实验评估.数据集可通过Stanford大学的SNAP项目在线获取[32].在Brightkite和Gowalla中，分别有11.4%和45.6%的用户无位置坐标，对于这部分用户，根据其朋友位置坐标的均值对其进行位置分配.处理后的数据集信息如表2所示:
Table 2 Statistics of the Datasets
表2 数据集统计信息
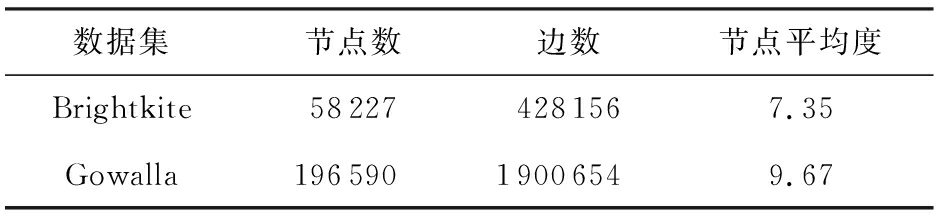
数据集节点数边数节点平均度Brightkite582274281567.35Gowalla19659019006549.67
实验测试的算法均使用C++语言编写，并在g++13编译器下编译优化.所有实验在配备有Intel i-7 2.9 GHz主频CPU，64 GB内存的PC机上运行，安装的操作系统为Ubuntu 14.04.
4.2 实验设定
1) 传播概率设定.参考当前IM研究领域中广泛使用的方法[8-9,19-22]，本文采用加权级联(weighted cascade)模型对社交网络图边上影响力传播概率进行分配：p(u,v)=1/|Nin(v)|，其中|Nin(v)|表示用户v在社交网络中的入度.
2) 用户权重设置.本文根据文献[9]在单目标位置推广时的用户权重设置方法，对式(2)中相关参数进行设置.其中最大用户权重c=1，权重衰减系数β=0.01.此外，考虑到
中对象具有空间邻近的特点(同一个城市的连锁门店)，故根据式(2)，社交网络中将存在大量权重无限接近0的用户，这部分用户对问题最终结果几乎不产生影响.为降低用户权重计算的开销，本文默认当用户与推广目标位置间距离大于100 km时，其权重为0.
3) 影响力收益值评估.为客观评估不同算法所求结果的质量，实验对种子影响力传播过程进行10 000次蒙特卡罗(Monte Carlo, MC)模拟[8-9,12]，并将此过程中被激活用户权重和的均值作为种子影响力收益.
4) 参数设定.为评估不同参数设置对算法的影响，我们在不同参数设定下对算法性能进行评估.各参数设定值的范围如表3所示，每行中黑体数字表示各参数的默认设定值.在评估参数性能时，我们仅改变其中某个参数的值，而固定其余参数为默认设定值.
Table 3 Parameter Settings
表3 参数设定信息表
参数设定值k(影响力种子集合大小)5,10,15,20,25m(推广目标集合大小)2,3,4,5,6| c|(候选位置集合大小)10,20,30,40,50
注：黑体数字为默认值.
4.3 有效性评估
为了验证本文研究内容在空间感知影响力联合推广中的有效性，本节将LA-JIP策略下产生的影响力收益情况与下述策略进行对比：
1) IM+DBSCAN策略.利用传统的IM处理算法[21-22]选取k个用户作为影响力种子集S*，利用密度聚类算法DBSCAN[34]从候选目标位置集
中选取用户签到密度最大的m个位置作为推广位置集L*；
2) DAIM策略.使用DAIM[9,32]算法对候选位置集
中各位置点单独作用下的影响力收益进行评估，并从中选择拥有最大收益的m个位置作为推广目标L*,同时合并各位置下选出的影响力种子，从中抽取频率最大的k个用户作为整体的影响力种子S*；
3) Baseline策略.本文所提算法1(基准算法)，即解决问题的启发式算法；
4) LA-JIP策略.本文所提算法2(多轮迭代处理算法)，即求得的结果有理论精度保障的近似算法.
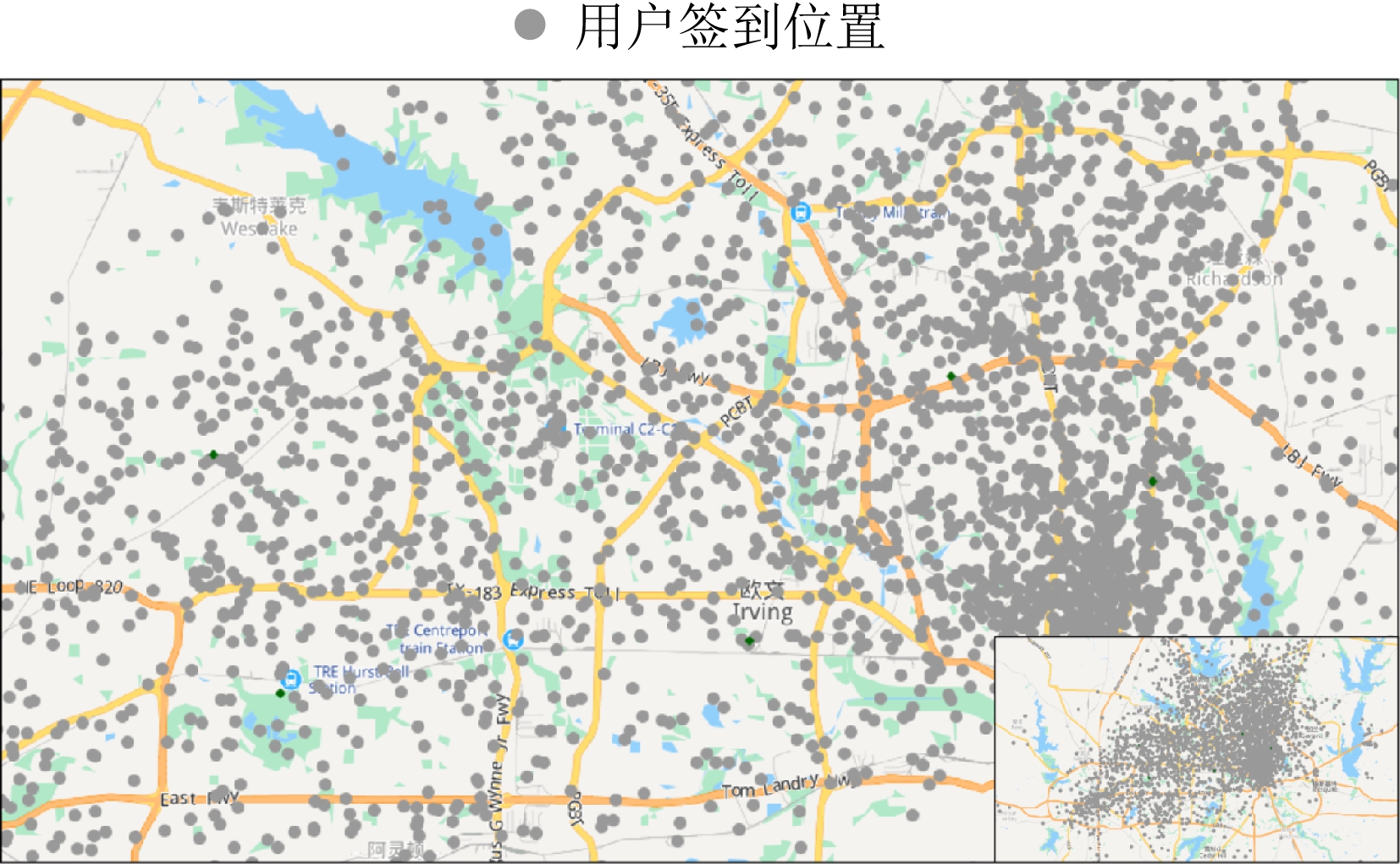
Fig. 3 The distribution of the users located in Dallas
图3 达拉斯市区范围内用户分布情况
通过对Gowalla数据集的分析，我们发现美国得克萨斯州达拉斯市区有稠密的用户分布(如图3所示)，故认为达拉斯市区范围内的兴趣点有较高推广潜力，因此将该城市作为影响力推广效果测试区域；其次利用百度API，爬取达拉斯市区领域的所有兴趣点，根据标签信息，将兴趣点进行分类，分别获得酒吧、商场、餐厅等的兴趣点组；我们将隶属同组的兴趣点集合作为
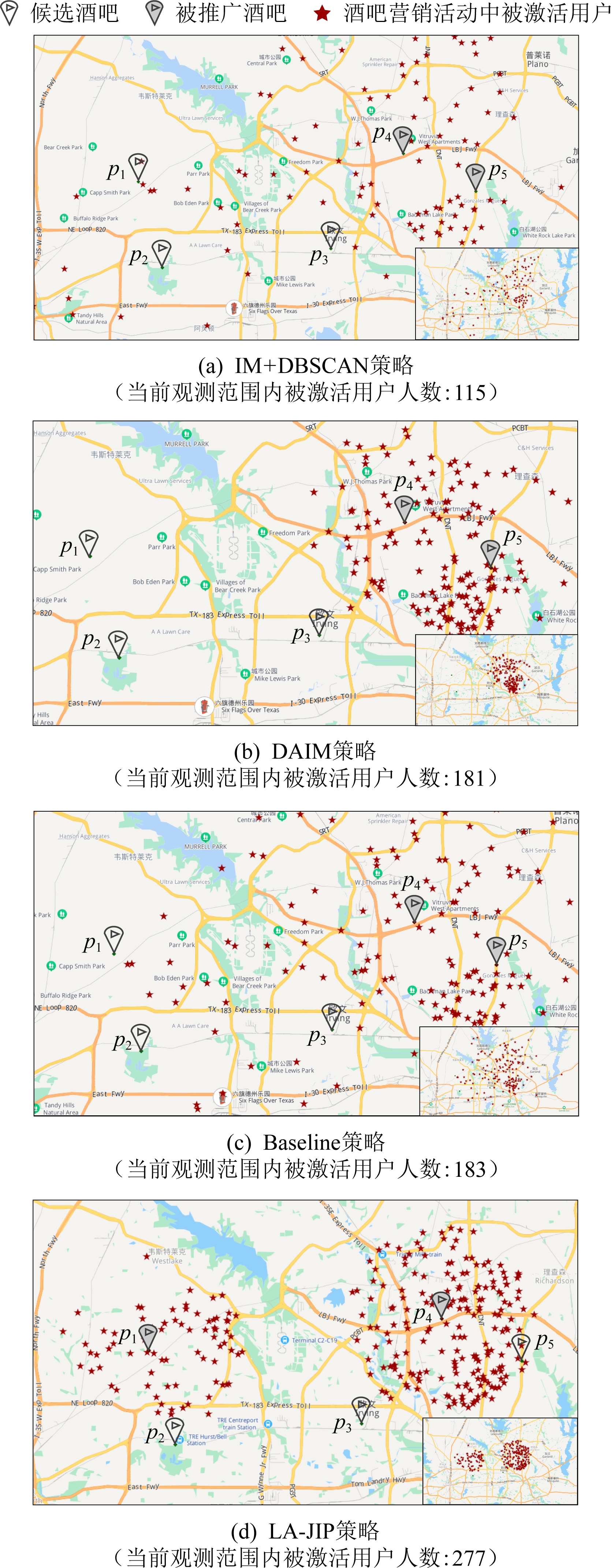
Fig. 4 The performance comparison of influence promotion for bars by different strategies
图4 酒吧类兴趣点集合下不同策略的影响力 推广效果对比
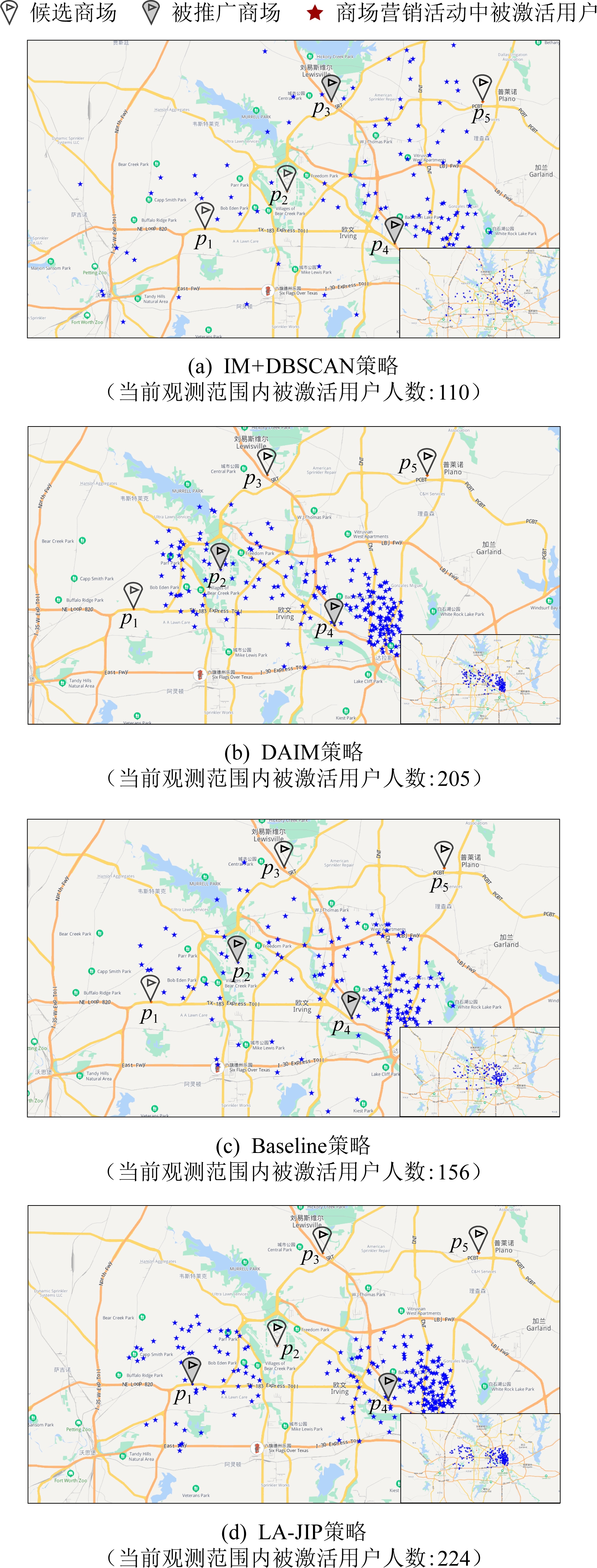
Fig. 5 The performance comparison of influence promotion for markets by different strategies
图5 商场类兴趣点集合下不同策略的影响力 推广效果对比
设置m=2，k=10，测试上述推广策略的执行效果.对不同策略返回的结果(推广位置集+种子集)执行蒙特卡洛模拟评估其影响力传播情况，使用百度地图API对传播中激活用户的位置进行可视化展示.由于各类兴趣点组下策略间的性能差异大体相同，本节仅对酒吧、商场这2类兴趣点集合下的结果进行展示(图4与图5).由图中结果可知，IM+DBSCAN策略在空间感知影响力推广中的效果最差，该策略激活用户的空间分布十分离散且与推广位置间无明显邻近关系；DAIM策略由于考虑了用户权重，故影响力传播相对推广位置有明显的空间聚合趋势.然而，由于该策略忽略了对推广位置的优化，推广位置个体间仍存在较多的影响力重叠，整体推广效果依旧不佳；Baseline策略由于在贪婪策略中对种子集与位置集进行了同步优化，故相比仅分开优化2组集合的IM+DBSCAN策略，影响力推广效果有明显的提升.
但由于Baseline策略无理论精度保障，因此优化性能并不稳定，在某些输入情况下Baseline策略的效果将劣于DAIM策略.作为对比，LA-JIP策略在各类兴趣点集合下始终中展现了全局最优的特点，且相比Baseline策略，LA-JIP策略整体性能更加稳定，产生的影响力分布情况相对推广目标的位置分布也更具空间聚合性.此外，由于LA-JIP策略进一步优化了推广位置的空间布局，因此LA-JIP相比DAIM减少了更多内部的影响力重叠，故在多目标组合下有更优影响力全局推广效果.
4.4 算法性能评估
本节在Brightkite和Gowalla两组数据集上，对基准算法(baseline, BA)、迭代算法(iterative, IT)的处理性能进行全面评估.实验比较了算法在不同种子个数、推广目标位置个数、侯选位置集合大小下的性能变化趋势.本文以算法的响应时间和所求结果的影响力传播收益作为衡量算法性能的2项指标.本文对每组实验重复5次测试，并取平均值作为最终结果.
4.4.1 种子个数对性能的影响
本文在Brightkite和Gowalla两组数据集下测试不同的种子个数(5,10,15,20,25)对BA与IT算法性能的影响，结果如图6所示.从图6结果可知，IT算法能够在BA算法基础上进一步提升10%～50%的影响力传播收益，且运行效率有1～2个数量级的提升.这验证了本文第3节中所提方法的有效性.此外，随着种子个数的增多，所有算法的响应时间及影响力传播收益均呈现增长趋势.这是因为较多的种子能触发更大的影响力传播范围，从而提高了影响力在用户中传播所能获得的收益；这同时也增加了算法在评估种子影响力过程中的开销.值得注意的是，所有算法在Gowalla数据集下均获得了比Brightkite数据集下更高的影响力收益.这是因为Gowalla相比Brightkite拥有更大的社交网络以及更为稠密的用户空间分布，因而Gowalla数据集下产生的种子能够激活更多高权重的用户，从而利于影响力在传播过程中积累到更多收益.这一对比结果体现了迭代算法在大规模社交图下实现空间感知影响力推广的性能优势.
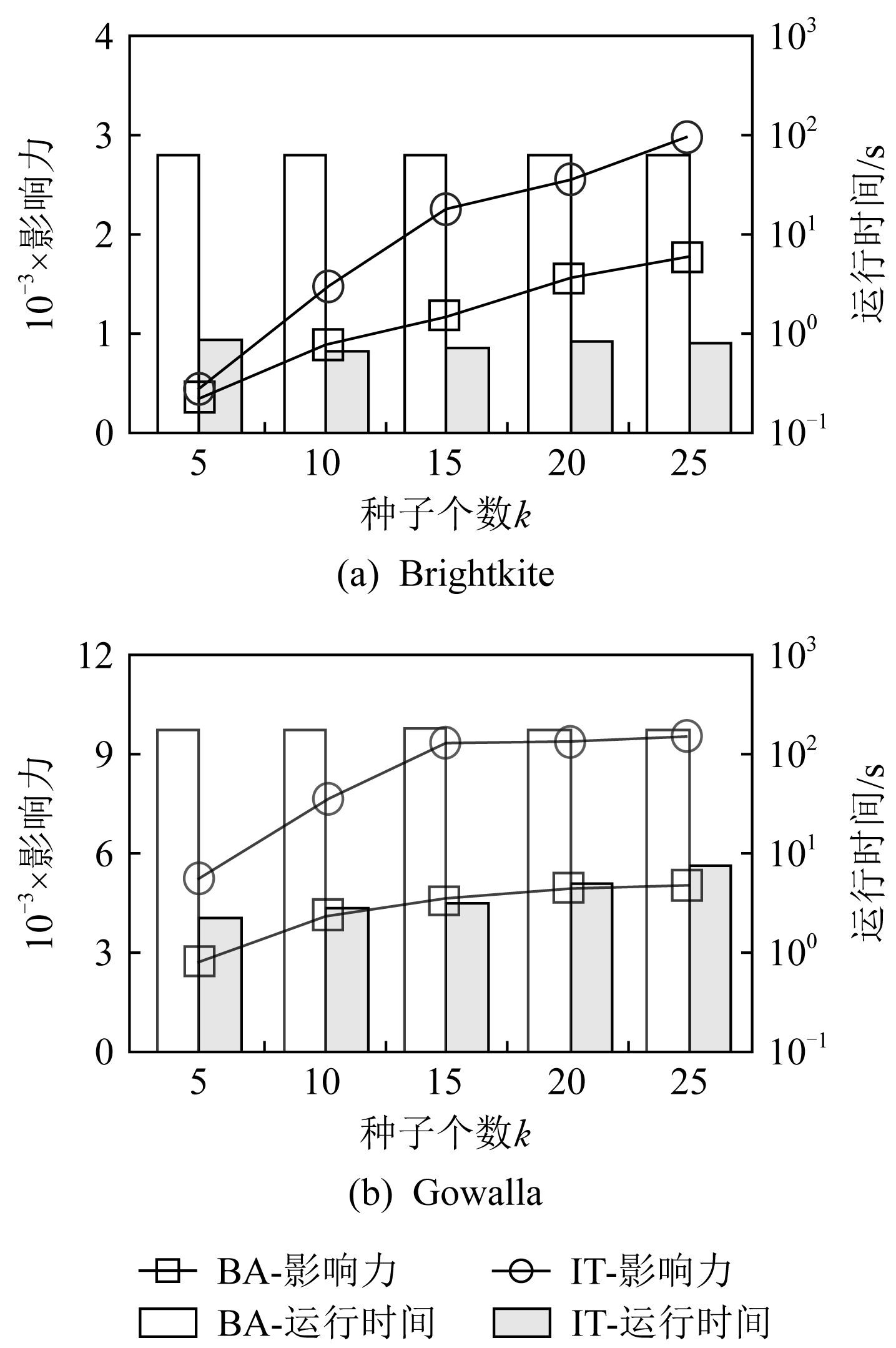
Fig. 6 The effect of varying k on performance
图6 种子个数k变化对算法性能的影响
4.4.2 推广目标位置个数对性能的影响
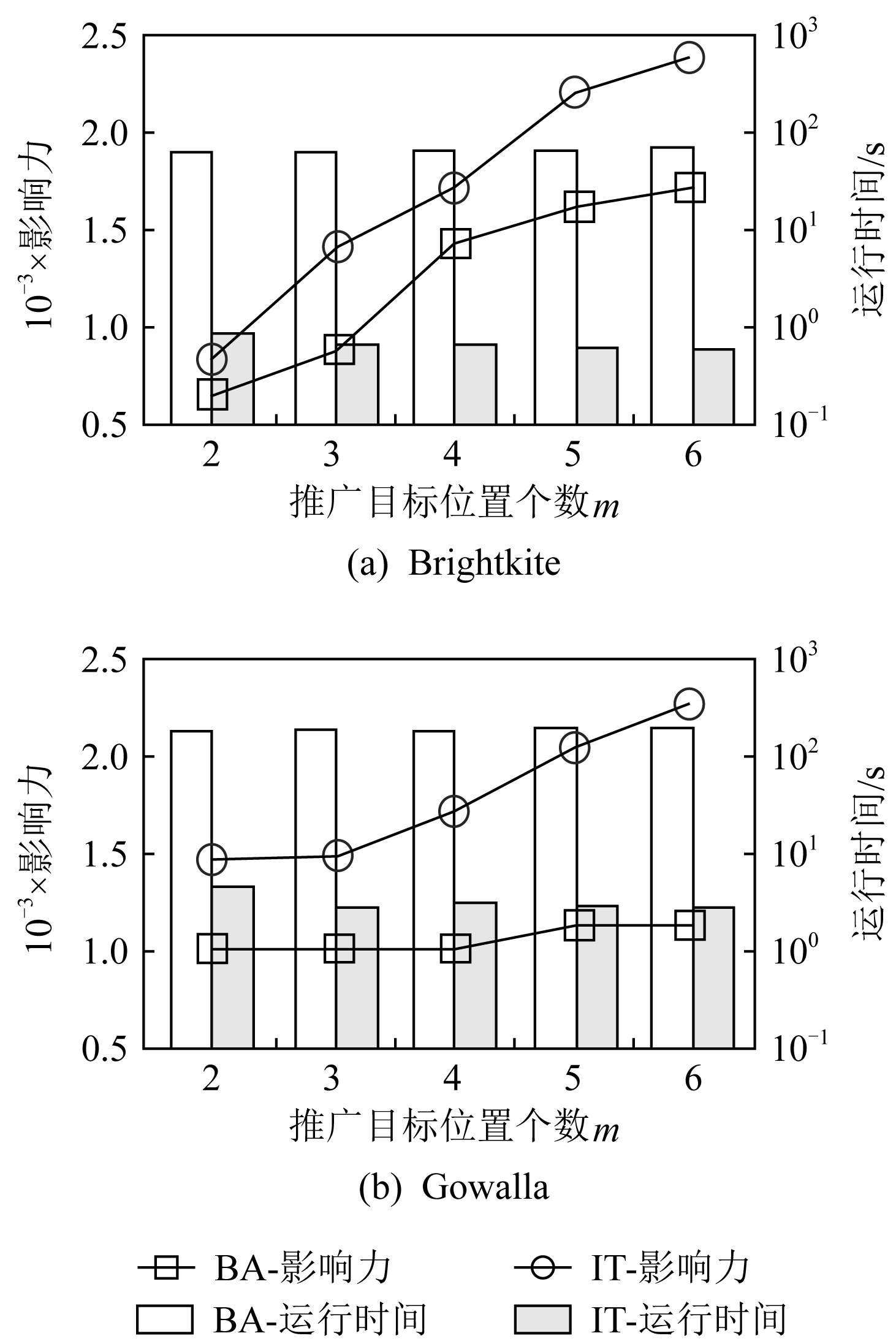
Fig. 7 The effect of varying m on performance
图7 推广目标位置个数m变化对算法性能的影响
图7展示了推广目标位置个数对算法性能的影响.在不同的位置个数设定下，迭代算法的性能均明显优于基准算法，且在更大规模的Gowalla数据集上迭代算法较基准算法的性能优势更为明显.随着推广目标位置个数的增多，各算法取得的影响力收益均呈现增长趋势.这是因为推广位置的增加将使更多用户因邻近空间对象而拥有更大的推广权重，因而影响力传播过程将获得更大的收益.值得注意的是，当推广位置较多时(|L|≥4)，基准算法与迭代算法间性能分化趋势更为明显，这进一步体现了迭代算法在多目标组合优化处理中的优势.
4.4.3 侯选位置集合大小对性能的影响
图8展示了候选位置集合大小的变化对算法性能的影响.在不同规模的候选位置集合下，迭代算法的性能均明显优于基准算法.此外，随着候选位置集合的增大，各算法所得结果的影响力收益呈现先增加后逐渐趋于稳定的趋势.这是因为当候选位置集合规模较小时，加入更多的位置可使算法构建出与影响力空间分布更为拟合的推广目标位置分布.然而，当候选位置集增加至一定规模后，集合中的大量位置之间将存在较多的影响力重叠，从而使得影响力传播收益的增幅呈现减缓趋势.
Fig. 8 The effect of varying 
on performance
图8 候选位置集合大小变化对算法性能的影响
4.5 对ε参数设定的评估
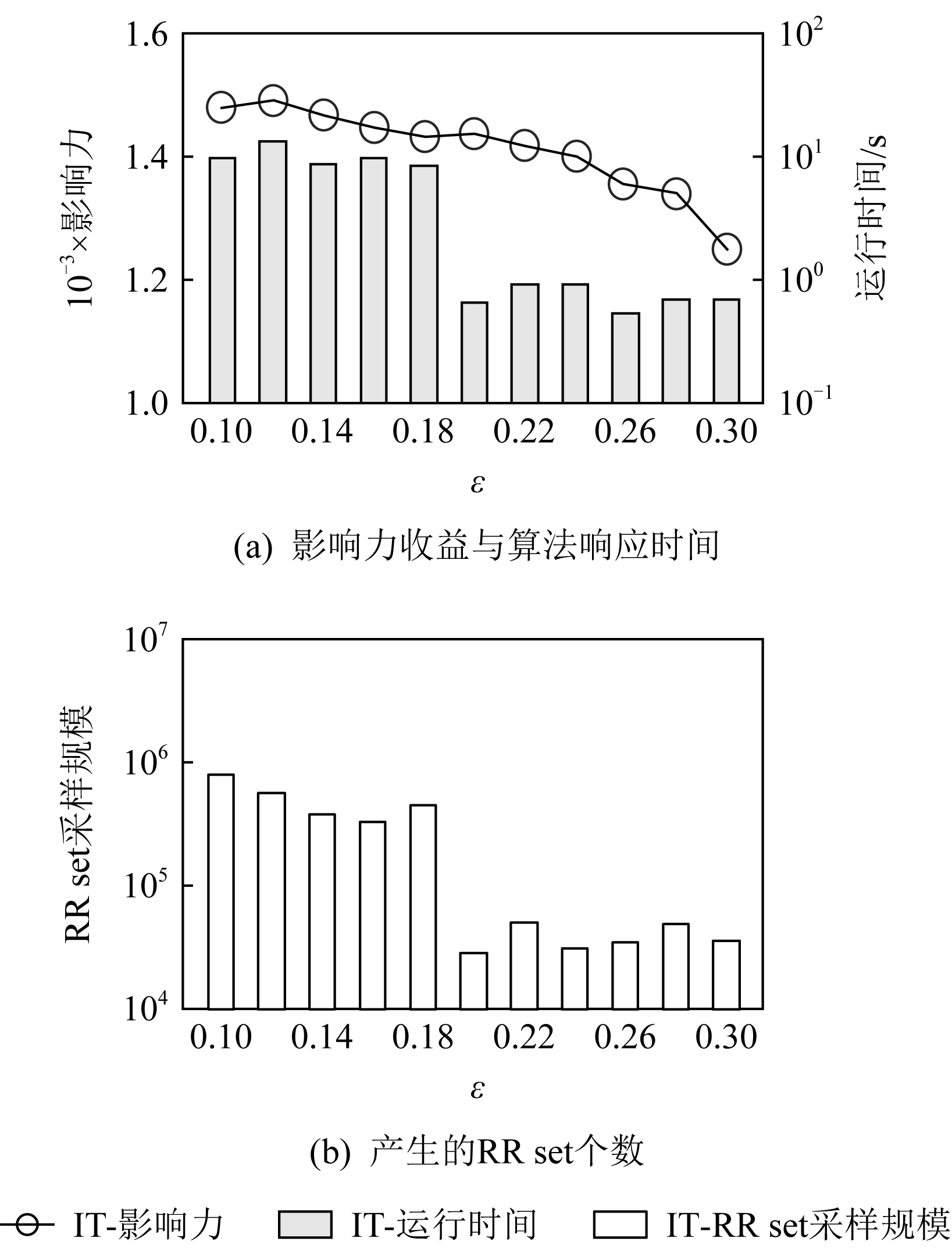
Fig. 9 Evaluate parameter ε in Brightkite dataset
图9 Brightkite数据集下评估参数ε
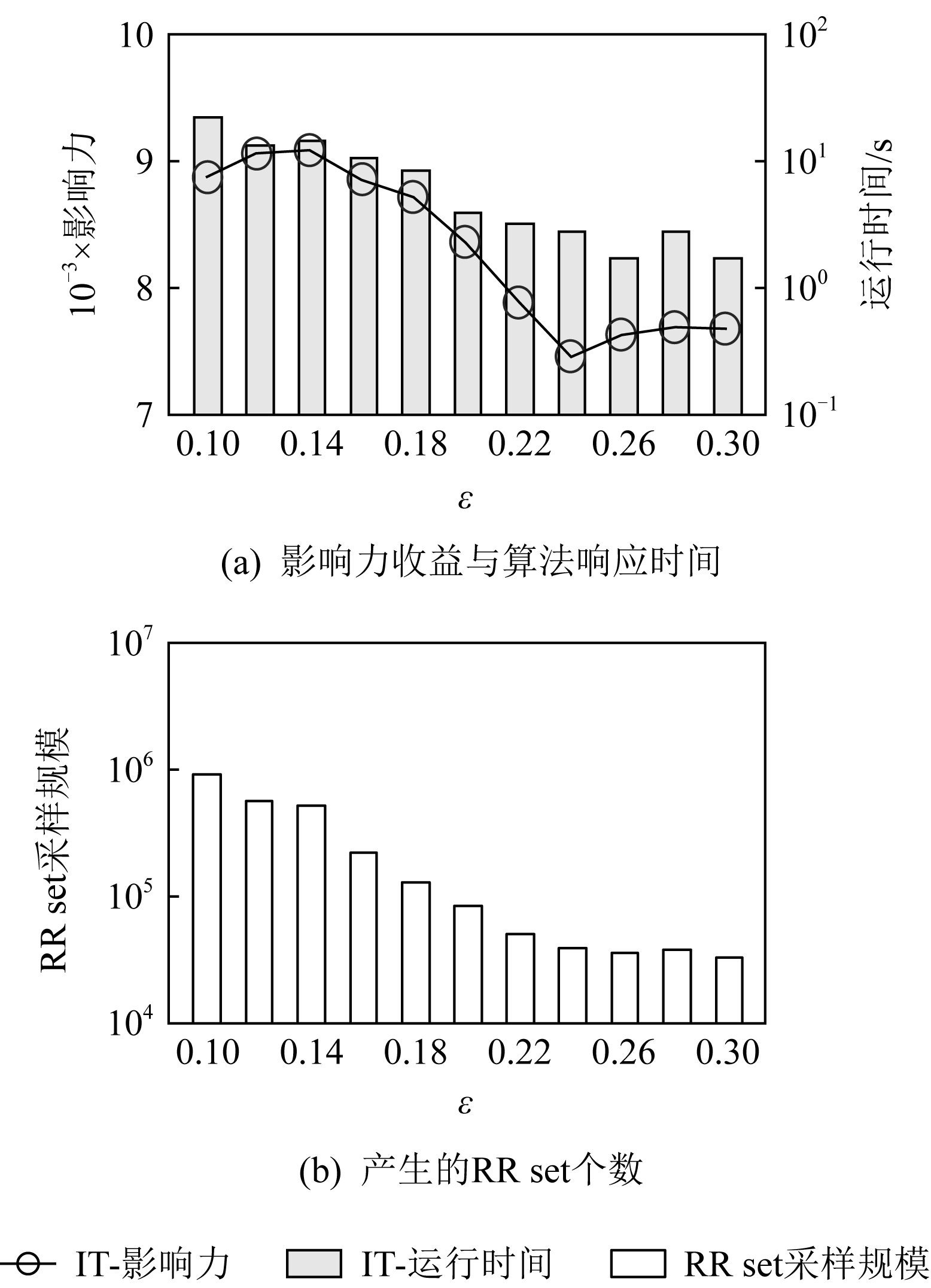
Fig. 10 Evaluate parameter ε in Gowalla dataset
图10 Gowalla数据集下评估参数ε
本节进一步探索迭代算法中对精度误差参数ε的合理设定.图9～10展示了迭代算法在Brightkite数据集以及Gowalla数据集下基于不同精度误差参数ε的运行结果(影响力收益、响应时间、RR set采样规模).从图9中结果可知，当ε值较小时(ε<0.20)，进一步减小ε对算法返回的结果精度提升效果并不明显；相反，还将导致算法的响应时间急剧增长，并在处理过程中耗费大量的内存开销(大量RR set被采样产生并作为中间结果常驻内存).当精度误差参数设定较大时(ε≥0.20)，算法时间空间上的开销都明显降低，但结果精度损失却下降明显.权衡算法的求解效率与返回结果的质量，本文将ε=0.20作为迭代算法的默认精度误差参数.
5 总 结
本文研究了地理社交网络中基于多目标组合优化的空间感知影响力联合推广问题(LA-JIP).该问题考虑了影响力在位置相关用户中的推广差异，通过构建推广目标位置与影响力种子间的最优搭配，实现全局利益最大化的商家营销推广.为了有效地解决LA-JIP问题，本文拓展了现有的反向影响力采样技术，提出了有理论保障的影响力收益上下界评估方法，并基于此通过多轮迭代对问题进行了高效的近似求解.最终，在真实的数据集下实验结果验证了本文所提出的技术能有效地提升多目标组合下空间感知影响力推广.在未来工作中，我们将考虑引入更多的地理空间因素(如营销点的空间分布密集、营销位置相对各用户的k近邻排序等)来设计更为合理的用户权重度量函数，以使LA-JIP问题适应更多复杂的应用场景.此外进一步优化提升本文提出的近似算法的理论精度也是未来努力的方向之一.
作者贡献声明：金鹏飞负责提出问题研究的动机与思路、算法设计方案、实验方案并撰写论文；常雪芹负责算法方案实现、实验测试、结果评估并协助撰写论文；房子荃与李淼提出指导意见并修改完善论文.
[1]Zhang Xin. The 2020 financial report of Meituan company: The annual revenue breaks 100 billion for the first time, please continue to invest new businesses[OL]. [2021-08-31]. https://t.ynet.cn/baijia/30565973.html (in Chinese)(张鑫. 美团2020年财报: 全年营收首破千亿 继续坚定投入新业务[OL]. [2021-08-31]. https://t.ynet.cn/baijia/30565973.html)
[2]Foursquare. Understand the world with Foursquare Places data[OL]. [2021-08-31]. https://enterprise.foursquare.com/products/places
[3]Jacob G, Barak L, Eitan M. Using complex systems analysis to advance marketing theory development: Modeling heterogeneity effects on new product growth through stochastic cellular automata[J]. Journal Academy of Marketing Science Review, 2001, 9(3): 1-18
[4]Jacqueline B, Peter H. R. Social ties and word-of-mouth referral behavior[J]. Journal of Consumer Research, 1987,14(3): 350-362
[5]Goldenberg J, Libai B, Muller E. Talk of the network: A complex systems look at the underlying process of word-of-mouth[J]. Marketing Letters, 2001, 12(3): 211-223
[6]Domingo P, Richardson M. Mining the network value of customers[C] //Proc of the 7th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2001: 57-66
[7]Ethan J. Local advertising will rebound steadily in 2021, new report predicts[OL].[2021-08-31]. https://adage.com/article/media/local-advertising-will-rebound-steadily-2021-new-report-predicts/
[8]Li Guoliang, Chen Shuo, Feng Jianhua, et al. Efficient location-aware influence maximization[C] //Proc of the 7th ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2014: 87-98
[9]Wang Xiaoyang, Zhang Ying, Lin Xuemin, et al. Distance-aware influence maximization in geo-social network[C] //Proc of the 32nd Int Conf on Data Engineering. Los Alamitos, CA: IEEE Computer Society, 2016: 1-12
[10]Wang Ziyang. Starbucks has 5000 stores in China Mainland[OL]. [2021-08-31]. https://baijiahao.baidu.com/s?id=1698182374129201961&wfr=spider&for=pc (in Chinese)(王子扬. 星巴克中国内地门店数量达5000家[OL]. [2021-08-31]. https://baijiahao.baidu.com/s?id=169818237412920 1961&wfr=spider&for=pc)
[11]Richardson M, Domingo P. Mining knowledge-sharing sites for viral marketing[C] //Proc of the 8th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2002: 61-70
[12]Kempe D, Kleinberg J. Maximizing the spread of influence through a social network[C] //Proc of the 9th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2003: 137-146
[13]Chen Wei, Wang Yajun, Yang Siyu. Efficient influence maximization in social networks[C] //Proc of the 15th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2009: 199-208
[14]Chen Wei, Wang Chi, Wang Yajun. Scalable influence maximization foe prevalent viral marketing in large-scale social networks[C] //Proc of the 16th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2010: 1029-1038
[15]Jung K, Heo W, Chen Wei. IRIE: Scalable and robust influence maximization in social networks[C] //Proc of the 12th IEEE Int Conf Data Mining(ICDM). Piscataway, NJ: IEEE, 2012: 918-923
[16]Wang Zhefeng, Wang Han, Liu Qi, et al. Influential nodes selection: A data reconstruction perspective[C] //Proc of the 37th Int ACM SIGIR Conf on Research & Development in Information Retrieval. New York: ACM, 2014: 879-882
[17]Borgs C, Brautbar M, Chayes J, et al. Maximizing social influence in nearly optimal time[C] //Proc of the 25th Annual ACM-SIAM Symp on Discrete Algorithms. Philadelphia, PA: SIAM, 2014: 946-957
[18]Tang Youze, Xiao Xiaokui, Shi Yanchen. Influence maximization: Near-optimal time complexity meets practical efficiency[C] //Proc of the 7th ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2014: 75-86
[19]Tang Youze, Shi Yanchen, Xiao Xiaokui. Influence maximization in near-linear time: A martingale approach[C] //Proc of the 8th ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2015: 1539-1554
[20]Hung T N, My T T, Thang N D. Stop-and-stare: Optimal sampling algorithms for viral marketing in billion-scale networks[C] //Proc of the 9th ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2016: 695-710
[21]Tang Jing, Tang Xueyan, Xiao Xiaokui, et al. Online processing algorithms for influence maximization[C] //Proc of the 11th ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2018: 991-1005
[22]Guo Qintian, Wang Sibo, Wei Zhewei, et al. Influence maximization revisited: Efficient reverse reachable set generation with bound tightened[C] //Proc of the 13th ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2020: 2167-2181
[23]Song Chonggang, Hsu W, Lee M. Targeted influence maximization in social networks[C] //Proc of the 25th ACM ICKM Int Conf on Information and Knowledge Management. New York: ACM, 2016: 1683-1692
[24]Li Jianxin, Timos S, J. Shane C, et al. Geo-social influence spanning maximization[J]. IEEE Transactions on Knowledge and Data Engineering, 2017, 29(8): 1653-1666
[25]Zhong Ming, Zeng Qian, Zhu Yuanyuan, et al. Sample location selection for efficient distance-aware influence maximization in geo-social networks[C] //Proc of Conf on Database Systems for Advanced Applications. Berlin: Springer, 2018: 355-371
[26]Wang Yanhao, Li Yuchen, Fan Ju, et al. Location-aware influence maximization over dynamic social streams[J]. ACM Transactions on Information Systems, 2018, 36(4): 43:1-43:35
[27]Shi Qihao, Wang Can, Chen Jiawei, et al. Location driven influence maximization: Online spread via offline deployment[J]. Knowledge Based Systems, 2019, 166(2): 30-41
[28]Yu Yaxin, Wang Lei. An advertising game theory decision-making mechanism for overlapping seeds[J]. Journal of Computer Research and Development, 2019, 56(6): 1302-1311 (in Chinese)(于亚新, 王磊. 地理社交网络中重叠种子的广告博弈决策机制[J]. 计算机研究与发展, 2019, 56(6): 1302-1311)
[29]Wang Liang, Yu Zhiwen, Xiong Fei, et al. Influence spread in geo-social networks: a multi-objective optimization perspective[J]. IEEE Transactions on Cybernetics, 2021, 51(5): 2663-2675
[30]Li Yuchen, Fan Ju, Wang Yanhao, et al. Influence maximization on social graphs: A survey[J]. IEEE Transactions on Knowledge and Data Engineering, 2018, 30(10): 1852-1872
[31]Goyal A, Lu Wei, Lakshmanan Laks. CELF++: Optimizing the greedy algorithm for influence maximization in social networks[C] //Proc of the 20th Int Conf on World Wide Web. New York: ACM, 2011: 47-48
[32]Wang Xiaoyang, Zhang Ying, Zhang Wenjie, et al. Efficient distance-aware influence maximization in geo-social networks[J]. IEEE Transactions on Knowledge and Data Engineering, 2017, 29(3): 599-612
[33]SNAP. Stanford large network dataset collection[OL]. [2021-08-31]. http://snap.stanford.edu/data/
[34]Ester M, Kriegel H P, Sander J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C] //Proc of the 2nd ACM International Conf on Knowledge Discovery and Data Mining. New York: ACM, 1996: 226-231
