数据的可靠性是存储系统需要考虑的首要问题,而随着信息技术的发展以及向各个行业领域的渗透,需要存储的数据量正持续地爆炸式增长.为了应对海量数据存储的可靠性问题,同时也为了提高数据访问的并发效率,通常有效的做法是使用多个存储节点共同构建1个存储系统,比如集中式的磁盘阵列(redundant arrays of independent disks, RAID)系统或基于网络的分布式存储系统等,而每个存储节点可以是1个磁盘、1台PC、1台服务器或1个移动终端等可用作数据存储的设备.与过去相比,当前单个存储设备的稳定性已经较高,但是对于由众多节点构成的大规模存储系统而言,节点故障事件仍然会频繁发生[1-2].关于如何在部分节点故障后能保证数据不丢失,并且在故障节点被替换后能迅速恢复失效数据是近年来存储领域研究的热点.早期的多节点存储系统多采用副本技术来为数据的可靠性提供保障,该技术把多个相同的数据副本存储到不同的节点上,相同数据的不同副本之间可互为备份,当有存储节点失效时,替换的节点可从任意1个或多个拥有相同数据副本的节点传入数据进行数据重构.但副本技术会导致系统存储效率过低的问题,如果需要在k(≥1)个节点同时失效后能有效重构数据,则需要把原始数据复制k份并分别存放在不同的节点上,整个系统的存储效率仅有1/(k+1).因此,目前更多的研究集中在如何利用纠删码技术来保证存储系统中的数据可靠性.与副本技术相比,使用纠删码来构建存储系统的容错机制可在相同容错能力的条件下,极大地提高了存储效率.
从编译码运算方式的角度看,大体可以把存储系统中使用的纠删码分为2类:1)XOR类纠删码,这类编码的编译码运算过程可以仅使用二进制的异或运算,因此编译码的速度很高,包括了阵列码[2-8]和低密度奇偶校验码[9-11](low density parity check code, LDPC)等.阵列码具有2维编码结构,且通常有几何形式的构造方法,工程实现时简洁直观,但具备极大距离可分(maximum distance deparable, MDS)性质的阵列码通常容错能力不超过3个[5-7],导致其对当前实用的大规模存储系统适应性不足.近年来,也有更高容错能力的阵列码被提出[2,8],但是一般都会付出巨大的存储效率代价.LDPC码可以使得存储效率逼近最优,但该码更适合构造长码,且其成功译码具有概率性,因此目前在存储系统中的使用较少.2)RS(Reed-Solomon codes)类纠删码[12-14],此类编码能达到理论最优的存储效率,即具有MDS性质,且能根据具体环境构造出任意容错能力的码字,具有很强的应用灵活性.由于它独特的优势,目前的存储系统也更多是偏向以RS类纠删码为基础构建其容错机制.但是,RS类纠删码的运算需要在多元有限域上进行,这导致RS类纠删码的计算效率大大低于XOR(exclusive-OR, XOR)类纠删码.对于RS类纠删码而言,其译码运算复杂度又远高于其编码运算.
针对这一问题,多年来不断有学者积极寻求着解决方案.但是,相比于XOR类编码,RS类纠删码很难在数据元素和校验元素之间寻找到有几何规律的码链关系,从而在方法论的层面提升RS类纠删码计算的时间效率相对困难.现在对于RS类纠删码的译码方法研究更多集中在如何提高单节点失效后的重构效率[13]或者减少修复带宽[14],对能整体降低RS类纠删码删除错误重构计算时间开销的方法研究较少[15-16].目前RS类纠删码最为工程领域接受的计算效率提升途径为,使用一些专门针对有限域运算进行优化的指令集或底层方法来达到降低RS类纠删码计算时间成本的目的,其中比较常见的包括GF-Complete[17],Jerasure[18]以及Intel公司推出的ISA-L library[19],但是此类技术路线与本文研究内容关联度不大,故不再详述.
本文工作的主要贡献包括3个方面:
1) 提出了一种针对RS类纠删码码删除错误的译码方法,适用于存储系统中的失效数据重构,由于不再使用计算复杂度很高的矩阵求逆运算,能很大程度节省RS类纠删码的译码时间开销;
2) 新的译码方法也可以推广到所有的二进制XOR类纠删码;
3) 对该译码方法的研究表明:该方法还能在数据重构时规避某些节点的参与,可用于大规模存储系统的数据重构时对重构参与节点的使用进行整体规划.
1 相关工作及研究动机
为了便于叙述,在此做约定:存储系统有n个存储节点,使用某一类(n,k)纠删码作为容错的核心方法,其要点是:数据存储前将原始数据分为k个大小相同的数据块,k个数据块对应着编码的k个数据元素(长度为k的数据列向量D=(d0,d1,…,dk-1)T),编码后形成n个数据块,分别存储于存储系统的n个不同节点上,而编码得到的1个码字C则分别对应着码字的n个码元(长度为n的码字列向量C=(d0,d1,…,dk-1,c0,c1,…,cn-k-1)T=(c0,c1,…,ck-1,…,cn-1)T,ci为码字的码元),其中k和n均为正整数,k为原始数据分组的长度,n为码字的长度,且n>k,0≤i≤n-1.文中若提到码元失效亦指该码元对应的存储节点失效,而存储节点失效可以理解为该存储节点上的全部数据丢失(亦即最坏的情况),反之亦然.而本文的所有方法叙述中,若无特别说明,编码的容错能力即指对删除错误的最大恢复能力,对于全部矩阵及存储阵列的行列的计数从0开始,且不妨假设所有运算有限域的特征为2.下面,本节将首先以示例的形式简要描述当前纠删码最常用的3类译码方法.
1.1 基于码链的译码方法
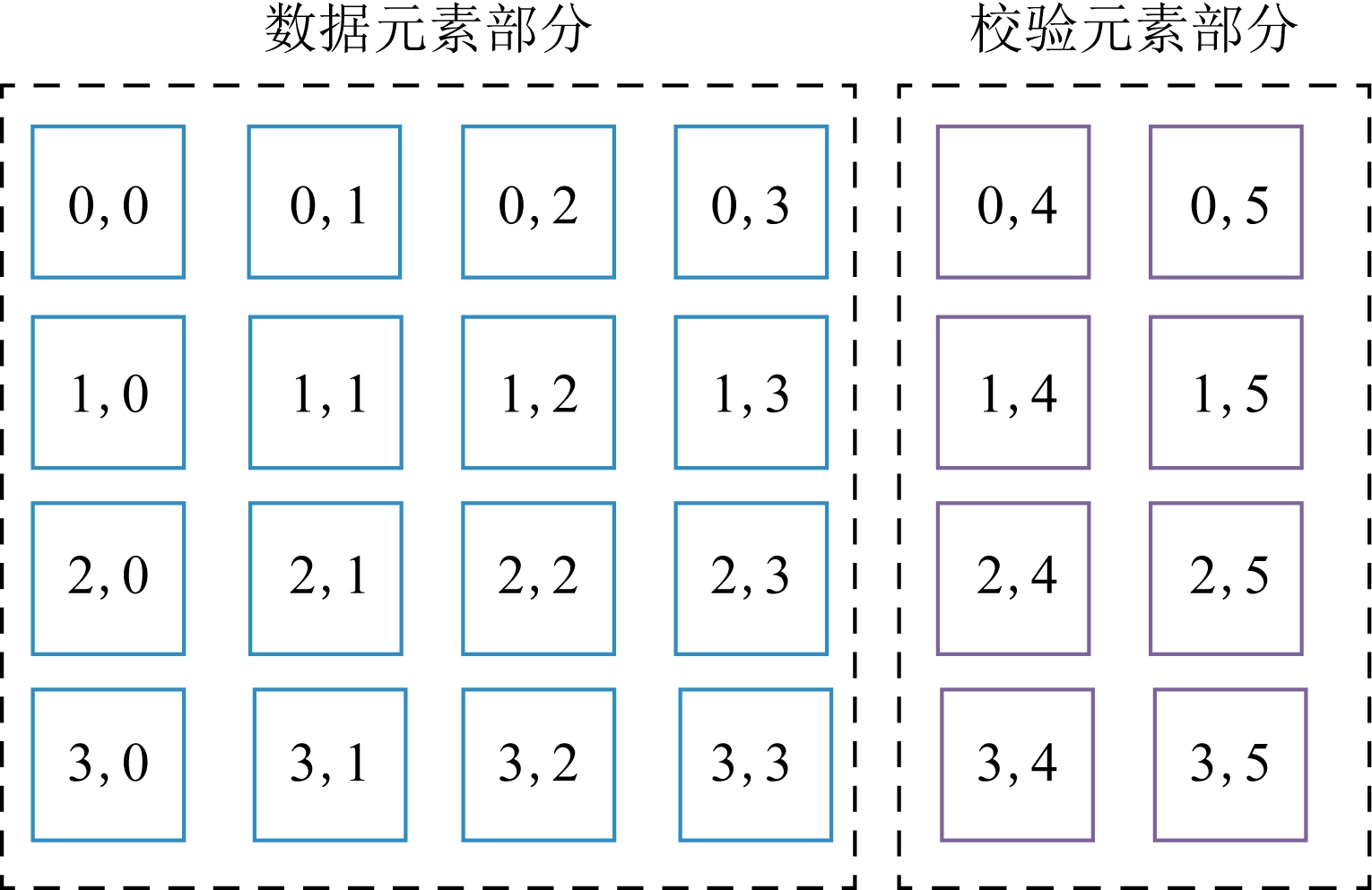
Fig. 1 Data layout of RDP code
图1 RDP码的布局结构
大多XOR类纠删码的构造可以由几何形式表示,即码字中所有存在校验关系的数据位和校验位的集合可以看作1条码链[2],1条码链即对应1个校验方程.特别是在阵列码中,如果用线连接码链上的所有码元则通常具有一定的几何规律.
以RDP码[6]为例,使用素数5构造出RDP码的码字结构如图1所示:
根据RDP码的编码规则,图2中用箭头连接起来的元素和所有图形相同的码元被称为码链,每条码链上所有码元的异或结果为0.而简单来说,基于码链关系的译码方法,即是按照一定规则搜索仅有1个失效码元的码链,利用码链上其他有效码元的异或求得失效码元的值.
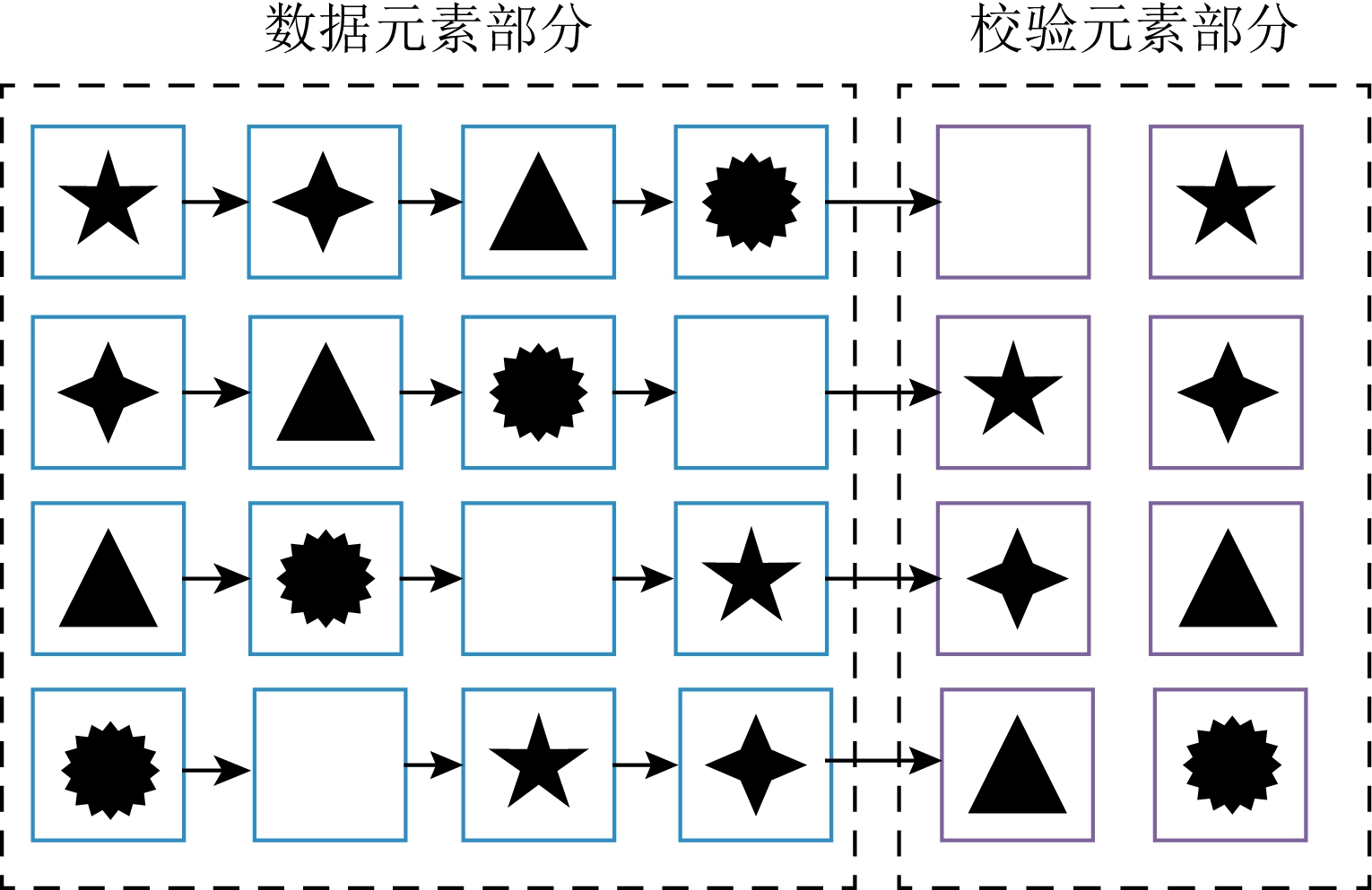
Fig. 2 Check relationship of RDP code
图2 RDP码的校验关系
假设在本示例中RDP码的第0列和第2列对应的存储节点失效,则基于码链的数据重构方法操作过程为:首先搜索到码链[(0,1),(1,0),(1,5),(2,4),(3,3)]中仅有1个失效码元(1,0),则将该码链上其他所有码元异或,从而得到码元(1,0)的值;码元(1,0)数据恢复后,其所在的另一条码链[(1,0),(1,1),(1,2),(1,3),(1,4)]上也就仅存在1个失效码元(1,2),异或该码链上所有有效码元则失效码元(1,2)得到恢复;码元(1,2)数据恢复后,其所在的另一条码链[(0,3),(1,2),(2,1),(3,0),(3,5)]上也就仅存在1个失效码元(3,0),异或该码链上所有有效码元则失效码元(3,0)得到恢复;以此类推,可以按照上述规律逐渐按序恢复出其他的失效码元(3,0),(3,2),(0,0),(0,2),(2,0),(2,2).
很多XOR类纠删码均可以用该译码方法进行数据重构,而基于码链的译码方法逻辑简单清晰,便于软硬件实现,因此在实际工程中被广泛使用.将运算的有限域GF(2w)上的所有数值替换为对应的w×w的2元域矩阵后,基于码链的译码方法也能勉强用于RS类纠删码的译码,其中w为正整数.但是,RS类纠删码的构造方法与XOR类纠删码差异较大,一般没有清晰的几何编码结构,因此用该译码方法将有较大概率不能完全重构本应该可以恢复的失效码元.
1.2 基于生成矩阵的译码方法
RS类纠删码的编码通常是采用生成矩阵乘以数据向量的做法,假设数据向量为D,生成矩阵为G,生成矩阵可以是由范德蒙矩阵或者柯西矩阵生成,但是本质上没有太大差异.
图3显示了1个(7,4)RS纠删码的编码过程,生成矩阵的上半部分为1个单位矩阵I,下半部分为1个3×4的柯西矩阵P,显然这是1个容错能力为3的系统柯西RS纠删码.
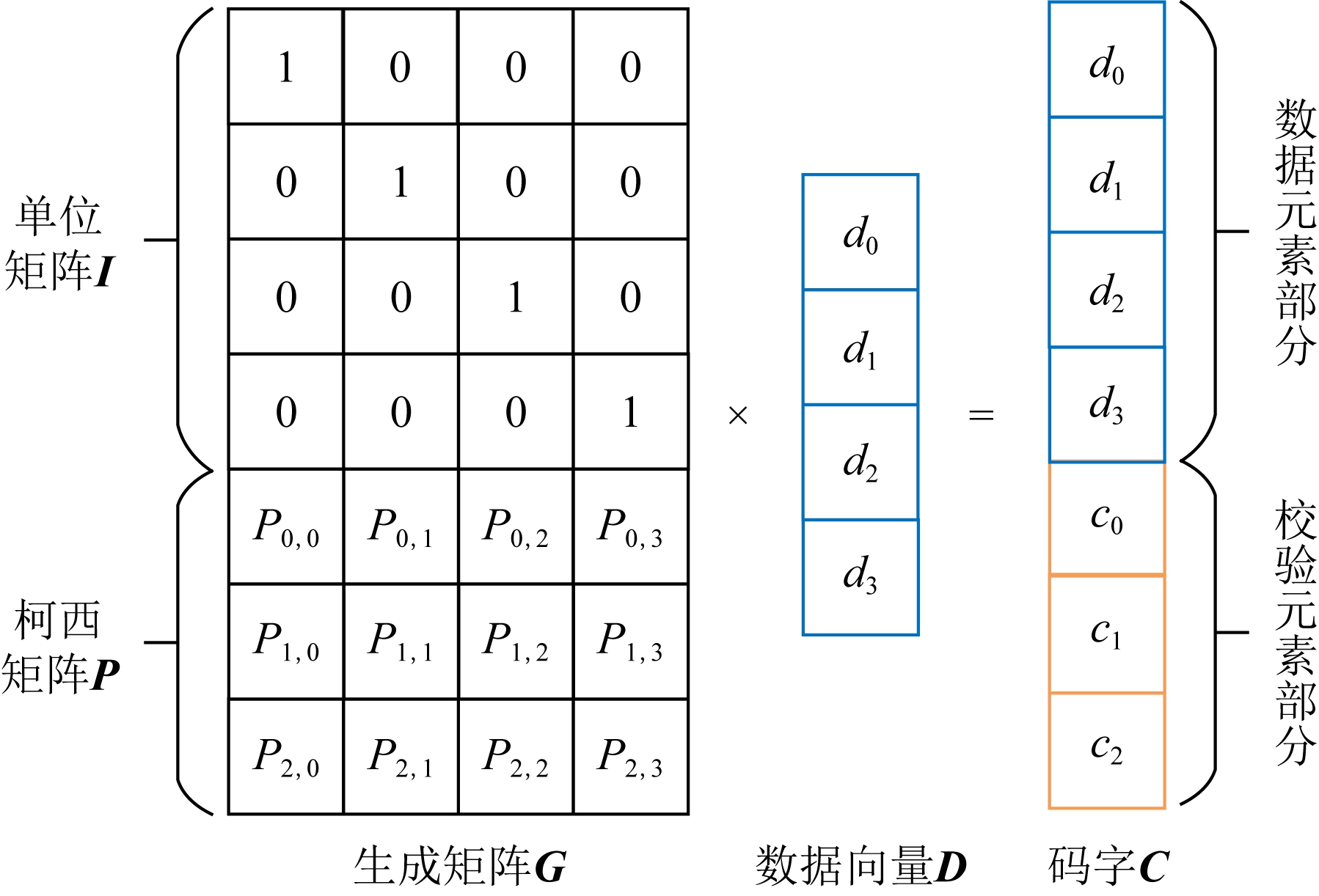
Fig. 3 Encoding process of RS code
图3 RS码的编码过程
其编码过程可表达为G×D=C,其中的参数D=(d0,d1,…,dk-1)T,C=(d0,d1,…,dk-1,c0,c1,…,cn-k-1)T.
使用生成矩阵乘以由数据元素组成的列向量,从而得到由各码字元素构成的码字列向量.由矩阵的乘法定义可知,生成矩阵的第i行构成的行向量乘以数据元素构成的列向量得到码字向量的第i个码元,因此生成矩阵的第i行与码字向量的第i个码元存在对应关系.换句话说,抽取生成矩阵的任意行而组成的子矩阵,乘以数据元素构成的列向量,如果也选取码字向量中与生成矩阵抽取行相同位置的码元构成新的列向量,则图3中的等式仍然成立.
假设码字C中的元素d0和d2这2个码元失效,我们可以去除码字这2个码元以及生成矩阵中对应的2行,等式仍然成立,如图4所示.
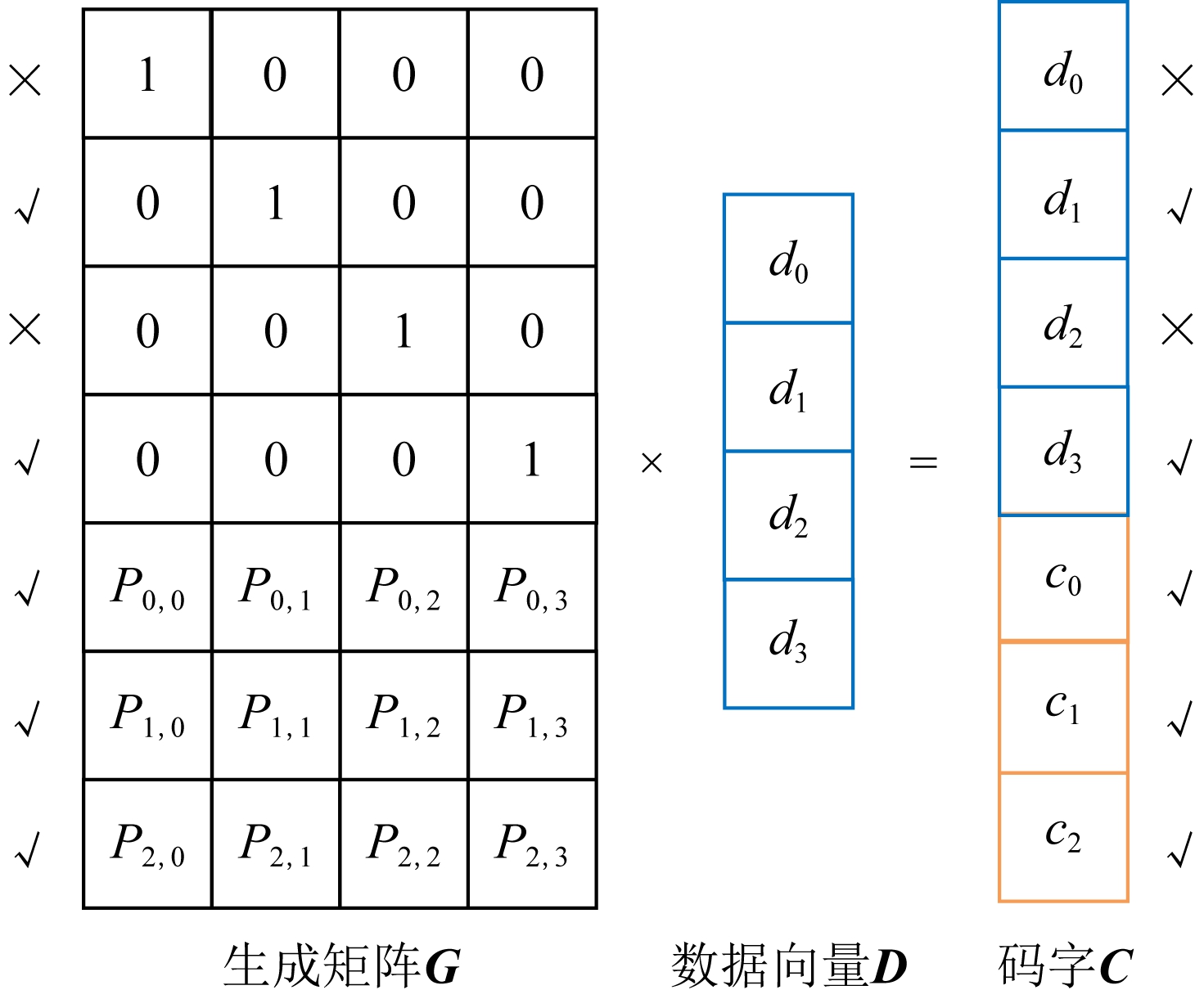
Fig. 4 Decoding process based on the generating matrix
图4 基于生成矩阵的译码过程
此时,从仍然有效的码元中任意选取4个(比如最后4个码元),构成列向量C′=(d3,c1,c2,c3),并使用生成矩阵中与列向量C′中码元相同位置的第4~7行,构成1个矩阵G′,若将数据元素列向量记作D,则显然G′×D=C′成立,此时在该等式两边同时乘以矩阵B的逆,则能恢复出数据元素D=G′-1×C′.而矩阵B的可逆性则由柯西矩阵或者范德蒙矩阵的性质来保证,此处不再赘述.这就是基于生成矩阵译码的基本原理,也可用于任意纠删码的译码.
基于生成矩阵的译码方法,也有不少学者提出过改进方案.其中最典型的是Blomer等人[20]提出的降低有限域维度方案,该方案将运算在有限域GF(2w)上生成矩阵中的每个元素用1个w阶的0-1方阵表示,源文件分为k个数据块,每个数据块由相同数量的运算单位构成,每个运算单位是1个w位的0-1比特串(看作是1个w维列向量),这样,编译码运算时均只需进行2元域的运算,从而提高计算速度.而此后Plank等人[21]又在此基础之上提出如何减少生成矩阵中数值1的方法,从而进一步减少运算时间.不过,文献[20-21]改进方案本质上是通过降低运算有限域的维度达到的,方法本身和本节叙述的原理没有实质的差异.此外,随着对容错能力要求的提高,此类改进方案可能会导致生成矩阵的尺寸膨胀过快,从而译码运算时将面临高复杂度的大矩阵求逆运算的问题.
1.3 基于校验矩阵的译码方法
基于生成矩阵译码方法的问题为,对1个容错能力为k(k>1)的RS纠删码,1个码元失效和k个码元失效,在译码过程中使用到的矩阵求逆运算的次数和所需求逆矩阵的尺寸是相同的.如果码字的数据元素和校验元素同时出现了失效,则使用该方法译码则需要先恢复数据元素,再重新进行编码以恢复校验元素,比较繁琐,也增加了本来不必要的计算工作量.而基于校验矩阵的译码方法可以在很大程度解决上述问题.基于校验矩阵的译码方法几经改进[15-16,22],但译码原理总体一致,本节根据文献[16]的方法,并以1.2节的(7,4)柯西RS纠删码为例进行简要叙述.
1个(7,4)柯西RS纠删码的校验矩阵的尺寸为3×7,其中校验矩阵的前半部分为1个3×4的柯西矩阵P(和1.2节示例中的矩阵P相同),后半部分为1个单位矩阵I,如图5所示:
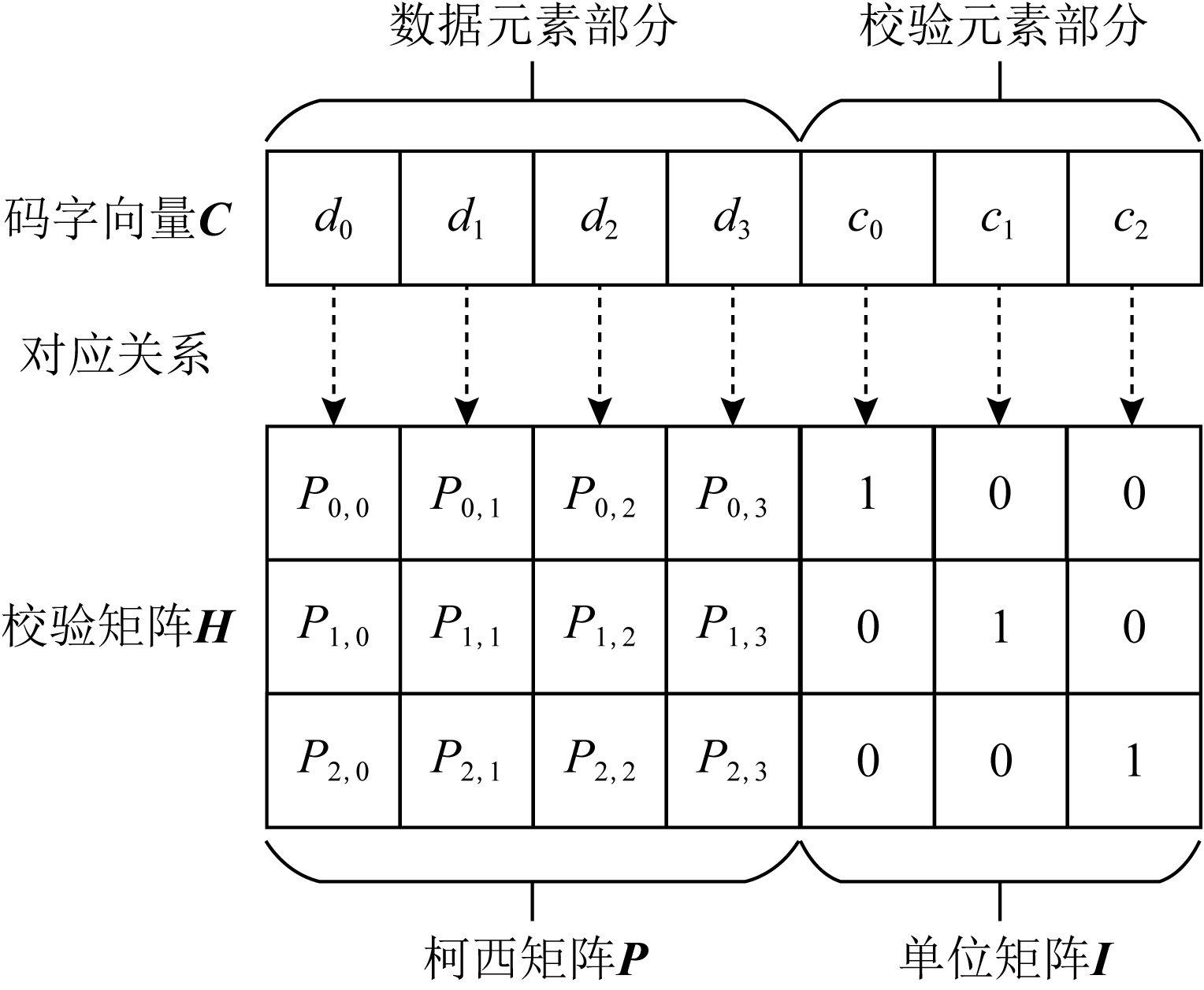
Fig. 5 The check matrix and correspondence between its column vectors and code elements
图5 校验矩阵及列向量与码字元素的对应关系
由校验矩阵的定义可知,校验矩阵的每一列与码字中的各个码元一一对应:
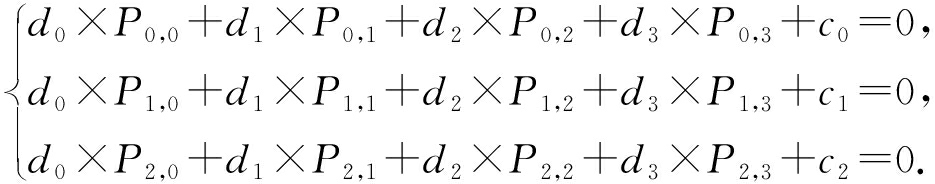
(1)
将校验矩阵记作H,码字向量记作C,则在所有码元没有错误发生时恒有等式H×C=0成立.
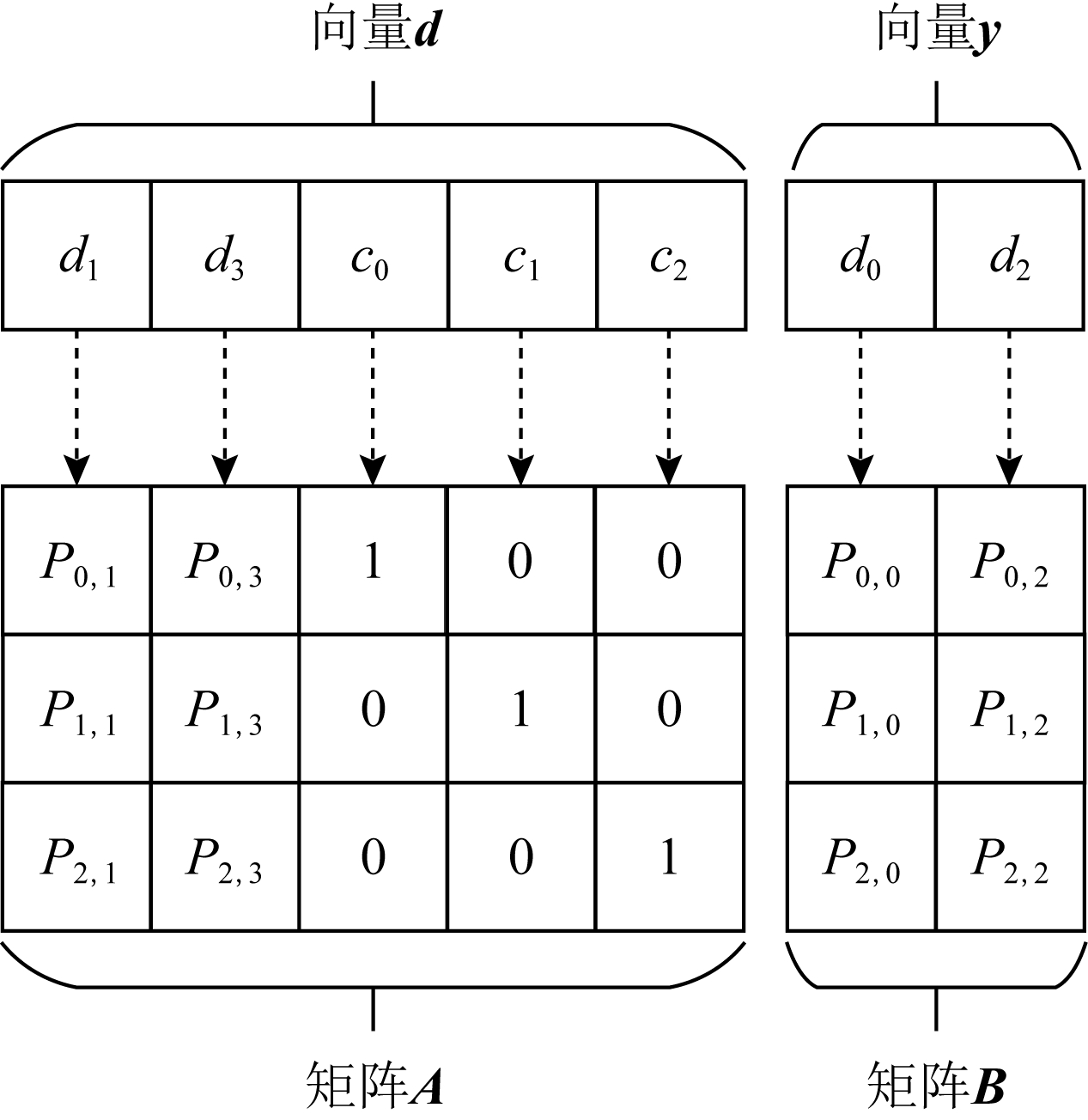
Fig. 6 Adjustment of position of column vectors and code elements in the check matrix
图6 调整校验矩阵中列向量与码字元素的位置
此时仍然假设码字中的第0个和第2个码元,即d0和d2失效,则做操作:如图6所示,移动码字向量C中的失效码元到最右边,并将其作为1个子向量记作y,剩余的有效码元也记作1个新的子向量d,d和y组成的向量记作向量C=(d|y);然后按照当前向量C中各码元和校验矩阵中各列向量的对应关系,重新排列校验矩阵中的各列,将向量d中码元对应校验矩阵中的各列组成的子矩阵记作A,向量d中码元对应校验矩阵中的各列组成的子矩阵记作B,因此校验矩阵可以表示为H=(A|B),显然等式H×C=A×d+B×y=0成立,因为运算有限域的特征为2,则等式A×d=B×y成立.
当码元d0和d2失效,则向量y变为未知,此时方程式A×d=B×y中的未知向量y有解,当且仅当矩阵B中存在2(失效码元数量)行线性无关,即B中存在1个可逆的2×2的子矩阵.取出矩阵B中的2行,构成新的矩阵记作![]() 再从矩阵A中取出和作
再从矩阵A中取出和作![]() 中相同位置的2行,构成新的矩阵,记作
中相同位置的2行,构成新的矩阵,记作![]() 则等式
则等式![]() 显然成立.此时,未知向量可由方程
显然成立.此时,未知向量可由方程![]() 得出.而矩阵
得出.而矩阵![]() 的可逆性由柯西矩阵或者范德蒙矩阵的性质保证.
的可逆性由柯西矩阵或者范德蒙矩阵的性质保证.
与基于生成矩阵的译码方法相比,本节方法在译码时能减小需要进行求逆运算的矩阵尺寸,对于1个r容错的RS类纠删码而言,如果失效码元数量为f(f≤r),则需要进行求逆运算的矩阵尺寸为f×f,当仅有1个失效码元需要重构时,则求1个特定数值在运算有限域上的乘法逆元即可.因此,此类译码方法的计算效率与基于生成矩阵的译码方法相比有了较为明显的提高.
1.4 本文的研究动机
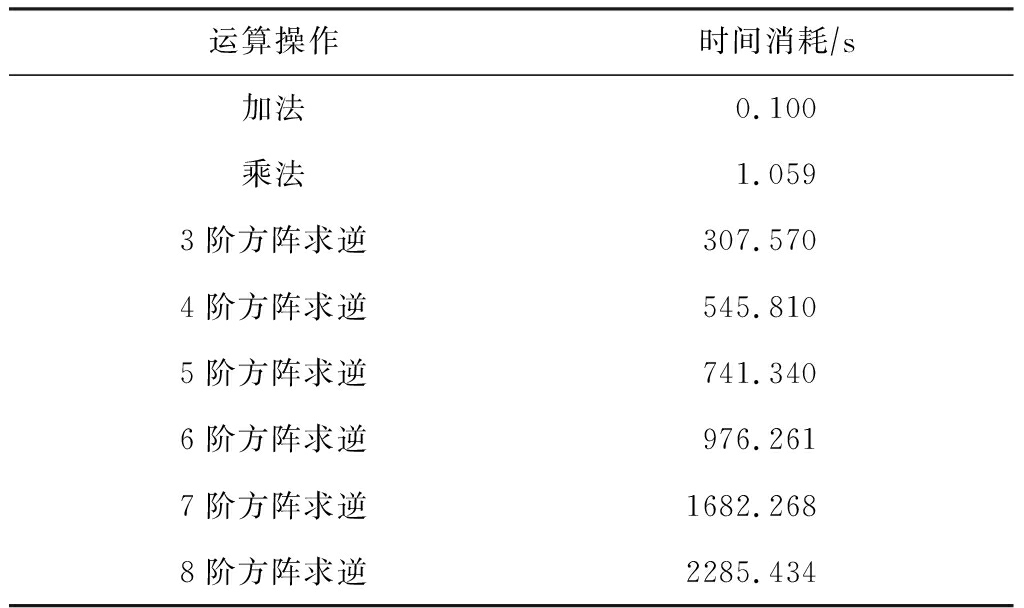
由于RS类纠删码使用了有限域上的计算操作,从而导致了很高的计算时间成本.不过,我们的实验表明,与有限域上的加法及乘法相比,RS类纠删码译码操作中需要频繁使用到的矩阵求逆运算才是导致RS码计算效率低的最重要因素.表1显示了在同一台电脑上进行5 000次有限域GF(28)上的加法、乘法,以及不同阶次方阵求逆运算的时间消耗对比.不难看出,有限域上加法和乘法操作的时间开销基本相当,而矩阵求逆运算的时间开销则是要高出加法和乘法运算好几个数量级的,且随着求逆矩阵尺寸的增加而成倍增长,从复杂度上来讲,对于规模为n×n的矩阵来讲,矩阵求逆的运算复杂度为O(n3),这也是为什么基于校验矩阵的译码方法时间效率优于基于生成矩阵译码方法的原因.但是,基于校验矩阵的译码方法并没有消除矩阵求逆运算,只是减小了需要进行求逆运算的矩阵尺寸.如果能在译码过程中完全消除矩阵的求逆运算,则能更大程度减小RS类纠删码的译码时间开销.这也是本文研究的出发点和动机.
Table 1 Time Cost Comparison of 5 000 Operations over the Finite Field GF(28)
表1 有限域GF(28)上5000次运算操作的时间消耗对比
运算操作时间消耗∕s加法0.100乘法1.0593阶方阵求逆307.5704阶方阵求逆545.8105阶方阵求逆741.3406阶方阵求逆976.2617阶方阵求逆1682.2688阶方阵求逆2285.434
2 一类新的RS类纠删码的译码方法
本节将提出一类新的RS类纠删码译码方法,该方法能完全消除译码过程中的矩阵求逆运算操作,从而降低译码操作的译码时间复杂度.在介绍新的方法之前,首先引入码元关系矩阵的概念,并对重要性质进行说明.
2.1 码元关系矩阵
有限域GF(q)上的所有(n,k)线性分组码,码字C=(c0,c1,c2…,cn-1)T中任意1个码元ci,i为整数且0≤i≤n-1,均可由所有码元的线性组合进行表示,则所有码元可表示为
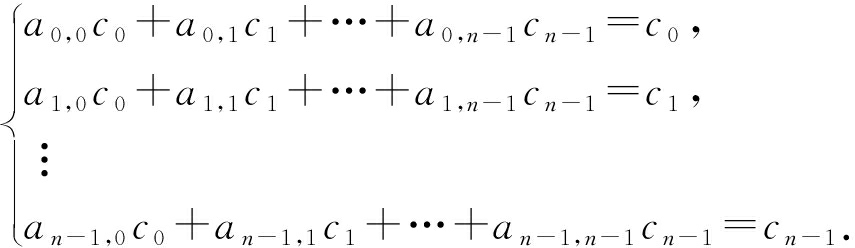
(2)
本文将该非齐次线性方程组的系数矩阵定义为码元关系矩阵W.
显然,对于任意1个(n,k)线性分组码,其码元关系矩阵一定是1个n×n的方阵:
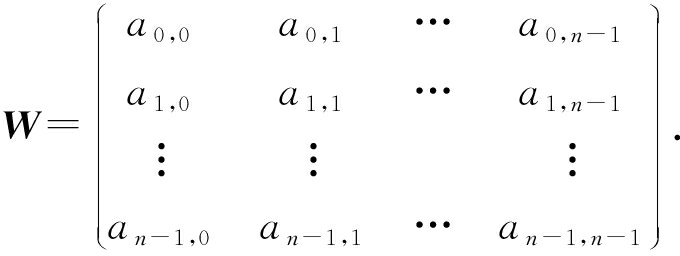
(3)
由码元关系矩阵的定义可知,W的第i行Wi=(ai,0,ai,1,…,ai,n-1)代表了码字第i个码元ci的一类线性表示方法,即ci=ai,0c0+ai,1c1+…+ai,n-1cn-1,i为整数且0≤i≤n-1,矩阵W的第j列对应着参与计算的码字中的第j个码元,j为整数且0≤j≤n-1.
对于任意线性分组码,其码元关系矩阵W通常不会是唯一的,但是单位矩阵显然是码元关系矩阵,它表示每一个码元和自身相等.下面给出码元关系矩阵的2个性质:
性质1. 对码元关系矩阵进行任何初等行变换后的结果不再是码元关系矩阵.
证明. 在有限域GF(q)中,矩阵的初等行变换包含3类变换[23]:
1) 以1个非0的数t乘以矩阵的某一行,其中t∈GF(q);
2) 把矩阵的某一行的t倍加到另一行,其中t为GF(q)中非0元素;
3) 互换矩阵中任意2行的位置.
下面就这3类初等行变换进行分别说明:
1) 根据定义,线性关系矩阵中的第i行代表了码字C=(c0,c1,…,cn-1)中第i个码元由所有码元的1种线性表示方式:ci=ai,0c0+ai,1c1+…+ai,n-1cn-1,其中i为整数且0≤i≤n-1.对其中1行乘以1个非0数t则等价于把该码元也乘以t: t×ci=t×(ai,0c0+ai,1c1+…+ai,n-1cn-1).显然,由于t为非0数,则ci≠t×(ai,0c0+ai,1c1+…+ai,n-1cn-1).因此,在线性关系矩阵中,第i行乘以t后得到的新的第i行(t×ai,0,t×ai,1,…+t×ai,n-1)不再是第i个元素ci的线性表达,所以1个非0数t乘以原始码元关系矩阵的某一行后的结果不再是线性关系矩阵.
2) 不妨假设将第j行的t倍加到i行上,可以表示为:t×cj+ci=(t×aj,0+ai,0)c0+(t×aj,1+ai,1)c1+…+(t×aj,n-1+ai,n-1)cn-1,其中i和j为整数且0≤i≤n-1.除非t=0,否则t×cj+ci≠ci.因此,第j行的t倍加到第i行的新的第i行(t×aj,0+ai,0,t×aj,1+ai,1,…,t×aj,n-1+ai,n-1)已经不再是第i个元素ci的线性表达,因此,在线性关系矩阵中,把矩阵的某一行的t倍加到另一行之后的结果不再是线性关系矩阵.
3) 根据码元关系矩阵的定义可知,线性关系矩阵的每一行代表了不同的元素,显然任意2行相互交换后的结果不再是线性关系矩阵.
证毕.
性质2. 对于任意长度为n的行向量v=(v0,v1,…,vn-1),将v的t倍加到码字C=(c0,c1,…,cn-1)对应的码元关系矩阵的任意行,其结果仍然为码元关系矩阵,其中v0c0+v1c1+…+vn-1cn-1=0,且ci,vi,t∈GF(q).
证明. 根据码元关系矩阵的定义可知,码元关系矩阵的第i行Wi=(ai,0,ai,1,…,ai,n-1)为码字C中第i个码元ci由所有码元的其中1种线性表示:ci=ai,0c0+ai,1c1+…+ai,n-1cn-1.则等式ci=ai,0c0+ai,1c1+…+ai,n-1cn-1+0显然成立.而根据前提条件,对于向量v,有等式v0c0+v1c1+…+vn-1cn-1=0成立.则等式tv0c0+tv1c1+…+tvn-1cn-1=t×0=0也成立.那么,等式ci=(ai,0c0+ai,1c1+…+ai,n-1cn-1)+(tv0c0+ tv1c1+…+tvn-1cn-1)也成立,对该等式归并同类项后得到等式:ci=(ai,0+tv0)c0+(ai,1+tv1)c1+…+(ai,n-1+tvn-1)cn-1.
显然,这也是对第i个码元ci的一类线性表示.因此,将向量v的t倍加到线性关系矩阵任意行后的结果仍然是同一码字的码元关系矩阵.
证毕.
2.2 失效数据恢复步骤
不妨假设在有限域GF(q)上构建1个(n,k)RS纠删码,其中q=pw,p为素数,w,n,k均为正整数,且k<n.假设为原始信息分成k组后,经过编码生成码字C=(c0,c1,…,ck-1,ck,…,cn-1)T,将其校验矩阵记作H,显然H的尺寸为(n-k)×n,并且H×C=0,该编码最大可以容忍n-k个码元丢失.
假设其中有f个码元失效,f≤n-k,将失效码元组成的集合标记为F,F={F1,F2,…,Ff},即{F1,F2,…,Ff}={cs1,cs2,…,csf},其中下标{s1,s2,…,sf}∈{0,1,2,…,n-1},也就是下标为失效码元位置.
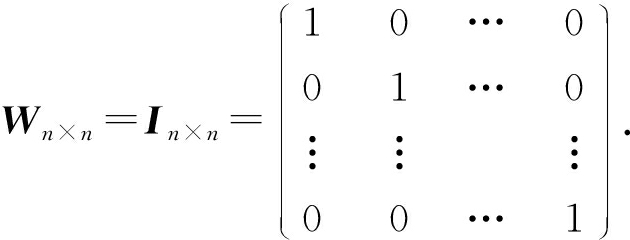
步骤1. 初始化码元关系矩阵.生成1个尺寸为n×n的单位矩阵In×n,根据码元关系矩阵的定义,因为ci=ci,i为整数且0≤i≤n-1,因此In×n可以作为初始的码元关系矩阵Wn×n,记作:
(4)
步骤2. 定义译码变换矩阵并初始化.将码元关系矩阵Wn×n和校验矩阵H(n-k)×n拼接成1个矩阵,称为初始译码变换矩阵,记作S0:
(5)
显然,矩阵S0的尺寸为(2n-k)×n,这里的矩阵的下标从0开始,将S0中前n行构成的子矩阵记作S_up0,而将其最后n-k行构成的子矩阵记作S_down0.
在该译码过程中,对于f个丢失码元,需要对初始译码变换矩阵S0进行f次变换操作.将经过第i次矩阵变换之后更新的译码变换矩阵Si中前n行构成的子矩阵记作S_upi,而将其最后n-k行构成的子矩阵记作作S_downi,i为整数且1≤i≤f.
在每次进行译码变换矩阵的变换过程中,由于只进行了行变换,那么对于S_upi和S_downi,第i列均对应着码字中的第i个码元,因此译码变换矩阵Si的每一列与码元也有相同的对应关系.
步骤3. 对于丢失码元集合F,{F1,F2,…,Ff}={cs1,cs2,…,csf},按序取出失效码元集合F中的1个元素csi,其中{s1,s2,…,sf}∈{0,1,…,n-1}.在矩阵Si-1的丢失码元csi对应的第si列上寻找非0元素,所有满足条件的非0元素的行编号形成集合,标记为![]() 其中的元素实际为q个非0元素所在行的位置,并且
其中的元素实际为q个非0元素所在行的位置,并且![]()
步骤4. 在集合Rsi中搜索一个大于等于n的元素,若存在则将该元素标记为![]() 并从Rsi中删除,然后转到步骤5;否则表明该列对应的码元csi不可恢复,终止.
并从Rsi中删除,然后转到步骤5;否则表明该列对应的码元csi不可恢复,终止.
步骤5. 按序取出![]() 中的一个不等于id_row的元素
中的一个不等于id_row的元素![]() 并做计算:
并做计算:![]() 计算完成从集合Rsi中删除元素
计算完成从集合Rsi中删除元素![]()
步骤6. 反复执行第5步,直到集合Rsi为空.将矩阵Si的第id_row行上所有元素置为0,然后将集合F中的元素csi删除.
步骤7. 判断矩阵Si的子矩阵S_downi是否所有元素均为0,若是则表明不能再恢复任何失效码元,若此时集合F中还存在元素则表明这些失效码元不可恢复,终止.
步骤8. 重复步骤3~7,直到失效码元集合F为空,即所有失效码元可成功恢复,转到步骤9.当存在失效码元不可恢复时,终止.
步骤9. 此时Si的上半部分子矩阵S_upi仍然为码元关系矩阵,其中包含着有效码元对失效码元的线性关系,也可简称为译码矩阵,记R,R=S_upi,显然,矩阵R的尺寸为n×n,而矩阵R的第si行(列)对应码字的第si个码元.那么失效码元csi可以进行恢复:
(6)
其中,1≤i≤f,0≤u≤n-1.
使用步骤1~9,可以对有限域GF(q)上的RS类纠删码的失效码元进行恢复,或者是所有失效码元能被恢复成功,若不能将所有码元成功恢复也能清楚地知道哪些码元可恢复而哪些不能恢复.
2.3 方法的正确性及分析
本节首先对和新译码方法相关的一些重要定理进行阐述,并在此基础上说明本文方法的正确性.
定理1. 对于有限域GF(q),S为(n,k)线性分组码的译码变换矩阵,则将矩阵S第i行乘以t后,矩阵S的子矩阵S_down仍然为校验矩阵.其中q=pm,p为素数,t≠0,t∈GF(q),i为整数且n≤i≤n+k-1.
证明. 由译码变换矩阵S的构造方法可知,该矩阵最上面n行为码元关系矩阵,而下面的n-k行为该编码的校验矩阵.因此,在译码变换矩阵S中最下面的n-k行均代表码字的校验方程:ai,0c0+ai,1c1+…+ai,k-1ck,其中i为整数且n≤i≤n+k-1.对译码变换矩阵S第i行乘以t,则等价于t×ai,0×c0+t×ai,1×c1+…+t×ai,k-1×ck-1=t×(ai,0c0+ai,1c1+…+ai,k-1ck-1)=0.因此,对于译码变换矩阵S而言,在其最下面的n-k行的任意1行上乘以1个非0数t后,组成的子矩阵S_down仍然为校验矩阵.
证毕.
定理2. 对于任意有限域GF(q),S为n-k线性分组码的译码变换矩阵,则将矩阵S第j行乘以t并加到第i行后,矩阵S的子矩阵S_up仍然为码元关系矩阵.其中q=pm,p为素数,t≠0,t∈GF(q),i和j均为整数且n≤j≤n+k-1,0≤i≤n+k-1.
证明. 分2种情况讨论:
1) 当n≤i≤2n-k-1时.此时对译码变换矩阵S的变换集中在该矩阵的最下面n-k行,该部分由编码的校验矩阵初始化.此时第i行对应的校验方程为ai,0c0+ai,1c1+…+ai,k-1ck-1=0,第j行对应的校验方程为aj,0c0+aj,1c1+…+aj,k-1ck-1=0,则将矩阵S第j行乘以t后加到第i行则等价于(taj,0+ai,0)c0+(taj,1+ai,1)c1+…+(taj,k-1+ai,k-1)ck-1=0,显然成立.
2) 当0≤i≤n-1时.此时,译码变换矩阵S的第i行对应的是码元线性关系方程ci=ai,0c0+ai,1c1+…+ai,n-1cn-1,而译码变换矩阵S的第j行对应的为该编码的校验方程aj,0c0+aj,1c1+…+aj,k-1ck-1=0.将矩阵S第j行乘以t加到第i行则等价于:ci=ai,0c0+ai,1c1+…+ai,n-1cn-1+0,显然也成立.这与线性关系矩阵的性质2也刚好吻合.因此,定理2成立.
证毕.
根据2.2节的描述,新的译码方法总是在译码变换矩阵S的最下面n-k行中选取符合条件的行,标记为第i行,然后将第i行乘以1个数后加到矩阵S的另外1行或多行上.换句话说,即对译码变换矩阵S进行有一定限制条件的初等变换.由于方法每次选取的第i行均满足条件n≤i≤n+k-1.根据定理1和定理2,虽然译码变换矩阵S在不断地进行变换和运算,其子矩阵S_up一直是码元关系矩阵,并能最终作为失效码元恢复的译码矩阵.综上所述,新方法可以对RS码字中的删除错误进行恢复.
该方法与文献[24]中的基于生成矩阵译码方法的译码方法,及文献[16]的基于校验矩阵的译码方法对比,主要存在2个方面的创新及优势:
1) 算法复杂度较低
对于1个(n,k)RS编码而言,k<n.当有f个丢失码元时,采用本文所述方法恢复f个丢失码元的时间复杂度为O(f×n).
证明. 本文所提的译码恢复方法的主要运算除了最后步骤9中如式(6)恢复计算f个失效码元固定次数E0=f×n的译码恢复运算,其余主要的运算集中在当i=1:f循环执行的步骤3~7对f个丢失码元的译码变换矩阵Si的更新操作,1≤i≤f.
在i=1:f的每次循环中,其主要的有限域计算主要是步骤5中的对于j=1:p且j≠v循环执行的公式所述的运算,这里需要循环的次数为p-1,p为对应列非0元素的个数.
在j=1:p且j≠v的每次循环中,根据步骤5中的执行公式,可以得出需要执行n次乘法运算,故译码变换运算需执行的运算次数E1≤f×p×n,因此可得总体的运算次数E=E0+E1≤(p+1)×f×n,可以得出该方法的时间复杂度为O(f×n).
而文献[24]所采用的生成矩阵求逆方法运算复杂度约为O(n3),1个(n,k)线性分组码作为纠删码时,当丢失的码元数量小于其分组码的最小码距的时候,这个纠删码的译码是可解的.文献[16]中采用基于校验矩阵的译码方法,根据1.3节中的方法描述,当其中有f个码元丢失时,其所需要进行的是对校验矩阵提取的对应的f×f满秩的子矩阵进行矩阵求逆,以进行后续的f个丢失码元的恢复,故其复杂度为O(f3).而文献[25]中的方法根据文中的描述,其复杂度为O(f×n2).
证毕.
2) 可同时恢复原始数据码元和校验码元
本文所述方法中丢失的校验码元可在译码过程中直接求得,无需额外计算.该方法可通过变换1次性的同时求得原始数据码元以及校验码元,这也有益于减少译码运算,降低所有失效元素恢复的时间.
而文献[24]和文献[25]所述方法中需要先求得原始数据,再通过式(2)所示方程组进行运算得到丢失的校验码元,增加了运算次数.
2.4 新方法示例
我们以在第1节中提到的RS纠删码为例来说明新方法的执行过程,如1.2节所述,这是1个(7,4)系统码,首先在有限域GF(28)上构造出该码的生成矩阵G(其中的子矩阵P为柯西矩阵):
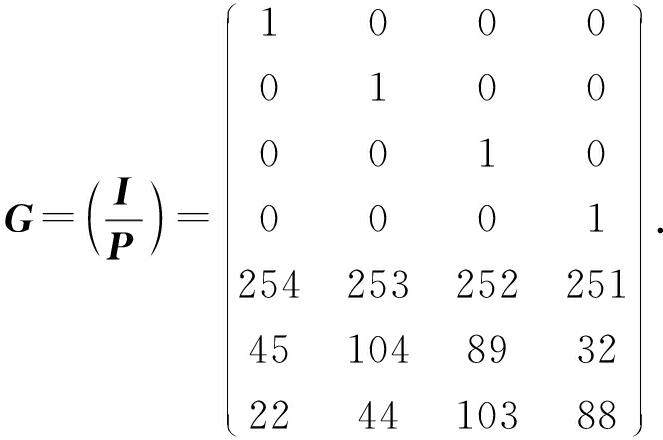
(7)
不妨假设数据元素向量为D=(1,2,3,4)T,则码字向量C=(c0,c1,…,c6)T能计算得出:C=G×D=(1,2,3,4,0,241,160)T.其中有限域的构建方法可参考文献[26],由于篇幅原因本文不再叙述.
仍然假设码字中的第0和第2个元素失效,则失效码元集合为F={c0,c2}.首先初始化译码变换矩阵S0(子矩阵W为单位矩阵、而子矩阵H为该编码的校验矩阵):
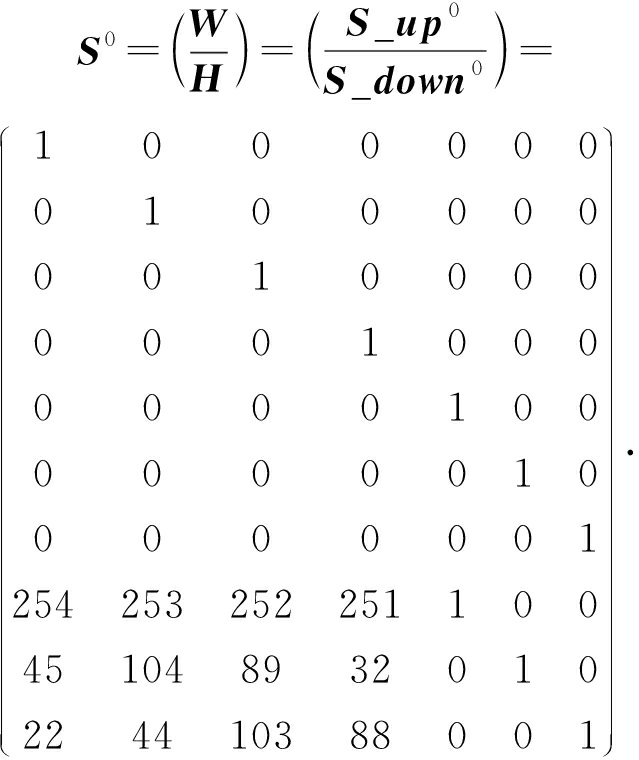
(8)
首先,从失效码元序号集合F中取出第1个元素cs1=c0,搜索该元素对应的矩阵S0中的第s1=0列,发现该列中的第0,7,8,9行上元素非0,形成集合Rs1={0,7,8,9}.从集合Rs1中找出不小于7的元素![]() 并从集合Rs1中删除 ,然后从集合Rs1中按序取出各元素
并从集合Rs1中删除 ,然后从集合Rs1中按序取出各元素![]() 对译码变换矩阵做操作:
对译码变换矩阵做操作:
操作完成后将元素![]() 从集合Rs1中删除.反复从集合Rs1中取出元素
从集合Rs1中删除.反复从集合Rs1中取出元素![]() 并执行上述操作,直到集合Rs1为空,则从F中删除元素c0.此时,译码变换矩阵S1:
并执行上述操作,直到集合Rs1为空,则从F中删除元素c0.此时,译码变换矩阵S1:
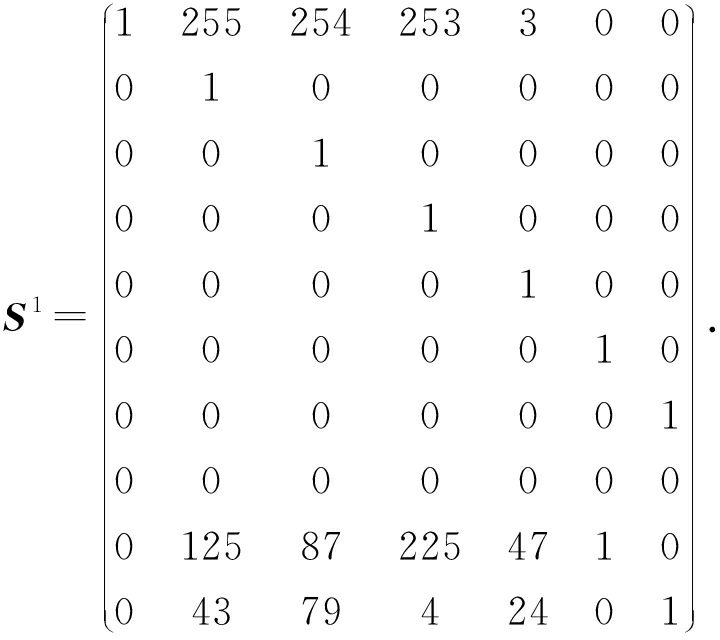
(9)
当i=2时,从失效码元序号集合F中取出第2个元素cs2=c2,搜索该元素对应的矩阵S1中的第s2=2的列,发现该列中的第0,2,8,9行上元素非0,形成集合Rs2={0,2,8,9}.从集合Rs2中找出数值不小于码长7的元素![]() 并从Rs2中删除id_row,然后从集合Rs2中按序取出各元素
并从Rs2中删除id_row,然后从集合Rs2中按序取出各元素![]() 对译码变换矩阵做操作:
对译码变换矩阵做操作:
反复从集合Rs2中取出元素并执行2.2节中详细步骤操作,直到集合Rs2为空.并删除元素c2后,集合F为空,循环退出.所有变换完成后,矩阵S2:
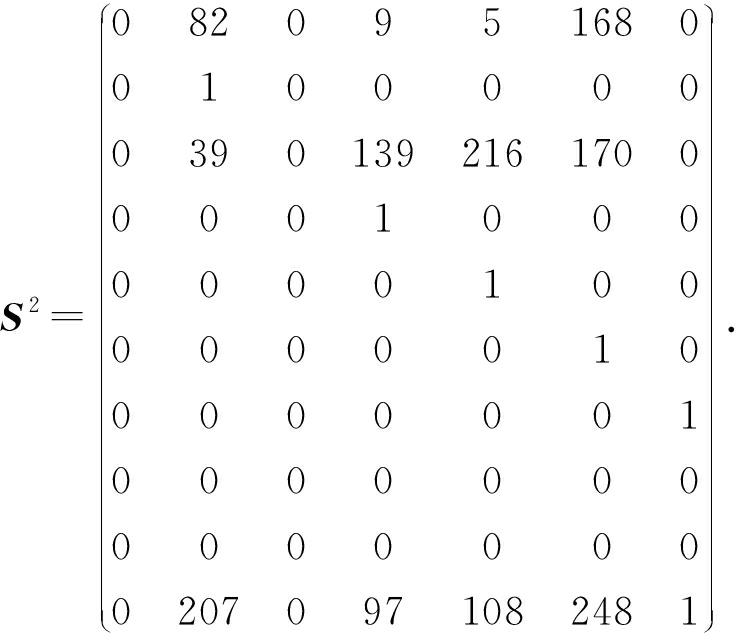
(10)
其中的前7行构成的子矩阵S_up2即为可用作失效元素恢复的码元关系矩阵,即译码矩阵R.
根据码元关系矩阵的定义可以,2个失效码元可以计算得出:
(11)
3 新方法的性能分析及应用扩展
首先说明实验运行的平台信息(以下简称为实验平台),实验平台使用了Ceph v13.2.3进行分布式存储系统的搭建,所有纠删码代码由Python2.7实现,但是为了编译码方法代码构建与分析的方便,没有直接使用ceph的逻辑存储关系,系统中使用完全相同的计算机作为存储节点.其主要配置信息为:CPU为Intel i5-4570U,6 MB缓存,内存容量为8 GB,而每台计算机上仅搭建1个OSD(object storage daemon).在实验时,每个存储节点对应码字中相同位置的1个码元,码元失效即对应的节点失效.
3.1 RS类纠删码译码的时间开销
本节实验除了使用到本文的译码方法,一方面我们还选用了文献[24]中的译码方法作为基于生成矩阵译码方法的代表,选用了文献[16]的译码方法作为基于校验矩阵的译码方法,以及文献[25]中的译码方法,在同样的环境下进行运行测试.另一方面,选用了硬件加速方法[18]及降低有限域规模的方法[20]进行对比.在这些实验中,若无特别说明,用于编译码测试的原始数据均为10 MB.
实验1. 在实验平台上分别构建(4,2),(5,3),(7,4),(7,3)柯西RS纠删码作为容错方法,计算有限域为GF(28).将10 MB原始数据编码后按序存储到各个存储节点中,分别使其中的1个和2个存储节点失效,在用新的节点替换后,分别采用基于生成矩阵的译码方法[24]、基于校验矩阵的译码方法[16]、文献[25]中的译码方法及本文方法重构数据,其数据重构的时间开销分别如图7和图8所示.
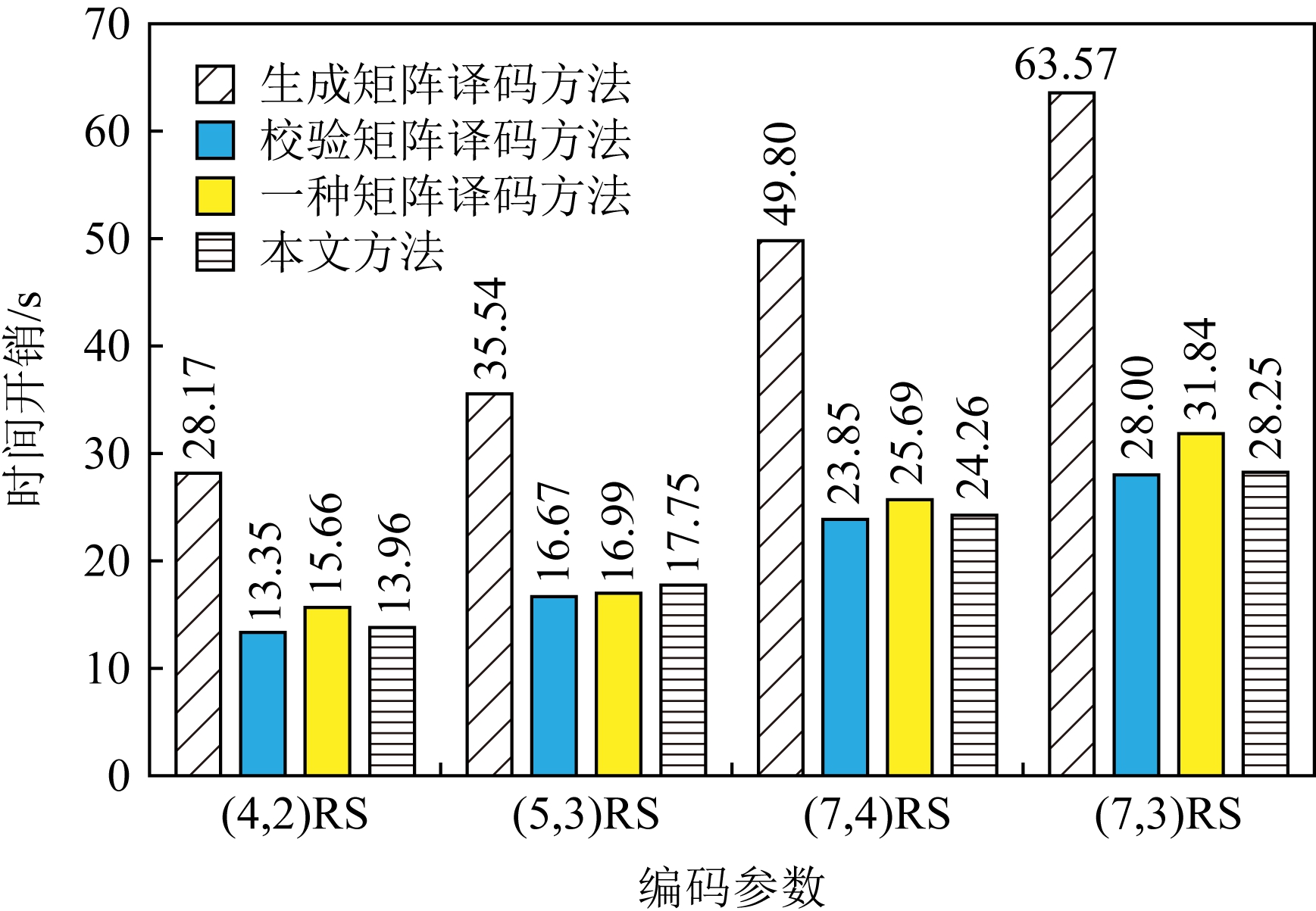
Fig. 7 Comparison of the time cost of four different methods to reconstruct a single failed node
图7 4种不同方法重构单个失效节点的时间开销对比
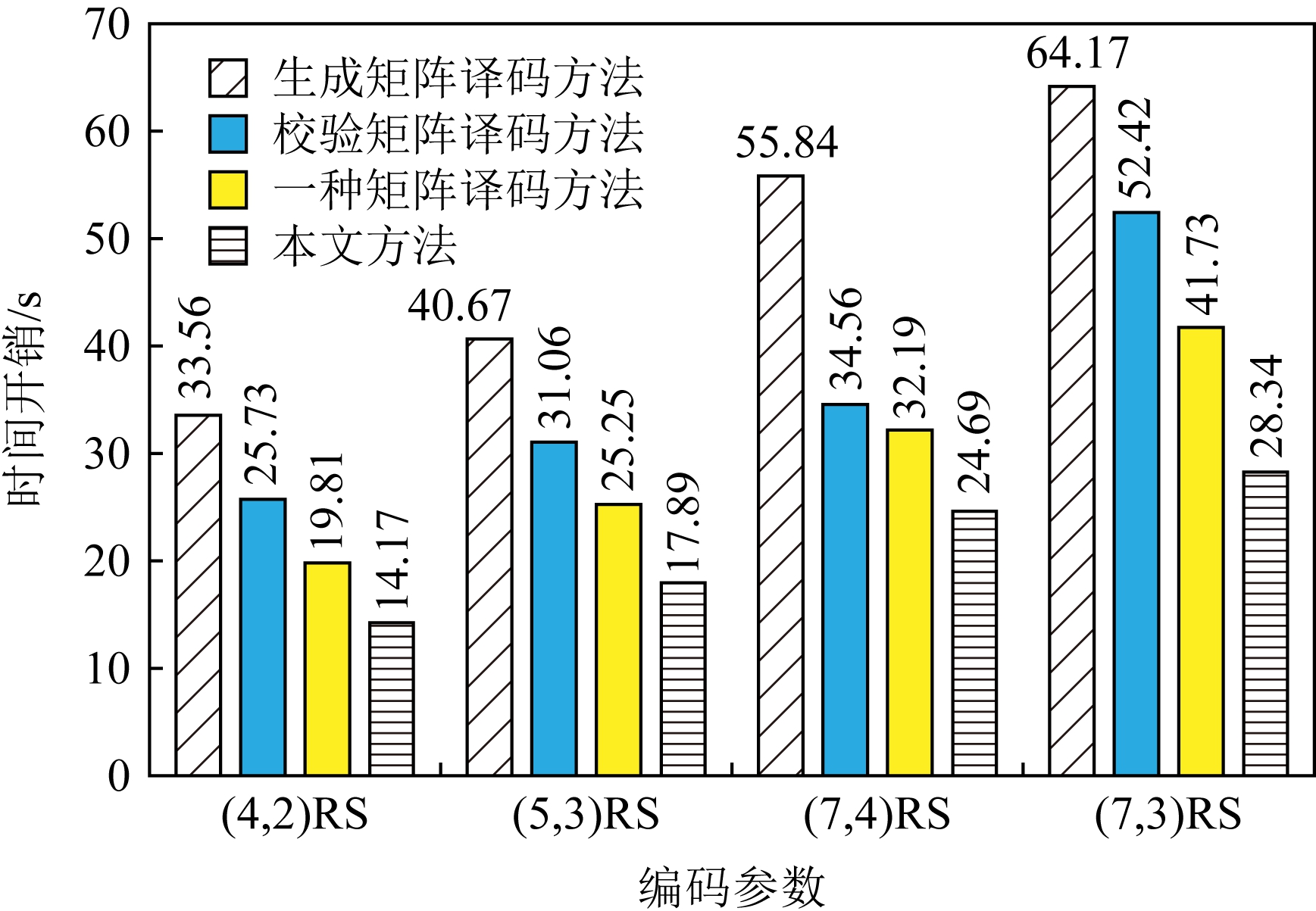
Fig. 8 Comparison of the time cost of four different methods to reconstruct two failed nodes
图8 4种不同方法重构2个失效节点的时间开销对比
总体来看,单个失效节点失效时采用基于校验矩阵的译码方法进行数据重构的时间开销最低,新方法略高于此,但是从2个失效节点开始,采用新译码方法进行数据重构的时间开销就低于另外3种方法.
实验2. 在实验平台上同样构建(4,2),(5,3),(7,4),(7,3)柯西RS纠删码作为容错方法,计算有限域为GF(28).将原始数据编码后按序存储到各个存储节点中,采用的原始数据文件大小分别为10 MB,50 MB,100 MB,文件分块大小分别为1 KB,4 KB,1 MB.分别使其中的1个和2个存储节点失效,分别采用基于生成矩阵的译码方法[24]、基于校验矩阵的译码方法[16]、文献[25]中的译码方法及本文方法重构数据,其数据重构的时间开销分别如表2和表3所示.从实验结果来看,在不同的文件分块大小情况下,本文所提的方法总体上较其他方法的译码时间开销更低.
实验3. 在实验平台上构建(9,4)柯西RS纠删码作为容错方法,将原始数据编码后按序存储到各个存储节点中,计算有限域为GF(28).可知该存储系统的节点容错能力为5,即最多5个节点失效后,其数据可以得到有效恢复.分别使其中的1~5个存储节点失效,并用新的节点替换后,采用文中的方法与本文方法进行数据重构,数据重构的时间开销变化如图9所示.
Table 2 Comparison of the Time Cost of Reconstructing a Single Failed Node
表2 重构单个失效节点时间开销对比
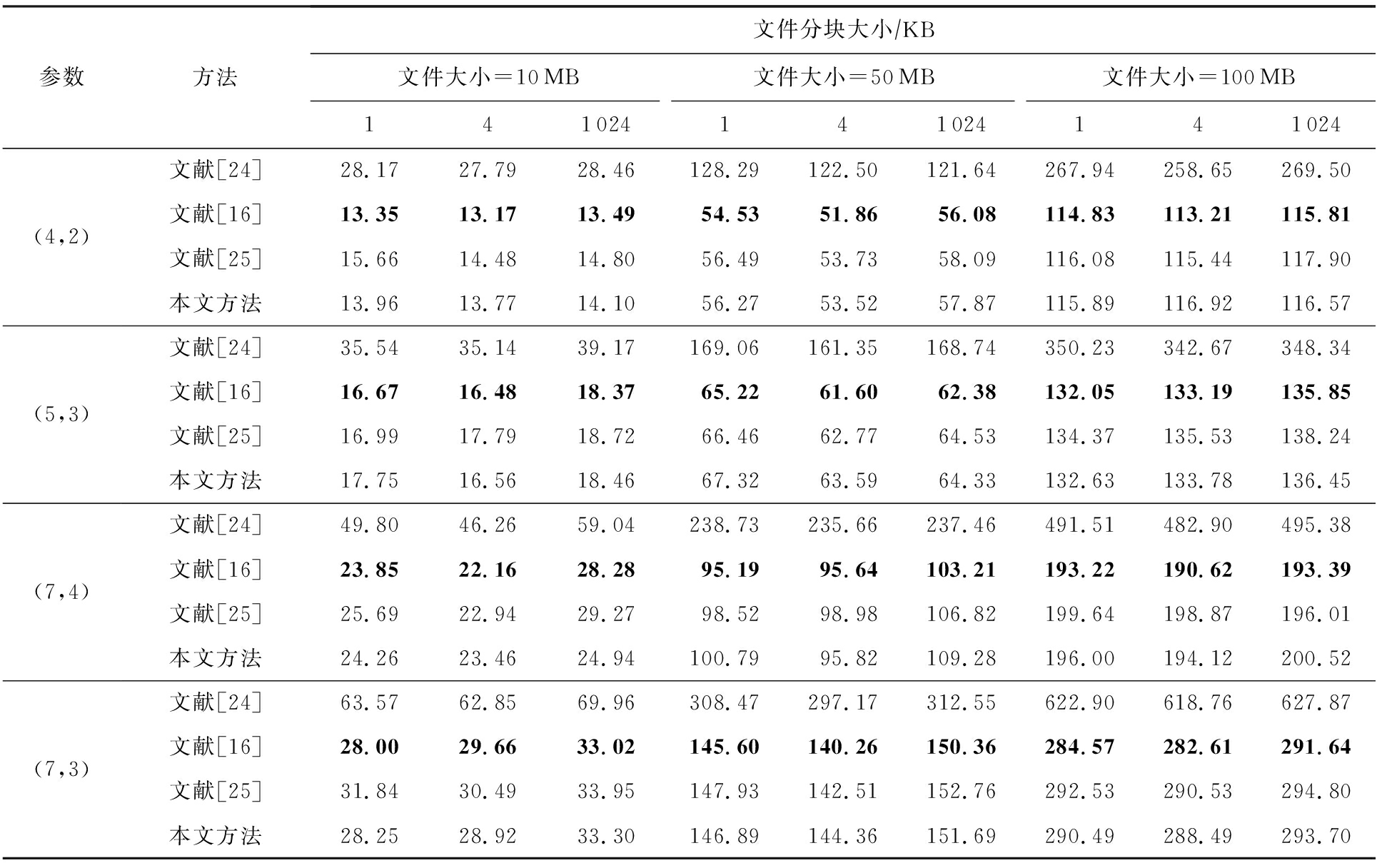
参数方法文件分块大小∕KB文件大小=10MB文件大小=50MB文件大小=100MB141024141024141024(4,2)(5,3)(7,4)(7,3)文献[24]28.1727.7928.46128.29122.50121.64267.94258.65269.50文献[16]13.3513.1713.4954.5351.8656.08114.83113.21115.81文献[25]15.6614.4814.8056.4953.7358.09116.08115.44117.90本文方法13.9613.7714.1056.2753.5257.87115.89116.92116.57文献[24]35.5435.1439.17169.06161.35168.74350.23342.67348.34文献[16]16.6716.4818.3765.2261.6062.38132.05133.19135.85文献[25]16.9917.7918.7266.4662.7764.53134.37135.53138.24本文方法17.7516.5618.4667.3263.5964.33132.63133.78136.45文献[24]49.8046.2659.04238.73235.66237.46491.51482.90495.38文献[16]23.8522.1628.2895.1995.64103.21193.22190.62193.39文献[25]25.6922.9429.2798.5298.98106.82199.64198.87196.01本文方法24.2623.4624.94100.7995.82109.28196.00194.12200.52文献[24]63.5762.8569.96308.47297.17312.55622.90618.76627.87文献[16]28.0029.6633.02145.60140.26150.36284.57282.61291.64文献[25]31.8430.4933.95147.93142.51152.76292.53290.53294.80本文方法28.2528.9233.30146.89144.36151.69290.49288.49293.70
注:黑体数字表示译码修复时间最短的.
Table 3 Comparison of the Time Cost of Reconstructing Two Failed Nodes
表3 重构2个失效节点时间开销对比
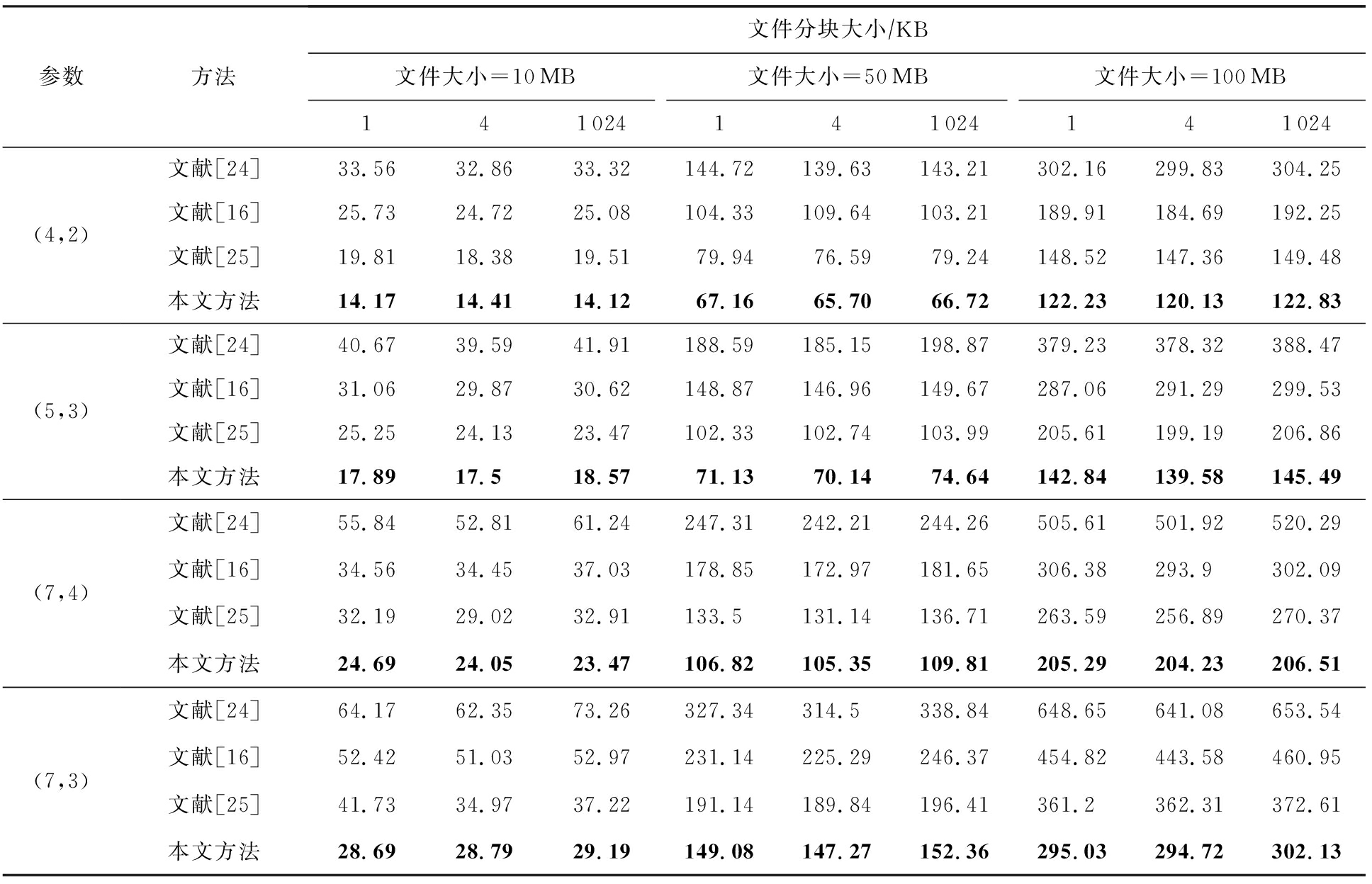
参数方法文件分块大小∕KB文件大小=10MB文件大小=50MB文件大小=100MB141024141024141024(4,2)(5,3)(7,4)(7,3)文献[24]33.5632.8633.32144.72139.63143.21302.16299.83304.25文献[16]25.7324.7225.08104.33109.64103.21189.91184.69192.25文献[25]19.8118.3819.5179.9476.5979.24148.52147.36149.48本文方法14.1714.4114.1267.1665.7066.72122.23120.13122.83文献[24]40.6739.5941.91188.59185.15198.87379.23378.32388.47文献[16]31.0629.8730.62148.87146.96149.67287.06291.29299.53文献[25]25.2524.1323.47102.33102.74103.99205.61199.19206.86本文方法17.8917.518.5771.1370.1474.64142.84139.58145.49文献[24]55.8452.8161.24247.31242.21244.26505.61501.92520.29文献[16]34.5634.4537.03178.85172.97181.65306.38293.9302.09文献[25]32.1929.0232.91133.5131.14136.71263.59256.89270.37本文方法24.6924.0523.47106.82105.35109.81205.29204.23206.51文献[24]64.1762.3573.26327.34314.5338.84648.65641.08653.54文献[16]52.4251.0352.97231.14225.29246.37454.82443.58460.95文献[25]41.7334.9737.22191.14189.84196.41361.2362.31372.61本文方法28.6928.7929.19149.08147.27152.36295.03294.72302.13
注:黑体数字表示译码修复时间最短的.
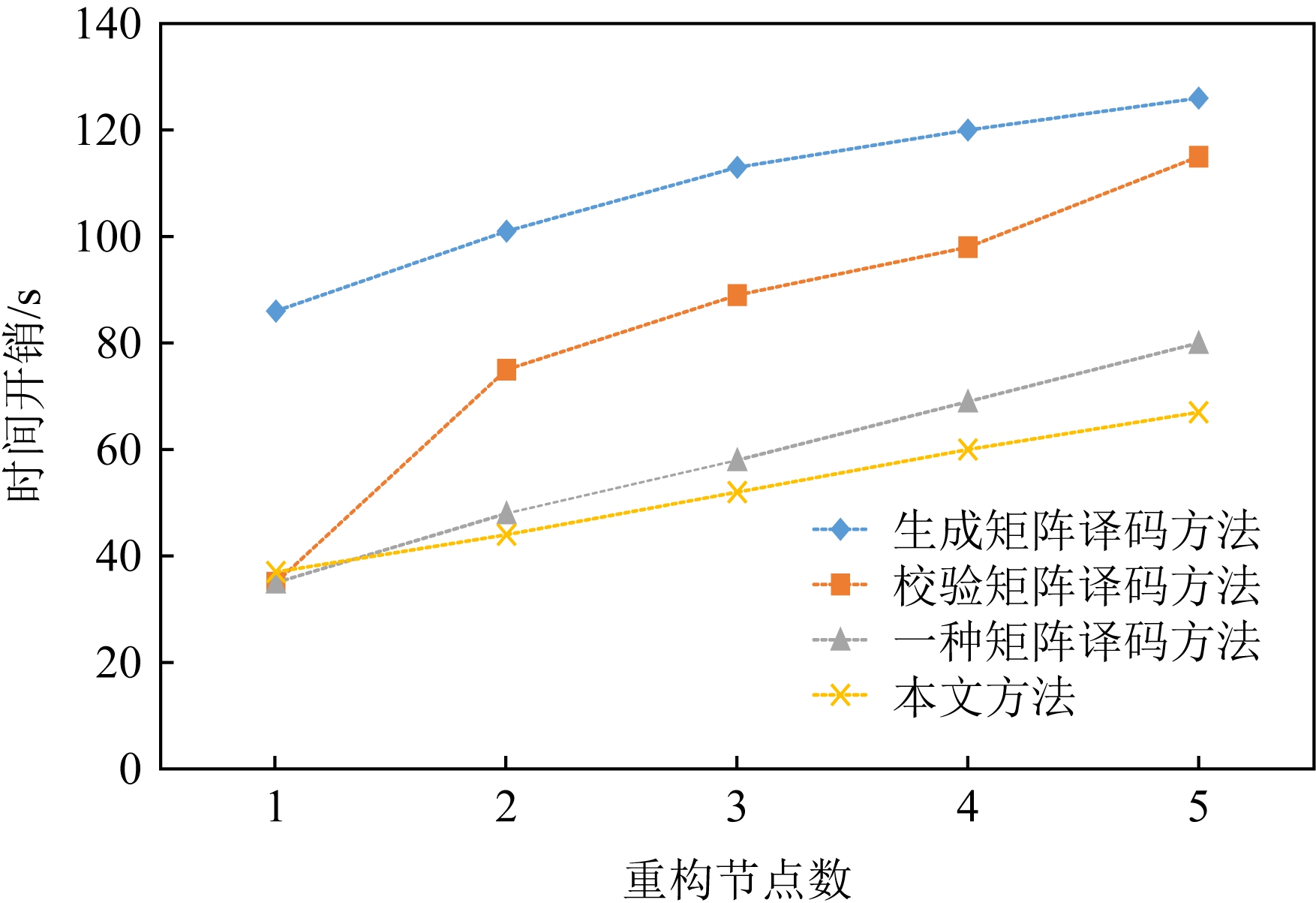
Fig. 9 Comparison of the time cost of four different
methods to reconstruct different number of failed nodes
图9 4种不同方法重构不同数量失效节点的时间开销 对比
不难看出,采用基于校验矩阵的译码方法进行数据重构的时间开销会随着所需重构节点数的增加而逼近基于生成矩阵的译码方法,文中的方法整体时间开销比本文要高一些,而采用新方法进行数据重构的时间开销则总体随着所需重构数据量的增加而线性增加.
实验4和实验5主要是将本文所提方法与硬件加速方法Jerasure[18]、降低有限域规模的方法[20]进行比较.Jerasure[18]采用了硬件加速方法,属于硬件类方法,其通过SSE指令集来加速编解码的速度,并且支持不同的有限域上的编码运算,对RS编码和柯西RS编码的支持较好.Jerasure已经发展到2.0版本,该方法在仅使用SSE的情况下,依然能够有效地提升RS类纠删码的编译码表现.降低有限域规模的方法主要是将运算进行分解以便在较小的有限域上执行以降低有限域运算的开销.
实验4. 在分布式存储实验平台上以柯西RS纠删码作为其存储编码方法,柯西RS编码参数分别为(4,2),(5,3),(7,4),(7,3),计算有限域同样为GF(28).对原始文件采用相应的编码方法进行编码后将编码分片存储到各个存储节点中,当1个和2个存储节点失效,分别采用硬件加速方法Jerasure[18]、降低有限域规模的方法[20]和本文方法进行重构,数据重构的时间开销分别如图10和图11所示.
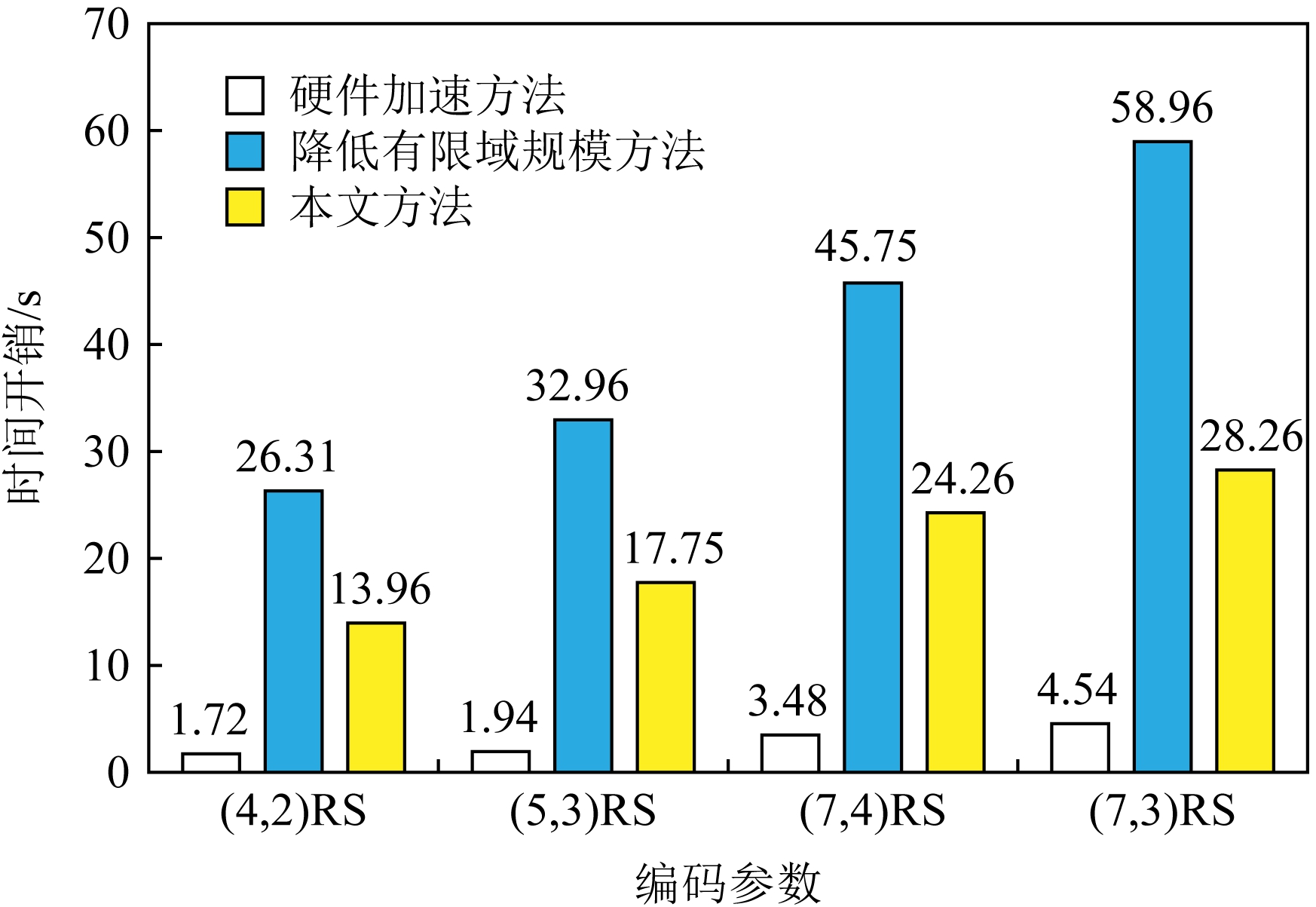
Fig. 10 Comparison of the time cost of three different methods to reconstruct a single failed node
图10 3种不同方法重构单个失效节点的时间开销对比
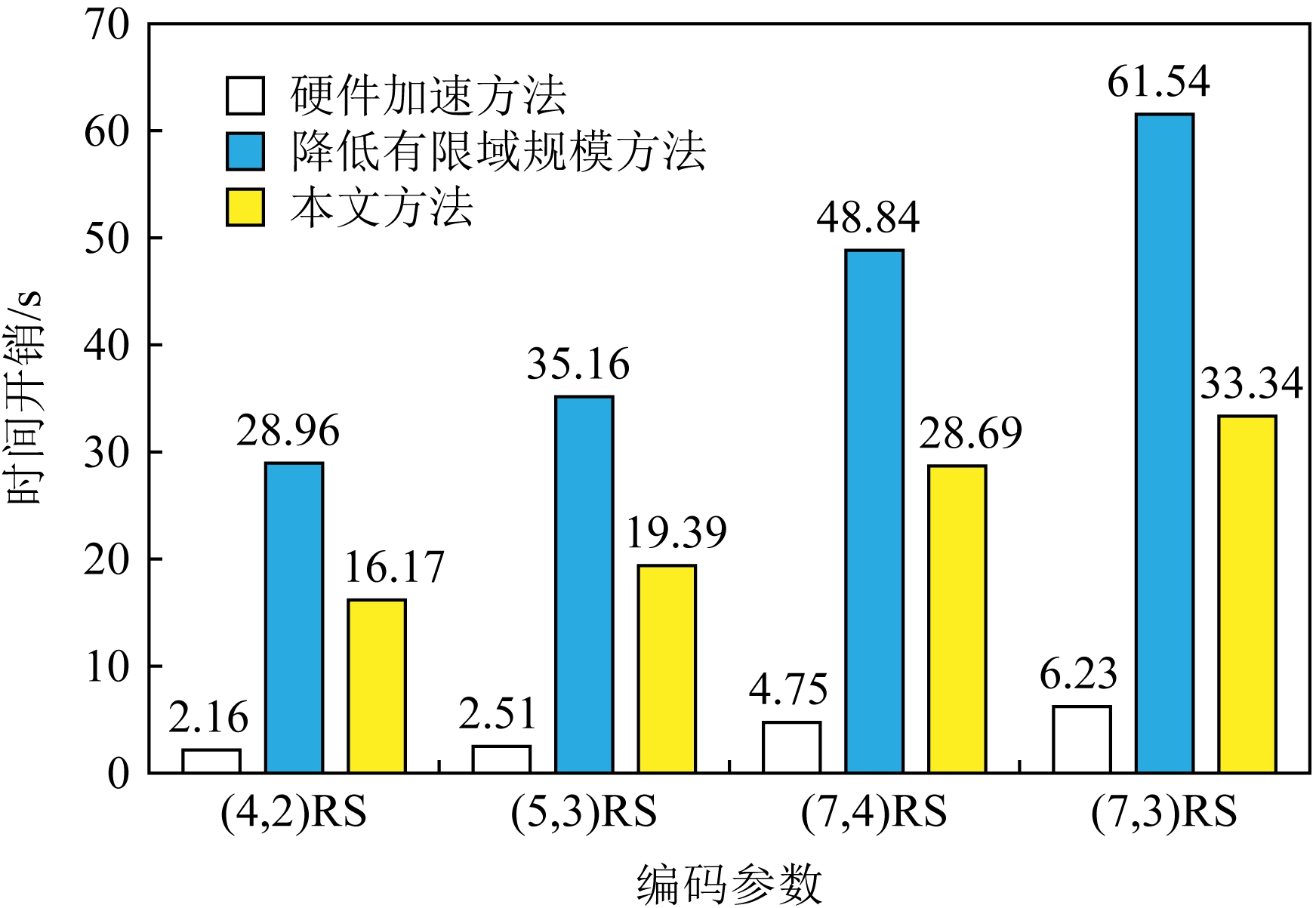
Fig. 11 Comparison of the time cost of three different methods to reconstruct two failed nodes
图11 3种不同方法重构2个失效节点的时间开销对比
可以看出,该方法与文献[20]中基于降低有限域规模的方法相比其译码效率显著提高,而稍差于硬件加速方法Jerasure[18].
实验5. 在实验平台上以柯西RS纠删码作为存储容错方法,编码参数为(8,4),计算有限域为GF(28).经过编码后将数据分存在不同节点,节点失效数目从1开始逐渐增大到4,即最大容错能力.分别采用硬件加速方法[18]、降低有限域规模的方法[20]与本文方法进行数据重构,其数据重构时间开销如图12所示.
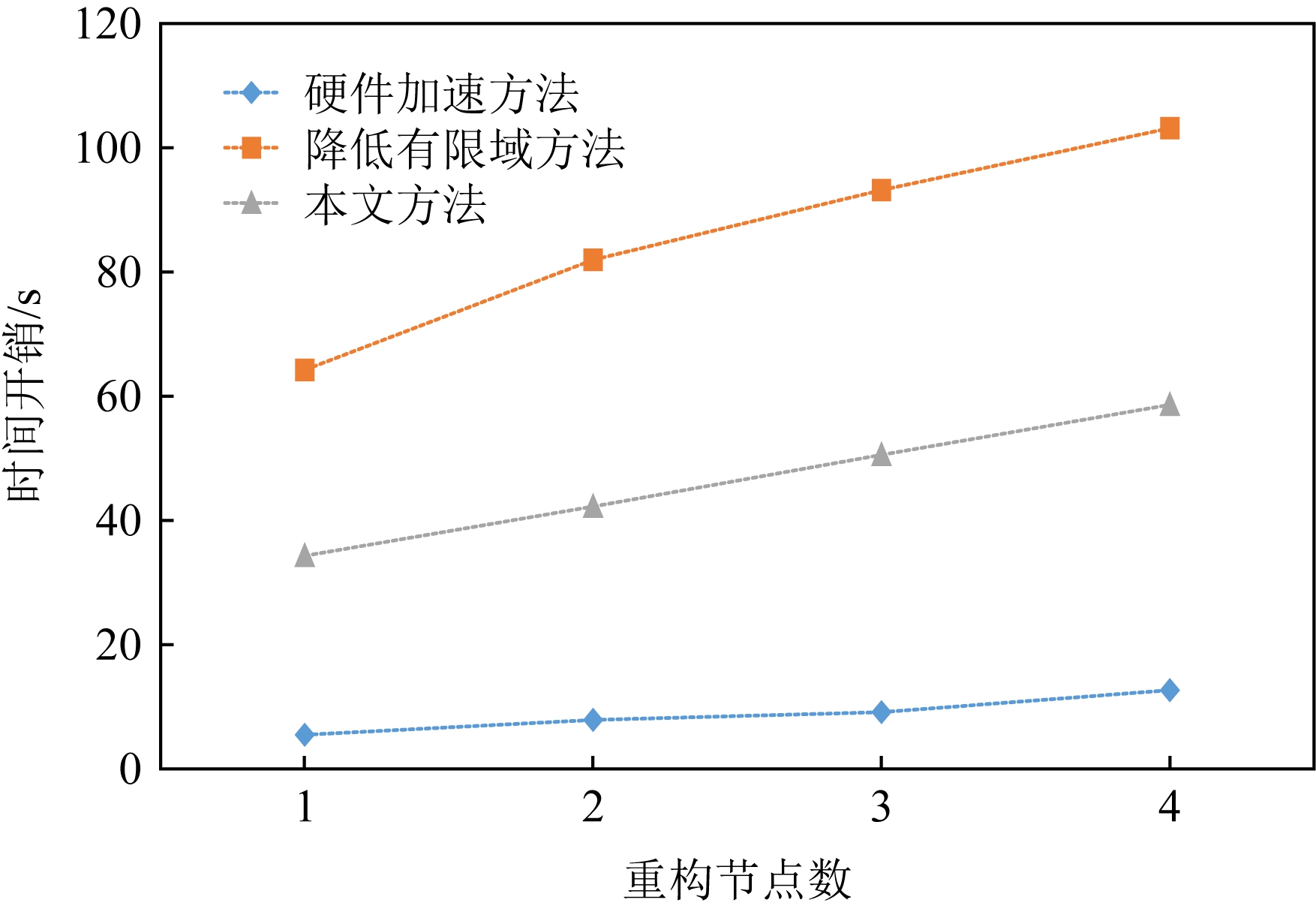
Fig. 12 Comparison of the time cost of three different
methods to reconstruct different number of failed nodes
图12 3种不同方法重构不同数量失效节点的时间开销 对比
从图12中可以看出,本文所述方法的译码时间较降低有限域规模方法大幅降低,较硬件加速方法偏高,并随着失效节点数目的增加译码时间增长速度较缓.
从实验4和实验5的结果来看,本文所提的方法的译码表现比同属于软件类的非理论改进的降低有限域规模的方法[20]的表现要好,比基于硬件加速方法的Jerasure[18]表现要差一些.因本文的研究内容及改进方法都是属于软件方法领域,故从软件方法的角度来讲,本文所提的方法比其他软件理论改进方法要优,而本文所提的理论方法改进与硬件方法的改进并不是对立的,可以将理论方法改进与硬件加速结合来进一步提升编译码效率,这可以作为以后的一个研究方向.
3.2 适用于XOR类纠删码译码
一般而言,XOR类纠删码的构造均有一定几何形式的规律,在编译码操作中通常会基于码链关系进行,这种做法直观形象且更加容易理解,因此最频繁使用的是二进制的异或运算.和RS类纠删码一样,XOR类纠删码也是线性码的1个子类,它继承了线性码的所有性质,而对所有线性码的译码方法也能适用.比如,在本文第1节中构造的RDP码,它的生成矩阵即为1个24×16的矩阵G,而原始数据元素也可以表示为1个16×1的列向量D,RDP码的码字仍然可以计算得出:C=G×D,其中矩阵G、数据向量D和码字向量C中的元素均为0或者1.所有操作涉及的乘法即为二进制与,而加法则为二进制异或,换句话说XOR类纠删码的运算在有限域GF(2)上进行.而在GF(2)中,1+1=0,显然其特征为2,所以,本文中讲到的基于生成矩阵译码的方法、基于校验矩阵译码的方法和本文提出的新方法均能适用于XOR类纠删码.
实验6. 在实验平台上,使用素数5构建1个RDP码作为容错方法,其存储阵列尺寸为4×6,计算有限域为GF(2).将原始数据编码后按序存储到各个存储节点中,分别使其中的第0个存储节点失效,以及第0个和第2个存储节点同时失效,并用新的节点替换后,数据重构的时间开销如图13所示.
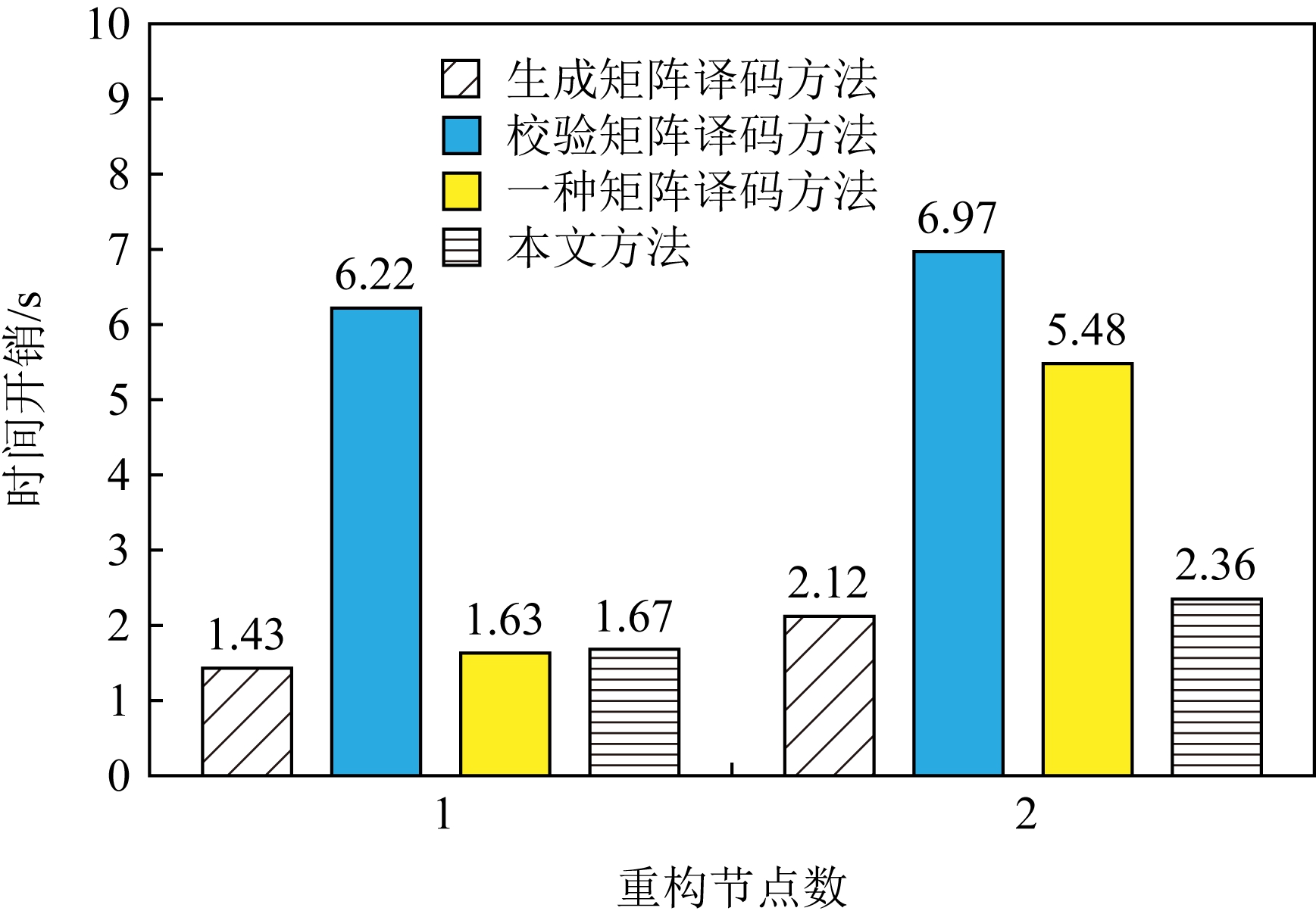
Fig. 13 Time cost of reconstructing in the RDP codes storage system
图13 基于RDP码存储系统中的数据重构时间开销
不难看出,对于基于二进制运算的纠删码译码,采用基于码链关系的译码方法的计算时间开销最小,本文的新方法在计算时间开销上相比略高.
但是,如第1节所述,成功使用基于码链的译码方法进行数据重构的关键为能找到仅有1个失效元素的码链,而如果不存在这样的码链,则显然无法使用该方法.容易验证,使用素数5构造的EVENODD码,假设其第0列和第2列发生错误失效(并没有超过EVENODD码的容错能力),则无法使用基于码链的译码方法恢复失效数据.而使用本文提出的译码方法则能顺利恢复所有失效数据.
3.3 数据重构的参与节点规划
将纠删码作为容错方法的存储系统中,失效节点的数据重构过程,是从有效节点中传入与失效数据有相关性的数据并通过计算达到恢复丢失数据的目的.通常而言,恢复丢失数据可以有不止1种重构方案,换句话说,码元的线性表达式一般不止1个.如果在实际存储系统的运行过程中,存在某些负载过重的节点,则从系统整体运行效率的角度而言是不希望这些节点再参与到重构过程中的.本节将通过1个典型示例说明如何使用本文的译码方法规划参与数据重构的有效节点.
继续沿用2.2节中的示例,在实验平台上构建(7,4)柯西RS纠删码作为容错方法,将原始数据编码后生成的各个码元按序存储到各对应存储节点中,计算有限域为GF(28).该柯西RS纠删码的生成矩阵如式(7)所示,若数据元素向量为D=(1,2,3,4)T,则计算得到的码元向量为C=(1,2,3,4,0,241,160)T.仍然假设码元C0和C2失效,即存储系统中第0个和第2个节点失效.将2.4节计算出的译码矩阵记作R:
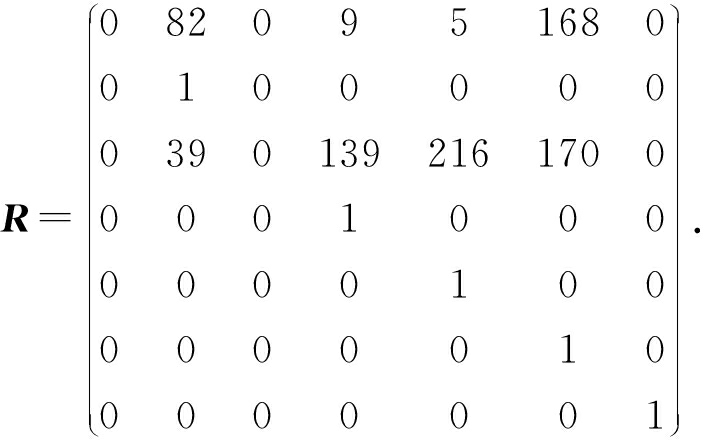
(12)
因此根据译码矩阵R的第0行和第2行可知,这2个失效节点上的数据全部可由式(11)计算得出.恢复失效码元用到的有效码元为c1,c3,c4,c5,即存储系统中对应的第1,3,4,5个节点上的数据参与了数据重构的过程.
若在存储系统的运行过程中,某个有效节点的负载较重,不希望其参与数据重构的过程,则可以检查此时的译码变换矩阵的子矩阵S_down,在矩阵S_down中,若该节点对应的列上存在非0元素则可以规划该节点不参加重构运算,若该节点对应的列上元素全部为0,则该节点必需参加到失效节点的重构中.
具体操作时,首先检查某有效节点对应矩阵S_down中的列是否为全0,若不是则可以在译码方法执行时将该列对应的码元看作失效.比如2.2节的示例中,假设我们不希望节点1参与重构运算,则首先检查矩阵S_down的第1列,发现该列为(0,0,207)T,不是全0列,因此节点1可以不参与重构运算.在译码时将节点1也作为失效节点对待,即设置F={c0,c1,c2},然后再执行译码方法进行数据重构.这样最终得到的译码矩阵R:

(13)
根据译码矩阵R,2个失效节点上的数据可计算得出:
(14)
显然节点1此时不再参与失效数据的重构.
当然,计算完成后,译码变换矩阵的子矩阵S_down也变为了零矩阵,换句话说,3个删除错误已经达到了该编码的最大容错能力,任意的第4个节点如果失效将导致所有数据丢失不可恢复.将本来有效的节点作为失效节点,我们是使用这一策略来规避该有效节点参与重构运算.所以,使用本文方法来进行重构运算的节点规划时有如下结论成立:
对于r容错能力的纠删码,当有f个节点失效时,我们最多能避免r-f个有效节点参与重构运算,其中r,f为正整数,且f≤r.
4 总 结
本文提出了一类新的RS类纠删码的译码方法,该方法完全避免了在有限域上计算复杂度很高的矩阵求逆运算,仅通过简单的矩阵初等变换,使用加法和乘法即可对失效数据进行重构.经实验表明,该方法与目前RS类纠删码译码主要使用的基于生成矩阵和校验矩阵的方法相比,整体译码的计算时间开销有较大幅度的降低.虽然是为了降低RS类纠删码译码计算代价提出,但该方法同样适用于XOR类纠删码等其他类型的纠删码.此外,新的方法经过少量改动,即可对参与重构运算的有效节点做出动态规划,有利于平衡存储系统的整体性能.
作者贡献声明:唐聃提出了算法思路和实验方案;蔡红亮提出指导意见并修改论文;耿微负责完成实验并撰写论文.
[1]Rashmi K V, Shah N B, GuDikang, et al. A solution to the network challenges of data recovery in erasure-coded distributed storage systems: A study on the Facebook warehouse cluster[C/OL] //Proc of the 5th USENIX Workshop on Hot Topics in Storage and File Systems. Berkeley, CA: USENIX Association, 2013 [2020-03-07]. https://www.usenix.org/conference/hotstorage13/workshop-program/presentation/rashmi
[2]Tang Dan, Shu Hongping. A class of array erasure codes with high fault tolerance[J]. Scientia Sinica Informationis, 2016, 46(4): 523-538 (in Chinese)(唐聃, 舒红平. 一类多容错的阵列纠删码[J]. 中国科学: 信息科学, 2016, 46(4): 523-538)
[3]Wang Yijie, Xu Fangliang, Pei Xiaoqiang. Research on erasure code-based fault-tolerant technology for distributed storage[J]. Chinese Journal of Computers, 2017, 40(1): 236-255 (in Chinese)(王意洁, 许方亮, 裴晓强. 分布式存储中的纠删码容错技术研究[J]. 计算机学报, 2017, 40(1): 236-255)
[4]Fu Yingxun, Shu Jiwu. D-Code: An efficient RAID-6 code to optimize I/O loads and read performance[C] //Proc of the 29th IEEE Int Parallel and Distributed Processing Symp. Piscataway, NJ: IEEE, 2015: 603-612
[5]Plank J S, Blaum M. Sector-disk (SD) erasure codes for mixed failure modes in RAID systems[J]. ACM Transactions on Storage, 2014, 10(1): 1-17
[6]Corbett P, English B, Goel A, et al. Row-diagonal parity for double disk failure correction[C/OL] //Proc of the 3rd USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2004 [2019-10-18]. https://www.usenix.org/legacy/events/fast04/tech/corbett.html
[7]Cheng Huang, Xu Lihao. STAR: An efficient coding scheme for correcting triple storage node failures[J]. IEEE Transactions on Computers, 2008, 57(7): 889-901
[8]Hafner J L. Weavercodes: Highly fault tolerant erasure codes for storage systems[C] //Proc of the 4th USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2005: 211-224
[9]Gallager R. Low-density parity-check codes[J]. IRE Transactions on Information Theory, 1962, 8(1): 21-28
[10]Elkelesh A, Ebada M, Cammerer S, et al. Decoder-in-the-loop: Genetic optimization-based LDPC code design[J]. IEEE Access, 2019, 7: 141161-141170
[11]Karimi B, Banihashemi A H. Construction of QC LDPC codes with low error floor by efficient systematic search andelimination of trapping sets[J]. IEEE Transactions on Communications, 2019, 68(2): 697-712
[12]Vajha M, Ramkumar V, Puranik B, et al. Clay codes:Moulding MDS codes to yield an MSR code[C] //Proc of the 16th USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2018: 139- 154
[13]Li Weiqi, Wang Zhiying, Jafarkhani H. Repairing Reed-Solomon codes over GF(2l)[J]. IEEE Communications Letters, 2020, 24(1): 34-37
[14]Dau S H, Duursma I M, Kiah H M, et al. Repairing Reed-Solomon codes with multiple erasures[J]. IEEE Transactions on Information Theory, 2018, 64(10): 6567-6582
[15]Hellerstein L, Gibson G A, Karp R M, et al. Coding techniques for handling failures in large disk arrays[J]. Algorithmica, 1994,12(2/3):182-208
[16]Zhang Yongzhe, Wu Chentao, Li Jie, et al. PCM: A parity-check matrix based approach to improve decoding performance of xor-based erasure codes[C] //Proc of the 34th IEEE Symp on Reliable Distributed Systems. Piscataway, NJ: IEEE, 2015: 182-191
[17]Plank J S, Miller E L, Houston W B. GF-complete: A comprehensive open source library for galois field arithmetic version 1.0[J/OL]. Electrical Engineering and Computer Sciences, 2013 [2020-03-21]. https://xueshu.baidu.com/usercenter/paper/show?paperid=9c12bc31188f86982e7939de 1e09c65a&site=xueshu_se&hitarticle=1
[18]Plank J S, Greenan K M. Jerasure: A library in C facilitating erasure coding for storage applications version 2.0[R/OL]. Knoxville: University of Tennessee, 2014 [2019-09-20]. http://web.eecs.utk.edu/~jplank/plank/papers/Jerasure-2-0-Archive.pdf
[19]Plank J S, Greenan K M, Miller E L. Screaming fast galois field arithmetic using Intel SIMD instructions[C] //Proc of the 11th USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2013: 299-306
[20]Blomer J, Kalfane M, Karp R,et al. An XOR-based erasure-resilient coding scheme[R/OL]. Berkeley, CA: International Computer Science Institute (ICSI), 1995 [2020-00-00]. https://www.cs.utexas.edu/users/diz/pubs/erasure.pdf
[21]Plank J S, Xu Lihao. Optimizing cauchy Reed-Solomon codes for fault-tolerant network storage applications[C] //Proc of the 5th IEEE Int Symp on Network Computing and Applications. Piscataway, NJ: IEEE, 2006:173-180
[22]Tang Dan. Research of methods for lost data reconstruction in erasure codes over binary fields[J]. Journal of Electronic Science and Technology, 2010, 14(1): 43-48
[23]Huffman W C, Brualdi R A, Pless V S. Handbook of Coding Theory[M]. Amsterdam: Elsevier, 1998
[24]Plank J S. A tutorial on Reed-Solomon coding for fault-tolerance in RAID-like systems[J]. Software Practice and Experience, 1997, 27(9): 995-1012
[25]Hafner J L, Deenadhayalan V, Rao K K, et al. Matrix methods for lost data reconstruction in erasure codes[C] //Proc of the 4th USENIX Conf on File and Storage Technologies. Berkeley, CA: USENIX Association, 2005: 183-196
[26]Lidl R, Niederreiter H. Introduction to Finite Fields and Their Applications[M]. Cambridge, UK: Cambridge University Press, 1994


