随着互联网的普及和移动技术的发展,当前软件技术的发展呈现出了明显的网络化趋势,越来越多的软件应用选择将业务或服务拆分后布置在不同的硬件设施上,通过互联网通信协同完成工作,以实现更多样化的功能.这类以网络为媒介,以信息或服务资源为元素,以元素间的协同与互操作为构造手段,所建立的软件密集型混合系统被称为网络化软件[1].《中国互联网发展报告(2021)》显示,2020年我国工业互联网市场规模已超9 000亿元,物联网市场规模达1.7万亿元,网络化软件的研究和发展有着广阔的前景.
近年来,互联网应用规模扩展迅速,网络化软件在互联网中的部署越来越复杂,节点故障、通信拥塞、激增的用户请求等突发因素为软件的平稳运行带来了巨大挑战,导致软件性能和服务质量的下降,造成重大的损失.例如,2019年6月,谷歌的云服务器出现约4 h的宕机故障,大量基于该服务的网站或应用服务加载缓慢、无法登录,其中,大型视频网站YouTube的全球观看人数减少了10%;2021年3月,苹果App Store,iCloud等服务出现大规模故障,大量用户访问相关服务缓慢或失败.因此,网络化软件需要实现优化调整功能,主动调节各类参数,以保障软件的正常运行,防止性能下降,提高系统的稳定性.
网络化软件部署在异构的联网设备上,根据功能或服务范围由数量不等的计算设备组成软件节点,完成发送、汇集与处理数据的任务.软件节点的大量部署使网络化软件产生了高度分布的特征.在此背景下,网络化软件的发展呈现出去中心化的趋势,系统架构越发开放和平等,系统中每个节点高度自治,不具备强制性的中心控制[2].然而,由于网络化软件高度分布的特点,软件节点之间存在的通信延迟阻碍了节点间的信息共享,导致各个节点在进行自主优化调整时出现个体与集体信念的不一致,为网络化软件系统的优化调整带来了困难.
针对网络化软件性能优化中存在的节点间信息交流问题,本文研究了一种基于多智能体博弈的分布式优化框架,将智能体设置在不同的软件节点上,各个智能体使用有限的信息估计系统状态并做出决策对软件的参数进行管理,实现软件性能的优化.此外,本文针对现有方法易发散、参数选取困难的问题提出了自适应步长机制和强制协调机制,根据各个智能体的估计误差调整当前决策寻优步长,防止由于智能体之间估计偏差过大带来的发散问题,同时保证了方法的收敛速度.
1 相关工作
目前软件在线优化的研究主要集中于如何通过合理的资源分配和任务调度提高软件的服务质量或降低资源消耗和运营成本.阿里巴巴的云服务器集群采用了集中式任务管理机制,在阿里巴巴的混部集群中,由Sigma和Fuxi两种管理中心汇总各个服务器的运行信息并对进程合理调度以提升资源的利用率[3];Sahni等人[4]提出了一种启发式的云计算资源弹性伸缩方法,该方法通过资源提供历史和在线的工作负载分析估计后续任务的资源需求,之后使用贪心算法给出一组最优的资源配置,以更低的资源消耗和更高的资源利用率满足软件的服务质量需求;Chen等人[5]基于反馈控制实现了一种组合服务的自优化机制,设置函数数值化计算当前的服务质量,根据计算结果使用比例积分微分控制器对影响服务质量的因素进行重要性排序,产生优化调整的策略;Das等人[6]针对流处理系统的容错和效率问题,提出了一种基于不动点迭代的控制算法,自适应地调整批处理作业的大小,使工作负载能够适应系统当前的情况.现有研究以软件控制的自动化和智能化为目的,但大多着眼于使用集中控制方法对软件系统进行调控,然而,这种方法无法完全适用于愈发庞大、愈发复杂的网络化软件系统.首先,在集中控制的情况下,中心控制节点的故障将会导致调控机制停摆,缺乏可靠性;其次,集中为所有软件节点提供控制策略需要收集大量的节点信息并产生巨大的计算开销,效率低下;最后,在部署或移除软件节点时,需要为中心节点更新控制逻辑,难以应用于动态变化的大型系统.
本文采用多智能体博弈的方法对网络化软件进行优化,将智能体设置在不同的软件节点上,实现分布式的优化决策与控制,相关研究聚焦于智能体的收益函数的设计和博弈决策方法上.收益函数的设计很大程度影响了博弈优化的收敛效果,为了保证系统能在多轮博弈后达到纳什均衡,常见的做法是根据实际情况将收益函数设计成符合势博弈(potential games)[7]和凸博弈(convex games)[8]等具有良好收敛性质的形式.Li等人[9]通过改造系统的全局目标函数作为各个智能体的收益函数,设计了一种使用非完全信息的势博弈分布式优化模型;Wu等人[10]为多智能体任务分配问题设计了一种势博弈模型,该模型将各智能体的收益函数设置为任务收益的指数形式,保证重要的任务被优先完成,此外,将实际需求与参与智能体数目之差作为指数,防止过多的智能体被分配于同一任务造成浪费.博弈决策的目的是如何让智能体做出决策优化自身收益函数的值,常见的决策方法有沿收益函数的梯度调整的梯度博弈(gradient-play)[11]、根据历史博弈记录计算最佳决策的虚拟博弈(fictitious play)[12]、根据概率分布选择策略的对数线性学习(log-linear learning)[13]等.Ye等人[14]对梯度博弈进行了扩展,在收益函数中使用对所有智能体值的估计值计算梯度,使其能让系统中的各个智能体在不了解全局信息的情况下收敛至纳什均衡;Heinrich等人[15]使用强化学习过程寻找最优近似代替虚拟博弈中的最优策略选取,改善了此类方法在大规模的博弈场景中的表现.
在分布式多智能体博弈中,智能体之间的信念冲突是导致博弈无法达到纳什均衡的主要原因之一,本文采用多智能体一致性协议(consensus protocols)缓解系统中各个智能体之间的信念差异,该技术来源于自动化和控制理论领域,是一种通过智能体间信息交换实现信念趋同和协同合作的技术.Saber等人在文献[16]中提出了多智能体一致性协议的基础形式和收敛分析,并在文献[17]中进一步分析了收敛速度与智能体网络的连通度和网络类型之间的关系;Xie等人[18]在基础的一致性协议上增加了基于智能体当前状态的反馈控制机制,该协议能在变化的网络连接状态下收敛;Zuo等人[19]根据不等式关系进一步改造了一致性协议,使其能在有外部干扰的情况下以任意初始状态在有限时间内收敛.
2 优化模型
2.1 系统模型
为了便于读者理解本文的优化决策机制,首先给出本文的系统模型.本文系统模型的构建基于广泛应用于自主计算领域的感知—分析—决策—执行(monitor-analyze-plan-execute, MAPE)控制方法[20],如图1所示,MAPE循环包括4个主要阶段:
1) 感知(monitor)阶段.该阶段收集系统信息,对系统参数和结构的变化情况进行监控,并将变化数值化传递给分析阶段.
2) 分析(analyze)阶段.该阶段根据感知阶段收集的信息确定系统的当前状态和变化趋势.
3) 决策(plan)阶段.该阶段针对当前系统的状态和问题产生调整策略,以保证系统的稳定运行或优化系统的性能.
4) 执行(execute)阶段.该阶段根据决策阶段产生的策略调整系统行为,在执行阶段结束后,将再次进入感知阶段开启下轮MAPE控制循环.
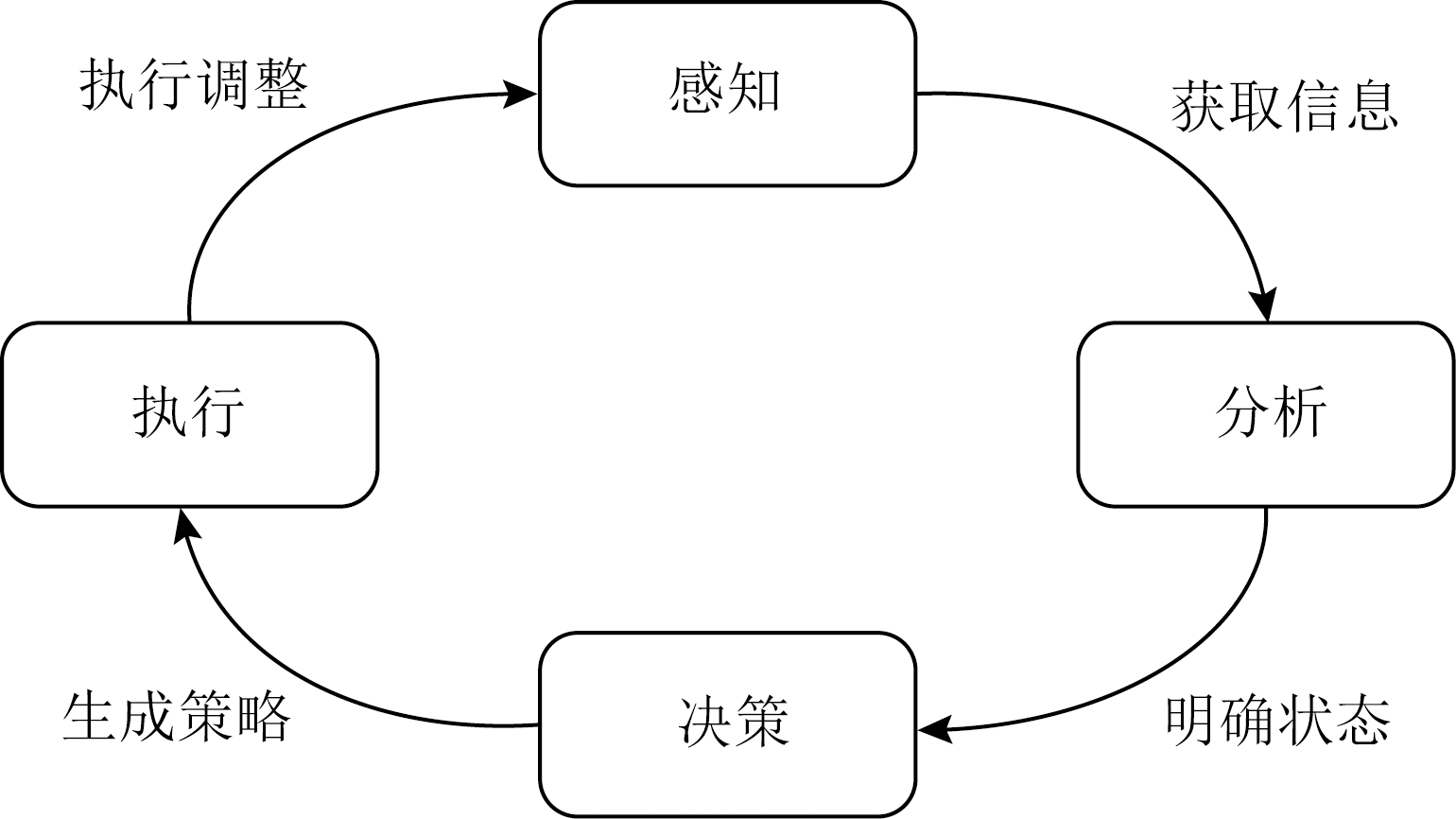
Fig. 1 MAPE loop
图1 MAPE循环
本文的系统模型如图2所示,在网络化软件系统中设置分析预测节点负责感知阶段和分析阶段的工作,收集节点信息,分析预测节点根据与软件节点间的网络延迟确定管理范围,对分析范围内的软件系统状态建模并分析预测系统性能的变化情况,生成节点数据与该区域系统总体效益之间的函数[21].分析完成后,各个分析预测节点将结果分发给网络中的软件节点,部署在各个软件节点上的智能体以此为依据对节点的参数进行调整,实现系统性能的整体优化.
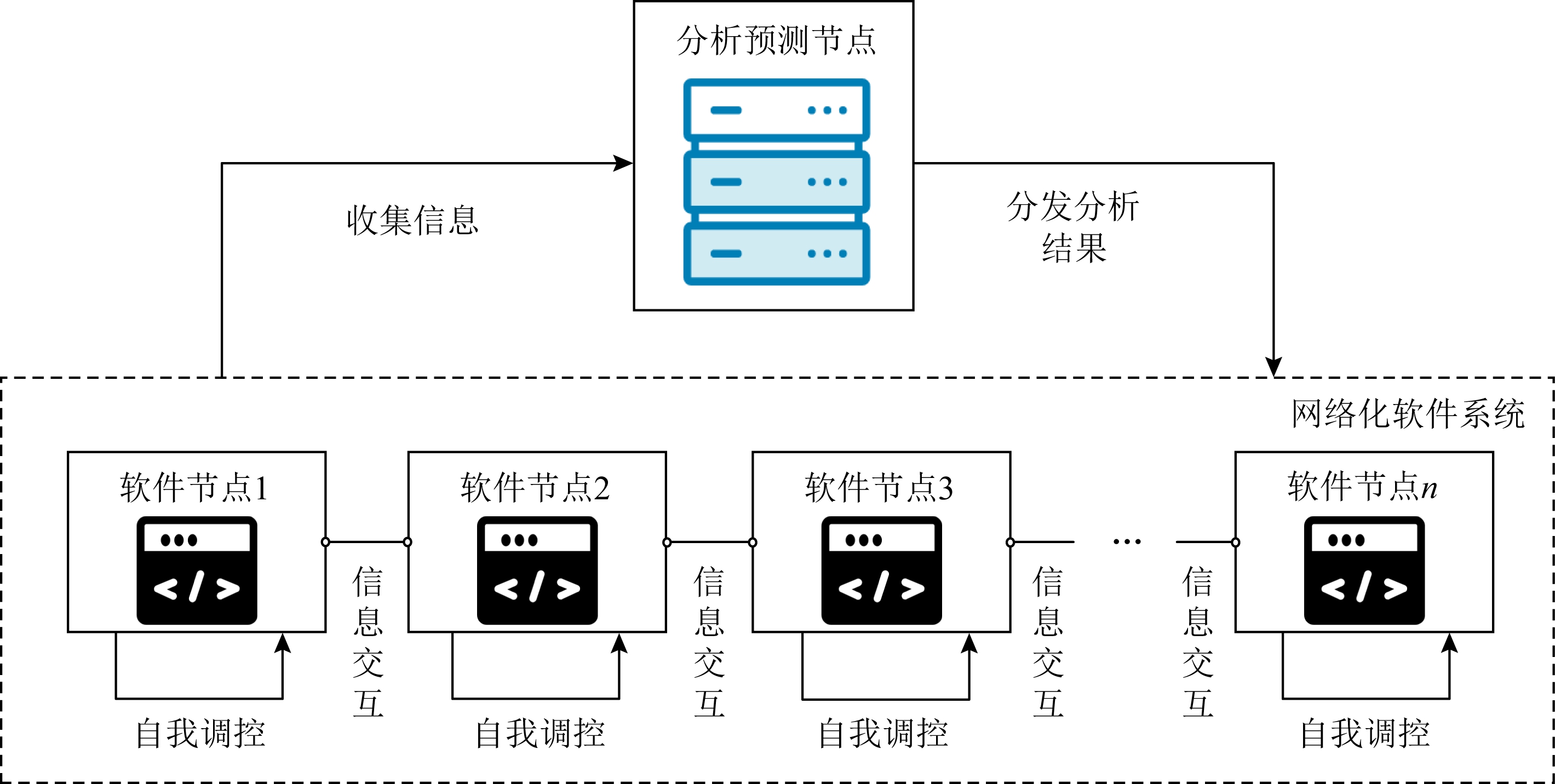
Fig. 2 System model of networked software
图2 网络化软件系统模型
在这个过程中,由于网络化软件系统的性能受各个软件节点状态的影响,分析预测节点得到的函数变量中包含多个软件节点的参数,部署在软件节点上的智能体需要拥有其他节点的信息才能做出优化决策.然而,分布在各处的软件节点虽然能够通过网络相互通信间接获取全局的节点信息,但长距离通信的延迟和不稳定会导致信息传递缓慢,进而影响优化决策的效率,该问题会随软件部署的规模扩大而加深.因此本文让每个节点通过不完全的节点信息,相互博弈做出决策,具体做法是根据每次优化的最大时间限制和迭代次数上限计算出通信时延的阈值,各个节点选择与自己通信稳定且通信时延较符合阈值的节点建立连接,智能体使用不完全的节点信息做出决策来优化软件性能.
2.2 博弈模型
本文的主要研究内容是通过分布在软件节点上智能体间的博弈实现网络化软件优化机制,一个博弈场景G描述为G={N,v,V,F,J},下面分别介绍.
1) N={A1,A2,…,An}为网络中的智能体集合,其中n为集合的大小,即网络化软件的节点数量.
2) v=(v1,v2,…,vn),其中vi为各个智能体维护的取值(value),取值可以代表节点的最大硬件负载、最大任务排队量等参数,智能体通过调整自身的取值实现各类优化决策.
3) V=V1×V2×…×Vn,其中Vi为各个智能体的取值空间(value space),取值空间是对智能体取值的限制,对于每个智能体的值有vi∈Vi,即智能体只能在取值空间规定的范围内调整自身的取值.
4) F:V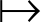
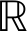 为全局效益函数,是一个关于智能体取值的函数,由所有分析预测节点根据系统的情况给出,用于衡量系统的整体性能.本文中的效益函数F的结果为系统功耗、响应时间等与软件系统性能负相关的指标,系统的优化目标等价于优化问题:
为全局效益函数,是一个关于智能体取值的函数,由所有分析预测节点根据系统的情况给出,用于衡量系统的整体性能.本文中的效益函数F的结果为系统功耗、响应时间等与软件系统性能负相关的指标,系统的优化目标等价于优化问题:
(1)
5) J={J1,J2,…,Jn}为各个智能体的收益函数集合,其中Ji:V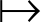
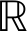 ,收益函数由分析预测节点赋予智能体,是智能体进行决策的标准,各个智能体在多轮博弈中通过调整自身取值获取更高的收益函数值,并最终让整个系统达到纳什均衡(Nash equilibrium),从而产生调整策略,纳什均衡的定义如下.
,收益函数由分析预测节点赋予智能体,是智能体进行决策的标准,各个智能体在多轮博弈中通过调整自身取值获取更高的收益函数值,并最终让整个系统达到纳什均衡(Nash equilibrium),从而产生调整策略,纳什均衡的定义如下.
定义1. 纳什均衡[22].如果在博弈G={N,v,V,F,J}中,对于网络中各个节点上的智能体Ai (i=1,2,…,n)的收益函数Ji和∀vi∈Vi,存在取值![]() 满足:
满足:
则称v*为博弈G的一个纳什均衡,其中![]() 代表v*中除
代表v*中除![]() 外的序列,即
外的序列,即![]()
在纳什均衡下,网络中所有的智能体都无法仅通过改变自身的取值使得自身的收益函数结果变得更好,当博弈到达纳什均衡时,各个智能体的取值将趋于稳定.通过合理地构造智能体的收益函数,可以让博弈的纳什均衡充分接近如式(1)所示的优化问题的解.本文使用一种简单的博弈构造方法,对于网络中的所有智能体Ai,令
这种方式构造出的是一类具有良好特性的博弈:势博弈(potential games).
定义2. 势博弈[7].对于一个博弈G={N,v,V,F,J}中任意智能体Ai的取值![]() 和收益函数Ji,如果存在一个函数Φ:V
和收益函数Ji,如果存在一个函数Φ:V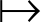
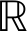 ,令
,令
则称博弈G为势博弈,Φ为G的势函数.
显然,使用上文方法构造出的全局效益函数F是对应博弈的势函数.在势博弈中,单个智能体的取值改变对其自身的收益函数的影响和对全局效益函数的影响相同,有限势博弈一定存在纳什均衡,这为本文的优化决策设计提供了收敛保证.由于各个智能体不能完全掌握网络中所有智能体的取值情况,所以无法直接计算收益函数.为了解决这个问题,引入智能体的取值估计(estimation)[9]:e=(e1,e2,…,en)替代真实的取值计算收益函数,其中ei= (ei1,ei2,…,ein),eij表示智能体Ai对智能体Aj取值的估计,用于替代智能体Ai可能无法得知的智能体Aj的取值vj.在第3节中将介绍如何让取值估计在博弈迭代过程中接近各个智能体的真实取值,以使得这种决策方式是有效的.
3 网络化软件博弈优化机制
3.1 基于多智能体一致性的梯度博弈
本文考虑连续博弈(continuous games),即F和Ji均为连续函数的博弈决策问题,如带宽控制等采用连续取值空间的优化问题需要使用连续博弈解决,服务降级、CPU核心、成块的内存分配等离散目标则需要先转换为连续的优化问题.梯度博弈是一种常用的连续博弈决策方法[23],在每轮博弈中,各个智能体将取值估计代入收益函数,沿自身取值的梯度方向对取值进行调整:
(2)
其中:vi(t)表示智能体Ai在第t轮迭代时的取值;εi>0,为每轮更新取值的步长;符号[·]+表示第t轮时梯度在智能体Ai可选取值变化集合上的投影,防止取值超出该节点可以选择的范围.对于第2节中构造的博弈G={N,v,V,F,J},设F在V上具有凸性,则G能使用梯度博弈以合适的步长收敛至纳什均衡[9,23],大部分的软件优化问题满足该条件或可转化为满足该条件的等价问题[24-25],如果无法满足该条件则无法使用此类方法求解纳什均衡.与常规的梯度博弈不同,式(2)在更新取值时使用的不是真实的梯度,而是根据估计值ei计算出的虚拟梯度,显然,如果在博弈迭代中智能体无法正确估计全局的取值情况,梯度博弈将由于错误的梯度而无法收敛至纳什均衡.
为了让智能体正确估计其余智能体的取值,基于一致性协议对各个智能体的估计值进行修正,使其接近系统中各个节点的真实状态.在每轮博弈的取值调整前,每个智能体向与其建立连接的智能体集合Ni发送自己的取值和估计信息,并在调整结束后利用这些信息:
1) 通过一致性协议[16]减少各个智能体之间的估计误差,令
(3)
其中Ni为与Ai建立连接的智能体集合(包括Ai自身).
2) 让各自的估计值向可获取的真实取值信息靠近[14],令![]() 其中
其中
(4)
注意,虽然每个智能体能在博弈当中获取一定的真实取值信息,但不能通过持续将其代入收益函数的方式计算梯度,因为这样会破坏式(3)的信息交换,可能会引起算法失效.
3) 更新估计值
(5)
其中α1和α2为比例系数,0<α1<1,0<α2<1,α1和α2用于约束估计值的变化速度.与常规的一致性协议不同,以上方法中除了需要让智能体与相邻智能体的估计趋于一致外,还要让估计值接近一组不断变化的真实取值.
综合第2节中的系统模型和本节的博弈机制,基于Li等人[9]和Ye等人[14]的工作,我们总结了基于多智能体一致性和梯度博弈的分布式优化(distributed optimization based on consensus and gradient-play, DOCG)算法.
算法1. DOCG算法.
输入:迭代次数上限l、各个智能体的初始取值vi(0)、梯度博弈步长εi、比例系数α1和α2;
输出:更新完成后的各个智能体取值v′.
① for each Agent I in N
② ei(0)←v(0); /*通过网络通信初始化各
个智能体的估计值*/
③ end for
④ iter_count←0;
⑤ while iter_count<l 并且没有达到纳什均衡
⑥ for each Agent I in N
⑦ getinfo();
/*从相邻的智能体获取信息*/
⑧ gradient_play(ei(iter_count),εi);
/*使用估计值和梯度博弈更新取值*/
⑨ estimation_update();/*基于相邻智
能体的信息更新估计值*/
⑩ end for
 iter_count←iter_count+1;
iter_count←iter_count+1;
 end while
end while
 return v′.
return v′.
显然,智能体间到达纳什均衡的充要条件为所有智能体的估计值等于其可获得的真实取值,且在多轮迭代中不再变化.当智能体的估计值与相邻智能体取值相等且稳定时,根据梯度博弈的原理,任何智能体对取值做出的调整都会让自身的收益函数结果变差,根据定义1,此时博弈已达到纳什均衡;另一方面,假设存在智能体的估计值与相邻智能体的估计或真实取值序列存在偏差,那么在接下来的迭代中该智能体仍会根据式(5)修正自身的估计值,此时智能体间并不是纳什均衡状态.基于Ye等人[14]的分析,在效益函数满足一定条件时,使用算法1控制的系统达到的纳什均衡是Lyapunov稳定的,软件系统本质上也是一种控制系统[26],但算法1中的梯度博弈的步长和估计修正中的比例系数很大程度上影响了方法的收敛能力.在3.2节和3.3节中,将探究如何设置和控制这2类参数以提升算法的收敛能力.
3.2 自适应梯度步长机制
在算法1中,取值更新和估计修正过程是相互影响的,过大的估计误差会造成梯度方向的偏移,使取值越来越偏离应有的更新方向,同时取值的错误更新也会反作用于估计值的修正,进而造成恶性循环让取值点“迷失”在高维曲面上无法到达对应纳什均衡的取值点.对于更新步长ε=(εi)和比例系数α1,α2各存在一组范围上限,当ε和α1,α2均在范围限制之内时,算法1能保证收敛至纳什均衡,但这2类上限的严格计算都和全局效益函数F有关,且对于每个智能体,计算这2类上限的时间复杂度均在O(n2)以上[14].显然通过计算确定这2种参数是不明智的,而为了保证方法收敛保守地选择参数则会降低算法的效率.
对于算法1,假设比例系数符合收敛限制,暂时停止取值的更新(暂时令步长ε=0)并让各个智能体以式(5)的方法修正估计值,各个智能体的估计值将在迭代中逐渐统一并收敛于真实的取值.这时使用式(2)计算的梯度将趋于真实的梯度,之后当估计误差过大时再次停止更新取值并修正估计值,重复这个过程能让各个智能体将取值调整至纳什均衡的某个邻域当中,但这种做法会大幅降低算法的效率.基于以上讨论,我们提出一种随迭代过程变化的步长选取方法,令
(6)
其中
为智能体估计值与相邻智能体真实取值之间的误差;εmax i为该智能体沿虚拟梯度更新的最大步长,当智能体对相邻智能体的估计值没有误差时,可以以最大步长更新自身的取值;τi为衰减系数,0<τi<1,让取值的迭代步长随估计误差的增大而减小,实现在误差过大时减缓取值的更新速度.
可变步长可以防止上文中提到的“取值迷失”情况并为步长提供了更大的选择空间,但同时也带来了新的问题.在算法执行后期各个智能体之间的估计值和取值差异将逐步收敛,此时可变步长也将趋于最大步长,如图3所示,当最大步长过大时算法会在纳什均衡点附近发生震荡,这种现象会随着最大步长的增加而变得越发严重.根据3.1节中关于算法1的纳什均衡条件的讨论,当震荡现象发生时降低最大步长即可让算法收敛,具体做法为:为式(3)的估计误差设定范围判断其是否接近收敛状态,在几轮迭代后,若估计误差接近算法却没有达到纳什均衡,则逐步下调最大步长,该机制的具体执行方式见3.4节.
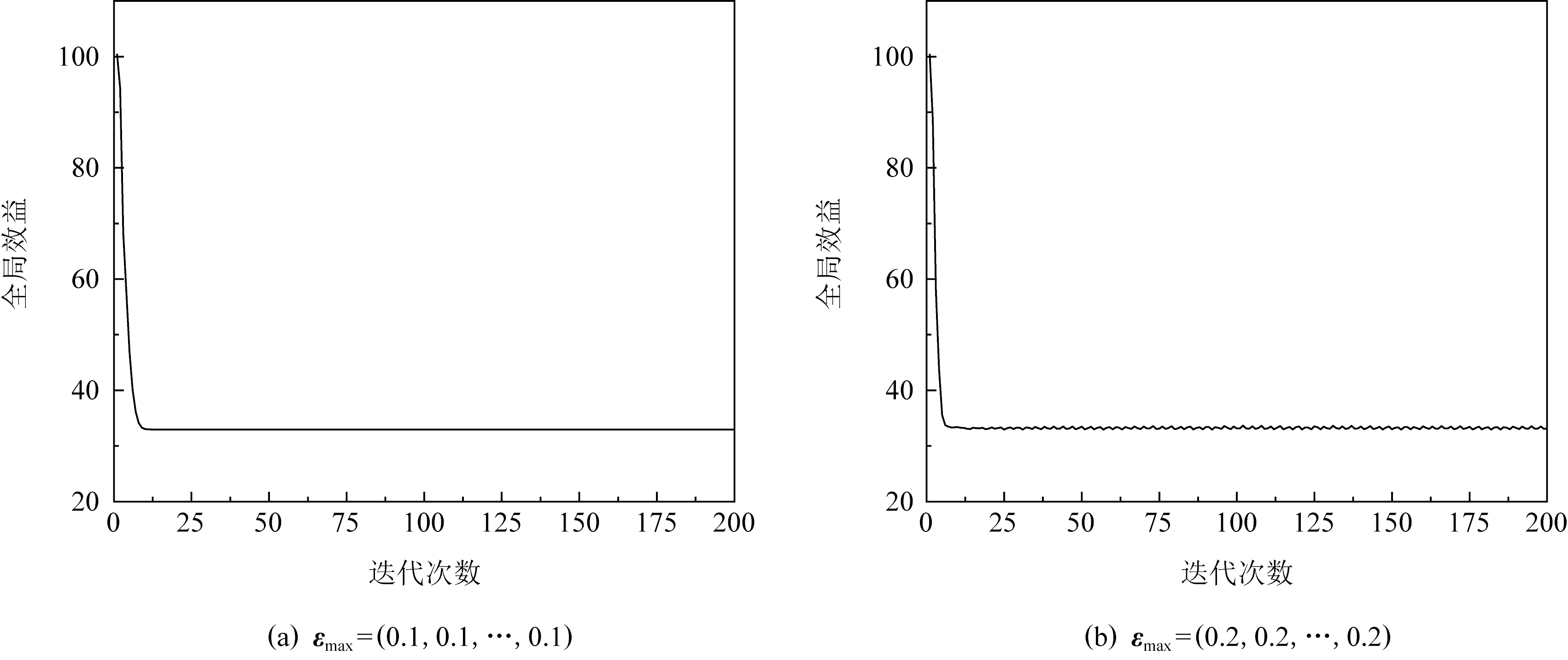
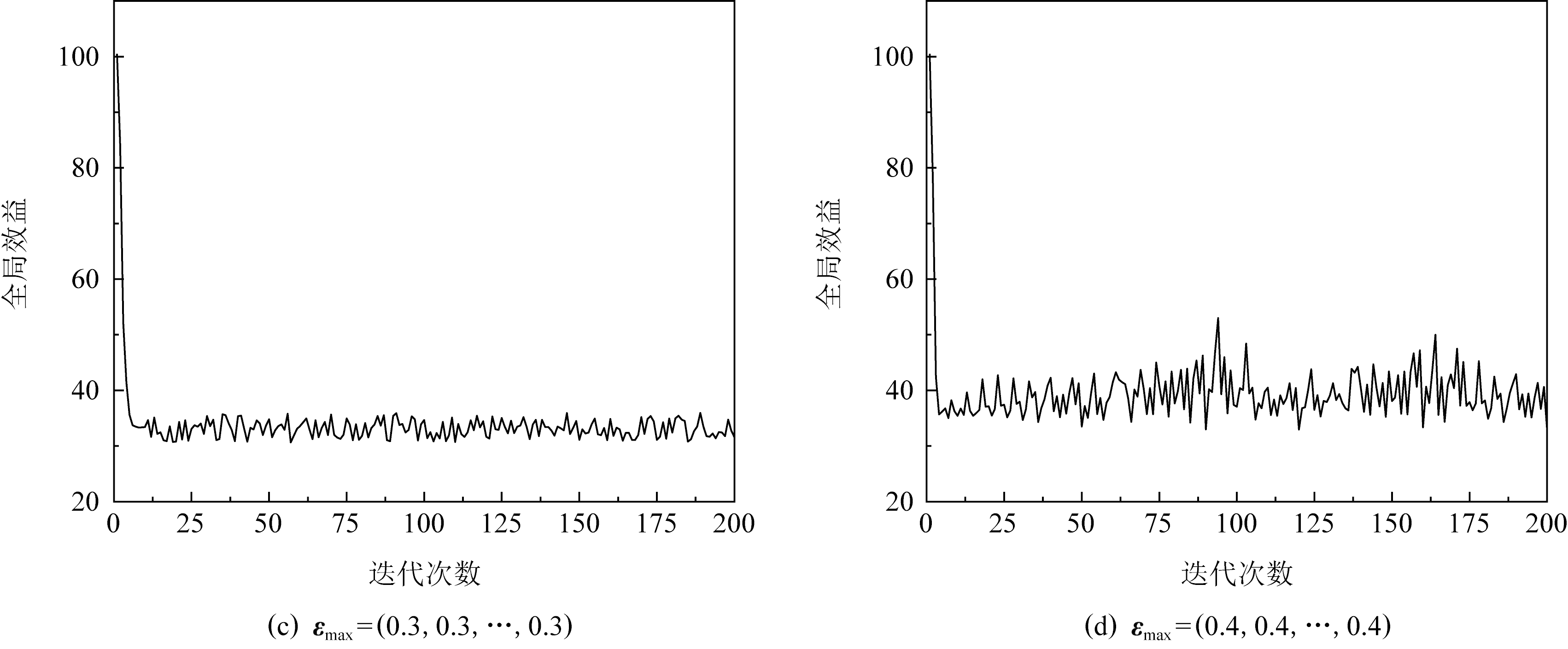
Fig. 3 Oscillation phenomenon
图3 震荡现象
3.3 强制协调机制
3.2节中,我们在比例系数符合收敛条件的情况下讨论了步长的设计与调整,然而,不当的比例系数将导致估计值与真实取值之间的误差越来越大,让式(6)的可变步长逐渐趋于0,最终智能体的取值不再更新,算法呈现出如图4所示的过早收敛现象.
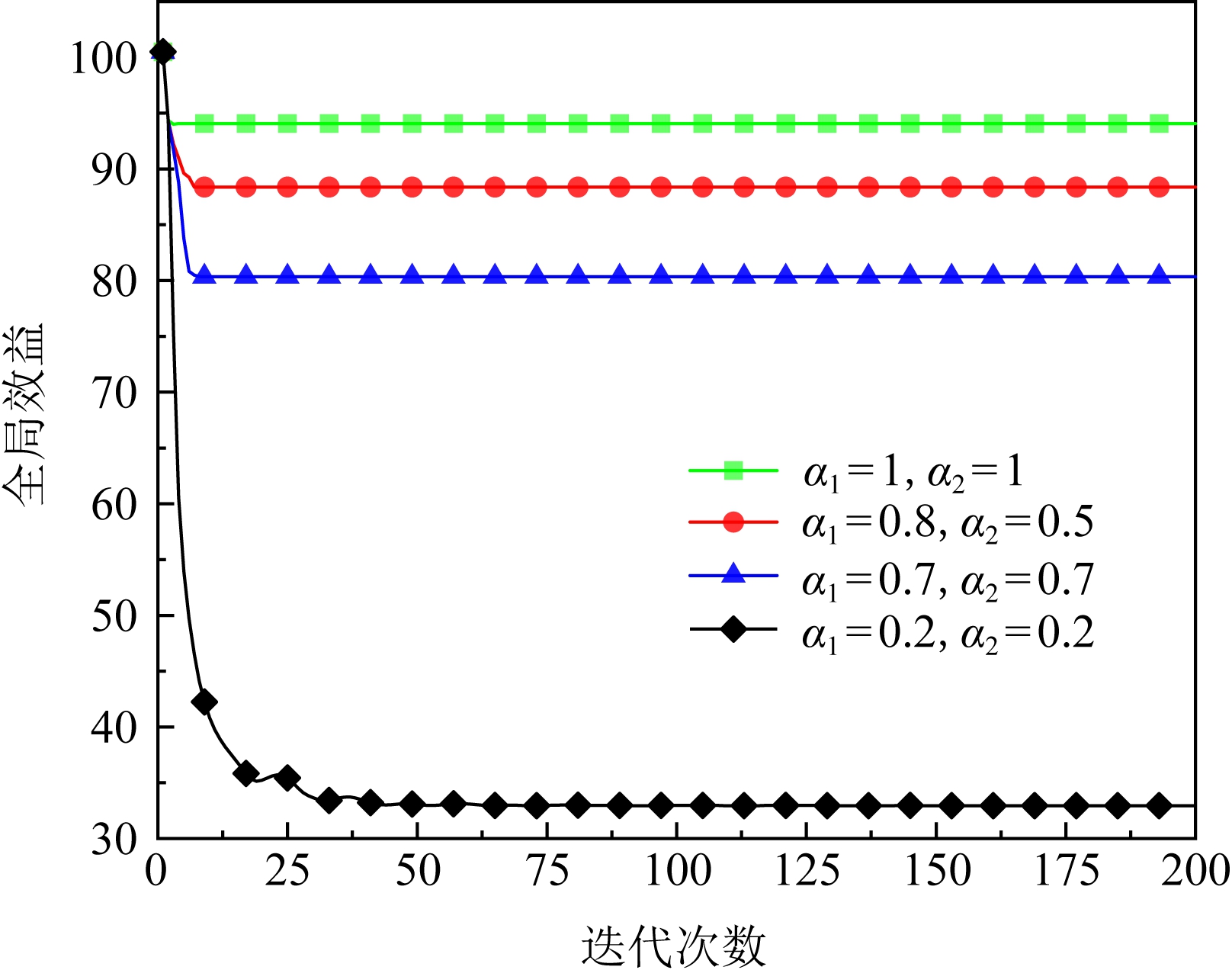
Fig. 4 Premature convergence phenomenon
图4 过早收敛现象
为了防止因不当的比例系数引起的算法过早收敛,我们为基于可变步长的算法1研究一种比例系数调整和误差协调机制.类似于3.2节中的最大步长调整方法,为智能体的可变步长设置下限δε,当可变步长小于δε时,触发强制协调:
1) 由于旧的比例系数无法有效地修正估计值,首先需要尝试降低当前的比例系数,让比例系数以某种方式降低,比例系数降低后,误差的扩大速度将减慢,如果此时的比例系数仍会引起过早收敛,使用原先的判断条件触发强制协调需要更多的迭代轮数,需要更加严格地对误差大小进行限制,合理地提高判断误差过大的可变步长下限δε;
2) 另一方面,触发强制协调机制时各个智能体的估计误差很大,考虑到使用式(5)的迭代方法修正误差的效率,且调整后的比例系数可能仍不符合收敛条件,会继续扩大误差,因此在触发强制协调时将各个智能体当前可获得的取值信息赋值于其估计值,即让
eij=vj, Aj∈Nj.
强制协调完成后,智能体继续执行算法直至发现误差过大再次进行协调或达到纳什均衡.强制协调的本质是限制智能体之间估计误差的大小并在必要时修正比例系数和重启算法,提高收敛速度.
3.4 决策算法
将3.2节中的自适应步长机制和强制协调机制综合到算法1中,本文的网络化软件优化决策机制可以总结为算法2.
算法2. DOCGAC(distributed optimization based on consensus and gradient-play with adaptive step size and coordination)算法.
输入:迭代次数上限l、各个智能体的初始取值vi(0)、最大步长εmax i、衰减系数τi、初始比例系数α1和α2、判别震荡的估计误差范围δerr、判别过早收敛的可变步长下限δε;
输出:更新完成后的各个智能体取值v′.
① for each Agent I in N
② ei(0)←v(0);
③ end for
④ iter_count←0;
⑤ while iter_count<l 并且没有达到纳什均衡
⑥ for each Agent I in N
⑦ getinfo();
⑧ εi←variable_step_size(ei(iter_count),
{vj(iter_count)},εmax i,τi) ;
/*可变步长*/
⑨ gradient_play(vi(iter_count),
ei(iter_count),εi);
⑩ estimation_update(); /*更新估计值*/
 if erri(iter_count)<δerr
if erri(iter_count)<δerr
 εmax i←εmax i×0.8; /*降低最大步长*/
εmax i←εmax i×0.8; /*降低最大步长*/
 end if
end if
 if εi<δε
if εi<δε
 α1←α1/2,α2←α2×0.8,δε←δε×10;
α1←α1/2,α2←α2×0.8,δε←δε×10;
 coordination(); /*强制协调*/
coordination(); /*强制协调*/
 end if
end if
 end for
end for
 iter_count←iter_count+1;
iter_count←iter_count+1;
 end while
end while
 return v′.
return v′.
算法2使用了按比例减小的方法搜索合适的参数.在最大步长和比例系数的下调方面,只要让它们进入收敛条件的范围即可,保守的下调可能导致频繁触发调整机制,而过于激进的下调方式反而会让参数变得过小影响方法的收敛速度,甚至引起类似于提前收敛的情况,按比例缩小是一种较为折中的选择.另一方面,合理的初始值能够减少参数下调触发的次数,提高算法的收敛速度.对于最大步长,其合理的初始取值受网络规模和效益函数的复杂程度影响,在实际使用中,由于系统在运行过程中会多次执行优化机制,因此可以根据同类型优化问题处理时的历史数据对初始值进行调整,如果智能体在连续的r轮迭代中都未触发步长下调,则可以谨慎地提高初始值以提高算法的收敛速度,更新最大步长为
其中β为大于1的数,可以选用下调最大步长时使用乘数的倒数,反之,如果在1轮算法中需要多次下调步长,则需要在下次算法开始前降低初始值.智能体在执行算法时记录本次算法中触发下调最大步长的次数c,令新的最大步长为
最大步长会在长期的优化过程中趋于稳定.对于比例系数α1,α1限制的是式(3)中基于一致性协议的估计修正速率,该值与智能体的相邻智能体个数有关,相邻智能体的个数越多,误差的累积效应就越强,一种简单的选取方法是让每个智能体的初始比例系数α1与其邻接智能体的个数成反比,如令
(7)
而α2限制的式(4)只和单个相邻智能体的取值有关,其本质是估计值向取值的靠近速度,与梯度博弈中的步长类似,因此可让其初始值与最大步长的初始值保持一致.
4 实验分析
为了验证方法的有效性,我们将在4.1节和4.2节对本团队前期开发的网上商城系统[27]进行了仿真实验,该软件是典型的互联网应用,通过集群节点协同为用户提供服务,其整体性能受各个节点的状态影响,适合使用本文的方法进行调控.我们基于团队在软件状态分析方面的工作[21]分析了该系统某一时段的各个节点带宽与总体响应延迟之间的关系,建立了模拟该系统的10个虚拟节点,以图5所示的方式进行连接,通过本文提出的方法让各个智能体调节软件节点的带宽,以系统响应时间的预测值为指标方法验证有效性,初始带宽的取值使用了分析时的日志记录值.
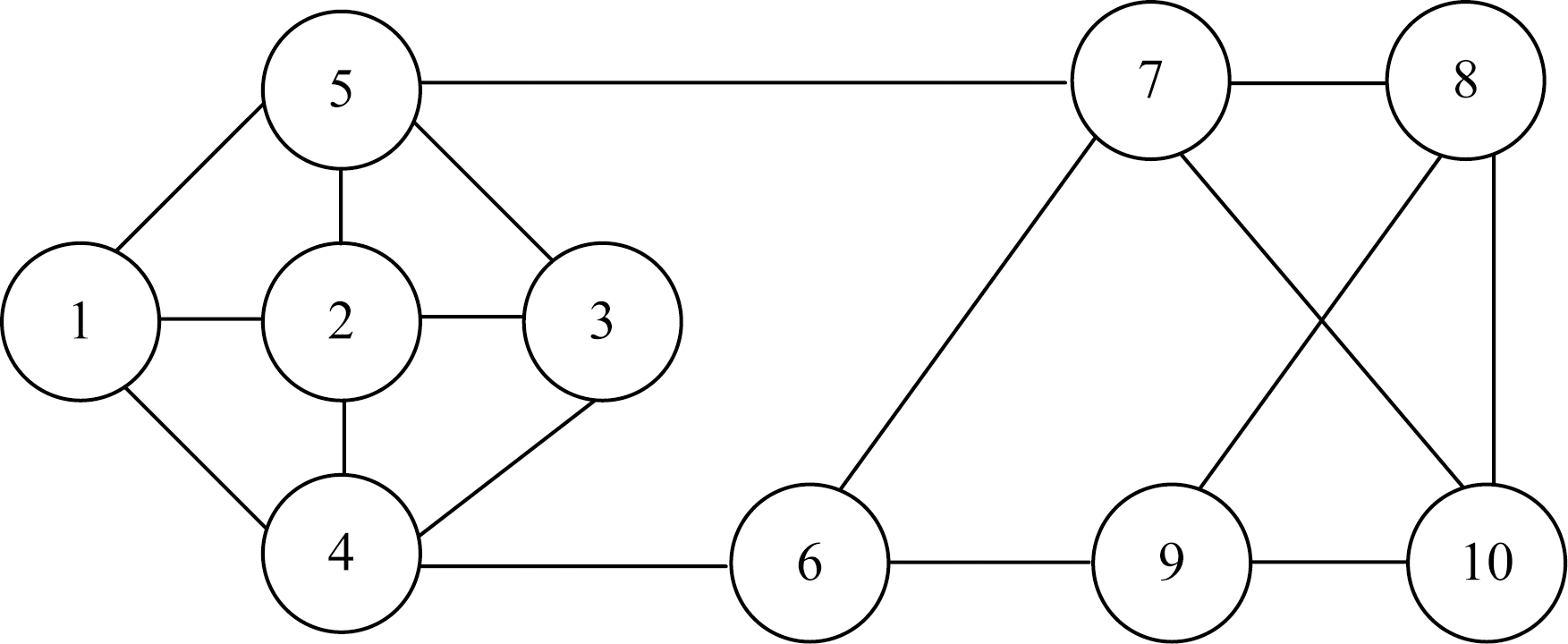
Fig. 5 Connectivity of agents in our simulation
图5 本文仿真实验智能体连接方式
4.1 机制触发
在本节中,我们对3.2节和3.3节提出的2类机制触发和效果分别进行了测试,以验证它们的效果.
1) 自适应梯度步长机制的触发
本文的自适应梯度步长机制分为可变步长和最大步长的调整过程,本节分别对完整的自适应梯度步长机制、只使用可变步长以及只使用最大步长下调的情况进行了实验,实验结果分别如图6所示.本轮实验中,各个智能体的最大步长εmax i均取0.3,衰减系数τi均取0.5,比例系数α1,α2均分别取0.2,0.4,其中,在只使用最大步长下调的情况下使用的最大步长为0.1.
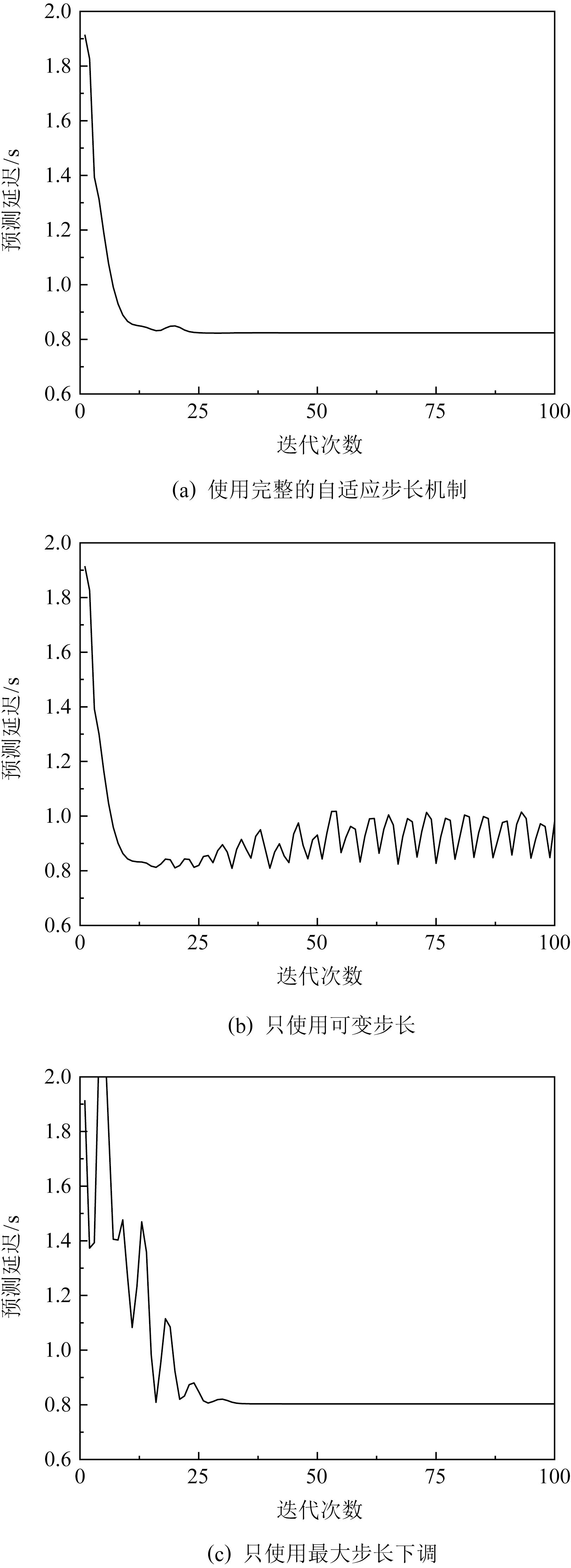
Fig. 6 Triggering of adaptive step size mechanism
图6 自适应步长机制的触发情况
从图6中可以看出,如果不使用步长下调,算法会在即将到达纳什均衡时由于过大的步长发生震荡现象;如果不使用可变步长,算法虽然能在合适的步长下收敛至纳什均衡,但在收敛过程中会受到估计误差的影响,出现频繁的震动,此时比例系数稍有不当就会让估计值与真实值的误差越来越大进而导致算法发散.
2) 强制协调机制

Fig. 7 Triggering of forced coordination mechanism
图7 强制协调机制的触发情况
我们首先测试了在使用可变步长时强制协调机制的触发情况,分别对使用和不使用强制协调下的方法迭代情况进行了实验测试.令所有智能体的初始最大步长εmax i=0.2,衰减系数τi=0.5,比例系数α1的初始值按式(7)的方法选取,α2的初始值均取0.8,实验结果如图7(a)所示.在不使用强制协调的情况下,由于估计误差过大可变步长归零导致算法在迭代刚刚开始时就停止更新,而强制协调机制能够对比例系数进行搜索并有效避免过早收敛现象.另一方面,不使用可变步长,在步长合适的情况下,使用强制协调机制也能实现对比例系数的搜索.如图7(b)所示,将所有智能体的步长均固定为0.1,用于判断估计误差大小的最大步长设置为0.08(虽然不使用可变步长,但强制协调机制的触发条件是该值的大小,本轮实验中的可变步长仅用于判断估计误差大小,不用于计算取值更新),算法在经过几次比例系数的下调后成功收敛到纳什均衡,相同的参数选取下不使用强制协调机制算法会发散.
4.2 对比实验
根据4.1节的讨论,算法2主要在收敛速度、参数选取等方面对算法1进行了改进,我们分别使用算法1和算法2对本节开始时提到的优化问题进行了处理,同时,为了进一步验证本文方法相较于传统方法的优势,我们选取了经典的最佳响应(best response, BR)和虚拟博弈 (fictitious play, FP)[12]作为参照.BR,FP以及本文使用的梯度方法是机器博弈研究中3类常见的决策方法,当前该领域的研究大多是在这3类方法的基础上改进而来,目前仍有很多相关的研究和讨论,其中最主要的研究是通过近似值替代最佳值的方式克服大量数据带来的求解问题[15,28-29],在本文的实验条件下近似值会影响求解精度和收敛轮数,此处使用精确的最佳值反映3种方法间的区别以及不完全信息带来的影响.本轮实验中,算法1的参数选取:为了防止发散,步长εi均使用0.05,比例系数α1,α2均分别设定为0.2,0.8;算法2的参数选取:初始最大步长εmax i均设置为表现较为平均的0.3,衰减系数τi均使用较为保守的0.5,比例系数α1的初始值使用式(7)的选取方法,α2的初始值均设置为0.8;BR和FP均使用估计值计算收益函数,为了确保能够顺利执行,这2种算法的比例系数组合都选取为0.2和0.3.
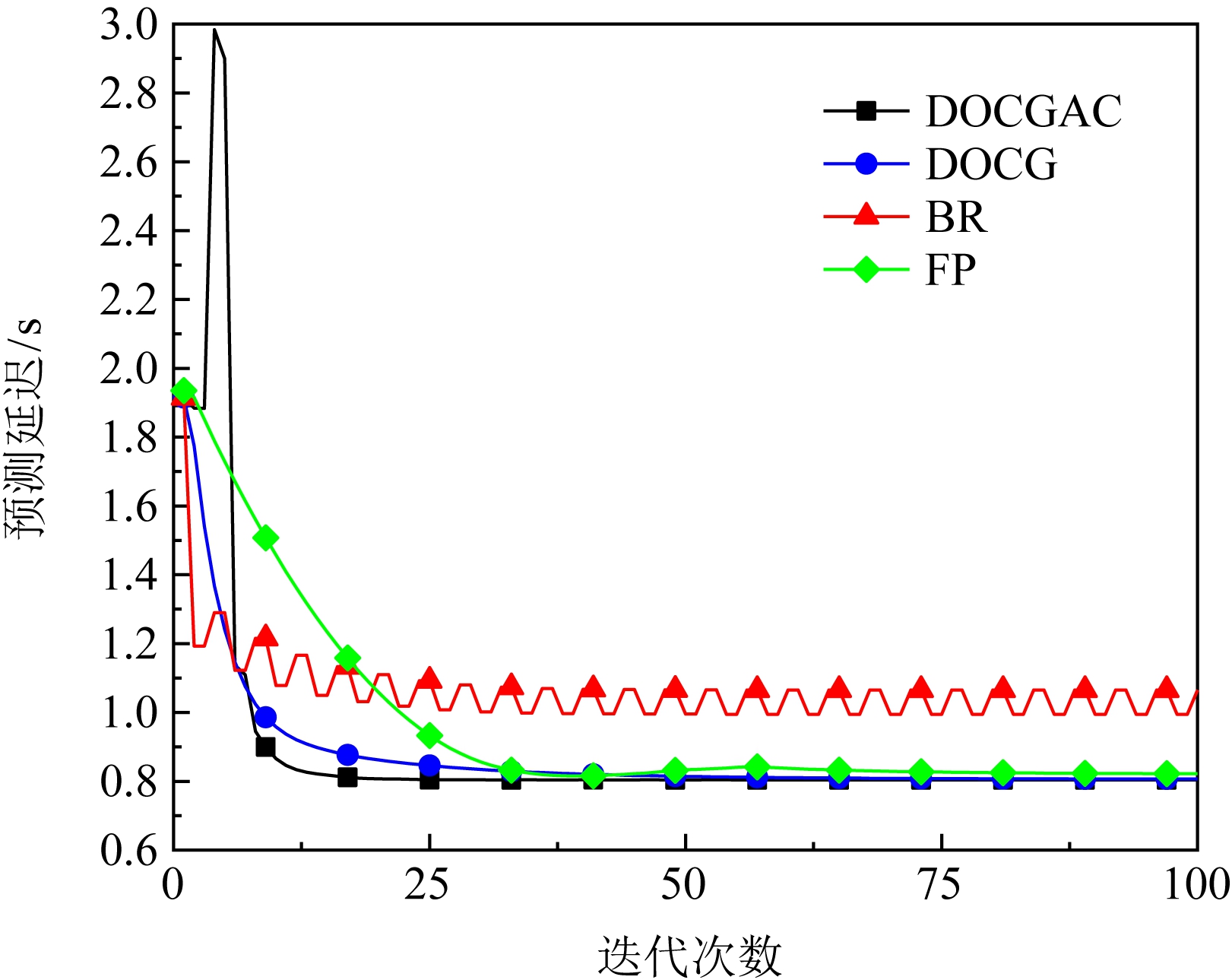
Fig. 8 Convergence performance of algorithms
图8 各类算法的效果对比
实验结果如图8所示,可以看出算法1使用较为保守的参数平稳地收敛到纳什均衡,而算法2由于在执行初期更新取值时使用了最大步长,各个智能体间的博弈导致预期结果发生了巨大的波动,但在接下来的几轮博弈中在可变步长和强制协调机制的控制下,各个智能体放慢了更新幅度并修正了自身对其他智能体的估计,将取值更新重新拉回了正确的方向,最后比改进前的算法更快速地收敛到了纳什均衡.BR由于各个智能体激进地追求自身的最佳收益,无法完全达成平衡;FP通过根据历史平均采取最佳响应,稳定地收敛到了平衡状态,但收敛速度不如前2种方法.
4.3 复杂网络实验
为了验证方法在复杂网络中的效果,我们进行了更大规模的实验,设置了1 000个模拟节点.由于可供使用的节点数据不足,我们模仿文献[14]中的方法进行了数值实验,在3种典型的网络结构:随机网络、小世界网络、无标度网络上对算法2进行了测试.在随机网络中设置连边概率p分别为0.1,0.2,0.4,0.8;在小世界网络中,邻边数k分别取20,40,80,100,重连概率被固定为0.2;在无标度网络中,每次加入的边数m分别设置为10,20,40,50,每种网络随机生成后进行测试记录结果,各重复20次取平均值,实验结果如图9所示.由图9可知,在随机网络中,随着智能体间的连边增加,算法的收敛速度会大幅减慢,但不会引起发散.这与我们的设想相反,因为一致性协议修正估计值的速度会随连边的增加而加快[17],且在全连接实验中,算法的收敛表现非常好.引起这种情况的原因是复杂的网络构成让智能体间的估计相互影响,导致估计修正速度变慢,进而减慢了达到纳什均衡的速度.而在小世界网络和无标度网络中,由于在局部的网络结构中出现了近似于全连接的状态,降低了该问题的影响,因此在这2种网络中,连边数量的增加对收敛性能的影响不大.网络的复杂性会一定程度上降低算法的收敛效率,但不会导致算法失效.
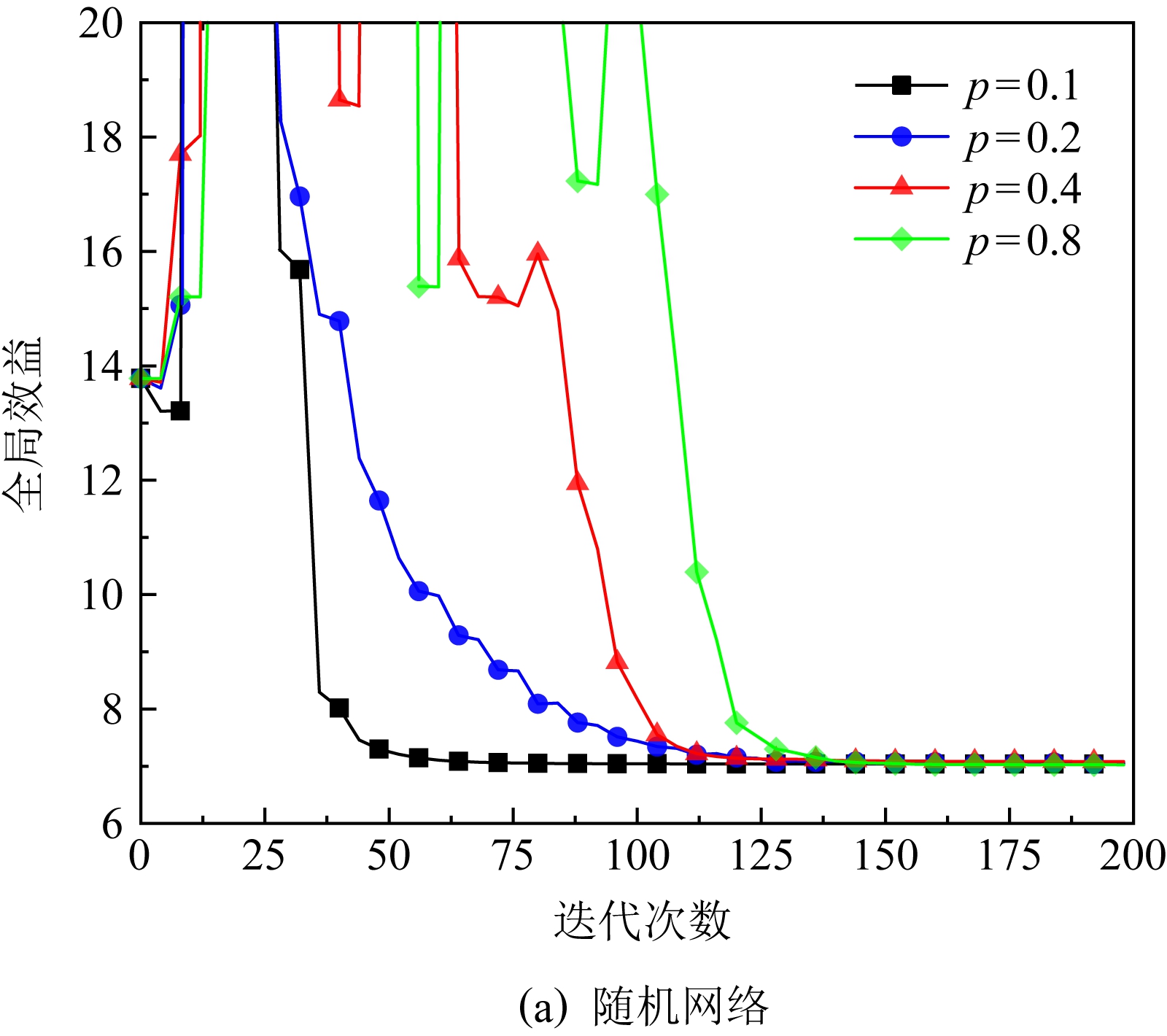
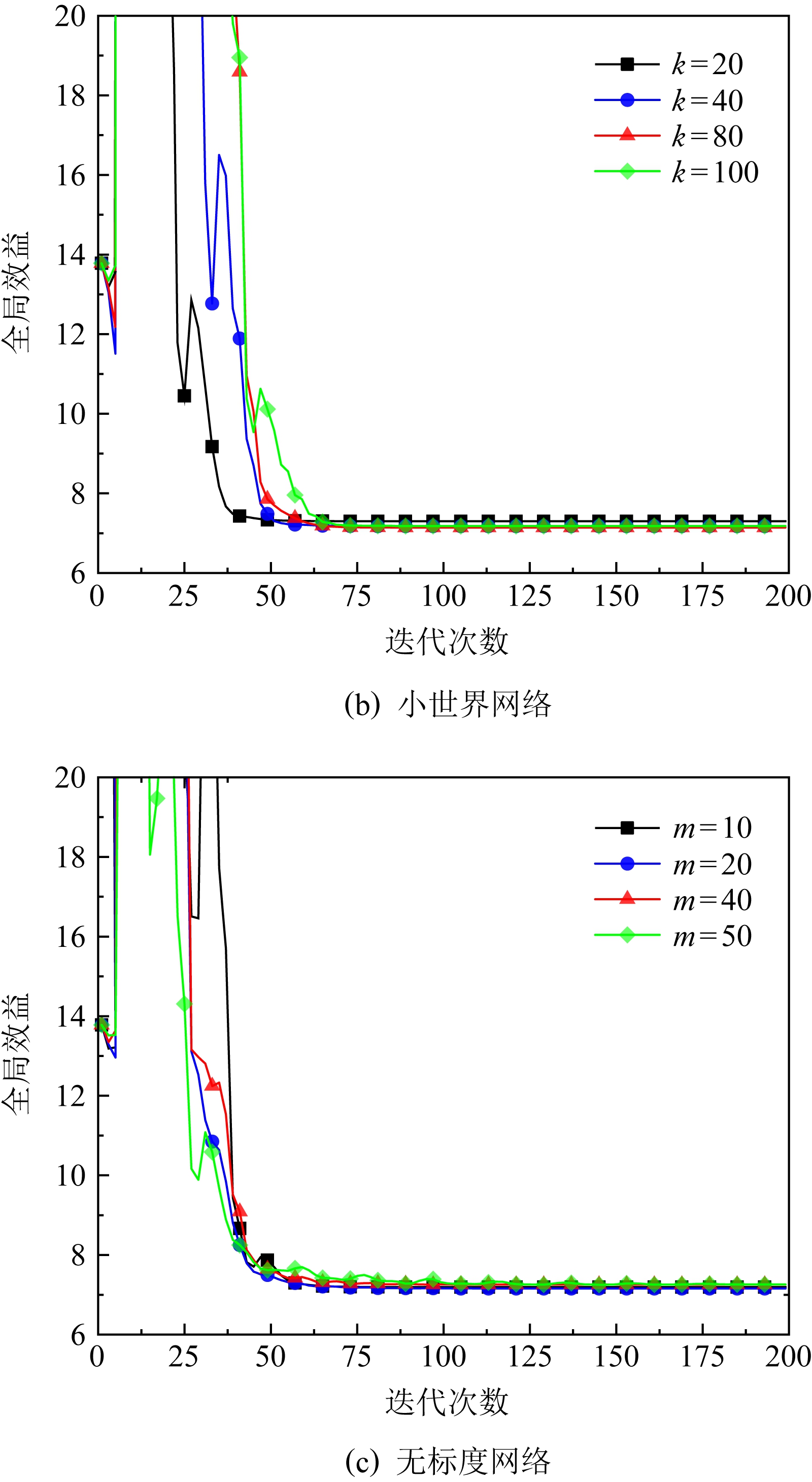
Fig. 9 Experimental results of algorithm in complex networks
图9 复杂网络的算法实验结果
5 总结与展望
在本文中,我们针对网络化软件的优化决策问题建立了系统模型,将现有的基于多智能体一致性的分布式梯度博弈方法研究总结为了DOCG算法,并提出了将其应用在网络化软件的优化决策问题中的方法.此外,我们对该算法进行了改进,研究了能调节寻优速度和自动搜索合适参数的自适应步长机制和强制协调机制,提出了DOCGAC算法,为软件在连续工作中的持续参数优化提供了一种解决方案.实验结果表明,改进后的算法能更快地收敛至纳什均衡,并且降低了方法对参数选取的要求,使此类算法能够应用于网络化软件系统的优化任务中.
我们的方法也存在一定的不足,与原算法相同,DOCGAC收敛到的纳什均衡无法保证是对应优化问题的全局最优解.在未来的工作中,我们将探索如何让此类方法的纳什均衡更靠近理论最优值,并在真实的大规模网络化软件中进一步测试和改进我们的方法.
作者贡献声明:舒畅提出核心方法,参与实验框架的设计和实验编程,并最终完成了论文的撰写;李青山拟定研究方向,设计了具体的研究方案;王璐设计了实验框架和方法,完善研究方案;王子奇负责实验编程及论文撰写;计亚江负责实验数据收集和论文核定.
[1]Schmidt D C,Mccormick Z. Producing and delivering a coursera MOOC on pattern-oriented software architecture for concurrent and networked software[C]//Proc of the 2013 Companion Publication for Conf on Systems, Programming, and Applications: Software for Humanity. New York: ACM, 2013: 167-176
[2]Namiot D, Sneps-Sneppe M. On micro-services architecture[J]. International Journal of Open Information Technologies, 2014, 2(9): 24-27
[3]Jing Guo, Chang Zihao, Wang Sa, et al. Who limits the resource efficiency of my datacenter: An analysis of Alibaba datacenter traces[C] //Proc of the 2019 Int Symp on Quality of Service. New York: ACM, 2019: 39:1-39:10
[4]Sahni J, Vidyarthi D P. Heterogeneity-aware adaptive auto-scaling heuristic for improved QoS and resource usage in cloud environments[J]. Computing: Archives for Informatics and Numerical Computation, 2017, 99(4): 351-381
[5]Chen Bihuan, Peng Xin, Yu Yijun, et al. Requirements-driven self-optimization of composite services using feedback control[J]. IEEE Transactions on Services Computing, 2015, 8(1): 107-120
[6]Das T, Zhong Yuan, Stoica I, et al. Adaptive stream processing using dynamic batch sizing[C] //Proc of the 5th ACM Symp on Cloud Computing(SoCC’14). New York: ACM, 2014: 16:1-16:13
[7]Monderer D, Shapley L S. Potential games[J]. Games & Economic Behavior, 1996, 14(1): 124-143
[8]Rosen J B. Existence and uniqueness of equilibrium points for concave n-person games[J]. Econometrica, 1964, 33(1): 520-534
[9]Li Na, Marden J R. Designing games for distributed optimization[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(2): 230-242
[10]Wu Han, Shang Huiliang. Potential game for dynamic task allocation in multi-agent system[J]. ISA Transactions, 2020, 102(1): 208-220
[11]Flåm S D. Equilibrium, evolutionary stability and gradient dynamics[J]. International Game Theory Review, 2002, 4(4): 357-370
[12]Brown G W. Iterative solution of games by fictitious play[J]. Activity Analysis of Production and Allocation, 1951, 13(1): 374-376
[13]Blume L E. The statistical mechanics of strategic interaction[J]. Games and Economic Behavior, 1993, 5(3): 387-424
[14]Ye Maojiao, Hu Guoqiang. Distributed Nash equilibrium seeking by a consensus based approach[J]. IEEE Transactions on Automatic Control, 2017, 62(9): 4811-4818
[15]Heinrich J, Lanctot M, Silver D. Fictitious self-play in extensive-form games[C] //Proc of the 32nd Int Conf on Machine Learning(ICML’15). New York: ACM, 2015: 805-813
[16]Saber R O, Murray R M. Consensus protocols for networks of dynamic agents[C] //Proc of the 2003 American Control Conf. Piscataway, NJ: IEEE, 2003: 951-956
[17]Saber R O, Fax J A, Murray R M. Consensus and cooperation in networked multi-agent systems[J]. Proceedings of the IEEE, 2007, 95(1): 215-233
[18]Xie Guangming, Wang Long. Consensus control for a class of networks of dynamic agents[J]. International Journal of Robust & Nonlinear Control, 2007, 17(10/11): 941-959
[19]Zuo Zongyu, Tie Lin. Distributed robust finite-time nonlinear consensus protocols for multi-agent systems[J]. International Journal of Systems Science, 2016, 47(6): 1366-1375
[20]Krupitzer C, Roth F M, VanSyckel S, et al. A survey on engineering approaches for self-adaptive systems[J]. Pervasive and Mobile Computing, 2015, 17: 184-206
[21]Wang Lu, Li Qingshan, Lü Wenqi, et al. Self-adaptation analysis method for recognition quality assurance using event relationships[J]. Journal of Software, 2021, 32(7): 1978-1998 (in Chinese)(王璐, 李青山, 吕文琪, 等.基于事件关系保障识别质量的自适应分析方法[J]. 软件学报, 2021, 32(7): 1978-1998)
[22]Nash J F. Non-cooperative games[J]. Annals of Mathematics, 1951, 54(2): 286-295
[23]Mazumdar E, Ratliff L J, Sastry S S. On gradient-based learning in continuous games[J]. SIAM Journal on Mathematics of Data Science, 2020, 2(1): 103-131
[24]Wen Wanli, Cui Ying, Quek T, et al. Joint optimal software caching, computation offloading and communications resource allocation for mobile edge computing[J]. IEEE Transactions on Vehicular Technology, 2020, 69(7): 7879-7894
[25]Roozbehani M, Megretski A, Feron E. Optimization of Lyapunov invariants in verification of software systems[J]. IEEE Transactions on Automatic Control, 2013, 58(3): 696-711
[26]Cai Kaiyuan, Sun Chang’ai, Nie Changhai. Software reliability assessment: A software cybernetics perspective[J]. SCIENTIA SINICA Informationis, 2019, 49(11): 1528-1531 (in Chinese)(蔡开元, 孙昌爱, 聂长海. 软件可靠性评估的控制论观点[J]. 中国科学: 信息科学, 2019, 49(11): 1528-1531)
[27]Zhang He, Li Qingshan, Wang Lu, et al. Self-Adaptive software changes analysis method based on “detection-recognition” mechanism(s)[C] //Proc of the 31st Int Conf on Software Engineering and Knowledge Engineering. Pittsburgh, PA: KSI, 2019: 287-290
[28]Brian S, Soummya K, Joao X. Single sample fictitious play[J]. IEEE Transactions on Automatic Control, 2017, 62(11): 6026-6031
[29]Sarper A, Ceyhun E. Decentralized inertial best-response with voluntary and limited communication in random communication networks[J]. arXiv preprint, arXiv:2106.07079, 2021




