自适应软件系统是一类通过动态调整自己的行为,以适应系统自身和运行环境的非确定性,从而持续满足系统目标的软件系统[1].基于这一理念,一个自适应软件系统主要由实现系统应用逻辑的被管理系统(managed system)模块和实现自适应逻辑的管理系统(managing system)模块2部分组成[2].
近年来,控制论在自适应软件系统的开发中得到了广泛应用[3-4].这类控制型自适应软件系统通常是基于一个辨识而得的、用于描述被管理系统行为的标称模型,依据控制论自动合成所需的管理系统.这类系统利用反馈机制支撑被管理系统的自适应,并由控制论从数学上保证所设计、实现的自适应软件系统的优化性和可靠性[5-8].然而,软件系统运行环境的非确定性,使得标称模型的实际参数值在运行时常偏离其辨识值,这种现象被称为自适应软件系统的模型偏差(model deviation).模型偏差会使控制论提供的优化性和可靠性失效,威胁控制型自适应软件系统的安全运行.因此,各种模型偏差检测方法被提出用以解决这一问题.
自适应软件系统的运行环境具有动态、开放的特点[9-10],同时系统与环境的交互也受到非确定性的影响[11-12].因此,在其运行过程中,被管理系统标称模型的实际参数值可能以多种开发人员无法预先描述的方式偏离其辨识值,使得模型偏差表现出多种不同的形态.本文使用场景来区分模型偏差的不同形态,而模型偏差的形态差异导致模型偏差检测方法在不同偏差场景下的检测有效性不同.
因此,除了在技术层面上改进模型偏差检测方法,对不同模型偏差检测方法适用的模型偏差场景进行研究,也有助于提高自适应软件系统的整体可靠性.通常从检测时延和检测准确度2方面描述模型偏差检测方法的有效性,即检测时延越低且检测准确度越高,则检测方法的有效性越好.
在传统控制论中,通常依据被管理系统的物理特性,选取有效的模型偏差检测方法[13-14].然而,自适应软件系统通常不存在可使用数学模型精确描述的物理特性.因此,为自适应软件系统选取有效的模型偏差检测方法的挑战在于如何建立一套特性体系,用于描述不同的模型偏差场景.
针对这一挑战,本文提出了模型偏差检测的理论框架,刻画了模型偏差检测方法的重点要素.基于该框架,本文进一步分析、归纳了3个影响模型偏差检测有效性的主要因素,包括控制信号(被管理系统从管理系统获得的调节命令)、环境输入(被管理系统受外部环境的影响),以及非确定性(被管理系统中存在的观测误差和系统噪声).一旦某检测方法没有考虑偏差场景下影响检测有效性的主要因素,则此检测方法将不能够有效检测该场景的模型偏差.根据这3个主要因素,本文提出了3个模型偏差场景特性指标,用于建立描述偏差场景特性的评价体系.通过使用不同实验对象和不同配置的实证实验,探索了现有主流模型偏差检测方法对于不同模型偏差场景的适用性.
本文的主要贡献有3个方面:
1) 构建了一个控制型自适应软件系统的模型偏差检测框架,为模型偏差检测方法的适用性研究提供理论依据.
2) 提出了一套基于模型偏差检测框架的特性指标,用于描述不同的模型偏差场景,并评估模型偏差检测方法的适用性.
3) 进行了基于大量实验的模型偏差检测方法适用性研究.依据划分的6种特性场景,总结各检测方法适用的特性范围,用于指导如何在不同的场景特性下选取有效的模型偏差检测方法.
1 相关背景
本节首先介绍自适应软件系统的背景知识,然后以安全水处理(secure water treatment, SWaT)系统为例介绍控制型自适应软件系统的设计和运行过程.
1.1 自适应软件系统
现代软件系统面临着非确定性的挑战,包括动态、开放的运行环境以及不断变化的系统需求.为了应对这一挑战,自适应软件系统应运而生[15-17].自适应软件系统通过自我监测和重新配置自身,以持续适应不断变化的环境和系统需求.一个自适应软件系统可分为2个不同的部分:1)被管理系统,与软件用户交互,负责系统业务逻辑的实现;2)管理系统,与软件运行环境交互,负责监测被管理系统的行为,并在必要的时候对其进行重新配置.例如,对于一个自适应Web服务系统而言,其被管理系统就是实现用户访问的软件模块,包括Web前端、负载均衡器、服务器及其访问接口等.其管理系统需要定时获取用户访问的平均响应时间,并根据用户的响应需求进行服务和负载的伸缩.
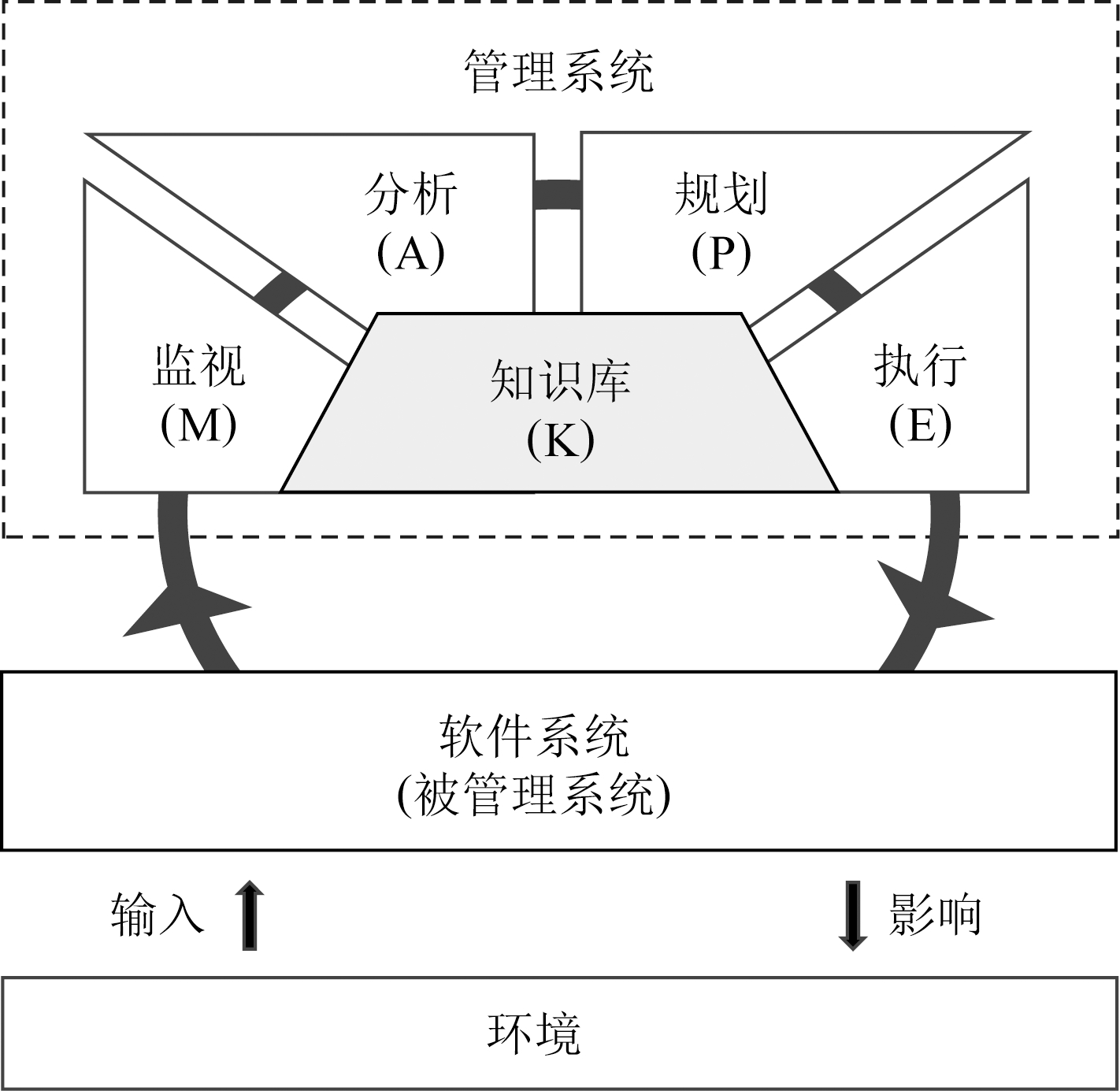
Fig. 1 MAPE-K loop
图1 MAPE-K环
实现自适应软件系统的关键在于管理系统中自适应逻辑的设计.传统自适应软件理论使用监视、分析、规划和执行4个模块外加1个共享知识库共同实现的循环,即MAPE-K环(monitor-analyze-plan-execute loop with knowledge, MAPE-K loop)来指导自适应软件系统的开发[18],如图1所示.软件的自适应表现为循环顺序运行这4个模块.4个模块的迭代执行构成了自适应软件系统的自适应环,通常使用自适应环的迭代序号k代指在该次迭代中自适应软件系统的状态和执行过程.在基于MAPE-K环实现的自适应Web服务系统中,监视模块实现定时观测用户访问的平均响应时间,分析模块对比观测的平均响应时间是否大于或者远小于目标响应时间,规划模块根据实际观测的平均响应时间与目标响应时间,计算适合的服务器数量,执行模块调用接口添加或删减对应数量的服务器,共享知识库提供了用户负载、服务器数量和平均响应时间的排队论模型以及目标响应时间.MAPE-K环为自适应软件系统提供了基本的实现框架,但各模块的实现无具体方法指导,且需要设计额外的机制去保证所实现的自适应软件系统的可靠运行.
1.2 控制型自适应软件系统
近年来,基于控制论的控制型自适应软件系统因其开发过程的自动化支撑和整体系统的理论保障,成为自适应软件领域的研究热点[1,19].
图2所示为控制型自适应软件系统的基本架构.其中,管理系统被实现为控制器,系统输出是被管理系统行为的观测变量,控制信号是改变被管理系统行为的可调参数.在该反馈控制环中,面对环境输入的扰动,被管理系统的系统输出在控制器的作用下能够追踪系统目标.基于反馈控制环,Filieri等人[9]首先提出了一个框架PBM(push-button method)来支持控制型自适应软件系统的开发.该实现框架基于数据收集和模型拟合(即系统辨识[20])得到的标称模型,提供控制论指导的控制器设计(即控制器合成[21])和整个自适应软件系统优化且可靠运行的理论保证.
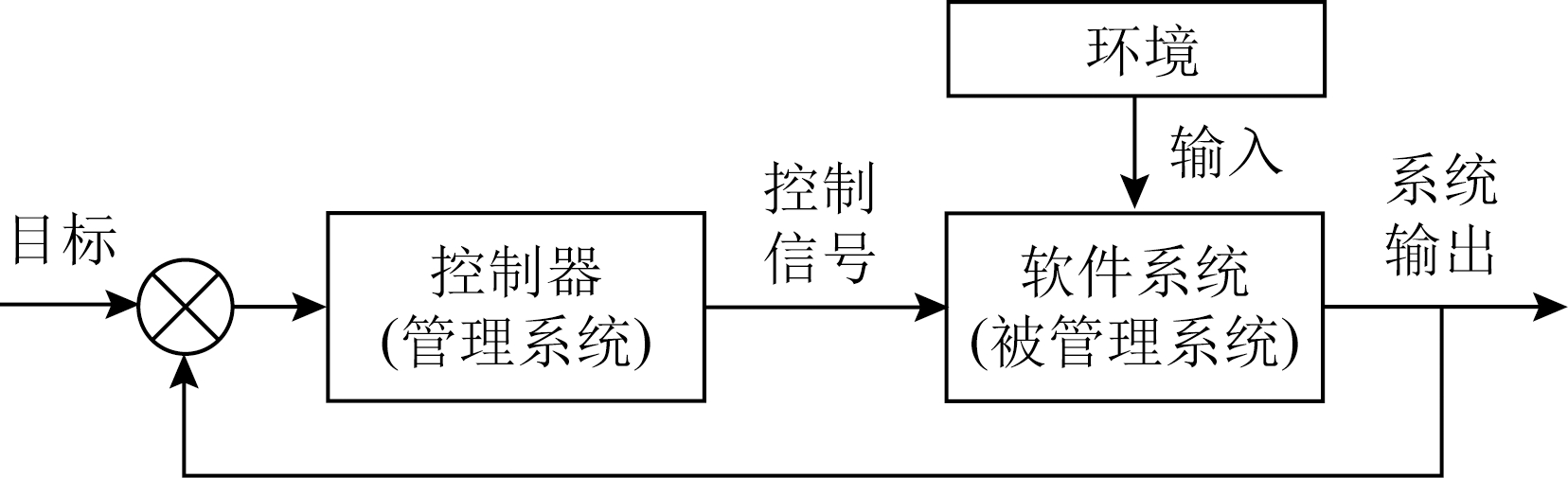
Fig. 2 Control-based self-adaptive software systems
图2 控制型自适应软件系统
系统辨识将被管理系统建模为一个定量的标称模型.系统辨识可以构建多种类型的标称模型来支持不同场景下的自适应,包括线性时不变系统[11,22-23]、线性时变系统[24]和非线性时不变系统[25].根据系统化采样的各运行环境下的控制信号及其系统输出,拟合选定类型标称模型的参数值,得到辨识标称模型.
基于辨识标称模型,控制器合成利用各种控制论技术来设计不同自适应场景下的控制器.其中,最流行的2种技术是比例-积分-微分(proportional-integral-derivative, PID)控制[5,26-28]和模型预测控制(model predictive control, MPC)[23,29-32].在控制论的支持下,自动合成的控制器使整个自适应软件系统的行为理论上遵循所需的控制属性[33],如稳定性、准确性、趋稳性和低超调性.这些理论保证的控制属性使得实现的自适应软件系统在运行中能够优化且可靠地满足系统目标.
下面基于SWaT系统[34]进一步说明控制型自适应软件系统的运行架构和开发过程.如图3所示,SWaT是一个缩小版的水处理系统,可生产双重过滤的饮用水.该系统主要通过管理控制5个相连的水箱及其各自的进水阀/出水阀以完成系统需求.自适应SWaT的目标是在不同的环境条件下(如5个水箱的不同初始水位),保障水过滤过程的可靠性(如无水箱溢出和空箱),并尽可能提升水处理过程的优化性(如饮用水产量最大化).

Fig. 3 Secure water treatment testbed (SWaT)[34]
图3 安全水处理系统[34]
实现控制型自适应SWaT,首先可使用线性时不变系统来描述SWaT:
(1)
其中,x(k)表示当前运行状态(即5个水箱当前进、出水状态),x(k-1)表示历史运行状态(即5个水箱历史进、出水状态),y(k)表示系统输出(即5个水箱水位实测值),u(k-1)表示控制信号(即在一个自适应环里各阀门打开的时间).模型参数(即A,B,C)无法直接观测,需要辨识确定.每一个参数都代表SWaT特定的动态属性.A代表系统的延迟属性,它描述了控制器请求打开或关闭阀门的时间与阀门打开或关闭的时间之间的间隔;B代表系统的可控属性,它描述了打开或关闭阀门对系统运行状态的影响;C代表系统的可观测属性,它描述了每个水箱的进、出水状态与水箱水位之间的关系.根据系统化采样的阀门不同打开时间及其水箱水位实测值,线性拟合模型参数(即![]() 得到辨识标称模型.
得到辨识标称模型.
基于辨识的标称模型,开发人员可以利用On-Off控制[35]一套控制器,使SWaT能够适应不同的运行环境.控制论保证了所设计的自适应SWaT遵循趋稳性(即所有水箱的水位应快速达到所需水位,实现饮用水产量最大化)和低超调性(即所有水箱水位不会高/低于上/下警戒线过多,避免水箱溢出或空箱),保障水处理过程优化且可靠地运行.
2 模型偏差检测
2.1 模型偏差及其检测
自适应软件系统常运行于动态、开放环境,这使管理系统需要面对可能超出其设计能力范围的环境状况,这对控制型自适应软件系统而言,将导致标称模型的实际参数值偏离其辨识值.这一偏差会导致自动设计的控制器与被管理系统的实际行为不匹配,从而使控制器不再严格遵守控制属性,严重时会导致软件系统的异常行为,威胁整个自适应软件系统的安全.例如,自适应SWaT在面临阀门磨损场景[36]时,其对应阀门的水流量减小,会使控制器的趋稳性失效,降低饮用水产量.该系统在传感器数据篡改场景[25]时,控制器会生成错误的控制信号,使其反馈控制环的趋稳性和低超调性失效,直接导致水箱溢出或空箱.
实际运行环境中,根据不同的模型偏差产生原因,模型偏差场景会体现出不同的特性.在上文的例子中,阀门磨损会导致被管理系统标称模型可控属性对应参数值缓慢、定向变化,外在表现为水位实测值的缓慢变化;而篡改传感器数据会导致被管理系统标称模型可控属性对应参数值的快速、非定向变化,外在表现为水位实测值的快速变化.
现有模型偏差检测方法在面对不同特性的模型偏差场景时会展现出不同的性能.Tong等人[10]基于自适应SWaT的实验表明,同一种检测方法在不同场景下性能的差异程度会相当显著.例如,基于滑窗的系统输出检测方法(即检测水箱水位变化是否超出给定范围)在阀门磨损场景下,其性能显著差于其他2种比较方法;而在传感器数据篡改场景下,该检测方法的性能以微弱优势领先Tong等人[10]提出的最新方法,并大幅领先另一比较方法.
基于这一观察,本文认为除了在技术层面上改进模型偏差检测方法,对不同模型偏差检测方法适用的模型偏差场景进行研究,也有助于提高自适应软件系统的整体可靠性.因此本文的研究问题是如何为控制型自适应软件系统选取有效的模型偏差检测方法.
具体而言,使用检测时延和检测准确度2个方面评价模型偏差检测方法的有效性.其中,检测时延是指从自适应软件系统发生模型偏差到检测方法发现该模型偏差的时间间隔.检测准确度包括2个维度,即漏报率和误报率.漏报率是指在模型偏差场景下,检测方法没有发现模型偏差的概率;而误报率是指在正常运行场景下,检测方法错误报告模型偏差的概率.基于这3个指标,有效的模型偏差检测方法即指检测的时延低、漏报率低和误报率低.
2.2 检测框架
为了探索各检测方法的适用性,需构建模型偏差检测框架,分析影响模型偏差检测有效性的因素.基于对现有模型偏差检测过程的观察,控制型自适应软件系统的模型偏差检测方法主要由系统建模、检测变量估计、模型偏差表示以及模型偏差判断4个部分组成.由此,本文提出可以使用式(2)~(5)组成的框架统一描述分析模型偏差检测方法.
系统建模:
(2)
检测变量估计:
PΣ(T)=Φ(Σ(P)|D(T)).
(3)
模型偏差表示:
ΘMD=Ψ(Σ(P)).
(4)
模型偏差判断:
Alarm(T)=I(PΣ(T)|ΘMD).
(5)
式(2)表示控制型自适应软件系统的模型,通常为一个基于控制论通过系统辨识而得的微分方程.其中Y(k)表示模型输出矩阵,包括系统输出、系统内部状态等;N(k)表示模型输入矩阵,包括历史系统输出、控制信号和环境输入等;P表示模型参数矩阵,可根据正常情况下自适应软件系统的运行记录辨识其元素值,所得到的矩阵称作辨识模型参数矩阵![]() 对于自适应SWaT基于式(2),Tong等人[10]提出的MoD2检测方法对该自适应软件系统的建模中模型输出矩阵为
对于自适应SWaT基于式(2),Tong等人[10]提出的MoD2检测方法对该自适应软件系统的建模中模型输出矩阵为
x(k)表示5个水箱当前进、出水状态,y(k)表示5个水箱水位实测值.模型输入矩阵为
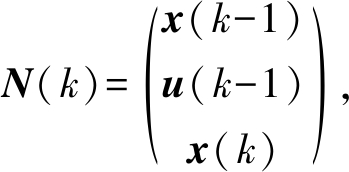
x(k-1)表示5个水箱历史进、出水状态,u(k-1)表示所有阀门当前的控制信号.模型参数矩阵为
A代表系统的延迟属性,B代表系统的可控属性,C代表系统的可观测属性.则其辨识模型参数矩阵为
![]() 分别表示系统延迟属性、可控属性和可观测属性对应的辨识模型参数值.
分别表示系统延迟属性、可控属性和可观测属性对应的辨识模型参数值.
式(3)描述了模型偏差检测方法选取检测变量及对检测变量进行的估测.具体而言,首先确定检测的模型参数(即检测变量PΣ),再根据观测变量序列D(T)(即包含模型输入、输出矩阵变量的序列)估计检测变量值.其中Σ表示模型参数的选择运算.对于自适应SWaT,基于式(3),Tong等人[10]提出的MoD2检测方法的检测周期取值为1次自适应环迭代(即检测周期等同于自适应周期),并选择可控属性对应的模型参数(即B)作为检测变量.MoD2检测方法依据的观测变量序列包括水箱水位值序列和阀门控制信号序列.
式(4)所示确定自适应软件系统的模型偏差表示.其中Ψ表示使用数据驱动、人工经验或理论推导等方法获取检测变量值的安全区域.检测变量值在这个安全区域内,控制型自适应软件系统的可靠和优化运行存在理论保证,而检测变量值一旦超出这个安全区域,理论保证将会失效,可能导致系统行为异常.因此,模型偏差表示ΘMD可描述为检测变量值安全区域的补集.对于自适应SWaT,基于式(4),Tong等人[10]提出的MoD2检测方法通过频域分析决定其安全区域Ψ.具体而言,Ψ描述了可使自适应SWaT的控制器正常运作的控制参数B的取值范围.
式(5)所示每个检测周期判断检测变量估计值是否符合模型偏差表示.如果符合,则发出警报,即Alarm(T)=1,可触发模型偏差补救机制.对于自适应SWaT,基于式(5),Tong等人[10]提出的MoD2检测方法通过计算当前估测的控制参数值处于安全区间内的置信度,决定该系统是否出现模型偏差现象.
2.3 主流检测方法
基于前述的模型偏差检测理论框架,介绍4种主流模型偏差检测方法(基于式(2)~(5)的详细描述请见技术文档[37]).
基于滑窗的系统输出检测方法SWDetector通过实时监测系统输出变化是否符合给定数值范围来检测模型偏差,并使用滑动窗口平滑非确定性的影响[38].Filieri等人[9]在引入控制论实现自适应时,也一并引入该检测方法以应对模型偏差问题.
在系统模型方面,SWDetector使用自回归模型描述控制型自适应软件系统.在检测变量估计方面,SWDetector使用系统输出的变化量(即前后2次自适应迭代中系统输出的差值)作为其检测变量,并通过滑动窗口平滑观测误差对该变化量的影响.在模型偏差表示方面,SWDetector基于观测数据决定系统输出变化值的安全区域.首先使用系统化采样的方法收集被管理系统正常运行时的运行数据,再根据系统模型计算出正常运行下被管理系统系统输出变化的取值范围作为安全区域.在模型偏差判断方面,SWDetector通过比较当前估计的系统输出变化值是否处于其安全区域内,决定该系统是否出现模型偏差现象.
基于滑窗的系统输出检测方法ARMA通过监测系统输出模型预测值和当前实际测量值之间的差值是否超出正常误差范围来判断是否发生模型偏差[39-45].He等人[22]引入该方法检测由于软件缺陷导致的模型偏差.
在系统模型方面,ARMA同样使用自回归模型描述控制型自适应软件系统[46].在检测变量估计方面,ARMA使用系统输出的预测误差(即基于系统模型的系统输出预测值和基于实际观测的系统输出实测值的差)作为检测变量.ARMA同样通过滑动窗口平滑观测误差对该检测变量的影响.在模型偏差表示方面,ARMA亦基于观测数据决定检测变量的安全区域.与SWDetector不同的是,ARMA使用检测变量的概率分布,而非取值范围,作为其安全区域的基础.在模型偏差判断方面,ARMA通过计算当前估计的辨识误差值处于概率分布3 sigma或6 sigma范围内的置信度[22],决定该系统是否出现模型偏差现象.
基于矩阵计算的参数检测方法Direct通过监测矩阵计算得出的实际参数值是否超出安全区域来判断是否发生模型偏差[24,47-48],并使用滑动窗口平滑非确定性的影响.
在系统模型方面,Direct使用线性时不变系统为描述自适应软件系统的基础模型,并引入环境输入补偿项对系统模型进行精化.在检测变量估计方面,Direct关注于系统模型的内部参数(即模型参数矩阵P的某一分量),基于当前(本自适应环中的)观测值直接推导该参数的当前值.Direct同样通过滑动窗口平滑观测误差对该检测变量的影响在模型偏差表示方面,Direct通过频域分析推导可使控制型自适应软件系统的控制器正常运作的内部参数的取值范围.在模型偏差判断方面,Direct通过比较当前估计的控制参数值是否处于其正常取值范围,决定该系统是否出现模型偏差现象.
基于贝叶斯的参数估计检测方法MoD2通过监测估计的模型参数后验分布是否处于安全区域来判断是否发生模型偏差[49-50].Tong等人[10]考虑模型参数值的内部抖动和各种观测误差提出了基于贝叶斯的模型导向偏差检测方法.
在系统模型方面,MoD2同样使用线性时不变系统为描述自适应软件系统的基础模型,并引入非确定性补偿项对系统模型进行精化.在检测变量估计方面,MoD2关注于系统模型的内部参数(即模型参数矩阵P的某一分量).MoD2额外考虑该参数随时间变化的系统噪声,将其建模为线性时变随机变量,通过贝叶斯过程实时估算该参数的概率分布.在模型偏差表示方面,MoD2通过频域分析推导可使控制型自适应软件系统的控制器正常运作的内部参数的取值范围,并将该范围作为安全区域.在模型偏差判断方面,MoD2通过计算当前估测的控制参数值处于安全区域内的置信度,决定该系统是否出现模型偏差现象.
2.4 影响检测有效性的因素
模型偏差检测的理论框架刻画了现有模型偏差检测方法的主要流程.结合图2所示的控制型自适应软件系统的基本架构,本文认为,影响检测有效性的主要因素包括控制信号、环境输入以及非确定性这3方面.下面分别对其进行讨论.
控制信号是控制型自适应软件系统中连接控制器和被管理系统的变量,直接决定了控制型自适应软件系统应对运行环境变化的适应能力.在模型偏差发生的过程中,控制器依照原有系统模型(式(2))所产生的控制信号不再能够高效、可靠地调节被管理系统的行为,这是导致系统异常状态的直接原因.因此检测方法能否有效刻画控制信号在控制型自适应软件系统中的作用,决定了其能否准确描述因模型偏差导致的系统行为,也就决定了其能否有效地检测模型偏差现象.
控制信号除了是系统模型(式(2))中的重要变量外,也对检测变量估计(式(3))和模型偏差表示(式(4))产生了一定的影响.在检测变量估计中,控制信号决定了观测变量序列D(T)到检测变量PΣ的映射关系.当控制信号能有效调节被管理系统行为时,该映射关系应符合系统模型的描述,即表示检测方法能够获取较准确的检测变量值;反之,检测方法对于检测变量的估算会存在较大的误差.在模型偏差表示中,控制信号主要影响安全区域所依赖的检测变量的个数,即需要从多少个自适应环中估算其对应的检测变量.如果控制信号在被管理系统的行为上存在放大效应(即控制信号的微小改变会引起被管理系统行为的较大波动),则安全区域所依赖的检测变量的个数应当尽可能小,以防止模型偏差导致正常系统行为在较短时间内快速发展为异常系统行为.反之,若控制信号在被管理系统的行为上存在缩小效应,则安全区域所依赖的检测变量的个数可以适量增加,牺牲及时性以换取模型偏差检测的准确性.
环境输入描述了控制型自适应软件系统获取到的外部环境信息.控制型自适应软件系统需要根据环境输入判断外部环境状况并调整自身行为.为了增强自适应系统应对不同环境的能力,在设计开发此类系统时,通常会尽可能多地采样被控制系统在不同环境下的运行,并以此确定控制型自适应软件系统的适用范围.当系统运行于某一未采样的环境中时,若该环境的特性不同于已采样的环境,则系统在该环境中运行时有较大可能发生模型偏差现象.
从检测模型偏差的角度出发,环境输入的多样性反映了模型偏差表示(式(4))中的安全范围.设计阶段采样的环境输入多样性越高,则对应划定的安全范围越大.运行阶段实际的环境输入多样性越高,则当前环境特性超出已划定的安全范围的可能性就越高.因此模型偏差检测方法能否有效反映不同环境输入下对应的模型偏差安全范围,决定了其能否准确判断当前系统行为是否超出了安全范围,也就决定了其能否有效地检测模型偏差现象.
除此之外,环境输入也影响着模型偏差检测的系统模型(式(2))和检测变量估计(式(3)).对前者而言,在建模中补偿环境输入对系统输出的影响有利于模型对被管理系统行为的精确描述;对后者而言,环境输入决定了观测变量序列D(T)的特征(如系统输出序列的高、低抖动),影响对检测变量的估计.
非确定性描述了存在于控制型自适应软件系统观测变量(如控制信号、系统输出和环境输入)的误差.在模型误差检测的过程中,非确定性会使检测变量估计(式(3))中所依据的观测变量序列D(T)的值偏离其实际值.而这种数值上的偏离又具有累加效应.如对于线性时变系统这类保留历史状态信息的系统模型而言,观测变量的误差会导致对系统内部参数的估计误差,而估计误差会随着自适应环数量的增加而累计,最终造成对检测变量的估计产生较大的误导.因此,检测方法能否有效处理非确定性对检测变量估计的不良影响,决定了其能否准确地获取检测变量的估计值,也就决定了其对模型偏差检测的准确性.
非确定性除了对检测变量估计(式(3))具有重要影响外,还对系统建模(式(2))和模型偏差表示(式(4))具有一定的影响.对前者而言,刻画非确定性有助于更加精确地描述被管理系统的行为;对后者而言,收集的运行记录中各变量的不确定性也会为检测变量的估计引入误差,影响检测的准确度.
3 场景特性
基于模型偏差检测的理论框架,根据2.4节归纳得到的影响检测有效性的3个主要因素,即控制信号、环境输入和非确定性,提出了3个特性指标,即控制信号强度、环境输入强度和非确定性强度,用于建立偏差场景特性的评价体系,并定义了这3个指标的量化公式.具体而言,各特性指标的量化公式为一个比值,其分子部分定量描述了各因素变化范围的峰值,分母部分对该峰值基于系统输出变化范围进行归一化处理.以自适应SWaT为例,各量化公式的分子部分分别表示因控制强度、环境输入和非确定性变化导致的水箱水位的变化峰值,而分母部分统一为水箱水位的变化范围值.
3.1 控制信号强度
控制信号强度IC描述了自适应软件系统中控制信号变化对模型偏差检测有效性影响的强度,其量化公式为
(6)
其中,u表示控制信号,控制信号变化值可取单位值![]() 和
和![]() 分别表示自适应软件系统模型中可观测属性和可控属性对应的辨识参数;n表示采样的模型偏差场景运行记录数量;y(i,j)表示第i个运行记录在第j个自适应环的系统输出;max表示求取各维度系统输出变化的最大值;
分别表示自适应软件系统模型中可观测属性和可控属性对应的辨识参数;n表示采样的模型偏差场景运行记录数量;y(i,j)表示第i个运行记录在第j个自适应环的系统输出;max表示求取各维度系统输出变化的最大值;  表示矩阵的Hadamard除法,即2个矩阵对应位置的元素相除.
表示矩阵的Hadamard除法,即2个矩阵对应位置的元素相除.
在式(6)中,分子表示控制信号对应的系统输出变化预测值.某一场景下,控制信号强度IC值越高,说明该场景下的系统输出越接近正常情况下的系统输出;控制信号强度IC值越低,则说明该场景下的系统输出与正常情况系统输出的区分度越高.
在自适应SWaT中,![]() 和
和![]() 分别对应于辨识参数
分别对应于辨识参数![]() 和
和![]() 式(6)分子部分对应表示在控制器作用下,各水箱正常水位变化预测值.在某一模型偏差场景中,该特性指标越高说明此模型偏差场景与正常情况的实测水位变化区分度越低;反之则说明该模型偏差场景与正常情况的实测水位变化区分度高.
式(6)分子部分对应表示在控制器作用下,各水箱正常水位变化预测值.在某一模型偏差场景中,该特性指标越高说明此模型偏差场景与正常情况的实测水位变化区分度越低;反之则说明该模型偏差场景与正常情况的实测水位变化区分度高.
3.2 环境输入强度
环境输入强度IE描述了自适应软件系统中环境输入变化对模型偏差检测有效性影响的强度,其量化公式为
![]()

![]()
(7)
其中,γ表示环境输入对系统内部状态线性影响的系数,可在自适应软件系统设计阶段辨识获得;a(i,j)表示第i个运行记录在第j个自适应环的实测环境输入;其他符号表示同式(6).
在式(7)中,分子表示环境输入变化导致系统输出最大变化的预测值.某一场景下,环境输入强度IE值越高,说明该场景下因环境输入变化引起的系统输出抖动越大;环境输入强度IE值越低说明该场景下因环境输入变化引起的系统输出抖动越小.
在自适应SWaT中,式(7)分子部分对应表示物理环境输入变化导致各水箱水位最大变化的预测值.在某一模型偏差场景中,环境输入强度IE值越高,说明因环境输入变化导致的水箱水位抖动越大;环境输入强度IE值越低,说明因环境输入变化导致的水箱水位抖动越小.
3.3 非确定性强度
非确定性强度IU描述了自适应软件系统中非确定性对模型偏差检测有效性影响的强度.这里的非确定性主要是基于自适应软件系统模型的各类观测误差,包括对控制信号、环境输入和系统输出的观测误差等.由于大多数观测误差均可以使用均值为0、方差为σ的正态分布进行描述,因此本文使用一个均值为0、方差为R的正态分布统一描述观测误差:
(8)
其中Q,W,V分别为控制信号观测误差的方差、环境输入观测误差的方差和系统输出观测误差的方差.
基于R,非确定性强度的量化公式为
(9)
其中m表示系统输出变化最大误差值相对于综合观测误差标准差的倍数.例如,根据正态分布的3 sigma准则,m=6.其他符号表示同式(6).
在式(9)中,分子表示系统输出变化测量最大误差值.某一场景下,非确定性强度IU值越高说明该场景下的系统输出实测值的误差越大;非确定性强度IU值越低说明该场景下的系统输出实测值的误差越小.
在自适应SWaT中,式(9)分子部分对应表示各水箱水位变化测量最大误差值.在某一模型偏差场景中,非确定性强度IU值越高说明水箱水位的误差值越大;非确定性强度IU值越低说明水箱水位的误差值越小.
4 实 验
基于3个控制型自适应软件系统,本文设计了不同的运行场景(包括被管理系统发生模型偏差的偏差场景和未发生模型偏差的正常场景),并在这些运行场景下比较2.3节所述的4种模型偏差检测方法的有效性.实验目标在于回答2个研究问题:
问题1. 4种模型偏差检测方法,即SWDetector,ARMA,Direct,MoD2,在不同运行场景中对模型偏差现象的检测效果如何.
问题2. 4种模型偏差检测方法各自适用的运行场景,分别可以用哪些特性指标区间加以刻画.
所有实验运行于1台配有8个CPU、16 GB内存的阿里云ECS服务器上.
4.1 实验配置
4.1.1 实验对象
一个实验对象是由一个被管理系统及其对应的控制器共同组成的一个控制型自适应软件系统.从自适应软件系统相关研究中选取3个常用软件系统作为被管理系统,同时基于已有工作为每个被管理系统提供相应的控制器.具体的3个实验对象的被管理系统和控制器为:
1) SWaT.如1.2节所述,SWaT的被管理系统是一个生产双重过滤饮用水的水处理系统.其控制器是由SWaT的开发人员基于控制论和领域知识精心设计的可编程逻辑控制器[25],保障水箱无溢出和空箱且净水产量最大化.
2) RUBiS.RUBiS的被管理系统是一个网络拍卖系统,常作为控制型自适应研究的实验对象[12,26,51].其控制器是一个依据PBM框架[9]设计的PID控制器,通过对服务器数量、工作状态的伸缩来适应用户负载,保障网站运营的快速响应和高资源利用率.
3) Encoder.Encoder的被管理系统是一个在线视频压缩系统,也常作为控制型自适应研究的实验对象[30,32,52].同样地,其控制器是一个依据PBM框架[9]设计的PID控制器,通过调整压缩算法的参数以平衡视频吞吐量和视频质量,保障流畅和清晰的视频流传输.
4.1.2 场景设计
运行场景的设计是基于一个五元组(envini,envdev,paraini,paradev,t).其中,envini和envdev分别表示正常情况和模型偏差下的环境输入,paraini和paradev分别表示正常情况和模型偏差下的模型参数,t表示模型偏差发生的时间点.实验对象首先依据envini和paraini进行初始化,当发生模型偏差时,环境输入变为envdev,模型参数变为paradev.
基于五元组的表示方法,根据已有工作将3个实验对象的运行划分为9个不同的运行场景,包括4个正常运行场景和5个模型偏差场景.每个运行场景对应于1个场景配置集合,具体如表1所示:
Table 1 Scenario Configurations
表1 场景配置

场景(场景配置数量)环境输入envini模型参数paraini模型偏差envdev或paradevSWaT1(200)从真实测试平台[34]中提取例如:阀门的摩擦系数值文献[25]中阀门的原始设置例如:阀门的进、出水量SWaT2(200)从真实测试平台[34]中提取例如:阀门的摩擦系数值文献[25]中阀门的原始设置例如:阀门的进、出水量根据文献[25]向系统阀门注入操作干扰例如:envdev表示将摩擦系数的值从0.0改为一个(0.0,0.35)中的随机值SWaT3(125)从真实测试平台[34]中提取例如:阀门的摩擦系数值文献[25]中阀门的原始设置例如:阀门的进、出水量根据文献[25]向系统内部通信注入网络攻击篡改水位传感器数值例如:paradev表示传感器数值由900mm篡改为1200mmSWaT4(75)从真实测试平台[34]中提取例如:阀门的摩擦系数值文献[25]中阀门的原始设置例如:阀门的进、出水量根据文献[25]向系统内部通信注入网络攻击篡改阀门开关信号例如:paradev表示将阀门的控制信号从0(关闭)篡改为1(打开)RUBiS1(98)基于文献[53]的真实工作负载生成的用户负载数据例如:用户请求的时间间隔数组文献[12]中RUBiS的原始设置例如:服务器的工作状态RUBiS2(102)基于文献[54]的真实工作负载生成的用户负载数据例如:用户请求的时间间隔数组文献[12]中RUBiS的原始设置例如:服务器的工作状态RUBiS3(200)基于2个真实工作负载[53]生成的用户负载数据例如:用户请求的时间间隔数组文献[12]中RUBiS的原始设置例如:服务器的工作状态根据文献[55]向系统设置注入攻击使其与运行环境不匹配例如:paradev表示将服务器的工作状态值从“低保真”更改为“高保真”Encoder1(200)基于已发布数据集[9]采集的视频流例如:道路交通视频流文献[9]中视频编码器的原始设置例如:图像压缩算法参数值Encoder2(200)基于已发布数据集[9]采集的视频流例如:道路交通视频流文献[9]中视频编码器的原始设置例如:图像压缩算法参数值引入不同类型的视频流例如:envdev表示将道路交通视频流替换为广告视频流
在正常运行场景中,整个自适应软件系统的envini=envdev且paraini=paradev,该场景配置下的运行记录称为阴性运行记录.在模型偏差场景中,当发生模型偏差时,envini或paraini改变为不同的envdev或paradev,该场景配置下的运行记录称为阳性运行记录.
正常运行场景对应的场景配置集合(即SWaT1,RUBiS1,RUBiS2)覆盖了现有工作对实验对象的原始设置[12].由于原始数据不可获取,Encoder1不能覆盖文献[9]的原始设置,可根据文献的描述生成场景配置.SWaT模型偏差场景对应的场景配置集合(即SWaT2,SWaT3,SWaT4)覆盖了SWaT中报告的模型偏差[25],包括物理摩擦磨损阀门导致的模型偏差(即SWaT2)、网络攻击篡改水位传感器数值导致的模型偏差(即SWaT3)和网络攻击阀门控制信号导致的模型偏差(即SWaT4).RUBiS模型偏差场景对应的场景配置集合(即RUBiS3)覆盖了RUBiS系统已知的模型偏差设置[55],即系统配置和运行环境不匹配.Encoder模型偏差场景对应的场景配置集合(即Encoder2)根据经验设计生成.SWaT3,SWaT4,RUBiS1,RUBiS3分别含有125,75,98,102个场景配置,而其他场景配置集合皆含有200个场景配置.
4.1.3 场景划分
对于一个运行场景,基于第3节提出的3个特性指标的量化值,进一步分类为6种特性场景之一.根据控制论中被广泛使用的稳态下外部波动导致的系统输出变化幅度不超过实际系统输出变化范围的5%这一假设[22],本文使用0.05作为划分各特性指标量化值的阈值,因为特性指标量化值本身已经在系统输出变化范围上进行了归一化.
具体而言,根据控制信号强度值将运行场景划分为高控制影响场景IC↑(即控制信号强度矩阵IC中存在元素值大于0.05)和低控制影响场景IC↓(即控制信号强度矩阵IC的所有元素值都小于0.05).同理可划分高、低环境影响场景IE↑和IE↓与高、低非确定性影响场景IU↑和IU↓.
根据所提出的3个特性指标计算9个运行场景的特性指标,并归类到划分的6种特性场景中,具体如表2所示:
Table 2 Scenario Characteristics
表2 场景特性
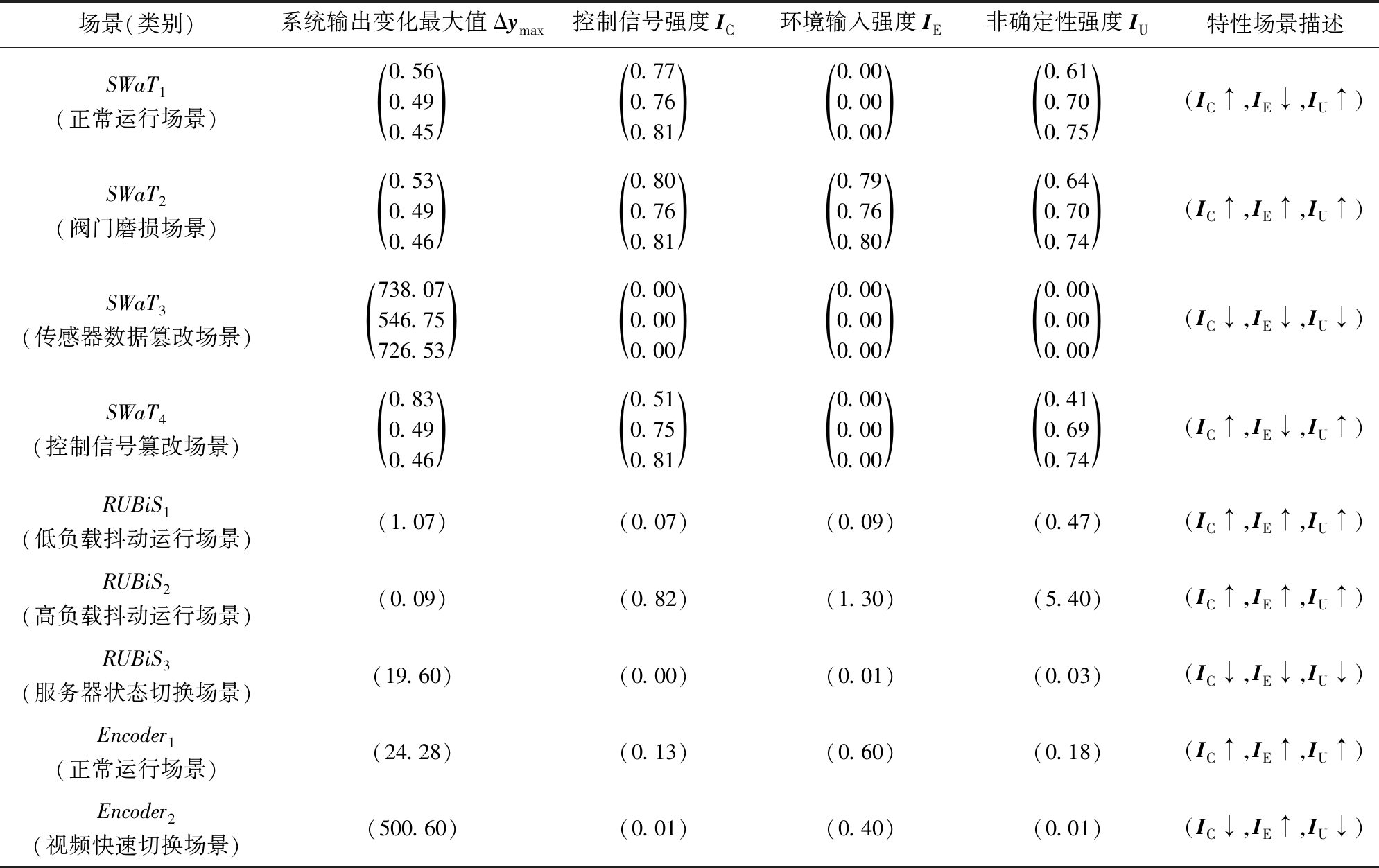
场景(类别)系统输出变化最大值Δymax控制信号强度IC环境输入强度IE非确定性强度IU特性场景描述SWaT1(正常运行场景)0.560.490.45()0.770.760.81()0.000.000.00()0.610.700.75()(IC↑,IE↓,IU↑)SWaT2(阀门磨损场景)0.530.490.46()0.800.760.81()0.790.760.80()0.640.700.74()(IC↑,IE↑,IU↑)SWaT3(传感器数据篡改场景)738.07546.75726.53()0.000.000.00()0.000.000.00()0.000.000.00()(IC↓,IE↓,IU↓)SWaT4(控制信号篡改场景)0.830.490.46()0.510.750.81()0.000.000.00()0.410.690.74()(IC↑,IE↓,IU↑)RUBiS1(低负载抖动运行场景)(1.07) (0.07)(0.09)(0.47)(IC↑,IE↑,IU↑)RUBiS2(高负载抖动运行场景)(0.09)(0.82)(1.30)(5.40)(IC↑,IE↑,IU↑)RUBiS3(服务器状态切换场景)(19.60)(0.00)(0.01)(0.03)(IC↓,IE↓,IU↓)Encoder1(正常运行场景)(24.28)(0.13)(0.60)(0.18)(IC↑,IE↑,IU↑)Encoder2(视频快速切换场景)(500.60)(0.01)(0.40)(0.01)(IC↓,IE↑,IU↓)
注:IC↑和IC↓表示高和低控制影响场景;IE↑和IE↓表示高和低环境影响场景;IU↑和IU↓表示高和低非确定性影响场景.
在SWaT中,传感器数据篡改场景(即SWaT3)下,系统输出变化显著,使其控制信号强度指标矩阵和非确定性强度指标矩阵元素值均为0.00,即SWaT3属于低控制影响场景和低非确定性影响场景,而其他3个运行场景(即SWaT1,SWaT2,SWaT4)下的系统输出变化较小,使其控制信号强度指标矩阵和非确定性强度指标矩阵元素值均大于0.05,即SWaT1,SWaT2,SWaT4属于高控制影响场景.阀门磨损场景(即SWaT2)下,阀门进、出水的流速因物理环境输入(即物理摩擦)显著变化,使其环境输入强度指标矩阵元素值大于0.05,即SWaT2属于高环境影响场景,而其他3个运行场景(即SWaT1,SWaT3,SWaT4)的环境输入对系统输出没有影响,即SWaT1,SWaT3,SWaT4属于低环境影响场景.
在RUBiS中,低、高负载抖动运行场景(即RUBiS1和RUBiS2)下的系统输出变化较小,使其3个特性指标矩阵元素值均大于0.05,即RUBiS1和RUBiS2都属于高控制影响场景、高环境影响场景和高非确定性影响场景.服务器状态切换场景(即RUBiS3)下系统输出变化较大,使其3个特性指标矩阵元素值均小于0.05,即RUBiS3属于低控制影响场景、低环境影响场景和低非确定性影响场景.
在Encoder中,正常运行场景(即Encoder1)下的系统输出变化较小,使其3个特性指标矩阵元素值均大于0.05,即Encoder1属于高控制影响场景、高环境影响场景和高非确定性影响场景.视频快速切换场景(即Encoder2)的系统输出变化显著,使其3个特性指标矩阵元素值均小于0.05,即Encoder2属于低控制影响场景、低环境影响场景和低非确定性影响场景.
4.1.4 评价标准
通过3个指标评价模型偏差检测方法在不同运行场景下检测的有效性.
1) 平均时间延迟(mean time delay, MTD).阳性运行记录从模型偏差时间点到检测报警时间点的平均时间间隔.
2) 漏报率(false negative, FN).阳性运行记录集合中被错误检测为阴性运行记录的百分比.
3) 误报率(false positive, FP).阴性运行记录集合中被错误检测为阳性运行记录的百分比,或者阳性运行记录集合中阴性部分被错误检测为阳性的百分比.
4.2 实验结果
实验针对问题1,统计9个运行场景下4种主流模型偏差检测方法的有效性,归一化对比分析每个运行场景的有效检测方法;针对问题2,统计6种特性场景下各检测方法的有效性指标均值,分析各检测方法适用的特性场景范围.
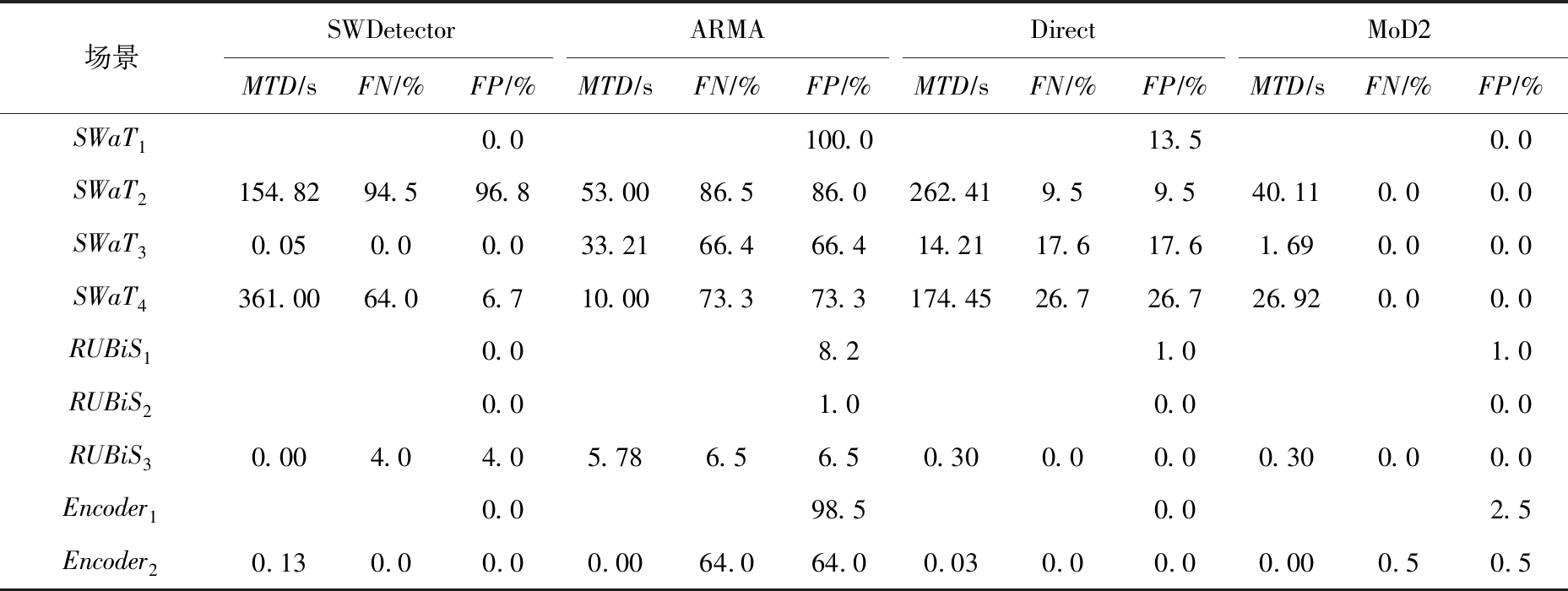
1) 针对问题1的方法有效性.表3显示了9个运行场景下4种主流模型偏差检测方法的有效性.其中,对于正常运行场景SWaT1,RUBiS1,RUBiS1和Encoder1,指标MTD和FN的值为空.
Table 3 Effectiveness of Different Scenarios with Each Detection Approach
表3 不同场景下各检测方法的有效性
场景SWDetectorARMADirectMoD2MTD∕sFN∕%FP∕%MTD∕sFN∕%FP∕%MTD∕sFN∕%FP∕%MTD∕sFN∕%FP∕%SWaT10.0100.013.50.0SWaT2154.8294.596.853.0086.586.0262.419.59.540.110.00.0SWaT30.050.00.033.2166.466.414.2117.617.61.690.00.0SWaT4361.0064.06.710.0073.373.3174.4526.726.726.920.00.0RUBiS10.08.21.01.0RUBiS20.01.00.00.0RUBiS30.004.04.05.786.56.50.300.00.00.300.00.0Encoder10.098.50.02.5Encoder20.130.00.00.0064.064.00.030.00.00.000.50.5
在SWaT正常运行场景SWaT1下,SWDetector和MoD2没有误报,Direct的FP值达到13.5%,而ARMA不适用于该运行场景(即FP值为100%).在SWaT阀门磨损场景SWaT2下,MoD2的3个指标值皆显著低于其他检测方法(即MTD值为40.11 s,FN值和FP值皆为0.0%);Direct的FN值和FP值皆显著低于SWDetector和ARMA,但MTD值最高(即262.41 s);ARMA的3个指标值皆低于SWDetector;SWDetector不仅MTD值高(仅低于Direct),而且FN值和FP值皆最高(即94.5%和96.8%).传感器数据篡改场景SWaT3下,SWDetector和MoD2的MTD值分别为0.05 s和1.69 s,且没有漏报和误报;Direct的3个指标值皆显著高于SWDetector和MoD2;而ARMA的3个指标值皆最高(即MTD值为33.21 s,FN值和FP值皆为66.4%).在控制信号篡改场景SWaT4下,MoD2的MTD值显著低于SWDetector和Direct,且没有漏报和误报;Direct的MTD值仅低于SWDetector,FP值仅低于ARMA;SWDetector虽然FP值显著低于ARMA和Direct,但MTD值最高(即361.00 s)且FN值高于Direct和MoD2;ARMA虽然MTD值最低(即10.00 s),但是FN值和FP值相同且皆最高(即73.3%).
在RUBiS的低负载抖动运行场景RUBiS1下,SWDetector没有误报,Direct和MoD2的FP值皆为1.0%,而ARMA的FP值为8.2%;在RUBiS的高负载抖动运行场景RUBiS2下,ARMA的FP值为1.0%,而其他3个检测方法没有误报;在RUBiS的服务器状态切换场景RUBiS3下,Direct和MoD2指标值相同(即MTD值为0.30 s,FN值和FP值皆为0.0%),SWDetector的MTD值最低(即0.00 s),但FN值和FP值皆高于Direct和MoD2,ARMA的MTD值、FN值和FP值皆最高(即5.78 s,6.5%,6.5%).
在Encoder正常运行场景Encoder1下,SWDetector和Direct皆没有误报,MoD2的FP值为2.5%,而ARMA的FP值高达98.5%.在Encoder的视频快速切换场景Encoder2下,MoD2的MTD值为0.00 s,FN值和FP值皆为0.5%;Direct和SWDetector的MTD值分别为0.03 s和0.13 s,且没有漏报和误报;ARMA的MTD值为0.00 s,但是FN值和FP值高达64.0%.
由于评价标准的3个指标描述了检测时延和检测准确度2个不同维度的有效性,需要对这3个指标做归一化和加权处理,从而获得一个归一化加权指标值来对比各检测方法的有效性.对于某一检测方法,其评价指标的归一化值为其评价指标值与各对比检测方法评价指标最小值之差和各对比检测方法评价指标值范围的比值.
由于检测时延的评价只使用MTD值这一个指标,而检测准确度的评价却使用FN值和FP值这2个不同角度的指标,考虑到检测时延和检测准确度2个维度的平衡,需为3个评价指标的归一化值添加相应的权重,即MTD值的归一化值权重为2,FN值和FP值的归一化值权重皆为1.则各检测方法有效性的归一化加权指标值为3个评价指标归一化值与权重乘积之和,其值越小表示有效性越好.具体如表4所示:
Table 4 Total Weight and Effectiveness Ranking of Different Scenarios with Each Detection Approach
表4 不同场景下各检测方法的总权重和有效性排序

场景SWDetector(S)ARMA(A)Direct(D)MoD2(M)检测有效性排序SWaT10.001.000.140.00S=M>D>ASWaT23.031.922.200.00M>A>D>SSWaT30.004.001.380.10S>M>D>ASWaT42.962.001.670.10M>D>A>SRUBiS10.001.000.120.12S>D=M>ARUBiS20.001.000.000.00S=D=M>ARUBiS31.234.000.100.10D=M>S>AEncoder10.001.000.000.03S=D>M>AEncoder22.002.000.460.02M>D>S=A
对于不同的运行场景,4种模型偏差检测方法的有效性排序存在差异.SWDetector在不同运行场景下的有效性差异最大,如该检测方法在SWaT的传感器数据篡改场景SWaT3下的有效性最好,却在SWaT的阀门磨损场景SWaT2下的有效性最差.ARMA在阀门磨损场景SWaT2下的有效性优于SWDetector和Direct,在控制信号篡改场景SWaT4下的有效性优于SWDetector,而其他运行场景皆差.Direct的有效性差异较大,如该检测方法在RUBiS的服务器状态切换场景RUBiS3下的有效性最好,而在SWaT3下的检测有效性劣于SWDetector和MoD2.MoD2在SWaT传感器数据篡改场景SWaT3下和RUBiS正常运行场景RUBiS1下的有效性劣于SWDetetor,在Encoder正常运行场景Encoder1下的有效性劣于SWDetector和Direct,而在其他运行场景下有效性皆优.
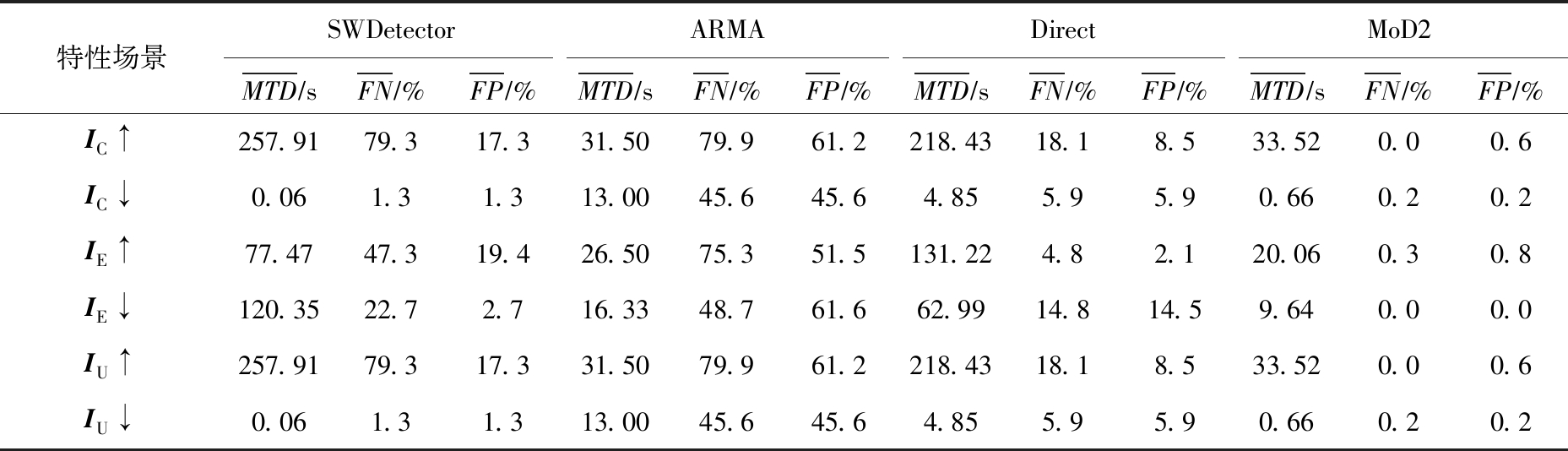
2) 针对问题2的方法适用性.表5显示了各模型偏差检测方法在划分的6种特性场景下的有效性,即MTD均值![]() 均值
均值![]() 和FP均值
和FP均值![]()
SWDetector在高控制影响场景和高非确定性影响场景(即IC↑和IU↑)下的![]() 皆为257.91 s,
皆为257.91 s,![]() 皆为
皆为![]() 皆为17.3%,而在低控制影响场景和低非确定性影响场景(即IC↓和IU↓)下的
皆为17.3%,而在低控制影响场景和低非确定性影响场景(即IC↓和IU↓)下的![]() 皆为
皆为![]() 和
和![]() 皆为1.3%.SWDetector在高环境影响场景(即IE↑)下的
皆为1.3%.SWDetector在高环境影响场景(即IE↑)下的![]() 和
和![]() 即47.3%和19.4%)约是其在低环境影响场景(即IE↓)下的2.1倍和7.2倍,而在IE↓下的
即47.3%和19.4%)约是其在低环境影响场景(即IE↓)下的2.1倍和7.2倍,而在IE↓下的![]() (即120.35 s)约是其在IE↑下的1.6倍.
(即120.35 s)约是其在IE↑下的1.6倍.
ARMA在高控制影响场景和高非确定性影响场景(即IC↑和IU↑)下的![]() 和
和![]() 即31.50 s,79.9%,61.2%)约是其在低控制影响场景和低非确定性影响场景(即IC↓和IU↓)下的2.4倍、1.8倍和1.3倍.ARMA在高环境影响场景(即IE↑)下的
即31.50 s,79.9%,61.2%)约是其在低控制影响场景和低非确定性影响场景(即IC↓和IU↓)下的2.4倍、1.8倍和1.3倍.ARMA在高环境影响场景(即IE↑)下的![]() 和
和![]() (即26.50 s和75.3%)约是其在低环境影响场景(即IE↓)下的1.6倍和1.5倍,而在IE↓下的
(即26.50 s和75.3%)约是其在低环境影响场景(即IE↓)下的1.6倍和1.5倍,而在IE↓下的![]() (即61.6%)约是其在IE↑下的1.2倍.
(即61.6%)约是其在IE↑下的1.2倍.
Direct在高控制影响场景和高非确定性影响场景(即IC↑和IU↑)下的![]() 皆为
皆为![]() 皆为
皆为![]() 皆为8.5%,而在低控制影响场景和低非确定性影响场景(即IC↓和IU↓)下的
皆为8.5%,而在低控制影响场景和低非确定性影响场景(即IC↓和IU↓)下的![]() 皆为
皆为![]() 和
和![]() 皆为5.9%.Direct在高环境影响场景(即IE↑)下的
皆为5.9%.Direct在高环境影响场景(即IE↑)下的![]() (即131.22 s)约是其在低环境影响场景(即IE↓)下的2.1倍,而在IE↓下的
(即131.22 s)约是其在低环境影响场景(即IE↓)下的2.1倍,而在IE↓下的![]() 和
和![]() (即14.8%和14.5%)约是其在IE↑下的3.1倍和6.9倍.
(即14.8%和14.5%)约是其在IE↑下的3.1倍和6.9倍.
MoD2在高控制影响场景和高非确定性影响场景(即IC↑和IU↑)下的![]() 皆为
皆为![]() 和
和![]() 分别为0.0%和0.6%,而在低控制影响场景和低非确定性影响场景(即IC↓和IU↓)下的
分别为0.0%和0.6%,而在低控制影响场景和低非确定性影响场景(即IC↓和IU↓)下的![]() 皆为
皆为![]() 和
和![]() 皆为0.2%.MoD2在高环境影响场景(即IE↑)下的
皆为0.2%.MoD2在高环境影响场景(即IE↑)下的![]() 为
为![]() 和
和![]() 分别为0.3%和0.8%,而在低环境影响场景(即IE↓)下的
分别为0.3%和0.8%,而在低环境影响场景(即IE↓)下的![]() 为9.64 s且没有漏报和误报.
为9.64 s且没有漏报和误报.
Table 5 Effectiveness of Each Detection Approach under Different Characteristic Scenarios
表5 各检测方法在不同特性场景下的有效性
特性场景SWDetectorARMADirectMoD2MTD∕sFN∕%FP∕%MTD∕sFN∕%FP∕%MTD∕sFN∕%FP∕%MTD∕sFN∕%FP∕%IC↑257.9179.317.331.5079.961.2218.4318.18.533.520.00.6IC↓0.061.31.313.0045.645.64.855.95.90.660.20.2IE↑77.4747.319.426.5075.351.5131.224.82.120.060.30.8IE↓120.3522.72.716.3348.761.662.9914.814.59.640.00.0IU↑257.9179.317.331.5079.961.2218.4318.18.533.520.00.6IU↓0.061.31.313.0045.645.64.855.95.90.660.20.2
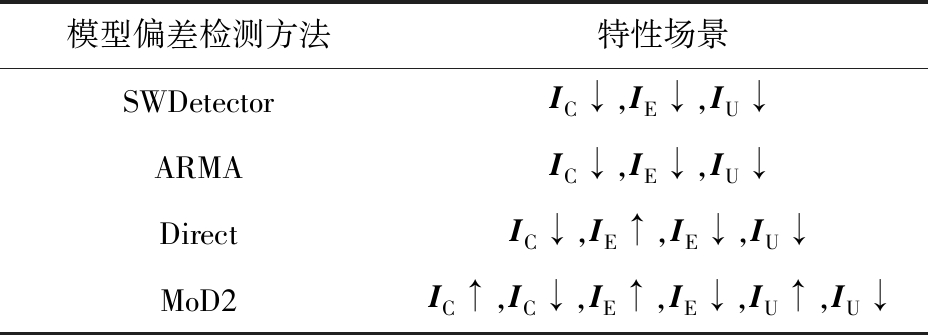
综上,4种主流模型偏差检测方法适用的特性场景如表6所示:
Table 6 Applicability of Each Detection Approach
表6 各检测方法适用性
模型偏差检测方法特性场景SWDetectorIC↓,IE↓,IU↓ARMAIC↓,IE↓,IU↓DirectIC↓,IE↑,IE↓,IU↓MoD2IC↑,IC↓,IE↑,IE↓,IU↑,IU↓
SWDetector通过自适应软件系统的系统输出变化检测模型偏差.如果自适应软件系统模型偏差场景下的系统输出变化与正常情况的区分度越大,则该检测方法的有效性越好,反之则没有考虑控制信号因素.因此,SWDetector适用于低控制影响场景IC↓.SWDetector通过滑动窗口综合考虑连续多次的系统输出值,从而平滑观测误差,但该补偿操作对于高非确定性因素的补偿效果有限.因此,SWDetector适用于低非确定性影响场景IU↓.由于SWDetector在建模自适应软件系统时未考虑环境输入,使环境输入导致的系统输出显著变化会降低检测的有效性,因此SWDetector适用于低环境影响场景IE↓.
ARMA使用自回归模型描述模型偏差对于系统输出的影响.自适应软件系统模型偏差场景下的系统输出变化与正常情况的区分度越大,则该方法的有效性越好,反之则难以检测.因此,ARMA适用于低控制影响场景IC↓.ARMA方法通常将环境输入和非确定性因素视为影响自适应软件系统整体行为的一个外部扰动,并通过控制系统的稳定性加以处理,并没有引入单独的机制进行应对.因此,ARMA适用于低环境影响场景IE↓和低非确定性影响场景IU↓.
Direct基于标称模型,引入环境输入建模自适应软件系统.因此,Direct适用于任何环境影响场景IE↑和IE↓.自适应软件系统模型偏差场景下的系统输出变化与正常情况的区分度越大,则模型参数估计值越容易超出安全区域,反之越容易被其他特性影响留在安全区域内.因此,Direct适用于低控制影响场景IC↓.由于控制信号的变化,Direct的补偿操作(即滑动窗口方法)不能有效平滑高非确定性因素.因此,Direct适用于低非确定性影响场景IU↓.
MoD2基于标称模型,建模了模型参数,添加了环境输入和各种非确定性补偿项,因此适用于所分类的6种特性场景.
由上述分析可知,MoD2在检测模型偏差时可以有效地覆盖不同的偏差场景.但相比于其他方法,MoD2需要开发人员在设计系统时额外计算更多的信息(如模型参数值的先验分布和非确定性补偿项的参数值),且在检测变量估计的过程中使用了计算量更大的贝叶斯方法,在性能上带来了额外的开销.这些额外的开销使得MoD2能够应对各种高影响场景(即IC↑,IE↑,IU↑),但却不能在低影响场景中相比其他部分方法提升其检测有效性.因此我们认为,在应对各种低影响场景时,可以综合使用滑窗这类的低成本检测方法,以平衡检测方法的有效性和性能开销.
4.3 有效性威胁
实证结论有效性的威胁包括实验对象、实现的模型偏差检测方法以及场景特性3个指标的内在联系.
本文只使用了3个自适应软件系统作为实验对象,这可能会影响实验结论的普遍性.为了进行实验,需要对被管理系统及其控制论设计的控制器有充分的了解.这一要求限制了对可能的实验对象的选择.尽管如此,所选择的实验对象代表了不同平台(包括网络系统和信息物理融合系统)和架构(包括单控制器和多控制器)的自适应软件系统.此外,所选自适应软件系统都被其他自适应研究人员广泛用作实验对象或研究案例.
本文实现了4个模型偏差检测方法.这4个检测方法的实现可能无法完全代表4种主流模型偏差检测方法的真实有效性.但是,这4个检测方法都是依据已有的文献描述实现,其有效性已经在相关文献中得到了证明.因此,所实现的检测方法可以比较好地反映所代表的模型偏差检测方法的有效性.
与控制论使用精确的数学模型去描述运行场景不同,基于模型偏差检测框架,对影响模型偏差检测方法的有效性的因素进行分析(即控制信号、环境输入和非确定性3个主要因素对模型偏差检测方法有效性的影响),由此定义了3个量化指标去描述运行场景在检测有效性影响层面上的特性.因此,3个指标代表自适应软件系统3个不同维度的检测有效性影响因素的特性.
5 相关工作
软件控制论是软件工程的一个重要分支,其核心在于使用控制论的方法来解决软件工程中的问题.现有工作中,软件控制论已广泛运用于软件的需求、实现、测试等各个方面[56].在软件需求方面,控制论将反馈控制环用于需求提升.Xu等人[57]使用控制论来定义一个需求工程过程控制系统.Liu等人[58]将数据驱动的需求激发过程表示为一个反馈控制系统,需求激发变成了对用户行为模型的不断优化.在软件设计实现方面,控制论关注将控制论系统地引入以提高软件的可靠性.Patikirikorala等人[3]系统总结了设计自适应软件系统的控制工程方法.Shevtsov等人[4]从系统建模、控制技术和控制属性3个方面系统分析了现有控制型自适应研究.在软件测试方面,控制论方法可以定量地预测测试过程的趋势,并帮助管理者分配测试资源.Cangussu等人[59]使用反馈控制来调整测试过程的参数.Zhang等人[60]遵循软件控制论,提出了基于历史的动态随机软件测试,改进了传统的随机测试和随机划分测试策略.
控制型自适应软件系统的开发首先需要建立被管理系统的标称模型.在早期,标称模型可从已知的复杂系统架构模型中推导获得.Checiu等人[61]从Web服务系统的服务器请求模型中推导出对应的常微分方程.Filieri等人[62-63]从应用程序的离散时间马尔可夫链模型中推导出对应的数学方程.推导出的标称模型虽然能够较好地描述软件系统的行为,但要求开发人员同时具备软件工程和控制论2方面的专业知识.为了降低开发人员的负担,同时更好地理解和推理实现的自适应软件系统的行为,Filieri等人[9]提出了PBM框架,该框架给出了自适应软件系统的自动化设计过程,理论保证实现的自适应软件系统具有所需的控制属性.基于PBM框架,不同类型的标称模型和各种控制技术被引入用来应对不同的软件自适应场景[5].然而,基于数据驱动的标称模型更加凸显模型偏差问题,使得各种模型偏差检测方法应运而生.面对各种检测方法,需要一个指导向的工作帮助选择有效的模型偏差检测方法,实现可靠运行的自适应软件系统.本文从模型偏差场景角度,分析了各模型偏差检测方法适用的特性场景,辅助检测方法的有效选择.
模型偏差问题自控制型自适应软件系统被提出以来一直备受关注.现有工作对模型偏差问题的处理方式大致分为3类:第1类是设计鲁棒控制器去容忍模型偏差.Baresi等人[51]使用灰盒离散时间反馈控制器实现鲁棒的自适应软件系统.第2类是采用学习、滤波等技术实现标称模型的在线更新.Filieri等人[28]使用学习机制保持标称模型参数辨识值在系统运行时不断更新.Maggio等人[30]使用卡尔曼滤波,通过更新标称模型的状态变量值达到修改标称模型参数辨识值的目的.这2类处理方式基本解决了标称模型参数辨识值的轻微偏差.第3类是模型偏差检测.该类处理方式关注会使自适应软件系统的理论保证失效,可能导致被管理系统行为异常的模型偏差.在线检测这类模型偏差对自适应软件系统的可靠运行至关重要.PBM框架也考虑了模型偏差问题,并提供了基于滑窗的系统输出检测方法实时检测由于模型偏差导致的系统异常行为.He等人[22]针对控制型CPS,提出了基于自回归的系统输出检测方法,用于检测由于软件bug导致的模型偏差.Tong等人[10]针对现有检测方法没有平衡检测及时性和准确性的问题,提出了基于贝叶斯参数估计的检测方法.对于模型偏差检测,现有工作专注于针对不同的被管理系统和模型偏差场景提出既快又准的检测方法.据我们所知,现有工作缺乏对不同偏差场景下各检测方法适用性的系统化研究.本文通过大量实验分析和描述了4种主流模型偏差检测方法的适用性,为实现可靠自适应软件系统时如何选择有效的检测方法提供了实证研究支持.
传统控制论同样关注模型偏差检测问题,并提出了各种检测方法.Webber等人[64]利用系统输出抖动与模型预测误差的相似度来检测模型偏差.Badwe等人[65]提出了一个基于分析控制信号和模型残差之间的偏相关性的检测方法.Ji等人[66]通过对比估计过程的频率响应与基于模型的频率响应,检测多变量模型预测控制的模型偏差.Wang等人[67]提出一种基于子空间法的模型偏差检测方法.Yin等人[68]提出了一种数据驱动方法来检测模型偏差,该方法结合子空间法和滑动窗口来估计标称模型的参数值.Tsai等人[69]使用2个系统辨识步骤来检测和定位模型偏差.控制领域关于偏差检测方法的实证研究关注在相同实例下对比各检测方法的优劣.Iqbal等人[70]对比了基于带输入自回归(autoregressive with exogenous inputs, ARX)模型和有限冲激响应(finite impulse response, FIR)模型的2种检测方法,表明在实例下基于ARX模型的检测方法要优于基于FIR模型的检测方法.Uddin等人[14]基于实例对比了ARX模型和带输入自回归滑动平均(autoregressive-moving-average with exogenous inputs, ARMAX)模型的2种偏差检测方法,表明使用ARMAX建模受控物理系统能以更少的模型阶数达到更好的检测效果.而本文的实证研究关注每个检测方法适用的实例有哪些特性.
6 总 结
本文通过实验对控制型自适应软件系统的模型偏差方法在不同模型偏差场景下的适用性进行研究.基于提出的模型偏差检测框架中对模型偏差检测有效性产生影响的3个维度(即控制信号、环境输入和非确定性),提出一套特性指标,即控制信号强度、环境输入强度和非确定性强度,来描述模型偏差场景,并根据系统输出稳定性假设,为3个特性指标划分6种不同特性场景.基于3个自适应软件系统生成的9个运行场景,实验分析4种主流模型偏差检测方法适用的特性场景范围.
作者贡献声明:童燕翔与秦逸完成研究构思、实验设计、数据分析和论文写作;马晓星指导研究选题、方法设计以及论文修改等.全体作者都阅读并同意最终的文本.
[1]De Lemos R, Giese H, Müller H A, et al. Software engineering for self-adaptive systems: A second research roadmap[M] //Software Engineering for Self-Adaptive Systems II.Berlin: Springer, 2013: 1-32
[2]Weyns D. Software engineering of self-adaptive systems[M] //Handbook of Software Engineering. Berlin: Springer, 2017: 399-443
[3]Patikirikorala T, Colman A, Han Jun,et al. A systematic survey on the design of self-adaptive software systems using control engineering approaches[C] //Proc of the 7th Int Symp on Software Engineering for Adaptive and Self-Managing Systems. Piscataway, NJ: IEEE, 2012: 33-42
[4]Shevtsov S, Berekmeri M, Weyns D, et al. Control-theoretical software adaptation: A systematic literature review[J]. IEEE Transactions on Software Engineering, 2017, 44(8): 784-810
[5]Shevtsov S, Weyns D. Keep it simplex: Satisfying multiple goals with guarantees in control-based self-adaptive systems[C] //Proc of the 24th ACM SIGSOFT Int Symp on Foundations of Software Engineering. New York: ACM, 2016: 229-241
[6]Filieri A, Maggio M, Angelopoulos K, et al. Software engineering meets control theory[C] //Proc of the 10th Int Symp on Software Engineering for Adaptive and Self-Managing Systems. Piscataway, NJ: IEEE, 2015: 71-82
[7]Litoiu M, Shaw M, Tamura G, et al. What can control theory teach us about assurances in self-adaptive software systems?[M] //Software Engineering for Self-Adaptive Systems III. Berlin: Springer, 2017: 90-134
[8]Zhu Xiaoyun, Uysal M, Wang Zhikui, et al. What does control theory bring to systems research?[J]. ACM SIGOPS Operating Systems Review, 2009, 43(1): 62-69
[9]Filieri A, Hoffmann H, Maggio M. Automated design of self-adaptive software with control-theoretical formal guarantees[C] //Proc of the 36th Int Conf on Software Engineering. New York: ACM, 2014: 299-310
[10]Tong Yanxiang, Qin Yi, Jiang Yanyan, et al. Timely and accurate detection of model deviation in self-adaptive software-intensive systems[C] //Proc of the 29th ACM Joint European Software Engineering Conf and Symp on the Foundations of Software Engineering. New York: ACM, 2021: 168-180
[11]Shevtsov S, Weyns D, Maggio M. SimCA*: A control-theoretic approach to handle uncertainty in self-adaptive systems with guarantees[J]. ACM Transactions on Autonomous and Adaptive Systems, 2019, 13(4): 1-34
[12]Moreno G A, Cámara J, Garlan D, et al. Proactive self-adaptation under uncertainty: A probabilistic model checking approach[C] //Proc of the 10th Joint Meeting on Foundations of Software Engineering. New York: ACM, 2015: 1-12
[13]Loeff M V, Kuramoto A S R, Garcia C. Structures’ influence on model-plant mismatch detection methods in MPC using partial correlation[C] //Proc of the 11th Portuguese Conf on Automatic Control. Berlin: Springer, 2015: 61-70
[14]Uddin F, Tufa L D, Yousif S M T, et al. Comparison of ARX and ARMAX decorrelation models for detecting model-plant mismatch[J]. Procedia Engineering, 2016, 148: 985-991
[15]Yang Zhuoqun, Jin Zhi. Self-adaptive decision making under uncertainty in environment and requirements[J]. Journal of Computer Research and Development, 2018, 55(5): 1014-1033 (in Chinese)(杨卓群, 金芝. 面向环境与需求不确定性的系统自适应决策[J]. 计算机研究与发展, 2018, 55(5): 1014-1033)
[16]Song Hui, Raj A, Hajebi S, et al. Model-based cross-layer monitoring and adaptation of multilayer systems[J]. Science China Information Sciences, 2013, 56(8): 1-15
[17]Chen Xing, Chen Shihong, Ma Yun, et al. An adaptive offloading framework for Android applications in mobile edge computing[J]. Science China Information Sciences, 2019, 62(8): 1-17
[18]Kephart J O, Chess D M. The vision of autonomic computing[J]. Computer, 2003, 36(1): 41-50
[19]Filieri A, Maggio M, Angelopoulos K, et al. Control strategies for self-adaptive software systems[J]. ACM Transactions on Autonomous and Adaptive Systems, 2017, 11(4): 1-31
[20]Ljung L.System Identification[M] //Signal Analysis and Prediction. Boston, MA: AP Professional, 1998: 163-173
[21]Datta A, Ho M T, Bhattacharyya S P.Structure and Synthesis of PID Controllers[M]. London: Springer, 1999
[22]He Zhijian, Chen Yao, Huang Enyan, et al. A system identification based Oracle for control-CPS software fault localization[C] //Proc of the 41st Int Conf on Software Engineering. Piscataway, NJ: IEEE, 2019: 116-127
[23]Angelopoulos K, Papadopoulos A V, Souza V E S, et al. Model predictive control for software systems with CobRA[C] //Proc of the 11th Int Symp on Software Engineering for Adaptive and Self-Managing Systems. Piscataway, NJ: IEEE, 2016: 35-46
[24]Incerto E, Tribastone M, Trubiani C. Software performance self-adaptation through efficient model predictive control[C] //Proc of the 32nd IEEE/ACM Int Conf on Automated Software Engineering. Piscataway, NJ: IEEE, 2017: 485-496
[25]Chen Yuqi, Poskitt C M, Sun Jun. Learning from mutants: Using code mutation to learn and monitor invariants of a cyber-physical system[C] //Proc of the 39th IEEE Symp on Security and Privacy. Piscataway, NJ: IEEE, 2018: 648-660
[26]Klein C, Maggio M, Årzén K E, et al. Brownout: Building more robust cloud applications[C] //Proc of the 36th Int Conf on Software Engineering. New York: ACM, 2014: 700-711
[27]Johnson M A, Moradi M H. PID Control[M]. London: Springer, 2005
[28]Filieri A, Hoffmann H, Maggio M. Automated multi-objective control for self-adaptive software design[C] //Proc of the 10th Joint Meeting on Foundations of Software Engineering. New York: ACM, 2015: 13-24
[29]Camacho E F, Alba C B. Model Predictive Control[M]. London: Springer, 2013
[30]Maggio M, Papadopoulos A V, Filieri A, et al. Automated control of multiple software goals using multiple actuators[C] //Proc of the 11th Joint Meeting on Foundations of Software Engineering. New York: ACM, 2017: 373-384
[31]Angelopoulos K, Papadopoulos A V, Souza V E S, et al. Engineering self-adaptive software systems: From requirements to model predictive control[J]. ACM Transactions on Autonomous and Adaptive Systems, 2018, 13(1): 1-27
[32]Mandrioli C, Maggio M. Testing self-adaptive software with probabilistic guarantees on performance metrics[C] //Proc of the 28th ACM Joint Meeting on European Software Engineering Conf and Symp on the Foundations of Software Engineering. New York: ACM, 2020: 1002-1014
[33]Hellerstein J L, Diao Yixin, Parekh S, et al. Feedback Control of Computing Systems[M]. Hoboken, NJ: John Wiley & Sons, 2004
[34]Aung K M.Secure Water Treatment Testbed (SWaT): An Overview[M/OL]. Singapore University of Technology and Design, 2015[2022-03-28]. https://itrust.sutd.edu.sg/wp-content/uploads/sites/3/2018/03/Brief-Introduction-to-SWaT-260318.pdf
[35]Vargas J V C, Parise J A R. Simulation in transient regime of a heat pump with closed-loop and on-off control[J]. International Journal of Refrigeration, 1995, 18(4): 235-243
[36]Fecarotta O, Martino R, Morani M C.Wastewater pump control under mechanical wear[J]. Water, 2019, 11(6): 1210
[37]Tong Yanxiang. Technical documentation of model deviation detection approaches[EB/OL]. (2021-12-21)[2022-03-28]. https://github.com/tongyanxiang/JournalCRD
[38]Gustafsson F. Adaptive Filtering and Change Detection[M]. New York: Wiley, 2000
[39]Eren U, Prach A, Koçer B B, et al. Model predictive control in aerospace systems: Current state and opportunities[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(7): 1541-1566
[40]Kannan S, Alamdari S A S, Dentler J, et al. Model predictive control for cooperative control of space robots[G] //AIP Conference Proceedings 1798: Proc of the 11th Int Conf on Mathematical Problems in Engineering, Aerospace and Sciences. Melville, NY: AIP Publishing LLC, 2016: 020068
[41]Dentler J, Kannan S, Mendez M A O, et al. A tracking error control approach for model predictive position control of a quadrotor with time varying reference[C] //Proc of the Int Conf on Robotics and Biomimetics. Piscataway, NJ: IEEE, 2016: 2051-2056
[42]Sebeke L, Luo Xi, De Jager B, et al. Model predictive control algorithm for large-area regional hyperthermia[J]. Journal of Therapeutic Ultrasound, 2016, 4(1): 107-113
[43]Yang Junxing, Grosu R, Smolka S A, et al. Love thy neighbor: V-formation as a problem of model predictive control[C] //Proc of the 27th Int Conf on Concurrency Theory. Dagstuhl, Germany: Schloss Dagstuhl, 2016: 4:1-4:5
[44]Jain A, Biyik E, Chakrabortty A. A model predictive control design for selective modal damping in power systems[C] //Proc of the American Control Conf. Piscataway, NJ: IEEE, 2015: 4314-4319
[45]Weiss A, Baldwin M, Erwin R S, et al. Model predictive control for spacecraft rendezvous and docking: Strategies for handling constraints and case studies[J]. IEEE Transactions on Control Systems Technology, 2015, 23(4): 1638-1647
[46]Choi B S. ARMA Model Identification[M]. Berlin: Springer, 2012
[47]Isermann R. Estimation of physical parameters for dynamic processes with application to an industrial robot[C] //Proc of the American Control Conf. Piscataway, NJ: IEEE, 1990: 1396-1401
[48]Ma Jianping, Jiang Jin. Applications of fault detection and diagnosis methods in nuclear power plants: A review[J]. Progress in Nuclear Energy, 2011, 53(3): 255-266
[49]Huang Biao. Bayesian methods for control loop monitoring and diagnosis[J]. Journal of Process Control, 2008, 18(9): 829-838
[50]Jiang Qingchao, Huang Biao. Distributed monitoring for large-scale processes based on multivariate statistical analysis and Bayesian method[J]. Journal of Process Control, 2016, 46: 75-83
[51]Baresi L, Guinea S, Leva A, et al. A discrete-time feedback controller for containerized cloud applications[C] //Proc of the 24th ACM SIGSOFT Int Symp on Foundations of Software Engineering. New York: ACM, 2016: 217-228
[52]Maggio M, Papadopoulos A V, Filieri A, et al. Self-adaptive video encoder: Comparison of multiple adaptation strategies made simple[C] //Proc of the 12th Int Symp on Software Engineering for Adaptive and Self-Managing Systems. Piscataway, NJ: IEEE, 2017: 123-128
[53]Arlitt M, Jin Tai. A workload characterization study of the 1998 world cup Web site[J]. IEEE Network, 2000, 14(3): 30-37
[54]Arlitt M F, Williamson C L. Web server workload characterization: The search for invariants[J]. ACM SIGMETRICS Performance Evaluation Review, 1996, 24(1): 126-137
[55]Alshahwan N, Harman M. Automated Web application testing using search based software engineering[C] //Proc of the 26th IEEE/ACM Int Conf on Automated Software Engineering. Piscataway, NJ: IEEE, 2011: 3-12
[56]Yang Hongji, Chen Feng, Aliyu S. Modern software cybernetics: New trends[J]. Journal of Systems and Software, 2017, 124: 169-186
[57]Xu Hong, Sawyer P, Sommerville I. Requirement process establishment and improvement from the viewpoint of cybernetics[J]. Journal of Systems and Software, 2006, 79(11): 1504-1513
[58]Liu Lin, Zhou Qing, Liu Jilei, et al. Requirements cybernetics: Elicitation based on user behavioral data[J]. Journal of Systems and Software, 2017, 124: 187-194
[59]Cangussu J W, DeCarlo R A, Mathur A P. A formal model of the software test process[J]. IEEE Transactions on Software Engineering, 2002, 28(8): 782-796
[60]Zhang Lei, Yin Beibei, Lü Junpeng, et al. A history-based dynamic random software testing[C] //Proc of the 38th Int Computer Software and Applications Conf Workshops. Piscataway, NJ: IEEE, 2014: 31-36
[61]Checiu L, Solomon B, Ionescu D, et al. Observability and controllability of autonomic computing systems for composed Web services[C] //Proc of the 6th IEEE Int Symp on Applied Computational Intelligence and Informatics. Piscataway, NJ: IEEE, 2011: 269-274
[62]Filieri A, Ghezzi C, Leva A, et al. Self-adaptive software meets control theory: A preliminary approach supporting reliability requirements[C] //Proc of the 26th IEEE/ACM Int Conf on Automated Software Engineering. Piscataway, NJ: IEEE, 2011: 283-292
[63]Filieri A, Ghezzi C, Leva A, et al. Reliability-driven dynamic binding via feedback control[C] //Proc of the 7th Int Symp on Software Engineering for Adaptive and Self-Managing Systems. Piscataway, NJ: IEEE, 2012: 43-52
[64]Webber J R, Gupta Y P. A closed-loop cross-correlation method for detecting model mismatch in MIMO model-based controllers[J]. ISA Transactions, 2008, 47(4): 395-400
[65]Badwe A S, Gudi R D, Patwardhan R S, et al. Detection of model-plant mismatch in MPC applications[J]. Journal of Process Control, 2009, 19(8): 1305-1313
[66]Ji Guoli, Zhang Kangkang, Zhu Yucai. A method of MPC model error detection[J]. Journal of Process Control, 2012, 22(3): 635-642
[67]Wang Hong, Song Zhihuan, Xie Lei. Parametric mismatch detection and isolation in model predictive control system[J]. IFAC Proceedings Volumes, 2012, 45(15): 154-159
[68]Yin Feng, Wang Hong, Xie Lei, et al. Data driven model mismatch detection based on statistical band of Markov parameters[J]. Computers & Electrical Engineering, 2014, 40(7): 2178-2192
[69]Tsai Y, Gopaluni R B, Marshman D, et al. A novel algorithm for model-plant mismatch detection for model predictive controllers[J]. IFAC-PapersOnLine, 2015, 48(8): 746-752
[70]Iqbal N H K, Yusoff N, Tufa L D. Comparison between ARX and FIR decorrelation models in detecting model-plant mismatch[J]. Journal of Applied Sciences, 2014, 14(15): 1711-1719


