在实际应用中,人们可能要在不同的粒度下对同一对象进行观察、表示、分析和决策,即对一个对象和某个属性,根据实际问题的不同粒度层次的需要,可取不同的值.针对上述多粒度描述的问题,Wu等人[1]提出了一种称为多尺度信息系统的知识表示系统.在多尺度信息系统中,一个对象根据不同的度量尺度,在每个属性上可以有多个不同取值,且不同尺度空间存在从细到粗的信息粒转换.多尺度广泛存在于地理空间分布、图像分析等多个研究领域[2-9].
目前,学者已经对多尺度信息系统进行了大量研究.Wu等人[1,10-11]介绍了多尺度决策系统的最优尺度选择方法及规则获取.从一致性角度考虑,Xu等人[12]及Wu等人[13-15]研究了多尺度决策系统的最优尺度选择方法.Hao等人[16]考虑到数据的动态变化,利用三支决策的方法研究了动态多尺度决策系统的最优尺度选择方法.铁文彦等人[17]讨论了对象动态更新情况下多粒度决策系统的最优粒度选择.顾沈明等人[18]定义了局部最优粒度,研究了多尺度决策系统的局部最优粒度和规则提取方法.Chen等人[19]为了简化最优尺度选择的计算过程,研究了基于矩阵的多尺度决策系统的最优尺度选择方法.以上研究假设多尺度信息系统中所有属性都具有相同尺度级数,Li等人[20]针对每个属性具有不同尺度级数的情况,定义了广义多尺度信息系统,并提出补充模型和格点模型来分析广义多尺度决策系统的最优尺度选择,此后又提出了基于属性重要度的逐步最优尺度选择方法[21].Wu等人[22]讨论了广义多尺度决策系统中几种最优尺度组合之间的关系.牛东苒等人[23]通过引入概率粗糙集,研究了可变精度下广义多尺度决策系统的最优尺度选择方法.Cheng等人[24-25]提出了基于序贯三支决策的最优尺度选择和属性约简方法.
文献[1-25]研究假设对象在属性各个尺度的取值都是唯一的,然而一些实际问题却不满足这一假设[26-31].为此,陈艳等人[32]提出了多尺度集值信息系统,给出了4种最优尺度选择方法,并讨论了在一致/不一致多尺度集值信息系统中它们之间的关系.该研究假设所有属性具有相同的尺度级数,使得属性只能在同一个尺度下进行组合.其次,最优尺度选择仅考虑决策系统的一致性或不确定性,忽略了实际应用中的代价问题,无法满足用户的个性化需求.
于是,针对不同属性具有不同数量的尺度及获取不同尺度数据的代价不同2个问题,本文对多尺度集值信息系统进行了扩展,提出具有代价的广义多尺度集值信息系统.在广义多尺度集值信息系统中,每个属性的尺度级数不同,在遍历每个属性的所有尺度时,针对尺度组合爆炸问题,提出了一种尺度空间更新方法,有效减少尺度空间中尺度组合数量;然后,综合考虑不确定性和代价2个因素的影响,提出了其最优尺度选择方法,可以快速地找到决策或分类结果最优且满足用户需求的尺度.
1 基本概念
本节主要介绍多尺度信息系统[1]及多尺度集值信息系统[32]的基本概念.
定义1[1,32]. 多尺度信息系统可以表示为一个四元组S=(U,A,V,F).其中,U={x1,x2,…,xn}为论域;A={a1,a2,…,am}是一个非空有限属性集,且每个属性aj∈A都是多尺度属性,即对于论域U中的每个对象,关于属性aj∈A在不同尺度下可得到不同的值;V是属性值的集合,即![]() 是属性aj在第k尺度的值域;F:U×A→V是对象x关于属性取值的映射函数.S=(U,A∪{d},V,F)称为多尺度决策系统,其中d∉A,d:U→Vd是单尺度决策属性.
是属性aj在第k尺度的值域;F:U×A→V是对象x关于属性取值的映射函数.S=(U,A∪{d},V,F)称为多尺度决策系统,其中d∉A,d:U→Vd是单尺度决策属性.
若F:U×A→2V,即对象x关于属性![]() 的取值
的取值![]() 是一个集值,则S=(U,A,V,F)称为多尺度集值信息系统,S=(U,A∪{d},V,F)称为多尺度集值决策系统.
是一个集值,则S=(U,A,V,F)称为多尺度集值信息系统,S=(U,A∪{d},V,F)称为多尺度集值决策系统.
假设所有的属性具有I个尺度,则多尺度集值决策系统可以表示为![]() 对于1≤k≤I-1,存在满射函数
对于1≤k≤I-1,存在满射函数![]() 满足
满足![]() 其中
其中![]() 称为信息粒转换函数.对于k∈{1,2,…,I},定义
称为信息粒转换函数.对于k∈{1,2,…,I},定义![]() 则多尺度集值决策系统S可分解成I个单尺度集值决策系统,表示为Sk=(U,Ak∪{d},V,F),k=1,2,…,I.
则多尺度集值决策系统S可分解成I个单尺度集值决策系统,表示为Sk=(U,Ak∪{d},V,F),k=1,2,…,I.
2 广义多尺度集值信息系统
本节主要给出广义多尺度集值信息系统的概念及相关性质,并讨论不同尺度组合下决策系统的不确定性和代价变化趋势.
2.1 广义多尺度集值信息系统
现有关于多尺度集值信息系统的研究假设每个属性的尺度级数都相同,然而实际问题中不同属性的尺度级数可能不同,因而需要对其做进一步推广.
定义![]() 1,2,…,m},V,F)=(U,A,V,F)是一个广义多尺度集值信息系统.其中,U为论域,A是一个非空有限属性集,且每个属性aj∈A具有Ij个尺度.V是属性值的集合
1,2,…,m},V,F)=(U,A,V,F)是一个广义多尺度集值信息系统.其中,U为论域,A是一个非空有限属性集,且每个属性aj∈A具有Ij个尺度.V是属性值的集合![]() 是属性aj关于第k尺度的值域.F:U×A→2V,即对象x关于属性
是属性aj关于第k尺度的值域.F:U×A→2V,即对象x关于属性![]() 的取值
的取值![]() 是一个集值.
是一个集值.
本文的研究基于集值的合取语义,即一个集值表示一个对象在某个属性下所有的值,并且它们都为真.
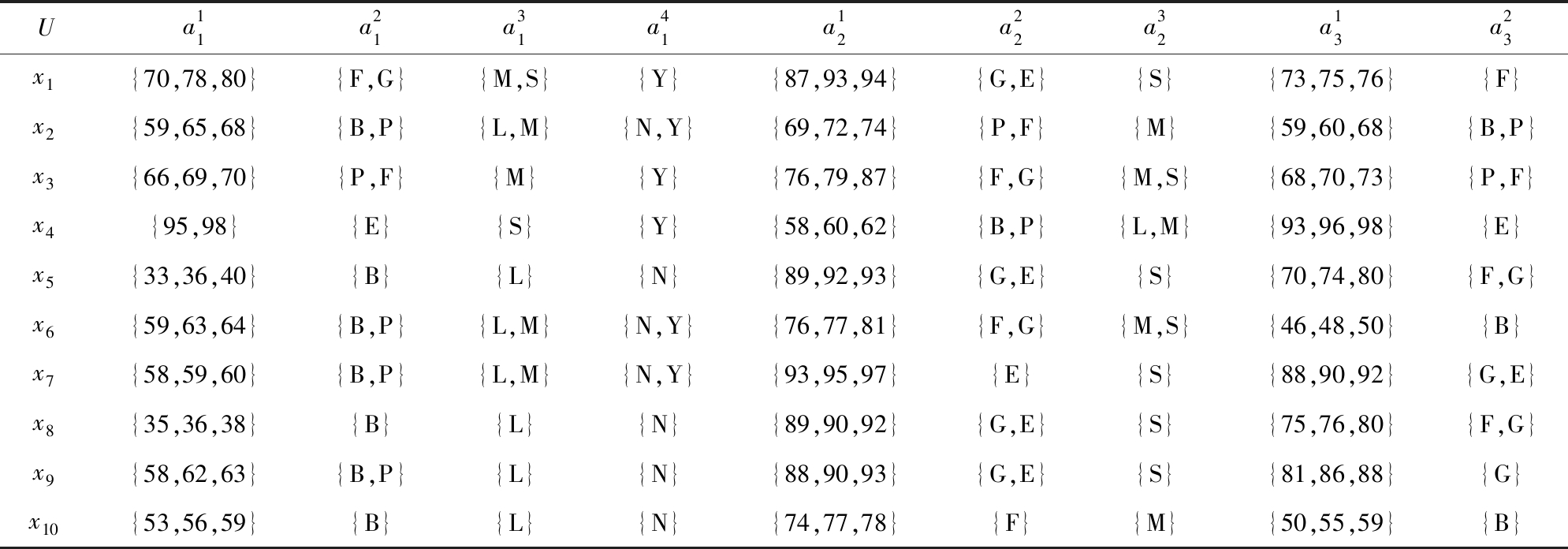
例1. 表1是某行业关于供应商的信息调查与评价,其中U={x1,x2,…,x10}表示10个供应商,属性a1,a2,a3分别代表产品质量、配送效率和服务水平,且它们拥有不同的尺度级数,即I1=4,I2=3,I3=2,属性取值“E”“G”“F”“P”“B”“S”“M”“L”“Y”“N”分别表示“Excellent”“Good”“Fair”“Pass”“Bad”“Super”“Middle”“Low”“Yes”“No”[33].
Table 1 A Generalized Multi-Scale Set-Valued Information System
表1 广义多尺度集值信息系统
Ua11a21a31a41a12a22a32a13a23x1{70,78,80}{F,G}{M,S}{Y}{87,93,94}{G,E}{S}{73,75,76}{F}x2{59,65,68}{B,P}{L,M}{N,Y}{69,72,74}{P,F}{M}{59,60,68}{B,P}x3{66,69,70}{P,F}{M}{Y}{76,79,87}{F,G}{M,S}{68,70,73}{P,F}x4{95,98}{E}{S}{Y}{58,60,62}{B,P}{L,M}{93,96,98}{E}x5{33,36,40}{B}{L}{N}{89,92,93}{G,E}{S}{70,74,80}{F,G}x6{59,63,64}{B,P}{L,M}{N,Y}{76,77,81}{F,G}{M,S}{46,48,50}{B}x7{58,59,60}{B,P}{L,M}{N,Y}{93,95,97}{E}{S}{88,90,92}{G,E}x8{35,36,38}{B}{L}{N}{89,90,92}{G,E}{S}{75,76,80}{F,G}x9{58,62,63}{B,P}{L}{N}{88,90,93}{G,E}{S}{81,86,88}{G}x10{53,56,59}{B}{L}{N}{74,77,78}{F}{M}{50,55,59}{B}
注:“E”“G”“F”“P”“B”“S”“M”“L”“Y”“N”分别代表“Excellent”“Good”“Fair”“Pass”“Bad”“Super”“Middle”“Low”“Yes”“No”.
定义3. 已知![]() 是一个广义多尺度信息系统,根据每个属性a1,a2,…,am在不同尺度下的组合得到一个单尺度集值信息系统SK=(U,AK,V,F),其中
是一个广义多尺度信息系统,根据每个属性a1,a2,…,am在不同尺度下的组合得到一个单尺度集值信息系统SK=(U,AK,V,F),其中![]() 称K是一个关于S的尺度组合.广义多尺度集值信息系统S的所有尺度组合形成一个尺度空间,定义为ψ={K=(l1,l2,…,lm)|1≤lj≤Ij,j=1,2,…,m}.
称K是一个关于S的尺度组合.广义多尺度集值信息系统S的所有尺度组合形成一个尺度空间,定义为ψ={K=(l1,l2,…,lm)|1≤lj≤Ij,j=1,2,…,m}.
例2. 在例1所示的广义多尺度集值信息系统中,其尺度空间ψ={(1,1,1),(2,1,1),(1,1,2),(1,2,1),(3,1,1),(2,1,2),(2,2,1),(1,2,2),(1,3,1),(4,1,1),(3,2,1),(3,1,2),(2,3,1),(2,2,2),(1,3,2),(4,2,1),(4,1,2),(3,3,1),(3,2,2),(2,3,2),(4,3,1),(4,2,2),(3,3,2),(4,3,2)}.
假设有2个尺度组合为![]() 若∀j∈{1,2,…,m}满足
若∀j∈{1,2,…,m}满足![]() 则称K较K′尺度更细或K′较K尺度更粗,记为K
则称K较K′尺度更细或K′较K尺度更粗,记为K K′.
K′.
定义4. 已知![]() 是一个广义多尺度集值信息系统,对于∀x,y∈U,x和y关于尺度组合K的相似关系为
是一个广义多尺度集值信息系统,对于∀x,y∈U,x和y关于尺度组合K的相似关系为![]() ={(x,y)∈U2|alj(x)∩alj(y)≠∅(∀a∈A,lj是K的尺度组合之一)}.
={(x,y)∈U2|alj(x)∩alj(y)≠∅(∀a∈A,lj是K的尺度组合之一)}.
对于∀x∈U,根据相似关系![]() 可得到关于论域U的一个信息粒
可得到关于论域U的一个信息粒![]() 也称为x的相似类.论域中所有对象的相似类构成了对论域U的一个覆盖U/
也称为x的相似类.论域中所有对象的相似类构成了对论域U的一个覆盖U/![]() ,即对于任意x∈U有
,即对于任意x∈U有![]() ≠∅,且
≠∅,且![]()
定义5. 已知目标集合X⊆U,K是S的一个尺度组合,则X关于K的上、下近似集分别为
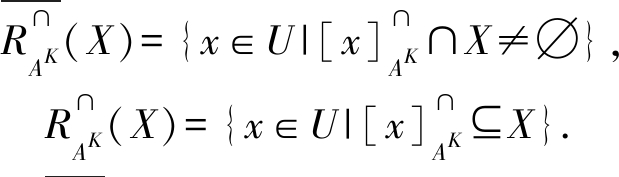
在尺度组合K下,通过上、下近似集,可将论域U划分为3个互不相交的区域,即正域、负域和边界域:
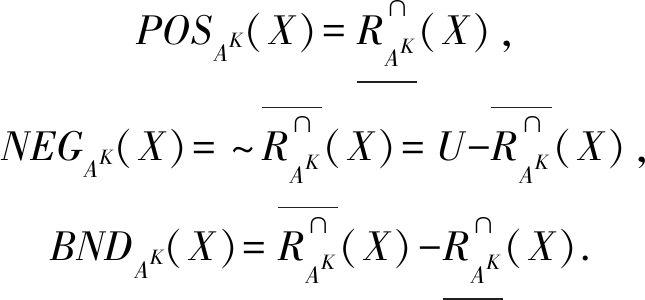
其中POSAK(X)表示一定属于X的对象集,NEGAK(X)表示一定不属于X的对象集,BNDAK(X)表示不能确定是否属于X的对象集.
由于不同尺度间存在信息粒转换函数![]() 当尺度组合K和K′满足K
当尺度组合K和K′满足K K′时,若aK(x)∩aK(y)≠∅,必有aK′(x)∩aK′(y)≠∅.则决策系统SK和SK′满足偏序关系
K′时,若aK(x)∩aK(y)≠∅,必有aK′(x)∩aK′(y)≠∅.则决策系统SK和SK′满足偏序关系![]() 及U/
及U/![]() 因此,目标集合X关于尺度组合K和K′的上、下近似满足
因此,目标集合X关于尺度组合K和K′的上、下近似满足![]() 和
和![]()
定义![]() 是一个广义多尺度集值决策系统,其中S=(U,A,V,F)是一个广义多尺度集值信息系统,d∉A,d:U→Vd为单尺度决策属性.
是一个广义多尺度集值决策系统,其中S=(U,A,V,F)是一个广义多尺度集值信息系统,d∉A,d:U→Vd为单尺度决策属性.
关于决策属性d的等价关系为Rd={(x,y)∈U×U|d(x)=d(y)},则可将论域划分为U/Rd={D1,D2,…,Dr},其中Dj,j=1,2,…,r表示不同的决策类.
定义7. 已知广义多尺度集值决策系统S可分解成若干个单尺度集值决策系统SK,其中K=(l1,l2,…,lm)是关于属性a1,a2,…,am的一个尺度组合.在单尺度集值决策系统SK中,若满足关系![]() ⊆Rd,则称SK是一致的,否则是不一致的.
⊆Rd,则称SK是一致的,否则是不一致的.
假设SK和SK′分别是广义多尺度集值决策系统S关于尺度组合K和K′的单尺度集值决策系统,且K K′.由定义7及
K′.由定义7及![]() 可知,若单尺度集值决策系统SK是不一致的,则SK′也是不一致的;并且,若单尺度集值决策系统SK′是一致的,则SK也是一致的.
可知,若单尺度集值决策系统SK是不一致的,则SK′也是不一致的;并且,若单尺度集值决策系统SK′是一致的,则SK也是一致的.
2.2 广义多尺度集值决策系统的不确定性
为了定量分析不同尺度下的不确定性,下面给出广义多尺度集值决策系统的不确定性度量.由于正域和负域的对象都是确定的,因此目标概念的不确定性仅来自边界域.于是,基于相似关系R,X⊆U关于尺度组合K的不确定性可以度量为[34]
![]()
(1-P(X|![]() )),
)),
其中,P(X|[x]R)为x相对于X的粗糙隶属函数[35],即![]()
定理1. 已知广义多尺度集值决策系统![]() 和K′是关于S的2个尺度组合,当K
和K′是关于S的2个尺度组合,当K K′时,可以得到
K′时,可以得到![]()
证明. 假设尺度组合K′下的边界域为![]() 尺度组合K下关于论域的覆盖为
尺度组合K下关于论域的覆盖为![]() 且仅存在
且仅存在![]() 是关于
是关于![]() 划分粒度较细的2个子粒.其中
划分粒度较细的2个子粒.其中![]() 于是有:
于是有:
1) 若![]() 且
且![]() 则
则![]() 于是有
于是有![]() 因此,
因此,![]()
2) 若![]() 且
且![]() 则
则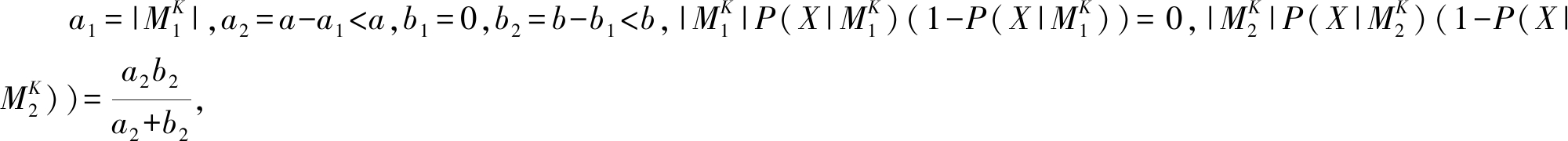 于是有
于是有![]()
![]() 因此
因此![]() 同样地,若
同样地,若![]() ∅且
∅且![]() 也可得到
也可得到![]()
3) 若![]() 且
且![]() 则
则![]() 于是有
于是有![]() 对其求解可以发现仅当
对其求解可以发现仅当![]() 且
且![]() 时有最大值
时有最大值![]() 则
则![]()
因此,若2个尺度组合满足K K′,则始终可以得到
K′,则始终可以得到![]()
证毕.
定理1表明,在广义多尺度集值决策系统中,尺度组合越粗,目标概念X的不确定性越大.
2.3 广义多尺度集值决策系统的代价
在决策过程中,不同尺度的数据,其测试代价往往不同,且对边界域对象进行延迟决策会产生延迟代价.本节主要讨论广义多尺度集值决策系统中的测试代价和延迟代价.
定义8. 已知![]() 是一个广义多尺度集值决策系统,且有
是一个广义多尺度集值决策系统,且有![]() 其中,
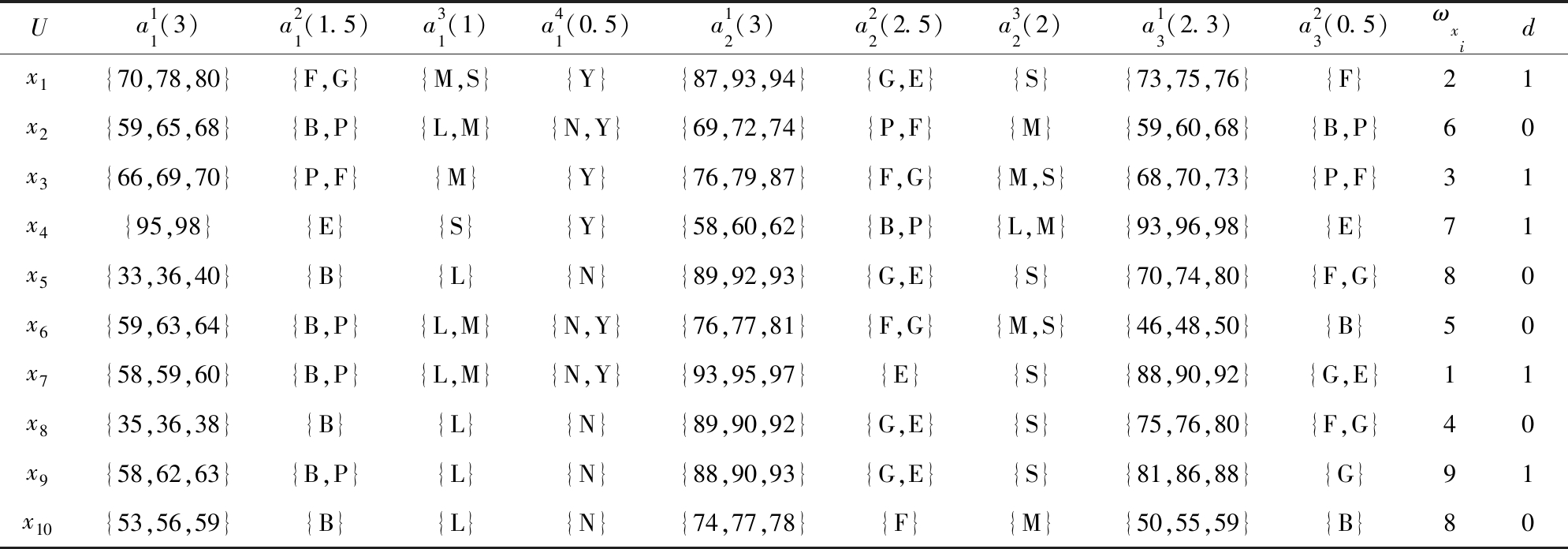
其中,![]() 表示获取属性aj在第k个尺度下属性值的测试代价,ωxi表示将对象xi划分到边界域进行延迟决策的延迟代价.于是,具有测试代价和延迟代价的广义多尺度集值决策系统可定义为S=(U,A∪{d},V,F,η,ω).如表2所示是一个具有测试代价和延迟代价的广义多尺度集值决策系统S[33].
表示获取属性aj在第k个尺度下属性值的测试代价,ωxi表示将对象xi划分到边界域进行延迟决策的延迟代价.于是,具有测试代价和延迟代价的广义多尺度集值决策系统可定义为S=(U,A∪{d},V,F,η,ω).如表2所示是一个具有测试代价和延迟代价的广义多尺度集值决策系统S[33].
Table 2 A Generalized Multi-Scale Set-Valued Information System with Test Cost and Delay Cost
表2 具有测试代价和延迟代价的广义多尺度集值决策系统
Ua11(3)a21(1.5)a31(1)a41(0.5)a12(3)a22(2.5)a32(2)a13(2.3)a23(0.5)ωxidx1{70,78,80}{F,G}{M,S}{Y}{87,93,94}{G,E}{S}{73,75,76}{F}21x2{59,65,68}{B,P}{L,M}{N,Y}{69,72,74}{P,F}{M}{59,60,68}{B,P}60x3{66,69,70}{P,F}{M}{Y}{76,79,87}{F,G}{M,S}{68,70,73}{P,F}31x4{95,98}{E}{S}{Y}{58,60,62}{B,P}{L,M}{93,96,98}{E}71x5{33,36,40}{B}{L}{N}{89,92,93}{G,E}{S}{70,74,80}{F,G}80x6{59,63,64}{B,P}{L,M}{N,Y}{76,77,81}{F,G}{M,S}{46,48,50}{B}50x7{58,59,60}{B,P}{L,M}{N,Y}{93,95,97}{E}{S}{88,90,92}{G,E}11x8{35,36,38}{B}{L}{N}{89,90,92}{G,E}{S}{75,76,80}{F,G}40x9{58,62,63}{B,P}{L}{N}{88,90,93}{G,E}{S}{81,86,88}{G}91x10{53,56,59}{B}{L}{N}{74,77,78}{F}{M}{50,55,59}{B}80
注:“E”“G”“F”“P”“B”“S”“M”“L”“Y”“N”分别代表“Excellent”“Good”“Fair”“Pass”“Bad”“Super”“Middle”“Low”“Yes”“No”.
定义9. 已知广义多尺度集值决策系统S=(U,A∪{d},V,F,η,ω),关于尺度组合K的决策系统SK的测试代价定义为
其中,![]() 是获取属性aj在第lj层尺度下属性值的测试代价,决策系统SK的测试代价为在尺度组合K下获取所有对象属性值的代价.
是获取属性aj在第lj层尺度下属性值的测试代价,决策系统SK的测试代价为在尺度组合K下获取所有对象属性值的代价.
定义10. 已知广义多尺度集值决策系统S=(U,A∪{d},V,F,η,ω),X⊆U.X关于尺度组合K的延迟代价定义为
其中,BNDAK(X)是在尺度组合K下的边界域对象集,ωxi是关于xi延迟决策的代价,即决策系统SK的延迟代价为尺度组合K下边界域对象集延迟决策的代价.
定义11. 在广义多尺度集值决策系统S=(U,A∪{d},V,F,η,ω)中,X⊆U.X关于尺度组合K的总代价为
COSTK(X)=TCK+DCK(X).
其中,TCK是在尺度组合K下获取所有对象属性值的测试代价,DCK(X)是在尺度组合K下边界域对象集的延迟代价.
定理2. 已知S=(U,A∪{d},V,F,η,ω)是一个具有测试代价和延迟价的广义多尺度集值决策系统,X⊆U.K和K′是关于S的2个尺度组合,当K K′时,可以得到TCK≤TCK′.
K′时,可以得到TCK≤TCK′.
证明. 已知关于尺度组合K的测试代价为TCK= ![]() 且
且![]() 满足关系K
满足关系K K′.在广义多尺度集值决策系统中,关于任意aj∈A,始终满足
K′.在广义多尺度集值决策系统中,关于任意aj∈A,始终满足![]() 因此,当K
因此,当K K′时,始终有
K′时,始终有![]() 于是可以得到TCK≤TCK′.
于是可以得到TCK≤TCK′.
证毕.
定理3. 已知S=(U,A∪{d},V,F,η,ω)是一个具有测试代价和延迟代价的广义多尺度集值决策系统,X⊆U.K和K′是关于S的2个尺度组合,当K K′时,可以得到DCK(X)≤DCK′(X).
K′时,可以得到DCK(X)≤DCK′(X).
证明. 假设尺度组合K下边界域为E1,尺度组合K′下边界域为E2,当K K′时,X关于尺度组合K和K′的粗糙近似关系有
K′时,X关于尺度组合K和K′的粗糙近似关系有![]() 及
及![]() 根据边界域定义可以得到E1⊆E2.因此,对于∀x∈BNDAK(X),始终满足x∈BNDAK′(X),于是得到DCK(X)≤DCK′(X).
根据边界域定义可以得到E1⊆E2.因此,对于∀x∈BNDAK(X),始终满足x∈BNDAK′(X),于是得到DCK(X)≤DCK′(X).
证毕.
可以看出,随着尺度组合变粗,其对应单尺度集值决策系统的延迟代价逐渐增大,测试代价逐渐减小,而总代价不具有单调性.
3 广义多尺度集值决策系统最优尺度选择
现有的最优尺度选择方法,大多是从决策系统的一致性或不确定性的角度出发,没有考虑到实际场景中的代价问题.因此,本节主要结合不确定性和代价,以用户需求为前提,找到决策或分类最优的尺度.
3.1 基于序贯三支决策的尺度空间更新
在广义多尺度集值决策系统中,当属性的尺度级数较大时,遍历每个属性的所有尺度将会导致尺度组合爆炸,计算成本较高.因此,这里基于序贯三支决策思想提出一种能有效减少一致性判断时间的尺度空间更新方法.
定义12. 假设存在尺度组合K∈ψ,那么关于K的上、下边界定义为
UBψ(K)={K′|K′∈ψ,K′≻K},
LBψ(K)={K′|K′∈ψ,K′ K}.
K}.
其中,UBψ(K)表示尺度空间ψ中所有较K更粗的尺度组合,LBψ(K)表示尺度空间ψ中所有较K更细的尺度组合.
根据定义12及决策系统的一致性可以得到,在广义多尺度集值决策系统![]() Ij,j=1,2,…,m}∪{d},V,F)中,若存在尺度组合K∈ψ,使得单尺度集值决策系统SK是不一致的,则对于任意K′∈UBψ(K),SK′一定是不一致的.
Ij,j=1,2,…,m}∪{d},V,F)中,若存在尺度组合K∈ψ,使得单尺度集值决策系统SK是不一致的,则对于任意K′∈UBψ(K),SK′一定是不一致的.
定义13. 已知![]() 1,2,…,m}∪{d},V,F)是一个广义多尺度集值决策系统,且ψ={K=(l1,l2,…,lm)|1≤lj≤Ij,j=1,2,…,m}为S的尺度空间.那么,关于尺度空间ψ的三支决策(接受、拒绝和不确定)分别定义为ACK(ψ),REJ(ψ),UNC(ψ),其中ACK(ψ)表示满足一致性的尺度组合,REJ(ψ)表示不满足一致性的尺度组合,UNC(ψ)表示需继续判断一致性的尺度组合.
1,2,…,m}∪{d},V,F)是一个广义多尺度集值决策系统,且ψ={K=(l1,l2,…,lm)|1≤lj≤Ij,j=1,2,…,m}为S的尺度空间.那么,关于尺度空间ψ的三支决策(接受、拒绝和不确定)分别定义为ACK(ψ),REJ(ψ),UNC(ψ),其中ACK(ψ)表示满足一致性的尺度组合,REJ(ψ)表示不满足一致性的尺度组合,UNC(ψ)表示需继续判断一致性的尺度组合.
假设需进行一致性判断的尺度组合集合为UNC(ψ0)=ψ,其中ψ是S的初始尺度空间,第i-1次更新后决策结果分别为ACK(ψi-1),REJ(ψi-1),UNC(ψi-1),则需进一步判断的尺度组合集合为ψi=UNC(ψi-1).通过引入序贯三支决策思想对UNC(ψi-1)中的尺度组合进行判断可得到第i次更新后尺度空间的决策结果分别为
ACK(ψi)={Ki}∪ACK(ψi-1),
REJ(ψi)={Kj}∪UBψi(Kj)∪REJ(ψi-1),
UNC(ψi)=ψi-ACK(ψi)-REJ(ψi).
其中,Ki是尺度空间第i层满足一致性的尺度组合,Kj是尺度空间第i层不满足一致性的尺度组合,UBψi(Kj)为尺度组合Kj的上边界,UNC(ψi)表示i次更新后需进行一致性判断的尺度组合.当UNC(ψi)=∅,可以得到S中所有一致的单尺度集值决策系统的尺度组合,即更新后的尺度空间ψ′=ACK(ψi).
因此,可得到尺度空间更新算法:
算法1. 广义多尺度集值决策系统尺度空间更新.
输入:广义多尺度集值决策系统S=(U,A∪{d},V,F);
输出:更新后的尺度空间ψ′.
① 初始化ψ={K=(l1,l2,…,lm)|1≤lj≤Ij,j=1,2,…,m},ACK(ψ0)=∅,
REJ(ψ0)=∅,UNC(ψ0)=ψ,
ψi=UNC(ψi-1)(i≥1);
② while UNC(ψi-1)≠∅ do
③ for each K∈UNC(ψi-1) do
④ if ![]() ⊆Rdin SKthen
⊆Rdin SKthen
⑤ ACK(ψi)←{K}∪ACK(ψi-1);
⑥ else
⑦ REJ(ψi)←{K}∪UBψi(K)∪
REJ(ψi-1);
⑧ end if
⑨ UNC(ψi)←UNC(ψi-1)-ACK(ψi)-REJ(ψi);
⑩ i++;
 end for
end for
 end while
end while
 ψ′=ACK(ψi);
ψ′=ACK(ψi);
 return ψ′.
return ψ′.
算法1首先计算了广义多尺度集值决策系统的尺度空间,时间复杂度为O(I1×I2×…×Im).然后针对尺度空间中尺度组合对应的决策系统进行一致性判断,其中每个相似类的计算需要时间复杂度为O(m×|U|).在最坏情况下,假设所有尺度组合的决策系统都是一致的,需进行|ψ|=I1×I2×…×Im次判断,所以算法1总的时间复杂度为O(m×|U|×|ψ|).
下面举例说明尺度空间更新的计算过程.
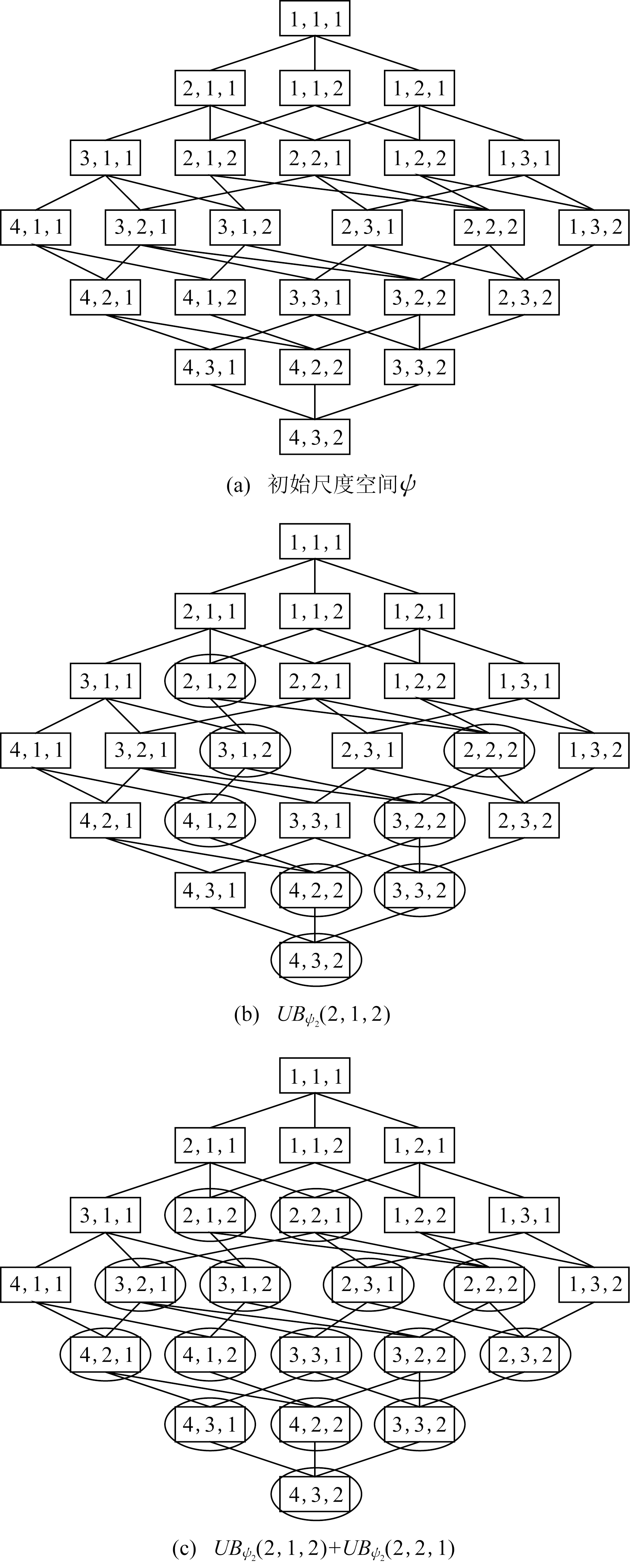
Fig. 1 The scale space of generalized multi-scaleset-valued decision system
图1 广义多尺度集值决策系统的尺度空间
例3. 根据例2可知,广义多尺度集值决策系统S的尺度空间如图1(a)所示.通过计算可以得到:
第1层关于尺度组合(1,1,1)的决策系统S(1,1,1)是一致的,则ACK(ψ0)={(1,1,1)},REJ(ψ0)=∅,UNC(ψ0)=ψ-ACK(ψ0)=ψ1.
第2层尺度组合(2,1,1),(1,1,2),(1,2,1)是一致的,则ACK(ψ1)={(1,1,1),(2,1,1),(1,1,2),(1,2,1)},REJ(ψ1)=∅,UNC(ψ1)=ψ1-ACK(ψ1)=ψ2.
第3层尺度组合(3,1,1),(1,2,2),(1,3,1)是一致的,(2,1,2),(2,2,1)是不一致的.根据图1(b)(c)可知UBψ2(2,1,2)={(3,1,2),(2,2,2),(4,1,2),(3,2,2),(4,2,2),(3,3,2),(4,3,2)},UBψ2(2,2,1)={(3,2,1),(2,3,1),(2,2,2),(4,2,1),(3,3,1),(3,2,2),(2,3,2),(4,3,1),(4,2,2),(3,3,2),(4,3,2)},则ACK(ψ2)={(1,1,1),(2,1,1),(1,1,2),(1,2,1),(3,1,1),(1,2,2),(1,3,1)},REJ(ψ2)={(2,1,2),(2,2,1)},UNC(ψ2)=ψ2-ACK(ψ2)-REJ(ψ2)={(4,1,1),(1,3,2)}=ψ3.
第4层尺度组合(4,1,1),(1,3,2)是一致的,则ACK(ψ3)={(1,1,1),(2,1,1),(1,1,2),(1,2,1),(3,1,1),(1,2,2),(1,3,1),(4,1,1),(1,3,2)},REJ(ψ3)={(2,1,2),(2,2,1)},UNC(ψ3)=∅.
于是,更新的尺度空间ψ′=ACK(ψ3)={(1,1,1),(2,1,1),(1,1,2),(1,2,1),(3,1,1),(1,2,2),(1,3,1),(4,1,1),(1,3,2)}.
可以发现,广义多尺度集值决策系统的初始尺度空间|ψ|=I1×I2×I3=24,即需进行24次一致性判断,而更新后的尺度空间|ψ′|=9,且只需11次一致性判断即可得到所有一致的单尺度集值决策系统.因此,对于尺度级数较高的广义多尺度集值决策系统,该尺度空间更新方法能有效地提高计算效率.
3.2 最优尺度选择
为了更好地综合考虑不同尺度组合的不确定性和代价2个因素,本文采用L2范式[35]对不确定性和代价进行归一化,消除不同维度的影响.通过数据标准化解决不确定性与代价间的不可比性.其归一化公式为![]() 其中
其中![]() 是LK的归一化结果.
是LK的归一化结果.
定义14. 已知S=(U,A∪{d},V,F,η,ω)是一个具有测试代价和延迟代价的广义多尺度集值决策系统,X⊆U.那么,X关于尺度组合K的评价为
其中,![]() 和
和![]() 分别表示X关于尺度组合K的不确定性和总代价的归一化结果.
分别表示X关于尺度组合K的不确定性和总代价的归一化结果.
因此,在满足用户需求的情况下,以最小化不确定性和代价为目标建立最优尺度选择模型,具体为:
其中,Huser和Costuser分别是用户对于不确定性和代价的需求.
该模型以用户需求为约束条件,根据最小化评价来选择最优尺度.对于一个广义多尺度集值决策系统,有可能存在一组满足用户需求的可行解.由于该模型需要同时优化2个目标且目标之间存在冲突,即一个目标性能的提高是以牺牲另一个目标为代价的.例如,在满足约束条件可行的解决方案中,有些是低代价高不确定性的,有些是低不确定性高代价的.为此,通过引入理想解来计算可行解与理想解的差值,差值越小则表明越接近理想解,那么最接近理想解的尺度为最优尺度.
定义15. 已知有一组可行解为![]() 其中
其中![]() 和
和![]() 分别为不确定性和代价的可行解.则理想解定义为
分别为不确定性和代价的可行解.则理想解定义为
其中,![]() 为
为![]() 中的最小值,
中的最小值,![]() 为
为![]() 中的最小值.
中的最小值.
定义16. 已知S=(U,A∪{d},V,F,η,ω)是一个具有测试代价和延迟代价的广义多尺度集值决策系统,基于加权的最优尺度选择模型为
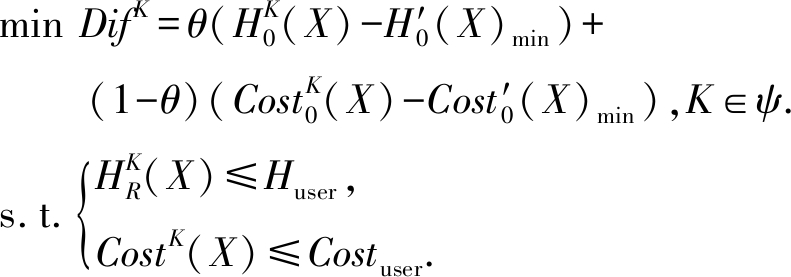
其中,DifK表示加权差异程度,θ∈[0,1]表示加权系数.加权系数θ可根据用户需求进行设置,当θ=0时,该模型退化为基于代价的最优尺度选择;当θ=1时,该模型退化为基于不确定性的最优尺度选择.
因此,可以设计广义多尺度集值决策系统最优尺度选择算法为:
算法2. 广义多尺度集值决策系统最优尺度选择.
输入:广义多尺度集值决策系统S=(U,A∪{d},V,F,η,ω),Huser,Costuser,θ,X;
输出:最优尺度组合K′.
① 初始化![]()
② 调用算法1更新尺度空间为ψ′;
③ for each K∈ψ′ do
④ 得到POSAK(X),NEGAK(X),BNDAK(X);
⑤ 计算不确定性![]() 和代价CostK(X);
和代价CostK(X);
⑥ end for
⑦ for each K∈ψ′ do
⑧ 计算![]()
⑨ if![]() 且CostK(X)≤
且CostK(X)≤
Costuser then
⑩ ![]()
 end if
end if
 end for
end for
 for each K∈ψ′ do
for each K∈ψ′ do

![]()
 end for
end for
 最优尺度组合K′={K∈ψ′|min DifK};
最优尺度组合K′={K∈ψ′|min DifK};
 return K′.
return K′.
在最坏情况下来分析算法2的时间复杂度,即假设每个对象都是一个独立于条件和决策属性的概念.在算法2中,步骤③~⑥在不同尺度下计算不确定性和代价,它的时间复杂度是O(|ψ′|×|U|2).步骤⑦~ 的目的是获取满足用户需求的可行解,时间复杂度为O(|ψ′|).在最坏的情况下,初始尺度空间ψ中的所有尺度组合K的单尺度集值决策系统SK都是一致的,即|ψ|=|ψ′|.根据分析可知,该算法的时间复杂度为O(|ψ|×|U|2).下面举例说明最优尺度选择的计算过程.
的目的是获取满足用户需求的可行解,时间复杂度为O(|ψ′|).在最坏的情况下,初始尺度空间ψ中的所有尺度组合K的单尺度集值决策系统SK都是一致的,即|ψ|=|ψ′|.根据分析可知,该算法的时间复杂度为O(|ψ|×|U|2).下面举例说明最优尺度选择的计算过程.
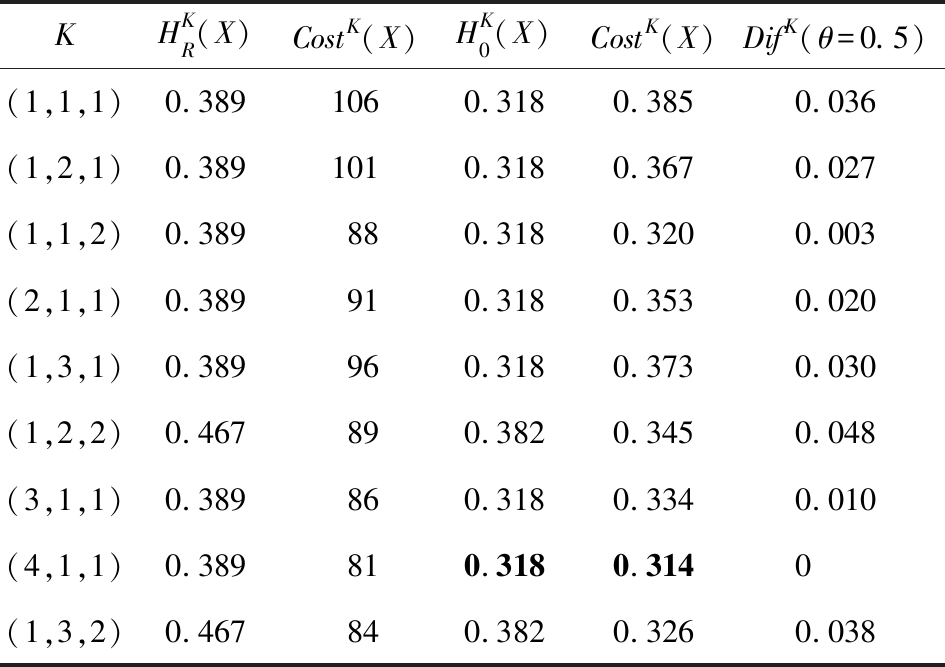
例4. 在表2给出的具有测试代价和延迟代价的广义多尺度集值决策系统S=(U,A∪{d},V,F,η,ω)中U={x1,x2,…,x10},X={x1,x2,x3,x9,x10},关于决策属性的论域划分结果为U/Rd={(x1,x3,x4,x7,x9),(x2,x5,x6,x8,x10)}.根据例3可知:更新的尺度空间ψ′={(1,1,1),(2,1,1),(1,1,2),(1,2,1),(3,1,1),(1,2,2),(1,3,1),(4,1,1),(1,3,2)},其中BNDA(1,1,1)(X)=BNDA(2,1,1)(X)=BNDA(1,1,2)(X)=BNDA(1,2,1)(X)=BNDA(3,1,1)(X)=BNDA(1,3,1)(X)=BNDA(4,1,1)(X)={x6,x7,x9,x10},BNDA(1,2,2)(X)=BNDA(1,3,2)(X)={x2,x6,x7,x9,x10}.根据定义14~16及归一化处理,其计算结果如表3所示,表3中粗体数据表明:在当前尺度组合下决策系统的不确定性或代价是最小的.当用户对不确定性和代价需求分别是Huser=0.4,Costuser=100时,根据最优尺度选择模型,可得到不确定性和代价最小的最优尺度组合是K=(4,1,1).
Table 3 The Results Based on Weighted Optimal ScaleSelection Model
表3 基于加权的最优尺度选择模型计算结果
KHKR(X)CostK(X)HK0(X)CostK(X)DifK(θ=0.5)(1,1,1)0.3891060.3180.3850.036(1,2,1)0.3891010.3180.3670.027(1,1,2)0.389880.3180.3200.003(2,1,1)0.389910.3180.3530.020(1,3,1)0.389960.3180.3730.030(1,2,2)0.467890.3820.3450.048(3,1,1)0.389860.3180.3340.010(4,1,1)0.389810.3180.3140(1,3,2)0.467840.3820.3260.038
注:黑体数字表示该尺度组合下的代价是最小的.
例4中,根据最优尺度选择模型可得到唯一的尺度组合解,但在有些广义多尺度集值决策系统中,根据最优尺度模型可能得到一组可行解.假设在例4模型中,满足用户需求的尺度组合为(1,1,2),(2,1,1),(1,3,1),(3,1,1),(4,1,1),于是可以得到其理想解为Ide=[0.318,0.314].在基于加权的最优尺度选择模型中,假设用户给定的加权系数θ=0.5,可以计算出Dif(1,1,2)=0.003,Dif(2,1,1)=0.020,Dif(1,3,1)=0.030,Dif(3,1,1)=0.010,Dif(4,1,1)=0.因此,可以得到(4,1,1)是最优尺度组合.
例4说明算法2在得到唯一解或一组可行解情况下,其最优尺度选择的一致性.
4 实验结果与分析
为了验证本文提出的最优尺度选择算法的可行性和有效性,从UCI数据库中选取了6个数据集进行数值模拟,其详细信息如表4所示.
为了满足实验要求,本文参照文献[16]中提出的方法构造多尺度决策系统.具体而言,首先对条件属性进行扩展.若条件属性值为离散型,则尽量对属性值进行合并,保证其不重复;若条件属性值为连续型,则将属性值划分为多个区间,并将每个区间看作一个属性值.然后,随机丢失部分数据值,其取值为该属性相应尺度下的值域,即可得到广义多尺度集值决策系统.表5列出了经过预处理后数据集的信息.
Table 4 The Original Dataset Information
表4 原始数据集信息
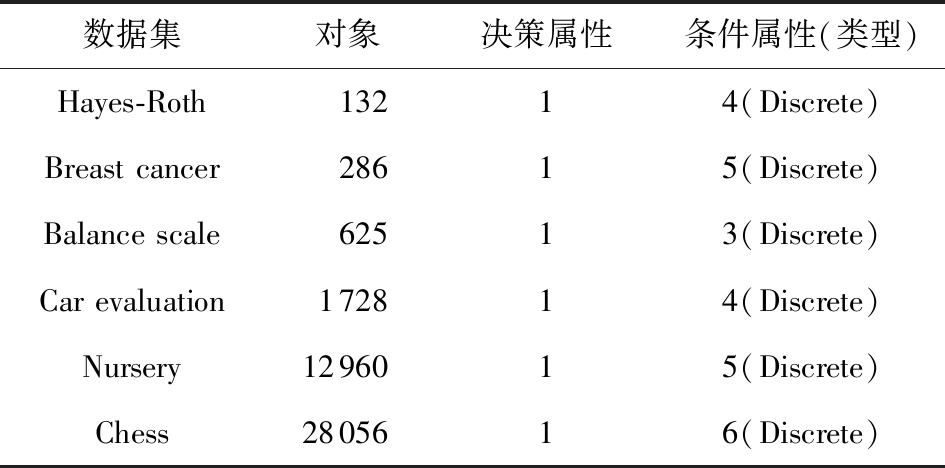
数据集对象决策属性条件属性(类型)Hayes-Roth13214(Discrete)Breast cancer28615(Discrete)Balance scale62513(Discrete)Car evaluation172814(Discrete)Nursery1296015(Discrete)Chess2805616(Discrete)
Table 5 The Dataset Information after Preprocessing
表5 预处理后的数据集信息
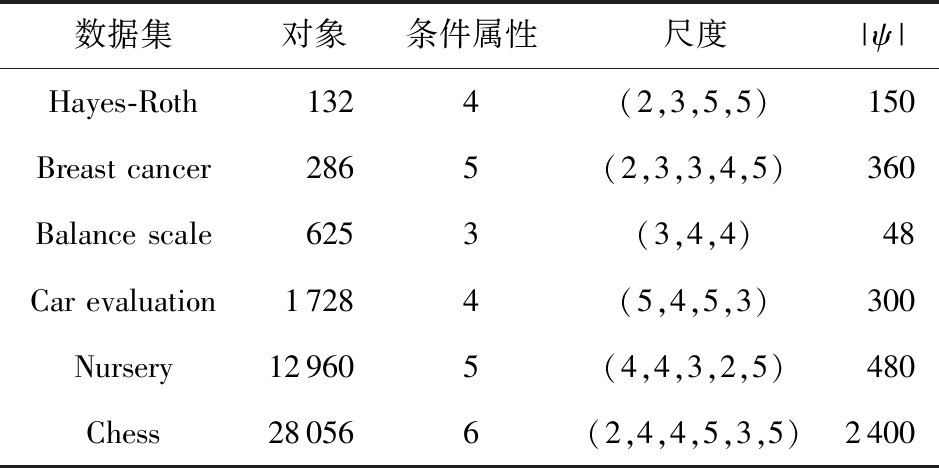
数据集对象条件属性尺度|ψ|Hayes-Roth1324(2,3,5,5)150Breast cancer2865(2,3,3,4,5)360Balance scale6253(3,4,4)48Car evaluation17284(5,4,5,3)300Nursery129605(4,4,3,2,5)480Chess280566(2,4,4,5,3,5)2400
实验使用不同的代价参数来处理每个数据集,其详细代价参数信息如表6所示.属性在不同尺度下的测试代价参数![]() 是在一定范围内递减的随机数.对象xi的延迟代价参数ωxi是一个固定范围内的随机数.另外,随机选取部分对象作为目标概念X.
是在一定范围内递减的随机数.对象xi的延迟代价参数ωxi是一个固定范围内的随机数.另外,随机选取部分对象作为目标概念X.
Table 6 The Related Cost Parameters of Datasets
表6 数据集的相关代价参数

数据集测试代价延迟代价Hayes-Roth(1,10) Random(1,10) RandomBreast cancer(1,20) Random(1,20) RandomBalance scale(1,30) Random(1,20) RandomCar evaluation(1,20) Random(1,10) RandomNursery(1,10) Random(1,20) RandomChess(1,10) Random(1,30) Random
使用算法1对每个数据集进行尺度空间更新,结果如图2所示,其中横坐标表示数据集,纵坐标表示数据集的尺度组合数量.与LM(lattice mode)模型[20]相比,该尺度空间更新方法显著减少了尺度组合数量,从而可以减少决策系统一致性判断次数.
由于测试代价和延迟代价的变化趋势不同,总代价并不总是与不确定性的变化趋势相同,实验将不确定性和总代价进行归一化处理.如表7是6个数据集进行最优尺度选择的结果.
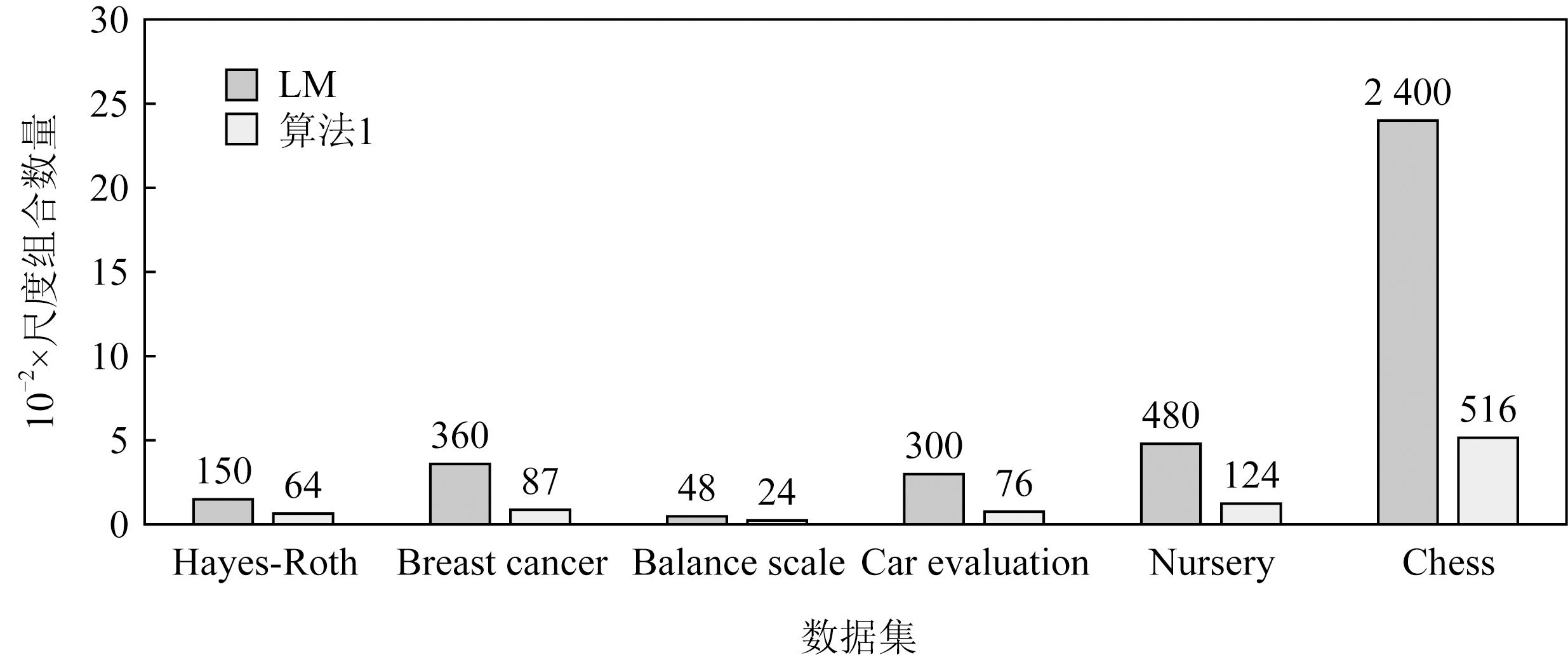
Fig. 2 The scale space update results
图2 尺度空间更新结果
Table 7 The Optimal Scale Selection Results
表7 最优尺度选择结果
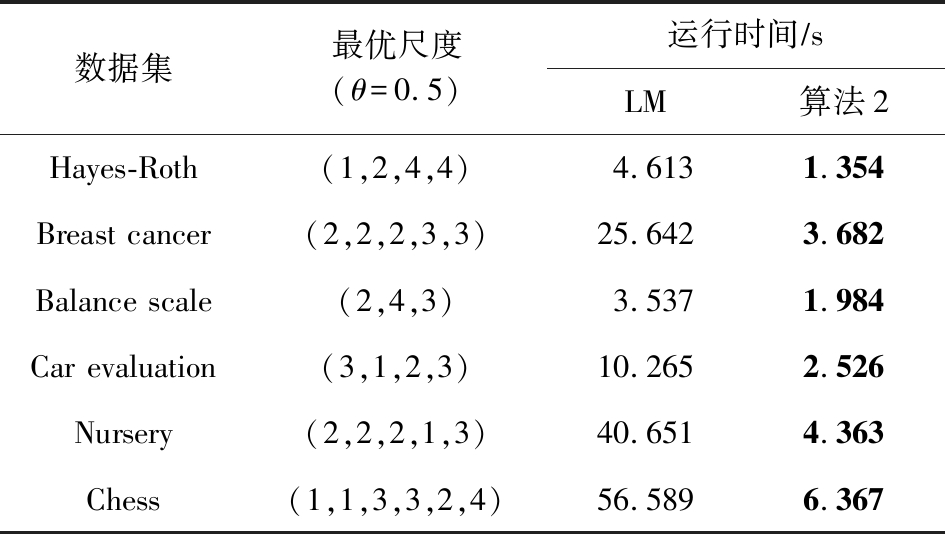
数据集最优尺度(θ=0.5)运行时间∕sLM算法2Hayes-Roth(1,2,4,4)4.6131.354Breast cancer(2,2,2,3,3)25.6423.682Balance scale(2,4,3)3.5371.984Car evaluation(3,1,2,3)10.2652.526Nursery(2,2,2,1,3)40.6514.363Chess(1,1,3,3,2,4)56.5896.367
注:黑体数字表示本文的算法2与传统LM算法相比耗时更少.
为了分析不确定和代价对最优尺度选择的影响,本文分别在2组不同的参数下对Hayes-Roth数据集进行实验,其结果如图3和图4所示.在图3和图4中,横坐标代表更新尺度空间后决策系统的尺度组合数量,根据图2中的数据可知,经过尺度空间更新后,Hayes-Roth的尺度空间大小为64;纵坐标代表决策系统的不确定性或代价;曲线H表示不同尺度组合下决策系统的不确定性;曲线Cost表示不同尺度组合下决策系统的代价;曲线Dif表示在2种加权系数下,决策系统的不确定性和代价与理想解的差异程度.其中,在第1组参数下,测试代价和延迟代价都为1~10范围内的随机数,用户对不确定性和代价的需求分别为Huser=0.36和Costuser=300,其最优尺度组合为图3所标出的结果,即K=(1,2,4,4).在第2组参数下,测试代价和延迟代价都为1~15范围内的随机数,用户对不确定性和代价的需求分别为Huser=0.36和Costuser=600,其最优尺度组合为图4所标出的结果,即K=(1,1,4,4).可以发现,在2组不同的参数设定下,决策系统的不确定性和代价不同,但通过本文提出的方法均可得到满足用户需求的最优尺度.
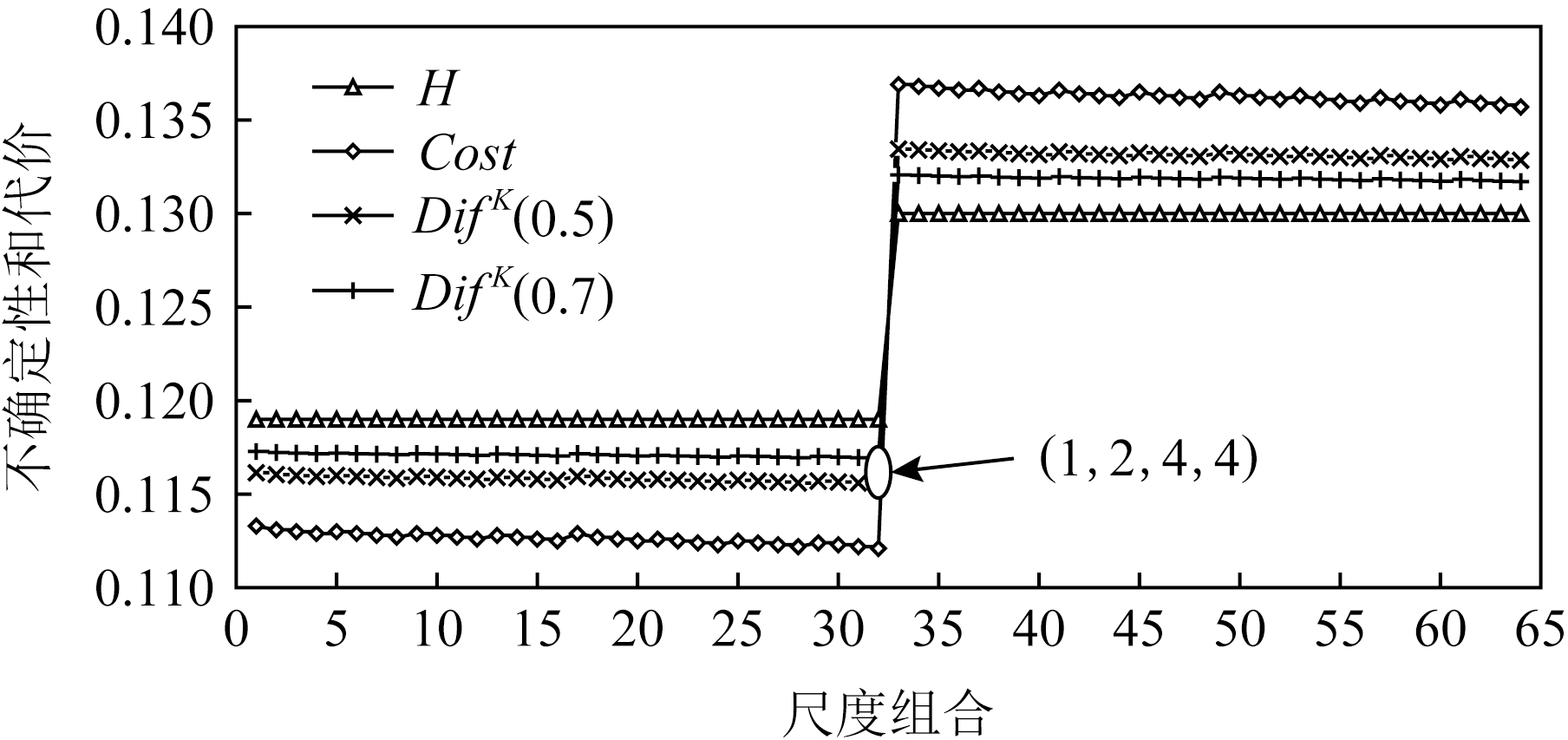
Fig. 3 The optimal scale of Hayes-Roth underthe first set of parameters
图3 第1组参数下Hayes-Roth的最优尺度
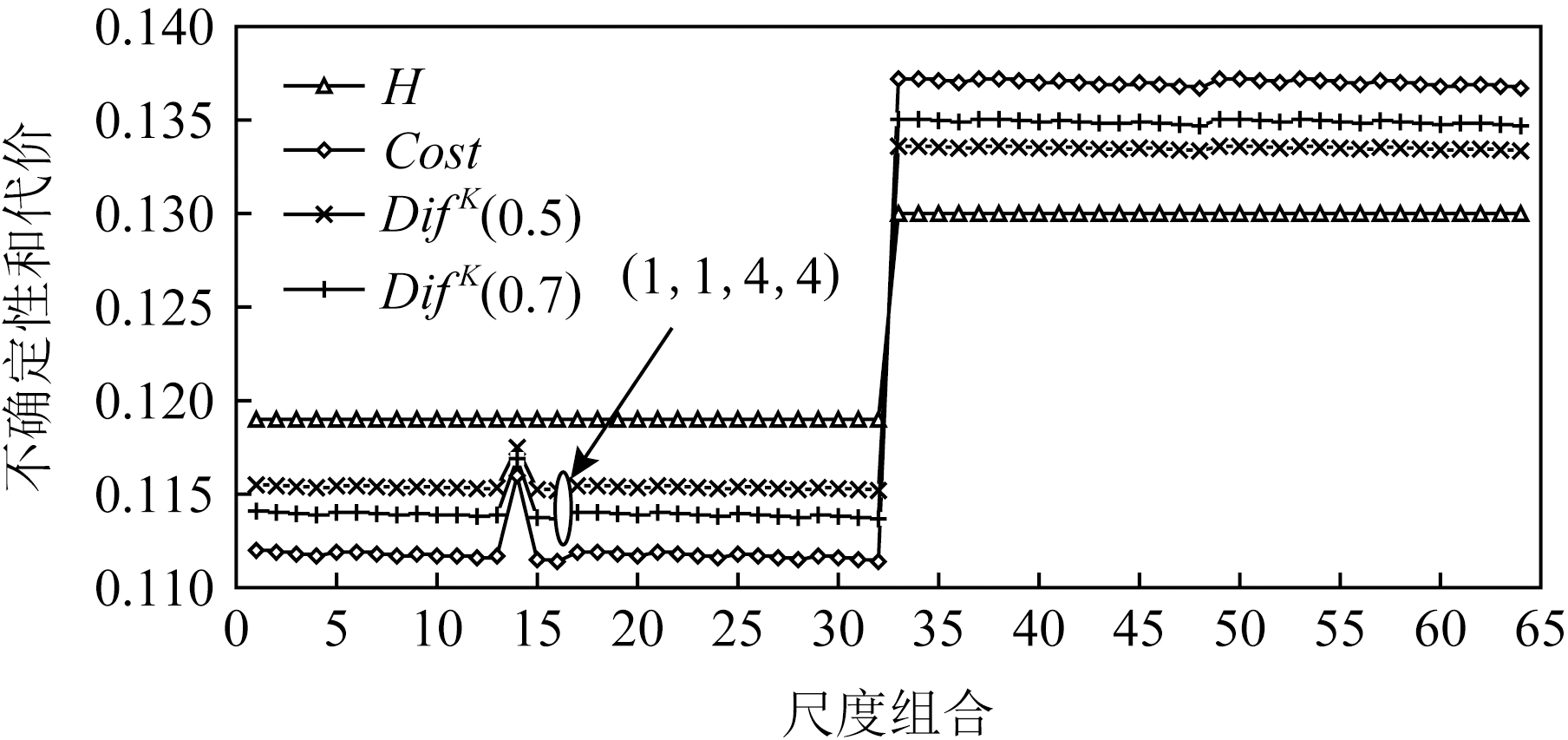
Fig. 4 The optimal scale of Hayes-Roth under thesecond set of parameters
图4 第2组参数下Hayes-Roth的最优尺度
5 总 结
本文主要研究了广义多尺度集值决策系统的最优尺度选择问题.首先,定义了广义多尺度集值决策系统的概念,并讨论了不同尺度组合下决策系统的不确定性和代价.然后,引入序贯三支决策思想对决策系统的尺度空间进行更新,减少了决策系统的一致性判断次数.在此基础上,提出了一种综合考虑不确定性和代价的最优尺度选择方法,并通过引入具有用户偏好的理想解对其进行优化.最后,通过实验证明该方法能够快速地得到一个满足用户需求的最优尺度.
作者贡献声明:胡军提出论文研究内容,并指导论文写作;陈艳负责研究内容的实现和论文写作;张清华、王国胤参与论文的研讨与修改.
[1]Wu Weizhi, Leung Y. Theory and applications of granular labelled partitions in multi-scale decision tables[J]. Information Sciences, 2011, 181(18): 3878-3897
[2]Kendall M S, Christensen J D, Hillis-Starr Z. Multi-scale data used to analyze the spatial distribution of French grunts,Haemulon flavolineatum, relative to hard and soft bottom in a benthic landscape[J]. Environmental Biology of Fishes, 2003, 66(1): 19-26
[3]Brown M, Szeliski R, Winder S. Multi-image matching using multi-scale oriented patches[C] //Proc of the Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2005: 510-517
[4]Pauly M, Keiser R, Gross M. Multi-scale feature extraction on point-sampled surfaces[J]. Computer Graphics Forum, 2003, 22(3): 281-289
[5]Huang Bing, Wu Weizhi, Yan Jinjiang, et al. Inclusion measure-based multi-granulation decision-theoretic rough sets in multi-scale intuitionistic fuzzy information tables[J]. Information Sciences, 2020, 507: 421-448
[6]Luo Chuan, Li Tianrui, Huang Yanyong, et al. Updating three-way decisions in incomplete multi-scale information systems[J]. Information Sciences, 2019, 476: 274-289
[7]Xie Junping, Yang Minhua, Li Jinhai, et al. Rule acquisition and optimal scale selection in multi-scale formal decision contexts and their applications to smart city[J]. Future Generation Computer Systems, 2018, 83: 564-581
[8]Li Chao, Zhao Shuliang, Zhao Junpeng, et al. Scaling-up algorithm of multi-scale association rules[J]. Computer Science, 2017, 44(8): 285-289 (in Chinese)(李超, 赵书良, 赵骏鹏, 等. 多尺度关联规则尺度上推算法[J]. 计算机科学, 2017, 44(8): 285-289)
[9]Zhao Junpeng, Zhao Shuliang, Li Chao, et al. Upscale algorithm of multi-scale clustering based on granular computing[J]. Application Research of Computers, 2018, 35(2): 362-366 (in Chinese)(赵骏鹏, 赵书良, 李超, 等. 基于粒计算的多尺度聚类尺度上推算法[J]. 计算机应用研究, 2018, 35(2): 362-366)
[10]Wu Weizhi, Qian Yuhua, Li Tongjun, et al. On rule acquisition in incomplete multi-scale decision tables[J]. Information Sciences, 2017, 378: 282-302
[11]Wu Weizhi, Leung Y. Optimal scale selection for multi-scale decision tables[J]. International Journal of Approximate Reasoning, 2013, 54(8): 1107-1129
[12]Xu Youhong, Wu Weizhi, Tan Anhui. Optimal scale selections in consistent generalize multi-scale decision tables[C] //Proc of the Int Joint Conf on Rough Sets. Berlin: Springer, 2017: 185-198
[13]Wu Weizhi, Chen Ying, Xu Youhong, et al. Optimal granularity selections in consistent incomplete multi-granular labeled decision systems[J]. Pattern Recognition and Artificial Intelligence, 2016, 29(2): 108-115 (in Chinese)(吴伟志, 陈颖, 徐优红, 等. 协调的不完备多粒度标记决策系统的最优粒度选择[J]. 模式识别与人工智能, 2016, 29(2): 108-115)
[14]Wu Weizhi, Zhuang Yubin, Tan Anhui, et al. Scale combinations in inconsistent generalized multi-scale decision systems[J]. Pattern Recognition and Artificial Intelligence, 2018, 31(6): 485-494 (in Chinese)(吴伟志, 庄宇斌, 谭安辉, 等. 不协调广义多尺度决策系统的尺度组合[J]. 模式识别和人工智能, 2018, 31(6): 485-494)
[15]Wu Weizhi, Chen Chaojun, Li Tongjun, et al. Comparative study on optimal granularities in inconsistent multi-granular labeled decision systems[J]. Pattern Recognition and Artificial Intelligence, 2016, 29(12): 1095-1103 (in Chinese)(吴伟志, 陈超君, 李同军, 等. 不协调多粒度标记决策系统最优粒度的对比[J]. 模式识别与人工智能, 2016, 29(12): 1095-1103)
[16]Hao Chen, Li Jinhai, Fan Min, et al. Optimal scale selection in dynamic multi-scale decision tables based on sequential three-way decisions[J]. Information Sciences, 2017, 415/416: 213-232
[17]Tie Wenyan, Fan Min, Li Jinhai. Optimal scale selection in multi-scale decision systems under environment of objects updating[J]. Computer Science, 2018, 45(1): 113-121 (in Chinese)(铁文彦, 范敏, 李金海. 对象更新环境下的多粒度决策系统的最优粒度选择[J]. 计算机科学, 2018, 45(1): 113-121)
[18]Gu Shenming, Gu Jinyan, Wu Weizhi, et al. Local optimal granularity selection in incomplete multi-granular decision systems[J]. Journal of Computer Research and Development, 2017, 54(7): 1500-1509 (in Chinese)(顾沈明, 顾金燕, 吴伟志, 等. 不完备多粒度决策系统的局部最优粒度选择[J]. 计算机研究与发展, 2017, 54(7): 1500-1509)
[19]Chen Yingsheng, Li Jinjin, Huang Jianxin. Matrix method for the optimal scale selection of multi-scale information decision systems[J]. Mathematics, 2019, 7(3): 1-17.DOI:10.3390/math7030290
[20]Li Feng, Hu Baoqing. A new approach of optimal scale selection to multi-scale decision tables[J]. Information Sciences, 2017, 381: 193-208
[21]Li Feng, Hu Baoqing, Wang Jun. Stepwise optimal scale selection for multi-scale decision tables via attribute significance[J]. Knowledge-Based Systems, 2017, 129: 4-16
[22]Wu Weizhi, Leung Y. A comparison study of optimal scale combination selection in generalized multi-scale decision tables[J]. International Journal of Machine Learning and Cybernetics, 2020, 11(5): 961-972
[23]Niu Dongran, Wu Weizhi, Li Tongjun. Variable precision based optimal scale combinations in generalized multi-scale decision systems[J]. Pattern Recognition and Artificial Intelligence, 2019, 32(11): 965-974 (in Chinese)(牛东苒, 吴伟志, 李同军. 广义多尺度决策系统中基于可变精度的最优尺度组合[J]. 模式识别与人工智能, 2019, 32(11): 965-974)
[24]Cheng Yunlong, Zhang Qinghua, Wang Guoyin, et al. Optimal scale selection and attribute reduction in multi-scale decision tables based on three-way decision[J]. Information Sciences, 2020, 541: 36-59
[25]Cheng Yunlong, Zhang Qinghua, Wang Guoyin. Optimal scale combination selection for multi-scale decision tables based on three-way decision[J]. Internatinal Journal of Machine Learning and Cybernetics, 2020, 12(2): 281-301
[26]Zhang Wenxiu, Mi Jusheng. Incomplete information system and its optimal selections[J]. Computers & Mathematics with Applications, 2004, 48(5): 691-698
[27]Qian Yuhua, Dang Chuanyin, Liang Jiye, et al. Set-valued ordered information systems[J]. Information Sciences, 2009, 179(16): 2809-2832
[28]Dai Jianhua, Tian Haowei. Fuzzy rough set model for set-valued data[J]. Fuzzy Sets & Systems, 2013, 229: 54-68
[29]Bao Zhongkui, Yang Shanlin. Attribute reduction for set-valued ordered fuzzy decision system[C] //Proc of the 6th Int Conf on Intelligent Human-Machine Systems & Cybernetics. Piscataway, NJ: IEEE, 2014: 96-99
[30]Orlowska E, Pawlak Z. Representation of nondeterministic information[J]. Theoretical Computer Science, 1984, 29(1): 27-39
[31]Zhao Xueyong, Hu Baoqing. Three-way decisions with decision-theoretic rough sets in multiset-valued information tables[J]. Information Sciences, 2020, 507: 684-699
[32]Chen Yan, Hu Jun, Zhang Qinghua, et al. Multi-scale set-valued information system and its optimal scale selection[J]. Journal of Shanxi University: Natural Science Edition, 2020, 43(4): 765-775 (in Chinese)
(陈艳, 胡军, 张清华, 等. 多尺度集值信息系统及其最优尺度选择[J]. 山西大学学报: 自然科学版, 2020, 43(4): 765-775)
[33]Chen Yan. Research on multi-scale set-valued information system and its application[D]. Chongqing: Chongqing University of Posts and Telecommunications, 2021 (in Chinese)(陈艳. 多尺度集值信息系统及其应用研究[D]. 重庆:重庆邮电大学, 2021)
[34]Zhang Xueqiu, Zhang Qinghua, Cheng Yunlong, et al. Optimal scale selection by integrating uncertainty and cost-sensitive learning in multi-scale decision tables[J]. International Journal of Machine Learning and Cybernetics, 2020, 11(5): 1095-1114
[35]Pawlak Z, Skowron A. Rough membership functions: A tool for reasoning with uncertainty[J]. Banach Center Publications, 1993, 28(1): 135-150



