随着大数据、人工智能技术、5G通信技术的高速发展,人们开始进入一个万物互联的物联网时代.根据华为《华为全球产业展望 GIV 2025》所述,到2025年,全球将有1 000亿台可以智能互联的设备,同时个人智能移动终端数量将达到400亿,智能家居及其他可穿戴设备数量将达到210亿,其中智能手机数量将达到80亿,平板和个人电脑数量将达到30亿,各类可穿戴设备数量将达到80亿.90%的人群将拥有个人智能助理,12%的家庭将享有智能服务机器人,20%的人将拥有10个以上的智能终端,平均每个人将拥有5个智能终端.各类数据利用率将剧增至80%,全球每年产生的数据将从2015年的8 ZB增长到1 800 ZB,而且全球人均日通信流量将达到4 GB,同时,人均日移动通信流量将达到1 GB.面对如此庞大的数据量,利用可持续和成本低廉的数据感知和收集方案变得越来越重要.群智感知系统[1-4]在此需求下应运而生,该系统利用人们拥有的无处不在的智能移动设备(如智能手机、可穿戴设备、智能车辆等)中嵌入的传感器(如照相机、陀螺仪等)来获取各种各样的数据[5-8],并将收集到的数据传给远程数据中心进行处理[9-11].
目前,群智感知系统已经成为了一种极具吸引力的大规模数据收集与分析的模式,为面积广袤、人流拥挤地区的信息收集提供了有效的解决方案[12-14].该系统强大而有效的数据收集能力使其成为现代智慧城市不可或缺的组成部分[15].此外,当前嵌入在可穿戴设备和智能手机中的各种传感器,使群智感知系统在学术界和工业界获得了相当大的关注,并被应用于环境监控[16]、智能交通[17]、智能车辆网络[18]、社交应用[19]、健康监测[20]以及其他许多方面[21-23].目前主流的群智感知系统有Mechanical Turk,Upwork,BikeNet和Uber等.
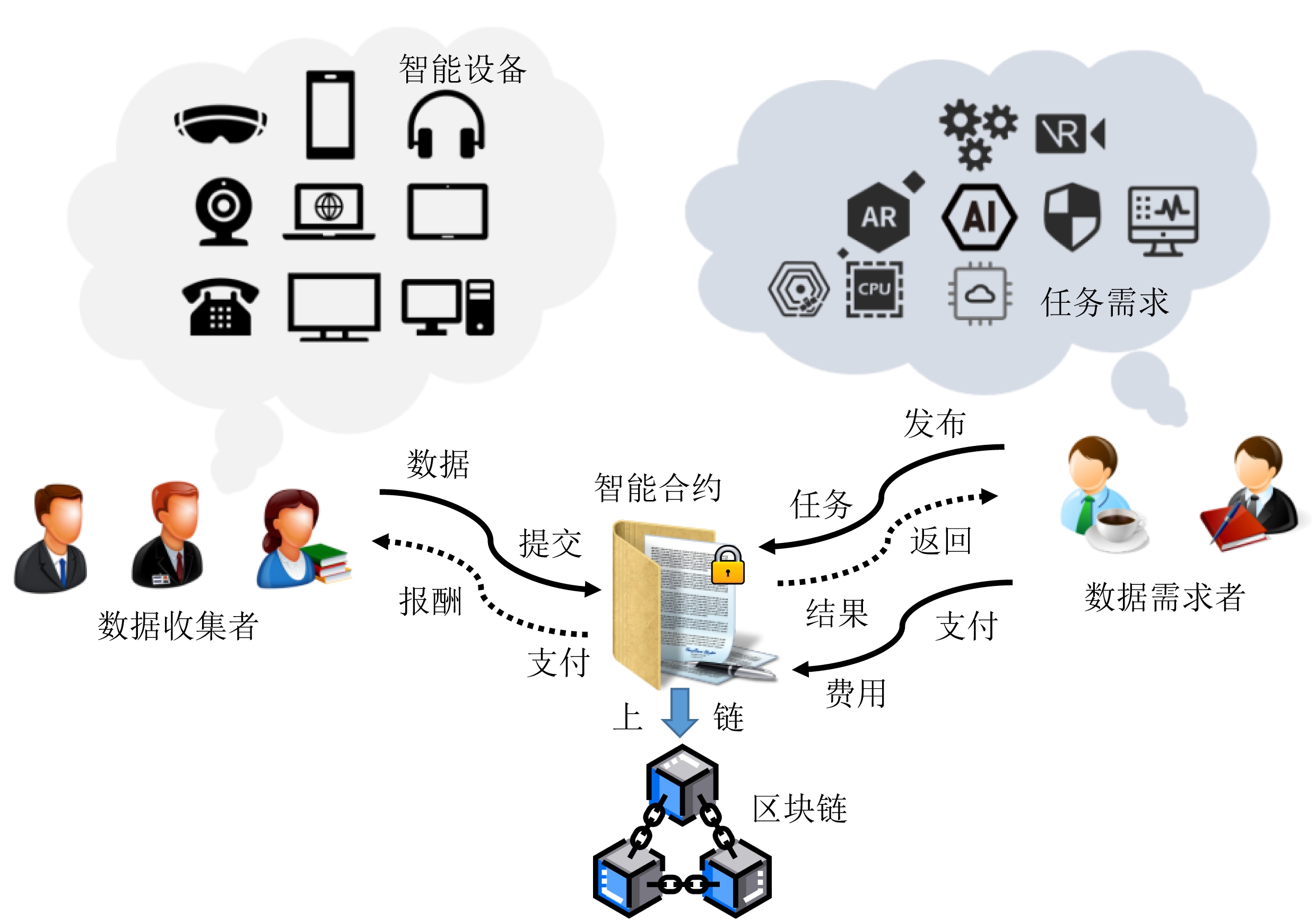
Fig.1 Blockchain-based mobile crowd sensing systems
图1 基于区块链的群智感知系统
尽管最近移动设备的普及推动了群智感知系统的大范围普及,但由于集中式平台和移动用户之间的大量数据处理操作和频繁的通信,此类系统会导致网络拥塞和严重延迟[24].不仅如此,由于移动用户参与群智感知系统会产生花费,所以需要设计激励机制来激励移动用户加入到该系统中[25],但是在该群智感知系统中,激励机制的实施依赖于一个可信的第三方,然而在实际应用中,这样一个可信第三方会带来许多新的问题:1)平台的功能可能会受到参与的移动用户或外部攻击者的损害[26];2)该平台可能不稳定[27];3)增加了大规模隐私泄露的风险[28].
最近,区块链作为一种分布式账本[29-31],以其去中心化、安全、透明、不可篡改等优越功能,被广泛应用于各种领域.同时,区块链中设置的智能合约[32]可以高效、准确、快捷地实现各种复杂的交易和功能[33-34].因此,本文利用区块链的智能合约,建立一类如图1所示的区块链群智感知系统中基于隐私保护数据真值估计的用户激励机制.该机制由数据真值估计模块和移动用户激励模块共同组成,该机制能够有效提高数据真值估计的准确度,并能够激励更多的移动用户参与到该系统中.
本文的主要贡献有3个方面:
1)机制设计.本文的第1个贡献是利用全同态加密算法构建了一类区块链群智感知系统中基于隐私保护数据真值估计的用户激励机制.该机制由数据真值估计模块(PATD)和参与者激励模块(PFPI)组成,能够实现高准确度的数据真值估计和参与者激励.据调研所知,本文尝试在全同态加密状态下实现具有数据真值估计功能的用户激励机制.与传统的机制不同,本文所提机制需要克服移动用户自私属性,提高数据真值估计的准确性,同时要保证全同态加密状态下机制运行的速率.从实验中可以看到,PATD的数据真值估计准确度相较于已有的方法提高了至少33%,而PFPI达到的社会福利相较于已有的方法提高了至少21%.同时,当系统具有128个数据感知任务时,整个系统的运行时间约为300 s,且通过不同的参数选择,还可以进一步加快机制运行速度,这表明该机制可被应用于实际的场景.
2)真值估计.本文的第2个贡献是实现了全同态加密状态下的数据真值估计,在保证真值估计的准确度和机制运行速度的同时,保护了用户的数据隐私.由于数据采集设备精确度不够等原因,用户收集的数据往往具有噪声,因此PATD对用户提交的含有噪声的数据的加密结果进行计算,并将解密后的计算结果作为相应数据真值的估计.因为所用的数据均是加密的,因此可以保护用户数据隐私,该性质在定理3中给出.同时,该机制还可以保证解密后的估计值具有较高的估计精度,可以从定理1中看到,估计误差呈指数衰减.就本文作者所知,CKKS是目前性能最好、计算速度最快的同态加密方案[35],且该方案被ZAMA所应用并进行了适当的改进[36].
3)用户激励.本文的第3个贡献是在全同态状态下保证数据真值估计准确性的同时实现了移动用户的激励.PFPI同样利用CKKS方案实现了竞价加密状态下用户激励,同时还从理论上证明了其满足真实性和个体合理性,并可以达到较高的社会福利,可以从定理2看到,PFPI在社会福利上达到了2的近似度,同时可以从定理4得到,PFPI可以保护用户竞价的隐私.
1 相关工作
目前,已有基于区块链的群智感知系统,它们利用区块链去中心化、安全、透明的性能构建了数据真值估计机制和移动用户激励机制,分别实现了高效的性能表现,但是这些机制都是分开来建立的,即只建立了数据真值估计机制或者只建立了移动用户激励机制.由这些机制组成的数据收集机制往往很难在实际的系统中实现较好的表现.接下来,我们将分别介绍基于区块链的数据真值估计机制和用户激励机制.
1.1 基于区块链的数据真值估计机制
Tian等人[37]提出了一个分布式数据真值估计机制,该机制可以有效地保护用户数据的隐私.该机制将数据融合和处理任务委托给分布式的参与者,通过利用区块链中的智能合约技术来执行和验证其行为.同时,由于区块链缺乏对链上数据保密性的支持,它们利用隐私保护解决方案防止数据泄露.此外,鉴于它们框架的去中心化性质,使得该框架还克服了单点故障的限制,增加了系统的稳定性.但是,该机制对数据隐私的保护是通过对原始数据加入高斯噪声实现的,由于无法消除高斯噪声对真值估计的影响,虽然在理论上可以证明其具有一定的真值估计准确度,但是在实际操作时往往无法达到很好的效果.
Wu等人[38]提出了一个基于区块链的数据真值估计机制,该机制可以提供可靠的数据真值.为了减轻恶意参与者的影响,该机制集成了一种具有隐私保护的感知验证协议.通过该协议,一些数据参与者可以在不知道任何数据的情况下协作验证真值估计结果.同时,该机制还可以通过经济激励,促使移动用户诚实地参与到群智感知系统中.但是该系统使用的是加法同态加密方案,由于该方案的局限性,使其无法保证数据真值估计的准确度.不仅如此,该机制在移动用户激励中,无法保护用户的隐私信息.
1.2 基于区块链的移动用户激励机制
Huang等人[39]通过区块链中的智能合约提出了一个基于完整信息动态博弈的激励机制,该机制利用完全信息的Stackelberg博弈来对用户数据进行选择,平台和移动用户都是根据对方可能的策略来选择自己的策略以保证自己在对方策略下的利益最大化,从而达到纳什均衡.该博弈具有唯一纳什平衡点,并应用基于区块链的同态水印技术来保护数据版权.但是该机制无法在用户激励过程中保护它们的隐私,所以无法在实际系统中取得很好的效果.
Zhang等人[40]提出了一种新颖的隐私保护和可靠的车辆移动群智感知系统.该机制包含一种具有隐私保护的车辆数据聚合方案,以保护参与车辆与感知数据之间的数据隐私和不可链接性.此外,还包括2个协议来保护数据隐私并为移动用户提供公平的回报.该系统实现了隐私保护、可靠性和公平性,且具有较高的计算和通信效率.但是该系统依据的同样是加法同态加密方案,所以无法实现在用户激励阶段的隐私保护.
Xie等人[41]提出了一种新颖的基于名誉激励的无人机辅助移动群智感知框架.该框架利用名誉激励方案来选择具有高名誉的无人机来执行数据感知任务,从而保护无人机和任务发布者之间的数据共享免受内部资源不足的无人机攻击.同时,该框架利用一种基于区块链的数据安全传输方案安全地记录无人机的数据交易.此外,由于资源有限的无人机难以执行计算密集型挖矿任务,因此结合边缘计算以增加区块创建的成功概率.无人机与边缘计算提供者之间的交互被建模为Stackelberg 博弈,以激励无人机参与区块创建过程,同时提供高质量的服务,在该博弈中,无人机和平台根据对方可能的策略来选择策略以保证自己在对方策略下的利益最大化,从而达到纳什均衡.但是与之前的机制类似,该框架只保护了无人机传输数据的隐私安全,但是并没有考虑用户激励过程中的隐私保护.
2 预备知识
本节分别介绍系统概述、数据真值估计、激励模型、同态加密方案和攻击模型.
2.1 系统概述
本文考虑一个基于区块链的群智感知系统,系统组成部分包括:智能合约、一个加密服务中心、一个数据收集者集合W={w1,w2,…,wm}、一个数据需求者集合R={r1,r2,…,rn}和感知任务需求集合T={τ1,τ2,…,τn},其中每个需求者ri的任务需求为τi.这些感知任务需要一些数据收集者在本地利用智能设备进行数据收集,然后将感知数据通过区块链发送给相应的需求者,其中,用户wj对于任务τi的感知数据表示为mi,j.为了消除每个移动用户设备差异带来的数据误差,对于每一个任务τi,智能合约会聚合相关收集者的数据以计算一个数据融合结果mi,该结果被视为任务τi的真值m*i的估计,其中m*i对参与者和数据收集者而言是未知的.因为智能合约是公开可见的,所以为了防止隐私信息在智能合约进行一些相关操作时泄露,每个数据需求者和数据收集者借助加密服务中心加密他们的信息(包括收集到的数据、上报的竞价),其中加密服务服务中心也是不可信任的,因此也需要防止中心对信息的窃取.图2所示为本文所提的基于区块链的群智感知系统中数据收集框架的工作流程.为了方便,表1列了一些重要的符号解释.

Fig.2 Workflow of data collection mechanism for blockchain-based mobile crowd sensing systems
图2 基于区块链的群智感知系统中数据收集机制工作流程
Table 1 Description of Some Important Symbols
表1 重要符号说明
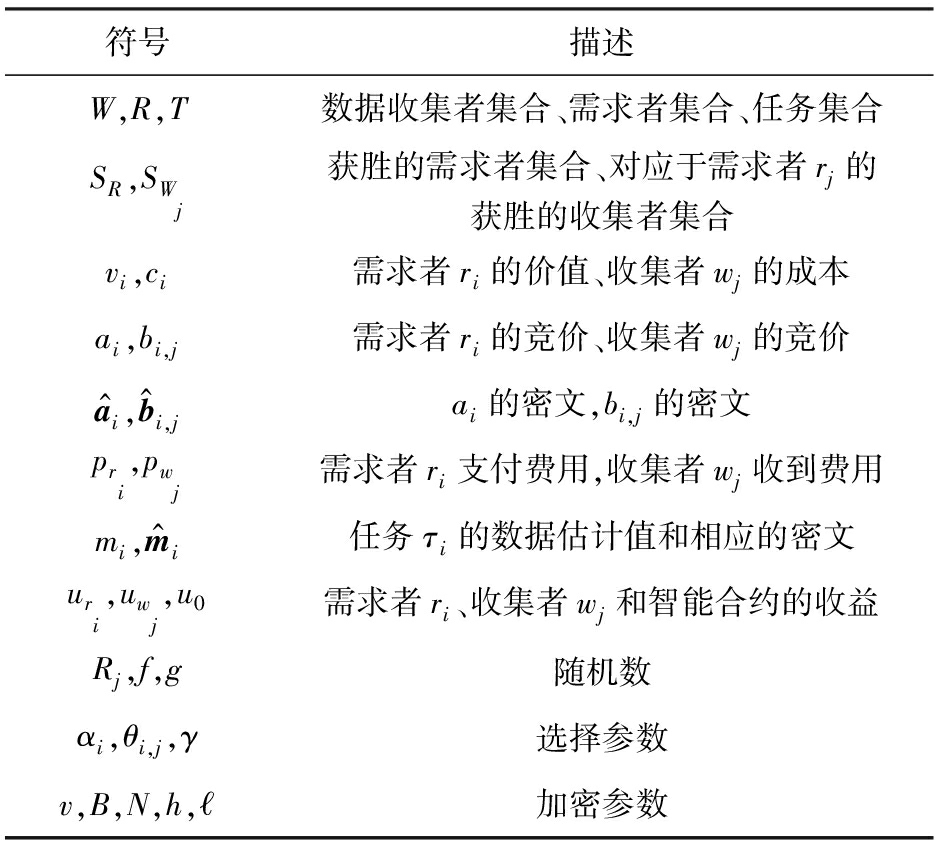
符号描述W,R,T 数据收集者集合、需求者集合、任务集合SR,SWj获胜的需求者集合、对应于需求者rj的获胜的收集者集合vi,ci需求者ri的价值、收集者wj的成本ai,bi,j需求者ri的竞价、收集者wj的竞价a^i,b^i,jai的密文,bi,j的密文pri,pwj需求者ri支付费用,收集者wj收到费用mi,m^i任务τi的数据估计值和相应的密文uri,uwj,u0需求者ri、收集者wj和智能合约的收益Rj,f,g 随机数αi,θi,j,γ选择参数v,B,N,h,ℓ加密参数
1)信息加密.每个数据需求者ri通过加密服务中心的公钥加密她的竞价ai,其中竞价ai表示任务τi被执行时她能够获得的价值(步骤①),然后向智能合约提交一个包含感知任务τi和加密竞价![]() 的数据收集请求(步骤②).智能合约对外公布数据收集任务集合T(步骤③).在接收任务后,每个数据收集者wj通过加密服务中心的公钥加密她的竞价bi,j,其中,bi,j表示执行任务τi时,收集者wj需要的花费(步骤④),之后收集者wj向智能合约提交她愿意执行的任务集合Γj⊆T和每个任务τi∈Γj的相关加密竞价
的数据收集请求(步骤②).智能合约对外公布数据收集任务集合T(步骤③).在接收任务后,每个数据收集者wj通过加密服务中心的公钥加密她的竞价bi,j,其中,bi,j表示执行任务τi时,收集者wj需要的花费(步骤④),之后收集者wj向智能合约提交她愿意执行的任务集合Γj⊆T和每个任务τi∈Γj的相关加密竞价![]() (步骤⑤).
(步骤⑤).
2)参与者激励.通过加密服务中心的协助,智能合约利用接收到的加密竞价来决定获胜的数据需求者集合SR和执行每个获胜需求者ri∈SR任务τi的获胜的数据收集者集合SWi、每个获胜需求者ri的需要支付的费用pri以及支付给每个获胜收集者wj的报酬pwi(步骤⑥).实际上,![]() 其中pi,j表示对于每个想要执行的任务τi,数据收集者wj从中获取的报酬.此外.注意,因为未获胜需求者的任务不会被执行,所以她们不会支付任何的费用.类似地,未被选中的收集者不会获得任何报酬因为她们不执行任何任务,此时她们各自收益都是0.
其中pi,j表示对于每个想要执行的任务τi,数据收集者wj从中获取的报酬.此外.注意,因为未获胜需求者的任务不会被执行,所以她们不会支付任何的费用.类似地,未被选中的收集者不会获得任何报酬因为她们不执行任何任务,此时她们各自收益都是0.
3)数据加密.每个被选中的数据收集者wj∈SWi通过加密服务中心的公钥,加密每个任务τi∈Γj收集到的数据mi,j(步骤⑦),然后向智能合约提交加密后的数据![]() (步骤⑧).
(步骤⑧).
4)数据融合.智能合约对于每个任务τi,计算获胜的收集者所提交加密数据的融合结果![]() (步骤⑨),然后借助加密服务中心解密得到明文mi(步骤⑩),并将mi发送给相应的获胜的数据需求者ri∈SR(步骤
(步骤⑨),然后借助加密服务中心解密得到明文mi(步骤⑩),并将mi发送给相应的获胜的数据需求者ri∈SR(步骤 )),其中mi便是智能合约计算的对于任务τi数据真值m*i的估计值.
)),其中mi便是智能合约计算的对于任务τi数据真值m*i的估计值.
5)报酬收集.最后,智能合约向获胜的需求者ri收取费用pri(步骤 )),并向被获胜的收集者wj支付报酬pwj(步骤
)),并向被获胜的收集者wj支付报酬pwj(步骤 )).
)).
2.2 数据真值估计
为了消除由于数据收集者设备差异带来的数据误差,对于每个任务,智能合约利用数据收集者的数据估计数据真值.因此,与已有的工作类似,本文也采用了Jin等人在文献[42]中提出的数据真值估计机制.为简便起见,在算法1中描述了相应的算法.需要注意的是,本文主要关注的是连续任务,而离散任务的真值估计则省略了,但是它可以用类似的方法获得.
算法1.数据真值估计算法.
输入:获胜需求者选择集合SR和对应的获胜收集者集合SWi,其中i:ri∈SR,每个任务τi的阈值参数αi,每个获胜收集者wj对于任务τi的置信度θi,j和收集的数据mi,j;
输出:每个获胜数据需求者ri的任务τi的数据真值的估计值mi.
/*智能合约的操作*/
for 获胜需求者ri∈SR的任务τi∈Γ do
① 计算:
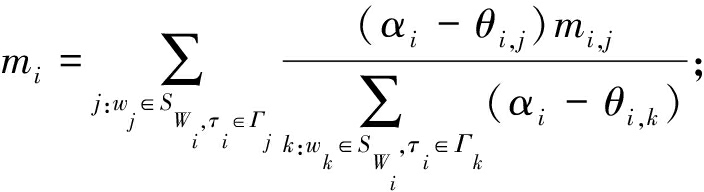
end for
如算法1所示,智能合约利用如下公式计算需求者ri的连续任务τi真值的估计值:
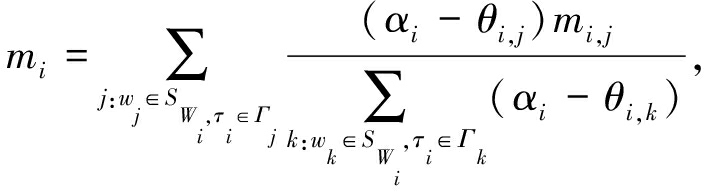
(1)
其中,αi表示智能合约选取的任务τi的阈值参数,满足![]() 表示收集者wj对于任务τi的置信水平,θi,j是智能合约已知的.因为在任务被执行之前,收集者wj关于每个任务τi的数据可被认作是一个随机变量Mi,j,θi,j的定义如定义1.
表示收集者wj对于任务τi的置信水平,θi,j是智能合约已知的.因为在任务被执行之前,收集者wj关于每个任务τi的数据可被认作是一个随机变量Mi,j,θi,j的定义如定义1.
定义1.收集者wj对于一个连续任务τi∈Γ的置信水平θi,j为
θi,j=E[|Mi,j-m*i|]∈[0,1],
(2)
其中数学期望是由于Mi,j的随机性.
此外,作为一个数据真值的估计需要具有较高的准确度.因此,定义2给出了连续任务(α,γ)-准确度的概念.
定义2.对于范围[0,1]内的2个随机变量Y1和Y2,当Pr[|Y1-Y2|≥α]≤γ时,我们称Y1对Y2是(α,γ)-准确的,其中α,γ∈(0,1).
这意味着一旦数据估计值和真值满足定义2,则它们有很高概率是相当接近的.
2.3 激励模型
数据收集者和数据请求者都是自私的,因此都希望最大化她们各自的收益.为了激励更多参与者加入到系统中,本文采用了类似于Jin等人在文献[43]中的双边激励模型,其定义如下.
定义3.在一个双边激励模型中,每个竞价为ai 的数据需求者ri拥有一个感知任务τi,该任务需要被多个数据收集者执行,其中竞价ai表示需求者能够从该任务中获得的价值.该任务被执行时产生一定的实际价值记为vi,需求者需向智能合约支付费用pri,需求者为了最大化收益可能谎报任务的价值,即ai≠vi.此外,每个数据收集者wj选择执行的任务集合为Γj⊆T,其中,对于每个任务τi∈Γj,她有一个竞价bi,j,该竞价表示她执行该任务时产生的花费.而收集者wj的实际开销为ci,j,并且将会从智能合约获取报酬pi,j,同样,为了最大化利益,收集者可能会谎报花费,即bi,j≠ci,j.为了保护隐私,需求者ri和收集者wj将会分别提交加密竞价![]() 和
和![]() 注意,每个需求者ri的任务τi所具有的价值vi和收集者wj的花费ci,j对于智能合约来说都是未知的.
注意,每个需求者ri的任务τi所具有的价值vi和收集者wj的花费ci,j对于智能合约来说都是未知的.
对于任务τi,当需求者ri∈R能够获得的价值为vi,需求者wj∈W的实际开销为ci,j 时,需求者ri的对应收益为
(3)
收集者wj的对应收益为

(4)
此外,智能合约的收益可以表示为
(5)
如式(3)~(5)所示,收益uri,uwj,u0实际分别是数据需求者ri、数据收集者wj和智能合约的净利润.由于收集者和需求者的自私和策略特性,对于每个任务τi,为了最大化收益,每个需求者ri可能会发送一个加密竞价![]() 其明文ai与实际价值vi不同.类似地,每个收集者wj可能发送一个加密竞价
其明文ai与实际价值vi不同.类似地,每个收集者wj可能发送一个加密竞价![]() 其明文bi,j与实际开销ci,j不同.这一问题可以通过激励模型的真实性来解决.
其明文bi,j与实际开销ci,j不同.这一问题可以通过激励模型的真实性来解决.
定义4.如果对于感知任务τi,收集者wj的收益在提交加密竞价![]() 的明文bi,j等于她的实际开销ci,j时达到最大,并且需求者ri的收益在提交加密竞价
的明文bi,j等于她的实际开销ci,j时达到最大,并且需求者ri的收益在提交加密竞价![]() 的明文ai等于获得的实际价值vi时达到最大,则一个激励模型被称为是双边真实的.
的明文ai等于获得的实际价值vi时达到最大,则一个激励模型被称为是双边真实的.
除了真实性,为了激励更多的参与者,设计的激励模块还需要满足个体合理性,具体定义如下.
定义5.如果需求者ri和收集者wj的收益分别满足uri>0和uwj>0,激励模型满足双边个体合理性.
定义6.基于区块链的群智感知系统的社会福利定义为
(6)
2.4 同态加密方案
每个数据收集者和数据需求者的信息(例如,收集的数据和提交的竞价)可能会被其他参与者窃听.因此,本文采用Cheon等人在文献[44]中提出的同态加密方案CKKS来保护它们的隐私.作为同态加密方案,CKKS支持实数和复数的近似计算.算法如下,其中 ![]() 为实数域,
为实数域,![]() 为复数域.
为复数域.
1)密钥生成操作KeyGen(L,1λ)
① 给定一个深度参数L和一个安全参数λ,算法选择一个2的幂整数N并设置密文的模值q =q0×p
=q0×p ,其中1≤
,其中1≤ ≤L,q0>0,p>0.q0是一个基本模数,p是一个底数,二者都是整数.
≤L,q0>0,p>0.q0是一个基本模数,p是一个底数,二者都是整数.
② 密钥分布χkey、误差分布χerr和加密分布χenc都在R
![]() [X]/(XN-1)多项式环上设置,其中
[X]/(XN-1)多项式环上设置,其中 ![]() 是整数环.
是整数环.
③ 算法选取一个密钥参数s←χkey并设置密钥为sk←(1,s).
④ 算法同时选取一个公共参数a←U(RqL),并选取一个误差参数e←χerr,其中U(RqL)为RqL上的均匀分布,RqL是一个多项式商环R/qLR.然后,算法根据选中的参数设置公钥为![]() 其中b是由前边参数确定的另外一个公共参数,其表达式为b←-a·s+e(mod qL).
其中b是由前边参数确定的另外一个公共参数,其表达式为b←-a·s+e(mod qL).
⑤ 算法采样一个计算参数![]() 和另一个误差参数e′←χerr,然后设置计算密钥为
和另一个误差参数e′←χerr,然后设置计算密钥为![]() 与④设置类似,
与④设置类似,![]() 是一个计算参数.其中 用于2个密文的乘法操作,也就是为了进行2个密文的乘法运算,必须使用计算密钥evk.
是一个计算参数.其中 用于2个密文的乘法操作,也就是为了进行2个密文的乘法运算,必须使用计算密钥evk.
2)加密操作Enc(pk,m)
① H={z∈![]()
![]() 其中
其中![]()
![]() N为z∈
N为z∈![]() N的共轭.在通过简单地复制明文m获取
N的共轭.在通过简单地复制明文m获取![]() 后,算法的加密操作利用同构映射π:H→
后,算法的加密操作利用同构映射π:H→![]() N/2计算
N/2计算![]() 在这之后,该算法进一步计算一个消息多项式
在这之后,该算法进一步计算一个消息多项式![]()
其中![]() y
y![]() 表示最接近y的整数,σ是后文定义中引入的规范化嵌入.
表示最接近y的整数,σ是后文定义中引入的规范化嵌入.
② 算法选取一个加密参数v←χenc和2个误差参数e0,e1←χerr,随后加密算法输出对应密文![]()
3)解密操作![]()
① 对于一个密文![]() 该解密算法通过进行计算估计得到的消息多项式
该解密算法通过进行计算估计得到的消息多项式![]()
② 用![]()
![]() N/2计算明文m′.
N/2计算明文m′.
注意,CKKS的加密过程引入了一个误差,因此它的解密值与输入值不完全相同.下面将介绍相应的同态运算,包括加法、乘法、标量乘法和缩放.
4)加法操作![]()
对于密文![]() 算法输出
算法输出![]()
5)乘法操作![]()
对于2个相应的密文![]()
![]() 乘法操作令
乘法操作令![]() 得到
得到![]() (mod q
(mod q ),从中可以看出,在CKKS全同态加密算法中,计算2个密文的乘法时,必须使用计算密钥evk,否则乘法操作将无法进行.
),从中可以看出,在CKKS全同态加密算法中,计算2个密文的乘法时,必须使用计算密钥evk,否则乘法操作将无法进行.
6)常量乘法![]()
对于常量![]() 和一个密文
和一个密文![]() 算法输出
算法输出![]()
7)缩放操作![]()
对于密文![]() 算法输出
算法输出![]() 说明
说明![]()
定义7.对于一个消息多项式![]() 的典范嵌入
的典范嵌入![]() 为在第M个N次割圆多项式ΦM=XN+1的根带入计算得到的对应值,也就是说有
为在第M个N次割圆多项式ΦM=XN+1的根带入计算得到的对应值,也就是说有![]()
![]() N,ζM=exp(-2πi/M)为一次本原单位根,
N,ζM=exp(-2πi/M)为一次本原单位根,![]()
![]()
定义8.对于一个实数消息多项式![]() 的典范嵌入范数
的典范嵌入范数![]() 为
为![]() 上的
上的 ∞-范数,表示为
∞-范数,表示为![]() 其中
其中![]()
![]() 和ζM的定义在定义7中给出.
和ζM的定义在定义7中给出.
对于一个消息多项式![]() 根据推导,加密实数消息多项式
根据推导,加密实数消息多项式![]() 可以被表示为
可以被表示为![]() 其中
其中![]() 是一个误差多项式.
是一个误差多项式.
定义9.如果对于常量ν和B,有![]() 则称方案
则称方案![]() 为
为![]() 的有效加密,其中
的有效加密,其中![]() 是加密深度为
是加密深度为 的密文.
的密文.
2.5 攻击模型
与之前在具有隐私保护的数据真值估计方面的工作类似,我们的安全目标是确保在整个数据真值估计过程中,数据收集者和数据需求者的竞价以及获胜收集者提交的数据受到保护,隐私信息不会被其他参与者获取.事实上,智能合约对于所有参与者是公开透明的,因此其他参与者可能通过窃听智能合约得到需求者和收集者的隐私信息,同时加密服务中心也是诚实但是好奇的,这意味着,加密服务中心能够诚实地遵循预先设计的通信协议,但也试图通过机制执行过程中收到的智能合约发送的信息推断参与者提交的竞价和感知数据.此外,所有其他数据收集者和数据需求者也诚实地遵循预先设计的通信协议,但是,他们也都对其他参与者提交的竞价和数据感到好奇.遵循现有工作中的类似假设,我们假设加密服务中心和其他参与者之间不存在共谋.特别注意,在机制执行过程中,加密服务中心不会主动对智能合约进行窃听并对加密数据进行解密,只会从智能合约发来的信息中推断参与者隐私信息.
需要注意的是,检测那些提交无效数据和竞价来故意破坏系统的恶意数据收集者和数据需求者并不是本文研究的内容.请注意,在本文提出的数据收集框架中,可以使用安全传输协议,例如SSL来验证不同参与方之间的通信.
3 具有隐私保护的数据真值估计模块
基于区块链的群智感知系统中数据收集框架由2部分组成,本节将详细介绍具有隐私保护的数据真值估计模块.
3.1 设计合理性
由于数据采集设备内部的各个器件本身尺寸具有误差,以及不同数据采集应用之间存在差异,移动用户利用不同设备不同应用对同一个任务采集到的数据往往带有噪声,即彼此数据并不相同.因此,为了能够准确得到数据的真值,需要利用收集到的大量用户数据进行真值估计.实际上,真值估计机制的设计是移动群智感知系统中一个重要的研究方向[1,8,12].
移动用户提交的数据往往含有用户的隐私信息,虽然因为设备和应用自身的差异使得采集到的数据具有噪声,但是这些噪声较为微小,因此这些数据虽然各不相同,但却都在一个较小的范围波动.得到这些数据后,仍然可以推测用户的隐私信息.例如测量移动用户所在地中午12点的气温,虽然测得的数据含有噪声,但是温度数据仅在很小的范围波动,因此可以利用这些数据推测用户所在地的一些信息.甚至有时候因为用户设备所带来的噪声,也会导致用户隐私泄露.例如用不同的手机拍摄同一个物品,因为设备的不同,照片的色温等参数可能不同.在得到这些照片后,可以从这些差别中分析用户使用的设备品牌.因此在利用用户采集的数据进行真值估计的同时,还需要保护用户的隐私信息,防止隐私泄露.为此本文利用全同态加密算法设计了数据真值估计机制,该机制在保护用户隐私的同时,具有较高的估计准确度.
3.2 设计细节
为防止隐私泄露,数据真值估计模块利用了CKKS同态加密方案对每个数据收集者和数据需求者提交的信息(包括竞价和感知数据)进行加密.利用式(1)对加密数据的真值进行估计,具有隐私保护的数据真值估计模块(PATD)的工作方式如下:
如算法2所示,加密服务中心应用CKKS的密钥生成操作生成一个公钥pk、一个密钥sk和一个计算密钥evk,然后将公钥pk发布给所有参与者,每个参与者按照CKKS加密操作对相关信息进行加密.注意,如CKKS的加密操作所示,消息![]()
![]() N/2.因此,每个获胜的收集者wj∈SW i将收集到的需求者ri的任务τi 的一维数据mi,j通过简单的复制操作扩展为N/2维数据,即
N/2.因此,每个获胜的收集者wj∈SW i将收集到的需求者ri的任务τi 的一维数据mi,j通过简单的复制操作扩展为N/2维数据,即![]() 利用数据向量
利用数据向量![]() 一个数据多项式
一个数据多项式![]() ∈R能够通过逆同构映射τ-1、π-1和预先定义的基底p获得.之后,通过公钥pk,每个获胜数据收集者wj根据CKKS的加密操作来加密要提交的数据,加密后的数据表示为
∈R能够通过逆同构映射τ-1、π-1和预先定义的基底p获得.之后,通过公钥pk,每个获胜数据收集者wj根据CKKS的加密操作来加密要提交的数据,加密后的数据表示为![]()
算法2.具有隐私保护的数据真值估计算法.
输入:获胜需求者集合SR和对应的获胜收集者集合SWi,其中i:ri∈SR,每个任务τi的阈值参数αi,每个获胜收集者wj对于任务τi的置信度θi,j和收集的加密数据![]()
输出:每个获胜数据需求者ri的任务τi数据的真值的估计值mi.
/*智能合约的操作*/
for 获胜需求者ri∈SR的任务τi∈T do
for 获胜收集者wj∈SWido
① 计算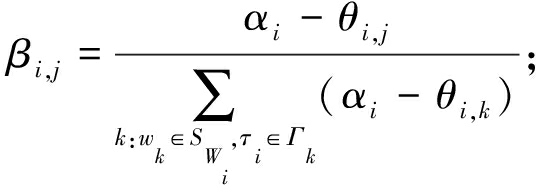
② 利用同态映射得到权重多项式![]()
end for
③ 利用数乘操作SMul(·,·)计算![]()
④ 利用缩放操作Res(·,·)计算
(mod q ′);
′);
for 获胜收集者wj∈SWi do
⑤ 利用加法操作Add(·,·)计算
end for
end for
此外,智能合约收集每个获胜收集者wj的对于任务τi的置信度θi,j并为任务τi设置阈值参数αi,满足![]() 然后,智能合约为每个任务集Γj中包含任务τi的获胜收集者wj∈SWi计算权重参数
然后,智能合约为每个任务集Γj中包含任务τi的获胜收集者wj∈SWi计算权重参数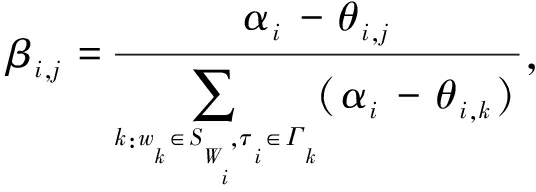 并通过简单复制操作获取N/2维权重参数向量
并通过简单复制操作获取N/2维权重参数向量![]() 利用
利用![]() 智能合约进一步通过逆同构映射τ-1和π-1获取权重参数多项式
智能合约进一步通过逆同构映射τ-1和π-1获取权重参数多项式![]()
当从获胜收集者wj∈SW处接得到为获胜需求者ri∈SR的任务τi提交的加密数据![]() 智能合约进行常量乘法操作
智能合约进行常量乘法操作![]() 在这之后,由于CKKS扩散的特性,智能合约需要通过缩放模数q
在这之后,由于CKKS扩散的特性,智能合约需要通过缩放模数q ′来执行缩放操作Res(·,·),该缩放值为
′来执行缩放操作Res(·,·),该缩放值为![]() 这里面有
这里面有 ′=
′= -1.最后,执行加法操作Add(·,·)得到加密数据估计结果
-1.最后,执行加法操作Add(·,·)得到加密数据估计结果![]()
注意整个操作实际是在输入为加密数据时计算式(1).智能合约随后提交任务τi的加密估计值![]() 到加密服务中心,并在CKKS解密操作后得到估计值mi.获胜数据需求者集合SW和获胜数据收集者集合SR的选择规则将在3.3节中描述.
到加密服务中心,并在CKKS解密操作后得到估计值mi.获胜数据需求者集合SW和获胜数据收集者集合SR的选择规则将在3.3节中描述.
3.3 理论分析
与其他已有的数据真值估计的工作类似,本节也分析了PATD模块的估计准确性.因为所用的CKKS同态加密方案是一个近似计算方案,所以需要设计参数来消除近似误差,为此有下面的引理.
引理1.对于明文数据为mi,j,若![]() 为数据多项式
为数据多项式![]() 的有效加密,其中ν>0,0<
的有效加密,其中ν>0,0< <L,那么
<L,那么![]() 是对应情况下的数据多项式
是对应情况下的数据多项式![]() 的有效加密,在这其中,
的有效加密,在这其中,![]()
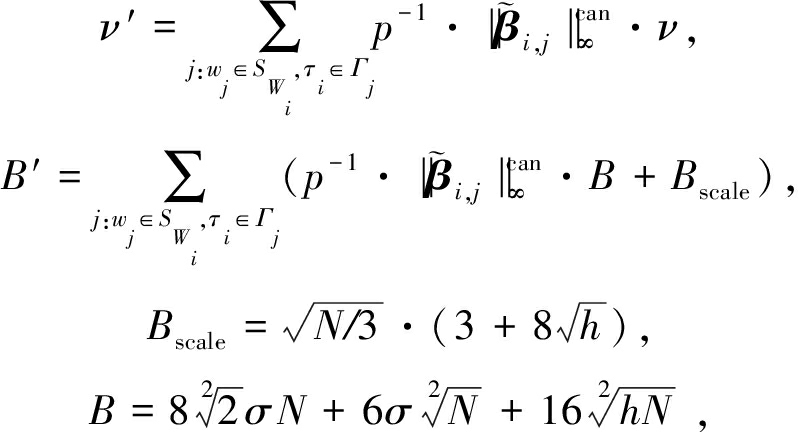
(7)
而h为密钥参数s的方差,σ2为每个![]() 的系数的方差,N为2的幂次整数.整数p>0为基底,
的系数的方差,N为2的幂次整数.整数p>0为基底,![]() 为由逆同构σ-1和π-1计算的权重参数多项式,其中,
为由逆同构σ-1和π-1计算的权重参数多项式,其中,![]() 为式(1)中相应权重系数.
为式(1)中相应权重系数.
证明.如算法2所示,智能合约对数据收集者wj为数据需求者ri的任务τi收集的加密数据![]() 进行了一次乘法操作和一次缩放操作,然后进行了一些加法操作.因此,借助Cheon等人在文献[44]的引理1~4可知,结论成立.
进行了一次乘法操作和一次缩放操作,然后进行了一些加法操作.因此,借助Cheon等人在文献[44]的引理1~4可知,结论成立.
证毕.
虽然如引理1所示,乘法操作、缩放操作和加法操作引入了一些噪声,但一些工作证明了解密后的值仍然确保较高的精度.为此,下面的定理分析PATD模块的准确性.
定理1.对于准确度参数为αi的获胜需求者ri∈SR的每个任务τi∈T,和获胜收集者wj∈SWi的置信度θi,j,用引理1设置相应参数,基底p满足![]() 时,PATD模块的Pr[|Mi-εi-m*i|≥αi]满足不等式
时,PATD模块的Pr[|Mi-εi-m*i|≥αi]满足不等式
Pr[|Mi-εi-m*i|≥αi]≤
此外,当
(8)
时,所提模块是(αi,γi)-准确的,也就是说对于误差满足Pr[|Mi-εi-m*i|≥αi]≤γi,其中εi是由CKKS加密方案引起的误差,m*i是任务τi的数据真值,Mi是随机变量,表示数据的估计值.
证明.为方便起见,需求者ri的任务τi的融合结果可以表示为
(9)
其中![]()
由于收集者wj关于每个任务τi的数据在该任务被执行之前可以被认作是随机变量Mi,j,这些数据的融合结果也能够被认作是随机变量.因此,有
(10)
其中,εi,j为加解密过程中CKKS引入的误差,因为CKKS的计算为近似结果.
该证明首先分析|εi|,由定理1可得
(11)
其中
(12)
![]() 是密文
是密文![]() 的解密输出.此外,根据Cheon等人在文献[44]中的引理1,对于一个消息向量
的解密输出.此外,根据Cheon等人在文献[44]中的引理1,对于一个消息向量![]()
![]() N/2,对于
N/2,对于![]() 的一个有效加密操作都是对的.
的一个有效加密操作都是对的.![]() 的一个有效加密,其相应的误差界为B″=B′+N/2.因此,如果p-1·B″<1/2,在CKKS解码算法中,可以通过舍入运算去除相应的误差多项式,即
的一个有效加密,其相应的误差界为B″=B′+N/2.因此,如果p-1·B″<1/2,在CKKS解码算法中,可以通过舍入运算去除相应的误差多项式,即
p(2|SWi|·Bscale+N)≤p2.
(13)
为了表示简便起见,这里令b′=2|SWi|·Bscale+![]() 因此,式(13)能够被改写为
因此,式(13)能够被改写为
(14)
其中,根据式(12),又因为对于极小x,利用无穷小代换有![]() 所以
所以![]() 成立.此外,将式(13)中的表达式b′和c′代入式(14)中,得
成立.此外,将式(13)中的表达式b′和c′代入式(14)中,得
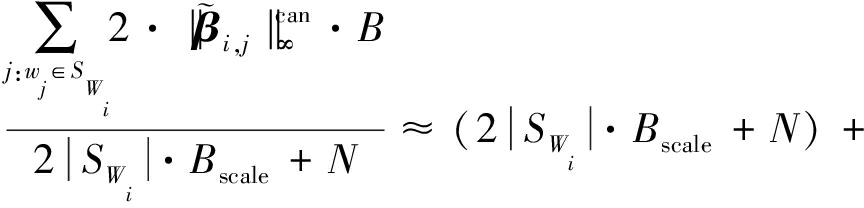
(15)
然后分析式(10)中不等式右边的第2项.为了分析误差,我们为每个任务τi定义一个随机变量![]() 该变量为随机变量Vi,j=|λi,j(Mi,j-m*i)|的和,可得
该变量为随机变量Vi,j=|λi,j(Mi,j-m*i)|的和,可得
(16)
因此,利用霍夫丁不等式,有
Pr[|Mi-m*i|≥αi]≤
![]() ⟹
⟹
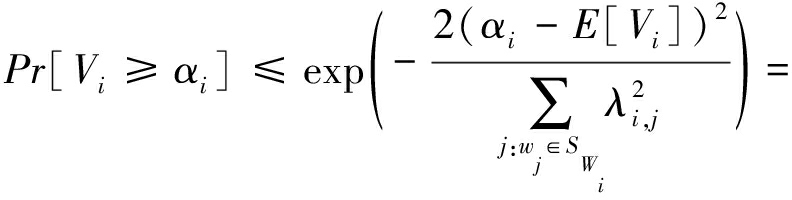
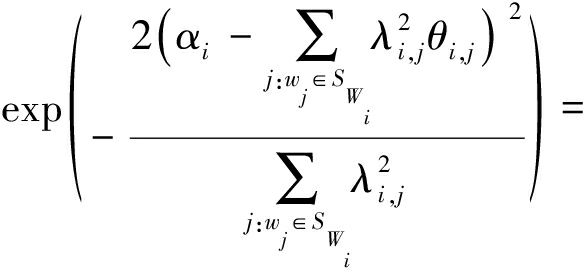
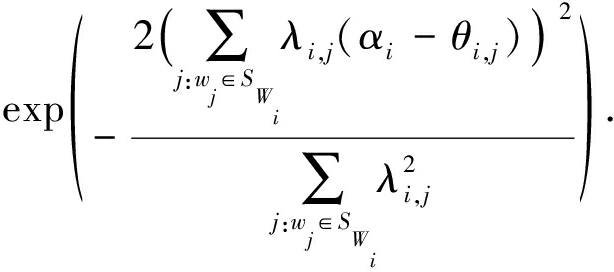
(17)
为了最小化式(17)最后一个等号后的式子,我们等价地最大化函数φ(λi),该函数定义为
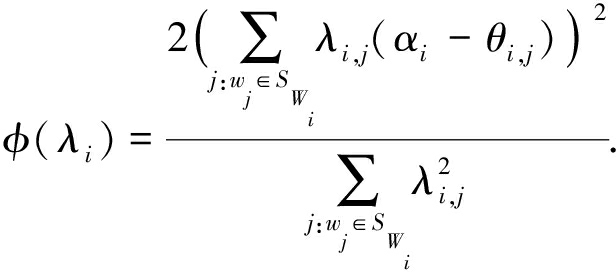
(18)
根据柯西-施瓦茨不等式,可得
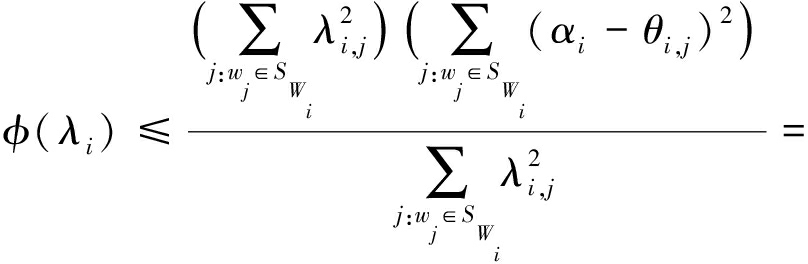
(19)
当λi,j∝(αi-θi,j),等式成立.又由![]()
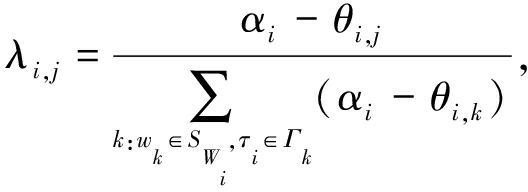
(20)
因此,当λi,j满足式(20),有
Pr[|Mi-εi-m*i|≥αi]≤
根据相应的定义,PATD模块是(αi,γi)-准确的,如果
(21)
即结论成立.
证毕.
4 具有隐私保护的用户激励模块
在介绍了PATD模块后,本节将接着介绍具有隐私保护的参与者激励(PFPI)模块,将分别介绍激励模块的数学优化模型、提出算法,并进行理论分析.
4.1 数学优化模型
数据真值的估计准确度与所收集的数据量有关,同时,所提框架希望能够最大化系统的社会福利,为此将建立式(22)数学优化模型.
优化问题.社会福利最大化:
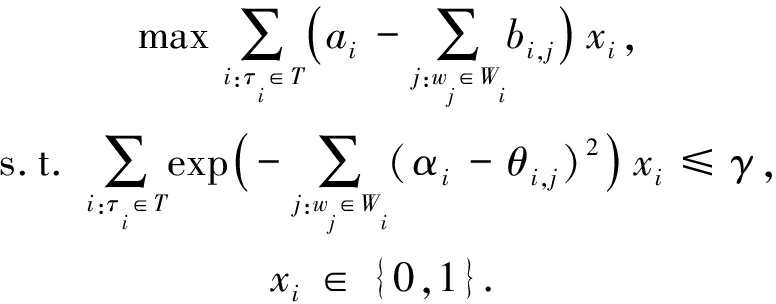
(22)
1)优化常数.社会福利最大化时,每一个任务τi所对应的数据收集者集合Wi,数据需求者ri的竞价ai,数据收集者wj的竞价bi,j,任务集合T,每个数据收集者wj的信任水平θi,j,准度参数αi和γ是常数,且γ=min{γi|i:ri∈SR}.
2)目标函数.为了能够保证PATD模块的准确度,对于任意一个任务τi,算法将该任务的所有数据都收集上来,并在此前提下最大化社会福利.
3)优化约束.根据式(8)和参数γ的选中,可知当约束不等式成立时,对于每一个任务τi,其数据真值估计都满足(αi,γi)-准确度.
4)优化变量.该优化问题中的优化变量为xi,当xi=1表示任务τi被智能合约选中并执行,当xi=0表示该任务没有被选中.
通过上述数学模型,可以得到该优化问题是NP难问题.
引理2.上述优化问题是NP难的.
证明.为了简化问题,令
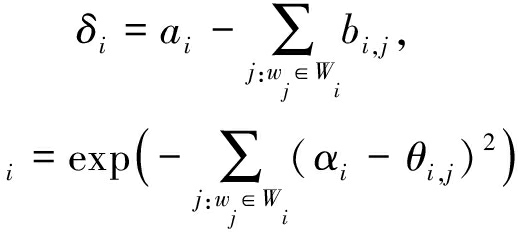
(23)
上述问题可简化为
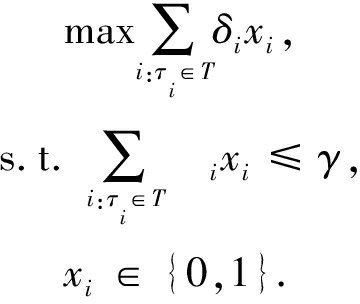
(24)
可以知道这是一个0-1背包问题,已知0-1背包问题为一个NP完全问题,所以可知,上述优化问题是一个NP难问题.
证毕.
由于该问题的NP困难属性,因此,4.2节将提出一个近似算法,高效地解决该问题.
4.2 算法设计
为了解决该问题,本节提出一个近似算法.该算法的伪代码如算法3所示,其具体流程如下.
具有隐私保护的用户激励算法由2部分组成,即参与者选择部分和报酬确定部分.
4.2.1 参与者选择部分
算法输入:收集者集合W、需求者集合R、每个数据需求者ri的加密竞价![]() 每个收集者wj对每个任务τi的加密竞价
每个收集者wj对每个任务τi的加密竞价![]() 和置信度θi,j、每个任务τi的阈值参数αi、在CKKS同态加密方案中的编码多项式.
和置信度θi,j、每个任务τi的阈值参数αi、在CKKS同态加密方案中的编码多项式.
算法主体:对于每一个任务τi,智能合约计算权重
(25)
以及权重编码多项式![]() 并计算加密状态下的收益
并计算加密状态下的收益
(26)
和加密状态下的加权收益![]() 之后,智能合约利用Hong等人在文献[45]中提出的K-加密排序算法将
之后,智能合约利用Hong等人在文献[45]中提出的K-加密排序算法将![]() 按照从大到小的顺序排序,我们假设K-加密排序算法输出左边第
按照从大到小的顺序排序,我们假设K-加密排序算法输出左边第 个密文为
个密文为![]() 即对应的明文φ
即对应的明文φ 有第
有第 大的值,注意序号
大的值,注意序号 是它在排序输出的位置,与
是它在排序输出的位置,与![]() 对应的算法输入
对应的算法输入![]() 的序号智能合约是不知道的.得到排序结果后,对于每一个任务τi,智能合约选择一个随机数Rj∈[0,1],该随机数只有智能合约自己知道,并利用密文
的序号智能合约是不知道的.得到排序结果后,对于每一个任务τi,智能合约选择一个随机数Rj∈[0,1],该随机数只有智能合约自己知道,并利用密文![]() 计算修正密文
计算修正密文![]()
(27)
其中![]() 是Rj的密文.并将
是Rj的密文.并将![]() 发送给加密服务中心,加密服务中心将其解密得到明文ζi,j,若ζi,j<η,则将序号i发送给智能合约,其中η是一个接近于0的随机数,智能合约将
发送给加密服务中心,加密服务中心将其解密得到明文ζi,j,若ζi,j<η,则将序号i发送给智能合约,其中η是一个接近于0的随机数,智能合约将![]() 排在第j个位置.为了方便,我们假设密文
排在第j个位置.为了方便,我们假设密文![]() 的对应明文δi/ϖi是第i大的值(注意,实际操作过程中往往不是).之后,智能合约计算按照序号依次计算ϖi+C.若ϖi+C≤β,则将数据需求者ri加入到需求者备选集合AR中,并得到收集者备选集合AWi=Wi.当ϖi+C>β时,智能合约利用K-加密排序算法比较
的对应明文δi/ϖi是第i大的值(注意,实际操作过程中往往不是).之后,智能合约计算按照序号依次计算ϖi+C.若ϖi+C≤β,则将数据需求者ri加入到需求者备选集合AR中,并得到收集者备选集合AWi=Wi.当ϖi+C>β时,智能合约利用K-加密排序算法比较![]() 和
和![]() 的大小,其中
的大小,其中![]() 是所有未获胜的数据需求者中其任务具有最大加权收益的,等价地可得
是所有未获胜的数据需求者中其任务具有最大加权收益的,等价地可得![]() 时,则输出SR=AR和SWi=AWi,其中i:ri∈SR,我们称这种情况下获胜的参与者分别为第1类获胜需求者和第1类获胜收集者.否则,得到
时,则输出SR=AR和SWi=AWi,其中i:ri∈SR,我们称这种情况下获胜的参与者分别为第1类获胜需求者和第1类获胜收集者.否则,得到![]() 并输出获胜需求者集合SR={ri*}和获胜收集者集合SWi*=Wi*,我们称这种情况下的获胜参与者分别为第2类获胜需求者和第2类获胜收集者.
并输出获胜需求者集合SR={ri*}和获胜收集者集合SWi*=Wi*,我们称这种情况下的获胜参与者分别为第2类获胜需求者和第2类获胜收集者.
算法输出:获胜需求者集合SR和每个获胜需求者ri对应的获胜收集者集合SWi,其中i:ri∈SR.
算法3.参与者选择部分.
输入:收集者集合W、需求者集合R、每个数据需求者ri的加密竞价![]() 每个收集者wj对每个任务τi的加密竞价
每个收集者wj对每个任务τi的加密竞价![]() 和置信度θi,j、每个任务τi的阈值参数αi;
和置信度θi,j、每个任务τi的阈值参数αi;
输出:获胜需求者集合SR和对应的获胜收集者集合SWi,其中i:ri∈SR.
/*智能合约的操作*/
① 定义需求者选择集合SR=∅和对应的收集者选择集合SWi=∅,其中i:ri∈SR,并定义常数C=0;
for 每一个τi∈T do
② 计算![]() 和权重编码多项式
和权重编码多项式![]()
③ 计算![]() 和
和![]()
end for
④ 利用K-加密排序算法将![]() 从大到小排序,记算法排序后第j个输出值为
从大到小排序,记算法排序后第j个输出值为![]()
for 每一个τi∈T do
for 每一个![]()
⑤ 选择一个随机数Rj;
⑥ 计算![]()
⑦ 发送![]() 给加密服务中心;
给加密服务中心;
end for
end for
⑧ go to 步骤 ;
;
⑨ 得到相应的排序数列![]() 其中
其中![]() 的明文δi/ϖi有第i大的值;
的明文δi/ϖi有第i大的值;
while ϖi+C≤β do
⑩ AR=AR∪{ri},AWi=Wi;
 C=C+ϖi;
C=C+ϖi;
end while
 比较
比较![]() 和
和![]() 大小;
大小;
 return SR=AR和所有SWi=AWi,
return SR=AR和所有SWi=AWi,
其中i:ri∈SR;
else
 计算
计算![]()
 SR={ri*},SWi*=Wi*;
SR={ri*},SWi*=Wi*;
 return SR和所有SWi*;
return SR和所有SWi*;
end if
/*加密服务中心的操作*/
for 每一个τi∈T do
for 每一个![]()
 解密
解密![]() 得到明文ζi,j;
得到明文ζi,j;
if ζi,j<η do
 将ζi,j的序号i发送给智能合约;
将ζi,j的序号i发送给智能合约;
end if
end for
end for
 go to 步骤⑦;
go to 步骤⑦;
在进行完参与者选择部分后,智能合约进入报酬确定部分.
4.2.2 报酬确定部分
算法输入:所有收集者wj的加密竞价![]() 和所有需求者的加密竞价
和所有需求者的加密竞价![]() 权重多项式
权重多项式![]() 获胜需求者集合SR和对应的获胜收集者集合SWi,其中i:ri∈SR.
获胜需求者集合SR和对应的获胜收集者集合SWi,其中i:ri∈SR.
算法主体:对于每一个获胜需求者ri∈SR,智能合约计算
(28)
其中 是未获胜需求者中加权收益明文值δ
是未获胜需求者中加权收益明文值δ /ϖ
/ϖ 最大的,即
最大的,即 =arg max{δj/ϖj|j:rj∉SR},而式(28)中相应的序号i′=arg max{δj|j:rj∈Ri},其中集合Ri={rk|rk∈R,δk<δi}.智能合约计算
=arg max{δj/ϖj|j:rj∉SR},而式(28)中相应的序号i′=arg max{δj|j:rj∈Ri},其中集合Ri={rk|rk∈R,δk<δi}.智能合约计算![]() 并将
并将![]() 发送给加密服务中心,其中
发送给加密服务中心,其中![]() 是g的密文而g<1是智能合约选择的一个随机数,该随机数只有智能合约自己知道.
是g的密文而g<1是智能合约选择的一个随机数,该随机数只有智能合约自己知道.
对于相应的获胜收集者wj∈SWi,智能合约计算
(29)
并计算![]() 并将
并将![]() 发送给加密服务中心,其中
发送给加密服务中心,其中![]() 是h的密文,而h>1是智能合约选择的一个随机数.
是h的密文,而h>1是智能合约选择的一个随机数.
加密服务中心收到![]() 和
和![]() 后,进行解密得到ρi和ρi,j,之后选择2个随机数f和d,其中f<1而d>1,该随机数只有中心自己知道,并计算pi=f·ρi和pi,j=d·ρi,j,然后将pi和pi,j发送给智能合约.
后,进行解密得到ρi和ρi,j,之后选择2个随机数f和d,其中f<1而d>1,该随机数只有中心自己知道,并计算pi=f·ρi和pi,j=d·ρi,j,然后将pi和pi,j发送给智能合约.
算法输出:每一个获胜需求者ri∈SR需要支付的费用pi和对应的获胜收集者wj∈SWi能够收到的报酬pi,j,其中i:ri∈SR.
算法4.报酬确定部分.
输入:所有收集者wj的加密竞价![]() 和所有需求者的加密竞价
和所有需求者的加密竞价![]() 权重多项式
权重多项式![]() 获胜需求者集合SR和对应的获胜收集者集合SWi,其中i:ri∈SR.
获胜需求者集合SR和对应的获胜收集者集合SWi,其中i:ri∈SR.
输出:获胜需求者ri∈SR的支付费用pi和对应获胜收集者wj∈SWi收到的报酬pi,j,其中i:ri∈SR.
① 智能合约选择2个随机数g<1和h>1,对应密文分别为![]() 和
和![]()
② 加密服务中心选择2个随机数f<1和d>1,其密文分别记为![]() 和
和![]()
/*智能合约的操作*/
for 每一个ri∈SRdo
③ 计算式(28);
④ 计算![]() 并将
并将![]() 发送给加密服务中心;
发送给加密服务中心;
⑤ go to 步骤 ;
;
for 每一个wj∈SWi do
⑥ 计算式(29);
⑦ 计算![]() 并发送
并发送![]() 给加密服务中心;
给加密服务中心;
⑧ go to 步骤 ;
;
⑨ return pi,j;
end for
⑩ return pi;
end for
/*加密服务中心的操作*/
for 每一个![]()
 解密得到明文ρi;
解密得到明文ρi;
 计算pi=f·ρi,并发送pi给智能合约;
计算pi=f·ρi,并发送pi给智能合约;
 go to 步骤⑥;
go to 步骤⑥;
end for
for 每一个![]()
 解密得到明文ρi,j;
解密得到明文ρi,j;
 计算pi,j=d·ρi,j,发送pi,j给智能合约;
计算pi,j=d·ρi,j,发送pi,j给智能合约;
 go to 步骤⑨;
go to 步骤⑨;
end for
在结束本节之前,我们给出一个例子来具体说明该算法的工作流程.
示例1.假设有3个数据需求者R={r1,r2,r3},他们的任务集合为T={τ1,τ2,τ3},与之相对应的竞价为{a1=0.5,a2=0.2,a3=0.1},以及3个数据收集者W={w1,w2,w3},各自感兴趣的任务为Γ1={τ1,τ2,τ3},每个任务的竞价为b1,1=0.2,b2,1=0.1,b3,1=0.02,Γ2={τ1,τ3},每个任务的竞价为b1,2=0.16,b3,2=0.024,Γ3={τ2},每个任务的竞价为b2,3=0.04.可以得到δ1=a1-b1,1-b1,2=0.14,δ2=0.06,δ3=0.056,为了方便,假设ϖ1=0.2,ϖ2=0.3,ϖ3=0.56,同时假设γ=0.2.因此,可以得到![]() 假设K-加密排序算法输出的值为φ1=0.699,φ2=0.198,φ3=0.101(注意,这些值在算法中都是密文).对于任务τ1,智能合约选择一个随机数R1=1,则可以得到
假设K-加密排序算法输出的值为φ1=0.699,φ2=0.198,φ3=0.101(注意,这些值在算法中都是密文).对于任务τ1,智能合约选择一个随机数R1=1,则可以得到![]() 加密服务中心解密将序号1发送给智能合约,对于任务τ2和τ3的操作类似.智能合约根据序号将密文位置进行相应调整,根据参与者选择部分的操作,可以得到获胜需求者集合为SR={r1},而获胜收集者集合SW1={w1,w2},因为ϖ1=γ,且δ1>δ2.之后进入报酬确定部分,根据相应的操作可得
加密服务中心解密将序号1发送给智能合约,对于任务τ2和τ3的操作类似.智能合约根据序号将密文位置进行相应调整,根据参与者选择部分的操作,可以得到获胜需求者集合为SR={r1},而获胜收集者集合SW1={w1,w2},因为ϖ1=γ,且δ1>δ2.之后进入报酬确定部分,根据相应的操作可得![]() 因此π1=min{0.40,0.42}=0.40,同样地,可以得到
因此π1=min{0.40,0.42}=0.40,同样地,可以得到![]() 类似地,可以得到π1,1=max{0.3,0.28}=0.3,同理π1,2=0.26.智能合约选择随机数g=0.9,h=1.1,加密服务中心选择随机数f=0.8,d=1.2,则最后可得数据需求者r1需要支付的费用为p1=0.284,数据收集者w1和w2得到的报酬为p1,1=0.396和p1,2=0.343.
类似地,可以得到π1,1=max{0.3,0.28}=0.3,同理π1,2=0.26.智能合约选择随机数g=0.9,h=1.1,加密服务中心选择随机数f=0.8,d=1.2,则最后可得数据需求者r1需要支付的费用为p1=0.284,数据收集者w1和w2得到的报酬为p1,1=0.396和p1,2=0.343.
4.3 激励属性
本节将证明所提出的PFPI模块满足双边真实性、双边个体合理性,同时在社会福利最大化中达到了2 的近似比.
引理3.PFPI对于每个需求者和收集者都满足真实性,这意味着每个需求者和收集者都诚实的报告竞价.
证明.我们通过证明PFPI满足单调性和临界报酬2个性质来说明参与的需求者具有真实性,而对于参与的收集者,可以用相似的方法得到结论,因此将省略相关的证明过程.注意,算法使用的CKKS是近似算法,但是由于算法的设计,使其在密文状态下的各种计算并没有改变相应的数值,因此在证明过程中所有变量均为明文.
单调性:假设需求者ri是获胜者,则相应的获胜数据收集者集合为SWi=Wi,如算法3所示,当满足![]() 时,可知如果需求者ri获胜了,则有ri∈SR且
时,可知如果需求者ri获胜了,则有ri∈SR且![]() 其中
其中![]() 而
而![]() 相似地,而其中与之相对应的变量δ
相似地,而其中与之相对应的变量δ 和ϖ
和ϖ 分别为
分别为![]() 和
和![]() 因为ϖi和ϖ
因为ϖi和ϖ 不变,所以如果需求者ri以竞价ai获胜,则当她以
不变,所以如果需求者ri以竞价ai获胜,则当她以![]() 竞价时,仍然会获胜.同时,当
竞价时,仍然会获胜.同时,当![]() 时,如果需求者ri获胜,因为
时,如果需求者ri获胜,因为![]() 是需求者集合R中收益最大的,所以如果需求者ri以竞价ai获胜,则当她以
是需求者集合R中收益最大的,所以如果需求者ri以竞价ai获胜,则当她以![]() 竞价时,仍然会获胜.因此该算法对于需求者而言,满足单调性.
竞价时,仍然会获胜.因此该算法对于需求者而言,满足单调性.
临界报酬:需求者ri支付费用pi=g·f·πi,其中![]() 序号
序号 =arg max{δj/ϖj|j:rj∉SR},同时,其中的序号i′=arg max{δj|j:rj∈Ri},其中集合Ri={rk|rk∈R,δk<δi}.而g<1且f<1.这里我们仅考虑
=arg max{δj/ϖj|j:rj∉SR},同时,其中的序号i′=arg max{δj|j:rj∈Ri},其中集合Ri={rk|rk∈R,δk<δi}.而g<1且f<1.这里我们仅考虑![]() 的情况,对于
的情况,对于![]() 的情况可以用类似的方法得到结论.在下面的证明中,为了方便表示,我们简单地令
的情况可以用类似的方法得到结论.在下面的证明中,为了方便表示,我们简单地令![]() 考虑需求者ri以
考虑需求者ri以![]() 的竞价参与竞争时的情况.
的竞价参与竞争时的情况.
当![]() 时,获胜的需求者需要支付的费用仍然是pi,非获胜需求者则需要支付的费用为0.因此,下面的证明只考虑
时,获胜的需求者需要支付的费用仍然是pi,非获胜需求者则需要支付的费用为0.因此,下面的证明只考虑![]() 的情况.在这种情况下,可以知道
的情况.在这种情况下,可以知道![]() 成立.根据算法3可知,如果需求者ri获胜,则她一定是第1类获胜者或第2类获胜者.但是当需求者ri以竞价
成立.根据算法3可知,如果需求者ri获胜,则她一定是第1类获胜者或第2类获胜者.但是当需求者ri以竞价![]() 进行竞争时,有
进行竞争时,有![]() 即
即![]() 可以得到
可以得到![]() 其中
其中![]() 根据算法3可知,需求者ri将不是第1类获胜者.同理可知,有
根据算法3可知,需求者ri将不是第1类获胜者.同理可知,有![]() 也就是说
也就是说![]() 可以得到
可以得到![]() 其中
其中![]() 因此,根据算法3可知,需求者ri将不是第2类获胜者.综上可知当
因此,根据算法3可知,需求者ri将不是第2类获胜者.综上可知当![]() 时,需求者ri不会获胜,因此,她的收益为0.
时,需求者ri不会获胜,因此,她的收益为0.
证毕.
除了真实性,还需要保证PFPI模块具有个体合理性.
引理4.PFPI模块满足每个需求者和收集者的个体合理性,这意味着每个需求者和收集者都可以得到非负的收益.
证明.这里只证明对于每个需求者,PFPI模块满足个体合理性,对于收集者的情况可以利用相同的方法得到结论.证明中所有变量都是明文.
当需求者ri获胜,则她需要支付的费用为pi=f·g·πi,其中f<1,g<1是2个随机数,而且![]() 序号
序号 =arg max{δj/ϖj|j:rj∉SR},同时,其中的序号i′=arg max{δj|j:rj∈Ri},其中集合Ri={rk|rk∈R,δk<δi}.这里我们仅证明情况为
=arg max{δj/ϖj|j:rj∉SR},同时,其中的序号i′=arg max{δj|j:rj∈Ri},其中集合Ri={rk|rk∈R,δk<δi}.这里我们仅证明情况为![]() 的结论,
的结论,![]() 时的情况可以用类似的方法证明.为了方便,在该证明中令
时的情况可以用类似的方法证明.为了方便,在该证明中令![]() 从引理2可知,每个数据需求者都诚实地报告她的竞价,即ai=vi,因此,她被获胜时的收益ui=vi-pi=ai-f·g·πi.如果她是第1类获胜者,则可以得到
从引理2可知,每个数据需求者都诚实地报告她的竞价,即ai=vi,因此,她被获胜时的收益ui=vi-pi=ai-f·g·πi.如果她是第1类获胜者,则可以得到![]() 化简后可得
化简后可得![]() 即ai>π
即ai>π ,因此ui>0.如果需求者ri是第2类获胜者,则根据算法3可知,δi=max{δj|j:τj∈T},因此δi>δi′,化简可得
,因此ui>0.如果需求者ri是第2类获胜者,则根据算法3可知,δi=max{δj|j:τj∈T},因此δi>δi′,化简可得![]() 即
即![]() 可知
可知![]() 因此,ui>0.综上可知结论成立.
因此,ui>0.综上可知结论成立.
证毕.
接下来将证明PFPI模块在系统的社会福利上达到了2的近似度.为了证明该结论,将利用分数背包问题,其定义如下.
问题.分数背包问题:
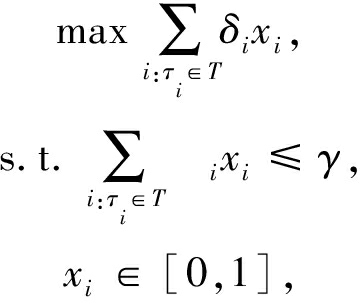
(30)
其中![]() 而与之项对应的变量则为
而与之项对应的变量则为![]() 与0-1背包问题中变量xi只能取0或1不同,分数背包问题中,变量xi可以取分数,即xi∈[0,1].对于该问题有下述引理.
与0-1背包问题中变量xi只能取0或1不同,分数背包问题中,变量xi可以取分数,即xi∈[0,1].对于该问题有下述引理.
引理5.假设当上述分数背包问题达到最大值OPTF时,xi*和xj*属于相应的最优解,那么如果有![]() 且xj*>0,则xi*=1.
且xj*>0,则xi*=1.
证明.利用反证法证明该结论.假设当上述分数背包问题达到最大值OPTF时,xi*和xj*属于相应的最优解,那么如果有![]() 且xj*>0,但是此时xi*<1.令
且xj*>0,但是此时xi*<1.令![]() 构造2个新的变量取值
构造2个新的变量取值![]() 和
和![]() 其余变量的取值均与最优算法得到的理想解完全相同.因为有
其余变量的取值均与最优算法得到的理想解完全相同.因为有![]() 可知新变量取值同样满足约束.根据ε定义可知
可知新变量取值同样满足约束.根据ε定义可知![]() 且
且![]() 因此可知新变量取值满足条件.而优化函数的取值变化量为
因此可知新变量取值满足条件.而优化函数的取值变化量为![]() 这意味着我们得到了另一组解,且达到了更高的收益,这与xi*和xj*属于相应的最优解矛盾,因此结论成立.
这意味着我们得到了另一组解,且达到了更高的收益,这与xi*和xj*属于相应的最优解矛盾,因此结论成立.
证毕.
利用引理5,可以得到如下定理.
定理2.PFPI模块在系统的社会福利上达到了2的近似比.
证明.根据引理4可知,令![]() 利用算法3可以得到相应的分数背包问题的最优解.因此可知当rj∉AR∪{r
利用算法3可以得到相应的分数背包问题的最优解.因此可知当rj∉AR∪{r },该需求者ri也不在相应的分数背包问题的最优解中,即x
},该需求者ri也不在相应的分数背包问题的最优解中,即x =0.由此可得
=0.由此可得
(31)
其中OPT是原始优化问题的最大值.由此可知
(32)
由算法3可知,选中需求者集合为SR=AR或SR={ri*},其中i*=arg max{δi|i:ri∈R},因此δi*≥δ .由此可知该算法满足
.由此可知该算法满足
(33)
所以结论成立.
证毕.
5 安全分析
如第3节和第4节所示,所提出的基于区块链的群智感知系统中数据收集框架利用 CKKS 保护数据需求者和数据收集者的数据以及竞价隐私.本节将详细分析所提框架的安全性.
定理3.PATD模块保证了收集者提交的数据对诚实但是好奇的窃听者的安全性,这意味着在执行算法过程中,加密服务中心和其他参与者除了最后的数据真值的估计值外无法获得其他关于数据的任何信息.
证明.如PATD模块所示,在提交数据之前,每个收集者使用加密服务中心生成的密钥对各自数据进行加密,然后智能合约根据加密数据估计数据真值.最后,加密状态的数据估计值由加密服务中心进行解密.在此过程中,CKKS的安全性保证了数据隐私.与现有的工作类似,假设加密服务中心和其他参与者(数据需求者和数据收集者)之间没有勾结,且加密服务中心不会在模块执行过程中主动解密收集者提交的加密数据,因此,除了最后公开的数据真值的估计值,没有人可以获得数据的任何信息.综上分析,PATD模块可以保证数据的安全性.
证毕.
值得注意的是,现有的许多具有隐私保护的数据真值估计算法为了得到最终的估计值需要在计算的过程中解密一些中间结果,而这些解密操作会导致数据隐私泄露,与这些工作不同,PATD模块不需要解密中间结果来得到最终的数据真值估计值,因此进一步保证了数据的安全性.此外,现在的一些已有工作在保护数据隐私的同时,还保护用户权重的隐私,因为研究者认为在估计真值过程中使用的用户权重也是隐私信息.与这些工作不同,在本文所提算法中,用户权重是他们的置信度,而这些置信度在区块链中是公开可见的,实际上,在区块链中,往往要根据每个参与者的置信度来决定谁有资格当矿工.
定理4.具有隐私保护的激励模块在面对半诚实但是好奇的攻击者时,可以保护数据需求者和数据收集者竞价的隐私安全,这意味着在执行算法过程中,智能合约、加密服务提供方和其他参与者除了最后的报酬外无法获得其他关于竞价的任何信息.
证明.根据算法3和算法4,数据需求者和数据收集者提交的是加密竞价,这意味着智能合约无法直接获取他们的竞价.该激励模块由2个子模块组成,参与者选择模块和报酬确定模块,因此下面的证明将分别从对2个子模块的安全性进行分析.
对于参与者选择模块,智能合约在收到数据需求者和数据收集者的加密竞价后,计算了每个任务的密态权重收益δi/ϖi,之后利用K-加密排序算法得到了相应的从小到大排序的输出![]() 并选择了一个只有自己知道的随机数Rj,其密文为
并选择了一个只有自己知道的随机数Rj,其密文为![]() 同时对于每一个密态加权收益
同时对于每一个密态加权收益![]() 计算
计算![]() 其中
其中![]() 是K-加密排序算法输出结果中排在第j个位置的密文,即
是K-加密排序算法输出结果中排在第j个位置的密文,即![]() 对应的明文φj在所有输出
对应的明文φj在所有输出![]() 对应的明文φi有第j大的值,其中i:τi∈T.在计算
对应的明文φi有第j大的值,其中i:τi∈T.在计算![]() 的过程中,所有变量均为加密状态,所以其他参与者无法得到竞价.之后智能合约将
的过程中,所有变量均为加密状态,所以其他参与者无法得到竞价.之后智能合约将![]() 发送给加密服务中心,中心解密后得到每个
发送给加密服务中心,中心解密后得到每个![]() 的明文ζi,j,因为随机数Rj只有智能合约知道,因此服务中心无法从ζi,j中得到竞价信息.服务中心将每个ζi,j对应的任务序号i发送给智能合约,智能合约只能得到每个密态加权收益的相对大小,无法知道每个竞价的信息.之后智能合约的操作同样是对密文进行的,所以无法获知竞价信息,用类似的方法对其他涉及比较操作的步骤进行分析可知同样不会泄露竞价.因此参与者选择部分能够保证竞价的隐私安全.
的明文ζi,j,因为随机数Rj只有智能合约知道,因此服务中心无法从ζi,j中得到竞价信息.服务中心将每个ζi,j对应的任务序号i发送给智能合约,智能合约只能得到每个密态加权收益的相对大小,无法知道每个竞价的信息.之后智能合约的操作同样是对密文进行的,所以无法获知竞价信息,用类似的方法对其他涉及比较操作的步骤进行分析可知同样不会泄露竞价.因此参与者选择部分能够保证竞价的隐私安全.
报酬确定部分涉及到数据需求者的费用确定和数据收集者的报酬确定,这里只分析需求者的费用确定部分,后者可以用类似的方法分析.智能合约在加密状态下计算每一个获胜需求者ri的![]() 时,涉及到一次比较操作,该操作与参与者选择阶段的比较操作流程一样,因此可知不会泄露竞价隐私.之后智能合约对每一个
时,涉及到一次比较操作,该操作与参与者选择阶段的比较操作流程一样,因此可知不会泄露竞价隐私.之后智能合约对每一个![]() 计算
计算![]() 其中
其中![]() 是随机数g的密文,且g只有智能合约知道.由于
是随机数g的密文,且g只有智能合约知道.由于![]() 的存在,加密服务中心无法在解密得到
的存在,加密服务中心无法在解密得到![]() 的明文ρi后得到竞价信息,之后中心选择一个只有自己知道的随机数f,并将pi=f·g·πi发给智能合约,同样由于f的存在,其他参与者无法从智能合约收到的pi得知竞价信息.因此报酬确定部分也可以保证竞价的隐私安全.综合上述分析可知,PFPI模块可以保证数据需求者和数据收集者竞价的隐私安全.
的明文ρi后得到竞价信息,之后中心选择一个只有自己知道的随机数f,并将pi=f·g·πi发给智能合约,同样由于f的存在,其他参与者无法从智能合约收到的pi得知竞价信息.因此报酬确定部分也可以保证竞价的隐私安全.综合上述分析可知,PFPI模块可以保证数据需求者和数据收集者竞价的隐私安全.
证毕.
6 实验仿真
本节将从实验仿真的角度验证所提机制的性能,该节首先介绍比较基线,之后将说明实验仿真中的参数设置,最后将给出实验结果.
6.1 比较基线
本文所提的区块链群智感知系统中基于隐私保护数据的用户激励机制包含PATD模块和PFPI模块2部分,因此本节将验证这2个机制的性能.
1)具有隐私保护的数据真值估计机制.实验仿真考虑3种比较基线:第1种是均值估计基线(MEAN),该基线将数据的均值作为最后的数据真值的估计值输出;第2种是中位数估计基线(MEDIAN),该基线将数据的中位数作为最后的数据真值估计的输出;第3种是迭代估计基线(IBTD),该基线由Zhang等人在文献[46]中提出,在每次迭代时,更新每个数据的权重,并利用更新后的权重计算数据真值估计,在达到迭代次数后,机制输出估计结果.注意,实验仿真过程中,均使用CKKS同态加密方案对数据进行加密.
2)具有隐私保护的参与者激励机制.因为目前没有基于同态加密方案的激励机制,因此实验仿真考虑2种基线:第1种基于收益的激励机制(BFI),该机制将每个任务τi的δi从大到小进行排序,然后从最大的开始选择获胜的数据需求者和收集者;第2种基于权重的激励机制(WFI),该机制将每个任务τi的权重ϖi按照从小到大排序,然后每次选择权重最小的任务确定相应的获胜数据需求者和收集者.
6.2 参数设置
为了方便,本节将实验的参数设置列在了表2中.与Jin等人的文献[43]类似,一些参数都是在某个区间均匀随机选择.具体而言,对于每一个任务τi,阈值参数αi和精度参数γi在[0.2,0.3]均匀随机选取,每个数据需求者ri能够获得的价值vi在[20,25]上均匀随机选取.同时,每个数据收集者wj的数据xi,j都是从均值为μi,j、方差为σi,j的截断高斯分布中采样得到的,即xi,j∈[0,1],且μi,j取值为[0,1],而σi,j取值为[1,2],数据置信度θi,j在[0,0.1]均匀选取,花费ci,j取值为[0,1],同时愿意执行的任务集合Γj中任务的数量|Γj|取值区间为[1,5].在仿真集合Ⅰ中,数据收集者的数量M从2变到512,而数据需求者的数量N保持100不变;在仿真集合Ⅱ中,数据需求者的数量N从2变到512,而数据收集者的数量M保持100不变.
Table 2 The Simulation Parameter Settings
表2 仿真参数设置

集合αiγi ci,jvi μi,jσi,j|Γj| θi,jM N Ⅰ[0.2,0.3][0.2,0.3][0,1][20,25][0,1][1,2][1,5][0,0.1][2,512]100Ⅱ[0.2,0.3][0.2,0.3][0,1][20,25][0,1][1,2][1,5][0,0.1]100[2,512]
此外,本文采用CKKS作为同态加密方案,因此,相关参数设置为:
维度参数N=213,缩放因子Δ=240,密文模数qL=21 503.同时,如Cheon等人在参考文献[47]中采用的多项式组合方法,本文也利用相同的方法,其中多项式fd和gd分别选取d=3,而相应的表达式为
f3(x)=(35x-35x3+21x5-5x7)/24,
g3(x)=(4 589x-16 577x3+25 614x5-
12 860x7)/210.
相应的组合参数分别为df和dg,其中fdf表示f∘f∘…∘f做df次组合,同样gdg表示g∘g∘…∘g做dg次组合.
本实验环境为Ubuntu 18.04.2 LTS,AMD Ryzen 7 5800H CPU,16 GB 内存,16线程.
6.3 仿真结果
本文仿真实验中的考察指标——社会福利,为整个机制运行完后对PFPI的性能评价指标,另一个考察指标——真值估计准确度,为整个机制运行完后对PATD的性能评价指标.最后一个评价指标——运行时间,为整个机制运行完成后所需的时间,但是因为PATD模块只涉及同态加法操作,运行时间较短,而PFPI涉及到排序操作和大量乘法操作,运行时间较长.
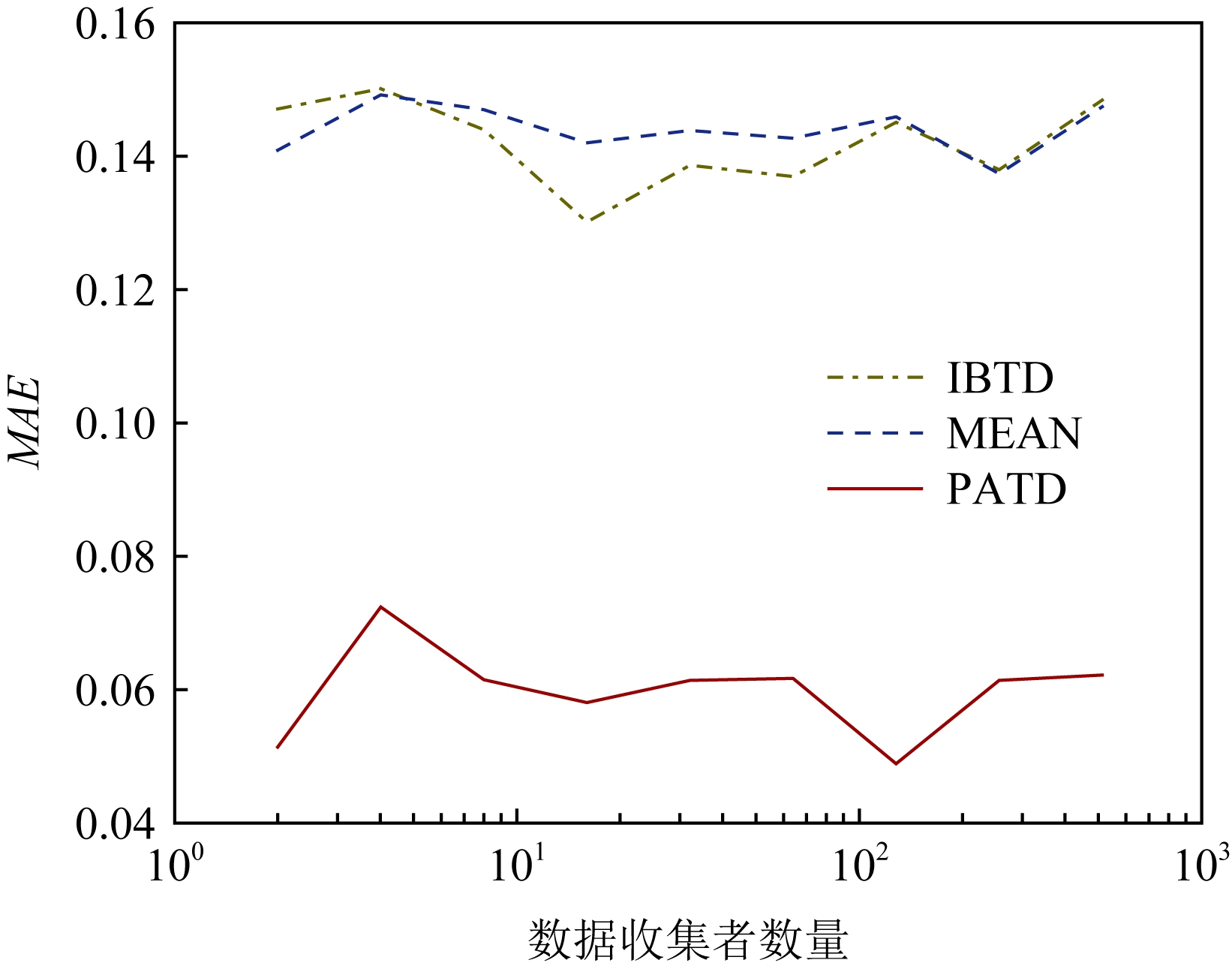
Fig.3 MAE under different number of data collectors
图3 不同数量的数据收集者时的MAE
图3、图4所示为PATD的仿真结果.图3为数据收集者数量不同时,各数据真值估计机制的MAE;而图4为数据需求者数量不同时,各数据真值估计机制的MAE.其中,MAE表示各数据的估计值与真值之间的平均距离,计算公式为
(34)

Fig.4 MAE under different number of data requesters
图4 不同数量的数据需求者时的MAE
从式(34)可以知道,MAE的值越小,表示算法的准确性越高.从图3和图4中可以看出,本文所提的PATD算法具有最小的MAE,因此,在所有比较的数据真值估计机制中具有最好的性能表现.在对IBTD机制进行仿真时,其迭代次数被设置为1 000次.
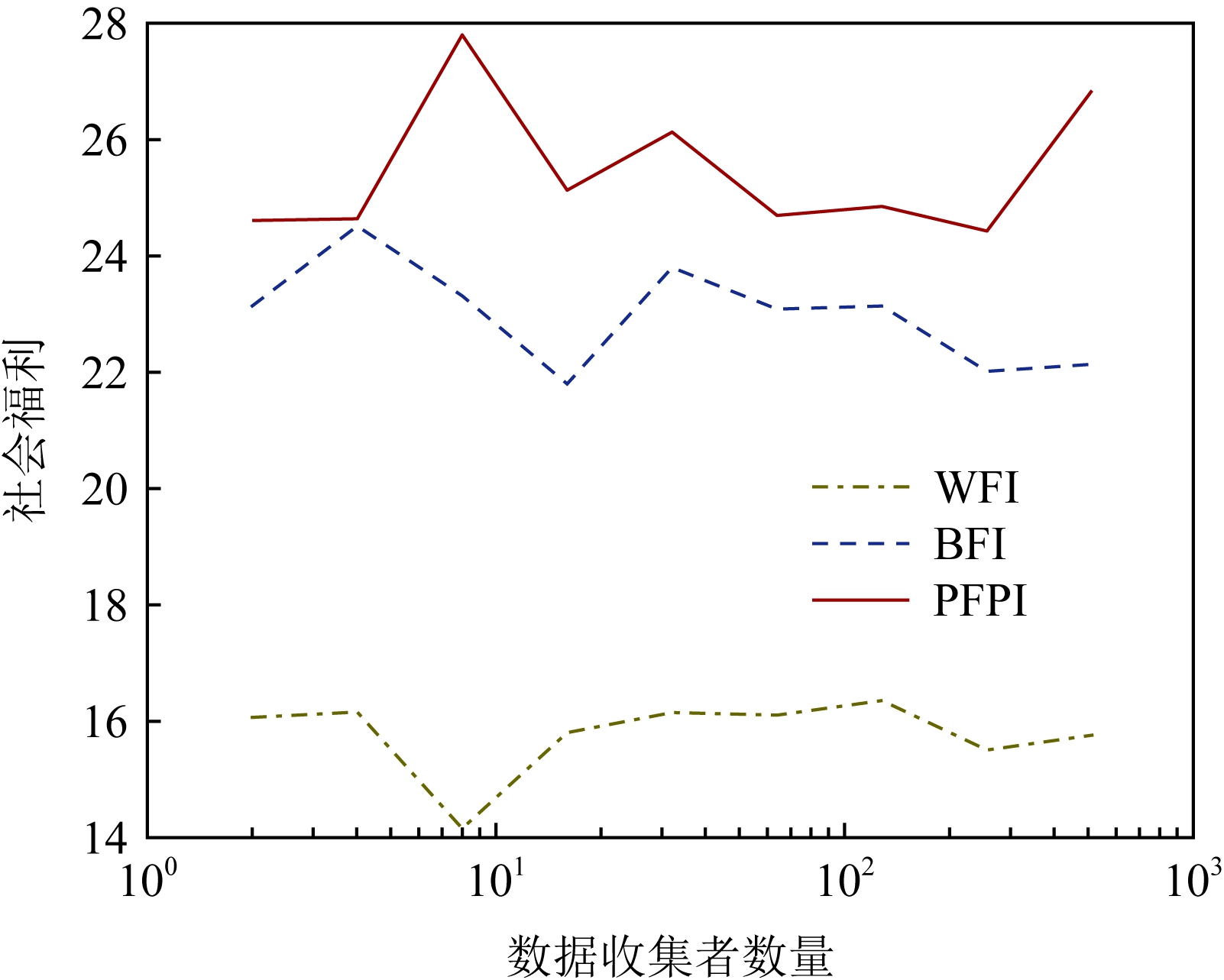
Fig.5 Social welfare under different number of data collectors
图5 不同数量的数据收集者时的社会福利
本文所提的区块链群智感知系统中基于隐私保护数据的用户激励机制包括2部分,即PATD和PFPI,在验证了PATD的性能后,接着对PFPI的性能进行验证.
图5、图6所示为PFPI的仿真结果.图5为数据收集者数量不同时,各具有隐私保护的激励机制达到的社会福利;而图6为数据需求者数量不同时,各具有隐私保护的激励机制达到的社会福利.需要指出的是,其中BFI机制可以满足真实性和个体合理性,而WFI机制只满足个体合理性但不满足真实性,在进行仿真的过程中,BFI和WFI中数据需求者和收集者提交的竞价都利用CKKS同态加密方案进行加密.从仿真结果可以看出PFPI达到的社会福利最高,这说明PFPI与其他基准激励机制相比具有更好的性能.同时,在图5和图6中可以看到,BFI的性能相较于WFI的性能更好.
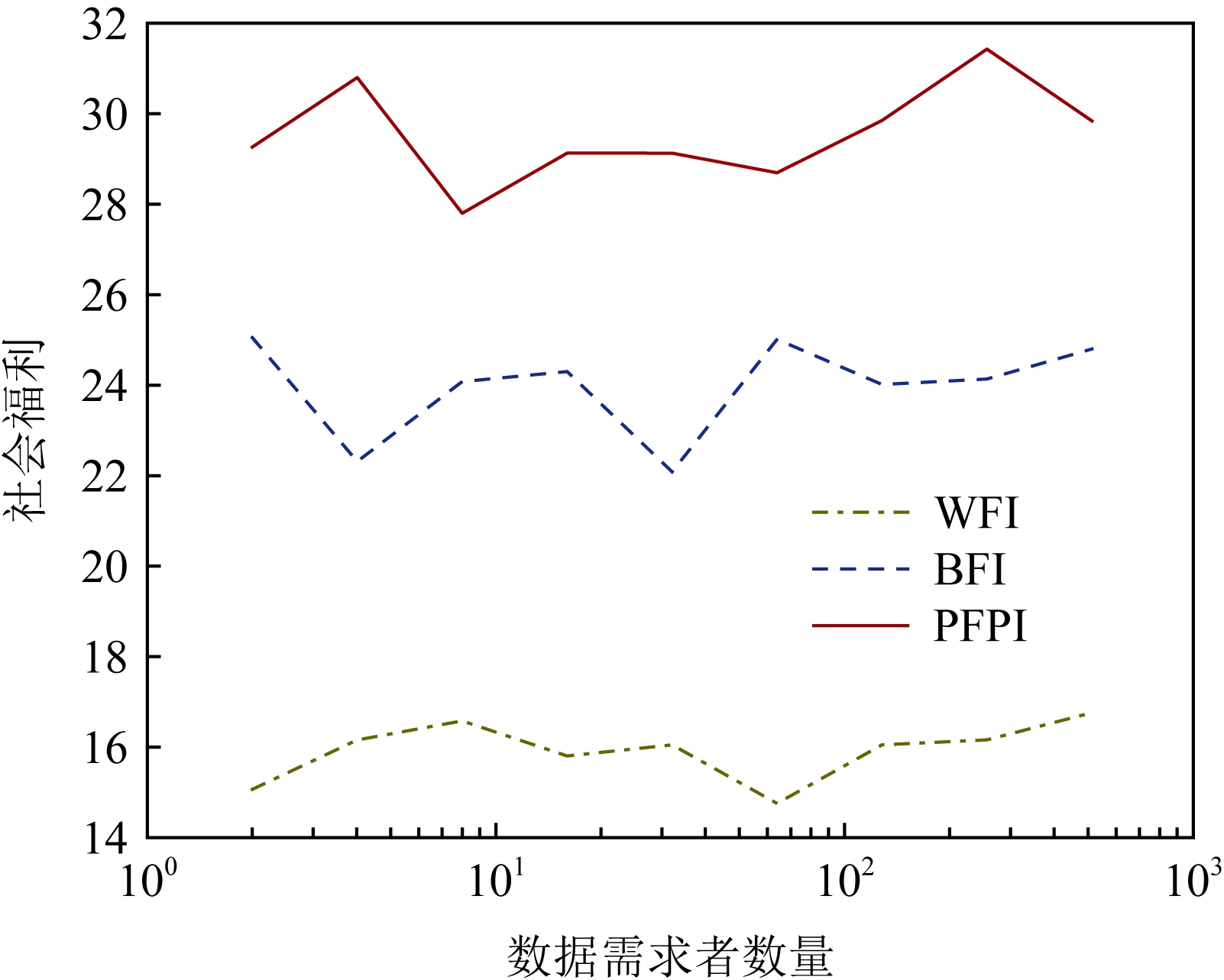
Fig.6 Social welfare under different number of data requesters
图6 不同数量的数据需求者时的社会福利
由于区块链每时每刻发生大量的交易,因此对于各种基于区块链的应用的运行速度有较高的要求,在性能仿真的最后,本节验证了利用本文所提区块链群智感知系统中基于隐私保护数据的用户激励机制的运行时间,并将仿真结果列于表3中.在表3中分别让(df,dg)取不同的组合,并统计任务数从2增加到512时,不同任务数所需的运行时间.从表3中可以看出,随着任务数的增加,所需要的运行时间在增加,这是因为需要的乘法操作在增加.同时可以看出不同的(df,dg)组合所需的时间不同,这是因为不同的组合需要计算的乘法操作次数是不同的,而且可以看出df的影响要比dg的影响大.
Table 3 Running Time of Different Parameters
表3 不同参数时的运行时间
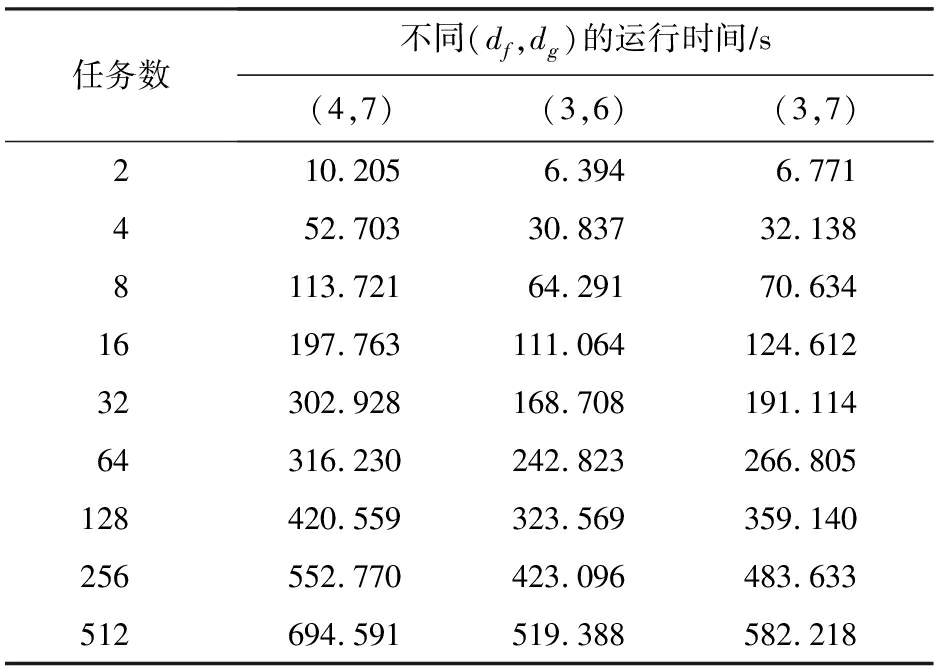
任务数不同(df,dg)的运行时间∕s(4,7)(3,6)(3,7)210.2056.3946.771452.70330.83732.1388113.72164.29170.63416197.763111.064124.61232302.928168.708191.11464316.230242.823266.805128420.559323.569359.140256552.770423.096483.633512694.591519.388582.218
表3为PFPI的运行速度,为了整个实验的完整性,本文最后对所提机制整体进行运行时间的仿真,以此来论证机制的合理性与连续性.
从表4可以看出,PFPI的运行时间相较于PATD要长得多,这是因为PATD模块仅涉及同态加法操作以及少量的明文与密文的乘法操作,这些操作所需时间较短.与之相反,PFPI在用户选择阶段和报酬确定阶段均涉及到排序操作,而排序操作需要大量的密文之间的同态乘法计算来完成,而乘法操作需要时间较长.从表4中可以看到,所提机制对时间敏感度不高的在线系统或者是完全线下的系统操作性较强.
Table 4 Running Time of the Whole Scheme
表4 机制整体的运行时间

任务数PATD运行时间∕sPFPI运行时间∕s(df=3,dg=5)总时间∕s20.0123.1873.19940.01826.51326.53180.02660.86560.891160.037103.944103.981320.049161.881161.930640.062226.06226.1221280.087308.02308.1072560.106396.442396.5485120.181489.292489.473
7 总结与展望
本文针对现有基于区块链群智感知系统的数据收集框架总是独立分离设计数据真值估计机制和参与者激励机制而导致其无法达到最佳性能的问题,提出一类新的具有隐私保护的数据收集机制.该机制由数据真值模块PATD和参与者激励模块PFPI共同构成.相较于分离设计的框架,该机制具有更好的性能.为了保护参与者的隐私信息,该机制利用CKKS同态加密方案.本文在提出数据收集机制后,从理论角度证明了PATD具有较高的真值估计准确度,同时证明了PFPI不仅满足真实性和个体合理性,而且具有较高的社会福利;从实验仿真的角度验证了PATD和PFPI的安全性能.从仿真结果可知,它们与各自的基准方案相比具有更好的安全性能.
作者贡献声明:应臣浩提出了算法思路和实验方案;夏福源负责完成实验仿真;李颉提出理论分析指导意见;斯雪明提出实验仿真指导意见;骆源提供论文修改意见.
[1]Peng Dan, Wu Fan, Chen Guihai.Data quality guided incentive mechanism design for crowdsensing[J].IEEE Transactions on Mobile Computing, 2017, 17(2): 307-319
[2]Ying Chenhao, Jin Haiming, Wang Xudong, et al.Double insurance: Incentivized federated learning with differential privacy in mobile crowdsensing[C]//Proc of 2020 IEEE Int Symp on Reliable Distributed Systems.Piscataway, NJ: IEEE, 2020: 81-90
[3]Ying Chenhao, Jin Haiming, Wang Xudong, et al.CHASTE: Incentive mechanism in edge-assisted mobile crowdsensing[C]//Proc of 2020 17th Annual IEEE Int Conf on Sensing, Communication, and Networking.Piscataway, NJ: IEEE, 2020: 1-9
[4]Jin Haiming, Guo Hongpeng, Su Lu, et al.Dynamic task pricing in multi-requester mobile crowd sensing with Markov correlated equilibrium[C]//Proc of 2019 IEEE Int Conf on Computer Communications.Piscataway, NJ: IEEE, 2019: 1063-1071
[5]Wang Xiumin, Wu Weiwei, Qi Deyu.Mobility-aware participant recruitment for vehicle-based mobile crowdsensing[J].IEEE Transactions on Vehicular Technology, 2017, 67(5): 4415-4426
[6]Tian Feng, Liu Bo, Sun Xiao, et al.Movement-based incentive for crowdsourcing[J].IEEE Transactions on Vehicular Technology, 2017, 66(8): 7223-7233
[7]Qu Yuben, Tang Shaojie, Dong Chao, et al.Posted pricing for chance constrained robust crowdsensing[J].IEEE Transactions on Mobile Computing, 2020, 19(1): 188-199
[8]Han Kai, Huang He, Luo Jun.Quality-aware pricing for mobile crowdsensing[J].IEEE/ACM Transactions on Networking, 2018, 26(4): 1728-1741
[9]Restuccia F, Ferraro P, Silvestri S, et al.IncentMe: Effective mechanism design to stimulate crowdsensing participants with uncertain mobility[J].IEEE Transactions on Mobile Computing, 2019, 18(7): 1571-1584
[10]Jin Wenqiang, Xiao Mingyan, Li Ming, et al.If you do not care about it, sell it: Trading location privacy in mobile crowd sensing[C]//Proc of 2019 IEEE Int Conf on Computer Communications.Piscataway, NJ: IEEE, 2019: 1045-1053
[11]Wang Liang, Yu Zhiwen, Han Qi, et al.Multi-objective optimization based allocation of heterogeneous spatial crowdsourcing tasks[J].IEEE Transactions on Mobile Computing, 2018, 17(7): 1637-1650
[12]Jin Haiming, Su Lu, Chen Danyang, et al.Thanos: Incentive mechanism with quality awareness for mobile crowd sensing[J].IEEE Transactions on Mobile Computing, 2018, 18(8): 1951-1964
[13]Karaliopoulos M, Koutsopoulos I, Spiliopoulos L.Optimal user choice engineering in mobile crowdsensing with bounded rational users[C]//Proc of 2019 IEEE Int Conf on Computer Communications.Piscataway, NJ: IEEE, 2019: 1054-1062
[14]Zhang Yanru, Gu Yunan, Pan Miao, et al.Multi-dimensional incentive mechanism in mobile crowdsourcing with moral hazard[J].IEEE Transactions on Mobile Computing, 2017, 17(3): 604-616
[15]Wang Jiangtao, Wang Yasha, Zhang Daqing, et al.Multi-task allocation in mobile crowd sensing with individual task quality assurance[J].IEEE Transactions on Mobile Computing, 2018, 17(9): 2101-2113
[16]Gao Yi, Dong Wei, Guo Kai, et al.Mosaic: A low-cost mobile sensing system for urban air quality monitoring[C]//Proc of IEEE Int Conf on Computer Communications.Piscataway, NJ: IEEE, 2016: 1-9
[17]Ganti R K, Pham N, Ahmadi H, et al.GreenGPS: A participatory sensing fuel-efficient maps application[C]//Proc of the 8th Int Conf on Mobile Systems, Applications, and Services.Piscataway, NJ: IEEE, 2010: 151-164
[18]Thiagarajan A, Ravindranath L, LaCurts K, et al.Vtrack: Accurate, energy-aware road traffic delay estimation using mobile phones[C]//Proc of the 7th ACM Conf on Embedded Networked Sensor Systems.New York: ACM, 2009: 85-98
[19]Eisenman S B, Miluzzo E, Lane N D, et al.BikeNet: A mobile sensing system for cyclist experience mapping[J].ACM Transactions on Sensor Networks, 2010, 6(1): 1-39
[20]Gao Chunming, Kong Fanyu, Tan Jindong.Healthaware: Tackling obesity with health aware smart phone systems[C]//Proc of 2009 IEEE Int Conf on Robotics and Biomimetics.Piscataway, NJ: IEEE, 2009: 1549-1554
[21]Hu Yidan, Zhang Rui.Differentially-private incentive mechanism for crowdsourced radio environment map construction[C]//Proc of 2019 IEEE Int Conf on Computer Communications.Piscataway, NJ: IEEE, 2019: 1594-1602
[22]Bhattacharjee S, Ghosh N, Shah V K, et al.QnQ: Quality and quantity based unified approach for secure and trustworthy mobile crowdsensing[J].IEEE Transactions on Mobile Computing, 2018, 19(1): 200-216
[23]Han Kai, Liu Huan, Tang Shaojie, et al.Differentially private mechanisms for budget limited mobile crowdsourcing[J].IEEE Transactions on Mobile Computing, 2018, 18(4): 934-946
[24]Gong Xiaowen, Shroff N B.Truthful mobile crowdsensing for strategic users with private data quality[J].IEEE/ACM Transactions on Networking, 2019, 27(5): 1959-1972
[25]Jin Haiming, Su Lu, Xiao Houping, et al.Incentive mechanism for privacy-aware data aggregation in mobile crowd sensing systems[J].IEEE/ACM Transactions on Networking, 2018, 26(5): 2019-2032
[26]Lin Jian, Yang Dejun, Wu Kun, et al.A sybil-resistant truth discovery framework for mobile crowdsensing[C]//Proc of 2019 IEEE 39th Int Conf on Distributed Computing Systems.Piscataway, NJ: IEEE, 2019: 871-880
[27]Zhang Zhikun, He Shibo, Chen Jiming, et al.REAP: An efficient incentive mechanism for reconciling aggregation accuracy and individual privacy in crowdsensing[J].IEEE Transactions on Information Forensics and Security, 2018, 13(12): 2995-3007
[28]Zhou Jun, Shen Huajie, Lin Zhongyun, et al.Research advances on privacy preserving in edge computing[J].Journal of Computer Research and Development, 2020, 57(10): 2027-2051(in Chinese)(周俊, 沈华杰, 林中允, 等.边缘计算隐私保护研究进展[J].计算机研究与发展, 2020, 57(10): 2027-2051)
[29]Luu L, Narayanan V, Zheng Chaodong, et al.A secure sharding protocol for open blockchains[C]//Proc of the 2016 ACM SIGSAC Conf on Computer and Communications Security.New York: ACM, 2016: 17-30
[30]Wang Chenxu, Cheng Jiacheng, Sang Xinxin, et al.Data privacy-preserving for blockchain: State of the art and trends[J].Journal of Computer Research and Development, 2021, 58(10): 2099-2119(in Chinese)(王晨旭, 程加成, 桑新欣, 等.区块链数据隐私保护:研究现状与展望[J].计算机研究与发展, 2021, 58(10): 2099-2119)
[31]Das P, Eckey L, Frassetto T, et al.FastKitten: Practical smart contracts on bitcoin[C]//Proc of the 28th USENIX Security Symp.New York: ACM, 2019: 801-818
[32]Zhang Peiyun, Zhou Mengchu.Security and trust in blockchains: Architecture, key technologies, and open issues[J].IEEE Transactions on Computational Social Systems, 2020, 7(3): 790-801
[33]Zheng Peiling, Xu Quanqing, Zheng Zibin, et al.Meepo: Sharded consortium blockchain[C]//Proc of 2021 IEEE 37th Int Conf on Data Engineering.Piscataway, NJ: IEEE, 2021: 1847-1852
[34]Huang Huawei, Yue Zhengyu, Peng Xiaowen, et al.Elastic resource allocation against imbalanced transaction assignments in sharding-based permissioned blockchains[J].IEEE Transactions on Parallel and Distributed Systems, 2022, 33(10): 2372-2385
[35]Aloufi A, Hu Peizhao, Song Y, et al.Computing blindfolded on data homomorphically encrypted under multiple keys: A survey[J].ACM Computing Surveys, 2022, 54(9): 1-37
[36]Chillotti I, Gama N, Georgieva M, et al.Tfhe: Fast fully homomorphic encryption over the torus[J].Journal of Cryptology, 2020, 33(1): 34-91
[37]Tian Yifan, Yuan Jiawei, Song Houbing.Secure and reliable decentralized truth discovery using blockchain[C]//Proc of 2019 IEEE Conf Communications and Network Security.Piscataway, NJ: IEEE, 2019: 1-8
[38]Wu Haiqin, Düdder B, Wang Liangmin, et al.Blockchain-based reliable and privacy-aware crowdsourcing with truth and fairness assurance[J].IEEE Internet of Things Journal, 2022, 9(5): 3586-3598
[39]Huang Zhiyuan, Zheng Jun, Xiao Mingjun.Privacy-enhanced crowdsourcing data trading based on blockchain and stackelberg game[C]//Proc of 2021 IEEE 18th Int Conf on Mobile Ad Hoc and Smart Systems.Piscataway, NJ: IEEE, 2021: 621-626
[40]Zhang Can, Zhu Liehuang, Xu Chang, et al.PRVB: Achieving privacy-preserving and reliable vehicular crowdsensing via blockchain oracle[J].IEEE Transactions on Vehicular Technology, 2021, 70(1): 831-843
[41]Xie Liang, Su Zhou, Chen Nan, et al.Secure data sharing in UAV-assisted crowdsensing: Integration of blockchain and reputation incentive[C]//Proc of 2021 IEEE Global Communications Conf.Piscataway, NJ: IEEE, 2021: 1-6
[42]Jin Haiming, Su Lu, Xiao Houping, et al.Incentive mechanism for privacy-aware data aggregation in mobile crowd sensing systems[J].IEEE/ACM Transactions on Networking, 2018, 26(5): 2019-2032
[43]Jin Haiming, Su Lu, Nahrstedt K.CENTURION: Incentivizing multi-requester mobile crowd sensing[C]//Proc of 2017 IEEE Int Conf on Computer Communications.Piscataway, NJ: IEEE, 2017: 1-9
[44]Cheon J H, Kim A, Kim M et al.Homomorphic encryption for arithmetic of approximate numbers[C]//Proc of Int Conf on the Theory and Application of Cryptology and Information Security.Berlin: Springer, 2017: 409-437
[45]Hong S, Kim S, Choi J et al.Efficient sorting of homomorphic encrypted data with k-way sorting network[J].IEEE Transactions on Information Forensics and Security, 2021, 16: 4389-4404
[46]Zhang Chuan, Zhu Liehuang, Xu Chang et al.Reliable and privacy-preserving truth discovery for mobile crowdsensing systems[J].IEEE Transactions on Dependable and Secure Computing, 2021, 18(3): 1245-1260
[47]Cheon J H, Kim D, Kim D.Efficient homomorphic comparison methods with optimal complexity[C]//Proc of Int Conf on the Theory and Application of Cryptology and Information Security.Berlin: Springer, 2020: 221-256




