随着联邦学习(federated learning)[1-3]、协同训练(collaborative training)[4-5]等开放网络下分布式深度学习系统在商业场景(如金融[6]、医疗[7]等)中的兴起,深度学习模型中间计算结果(如特征、梯度等)逐渐成为服务节点、计算节点和终端设备之间的主要传输内容.由于模型中间计算结果本质上是模型与数据共同计算的产物,那么其中将包含大量参与计算的数据信息.然而,现行数据保护规范大多未限制或明确给出对深度学习模型中间结果的保护标准[8],这也给潜伏在开放网络中的攻击者或不诚实的第三方服务节点带来可乘之机:利用新型攻击算法,从截获的明文的中间计算结果中,推断原始数据中的敏感信息.例如,Pan等人[9-10]指出,当一个开放网络中的攻击者截获通用语言模型(如Google的BERT[11]等)产生的深度文本编码后,可在几乎无先决条件的情况下,以接近100%的准确度逆向推断原始文本中是否存在目标关键词;而Melis等人[12]则发现攻击者可以从模型梯度中推断出训练样本的敏感属性信息.
本文针对分布式深度学习模型构建过程最重要的中间计算结果——模型平均梯度(简称“梯度”),对其数据泄露风险开展研究.如图1所示,在典型的分布式模型构建过程中,多个客户端(client)在服务器(server)的协调下,利用各自的本地数据,共同参与训练一个全局模型[13].具体地,每一轮训练过程为
1)服务器下发当前版本的全局模型给各个客户端(步骤1);
2)各客户端接收全局模型,复制到本地模型中,并根据该模型参数在一个本地训练批次(mini-batch)上计算模型梯度并上传(步骤2);
3)服务器聚合接收到的各客户端的梯度,并更新全局模型(步骤3).
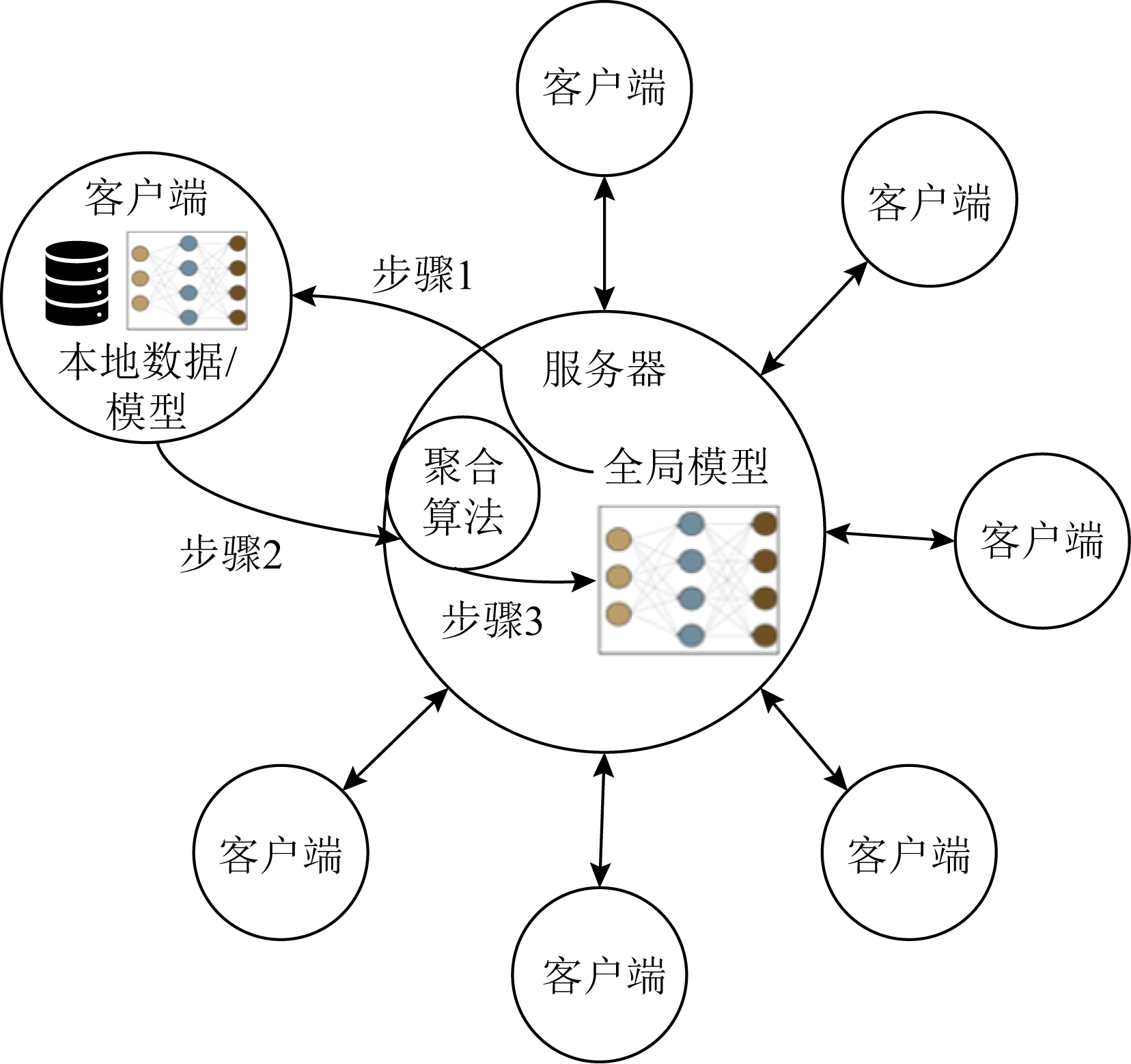
Fig.1 Overview of a typical distributed learning system
图1 典型分布式学习系统的架构概览
由于在联邦学习等场景下,客户端节点往往由用户或商业机构扮演,其参与训练的本地训练批次也往往包含大量敏感信息,这将诱使潜在攻击者尝试非法获取梯度,从中推断原始数据中的敏感信息,乃至披露原始数据本身.
本文聚焦基于平均梯度重建一个训练批次中各个原始数据样本的攻击场景,称作数据重建攻击(data reconstruction attack).如图1所示,当潜在攻击者通过中间人攻击或伪装成第三方服务器截获目标人脸识别模型时,在构建过程中无意泄露梯度信息后,数据重建攻击能被利用于恢复原始训练批次中的每张隐私人脸数据及相应标签.由于数据重建攻击造成的隐私泄露程度较大,Lyu等人[14]将数据重建攻击列为开放网络下分布式学习系统的重大安全威胁之一.
尽管此前数据重建攻击在大型深层神经网络和小训练批次的情况下已取得显著的攻击效果[15-18],这些工作大多仅停留在攻击方法设计和实验验证层面,对数据重建攻击中下述重要实验现象缺乏深层机理分析:
1)现有攻击仅能恢复少量样本组成的训练批次
Zhu等人[15]在实验过程中发现,随着训练批次的增大,提出的基于优化的攻击过程收敛缓慢.例如,当训练批次大小从1增加到8,攻击执行时间将从270 s快速增长至2 711 s(时间开销增加了9倍以上),仍无法保证在攻击不同训练批次时均能达到收敛.而Geiping等人[17]报告当利用基于优化的攻击算法尝试恢复大小为48的CIFAR-10图像训练批次时,其恢复图像中80%以上图像会模糊且无法辨识.
2)网络结构变浅变窄弱化现有攻击效果
在本文初步实验中发现,当目标模型神经网络层数减少为3层或层宽降低至100个神经元以下,现有基于优化梯度匹配目标的攻击效果出现明显下降,即在较浅的深度学习模型上已有的数据重建攻击远远无法达到在大型深层网络上的类似攻击效果,并同时伴随由于计算损失函数2阶微分带来的梯度匹配目标最小化过程的数值不稳定的情况.近期,文献[19]提出神经元激活独占性(neuron activation exclusivity),发现满足特定激活独占性条件的任意大小的训练数据批次能被攻击者从训练梯度中像素级重建,并远超此前工作的重建效果.然而,本文通过实证分析表明,在实际训练过程和设定中满足该条件的训练数据批次出现概率较低,较难造成实际泄露威胁.
本文主要做出4个方面的贡献:
1)对文献[19]中提出的基于神经元激活模式的新型数据重建攻击算法进行了系统化的机理剖析和复杂度分析,并披露了更多的理论和实现细节;
2)提出神经元激活模式控制算法,对给定多层全连接神经网络建立线性规划问题,从而为给定训练批次中的各训练样本求解微小扰动,以精确满足指定的神经元激活模式;
3)提出特定的神经元激活模式组合构造方法,通过在分布式训练端侧节点执行上述控制算法,主动诱导受害者的本地训练批次的平均梯度满足理论可重建性,从而有效松弛了文献[19]提出的攻击算法应用条件;
4)提出并行化策略优化了文献[19]的重建攻击算法的时间开销,速度提升近10倍.在5个涵盖智慧医疗、人脸识别等应用场景的数据集上的实验表明,本文提出的攻击流程优化方法将可重建训练批次大小从8张提升至实际应用的64张,且重建数据的均方误差与信噪比均与原始攻击算法持平.
1 基础知识和相关工作
1.1 深度神经网络、ReLU与神经元激活模式
1.1.1 相关记号
在过去10年里,深度神经网络(deep neural net-work, DNN)已在包括图像、文本、音频等的各类重要场景中得到广泛应用.直观地说,深度神经网络是一种逐层计算的机器学习模型.记一个用于K分类任务的H层的深度神经网络为f(·,θ):X(⊂![]() d)→Y,它通常具有如下的计算形式:
d)→Y,它通常具有如下的计算形式:
f(x;θ)=fH(σ(fH-1…σ(f1(x)))),
(1)
其中,f1,f2,…,fH表示第1到第H层神经网络,通常为包括全连接层(fully-connected layer)和卷积层(convolutional layer)在内的标准化神经网络组件,σ表示神经网络所采用的激活函数,θ表示神经网络中所有可学习的参数构成的集合.
沿着文献[19]的设定,本文同样以如下定义的多层全连接神经网络(multilayer fully-connected neural network)为主要的理论分析和攻击对象:
f(x)=WH(σ(WH-1…σ(W1x+b1)+bH-1))+bH,
(2)
其中,Wi∈![]() di×di-1,bi∈
di×di-1,bi∈![]() di分别表示第i个全连接层的权重(weight)矩阵和偏置(bias)向量,且满足dH=K和d0=d,即输入空间的维度.特别地,本文后续分析主要覆盖式(2)中激活函数σ为ReLU(rectified linear unit)函数的深度学习模型.
di分别表示第i个全连接层的权重(weight)矩阵和偏置(bias)向量,且满足dH=K和d0=d,即输入空间的维度.特别地,本文后续分析主要覆盖式(2)中激活函数σ为ReLU(rectified linear unit)函数的深度学习模型.
1.1.2 ReLU神经网络的前向计算性质
由于ReLU函数具有数值稳定性好和计算效率高等优势,目前ReLU函数已普遍应用于各种工业级的深度学习模型结构(例如ResNet,Inception等核心机器视觉模型).具体地,ReLU函数定义为
(3)
从式(3)可知,ReLU函数可被视作一种二值门控单元:当所属神经元输出到该ReLU函数的值a为非负数,则该输出值将被恒等地传递到下一层网络的计算中;否则,该输出值将被置为零.本文定义前者情形为该ReLU函数的所属神经元的激活态;后者情形为所属神经元的休眠态.
当整体考虑同层网络结构中包含的所有神经元,可将1.1.1节中式(2)给出的多层全连接神经网络的形式等价转化为
f(x)=WHDH-1(WH-1(…D1(W1x+b1)+
bH-1)+bH,
其中二值对角方阵Di∈![]()
![]() 刻画第i层全连接网络中的各个神经元的激活状态.例如,当Di中的第j个对角元素的值为1,则表示该层中的第j个神经元在x的输入下激活;反之,该神经元在x的输入下休眠.因此,本文称Di为输入x在第i层的激活状态矩阵.当输入x在神经网络中完成一次前向传播,收集每一层的各神经元的激活状态矩阵,得到该输入在神经网络中的激活模式
刻画第i层全连接网络中的各个神经元的激活状态.例如,当Di中的第j个对角元素的值为1,则表示该层中的第j个神经元在x的输入下激活;反之,该神经元在x的输入下休眠.因此,本文称Di为输入x在第i层的激活状态矩阵.当输入x在神经网络中完成一次前向传播,收集每一层的各神经元的激活状态矩阵,得到该输入在神经网络中的激活模式![]() 图2展示了在一个大小为2的ReLU隐藏层中输入数据x1,x2对应的2种不同的激活模式.
图2展示了在一个大小为2的ReLU隐藏层中输入数据x1,x2对应的2种不同的激活模式.

Fig.2 Examples of activation patterns in a ReLU MLP
图2 多层全连接ReLU网络中的激活模式示例
1.1.3 ReLU神经网络的后向传播性质
由1.1.2节中ReLU函数定义可知,ReLU函数在反向传播过程中满足:
(4)
由式(4)可推得,激活状态矩阵Di与求导算子∇θ具有对易性(commutability):∇θDiWi=Di∇θWi,即激活状态矩阵在反向传播的计算中保持不变.在神经元层面,这意味着如下的重要现象:反向传播的损失函数信号仅在前向传播激活的路径上非零.该现象是理解并提升文献[19]中提出具有理论保证的攻击算法的核心环节.
记模型训练过程中在样本(x,y)上损失函数为 (f(x;θ),y).在分类任务中,
(f(x;θ),y).在分类任务中, 通常被定义为交叉熵损失函数-log py,其中py表示概率向量(p1,p2,…,pK)中真实类标签y对应的概率值,而该概率向量通常为经过softmax函数的模型输出,有
通常被定义为交叉熵损失函数-log py,其中py表示概率向量(p1,p2,…,pK)中真实类标签y对应的概率值,而该概率向量通常为经过softmax函数的模型输出,有![]() 对于一个训练批次
对于一个训练批次![]() 模型在第i层的平均梯度
模型在第i层的平均梯度![]() 为
为
![]() ∇Wi
∇Wi (f(xm;θ),ym),
(f(xm;θ),ym),
(5)
其中M表示训练批次的大小,在实际训练中通常M≥32.
1.2 基于优化的数据重建攻击
在2019年,Zhu等人[15]提出了基于平均梯度的数据重建攻击方法DLG,其演示的攻击效果表明,DLG在已知模型参数的条件下,能从残差神经网络ResNet的平均梯度中即可近乎无损地恢复一个大小为8的训练数据批次中的各个样本.从攻击设计上看,DLG是一种基于优化的攻击技术,将待重建的各训练样本和标签当作可训练参数(trainable parameters),利用模型参数计算在这些待恢复样本和标签上的梯度,计算和实际梯度之间的均方误差作为损失函数(称作“梯度匹配目标”),损失函数具体形式为
(6)
在上述梯度匹配目标下,DLG通过反向传播更新优化待解的训练样本和标签,试图恢复原始样本.在文献[15]提出的基于优化的攻击框架下,后续工作[16-18]通过改进梯度匹配过程中的损失函数,如Geiping等人[17]提出了基于余弦相似度的梯度匹配目标,根据模型梯度的解析性质预先确定部分/全部样本的标签,如Zhao等人[16]提出根据模型最后一层偏置向量的梯度的正负号推断单张图片的标签,并引入相应的正则化项约束恢复图像的先验分布,如Yin等人[18]提出了利用批正则化层均值和方差的正则化项,进一步优化了文献[15]的恢复效果.
然而,已有数据重建攻击大多仅停留在攻击方法设计和实验验证层面,对数据重建攻击中重要实验现象缺乏深层机理分析.直观来看,数据重建攻击所依赖的平均梯度包含的信息量主要受到模型大小和训练批次大小2个因素的影响.本文通过实验研究发现,已有数据重建攻击将会随着训练批次扩大或模型尺寸缩小而弱化.例如,图3展示了在CIFAR-10训练集上进行训练的3层全连接网络上应用现有重建攻击的实验结果,其中网络结构为(3072,512,10),目标训练批次大小为8,攻击实现均为文献[15]给出的原始实现.可以看到,现有攻击算法均在攻击小型神经网络模型时存在瓶颈,导致图像重建效果显著下降.

Fig.3 Bottleneck of existing data reconstruction attacks on small-scale neural networks
图3 现有数据重建攻击在小型神经网络上存在瓶颈
现有攻击算法的瓶颈主要由于,DLG以及后续基于优化的数据重建均依赖优化算法迭代求解能满足真实平均梯度的训练批次.该过程并未设法分析各个训练样本从平均梯度中的可分离性,也未能化简神经网络的非线性,导致这类方法所需求解的梯度匹配优化目标具有很高的复杂性,优化过程很容易产生数值不稳定或陷入局部最优解.本文提出的攻击算法则通过将数据重建问题归约为训练批次中个体样本的激活模式差异,实现具有理论保证的数据重建攻击.
1.3 其他相关工作
由于梯度信息在开放网络下的分布式学习系统中易被攻击者获取,近年来已有一些研究工作开始着眼于梯度信息可能造成的用户敏感数据泄露问题.例如,Melis等人[12]发现,攻击者能通过模型梯度推断训练集样本是否包含特定的属性(例如,人脸样本是否佩戴眼镜).Hitaj等人[20]则利用分布式训练过程中传输的梯度信息训练生成对抗式网络(generative adversarial nets,GAN),从而推断端侧节点私有数据集中每一类样本的类平均(例如,平均脸).Nasr等人[21]则根据梯度信息进行成员推理攻击(membership inference attack),即推断给定目标样本是否属于用户的私有训练集.除文献[12,20-21]所述的这些利用梯度信息威胁训练样本私密性的研究进展,研究者也已尝试其他不同的信息泄露源实现隐私数据窃取.Ganju等人[22]和Carlini等人[23]提出利用模型参数推断训练集的全局隐私属性(例如,特定类样本占比).Fredrikson等人[24-25]和Pan等人[9-10]则利用数据深层表征分别重建类平均和推断对应样本的隐私属性,而Shokri等人[26]则提出利用模型可解释性输出结果,包括影响函数(influence function)等,进行成员推理攻击.不同于对全局数据集特征、个体数据的敏感属性或成员属性等进行推断,本文关注的数据重建攻击作为一种更具威胁性的深度学习数据隐私攻击,以直接恢复个体样本中尽可能多的原始数据为目标,造成更为严重的隐私泄露风险.与此同时,由于在相同或更弱的攻击假设下,数据重建攻击需要从几乎相同的信息源中破解更多的信息,因而带来了额外的技术挑战.
对于深度学习数据隐私的研究也不仅局限于训练集隐私,此前研究工作也已揭示了深度学习模型在测试时数据成员信息[27]、模型参数[28]、训练超参[29]、模型结构[30]以及模型功能[31]等层面的威胁.
2 神经元激活模式控制与数据泄露诱导方法
本节介绍了如何通过操控神经元激活模式主动满足独占性条件,以提升现有数据重建攻击的可重建训练批次大小和攻击效果,并介绍相应的系统层优化技术提升现有数据重建的攻击效率.首先给出本文所基于的威胁场景与攻击假设.
2.1 威胁场景与攻击假设
2.1.1 威胁场景
本文考察的威胁场景主要发生在开放网络中分布式深度学习模型的训练过程中.在引言部分介绍的典型分布式深度学习系统协议下,攻击者首先在网络传输过程中合法或非法地获取本地计算节点在一个本地的训练批次![]() 上传至服务器的平均梯度信息
上传至服务器的平均梯度信息![]() 希望根据该信息以尽可能低的误差重建原始训练批次中的各个输入样本xm及对应标签ym.在实际中,上述攻击者的角色由一个半诚实(honest-but-curious)的服务提供方或由一个实施中间人攻击的网络嗅探方进行.同时,由于服务提供方通常会在本地计算节点部署相应的数据预处理(preprocessing)模块(例如,对本地图像数据进行相应的归一化和裁剪),在本文考虑的威胁场景中,半诚实的服务提供方因此也能够部署特定的预处理算法,对数据施以微扰,以辅助下游数据开展重建攻击.
希望根据该信息以尽可能低的误差重建原始训练批次中的各个输入样本xm及对应标签ym.在实际中,上述攻击者的角色由一个半诚实(honest-but-curious)的服务提供方或由一个实施中间人攻击的网络嗅探方进行.同时,由于服务提供方通常会在本地计算节点部署相应的数据预处理(preprocessing)模块(例如,对本地图像数据进行相应的归一化和裁剪),在本文考虑的威胁场景中,半诚实的服务提供方因此也能够部署特定的预处理算法,对数据施以微扰,以辅助下游数据开展重建攻击.
2.1.2 攻击假设
具体地,本文假定攻击者拥有3方面的能力:
1)假设A.攻击者获得了目标训练批次上的明文平均梯度.
2)假设B.攻击者已知本地计算节点上的模型结构和参数.
3)假设C.攻击者能修改本地计算节点上的数据预处理算法.
假设A主要为攻击者准备了相应的攻击信道,即本地节点向服务器提交的平均梯度信息被攻击者获得.对于半诚实的服务提供方而言,满足假设A是简单的;而对于进行网络嗅探的中间人攻击而言,也可利用传输层漏洞等对网络包进行破解以获得明文平均梯度.假设B为攻击者分析平均梯度提供了基础,这是因为平均梯度正是在当前模型参数和模型结构上通过损失函数的反向传播而产生的,因而不论是类似于文献[15-18]中基于梯度匹配目标的数据重建攻击,还是文献[19]中基于独占性分析和线性方程求解的攻击算法,都需要依赖于模型参数和结构建立优化问题或目标方程组.假设B在实际中是合理的:在引言部分介绍的典型分布式深度学习系统协议下,各个参与节点和服务提供方均共享同样的模型结构,并在每轮的参数聚合、分发和同步的过程中,无论是作为服务提供方或者伪装成另一个参与训练的嗅探方,攻击者都能同步并获得目标训练批次所属的计算节点上的模型参数和结构.假设C为本文首次在数据重建攻击场景中引入,此前主要出现在针对分布式深度学习系统的属性推断攻击中[12].假设C的合理性在于,在现行的工业级分布式学习框架中(例如Tensorflow-Federated[32],PySyft[33]等),服务器在训练开始时,往往需要给端侧节点推送训练代码.因此一个半诚实的服务器即使在无法访问端侧节点本地数据的情况下,也可以给目标工作节点注入相应的恶意预训练处理算法.而由于深度学习训练流程往往涉及多种调参技术,实现逻辑较为复杂,也易于在不被用户察觉的情况下被攻击者操纵[34].
2.2 神经元独占性条件与数据重建
2.2.1 神经元激活独占性
本文提出的攻击算法基于神经元激活独占性的概念(简称“独占性”),该概念在文献[19]被提出.直观地,对于一组训练样本而言,本文称一个神经元是被独占的,即表示该神经元在这些训练样本的前向传播过程中被有且仅有一个样本激活.形式化地,当给定一组训练样本![]() 记它们在目标模型f中在第i层的激活状态矩阵分别为
记它们在目标模型f中在第i层的激活状态矩阵分别为![]() 则当满足条件:
则当满足条件:
(7)
其中符号[·]jk表示取操作数矩阵的第j行第k列的元素,则该层中第j个神经元被称为该组训练样本对应的独占神经元(exclusively activated neuron, ExAN).特别地,对于式(7)中唯一满足![]() 的样本索引m(j),本文称训练样本(xm(j),ym(j))独占第i层的第j个神经元.
的样本索引m(j),本文称训练样本(xm(j),ym(j))独占第i层的第j个神经元.
不同于此前基于优化的攻击算法,本文及文献[19]提出的数据重建攻击并非是经验性的攻击算法,而是将模型平均梯度能够泄露训练批次中的每个个体训练数据归结为训练批次中个体数据的神经元激活模式的独占性.从原理层面看,神经元独占性代表了平均梯度中个体样本的可分离性,即在前向和后向计算过程中,该训练批次中的样本单独占有至少一条或多条计算路径.2.2.2节表明,这类独有的计算路径的存在性保障了攻击者可在具有理论保证的精度误差下重建训练批次中的每个样本.
2.2.2 充分独占性条件下的重建算法
文献[19]基于独占性的概念,发现一种充分独占性条件(sufficient exclusivity condition):1个训练批次中的每个样本在多层全连接网络最后1个ReLU层都具有至少2个ExAN,而在其余层拥有至少1个ExAN.在充分独占性条件下,该工作构造攻击算法证明这样的训练批次中的每个样本可被几乎无损地从平均梯度中重建.归纳来看,Pan等人[19]构造的攻击算法主要由3个关键步骤组成.
1)推断样本标签和概率向量.根据最后1层的平均梯度信息,攻击算法通过对最后1层权重的梯度矩阵(即GH∈![]() K×dH-1)进行逐行的求比值操作,寻找每1行中具有重复值的位置.根据充分独占性条件中对于最后1层的假设,可证明具有重复值的位置索引对应的神经元为训练批次中某一样本的独占神经元,且当行索引中不包含该样本的真实标签对应的索引时,该重复值为其概率向量中对应类别概率之间的比值,因此恒为正值;否则,当分子(分母)行索引对应该样本的真实标签时,该重复值对应的分式中分子(分母)为对应概率减1,分母(分子)为相应的概率值,因此恒为负值.利用上述性质,攻击者可利用比值关系和概率归一化条件求解对应样本的概率向量,并通过对应重复值的正负性确定样本的标签.
K×dH-1)进行逐行的求比值操作,寻找每1行中具有重复值的位置.根据充分独占性条件中对于最后1层的假设,可证明具有重复值的位置索引对应的神经元为训练批次中某一样本的独占神经元,且当行索引中不包含该样本的真实标签对应的索引时,该重复值为其概率向量中对应类别概率之间的比值,因此恒为正值;否则,当分子(分母)行索引对应该样本的真实标签时,该重复值对应的分式中分子(分母)为对应概率减1,分母(分子)为相应的概率值,因此恒为负值.利用上述性质,攻击者可利用比值关系和概率归一化条件求解对应样本的概率向量,并通过对应重复值的正负性确定样本的标签.
2)推断各样本的激活模式.在步骤1)中攻击者求解得到最后一层中每个训练样本对应的ExAN,于是,利用在本文1.1.3节中介绍的ReLU神经网络后向传播的重要性质,即“后向传播的损失函数信号仅在前向传播激活的路径上非零”,可根据每个样本对应的最后一层独占神经元连接前层的参数梯度是否为0,确定前一层中相应的独占神经元.根据充分独占性条件中假设的其余层拥有至少1个ExAN,上述过程可递推地求得每个样本在各个ReLU层上的激活模式.
3)建立线性梯度方程求解.当通过上述2个步骤求得训练批次中每个样本的概率向量、标签和相应的激活模式后,攻击者根据神经网络参数和梯度运算规则建立相应关于输入样本的线性梯度匹配方程组.该步骤将输入样本中的每个标量记作一个符号,随后为该样本流经的每条边(即2个端点的神经元均激活的边)上的标量参数收集相应的线性方程.如图4所示(其中当i对应样本真实标签时,![]() 否则
否则![]() 对于当前收集位置对应的标量参数,相应的线性梯度方程中各个输入符号的系数为:从输入层对应位置到输出层每个神经元的所有路径集合中,经过当前收集位置的路径中各个权重与输出层
对于当前收集位置对应的标量参数,相应的线性梯度方程中各个输入符号的系数为:从输入层对应位置到输出层每个神经元的所有路径集合中,经过当前收集位置的路径中各个权重与输出层![]() (在步骤1)中解得)的乘积和.图4的符号化输入的系数为
(在步骤1)中解得)的乘积和.图4的符号化输入的系数为
(8)
其中,Pjk表示经过权重[W1]jk的所有路径端点的集合,c为输出层神经元的索引,i为符号化输入的索引,xm=(xm1,xm2,…,xmd).

Fig.4 A schematic diagram of collecting the linear gradient equations for an input sample
图4 为单张输入样本建立线性梯度方程组的方法示意图
2.2.3 充分独占性条件的严格性
从2.2.2节中充分独占性条件的表述可知,该条件直观上对于训练批次的要求较为严格,因而实际该重建攻击的应用面有限.为了进一步验证上述观点,本文统计了在CIFAR-10数据集上不同训练批次大小和不同隐藏层宽度的3层全连接网络中满足充分独占性条件的训练批次占比,相应结果在图5中展示.
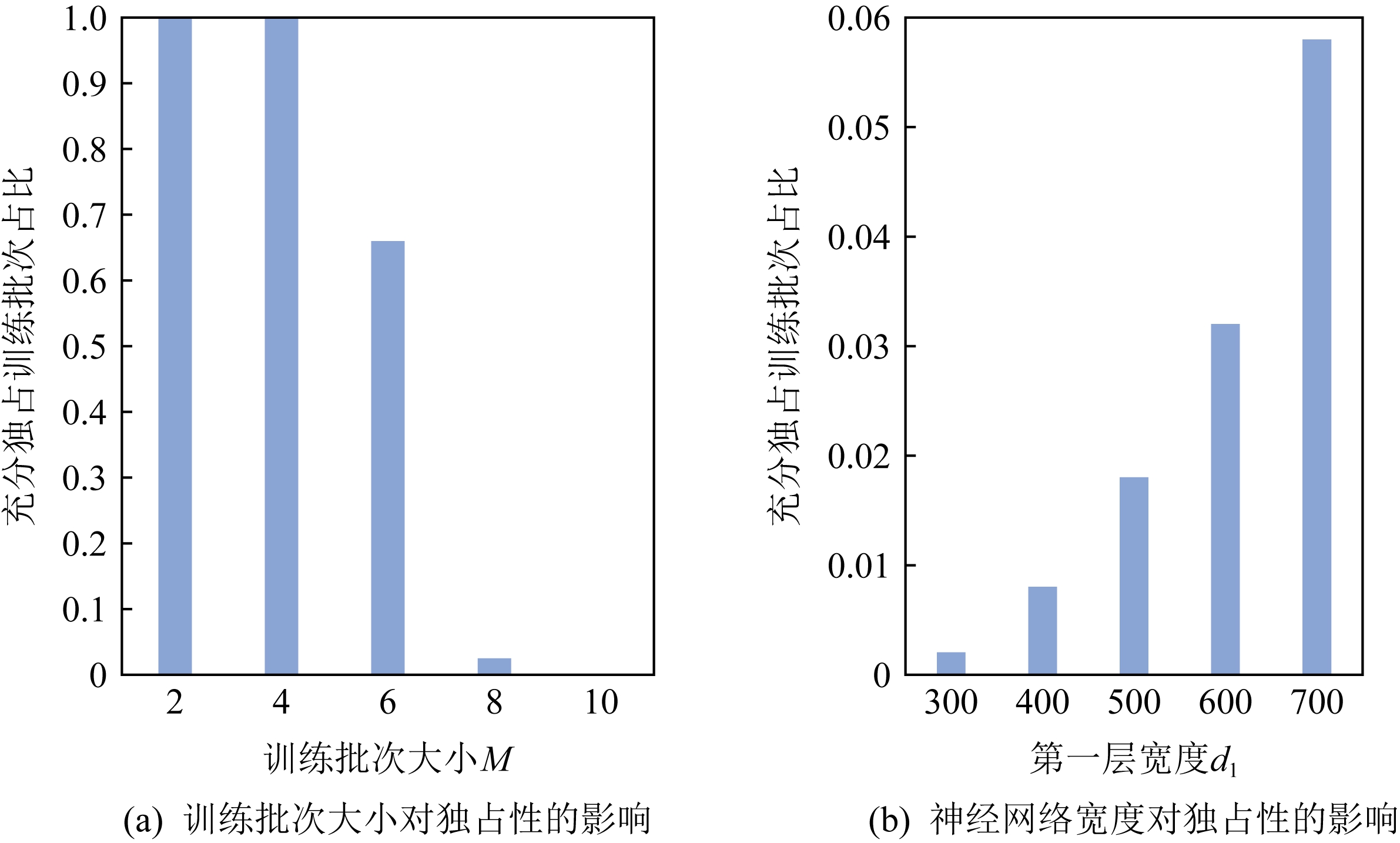
Fig.5 Percentage of batches in CIFAR-10 dataset satisfying the sufficient exclusivity condition with different configurations
图5 CIFAR-10数据集在不同设置下满足充分独占性条件训练批次占比变化情况
从图5中可以看到,一方面,随着训练批次大小M从2扩大到10,能满足充分独占性条件的批次比例从原来的接近100%快速衰减到不超过1%,如图5(a)所示;另一方面,当固定训练批次的大小为8,随着3层全连接网络中的隐藏层宽度从700个神经元缩小至300个神经元,能满足充分独占性条件的批次比例也从6%下降到不足1%.该实验现象表明,对于实际应用中的训练批次大小(如32,64等),一个训练批次满足充分独占性条件的概率非常低.因此,尽管Pan等人[19]提出的新型攻击算法对满足充分独占性条件的训练批次具有几乎无损的重建效果,该攻击在重建实际大小的训练批次时同样面临问题:一旦不满足充分独占性条件,2.2.2节中介绍的重建算法几乎无法执行.更一般地,图5展示的现象也为此前基于优化的数据重建攻击对大模型和小训练批次的强依赖提供了一种合理的解释:模型尺寸的缩小和训练批次的扩大均会导致批次满足充分独占性条件的概率降低,即同一批次中数据的独占性减弱,从而难以从平均化的梯度信息中分离.
2.3 基于线性规划的神经元激活模式控制
2.3.1 算法概述
为扩大2.2节中具有理论保证的数据重建算法的应用范围,同时松弛其对于训练批次的严格假设,2.3~2.4节进一步提出利用攻击者能够操控端侧节点的训练数据预处理算法这一环节,为一个本不满足充分独占性条件的训练批次生成微小的像素层面扰动,诱使该扰动后的训练批次满足充分独占性条件,从而结合2.2节的攻击算法,从平均梯度中对该训练批次的扰动版本实施破解.由于添加的扰动较小,攻击者因而仍能从重建的扰动数据中获得端侧节点的隐私信息.本节首先介绍作为本文提出攻击方法核心模块的算法SOW(Sleep-Or-Wake),即一种基于线性规划的神经元激活模式控制算法.
如图6所示,当攻击者指定当前训练样本x(例如,图6上部的实线样本)所需的神经元激活模式(例如,第1个隐藏层的激活模式为(0,1,0,0,1)),SOW算法会相应地建立线性规划问题,求解扰动规模最小的像素层面扰动Δ,使得扰动后样本x+Δ在网络前向传播过程中的确呈现指定的激活模式.具体地,本节后续将分别介绍单层激活模式控制和多层激活模式控制2部分.
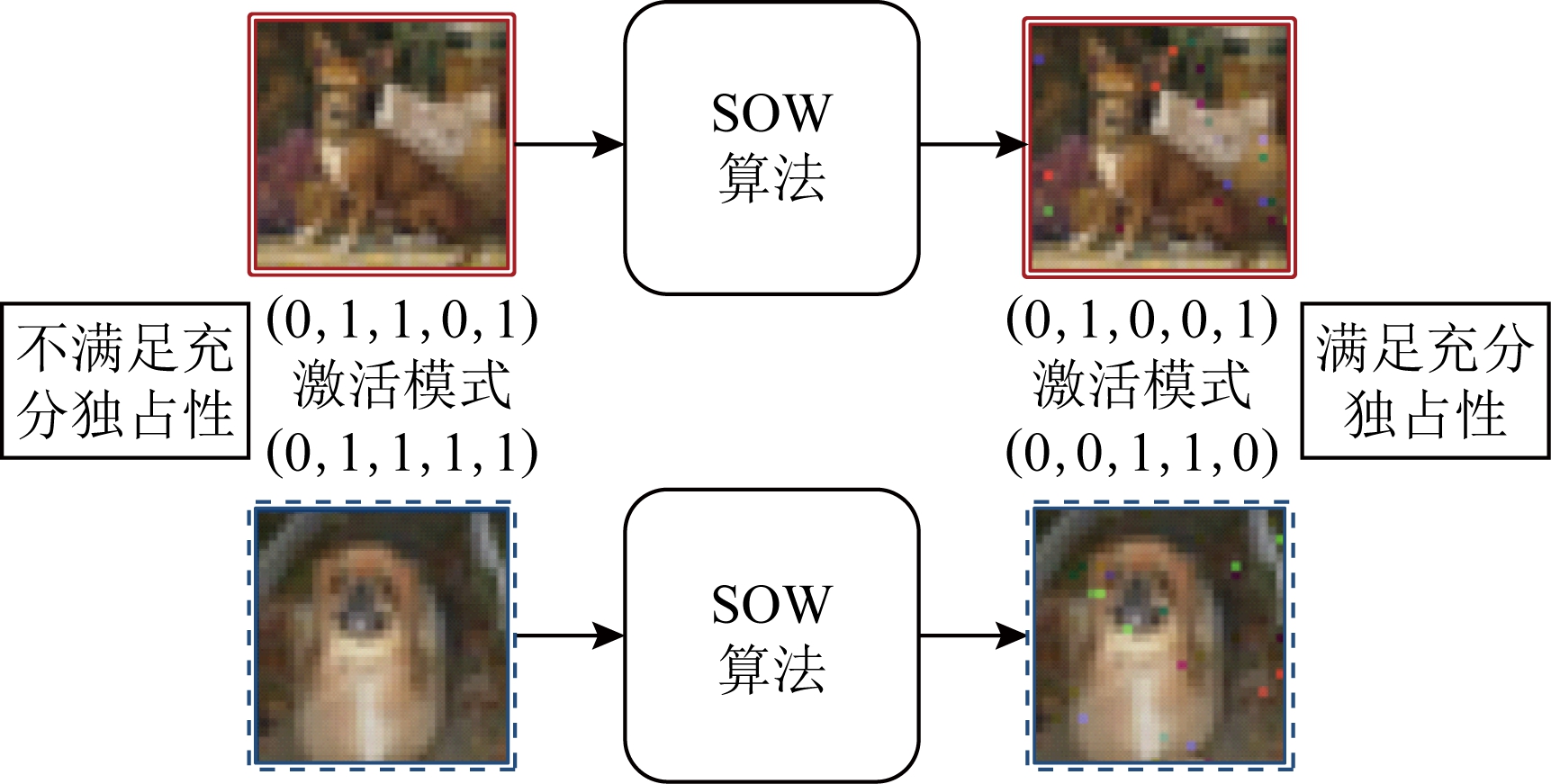
Fig.6 Neuron activation pattern manipulation by SOW algorithm
图6 通过SOW算法实现神经元激活模式控制
2.3.2 单层激活模式控制
首先,考虑在单层全连接网络f1(x)=D1(W1x+b1)中,攻击者希望找到最优的扰动Δ,使得输入数据X在该层的输出值经过ReLU函数后的激活模式为![]() 为此,可首先建立优化问题:
为此,可首先建立优化问题:
(9)
(10)
其中,L1范数![]() 表示扰动后输入在该层的激活模式,而约束x+Δ∈X要求扰动后输入仍然需要满足输入空间的定义.对于本文主要涉及的图像数据而言,归一化后的输入空间X定义为[-1,1]d,其中d=c×w×h,其中c,w,h分别表示图像的通道数、宽度和高度.
表示扰动后输入在该层的激活模式,而约束x+Δ∈X要求扰动后输入仍然需要满足输入空间的定义.对于本文主要涉及的图像数据而言,归一化后的输入空间X定义为[-1,1]d,其中d=c×w×h,其中c,w,h分别表示图像的通道数、宽度和高度.
然而,上述优化问题中对于激活模式的二值约束![]() 使得其形式上为组合优化问题,难以有效求解.为此,简记
使得其形式上为组合优化问题,难以有效求解.为此,简记![]() 的对角线向量为
的对角线向量为![]() 根据1.1.2节中介绍的ReLU函数的定义,该约束可进行如下线性转化:
根据1.1.2节中介绍的ReLU函数的定义,该约束可进行如下线性转化:
(11)
其中运算符⊙表示向量点乘, 表示向量间的逐维大于等于关系,超参ε为正常数(通常取10-8,用于容忍求解过程中存在的数值误差).
表示向量间的逐维大于等于关系,超参ε为正常数(通常取10-8,用于容忍求解过程中存在的数值误差).
直观地,上述约束条件要求X+Δ在单层全连接网络的激活前输出(pre-activation output)的符号需要匹配攻击者指定的激活模式:比如,当第j个神经元的激活模式指定为![]() 则有
则有![]() 对应地,扰动后输入样本x+Δ的激活前输出的第j位需要大于等于ε,即使得第j个神经元处于激活状态;反之,当
对应地,扰动后输入样本x+Δ的激活前输出的第j位需要大于等于ε,即使得第j个神经元处于激活状态;反之,当![]() 则有
则有![]() 相应地,激活前输出值需要小于等于-ε,即使得第j个神经元处于休眠状态.上述分析表明,该线性转化后的约束条件能准确反映指定神经元激活模式对于各个神经元输出值区间的充要条件.
相应地,激活前输出值需要小于等于-ε,即使得第j个神经元处于休眠状态.上述分析表明,该线性转化后的约束条件能准确反映指定神经元激活模式对于各个神经元输出值区间的充要条件.
至此,本节已将约束集合中的各个约束转化为标准线性规划问题中关于自变量Δ的线性不等式形式.最后,本节将继续对目标函数中的绝对值形式进行松弛变换,以适配标准线性规划问题形式.
为此,参考文献[35],本文引入额外非负变量组Δabs∈[0,1]d和额外约束条件:
-Δabs≼Δ≼Δabs,
(12)
则变量组Δabs的每个元素可被视作|Δ|中对应元素的紧致上界.因此,本节最初的优化问题中的目标函数转化为![]() 关于新变量Δabs的线性表示.
关于新变量Δabs的线性表示.
综上所述,下面给出SOW算法在控制单层神经元激活模式情形下构建的线性规划问题:
(13)
(14)
x+Δ∈[-1,1]d,-Δabs≼Δ≼Δabs.
(15)
在3.1节中,本文将通过实验验证上述松弛策略的有效性.
2.3.3 多层激活模式控制
在2.3.2节中构造的单层激活模式控制算法的基础上,本节进一步提出多层激活模式控制算法,从而能用于有效控制单张样本在多层全连接网络中每个ReLU层的激活模式,从而便于满足后续攻击所需的充分独占性条件.
从宏观上看,激活模式控制的关键在于约束每一个被指定激活状态的神经元的激活前输出值.因此,借鉴2.2.2节中所述的建立线性梯度方程的方法,本文提出将输入样本x+Δ符号化,从神经网络模型的输入层开始逐层向后传播.当传播路径上数据流遇到ReLU函数单元,则根据攻击者指定的0/1激活状态,收集相应的线性不等式约束.具体地,若当前ReLU函数单元的输入表达式为a,指定的激活状态为α∈{0,1},则收集的线性不等式约束为(2α-1)a≥ε.同时,若指定激活状态为1,则将输入表达式恒等地向下一层计算单元传递;否则,若指定激活状态为0,则向下一层计算单元传递0.执行上述步骤至完成最后一个ReLU层的不等式收集,攻击者可类似2.3.2节中建立关于输入扰动Δ的规划问题.最后,通过引入非负变量组Δabs∈[0,1]d和额外约束条件,可将多层激活模式控制问题转化为标准线性规划问题.在实现中,本文选用开源线性规划求解器PuLP[36]建立线性规划问题和进行求解.
2.4 攻击部署与数据泄露诱导
2.4.1 攻击部署模式
当利用SOW算法对给定样本生成微小扰动以操控该样本在目标网络中的神经元激活模式后,攻击者将实施3个攻击部署:
1)替换端侧数据预处理模块.首先,攻击者在其目标的端侧节点的训练过程中添加额外的SOW算法模块.具体地,该模块位于训练批次进入神经网络模型计算之前.
2)构造充分独占性的激活模式组合.SOW模块将自动构造满足充分独占性条件的激活模式集合.例如,在图6中,原本实线框样本和虚线框样本在最后1个ReLU层的激活模式分别为(0,1,1,0,1)和(0,1,1,1,1),不满足充分独占性条件中对于各样本均包含至少2个ExAN的要求.为此,该步骤将根据各正常样本的初始激活模式,构造修改神经元激活状态个数最少且满足充分独占性的激活模式集合.仍以图6为例,相应的激活模式为(0,1,0,0,1),(0,0,1,1,0).
3)执行SOW算法添加样本扰动.在这一步中,攻击者指定上一步中构造的激活模式,为训练批次中的每个样本执行SOW算法,寻找最优扰动以满足激活模式约束.随后,这些带扰动的样本将进入神经网络模块执行正常前向计算流程,产生平均损失值,反向传播获得平均梯度,最后提交至分布式训练服务提供方.
借助上述3个攻击部署,传输的平均梯度确保满足充分独占性条件,因而可被攻击者应用文献[19]的重建算法进行无损重建,恢复带扰动的私有训练样本.在实验中,本文将一并衡量重建样本和原始训练批次样本与带扰动的训练批次样本之间的误差,以评估本文提出的攻击部署造成的隐私泄露程度.
2.4.2 独占激活模式构造方式
作为2.4.1节所述步骤的补充,本节介绍当已知1个M大小的训练批次中各样本的初始激活模式组合为(A1,A2,…,AM)时,如何在翻转激活状态个数最少的前提下,构造相应的满足充分独占性条件的激活模式组合![]() 本文提出如下构造方法:在严格满足充分独占性条件下,实现近似最优翻转个数.
本文提出如下构造方法:在严格满足充分独占性条件下,实现近似最优翻转个数.
具体地,在多层全连接网络中的每一层,SOW算法均以逐神经元的方式进行.记当前第m个样本的激活模式中状态翻转个数为Sm(初始值均为0)和ExAN个数Nm(根据初始激活模式组合确定其初始值).当处理第j个神经元时,需要3个步骤:1)根据初始激活状态值(A1)j,(A2)j,…,(Am)j,找到其中非零值对应的样本索引集合I,其大小记作|I|.2)若|I|=1,则已满足条件;若|I|=0,则优先满足当前Nm=0的样本,将其对应的激活状态置为1;|I|≥2,则随机选择当前Nm值最小的样本(若有多个,选择其中状态翻转个数最多的样本),保留索引集合I中对应翻转个数最多的样本的激活状态.对于其他样本,设置其激活状态为0,并递增其翻转个数值Sm.3)重复执行上述步骤,便能构造满足设计要求的激活模式组合![]()
2.5 重建算法复杂性分析与优化
文献[19]中的数据重建攻击算法的主要效率瓶颈在于2.2.2节第3步中建立线性梯度匹配方程的过程.在该环节中,攻击者需要为模型中的每一个可学习参数收集经过该参数全部路径上的权重的乘积和.对于1个宽度为(d0,d1,…,dH)的全连接神经网络,其建立完整的线性梯度匹配方程组的浮点运算次数为![]() 对于CIFAR-10上的宽度为(3072,100,10)的全连接网络,也能达到1011的规模,运算开销较大.而Pan等人[19]在原始实现中并未对该攻击开销进行优化,存在较大提升空间.为此,本节提出2种优化策略:
对于CIFAR-10上的宽度为(3072,100,10)的全连接网络,也能达到1011的规模,运算开销较大.而Pan等人[19]在原始实现中并未对该攻击开销进行优化,存在较大提升空间.为此,本节提出2种优化策略:
1)网络预热机制(warm-up).在为每个参数计算经过路径的乘积和过程中,实际上存在很多被复用的乘积项.以图4为例,当重建算法为当前位置参数的输出神经元的后层参数建立方程时,同样需要复用先前经过当前位置参数的这些路径上的乘积项.为此,本文提出只需在一次正常神经网络的前向传播过程中,预先在每个神经元处缓存从输入层的每个符号变量到该神经元的路径上的权重乘积项,以及从输出层的所有类概率到该神经元的路径上的权重乘积和.那么,当实际需要为当前位置参数建立梯度方程时,只需从它所连接的首尾神经元中获取对应的乘积项进行拼接计算,便可快速获得该处梯度方程的形式.本文称上述的空间-时间置换策略为网络预热机制,所产生的额外空间复杂度为![]() 而相应的时间开销降低为
而相应的时间开销降低为![]() 2)并行化策略.注意到建立线性梯度方程组的过程符合Map-Reduce的模式,即该过程需要为每个可学习的标量参数收集并建立线性方程,而这些子问题之间两两独立.当完成对各个标量参数的方程收集后,仅通过集合并集操作便能得到完整的线性梯度方程组.同时,对于1个训练批次中不同样本的梯度方程组的收集同样相互独立,当所有子任务结束后,仅需将对应相同标量参数的标量梯度方程进行算数平均便可得到最终关于整个训练批次的梯度方程.为此,本文提出利用线程池方法从不同标量参数的方程收集和不同样本的方程收集2个层面进行并行化加速.3.3节的实验将验证该策略的有效性.
2)并行化策略.注意到建立线性梯度方程组的过程符合Map-Reduce的模式,即该过程需要为每个可学习的标量参数收集并建立线性方程,而这些子问题之间两两独立.当完成对各个标量参数的方程收集后,仅通过集合并集操作便能得到完整的线性梯度方程组.同时,对于1个训练批次中不同样本的梯度方程组的收集同样相互独立,当所有子任务结束后,仅需将对应相同标量参数的标量梯度方程进行算数平均便可得到最终关于整个训练批次的梯度方程.为此,本文提出利用线程池方法从不同标量参数的方程收集和不同样本的方程收集2个层面进行并行化加速.3.3节的实验将验证该策略的有效性.
2.6 数据集选取与评估指标
2.6.1 数据集简介
1)CIFAR-10[37].该数据集包含了60 000张来自10个不同类别(如狗、猫等)的日常事物图像,由Krizhevsky于2009年提出,被广泛应用于图像相关的深度学习研究.其中,每张图像均包含RGB通道,分辨率为32×32.
2)MedMNIST数据库[38].MedMNIST数据库包含了视网膜、皮肤肿瘤、组织切片等10余类医疗影像数据,由Yang等人于2014年从多家公开医疗数据库中分类收集,主要用于医疗智能诊断算法的评估.其中,不同类型的图像可能为灰度或RGB通道,分辨率统一为28×28.本文实验包含该数据库中的视网膜(RetinaMNIST)、皮肤肿瘤(DermaMNIST)、组织切片(OrganMNIST)数据集.
3)Facescrub数据集[39].Facescrub数据集包含530位男性和女性知名人物来自互联网的公开照片,共计10万以上.该数据集主要用于人脸识别模型的训练与评估.本文实验对Facescrub数据集降采样为20类分类任务,图像均包含RGB通道,像素大小缩放为32×32.
2.6.2 模型选取
为保持与文献[19]中原始实验设置相同,本文选取受害者的神经网络模型结构为(d,512,512,K)的4层全连接神经网络,其中d为输入图像的标量维度,K为类个数,该模型中包含2层神经元数目为512的隐藏层.
2.6.3 评估指标
假设目标训练批次为![]() 数据重建算法从平均训练梯度中得出的重建结果为
数据重建算法从平均训练梯度中得出的重建结果为![]() 考虑到训练批次作为1个集合存在无序性,因此类似于文献[19],本文在算法评估过程中,将以图像间均方误差作为距离度量,用匈牙利算法[40]匹配真实目标样本和对应的重建样本,记匹配后的重建结果为
考虑到训练批次作为1个集合存在无序性,因此类似于文献[19],本文在算法评估过程中,将以图像间均方误差作为距离度量,用匈牙利算法[40]匹配真实目标样本和对应的重建样本,记匹配后的重建结果为![]() 本文采用2个指标评判数据重建攻击的性能.
本文采用2个指标评判数据重建攻击的性能.
1)重建信噪比(PSNR).具体地,计算1对样本![]() 间的均方误差为
间的均方误差为![]() 其中d为输入样本的维度.那么,重建信噪比定义为
其中d为输入样本的维度.那么,重建信噪比定义为
(16)
特别地,PSNR能较好地反映重建图像的清晰程度,当PSNR≥20,则重建图像与真实图像在肉眼上几乎不存在差异[19].实验结果将以汇报数据重建攻击在目标训练批次上的平均重建信噪比为主,辅以可视化结果.
2)标签重建准确度(LAcc).此外,本文衡量重建样本和训练样本的标签一致性.具体地,定义数据重建算法的标签重建准确度为
(17)
3 实验结果与分析
本节首先给出基于2.3节的神经元控制算法的激活模式控制准确度,并给出相应的平均图像扰动大小和可视化结果;随后给出激活模式控制下恢复实际大小训练批次样本时的重建效果,并给出可视化;最后给出经过优化前后的数据重建攻击的时间和空间开销对比.
3.1 激活状态匹配准确度结果与分析
本节介绍了在各个数据集上利用本文提出的神经元激活模式控制算法对给定原始训练批次添加微小扰动,使得其满足特定的激活模式组合的准确度.特别地,本节设置原始训练批次的大小为64(8倍于此前工作通常考虑的大小为8的训练批次).根据2.4.2节提出的独占激活模式构造方式指定每个原始训练样本的目标激活模式.本节采用比特错误率(bit error rate, BER)衡量扰动后的训练样本的激活模式和目标激活模式之间的差异,定义为BER= ![]() 其中di表示相应隐藏层中包含的神经元个数;采用均方误差衡量扰动前后的样本差异.
其中di表示相应隐藏层中包含的神经元个数;采用均方误差衡量扰动前后的样本差异.
如表1所示,在5个图像数据集上,本文提出的神经元激活模式控制算法能够精确地操控数据样本在目标神经网络中的激活模式,在2个隐藏层上,扰动后样本的激活模式和指定的激活模式完全一致(即BER指标为0%,每个激活状态均匹配),这得益于本文将激活模式的控制问题转化为具有严格性的线性规划问题,因此得以精确求解.同时,由于在激活模式控制过程中,原始样本上所添加的扰动大小为线性规划问题的最小化目标,因此在完成激活模式控制的同时,扰动前后样本间的平均像素差异也被控制得较小.例如,在Facescrub上,均方误差(MSE)仅为0.006 3.为了提供给读者更为直观的体会,图7展示了在Facescrub数据集上扰动前后的训练批次中随机采样的4组对应样本.可以看到,本文的激活模式控制算法为每张样本添加散点状的微小扰动,不影响辨别原图所包含的人像,这也保证了后续通过从平均梯度中像素级重建扰动后样本,能实现对于原始训练样本的隐私窃取.
Table 1 Bit Error Rate of the Neuron Activation Pattern of the Perturbed Data Samples
表1 扰动数据样本的神经元激活模式的比特错误率
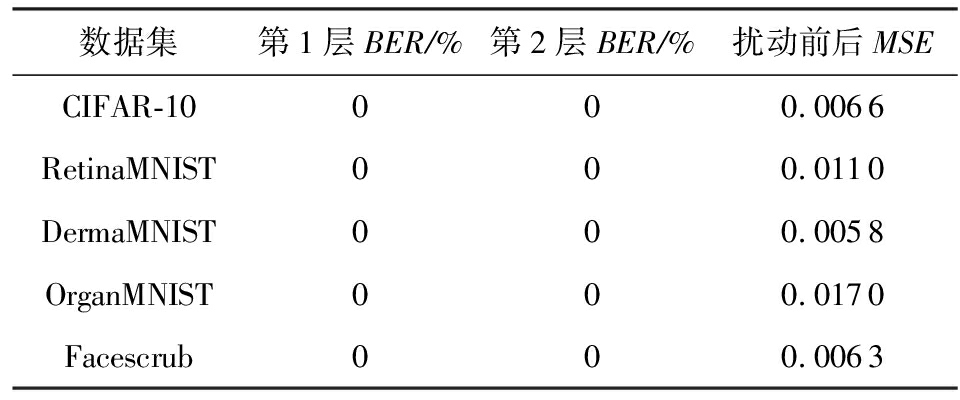
数据集第1层BER∕%第2层BER∕%扰动前后MSECIFAR-10000.0066RetinaMNIST000.0110DermaMNIST000.0058OrganMNIST000.0170Facescrub000.0063
3.2 数据重建攻击效果与分析
基于3.1节介绍的激活模式控制结果,本节进一步结合经优化后的文献[19]提出的攻击算法,对于扰动后的训练批次所计算产生的平均训练梯度进行数据重建攻击.具体地,本节同样设置训练批次大小M=64,先经过激活模式控制算法将训练批次扰动至满足充分独占性条件.在实际场景中,这些经由恶意预处理的样本将进入目标神经网络的学习过程,产生平均梯度并提交给服务器.通过截获该平均梯度,以文献[19]中同样的最优参数破解该梯度信息,获得重建后训练批次.本节以重建信噪比和标签重建准确度为评价指标,衡量重建后训练批次与扰动后训练批次(代表重建算法性能),以及与原始训练批次间的差异(代表实际隐私泄露程度).同时,对比基于优化的数据重建算法Inverting[17].需要注意的是,由于文献[19]的攻击算法在目标训练批次不满足充分独占性条件的情况而无法执行,因此不作为本节的基准方法进行对比实验.

Fig.7 Visualization of perturbed data samples which satisfy the sufficient exclusivity condition
图7 满足充分独占性条件的扰动数据样本可视化
从表2可知,首先激活模式控制算法使得文献[19]提出的数据重建算法得以重新应用于大小为64的实际训练批次,这是因为根据实验中间结果(如图5所示),这些原始训练批次均不满足该算法所要求的充分独占性条件,因此该数据重建算法将由于无法从最后1层的梯度信息中推断各个样本的独占神经元、概率向量和标签信息,从而导致后续重建步骤无法执行.相比之下,利用本文提出的激活模式控制算法,重建算法能有效破解包含64张图片的扰动后训练批次,得到与实际扰动后样本几乎无差异的重建结果.例如,在DermaMNIST皮肤病数据集上,64张重建后的图像与真实扰动后的训练样本的平均重建信噪比高达48.11(>20),意味着像素级重建.同时,表2中还进一步衡量了重建后样本与原始训练批次中的真实图片之间的差异,可以看到各个数据集上相应的PSNR也达到18以上,相较于此前基于优化的数据重建方法提升近1~4倍不等.这意味着,尽管激活模式控制算法为原始数据样本添加了微小扰动以使得文献[19]的重建算法得以应用,这样的代价是合理且具有实际意义的:一方面,重建的扰动后样本仍相比Inverting方法在真实梯度上的重建结果更接近原始数据;另一方面,这些扰动并不影响攻击者辨认私密数据中所包含的隐私信息(图7).为进一步直观地体现本文的攻击效果,图8展示了在Facescrub数据集上重建训练批次中随机采样的8张对应样本,并给出了相应的扰动后和原始的真实样本,从可视化的角度佐证了上述的分析和量化实验结果.
Table 2 Performance of Data Reconstruction Attacks Under Activation Pattern Manipulation
表2 激活模式控制下的数据重建攻击效果
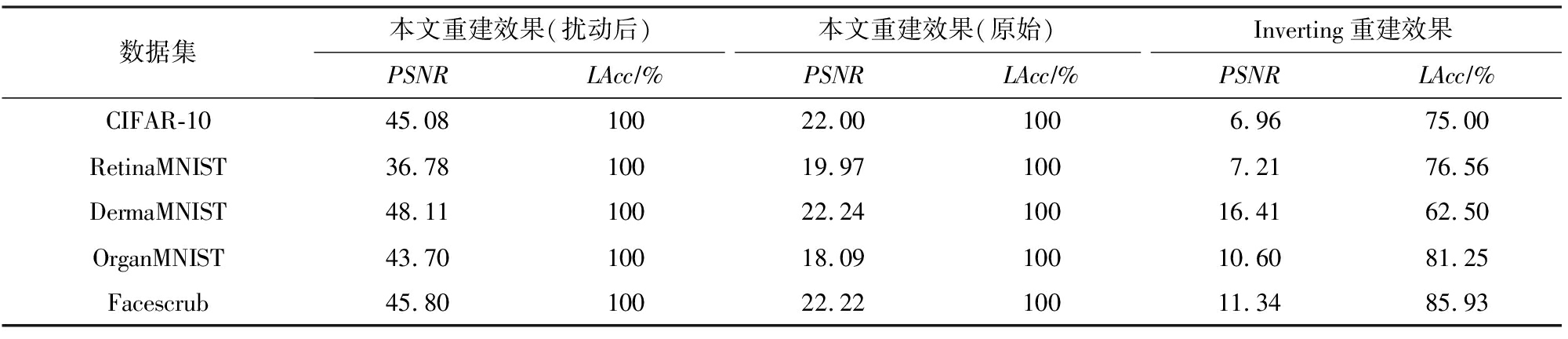
数据集本文重建效果(扰动后)本文重建效果(原始)Inverting重建效果PSNRLAcc∕%PSNRLAcc∕%PSNRLAcc∕%CIFAR-1045.0810022.001006.9675.00RetinaMNIST36.7810019.971007.2176.56DermaMNIST48.1110022.2410016.4162.50OrganMNIST43.7010018.0910010.6081.25Facescrub45.8010022.2210011.3485.93
3.3 攻击效率优化结果与分析
本节对比同时开启网络预热机制和并行化策略前后的数据重建算法运行效率.具体地,本节将以重建时间开销和内存开销作为衡量攻击效率的2个方面.本文的实验环境为1台安装Ubuntu 18.04操作系统的Linux服务器,CPU型号为AMD Ryzen Threadripper 2990WX(32线程),并配有2张NVIDIA GTX RTX2080显卡.以CIFAR-10数据集为例,本节将重建样本数从8张不断翻倍扩大至64张,在相同环境中分别重复运行重建算法10次,用Python time模块和memory_profiler模块监测优化前后算法的运行过程时间开销和空间开销.优化后的重建算法线程池大小设置为32.特别地,表2和图8的重建结果均为并行化优化后的实验结果,从实验层面证明了并行化策略的正确性.
图9对比了优化前后重建算法随着所需重建的训练批次扩大的时间开销和空间开销的增长情况.可以看到,本文优化后的数据重建攻击算法较先前在攻击所需时间开销层面具有显著降低,而空间开销维持相对接近.例如,当训练批次大小为64时,在仅增长约10%的内存空间开销的代价下,优化后的数据重建攻击的时间开销相较原始实现降低近90%.同时,随着训练批次的大小增加,得益于本文所实现的并行化策略,优化后算法的时间开销的增速远小于优化前算法,接近次线性增长.这也意味着,在同样的攻击时长下,本文优化后的数据重建攻击能破解更多的训练样本,因而造成更大的实际隐私风险.
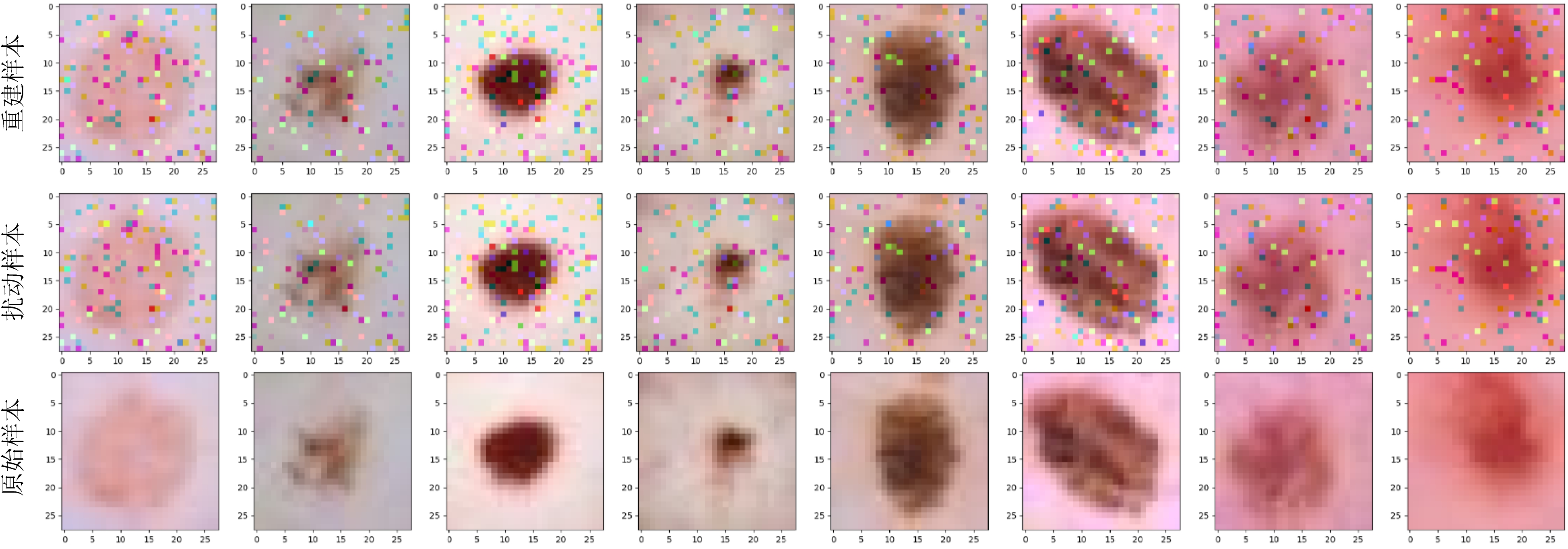
Fig.8 Visualization of reconstructed, perturbed and original samples from the DermaMNIST
图8 DermaMNIST数据集上的重建样本、扰动样本和原始样本的可视化
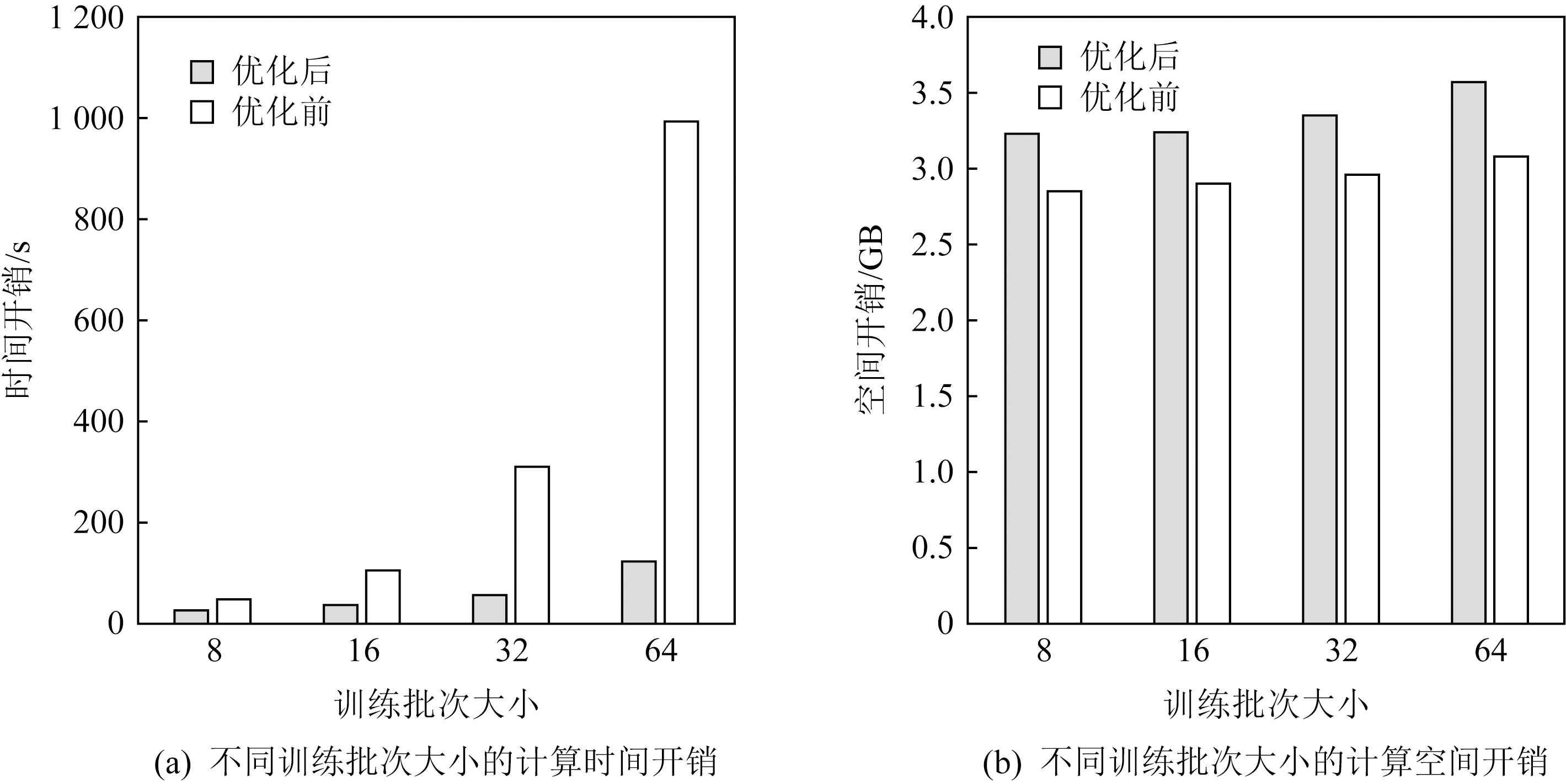
Fig.9 Time and memory cost of reconstruction attacks before and after optimization
图9 优化前后重建攻击的时空开销
4 总结与未来工作
联邦学习、共享学习等新型分布式训练算法的出现,使得训练梯度、深度表征等模型中间计算结果成为在开放网络中传输的主要媒介.在连接着数据孤岛、沟通多个深度学习模型的训练过程的同时,模型中间计算结果却无可避免地携带着模型、数据相关的私密信息,因此也极有可能成为中间人攻击和半诚实服务器觊觎的对象,用于破解端侧隐私数据.本文所研究的数据重建攻击,正是考虑在攻击者截获分布式训练过程中传递的平均训练梯度信息的情况下,如何从梯度中破解所涉及的训练批次中的每个私有样本及其标签的过程.本文创新性地提出了神经元激活模式控制算法,添加微小数据扰动以诱导端侧数据节点满足可重建性完备条件,即充分独占性条件,首次实现具有实际应用场景大小的训练批次的重建攻击.在实质性地扩大了文献[19]提出的攻击算法的应用范围的同时,算法的数据重建效果与原方法持平,从而能有效实现对于端侧隐私数据的破解.此外,本文利用网络预热和并行化策略将该重建算法的攻击效率提升10倍以上,有效增加了在相同时间内的数据破解效率.后续工作一方面可考虑将本文及文献[19]所提出的方法进一步扩展至更为复杂的卷积神经网络,以及具有残差连接的现代神经网络结构;另一方面,也可考虑将激活模式控制算法和神经元独占性分析技术应用于其他应用领域(如自然语言处理、语音识别)并结合其他攻击场景下的已有攻击算法(如模型窃取攻击等),用以松弛相应攻击条件,从而帮助模型使用者更为准确地把握这类攻击的实际威胁.同时,也希望后续研究者能够加紧研究如何有效反制这类具有严重危害的数据重建攻击(如通过梯度混淆、差分隐私等机制),在尽可能不影响分布式训练过程效能的情况下,降低乃至消除从平均梯度中恢复个体私有信息的可能性.
作者贡献声明:潘旭东负责思路提出、论文初稿撰写和实验设计;张谧和杨珉负责思路讨论、实验结果讨论和论文修改.
[1]Jakub K, McMahan B, Yu Xinnan, et al.Federated Learning: Strategies for improving communication efficiency[EB/OL].[2020-04-01].https://arxiv.org/abs/1610.05492
[2]Yang Qiang, Liu Yang, Chen Tianjian, et al.Federated machine learning: Concept and applications[J].ACM Transactions on Intelligent Systems and Technology, 2019, 10(2): 1-19
[3]Kairouz P, McMahan B, Avent B, et al.Advances and open problems in federated learning[J].Foundations and Trends in Machine Learning, 2021, 14(1): 1-210
[4]Jiang Zhanhong, Balu A, Hegde C, et al.Collaborative deep learning in fixed topology networks[C]//Proc of the 28th Annual Conf on Neural Information Processing Systems.New York: Curran Associates, 2017: 5906-5916
[5]Wang Haozhao, Guo Song, Qu Zhihao, et al.Error-compensated sparsification for communication-efficient decentralized training in edge environment[J].IEEE Transactions on Parallel and Distributed Systems, 2022, 33(1): 14-25
[6]Cheng Kewei, Fan Tao, Jin Yilun, et al.SecureBoost: A lossless federated learning framework[J].IEEE Intelligent Systems, 2021, 36(6): 87-98
[7]Jiang Meirui, Wang Zirui, Dou Qi.HarmoFL: Harmonizing local and global drifts in federated learning on heterogeneous medical images[C]//Proc of the 34th AAAI Conf on Artificial Intellilgence.Menlo Park: AAAI, 2020: 1087-1095
[8]China Academy of Information and Communications Technology.White Paper on Artificial Intelligence Security[EB/OL].[2021-04-05].http://www.caict.ac.cn/kxyj/qwfb/bps/201809/P020 180918473525332978.pdf(in Chinese)(中国信息通信研究院.人工智能安全白皮书[EB/OL].[2021-04-05].http://www.caict.ac.cn/kxyj/qwfb/bps/201809/P020 180918473525332978.pdf)
[9]Pan Xudong, Zhang Mi, Ji Shouling, et al.Privacy risks of general-purpose language models[C]//Proc of IEEE Symp on Security and Privacy.Piscataway, NJ: IEEE, 2020: 1314-1331
[10]Pan Xudong, Zhang Mi, Yan Yifan, et al.Evaluating privacy risks of deep learning based general-purpose language models[J].Journal of Computer Research and Development, 2021, 58(5): 1092-1105(in Chinese)(潘旭东, 张谧, 颜一帆, 等.通用深度学习语言模型的隐私风险评估[J].计算机研究与发展, 2021, 58(5): 1092-1105)
[11]Devlin J, Chang Mingwei, Lee K, et al.BERT: Pre-training of deep bidirectional transformers for language understanding[C]//Proc of the 20th Annual Conf of the North American Chapter of the Association for Computational Linguistics.Stroudsburg, PA: ACL, 2019: 4171-4186
[12]Melis L, Song Congzheng, Cristofaro E.Exploiting unintended feature leakage in collaborative learning[C]//Proc of the 40th IEEE Symp on Security and Privacy.Piscataway, NJ: IEEE, 2019: 691-706
[13]Pan Xudong, Zhang Mi, Wu Duocai, et al.Justinian’s GAAvernor: Robust distributed learning with gradient aggregation agent[C]//Proc of the 29th USENIX Security Symp.Berkeley, CA: USENIX Association, 2020: 1641-1658
[14]Lyu Lingjuan, Yu Han, Zhao Jun, et al.Threats to Federated Learning[G]//Federated Learning.Lecture Notes in Computer Science, vol 12500.Berlin: Springer, 2020: 3-16
[15]Zhu Ligeng, Liu Zhijian, Han Song.Deep leakage from gradients[C]//Proc of the 33rd Annual Conf on Neural Information Processing Systems.New York: Curran Associates, 2019: 14774-14784
[16]Zhao Bo, Mopuri K, Bilen H.iDLG: Improved deep leakage from gradients[EB/OL].[2020-02-01].https://arxiv.org/abs/2001.02610
[17]Geiping J, Bauermeister H, Dröge H, et al.Inverting gradients-how easy is it to break privacy in federated learning?[C]//Proc of the 34th Annual Conf on Neural Information Processing Systems.New York: Curran Associates, 2020: 16937-16947
[18]Yin Hongxu, Mallya A, Vahdat A, et al.See through gradients: Image batch recovery via GradInversion[C]//Proc of IEEE/CVF Conf on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE, 2020: 16332-16341
[19]Pan Xudong, Zhang Mi, Yan Yifan, et al.Exploring the security boundary of data reconstruction via neuron exclusivity analysis[C]//Proc of the 31st USENIX Security Symp.Berkeley, CA: USENIX Association, 2022[2022-06-17].https://www.usenix.org/system/files/sec22-pan-exploring.pdf
[20]Hitaj B, Ateniese G, Pérez F.Deepmodels under the GAN: Information leakage from collaborative deep learning[C]//Proc of the 24th ACM SIGSAC Conf on Computer and Communications Security.New York: ACM, 2017: 603-618
[21]Nasr M, Shokri R, Houmansadr A.Comprehensive privacy analysis of deep learning: Passive and active white-box inference attacks against centralized and federated learning[C]//Proc of IEEE Symp on Security and Privacy.Piscataway, NJ: IEEE, 2019: 739-753
[22]Ganju K, Wang Qi, Yang Wei, et al.Property inference attacks on fully connected neural networks using permutation invariant representations[C]//Proc of the 2018 ACM SIGSAC Conf on Computer and Communications Security.New York: ACM, 2018: 619-633
[23]Carlini N, Liu Chang, Erlingsson  , et al.The secret sharer: Evaluating and testing unintended memorization in neural networks[C]//Proc of the 26th USENIX Security Symp.Berkeley, CA: USENIX Association, 2017: 267-284
, et al.The secret sharer: Evaluating and testing unintended memorization in neural networks[C]//Proc of the 26th USENIX Security Symp.Berkeley, CA: USENIX Association, 2017: 267-284
[24]Fredrikson M, Jha S, Ristenpart T.Model inversion attacks that exploit confidence information and basic countermeasures[C]//Proc of the 2015 ACM SIGSAC Conf on Computer and Communications Security.New York: ACM, 2015: 1322-1333
[25]Fredrikson M, Lantz E, Jha S, et al.Privacy in pharmaco-genetics: An end-to-end case study of personalized warfarin dosing[C]//Proc of the 23rd USENIX Security Symp.Berkeley, CA: USENIX Association, 2014: 17-32
[26]Shokri R, Strobel M, Zick Y.Privacy risks of explaining machine learning models[EB/OL].[2020-04-01].https://arxiv.org/abs/1907.00164
[27]Shokri R, Stronati M, Song Congzheng, et al.Membership inference attacks against machine learning models[C]//Proc of IEEE Symp on Security and Privacy.Piscataway, NJ: IEEE, 2017: 3-18
[28]Jagielski M, Carlini N, Berthelot D, et al.High accuracy and high fidelity extraction of neural networks[C]//Proc of the 29th USENIX Security Symp.Berkeley, CA: USENIX Association, 2020: 1345-1362
[29]Wang Binghui, Gong Zhenqiang.Stealing hyperparameters in machine learning[C]//Proc of IEEE Symp on Security and Privacy.Piscataway, NJ: IEEE, 2018: 36-52
[30]Duddu V, Samanta D, Rao V, et al.Stealing neural networks via timing side channels[EB/OL].[2020-04-01].https://arxiv.org/abs/1812.11720
[31]Tramèr F, Zhang Fan, Juels A, et al.Stealing machine learning models via prediction APIs[C]//Proc of the 25th USENIX Security Symp.Berkeley, CA: USENIX Association, 2016: 601-618
[32]Bonawitz K, Eichner H, Grieskamp W, et al.Towards federated learning at scale: System design[EB/OL].[2019-10-11].https://arxiv.org/abs/1902.01046
[33]Ziller A, Trask A, Lopardo A, et al.PySyft: A Library for Easy Federated Learning[G]//Federated Learning Systems.Studies in Computational Intelligence, vol 965.Berlin: Springer, 2021: 111-139
[34]Bagdasaryan E, Shmatikov V.Blind backdoors in deep learning models[C]//Proc of the 30th USENIX Security Symp.Berkeley, CA: USENIX Association, 2021: 1505-1521
[35]Griffin C.Linear Programming: Penn State Math 484 Lecture Notes[EB/OL].[2021-04-05].http://www.personal.psu.edu/cxg286/Math484_V1.pdf
[36]Mitchell S, Sullivan O, Dunning I.PuLP: A linear programming toolkit for Python.[EB/OL].[2021-04-05].http://www.optimization-online.org/DB_FILE/2011/09/3178.pdf
[37]Krizhevsky A.Learning multiple layers of features from tiny images[M/OL].[2021-04-05].http://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf
[38]Yang Jiancheng, Shi Rui, Ni Bingbing.MedMNIST classification decathlon: A lightweight AutoML benchmark for medical image analysis[C]//Proc of the 18th IEEE Int Symp on Biomedical Imaging.Piscataway, NJ: IEEE, 2014: 191-195
[39]Ng H, Winkler S.A data-driven approach to cleaning large face datasets[C]//Proc of the 21st IEEE Int Conf on Image Processing.Piscataway, NJ: IEEE, 2014: 343-347
[40]Kuhn H.The Hungarian method for the assignment problem[J].Naval Research Logistics, 1955, 2(1): 83-97


