Overview of the Frontier Progress of Causal Machine Learning
-
摘要:
机器学习是实现人工智能的重要技术手段之一,在计算机视觉、自然语言处理、搜索引擎与推荐系统等领域有着重要应用.现有的机器学习方法往往注重数据中的相关关系而忽视其中的因果关系,而随着应用需求的提高,其弊端也逐渐开始显现,在可解释性、可迁移性、鲁棒性和公平性等方面面临一系列亟待解决的问题.为了解决这些问题,研究者们开始重新审视因果关系建模的必要性,相关方法也成为近期的研究热点之一.在此对近年来在机器学习领域中应用因果技术和思想解决实际问题的工作进行整理和总结,梳理出这一新兴研究方向的发展脉络.首先对与机器学习紧密相关的因果理论做简要介绍;然后以机器学习中的不同问题需求为划分依据对各工作进行分类介绍,从求解思路和技术手段的视角阐释其区别与联系;最后对因果机器学习的现状进行总结,并对未来发展趋势做出预测和展望.
Abstract:Machine learning is one of the important technical means to realize artificial intelligence, and it has important applications in the fields of computer vision, natural language processing, search engines and recommendation systems. Existing machine learning methods often focus on the correlations in the data and ignore the causality. With the increase in application requirements, their drawbacks have gradually begun to appear, facing a series of urgent problems in terms of interpretability, transferability, robustness, and fairness. In order to solve these problems, researchers have begun to re-examine the necessity of modeling causal relationship, and related methods have become one of the recent research hotspots. We organize and summarize the work of applying causal techniques and ideas to solve practical problems in the field of machine learning in recent years, and sort out the development venation of this emerging research direction. First, we briefly introduce the closely related causal theory to machine learning. Then, we classify and introduce each work based on the needs of different problems in machine learning, explain their differences and connections from the perspective of solution ideas and technical means. Finally, we summarize the current situation of causal machine learning, and make predictions and prospects for future development trends.
-
当预期的系统观测和真实的系统观测不一致时,这时系统就存在故障,需要对故障进行诊断.基于模型诊断(model-based diagnosis, MBD)[1]是根据系统的描述利用基于推理的方法解释系统观测不一致的过程.几十年来,MBD问题已经广泛应用于的各个领域,包括调试关系规范[2]、诊断系统调试[3]、电子表格调试[4]和软件故障定位[5]等领域.
文章的主要贡献包括3个方面:
1) 提出利用观测的扇入过滤边和扇出过滤边对边进行过滤的约简方法.这2种边都是冗余的,因为它们的值在进行诊断求解过程中是必须进行传播的值.
2) 提出利用观测的过滤节点来进行过滤的约简方法.对于基于观察的过滤节点而言,它所有的扇入和扇出都是固定的,即它的扇入和扇出之间不存在冲突.
3) 在ISCAS85和ITC99基准测试实例上的实验结果表明,提出的方法可以有效缩减MBD问题编码时生成的子句规模,进而降低最大可满足性问题(maximum satisfiability, MaxSAT)求解诊断问题的难度,有效地提高了诊断求解效率.
1. 相关工作
近几十年来,越来越多的研究者投入到MBD问题的研究中,提出了许多求解算法,其中包括单个观测的MBD算法[6-11]和多观测的MBD算法[12-15].目前用于解决单个观测下的MBD问题算法为:随机搜索算法[6,16]、基于编译的算法[7],基于广度优先搜索的算法[8]、基于可满足性问题(satisfiability,SAT)的算法[9-10]、基于冲突导向的算法[11]等[17-21].在这些算法中,基于广度优先搜索的算法及其改进算法利用了树结构.此类算法检查树的每个节点是否表示最小诊断解,这类方法是完备的.显然,只要有足够的时间,这类方法可以得到所有的诊断解.然而,这类方法是相当耗时的,它们在解决大型现实实例问题时是不太现实的.随着计算机处理器的快速发展,一些并行化技术也被用于MBD求解问题中,Jannach等人[8]通过并行地构造碰集树(hitting set-tree, HS-Tree)返回所有诊断.基于编译的方法通过利用给定的系统层次结构和DNF编码的方式[7]计算候选解的方法也显示出它们的优势.SAFARI算法[6]证明了在MBD问题上随机搜索算法的有效性.SAFARI随机删除一个组件,然后判断候选解是否仍然是一个诊断,直到没有组件可以删除.显然,SAFARI不能保证返回的诊断解是极小势诊断.近年来,随着SAT及MaxSAT求解器性能的大幅提升,使得基于SAT的诊断方法引起了广泛的关注.Feldman等人[6]提出将诊断的电路编码成MaxSAT问题,该方法比SAFARI运行时间更长.相比之下,Metodi等人[20]提出的SATbD考虑电路的直接统治者,并找出所有极小势诊断.2015年,Marques-Silva等人[22]提出一种面向统治者的编码(dominator oriented encoding, DOE)方法,通过过滤掉一些节点和一些边的方法将MBD编码为MaxSAT.作为一种先进的编码方法,DOE利用了系统的结构属性,有效地缩减了MBD问题编码后子句集的规模.虽然DOE保证返回基数最小的诊断,但它没有考虑与观察有关的多余带权重的合取范式(weighted conjunctive normal form, WCNF).本文提出一种面向观察的编码(observation-oriented encoding, OOE)方法,该方法在将MBD编码到Max SAT时能有效减少子句集规模.此外,本文在调用相同的MaxSAT求解器情况下,将OOE方法与基础编码(basic encoding, BE)和DOE进行了比较.实验结果表明,OOE方法有效提高了MBD问题的求解效率.
2. 基于模型的诊断问题
本节主要介绍MBD问题的相关定义及概念.
2.1 基本定义
诊断问题可以被定义为一个三元组
⟨ SD,Comps,Obs⟩ ,其中,SD表示诊断问题的系统描述,Comps代表组件的集合,Obs代表一个观测.假定所有组件的状态是正常的情况下,当系统的模型描述和观测出现不一致时,我们称存在一个诊断问题.也就是:SD∧Obs∧{¬AB(c)|c∈Comps}⊨⊥, (1) 其中,AB(c)=1代表组件c是故障的,相反,AB(c)=0代表组件c是正常的.下面我们给出诊断的定义.
定义1. 诊断[1].给定一个诊断问题D=
⟨ SD,Comps,Obs⟩ .一个诊断被定义为一组组件∆的集合,其中 ∆⋤ Comps,当SD∧Obs∧{AB(c)|c∈Δ}∧ \left\{\neg AB\left(c\right)\right|c\in Comps-\Delta \}\nvDash\perp . 其中
\Delta 是一个极小子集诊断当且仅当不存在当前诊断的一个子集{\Delta' }{\text{⋤}}\Delta 是一个诊断.诊断解的长度称为诊断的势,\Delta 是一个极小势诊断当且仅当不存在另外一个诊断解{\Delta '} 满足∣\Delta ∣>∣\Delta ' ∣.2.2 将诊断问题编码为MaxSAT
许多MBD问题在求解时先被编码为MaxSAT问题[14-15,22],下面本文介绍编码过程.当一个MBD问题被编码为一系列WCNF子句集时,诊断系统中的组件和电路线分别用变量表示,它们的值用文字表示.下面我们分别表示有2个输入的与非门(nand2)、与门(and2)、与或门(nor2)、或门(or2)的公式:
{F}_{\mathrm{n}\mathrm{a}\mathrm{n}\mathrm{d}2\_c}\triangleq Clauses({o}_{\mathrm{n}\mathrm{a}\mathrm{n}\mathrm{d}2\_c}\leftrightarrow \neg ({i}_{\mathrm{n}\mathrm{a}\mathrm{n}\mathrm{d}2\_c1}\wedge {i}_{\mathrm{n}\mathrm{a}\mathrm{n}\mathrm{d}2\_c2}\left)\right) , {F}_{\mathrm{a}\mathrm{n}\mathrm{d}2\_c}\triangleq Clauses({o}_{\mathrm{a}\mathrm{n}\mathrm{d}2\_c}\leftrightarrow ({i}_{\mathrm{a}\mathrm{n}\mathrm{d}2\_c1}\wedge {i}_{\mathrm{a}\mathrm{n}\mathrm{d}2\_c2}\left)\right) , {F}_{\mathrm{n}\mathrm{o}\mathrm{r}2\_c}\triangleq Clauses({o}_{\mathrm{n}\mathrm{o}\mathrm{r}2\_c}\leftrightarrow \neg ({i}_{\mathrm{n}\mathrm{o}\mathrm{r}2\_c1}\vee {i}_{\mathrm{n}\mathrm{o}\mathrm{r}2\_c2}\left)\right) , {F}_{\mathrm{o}\mathrm{r}2\_c}\triangleq Clauses({o}_{\mathrm{o}\mathrm{r}2\_c}\leftrightarrow ({i}_{\mathrm{o}\mathrm{r}2\_c1}\vee {i}_{\mathrm{o}\mathrm{r}2\_c2}\left)\right) . 例如,对于一个NAND组件c而言,
{i}_{\mathrm{nand}\_c1} 和{i}_{\mathrm{nand}\_c2} 分别代表组件c的输入,{o}_{\mathrm{n}\mathrm{a}\mathrm{n}\mathrm{d}\_c} 是组件c的输出.由一组组件组成的系统SD的表示公式为SD\triangleq \mathop \wedge\limits_{c\in Comps}\left(AB\right(c)\vee {F}_{\mathrm{nand}\mathrm{a}\mathrm{n}\mathrm{d}\_c}) , 此处,代表组件c的编码.在一个观测中,观测可以表示为
Obs\triangleq v .v 和一个电路的逻辑值相关,当v=1 代表电路逻辑值为正,当v=0 代表电路逻辑值为负.WCNF中的子句cl的权重用ω(cl)表示,我们分别设置SD,Comps,Obs相关的子句为:
1) 对于SD和Comps中的子句被设置为硬子句,
\mathrm{\omega }\left(cl\right):=num\left(Obs\right)+1 ,其中num\left(Obs\right) 代表观测的数量;2) Obs中的子句被设置为软子句,
\omega \left(cl\right):=1 .在基于SAT的方法中,MBD问题被编码为一组子句,然后通过迭代调用SAT或MaxSAT求解器来计算诊断.通过添加阻塞子句可以避免相同的诊断解被多次计算.利用诊断系统的结构属性是一种可行的方法,这种方法在许多基于SAT的诊断算法中得到了应用[23-24].相应地,诊断中的统治节点和顶层诊断(top-level diagnosis,TLD)也是重要的概念.
定义2. 统治节点[20].给定一个组件G1和G2,如果从G1到电路的输出的所有路径都包含G2,则称G2是G1的统治节点.换句话说,G1是被G2统治的节点.
定义3. 顶层诊断解[20].称
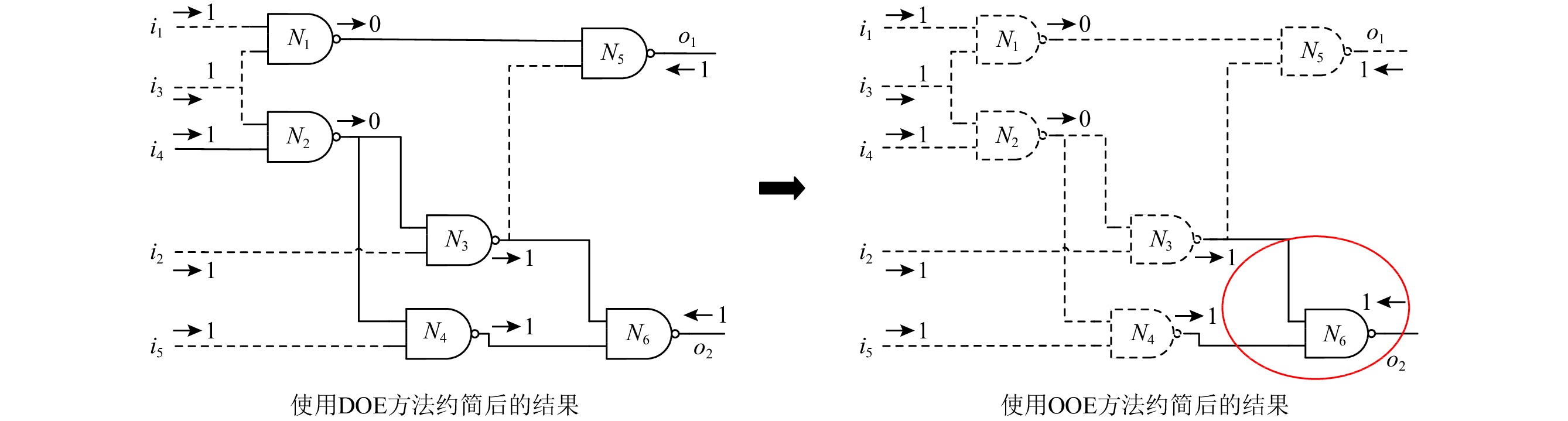
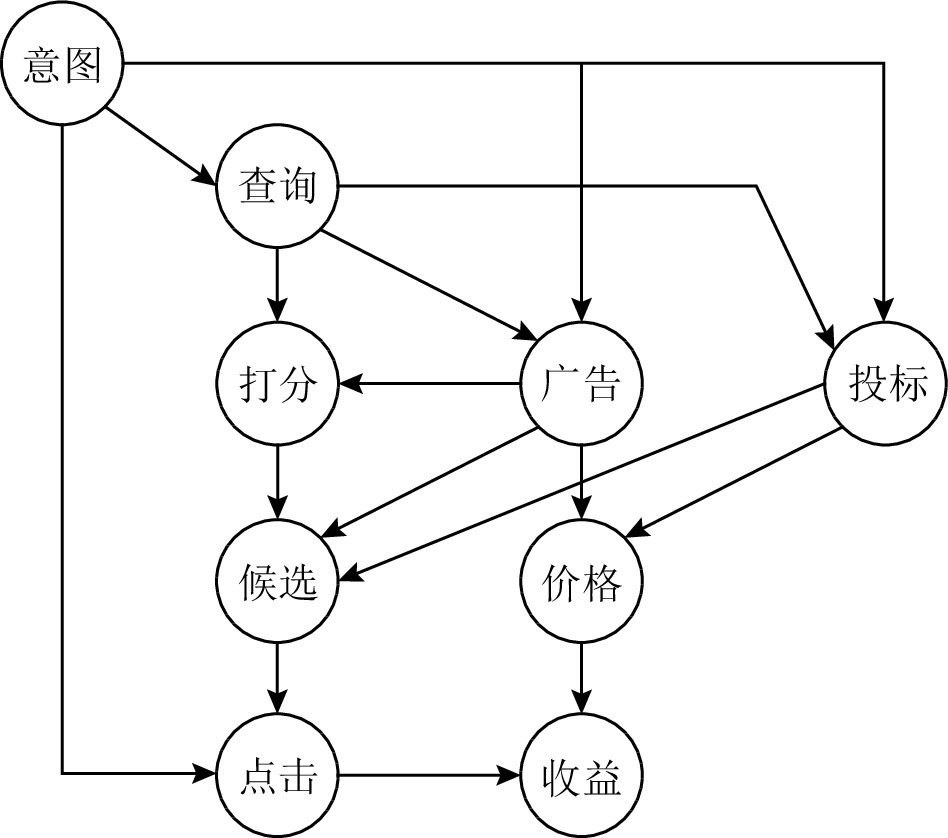
\Delta 为一个顶层诊断解,如果它是一个极小势诊断且不包含任何统治组件.以图1为例,由于N1到达系统输出的路径是唯一的,且包括N5,所以N1被N5统治.假定有观测i1= i2= i3= i5= o1= o2=1, i4=0, N6是一个TLD,因为N6不被任何组件统治.通过将统治组件编码到硬子句中 (即申明这些组件是健康的),就可以计算TLD.
3. 求解基于模型的诊断问题的DOE方法
为了简化MBD到MaxSAT的编码过程,缩减被编码的“门”生成的子句规模.DOE方法利用“门控制关系”,同时计算TLD.除此之外,一些曾在DOE方法中被提出的概念如阻塞连接及骨干组件,将在本节定义中给出解释.
定义4. 骨架节点(backbone node, B-Node)[22].我们称一个组件为骨架节点当且仅当其是一个被统治的组件且它的扇出对于任何一个TLD有固定的值.
考虑图1中组件N1,N1被N5统治,当给定一个观测时,N1的所有输入是固定的,也就是说,i1和i3有固定的值,当求解一个TLD时,N1的扇出就有固定的值,所以N1是一个B-Node.
定义5. 阻塞边(blocked edge,B-Edge)[22].我们称组件的一个扇入边E是一个阻塞边,如果边的值不会对该组件的扇出起作用.
考虑图1中的N2,当给定一个观测Obs={i4=0},N2的输出被确定为1,无论i3的值是什么,因此i3边是一个阻塞边.
定义6. 过滤节点[22].我们称组件B为一个过滤节点,如果它的所有扇出边都是过滤边.
定义7. 过滤边[22].我们称边E为一个过滤边,如果它是一个B-Node或者它的扇出组件是一个过滤节点.
由于N1是一个被统治组件,给定一个观测Obs={i1=1},当z1的值 (z1=0) 被传播后,z3的值将不会对N5的输出起作用.也就是说,N5的输出值是固定的.因此,
\langle N3,N5\rangle 是一个B-Edge,因此,\langle N3,N5\rangle 是一个过滤边.假定\langle N3,N6\rangle 也是一个过滤边,这时N3的所有输入边都是过滤边,那么组件N3是一个过滤节点.具体的DOE方法如算法1所示:算法1. 编码MBD到MaxSAT的DOE方法[22].
输入:SD,Comps,Obs;
输出:编译后的模型.
① repeat
② Dominators
\leftarrow 所有统治节点;③ BackboneComps
\leftarrow 所有骨架组件;④ BlockedConnections
\leftarrow 所有阻塞连接;⑤ if 到达最大迭代次数 then
⑥ break;
⑦ end if
⑧ until NoMoreChanges;
⑨
M\leftarrow 产生MaxSAT模型.4. OOE方法
文献[22]中的实验表明了DOE方法在求解MBD问题上的有效性.在本节中,我们将介绍OOE方法及该方法中为了改进基于MaxSAT的MBD编译过程用到的其他过滤节点和过滤边的概念.
定义8. 基于观测的扇入过滤边.我们称边E为一个基于观测的扇入过滤边,如果它是一个系统的输入或者它是一个统治组件的一个固定输出边.
此处继续讨论观测Obs = {i1 = 1, i2 = 1, i3 = 1, i4 = 1, i5 = 1, o1 = 1, o2 = 1},在第1次迭代中,i1, i2, i3, i4, i5是基于观测的扇入过滤边.在DOE方法过滤了一些节点和边之后,因为N1,N4,N3,N2依次成为统治节点之后,
\langle N1,N5\rangle ,\langle N3,N6\rangle ,\langle N2,N4\rangle ,\langle N4,N6\rangle 变成了基于观察的扇入过滤边.定义9. 基于观测的扇出过滤边.我们称边E为一个基于观测的扇出过滤边,如果它是一个系统的输出.
给定观测Obs={ i1 = 1, i2 = 1, i3 = 1, i4 = 1, i5 = 1, o1 = 1, o2 = 1},o1和o2 均为基于观测的扇出过滤边.
定义10. 基于观测的过滤边.我们称边E为一个基于观测的过滤边,如果它是一个基于观测的扇出过滤边或者它是一个基于观测的扇入过滤边.
初始状态下,系统的输入输出是固定的.因此,任何基于观测的边缘边都是固定的.
定义11. 基于观察的过滤节点.我们称一个组件B为基于观察的过滤节点,如果该组件的扇入和扇出都是固定的,并且扇出值与扇入值在逻辑上一致,或者该组件是一个B-Node.
给定一个观测Obs= { i1 = 1, i2 = 1, i3 = 1, i4 = 1, i5 = 1, o1 = 1, o2 = 1},在DOE编译过程中,因为N1,N2,N3,N4都是B-Node,所以它们都是基于观测的过滤节点.此外,N5也是一个基于观测的过滤节点因为它有一个输入值为0,这与它的输出值1是一致的.
在OOE方法中,被统治的组件编码为硬子句,这种设置与DOE方法中的设置是相同的.
在OOE编译方法的预处理过程中,不仅过滤边和过滤节点不被编码为WCNF,而且基于观测的过滤边和基于观测的过滤节点也不被编码为WCNF.
命题1. 假定ζ为使用DOE方法求解出的一个TLD,那么使用OOE方法可以求解出一个和ζ具有相同势的TLD,ζ ’.
考虑观测Obs = { i1 = 1, i2 = 1, i3 = 1, i4 = 1, i5 = 1, o1 = 1, o2 = 1},我们详细解释DOE方法和OOE方法在进行编码时的约简子句的细节.在第1次迭代中,被统治节点为{N1, N4}.N1被N5统治,N4被N6统治.之后N1的输出值0被传播, N5的输出值是固定的,所以
\langle N3,N5\rangle 是一个B-Edge.在第2次迭代时,因为过滤边\langle N3,N5\rangle ,所以N3被N6统治.随后, N2由N6统治.除此之外,i2,i5被过滤,成为过滤边.这就是所有的DOE方法的约简过程及贡献.剩余的组件{N5, N6}以及边\langle N1,N5\rangle ,\langle N3,N6\rangle ,\langle N4,N6\rangle 均在DOE方法中没有被考虑到.在OOE方法中,为了考虑将更多的节点和边进行约简,基于观测的过滤边和基于观测的过滤节点被提出用于减少生成的WCNF子句的数量.算法2概述了OOE方法的伪代码.
算法2. 编码MBD到MaxSAT的OOE方法.
输入:SD,Comps,Obs;
输出:编译后的WCNF子句.
① repeat
② Dominators
\leftarrow 所有统治节点;③ BackboneComps
\leftarrow 所有骨架组件;④ BlockedConnections
\leftarrow 所有阻塞连接;⑤ if 到达最大迭代次数 then
⑥ break;
⑦ end if
⑧ until NoMoreChanges;
⑨ edgeStack
\leftarrow 所有基于观测的过滤边;⑩ nodeStack
\leftarrow 所有基于观测的过滤节点;⑪ while edgeStack ≠ NULL do
⑫ e
\leftarrow edgeStack中的栈顶元素;⑬ Propagation(e);
⑭ node
\leftarrow nodeStack中的栈顶元素;⑮ Propagation(node);
⑯ if 获得一个新的基于观测的过滤 then
⑰ edgeStack
\leftarrow Push\left(E\right) ;⑱ end if
⑲ if 获得一个新的基于观测的过滤节点
node then
⑳ nodeStack
\leftarrow Push\left(node\right); ㉑ end if
㉒ end while
算法2一直迭代至没有发现新的基于观测的过滤边和过滤节点.其中,算法2的行①~⑧和文献[22]中提出的DOE方法的预处理部分相同,经过DOE预处理后,初步地,我们找到基于观测的过滤边和基于观测的过滤节点.算法2在行⑨~⑩分别将初步得到的基于观测的过滤边和基于观测的过滤节点压入栈中.在行⑪~㉒,算法2找出所有的基于观测的过滤边和基于观测的过滤节点,旨在减少生成的WCNF子句的数量.在行⑬和行⑮中,函数Propagation是一种单元传播技术用于传播行⑫和行⑭中的e和node变量的赋值.
给定观测Obs = { i1 = 1, i2 = 1, i3 = 1, i4 = 1, i5 = 1, o1 = 1, o2 = 1},图2分别为算法1和算法2的编译结果.在图2中,虚线表示过滤边(如图2(a)的
\langle N3, N5\rangle )或基于观测的过滤边(如图2(b)的\langle N1, N5\rangle ).同样地,虚线点表示的组件代表过滤节点或基于观测的过滤节点(如图2(a)的N1).过滤边、过滤节点、基于观测的过滤边和基于观测的过滤节点均将不会被编译成WCNF子句.如图2所示,仅有实线表示的元件和电路线被编码为WCNF子句,虚线表示的元件和电路线不被编码为WCNF子句.在这个例子中,在OOE方法之后,只有1个组件和3条电路线最终被编码为WCNF子句,图2(b)中用椭圆表示.5. 实验结果
在本节中,我们将在MBD中提出的预处理方法与目前最好的预处理方法DOE[22]及不用预处理过程的编码方法BE进行了对比.在编码为MaxSAT问题后求解诊断问题时,我们选择了一种MaxSAT求解器——UwrMaxSAT[19]进行求解, UwrMaxSAT在2020年MaxSAT评估中的加权组中表现最好.实验分别在ISCAS85和ITC99这2组测试实例上执行,这2组测试实例均在文献[22]中使用.其中,第1组测试实例包含9998个测试用例,第2个测试实例包含7822个测试用例.本文提出的OOE方法用C++实现并使用G++编译.我们的实验是在Ubuntu 16.04 Linux和Intel Xeon E5-1607@3.00 GHz, 16 GB RAM上进行.
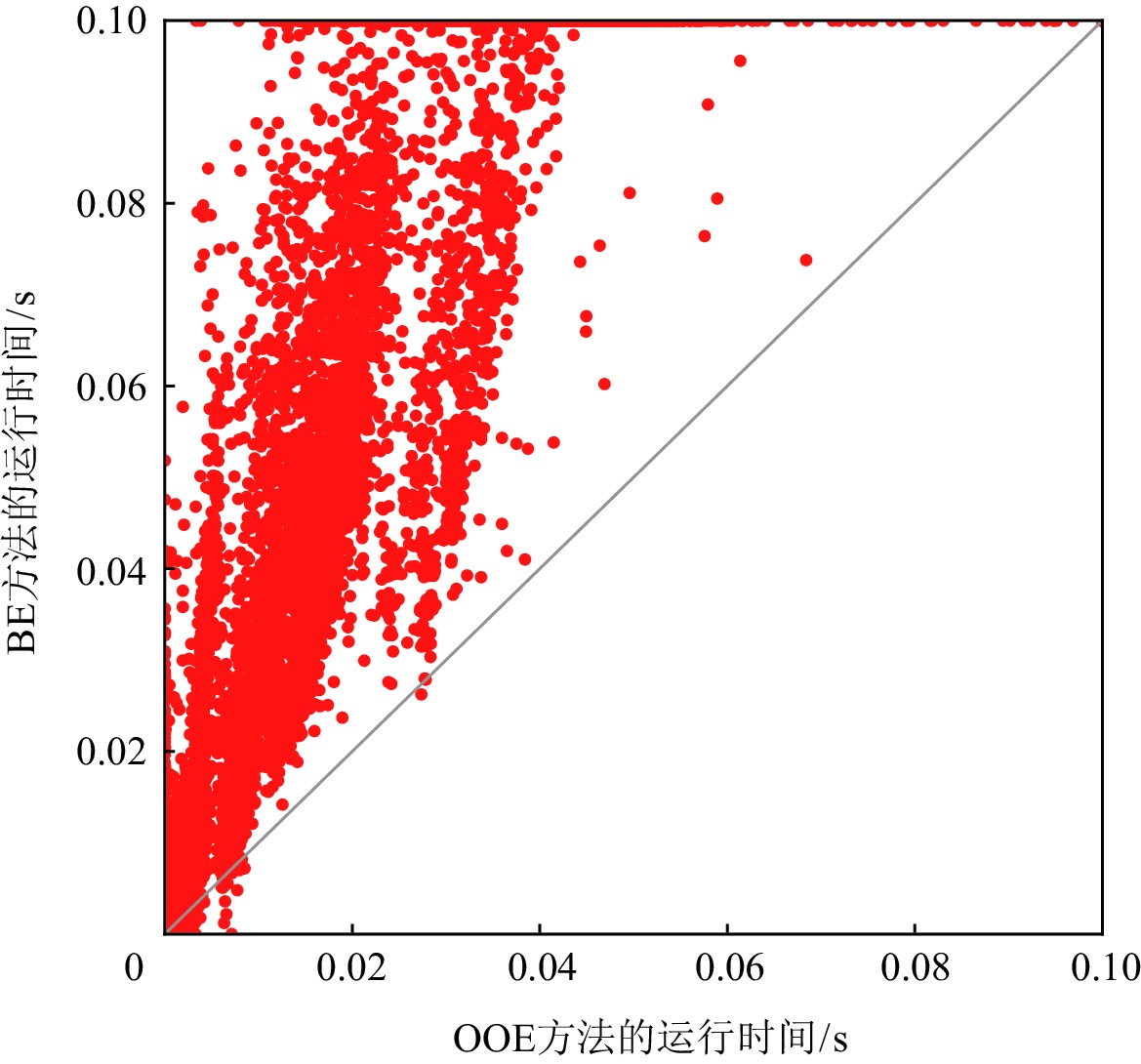
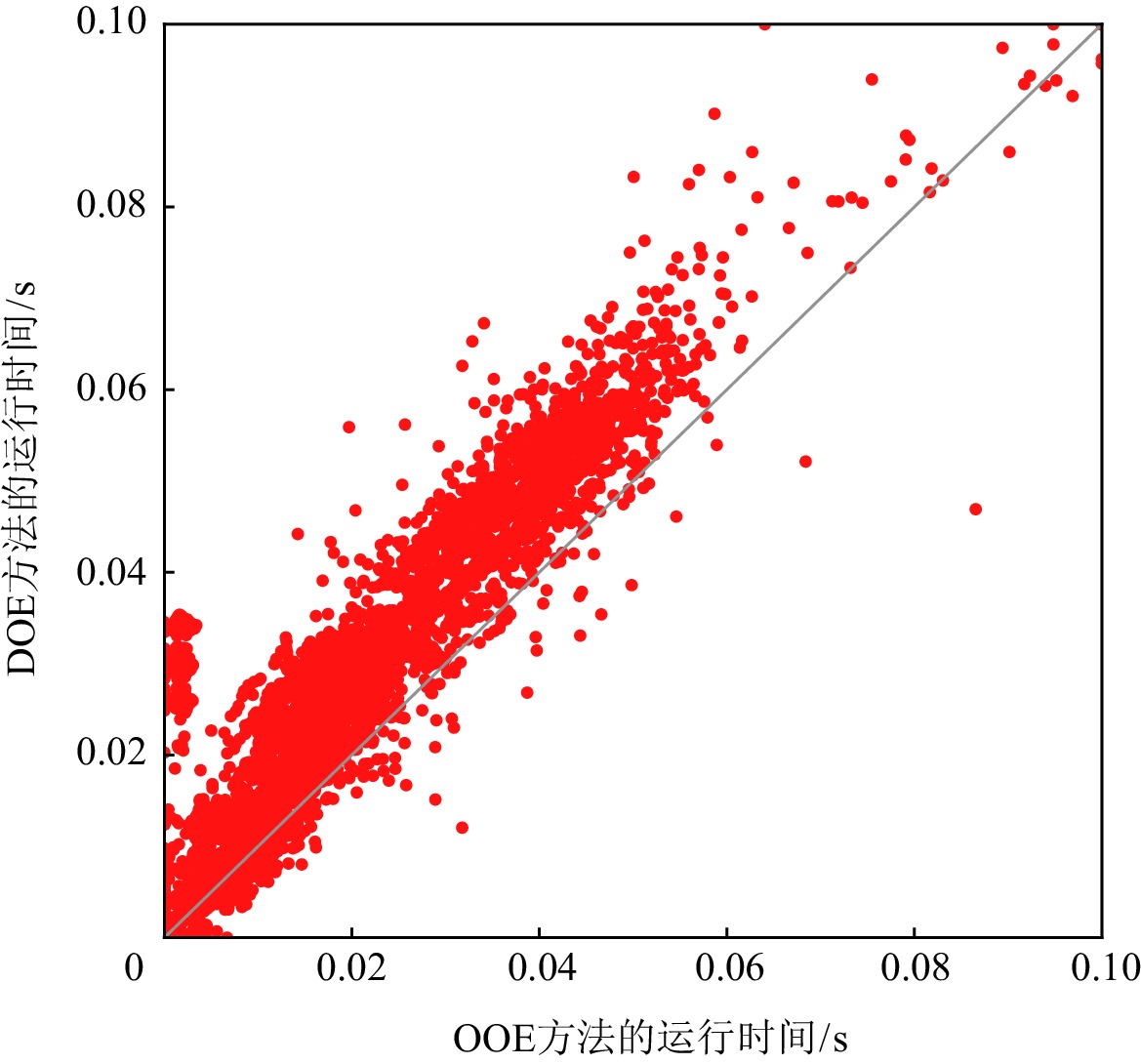
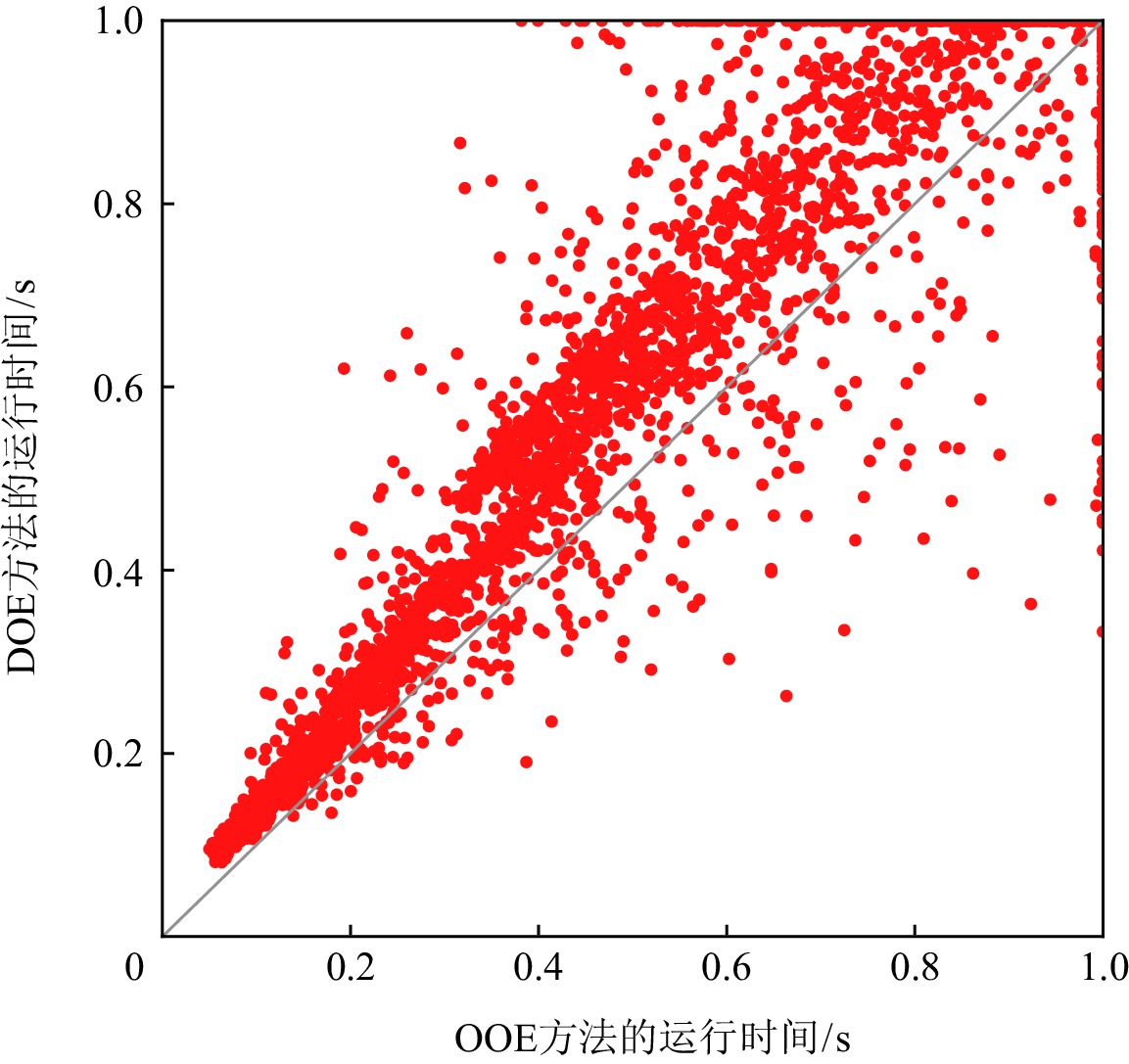
图3和图4分别给出OOE方法与BE方法和DOE方法在求解ISCAS85实例时,MaxSAT求解器求得一个诊断解的运行时间.在实验中,我们设置MaxSAT求解的时间上限为0.1 s.如图3和图4所示,对于大多数测试实例,OOE和DOE方法可以在0.1 s内通过MaxSAT求解器返回诊断结果.用BE方法求解时,有1431个测试实例不能在时间限制内得到一个诊断解;但是对于OOE和DOE方法,只有350个实例不能在0.1 s内得到一个诊断解.此外,如图4中所示,对于大多数测试实例,OOE方法要明显优于DOE方法.
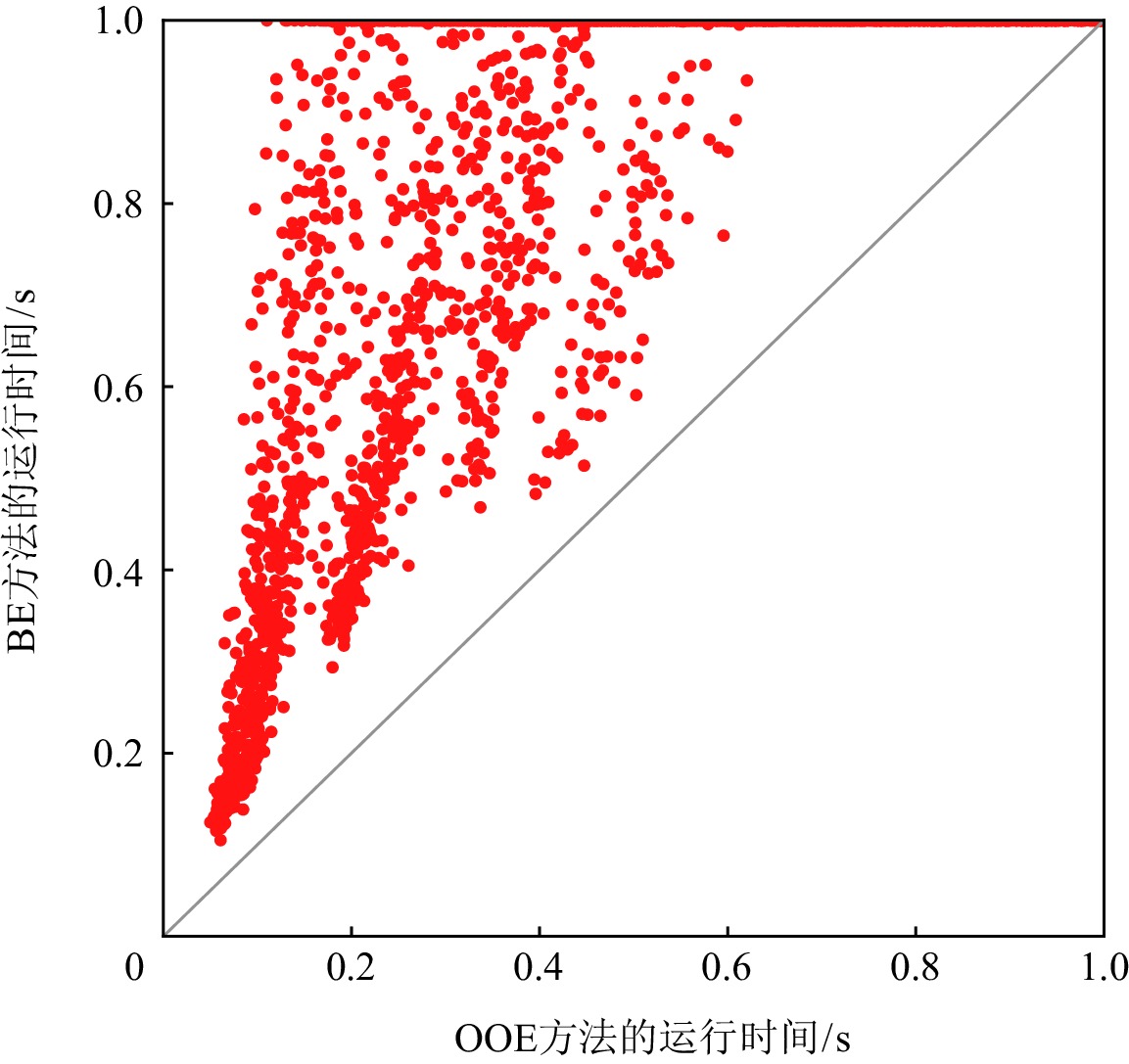
图5和图6分别显示了在ITC99实例上OOE方法与BE及DOE方法在求解诊断问题时MaxSAT求解器运行时间方面的比较.我们设置MaxSAT求解器的时间限制为1 s.坐标轴上的点表示在给定时间内无法求解的一些测试实例.使用OOE,DOE,BE方法不能得到一个解的测试实例的个数分别为4939,5197,6669.在求解实例个数上OOE方法明显优于BE和DOE方法,除此之外,在大多数情况下,相比于BE和DOE方法,使用OOE方法能在更短的时间内得到一个诊断解.
在ITC99 实例和ISCAS85实例上的详细实验结果分别如表1和表2所示:
表 1 在ITC99实例上的求解结果Table 1. Solved Results for ITC99 Benchmark电路名称 观测个数 所用时间比竞争
对手短的实例个数所用时间比竞争
对手短的实例个数OOE BE OOE DOE[22] b14 919 433 164 569 2 b15 995 663 188 819 2 b17 1000 946 54 1000 0 b18 1000 884 46 917 2 b19 1000 823 56 833 42 b20 997 596 222 782 0 b21 919 636 166 780 0 b22 992 722 223 932 0 在2组表中,我们分别列出了4组数据.第1列显示电路名称,第2列显示测试实例的数量.第3~6列显示OOE方法求解诊断时所用时间比竞争对手短的实例个数.从表1和表2可以看出,对每一个电路进行诊断问题求解时,OOE方法都是可行的,且求解结果显示,相比于DOE及 BE方法,OOE方法都有明显的优势.特别是在c880电路上,OOE方法在所有1182个测试实例中的实验结果均优于BE方法,有97.8%的实例的实验结果优于DOE方法.
表 2 在ISCAS85 实例上的求解结果Table 2. Solved Results for ISCAS85 Benchmark电路名称 观测个数 所用时间比竞争
对手短的实例个数所用时间比竞争
对手短的实例个数OOE BE OOE DOE[22] c17 63 48 14 56 7 c432 301 280 17 278 23 c499 835 734 96 760 71 c880 1182 1182 0 1157 20 c1355 836 719 113 832 4 c1908 864 664 182 834 12 c2670 1162 1128 34 1158 4 c3540 756 705 51 756 0 c5315 2038 2028 10 2038 0 c6288 404 246 158 398 6 c7552 1557 1536 21 1557 0 6. 总 结
目前,很多基于SAT的MBD方法把MaxSAT编码作为分析MBD问题的一个基本步骤.本文在面向支配者编码的方法研究基础之上,提出一种OOE的面向观测的编码方法,显著减少了MBD编码后子句的数量,进而降低了MaxSAT求解诊断的难度,提高了求解诊断的效率.本文提出了2种方法用于提高OOE的效率.首先,根据诊断系统的输入观测和输出观测对过滤边进行约简.其次,利用基于观测的过滤节点,在编码时对一些组件进行约简,进而不被编码到MBD问题的子句中.实验结果表明,通过找到更多的基于观测的过滤节点和基于观测的过滤边,能有效减少编码后子句集规模,进而提高基于MaxSAT计算诊断解的效率.OOE方法在ISCAS85系统和ITC99系统的基准测试实例上求解诊断是高效的.在未来的研究中,将探索多观测下OOE方法的扩展算法.
作者贡献声明:周慧思负责文章主体撰写和修订,文献资料的分析、整理及文章写作;欧阳丹彤负责确定综述选题,指导和督促完成相关文献资料的收集整理;田新亮负责文献资料的收集以及部分图表数据的绘制;张立明负责提出文章修改意见, 指导文章写作.
-
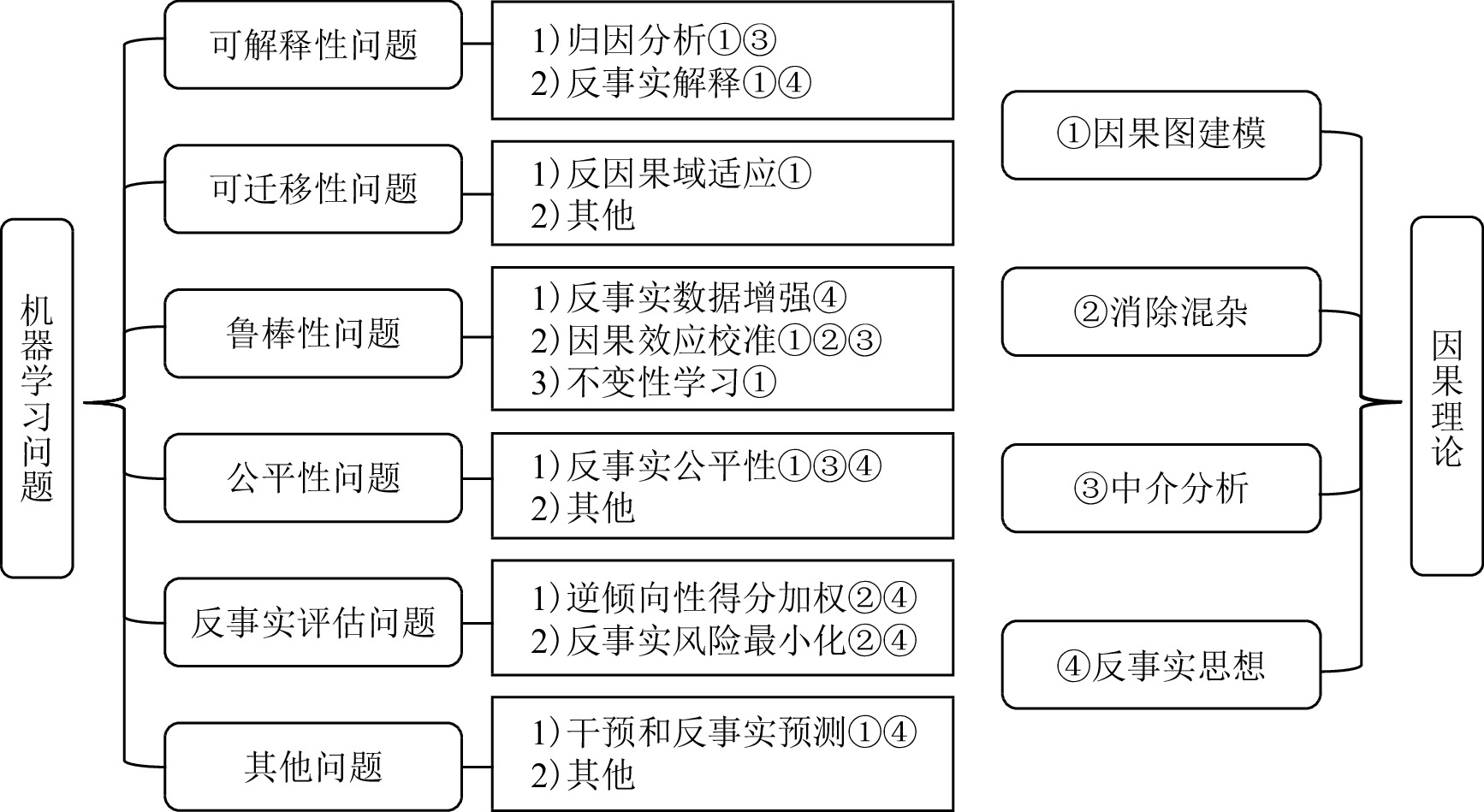
表 1 因果方法在可解释性问题上的应用
Table 1 Application of Causal Methods on Interpretability Problems
表 2 因果方法在可迁移性问题上的应用
Table 2 Application of Causal Methods on Transferability Problems
表 3 因果方法在鲁棒性问题上的应用
Table 3 Application of Causal Methods on Robustness Problems
分类 子类别 典型思路和方法 反事实数据增强 伪相关特征反事实 构造额外训练数据,在保持预测结果不变的前提下微调数据[88-93] 因果特征反事实 构造额外训练数据,更改关键因果特征并修改预测结果[92-95] 因果效应校准 基于后门调整 根据对问题的认识指出混杂因素,对其估计后消除影响[96-99] 基于中介分析 根据对问题的认识指出中介变量,对其估计后消除影响[97,100-102] 不变性学习 稳定学习 将每个特征视为处理变量,通过样本加权消除混杂,识别因果特征[103-107] 不变因果预测 基于多环境训练数据,利用假设检验确定因果特征集合[108-110] 不变风险最小化 基于多环境训练数据,在模型优化目标中添加跨环境不变约束,学习因果特征[111- 113] 表 4 因果方法在公平性问题上的应用
Table 4 Application of Causal Methods on Fairness Problems
-
[1] LeCun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(7553): 436−444
[2] He Kaiming, Zhang Xiangyu, Ren Shaoqing, et al. Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification[C] //Proc of the IEEE Int Conf on Computer Vision. Piscataway, NJ: IEEE, 2015: 1026−1034 [3] Brock A, Donahue J, Simonyan K. Large scale GAN training for high fidelity natural image synthesis [C/OL] //Proc of the 7th Int Conf on Learning Representations. 2019 [2021-11-03]. https://openreview.net/pdf?id=B1xsqj09Fm
[4] Brown T B, Mann B, Ryder N, et al. Language models are few-shot learners[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 1877−1901
[5] Silver D, Huang A, Maddison C J, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature, 2016, 529(7587): 484−489
[6] Senior A W, Evans R, Jumper J, et al. Improved protein structure prediction using potentials from deep learning[J]. Nature, 2020, 577(7792): 706−710
[7] Gunning D, Aha D. DARPA’s explainable artificial intelligence (XAI) program[J]. AI Magazine, 2019, 40(2): 44−58
[8] Szegedy C, Zaremba W, Sutskever I, et al. Intriguing properties of neural networks[C/OL] //Proc of the 2nd Int Conf on Learning Representations. 2014 [2021-11-03]. https://arxiv.org/abs/1312.6199
[9] Barocas S, Hardt M, Narayanan A. Fairness in machine learning [EB/OL]. 2017 [2021-11-13]. https://fairmlbook.org/pdf/fairmlbook.pdf
[10] Pearl J, Mackenzie D. The Book of Why: The New Science of Cause and Effect[M]. New York: Basic Books, 2018
[11] Pearl J. Theoretical impediments to machine learning with seven sparks from the causal revolution[J]. arXiv preprint, arXiv: 1801.04016, 2018
[12] 苗旺, 刘春辰, 耿直. 因果推断的统计方法[J]. 中国科学: 数学, 2018, 48(12): 1753-1778 Miao Wang, Liu Chunchen, Geng Zhi. Statistical approaches for causal inference [J]. SCIENTIA SINICA Mathematica, 2018, 48(12): 1753-1778 (in Chinese)
[13] Guo Ruocheng, Cheng Lu, Li Jundong, et al. A survey of learning causality with data: Problems and methods[J]. ACM Computing Surveys, 2020, 53(4): 1−37
[14] Kuang Kun, Li Lian, Geng Zhi, et al. Causal inference [J]. Engineering, 2020, 6(3): 253−263
[15] Schölkopf B. Causality for machine learning [J]. arXiv preprint, arXiv: 1911.10500, 2019
[16] Schölkopf B, Locatello F, Bauer S, et al. Toward causal representation learning[J]. Proceedings of the IEEE, 2021, 109(5): 612−634
[17] Splawa-Neyman J, Dabrowska D M, Speed T P. On the application of probability theory to agricultural experiments. Essay on principles. Section 9[J]. Statistical Science, 1990, 5(4): 465−472
[18] Rubin D B. Estimating causal effects of treatments in randomized and nonrandomized studies[J]. Journal of Educational Psychology, 1974, 66(5): 688−701
[19] Pearl J. Causality[M]. Cambridge, UK: Cambridge University Press, 2009
[20] Granger C W J. Investigating causal relations by econometric models and cross-spectral methods[J]. Econometrica, 1969, 37(3): 424−438
[21] Rubin D B. Randomization analysis of experimental data: The Fisher randomization test comment[J]. Journal of the American Statistical Association, 1980, 75(371): 591−593
[22] Rosenbaum P R, Rubin D B. The central role of the propensity score in observational studies for causal effects[J]. Biometrika, 1983, 70(1): 41−55
[23] Hirano K, Imbens G W, Ridder G. Efficient estimation of average treatment effects using the estimated propensity score[J]. Econometrica, 2003, 71(4): 1161−1189
[24] Robins J M, Rotnitzky A, Zhao Lueping. Estimation of regression coefficients when some regressors are not always observed[J]. Journal of the American Statistical Association, 1994, 89(427): 846−866
[25] Dudík M, Langford J, Li Lihong. Doubly robust policy evaluation and learning[C] //Proc of the 28th Int Conf on Machine Learning. Madison, WI: Omnipress, 2011: 1097−1104
[26] Kuang Kun, Cui Peng, Li Bo, et al. Estimating treatment effect in the wild via differentiated confounder balancing[C] //Proc of the 23rd ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2017: 265−274
[27] Imbens G W, Rubin D B. Causal Inference in Statistics, Social, and Biomedical Sciences[M]. Cambridge, UK: Cambridge University Press, 2015
[28] Yao Liuyi, Chu Zhixuan, Li Sheng, et al. A survey on causal inference [J]. arXiv preprint, arXiv: 2002.02770, 2020
[29] Pearl J. Causal diagrams for empirical research[J]. Biometrika, 1995, 82(4): 669−688
[30] Spirtes P, Glymour C. An algorithm for fast recovery of sparse causal graphs[J]. Social Science Computer Review, 1991, 9(1): 62−72
[31] Verma T, Pearl J. Equivalence and synthesis of causal models[C] //Proc of the 6th Annual Conf on Uncertainty in Artificial Intelligence. Amsterdam: Elsevier, 1990: 255−270
[32] Spirtes P, Glymour C N, Scheines R, et al. Causation, Prediction, and Search[M]. Cambridge, MA: MIT Press, 2000
[33] Schwarz G. Estimating the dimension of a model[J]. The Annals of Statistics, 1978, 6(2): 461−464
[34] Chickering D M. Optimal structure identification with greedy search[J]. Journal of Machine Learning Research, 2002, 3(Nov): 507−554 [35] Shimizu S, Hoyer P O, Hyvärinen A, et al. A linear non-Gaussian acyclic model for causal discovery[J]. Journal of Machine Learning Research, 2006, 7(10): 2003−2030
[36] Zhang Kun, Hyvärinen A. On the identifiability of the post-nonlinear causal model[C] //Proc of the 25th Conf on Uncertainty in Artificial Intelligence. Arlington, VA: AUAI Press, 2009: 647−655
[37] Pearl J. Direct and indirect effects[C] //Proc of the 17th Conf on Uncertainty in Artificial Intelligence. San Francisco, CA: Morgan Kaufmann Publishers Inc, 2001: 411−420
[38] VanderWeele T. Explanation in Causal Inference: Methods for Mediation and Interaction[M]. Oxford, UK: Oxford University Press, 2015
[39] 陈珂锐,孟小峰. 机器学习的可解释性[J]. 计算机研究与发展,2020,57(9):1971−1986 doi: 10.7544/issn1000-1239.2020.20190456 Chen Kerui, Meng Xiaofeng. Interpretation and understanding in machine learning[J]. Journal of Computer Research and Development, 2020, 57(9): 1971−1986 (in Chinese) doi: 10.7544/issn1000-1239.2020.20190456
[40] Ribeiro M T, Singh S, Guestrin C. “Why should I trust you?” Explaining the predictions of any classifier[C] //Proc of the 22nd ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2016: 1135−1144
[41] Selvaraju R R, Cogswell M, Das A, et al. Grad-CAM: Visual explanations from deep networks via gradient-based localization[C] //Proc of the IEEE Int Conf on Computer Vision. Piscataway, NJ: IEEE, 2017: 618-626 [42] Sundararajan M, Taly A, Yan Qiqi. Axiomatic attribution for deep networks[C] //Proc of the 34th Int Conf on Machine Learning. Cambridge, MA: JMLR, 2017: 3319−3328
[43] Lundberg S M, Lee S I. A unified approach to interpreting model predictions[C] //Proc of the 31st Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2017: 4765−4774
[44] Alvarez-Melis D, Jaakkola T. A causal framework for explaining the predictions of black-box sequence-to-sequence models[C] //Proc of the 2017 Conf on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2017: 412−421 [45] Schwab P, Karlen W. CXPlain: Causal explanations for model interpretation under uncertainty[C] //Proc of the 33rd Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2019: 10220−10230
[46] Chattopadhyay A, Manupriya P, Sarkar A, et al. Neural network attributions: A causal perspective[C] //Proc of the 36th Int Conf on Machine Learning. Cambridge, MA: JMLR, 2019: 981−990
[47] Frye C, Rowat C, Feige I. Asymmetric Shapley values: Incorporating causal knowledge into model-agnostic explainability[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 1229−1239
[48] Heskes T, Sijben E, Bucur I G, et al. Causal Shapley values: Exploiting causal knowledge to explain individual predictions of complex models [C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 4778−4789
[49] Goyal Y, Wu Ziyan, Ernst J, et al. Counterfactual visual explanations[C] //Proc of the 36th Int Conf on Machine Learning. Cambridge, MA: JMLR, 2019: 2376−2384
[50] Wang Pei, Vasconcelos N. SCOUT: Self-aware discriminant counterfactual explanations[C] //Proc of the 33rd IEEE/CVF Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2020: 8981−8990
[51] Hendricks L A, Hu Ronghang, Darrell T, et al. Generating counterfactual explanations with natural language[J]. arXiv preprint, arXiv: 1806.09809, 2018
[52] Chang Chunhao, Creager E, Goldenberg A, et al. Explaining image classifiers by counterfactual generation[C/OL] //Proc of the 7th Int Conf on Learning Representations, 2019 [2021-11-03]. https://openreview.net/pdf?id=B1MXz20cYQ
[53] Kanehira A, Takemoto K, Inayoshi S, et al. Multimodal explanations by predicting counterfactuality in videos[C] //Proc of the 32nd IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2019: 8594−8602
[54] Akula A R, Wang Shuai, Zhu Songchun. CoCoX: Generating conceptual and counterfactual explanations via fault-lines[C] //Proc of the 34th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2020: 2594−2601
[55] Madumal P, Miller T, Sonenberg L, et al. Explainable reinforcement learning through a causal lens[C] //Proc of the 34th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2020: 2493−2500
[56] Mothilal R K, Sharma A, Tan C. Explaining machine learning classifiers through diverse counterfactual explanations[C] //Proc of the 2020 Conf on Fairness, Accountability, and Transparency. New York: ACM, 2020: 607−617 [57] Albini E, Rago A, Baroni P, et al. Relation-based counterfactual explanations for Bayesian network classifiers[C] //Proc of the 29th Int Joint Conf on Artificial Intelligence, Red Hook, NY: Curran Associates Inc, 2020: 451−457
[58] Kenny E M, Keane M T. On generating plausible counterfactual and semi-factual explanations for deep learning[C] //Proc of the 35th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2021: 11575−11585
[59] Abrate C, Bonchi F. Counterfactual graphs for explainable classification of brain networks[J]. arXiv preprint, arXiv: 2106.08640, 2021
[60] Yang Fan, Alva S S, Chen Jiahao, et al. Model-based counterfactual synthesizer for interpretation[J]. arXiv preprint, arXiv: 2106.08971, 2021
[61] Parmentier A, Vidal T. Optimal counterfactual explanations in tree ensembles[J]. arXiv preprint, arXiv: 2106.06631, 2021
[62] Besserve M, Mehrjou A, Sun R, et al. Counterfactuals uncover the modular structure of deep generative models[C/OL] //Proc of the 8th Int Conf on Learning Representations. 2020 [2021-11-03]. https://openreview.net/pdf?id=SJxDDpEKvH
[63] Kanamori K, Takagi T, Kobayashi K, et al. DACE: Distribution-aware counterfactual explanation by mixed-integer linear optimization[C] //Proc of the 19th Int Joint Conf on Artificial Intelligence. Red Hook, NY: Curran Associates Inc, 2020: 2855−2862
[64] Kanamori K, Takagi T, Kobayashi K, et al. Ordered counterfactual explanation by mixed-integer linear optimization[C] //Proc of the 35th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2021: 11564−11574
[65] Tsirtsis S, Gomez-Rodriguez M. Decisions, counterfactual explanations and strategic behavior[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 16749−16760
[66] Karimi A H, von Kügelgen B J, Schölkopf B, et al. Algorithmic recourse under imperfect causal knowledge: A probabilistic approach[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 265−277
[67] Rojas-Carulla M, Schölkopf B, Turner R, et al. Invariant models for causal transfer learning[J]. The Journal of Machine Learning Research, 2018, 19(1): 1309−1342
[68] Guo Jiaxian, Gong Mingming, Liu Tongliang, et al. LTF: A label transformation framework for correcting target shift[C] //Proc of the 37th Int Conf on Machine Learning. Cambridge, MA: JMLR, 2020: 3843−3853
[69] Cai Ruichu, Li Zijian, Wei Pengfei, et al. Learning disentangled semantic representation for domain adaptation[C] //Proc of the 28th Int Joint Conf on Artificial Intelligence. Red Hook, NY: Curran Associates Inc, 2019: 2060−2066
[70] Zhang Kun, Schölkopf B, Muandet K, et al. Domain adaptation under target and conditional shift[C] //Proc of the 30th Int Conf on Machine Learning. Cambridge, MA: JMLR, 2013: 819−827
[71] Gong Mingming, Zhang Kun, Liu Tongliang, et al. Domain adaptation with conditional transferable components[C] //Proc of the 33rd Int Conf on Machine Learning. Cambridge, MA: JMLR, 2016: 2839−2848
[72] Teshima T, Sato I, Sugiyama M. Few-shot domain adaptation by causal mechanism transfer[C] //Proc of the 37th Int Conf on Machine Learning. Cambridge, MA: JMLR, 2020: 9458−9469
[73] Edmonds M, Ma Xiaojian, Qi Siyuan, et al. Theory-based causal transfer: Integrating instance-level induction and abstract-level structure learning[C] //Proc of the 34th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2020: 1283−1291
[74] Etesami J, Geiger P. Causal transfer for imitation learning and decision making under sensor-shift[C] //Proc of the 34th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2020: 10118−10125
[75] Yue Zhongqi, Zhang Hanwang, Sun Qianru, et al. Interventional few-shot learning[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 2734−2746
[76] Zhang Kun, Gong Mingming, Stojanov P, et al. Domain adaptation as a problem of inference on graphical models[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 4965−4976
[77] Schölkopf B, Janzing D, Peters J, et al. On causal and anticausal learning[C] //Proc of the 29th Int Conf on Machine Learning. Madison, WI: Omnipress, 2012: 459−466
[78] Zhang Kun, Gong Mingming, Schölkopf B. Multi-source domain adaptation: A causal view[C] //Proc of the 29th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2015: 3150−3157
[79] Bagnell J A. Robust supervised learning[C] //Proc of the 20th National Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2005: 714−719
[80] Hu Weihua, Niu Gang, Sato I, et al. Does distributionally robust supervised learning give robust classifiers?[C] //Proc of the 35th Int Conf on Machine Learning. Cambridge, MA: JMLR, 2018: 2029−2037
[81] Rahimian H, Mehrotra S. Distributionally robust optimization: A review[J]. arXiv preprint, arXiv: 1908.05659, 2019
[82] Goodfellow I J, Shlens J, Szegedy C. Explaining and harnessing adversarial examples[C/OL] //Proc of the 5th Int Conf on Learning Representations. 2017 [2021-11-14]. https://openreview.net/pdf?id=B1xsqj09Fm
[83] Xu Han, Ma Yao, Liu Haochen, et al. Adversarial attacks and defenses in images, graphs and text: A review[J]. International Journal of Automation and Computing, 2020, 17(2): 151−178
[84] Gururangan S, Swayamdipta S, Levy O, et al. Annotation artifacts in natural language inference data[C] //Proc of the 16th Conf of the North American Chapter of the ACL: Human Language Technologies, Vol 2. Stroudsburg, PA: ACL, 2018: 107−112
[85] Zhang Guanhua, Bai Bing, Liang Jian, et al. Selection bias explorations and debias methods for natural language sentence matching datasets[C] //Proc of the 57th Annual Meeting of the Association for Computational Linguistics. Stroudsburg, PA: ACL, 2019: 4418−4429
[86] Clark C, Yatskar M, Zettlemoyer L. Don’t take the easy way out: Ensemble based methods for avoiding known dataset biases[C] //Proc of the 2019 Conf on Empirical Methods in Natural Language Processing and the 9th Int Joint Conf on Natural Language Processing (EMNLP-IJCNLP). Stroudsburg, PA: ACL, 2019: 4060−4073 [87] Cadene R, Dancette C, Cord M, et al. Rubi: Reducing unimodal biases for visual question answering[C] //Proc of the 33rd Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2019: 841−852
[88] Lu Kaiji, Mardziel P, Wu Fangjing, et al. Gender bias in neural natural language processing[G] //LNCS 12300: Logic, Language, and Security: Essays Dedicated to Andre Scedrov on the Occasion of His 65th Birthday. Berlin: Springer, 2020: 189−202 [89] Maudslay R H, Gonen H, Cotterell R, et al. It’s all in the name: Mitigating gender bias with name-based counterfactual data substitution[C] //Proc of the 2019 Conf on Empirical Methods in Natural Language Processing and the 9th Int Joint Conf on Natural Language Processing (EMNLP-IJCNLP). Stroudsburg, PA: ACL, 2019: 5270−5278 [90] Zmigrod R, Mielke S J, Wallach H, et al. Counterfactual data augmentation for mitigating gender stereotypes in languages with rich morphology[C] //Proc of the 57th Annual Meeting of the ACL. Stroudsburg, PA: ACL, 2019: 1651−1661
[91] Kaushik D, Hovy E, Lipton Z. Learning the difference that makes a difference with counterfactually-augmented data[C/OL] //Proc of the 8th Int Conf on Learning Representations. 2020 [2021-11-14]. https://openreview.net/pdf?id=Sklgs0NFvr
[92] Agarwal V, Shetty R, Fritz M. Towards causal VQA: Revealing and reducing spurious correlations by invariant and covariant semantic editing[C] //Proc of the 33rd IEEE/CVF Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2020: 9690−9698
[93] Chang Chunhao, Adam G A, Goldenberg A. Towards robust classification model by counterfactual and invariant data generation[C] //Proc of the 34th IEEE/CVF Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2021: 15212−15221
[94] Wang Zhao, Culotta A. Robustness to spurious correlations in text classification via automatically generated counterfactuals[C] //Proc of the 35th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2021: 14024−14031
[95] Chen Long, Yan Xin, Xiao Jun, et al. Counterfactual samples synthesizing for robust visual question answering[C] //Proc of the 33rd IEEE/CVF Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2020: 10800−10809
[96] Wu Yiquan, Kuang Kun, Zhang Yating, et al. De-biased court’s view generation with causality[C] //Proc of the 2020 Conf on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2020: 763−780 [97] Qi Jia, Niu Yulei, Huang Jianqiang, et al. Two causal principles for improving visual dialog[C] //Proc of the 33rd IEEE/CVF Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2020: 10860−10869
[98] Wang Tan, Huang Jiangqiang, Zhang Hanwang, et al. Visual commonsense R-CNN[C] //Proc of the 33rd IEEE/CVF Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2020: 10760−10770
[99] Zhang Dong, Zhang Hanwang, Tang Jinhui, et al. Causal intervention for weakly-supervised semantic segmentation[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 655−666
[100] Tang Kaihua, Niu Yulei, Huang Jianqiang, et al. Unbiased scene graph generation from biased training[C] //Proc of the 33rd IEEE/CVF Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2020: 3716−3725
[101] Tang Kaihua, Huang Jianqiang, Zhang Hanwang. Long-tailed classification by keeping the good and removing the bad momentum causal effect[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 1513−1524
[102] Niu Yulei, Tang Kaihua, Zhang Hanwang, et al. Counterfactual VQA: A cause-effect look at language bias[C] //Proc of the 34th IEEE/CVF Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2021: 12700−12710
[103] Kuang Kun, Cui Peng, Athey S, et al. Stable prediction across unknown environments[C] //Proc of the 24th ACM SIGKDD Int Conf on Knowledge Discovery & Data Mining. New York: ACM, 2018: 1617−1626
[104] Shen Zheyan, Cui Peng, Kuang Kun, et al. Causally regularized learning with agnostic data selection bias[C] //Proc of the 26th ACM Int Conf on Multimedia. New York: ACM, 2018: 411−419
[105] Kuang Kun, Xiong Ruoxuan, Cui Peng, et al. Stable prediction with model misspecification and agnostic distribution shift[C] //Proc of the 34th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2020: 4485−4492
[106] Shen Zheyan, Cui Peng, Zhang Tong, et al. Stable learning via sample reweighting[C] //Proc of the 34th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2020: 5692−5699
[107] Zhang Xingxuan, Cui Peng, Xu Renzhe, et al. Deep stable learning for out-of-distribution generalization[J]. arXiv preprint, arXiv: 2104.07876, 2021
[108] Peters J, Bühlmann P, Meinshausen N. Causal inference by using invariant prediction: Identification and confidence intervals[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2016, 78(5): 947−1012
[109] Christina H D, Nicolai M, Jonas P. Invariant causal prediction for nonlinear models[J/OL]. Journal of Causal Inference, 2018, 6(2): 20170016 [2021-11-15]. https://www.degruyter.com/document/doi/10.1515/jci-2017-0016/pdf
[110] Pfister N, Bühlmann P, Peters J. Invariant causal prediction for sequential data[J]. Journal of the American Statistical Association, 2019, 114(527): 1264−1276
[111] Arjovsky M, Bottou L, Gulrajani I, et al. Invariant risk minimization[J]. arXiv preprint, arXiv: 1907.02893, 2019
[112] Zhang A, Lyle C, Sodhani S, et al. Invariant causal prediction for block MDPs[C] //Proc of the 37th Int Conf on Machine Learning. Cambridge, MA: JMLR, 2020: 11214−11224
[113] Creager E, Jacobsen J H, Zemel R. Environment inference for invariant learning[C] //Proc of the 38th Int Conf on Machine Learning. Cambridge, MA: JMLR, 2021: 2189−2200
[114] Kaushik D, Setlur A, Hovy E H, et al. Explaining the efficacy of counterfactually augmented data[C/OL] //Proc of the 9th Int Conf on Learning Representations. 2021 [2021-11-14]. https://openreview.net/pdf?id=HHiiQKWsOcV
[115] Abbasnejad E, Teney D, Parvaneh A, et al. Counterfactual vision and language learning[C] //Proc of the 33rd IEEE/CVF Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2020: 10044−10054
[116] Liang Zujie, Jiang Weitao, Hu Haifeng, et al. Learning to contrast the counterfactual samples for robust visual question answering[C] //Proc of the 2020 Conf on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2020: 3285−3292 [117] Teney D, Abbasnedjad E, van den Hengel A. Learning what makes a difference from counterfactual examples and gradient supervision[C] //Proc of the 16th European Conf on Computer Vision. Berlin: Springer, 2020: 580−599
[118] Fu T J, Wang X E, Peterson M F, et al. Counterfactual vision-and-language navigation via adversarial path sampler[C] //Proc of the 16th European Conf on Computer Vision. Berlin: Springer, 2020: 71−86
[119] Parvaneh A, Abbasnejad E, Teney D, et al. Counterfactual vision-and-language navigation: Unravelling the unseen[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 5296−5307
[120] Sauer A, Geiger A. Counterfactual generative networks[C/OL] //Proc of the 9th Int Conf on Learning Representations. 2021 [2021-11-14]. https://openreview.net/pdf?id=BXewfAYMmJw
[121] Mao Chengzhi, Cha A, Gupta A, et al. Generative interventions for causal learning[C] //Proc of the 34th IEEE/CVF Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2021: 3947−3956
[122] Zeng Xiangji, Li Yunliang, Zhai Yuchen, et al. Counterfactual generator: A weakly-supervised method for named entity recognition[C] //Proc of the 2020 Conf on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2020: 7270−7280 [123] Fu T J, Wang Xin, Grafton S, et al. Iterative language-based image editing via self-supervised counterfactual reasoning[C] //Proc of the 2020 Conf on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2020: 4413−4422 [124] Pitis S, Creager E, Garg A. Counterfactual data augmentation using locally factored dynamics[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 3976−3990
[125] Zhang Junzhe, Kumor D, Bareinboim E. Causal imitation learning with unobserved confounders[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 12263−12274
[126] Coston A, Kennedy E, Chouldechova A. Counterfactual predictions under runtime confounding[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 4150−4162
[127] Atzmon Y, Kreuk F, Shalit U, et al. A causal view of compositional zero-shot recognition[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 1462−1473
[128] Yang Zekun, Feng Juan. A causal inference method for reducing gender bias in word embedding relations[C] //Proc of the 34th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2020: 9434−9441
[129] Schölkopf B, Hogg D W, Wang Dun, et al. Modeling confounding by half-sibling regression[J]. Proceedings of the National Academy of Sciences, 2016, 113(27): 7391−7398 doi: 10.1073/pnas.1511656113
[130] Shin S, Song K, Jang J H, et al. Neutralizing gender bias in word embedding with latent disentanglement and counterfactual generation[C] //Proc of the 2020 Conf on Empirical Methods in Natural Language Processing: Findings. Stroudsburg, PA: ACL, 2020: 3126−3140 [131] Yang Zekun, Liu Tianlin. Causally denoise word embeddings using half-sibling regression[C] //Proc of the 34th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2020: 9426−9433
[132] Yang Xu, Zhang Hanwang, Qi Guojin, et al. Causal attention for vision-language tasks[C] //Proc of the 34th IEEE/CVF Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2021: 9847−9857
[133] Tople S, Sharma A, Nori A. Alleviating privacy attacks via causal learning[C] //Proc of the 37th Int Conf on Machine Learning. Cambridge, MA: JMLR, 2020: 9537−9547
[134] Zhang Cheng, Zhang Kun, Li Yingzhen. A causal view on robustness of neural networks[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 289−301
[135] Sun Xinwei, Wu Botong, Liu Chang, et al. Latent causal invariant model[J]. arXiv preprint, arXiv: 2011.02203, 2020
[136] Mitrovic J, McWilliams B, Walker J C, et al. Representation learning via invariant causal mechanisms[C/OL] //Proc of the 9th Int Conf on Learning Representations. 2021 [2021-11-14]. https://openreview.net/pdf?id=9p2ekP904Rs
[137] Mahajan D, Tople S, Sharma A. Domain generalization using causal matching[J]. arXiv preprint, arXiv: 2006.07500, 2020
[138] Zhang Weijia, Liu Lin, Li Jiuyong. Robust multi-instance learning with stable instances[C] //Proc of the 24th European Conf on Artificial Intelligence. Ohmsha: IOS, 2020: 1682−1689
[139] Kleinberg J, Mullainathan S, Raghavan M. Inherent trade-offs in the fair determination of risk scores[J]. arXiv preprint, arXiv: 1609.05807, 2016
[140] Grgic-Hlaca N, Zafar M B, Gummadi K P, et al. The case for process fairness in learning: Feature selection for fair decision making[C/OL] //Proc of Symp on Machine Learning and the Law at the 30th Conf on Neural Information Processing Systems. 2016 [2021-11-17]. http: //www.mlandthelaw.org/papers/grgic.pdf [141] Dwork C, Hardt M, Pitassi T, et al. Fairness through awareness[C] //Proc of the 3rd Innovations in Theoretical Computer Science Conf. New York: ACM, 2012: 214−226
[142] Calders T, Kamiran F, Pechenizkiy M. Building classifiers with independency constraints[C] //Proc of the 9th IEEE Int Conf on Data Mining Workshops. Piscataway, NJ: IEEE, 2009: 13−18
[143] Hardt M, Price E, Srebro N. Equality of opportunity in supervised learning[C] //Proc of the 30th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2016: 3315−3323
[144] Xu Renzhe, Cui Peng, Kuang Kun, et al. Algorithmic decision making with conditional fairness[C] //Proc of the 26th ACM SIGKDD Int Conf on Knowledge Discovery & Data Mining. New York: ACM, 2020: 2125−2135
[145] Kusner M J, Loftus J, Russell C, et al. Counterfactual fairness[C] //Proc of the 31st Int Conf on Neural Information Processing Systems. New York: ACM, 2017: 4066−4076
[146] Kilbertus N, Rojas-Carulla M, Parascandolo G, et al. Avoiding discrimination through causal reasoning[C] //Proc of the 31st Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2017: 656−666
[147] Nabi R, Shpitser I. Fair inference on outcomes[C] //Proc of the 32nd AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2018: 1931−1940
[148] Chiappa S. Path-specific counterfactual fairness[C] //Proc of the 33rd AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2019: 7801−7808
[149] Wu Yongkai, Zhang Lu, Wu Xintao, et al. PC-fairness: A unified framework for measuring causality-based fairness[C] //Proc of the 33rd Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2019: 3404−3414
[150] Wu Yongkai, Zhang Lu, Wu Xintao. Counterfactual fairness: Unidentification, bound and algorithm[C] //Proc of the 28th Int Joint Conf on Artificial Intelligence. Red Hook, NY: Curran Associates Inc, 2019: 1438−1444
[151] Huang P S, Zhang Huan, Jiang R, et al. Reducing sentiment bias in language models via counterfactual evaluation[C] //Proc of the 2020 Conf on Empirical Methods in Natural Language Processing: Findings. Stroudsburg, PA: ACL, 2020: 65−83 [152] Garg S, Perot V, Limtiaco N, et al. Counterfactual fairness in text classification through robustness[C] //Proc of the 33rd AAAI/ACM Conf on AI, Ethics, and Society. Menlo Park, CA: AAAI, 2019: 219−226
[153] Hu Yaowei, Wu Yongkai, Zhang Lu, et al. Fair multiple decision making through soft interventions[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 17965−17975
[154] Goel N, Amayuelas A, Deshpande A, et al. The importance of modeling data missingness in algorithmic fairness: A causal perspective[C] //Proc of the 35th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2021: 7564−7573
[155] Xu Depeng, Wu Yongkai, Yuan Shuhan, et al. Achieving causal fairness through generative adversarial networks[C] //Proc of the 28th Int Joint Conf on Artificial Intelligence. Red Hook, NY: Curran Associates Inc, 2019: 1452−1458
[156] Khademi A, Lee S, Foley D, et al. Fairness in algorithmic decision making: An excursion through the lens of causality[C] //Proc of the 28th World Wide Web Conf. New York: ACM, 2019: 2907−2914
[157] Zhang Junzhe, Bareinboim E. Fairness in decision-making—The causal explanation formula[C] //Proc of the 32nd AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2018: 2037−2045
[158] Zhang Junzhe, Bareinboim E. Equality of opportunity in classification: A causal approach[C] //Proc of the 32nd Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2018: 3671−3681
[159] Wang Hao, Ustun B, Calmon F. Repairing without retraining: Avoiding disparate impact with counterfactual distributions[C] //Proc of the 36th Int Conf on Machine Learning. Cambridge, MA: JMLR, 2019: 6618−6627
[160] Creager E, Madras D, Pitassi T, et al. Causal modeling for fairness in dynamical systems[C] //Proc of the 37th Int Conf on Machine Learning. Cambridge, MA: JMLR, 2020: 2185−2195
[161] Swaminathan A, Joachims T. Batch learning from logged bandit feedback through counterfactual risk minimization[J]. The Journal of Machine Learning Research, 2015, 16(1): 1731−1755
[162] Swaminathan A, Joachims T. The self-normalized estimator for counterfactual learning[C] //Proc of the 29th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2015: 3231−3239
[163] Wu Hang, Wang May. Variance regularized counterfactual risk minimization via variational divergence minimization[C] //Proc of the 35th Int Conf on Machine Learning. Cambridge, MA: JMLR, 2018: 5353−5362
[164] London B, Sandler T. Bayesian counterfactual risk minimization[C] //Proc of the 36th Int Conf on Machine Learning. Cambridge, MA: JMLR, 2019: 4125−4133
[165] Faury L, Tanielian U, Dohmatob E, et al. Distributionally robust counterfactual risk minimization[C] //Proc of the 34th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2020: 3850−3857
[166] Schnabel T, Swaminathan A, Singh A, et al. Recommendations as treatments: Debiasing learning and evaluation[C] //Proc of the 33rd Int Conf on Machine Learning. Cambridge, MA: JMLR, 2016: 1670−1679
[167] Yang Longqi, Cui Yin, Xuan Yuan, et al. Unbiased offline recommender evaluation for missing-not-at-random implicit feedback[C] //Proc of the 12th ACM Conf on Recommender Systems. New York: ACM, 2018: 279−287
[168] Bonner S, Vasile F. Causal embeddings for recommendation[C] //Proc of the 12th ACM Conf on Recommender Systems. New York: ACM, 2018: 104−112
[169] Narita Y, Yasui S, Yata K. Efficient counterfactual learning from bandit feedback[C] //Proc of the 33rd AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2019: 4634−4641
[170] Zou Hao, Cui Peng, Li Bo, et al. Counterfactual prediction for bundle treatment[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 19705−19715
[171] Xu Da, Ruan Chuanwei, Korpeoglu E, et al. Adversarial counterfactual learning and evaluation for recommender system[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 13515−13526
[172] Lopez R, Li Chenchen, Yan Xiang, et al. Cost-effective incentive allocation via structured counterfactual inference[C] //Proc of the 34th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2020: 4997−5004
[173] Joachims T, Swaminathan A, Schnabel T. Unbiased learning-to-rank with biased feedback[C] //Proc of the 10th ACM Int Conf on Web Search and Data Mining. New York: ACM, 2017: 781−789
[174] Wang Xuanhui, Golbandi N, Bendersky M, et al. Position bias estimation for unbiased learning to rank in personal search[C] //Proc of the 11th ACM Int Conf on Web Search and Data Mining. New York: ACM, 2018: 610−618
[175] Ai Qingyao, Bi Keping, Luo Cheng, et al. Unbiased learning to rank with unbiased propensity estimation[C] //Proc of the 41st Int ACM SIGIR Conf on Research and Development in Information Retrieval. New York: ACM, 2018: 385−394
[176] Agarwal A, Takatsu K, Zaitsev I, et al. A general framework for counterfactual learning-to-rank[C] //Proc of the 42nd Int ACM SIGIR Conf on Research and Development in Information Retrieval. New York: ACM, 2019: 5−14
[177] Jagerman R, de Rijke M. Accelerated convergence for counterfactual learning to rank[C] //Proc of the 43rd Int ACM SIGIR Conf on Research and Development in Information Retrieval. New York: ACM, 2020: 469−478
[178] Vardasbi A, de Rijke M, Markov I. Cascade model-based propensity estimation for counterfactual learning to rank[C] //Proc of the 43rd Int ACM SIGIR Conf on Research and Development in Information Retrieval. New York: ACM, 2020: 2089−2092
[179] Jagerman R, Oosterhuis H, de Rijke M. To model or to intervene: A comparison of counterfactual and online learning to rank from user interactions[C] //Proc of the 42nd Int ACM SIGIR Conf on Research and Development in Information Retrieval. New York: ACM, 2019: 15−24
[180] Bottou L, Peters J, Quiñonero-Candela J, et al. Counterfactual reasoning and learning systems: The example of computational advertising[J]. The Journal of Machine Learning Research, 2013, 14(1): 3207−3260
[181] Lawrence C, Riezler S. Improving a neural semantic parser by counterfactual learning from human bandit feedback[C] //Proc of the 56th Annual Meeting of the ACL, Vol 1. Stroudsburg, PA: ACL, 2018: 1820−1830
[182] Bareinboim E, Forney A, Pearl J. Bandits with unobserved confounders: A causal approach[C] //Proc of the 29th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2015: 1342−1350
[183] Lee S, Bareinboim E. Structural causal bandits: Where to intervene?[C] //Proc of the 32nd Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2018: 2568−2578
[184] Lee S, Bareinboim E. Structural causal bandits with non-manipulable variables[C] //Proc of the 33rd AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2019: 4164−4172
[185] Haan P, Jayaraman D, Levine S. Causal confusion in imitation learning[C] //Proc of the 33rd Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2019: 11698−11709
[186] Kyono T, Zhang Yao, van der Schaar M. CASTLE: Regularization via auxiliary causal graph discovery[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 1501−1512
[187] Yang Mengyue, Liu Frurui, Chen Zhitang, et al. CausalVAE: Disentangled representation learning via neural structural causal models[C] //Proc of the 34th IEEE/CVF Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2021: 9593−9602
[188] Zinkevich M, Johanson M, Bowling M, et al. Regret minimization in games with incomplete information[C] //Proc of the 20th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2007: 1729−1736
[189] Brown N, Lerer A, Gross S, et al. Deep counterfactual regret minimization[C] //Proc of the 36th Int Conf on Machine Learning. Cambridge, MA: JMLR, 2019: 793−802
[190] Farina G, Kroer C, Brown N, et al. Stable-predictive optimistic counterfactual regret minimization[C] //Proc of the 36th Int Conf on Machine Learning. Cambridge, MA: JMLR, 2019: 1853−1862
[191] Brown N, Sandholm T. Solving imperfect-information games via discounted regret minimization[C] //Proc of the 33rd AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2019: 1829−1836
[192] Li Hui, Hu Kailiang, Zhang Shaohua, et al. Double neural counterfactual regret minimization[C/OL] //Proc of the 8th Int Conf on Learning Representations. 2020 [2021-11-14]. https://openreview.net/pdf?id=ByedzkrKvH
[193] Oberst M, Sontag D. Counterfactual off-policy evaluation with Gumbel-max structural causal models[C] //Proc of the 36th Int Conf on Machine Learning. Cambridge, MA: JMLR, 2019: 4881−4890
[194] Buesing L, Weber T, Zwols Y, et al. Woulda, coulda, shoulda: Counterfactually-guided policy search[C/OL] //Proc of the 9th Int Conf on Learning Representations. 2019 [2021-11-14]. https://openreview.net/pdf?id=BJG0voC9YQ
[195] Chen Long, Zhang Hanwang, Xiao Jun, et al. Counterfactual critic multi-agent training for scene graph generation[C] //Proc of the 2019 IEEE/CVF Int Conf on Computer Vision. Piscataway, NJ: IEEE, 2019: 4613−4623 [196] Zhu Qingfu, Zhang Weinan, Liu Ting, et al. Counterfactual off-policy training for neural dialogue generation[C] //Proc of the 2020 Conf on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2020: 3438−3448 [197] Choi S, Park H, Yeo J, et al. Less is more: Attention supervision with counterfactuals for text classification[C] //Proc of the 2020 Conf on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2020: 6695−6704 [198] Zhang Zhu, Zhao Zhou, Lin Zhejie, et al. Counterfactual contrastive learning for weakly-supervised vision-language grounding[C] //Proc of the 34th Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2020: 655-666
[199] Kocaoglu M, Snyder C, Dimakis A G, et al. CausalGAN: Learning causal implicit generative models with adversarial training[C] //Proc of the 6th Int Conf on Learning Representations, 2018 [2021-11-03]. https://openreview.net/pdf?id=BJE-4xW0W
[200] Kim H, Shin S, Jang J H, et al. Counterfactual fairness with disentangled causal effect variational autoencoder[C] //Proc of the 35th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2021: 8128−8136
[201] Qin Lianhui, Bosselut A, Holtzman A, et al. Counterfactual story reasoning and generation[C] //Proc of the 2019 Conf on Empirical Methods in Natural Language Processing and the 9th Int Joint Conf on Natural Language Processing (EMNLP-IJCNLP). Stroudsburg, PA: ACL, 2019: 5046−5056 [202] Hao Changying, Pang Liang, Lan Yanyan, et al. Sketch and customize: A counterfactual story generator[C] //Proc of the 35th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2021: 12955−12962.
[203] Madaan N, Padhi I, Panwar N, et al. Generate your counterfactuals: Towards controlled counterfactual generation for text[C] //Proc of the 35th AAAI Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2021: 13516−13524
[204] Peysakhovich A, Kroer C, Lerer A. Robust multi-agent counterfactual prediction[C] //Proc of the 33rd Int Conf on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2019: 3083−3093
[205] Baradel F, Neverova N, Mille J, et al. CoPhy: Counterfactual learning of physical dynamics[C/OL] //Proc of the 8th Int Conf on Learning Representations. 2020 [2021-11-14]. https://openreview.net/pdf?id=SkeyppEFvS
-
期刊类型引用(2)
1. 史宏志 ,赵健 ,赵雅倩 ,李茹杨 ,魏辉 ,胡克坤 ,温东超 ,金良 . 大模型时代的混合专家系统优化综述. 计算机研究与发展. 2025(05): 1164-1189 .  本站查看
本站查看
2. 谢星丽,谢跃雷. 基于差分星座轨迹图的多任务802.11b/g信号识别方法. 电讯技术. 2023(11): 1771-1778 .  百度学术
百度学术
其他类型引用(0)



































 下载:
下载: