当预期的系统观测和真实的系统观测不一致时，这时系统就存在故障，需要对故障进行诊断.基于模型诊断(model-based diagnosis， MBD)^[1]是根据系统的描述利用基于推理的方法解释系统观测不一致的过程.几十年来，MBD问题已经广泛应用于的各个领域，包括调试关系规范^[2]、诊断系统调试^[3]、电子表格调试^[4]和软件故障定位^[5]等领域.

文章的主要贡献包括3个方面:

1) 提出利用观测的扇入过滤边和扇出过滤边对边进行过滤的约简方法.这2种边都是冗余的，因为它们的值在进行诊断求解过程中是必须进行传播的值.

2) 提出利用观测的过滤节点来进行过滤的约简方法.对于基于观察的过滤节点而言，它所有的扇入和扇出都是固定的，即它的扇入和扇出之间不存在冲突.

3) 在ISCAS85和ITC99基准测试实例上的实验结果表明，提出的方法可以有效缩减MBD问题编码时生成的子句规模，进而降低最大可满足性问题(maximum satisfiability， MaxSAT)求解诊断问题的难度，有效地提高了诊断求解效率.

1.   相关工作

近几十年来，越来越多的研究者投入到MBD问题的研究中，提出了许多求解算法，其中包括单个观测的MBD算法^[6-11]和多观测的MBD算法^[12-15].目前用于解决单个观测下的MBD问题算法为：随机搜索算法^[6,16]、基于编译的算法^[7]，基于广度优先搜索的算法^[8]、基于可满足性问题(satisfiability，SAT)的算法^[9-10]、基于冲突导向的算法^[11]等^[17-21].在这些算法中，基于广度优先搜索的算法及其改进算法利用了树结构.此类算法检查树的每个节点是否表示最小诊断解，这类方法是完备的.显然，只要有足够的时间，这类方法可以得到所有的诊断解.然而，这类方法是相当耗时的，它们在解决大型现实实例问题时是不太现实的.随着计算机处理器的快速发展，一些并行化技术也被用于MBD求解问题中，Jannach等人^[8]通过并行地构造碰集树(hitting set-tree， HS-Tree)返回所有诊断.基于编译的方法通过利用给定的系统层次结构和DNF编码的方式^[7]计算候选解的方法也显示出它们的优势.SAFARI算法^[6]证明了在MBD问题上随机搜索算法的有效性.SAFARI随机删除一个组件，然后判断候选解是否仍然是一个诊断，直到没有组件可以删除.显然，SAFARI不能保证返回的诊断解是极小势诊断.近年来，随着SAT及MaxSAT求解器性能的大幅提升，使得基于SAT的诊断方法引起了广泛的关注.Feldman等人^[6]提出将诊断的电路编码成MaxSAT问题，该方法比SAFARI运行时间更长.相比之下，Metodi等人^[20]提出的SATbD考虑电路的直接统治者，并找出所有极小势诊断.2015年，Marques-Silva等人^[22]提出一种面向统治者的编码(dominator oriented encoding， DOE)方法，通过过滤掉一些节点和一些边的方法将MBD编码为MaxSAT.作为一种先进的编码方法，DOE利用了系统的结构属性，有效地缩减了MBD问题编码后子句集的规模.虽然DOE保证返回基数最小的诊断，但它没有考虑与观察有关的多余带权重的合取范式(weighted conjunctive normal form， WCNF).本文提出一种面向观察的编码(observation-oriented encoding， OOE)方法，该方法在将MBD编码到Max SAT时能有效减少子句集规模.此外，本文在调用相同的MaxSAT求解器情况下，将OOE方法与基础编码（basic encoding， BE）和DOE进行了比较.实验结果表明，OOE方法有效提高了MBD问题的求解效率.

2.   基于模型的诊断问题

本节主要介绍MBD问题的相关定义及概念.

2.1   基本定义

诊断问题可以被定义为一个三元组$\langle$SD,Comps,Obs$\rangle$，其中，SD表示诊断问题的系统描述，Comps代表组件的集合，Obs代表一个观测.假定所有组件的状态是正常的情况下，当系统的模型描述和观测出现不一致时，我们称存在一个诊断问题.也就是:

其中，AB(c)=1代表组件c是故障的，相反，AB(c)=0代表组件c是正常的.下面我们给出诊断的定义.

定义1. 诊断^[1].给定一个诊断问题D=$\langle$SD,Comps,Obs$\rangle$.一个诊断被定义为一组组件∆的集合，其中 ∆ $\text{⋤}$ Comps，当

其中$\Delta$是一个极小子集诊断当且仅当不存在当前诊断的一个子集${\Delta' }{\text{⋤}}\Delta$是一个诊断.诊断解的长度称为诊断的势，$\Delta$是一个极小势诊断当且仅当不存在另外一个诊断解${\Delta '}$满足∣$\Delta$∣>∣$\Delta '$∣.

2.2   将诊断问题编码为MaxSAT

许多MBD问题在求解时先被编码为MaxSAT问题^[14-15,22]，下面本文介绍编码过程.当一个MBD问题被编码为一系列WCNF子句集时，诊断系统中的组件和电路线分别用变量表示，它们的值用文字表示.下面我们分别表示有2个输入的与非门(nand2)、与门(and2)、与或门(nor2)、或门(or2)的公式：

例如，对于一个NAND组件c而言，${i}_{\mathrm{nand}\_c1}$和${i}_{\mathrm{nand}\_c2}$分别代表组件c的输入，${o}_{\mathrm{n}\mathrm{a}\mathrm{n}\mathrm{d}\_c}$是组件c的输出.由一组组件组成的系统SD的表示公式为

此处，代表组件c的编码.在一个观测中，观测可以表示为

$Obs\triangleq v$.$v$和一个电路的逻辑值相关，当$v=1$代表电路逻辑值为正，当$v=0$代表电路逻辑值为负.

WCNF中的子句cl的权重用ω(cl)表示，我们分别设置SD，Comps，Obs相关的子句为：

1) 对于SD和Comps中的子句被设置为硬子句，$\mathrm{\omega }\left(cl\right):=num\left(Obs\right)+1$，其中$num\left(Obs\right)$代表观测的数量;

2) Obs中的子句被设置为软子句，$\omega \left(cl\right):=1$.

在基于SAT的方法中，MBD问题被编码为一组子句，然后通过迭代调用SAT或MaxSAT求解器来计算诊断.通过添加阻塞子句可以避免相同的诊断解被多次计算.利用诊断系统的结构属性是一种可行的方法，这种方法在许多基于SAT的诊断算法中得到了应用^[23-24].相应地，诊断中的统治节点和顶层诊断(top-level diagnosis，TLD)也是重要的概念.

定义2. 统治节点^[20].给定一个组件G₁和G₂，如果从G₁到电路的输出的所有路径都包含G₂，则称G₂是G₁的统治节点.换句话说，G₁是被G₂统治的节点.

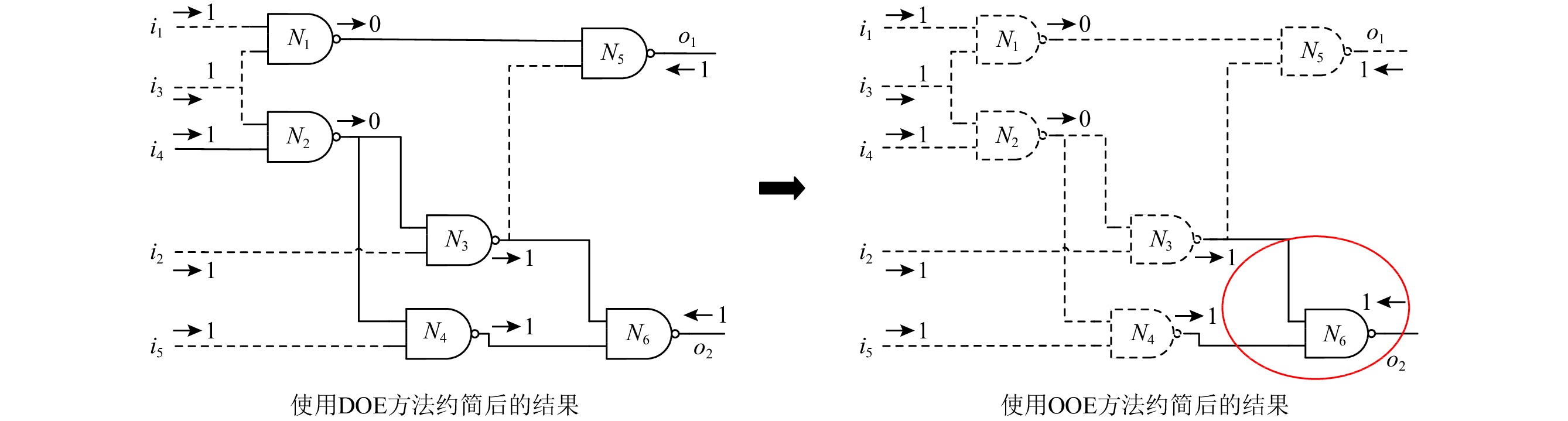
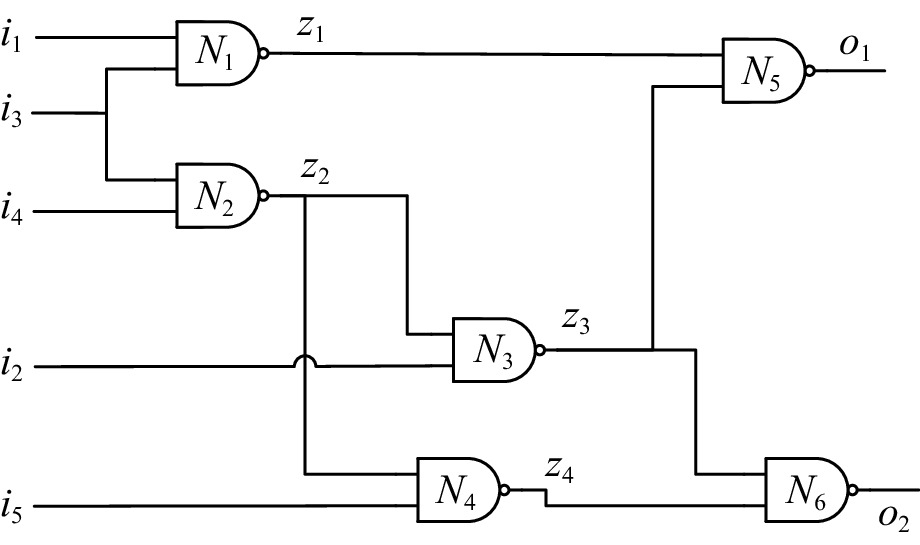
定义3. 顶层诊断解^[20].称$\Delta$为一个顶层诊断解，如果它是一个极小势诊断且不包含任何统治组件.

以图1为例，由于N₁到达系统输出的路径是唯一的，且包括N₅，所以N₁被N₅统治.假定有观测i₁= i₂= i₃= i₅= o₁= o₂=1, i₄=0, N₆是一个TLD，因为N₆不被任何组件统治.通过将统治组件编码到硬子句中 (即申明这些组件是健康的)，就可以计算TLD.

图  1  C17 电路

Figure  1.  C17 circuit

下载: 全尺寸图片 幻灯片

3.   求解基于模型的诊断问题的DOE方法

为了简化MBD到MaxSAT的编码过程，缩减被编码的“门”生成的子句规模.DOE方法利用“门控制关系”，同时计算TLD.除此之外，一些曾在DOE方法中被提出的概念如阻塞连接及骨干组件，将在本节定义中给出解释.

定义4. 骨架节点(backbone node, B-Node)^[22].我们称一个组件为骨架节点当且仅当其是一个被统治的组件且它的扇出对于任何一个TLD有固定的值.

考虑图1中组件N₁，N₁被N₅统治，当给定一个观测时，N₁的所有输入是固定的，也就是说，i₁和i₃有固定的值，当求解一个TLD时，N₁的扇出就有固定的值，所以N₁是一个B-Node.

定义5. 阻塞边(blocked edge，B-Edge)^[22].我们称组件的一个扇入边E是一个阻塞边，如果边的值不会对该组件的扇出起作用.

考虑图1中的N₂，当给定一个观测Obs={i₄=0}，N₂的输出被确定为1，无论i₃的值是什么，因此i₃边是一个阻塞边.

定义6. 过滤节点^[22].我们称组件B为一个过滤节点，如果它的所有扇出边都是过滤边.

定义7. 过滤边^[22].我们称边E为一个过滤边，如果它是一个B-Node或者它的扇出组件是一个过滤节点.

由于N₁是一个被统治组件，给定一个观测Obs={i₁=1}，当z₁的值 (z₁=0) 被传播后，z₃的值将不会对N₅的输出起作用.也就是说，N₅的输出值是固定的.因此，$\langle$N₃，N₅$\rangle$是一个B-Edge，因此，$\langle$N₃，N₅$\rangle$是一个过滤边.假定$\langle$N₃，N₆$\rangle$也是一个过滤边，这时N₃的所有输入边都是过滤边，那么组件N₃是一个过滤节点.具体的DOE方法如算法1所示:

算法1. 编码MBD到MaxSAT的DOE方法^[22].

输入：SD，Comps，Obs；

输出：编译后的模型.

① repeat

②　　Dominators $\leftarrow$所有统治节点；

③　　BackboneComps $\leftarrow$所有骨架组件；

④　　BlockedConnections $\leftarrow$所有阻塞连接；

⑤　　if 到达最大迭代次数 then

⑥　　　break；

⑦　　end if

⑧ until NoMoreChanges；

⑨ $M\leftarrow$ 产生MaxSAT模型.

4.   OOE方法

文献[22]中的实验表明了DOE方法在求解MBD问题上的有效性.在本节中，我们将介绍OOE方法及该方法中为了改进基于MaxSAT的MBD编译过程用到的其他过滤节点和过滤边的概念.

定义8. 基于观测的扇入过滤边.我们称边E为一个基于观测的扇入过滤边，如果它是一个系统的输入或者它是一个统治组件的一个固定输出边.

此处继续讨论观测Obs = {i₁ = 1, i₂ = 1, i₃ = 1, i₄ = 1, i₅ = 1, o₁ = 1, o₂ = 1}，在第1次迭代中，i₁, i₂, i₃, i₄, i₅是基于观测的扇入过滤边.在DOE方法过滤了一些节点和边之后，因为N₁，N₄，N₃，N₂依次成为统治节点之后，$\langle$N₁，N₅$\rangle$，$\langle$N₃，N₆$\rangle$，$\langle$N₂，N₄$\rangle$，$\langle$N₄，N₆$\rangle$变成了基于观察的扇入过滤边.

定义9. 基于观测的扇出过滤边.我们称边E为一个基于观测的扇出过滤边，如果它是一个系统的输出.

给定观测Obs={ i₁ = 1, i₂ = 1, i₃ = 1, i₄ = 1, i₅ = 1, o₁ = 1, o₂ = 1}，o₁和o₂ 均为基于观测的扇出过滤边.

定义10. 基于观测的过滤边.我们称边E为一个基于观测的过滤边，如果它是一个基于观测的扇出过滤边或者它是一个基于观测的扇入过滤边.

初始状态下，系统的输入输出是固定的.因此，任何基于观测的边缘边都是固定的.

定义11. 基于观察的过滤节点.我们称一个组件B为基于观察的过滤节点，如果该组件的扇入和扇出都是固定的，并且扇出值与扇入值在逻辑上一致，或者该组件是一个B-Node.

给定一个观测Obs= { i₁ = 1, i₂ = 1, i₃ = 1, i₄ = 1, i₅ = 1, o₁ = 1, o₂ = 1}，在DOE编译过程中，因为N₁，N₂，N₃，N₄都是B-Node，所以它们都是基于观测的过滤节点.此外，N₅也是一个基于观测的过滤节点因为它有一个输入值为0，这与它的输出值1是一致的.

在OOE方法中，被统治的组件编码为硬子句，这种设置与DOE方法中的设置是相同的.

在OOE编译方法的预处理过程中，不仅过滤边和过滤节点不被编码为WCNF，而且基于观测的过滤边和基于观测的过滤节点也不被编码为WCNF.

命题1. 假定ζ为使用DOE方法求解出的一个TLD，那么使用OOE方法可以求解出一个和ζ具有相同势的TLD，ζ ’.

考虑观测Obs = { i₁ = 1, i₂ = 1, i₃ = 1, i₄ = 1, i₅ = 1, o₁ = 1, o₂ = 1}，我们详细解释DOE方法和OOE方法在进行编码时的约简子句的细节.在第1次迭代中，被统治节点为{N₁, N₄}.N₁被N₅统治，N₄被N₆统治.之后N₁的输出值0被传播， N₅的输出值是固定的，所以$\langle$N₃，N₅$\rangle$是一个B-Edge.在第2次迭代时，因为过滤边$\langle$N₃，N₅$\rangle$，所以N₃被N₆统治.随后, N₂由N₆统治.除此之外，i₂，i₅被过滤，成为过滤边.这就是所有的DOE方法的约简过程及贡献.剩余的组件{N₅, N₆}以及边$\langle$N₁，N₅$\rangle$，$\langle$N₃，N₆$\rangle$，$\langle$N₄，N₆$\rangle$均在DOE方法中没有被考虑到.

在OOE方法中，为了考虑将更多的节点和边进行约简，基于观测的过滤边和基于观测的过滤节点被提出用于减少生成的WCNF子句的数量.算法2概述了OOE方法的伪代码.

算法2. 编码MBD到MaxSAT的OOE方法.

输入：SD，Comps，Obs；

输出：编译后的WCNF子句.

① repeat

②　　Dominators $\leftarrow$所有统治节点；

③　　BackboneComps $\leftarrow$所有骨架组件；

④　　BlockedConnections $\leftarrow$所有阻塞连接；

⑤　　if 到达最大迭代次数 then

⑥　　　break；

⑦　　end if

⑧ until NoMoreChanges；

⑨ edgeStack $\leftarrow$所有基于观测的过滤边；

⑩ nodeStack $\leftarrow$所有基于观测的过滤节点；

⑪ while edgeStack ≠ NULL do

⑫ 　　e$\leftarrow$edgeStack中的栈顶元素；

⑬ 　　Propagation(e)；

⑭　　node$\leftarrow$nodeStack中的栈顶元素；

⑮　　Propagation(node)；

⑯　　if 获得一个新的基于观测的过滤 then

⑰　　　　edgeStack $\leftarrow Push\left(E\right)$；

⑱　　end if

⑲　　if 获得一个新的基于观测的过滤节点

node then

⑳　　　 nodeStack $\leftarrow Push\left(node\right)；$

㉑　　end if

㉒ end while

算法2一直迭代至没有发现新的基于观测的过滤边和过滤节点.其中，算法2的行①~⑧和文献[22]中提出的DOE方法的预处理部分相同，经过DOE预处理后，初步地，我们找到基于观测的过滤边和基于观测的过滤节点.算法2在行⑨~⑩分别将初步得到的基于观测的过滤边和基于观测的过滤节点压入栈中.在行⑪~㉒，算法2找出所有的基于观测的过滤边和基于观测的过滤节点，旨在减少生成的WCNF子句的数量.在行⑬和行⑮中，函数Propagation是一种单元传播技术用于传播行⑫和行⑭中的e和node变量的赋值.

给定观测Obs = { i₁ = 1, i₂ = 1, i₃ = 1, i₄ = 1, i₅ = 1, o₁ = 1, o₂ = 1}，图2分别为算法1和算法2的编译结果.在图2中，虚线表示过滤边(如图2(a)的$\langle$N₃, N₅$\rangle$)或基于观测的过滤边(如图2(b)的$\langle$N₁, N₅$\rangle$).同样地，虚线点表示的组件代表过滤节点或基于观测的过滤节点(如图2(a)的N₁).过滤边、过滤节点、基于观测的过滤边和基于观测的过滤节点均将不会被编译成WCNF子句.如图2所示，仅有实线表示的元件和电路线被编码为WCNF子句，虚线表示的元件和电路线不被编码为WCNF子句.在这个例子中，在OOE方法之后，只有1个组件和3条电路线最终被编码为WCNF子句，图2(b)中用椭圆表示.

图  2  DOE方法和OOE方法在约简细节的比较

Figure  2.  Comparison between DOE and OOE in reduction detail

下载: 全尺寸图片 幻灯片

5.   实验结果

在本节中，我们将在MBD中提出的预处理方法与目前最好的预处理方法DOE^[22]及不用预处理过程的编码方法BE进行了对比.在编码为MaxSAT问题后求解诊断问题时，我们选择了一种MaxSAT求解器——UwrMaxSAT^[19]进行求解, UwrMaxSAT在2020年MaxSAT评估中的加权组中表现最好.实验分别在ISCAS85和ITC99这2组测试实例上执行，这2组测试实例均在文献[22]中使用.其中，第1组测试实例包含9998个测试用例，第2个测试实例包含7822个测试用例.本文提出的OOE方法用C++实现并使用G++编译.我们的实验是在Ubuntu 16.04 Linux和Intel Xeon E5-1607@3.00 GHz, 16 GB RAM上进行.

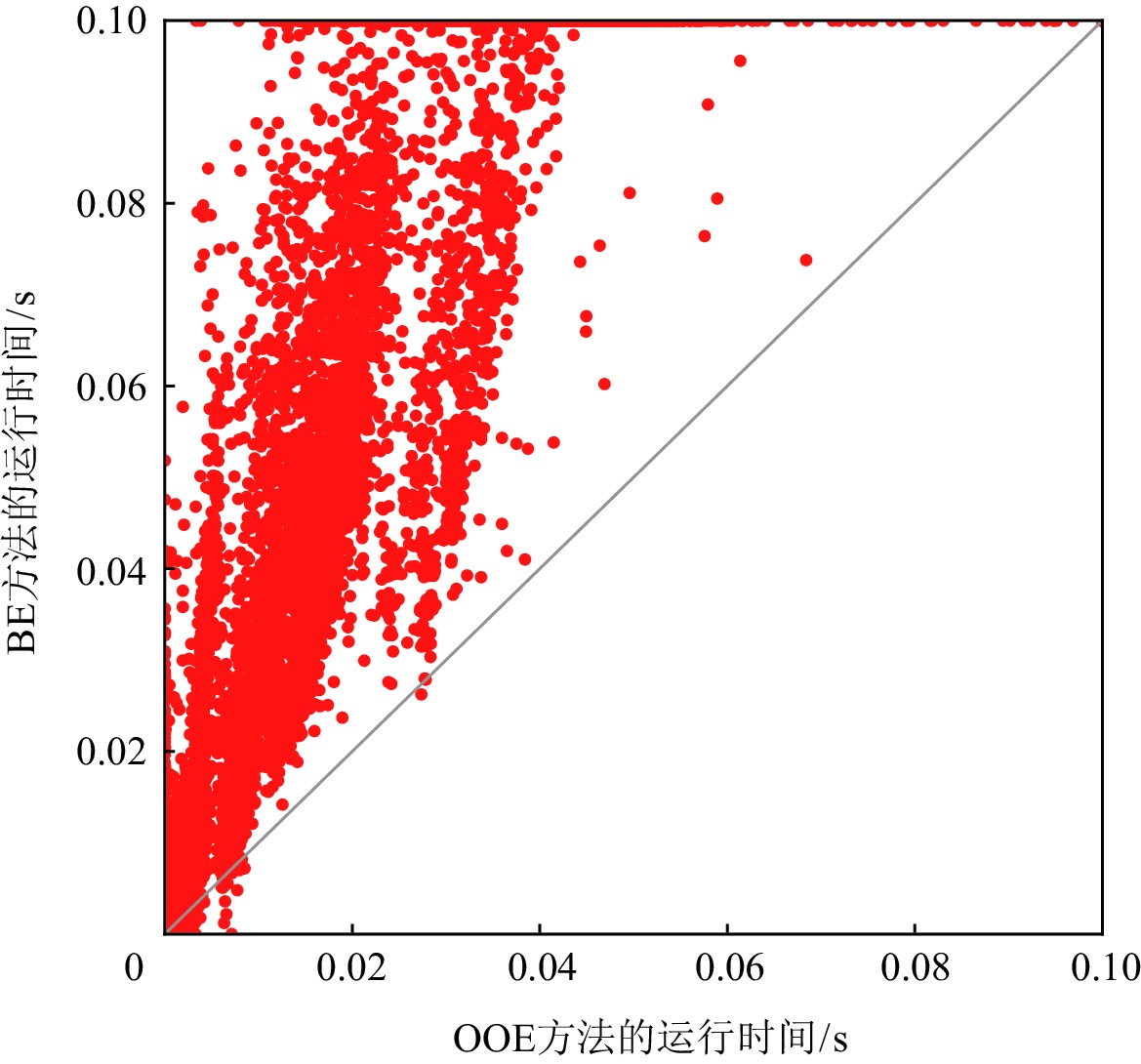
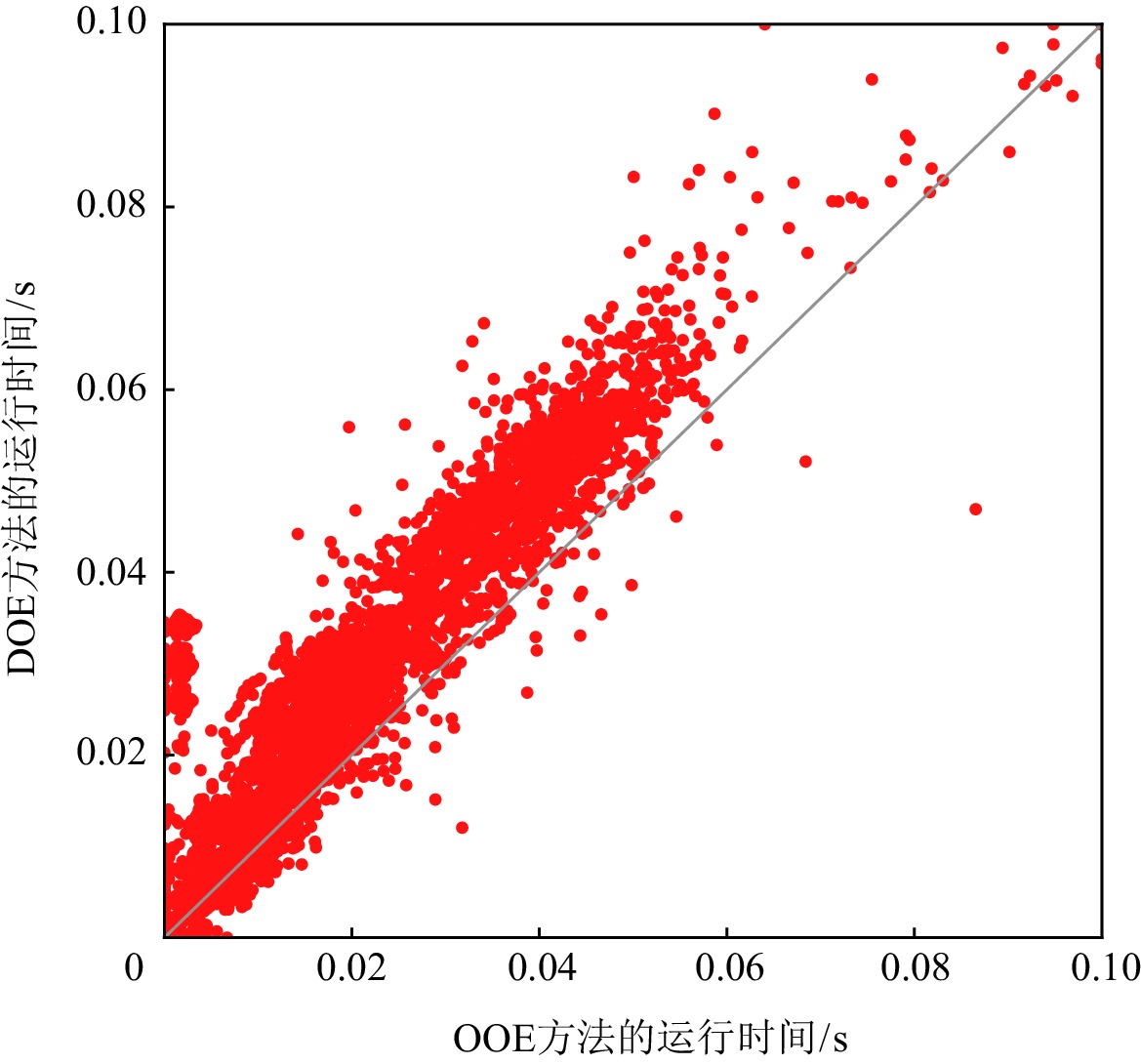
图3和图4分别给出OOE方法与BE方法和DOE方法在求解ISCAS85实例时，MaxSAT求解器求得一个诊断解的运行时间.在实验中，我们设置MaxSAT求解的时间上限为0.1 s.如图3和图4所示，对于大多数测试实例，OOE和DOE方法可以在0.1 s内通过MaxSAT求解器返回诊断结果.用BE方法求解时，有1431个测试实例不能在时间限制内得到一个诊断解；但是对于OOE和DOE方法，只有350个实例不能在0.1 s内得到一个诊断解.此外，如图4中所示，对于大多数测试实例，OOE方法要明显优于DOE方法.

图  3  BE和OOE方法在ISCAS85实例上的运行时间比较

Figure  3.  Comparison of the run time of BE and OOE approaches on ISCAS85 benchmark

下载: 全尺寸图片 幻灯片

图  4  DOE和OOE方法在ISCAS85实例上的运行时间比较

Figure  4.  Comparison of the run time of DOE and OOE approaches on ISCAS85 benchmark

下载: 全尺寸图片 幻灯片

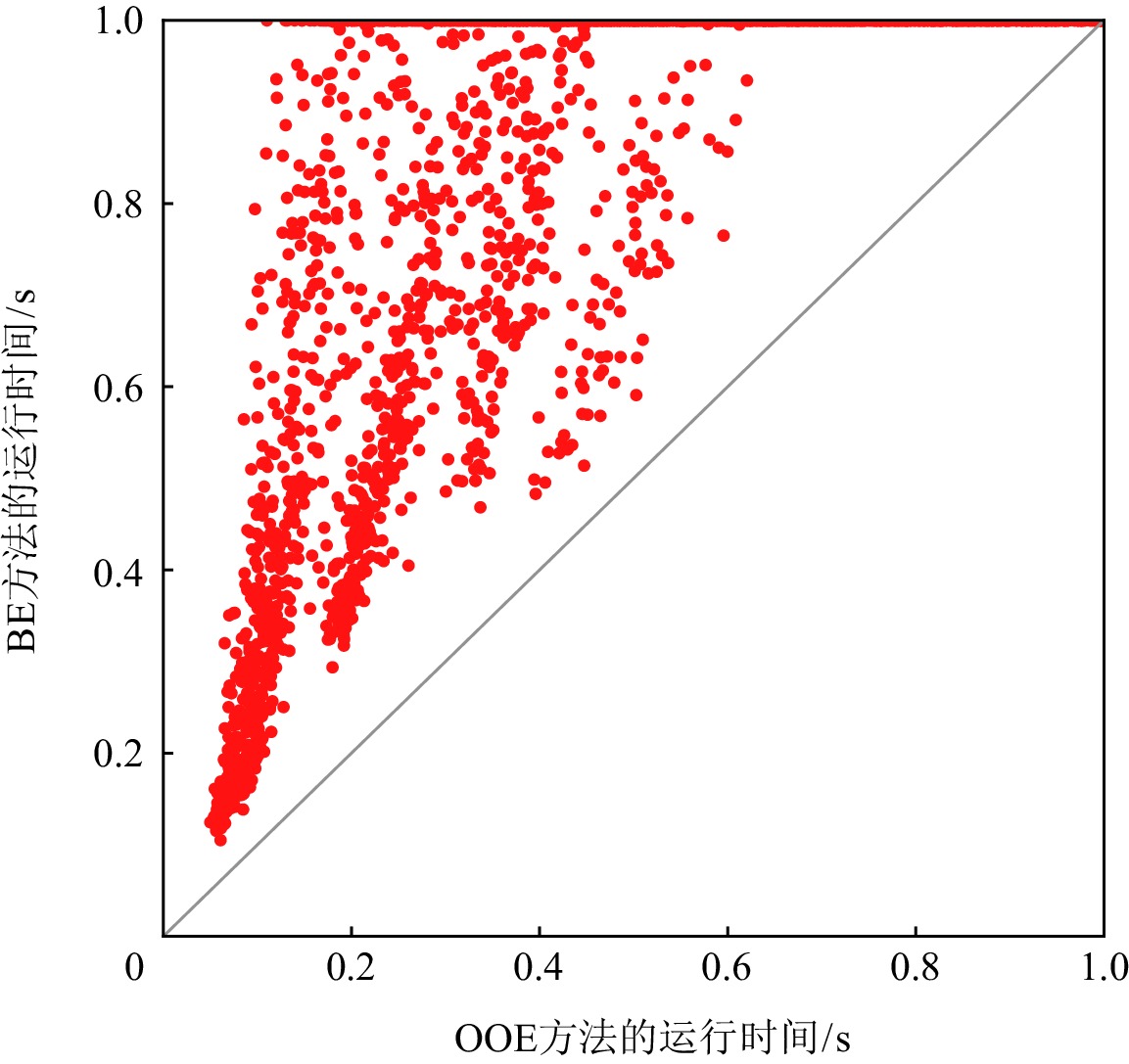
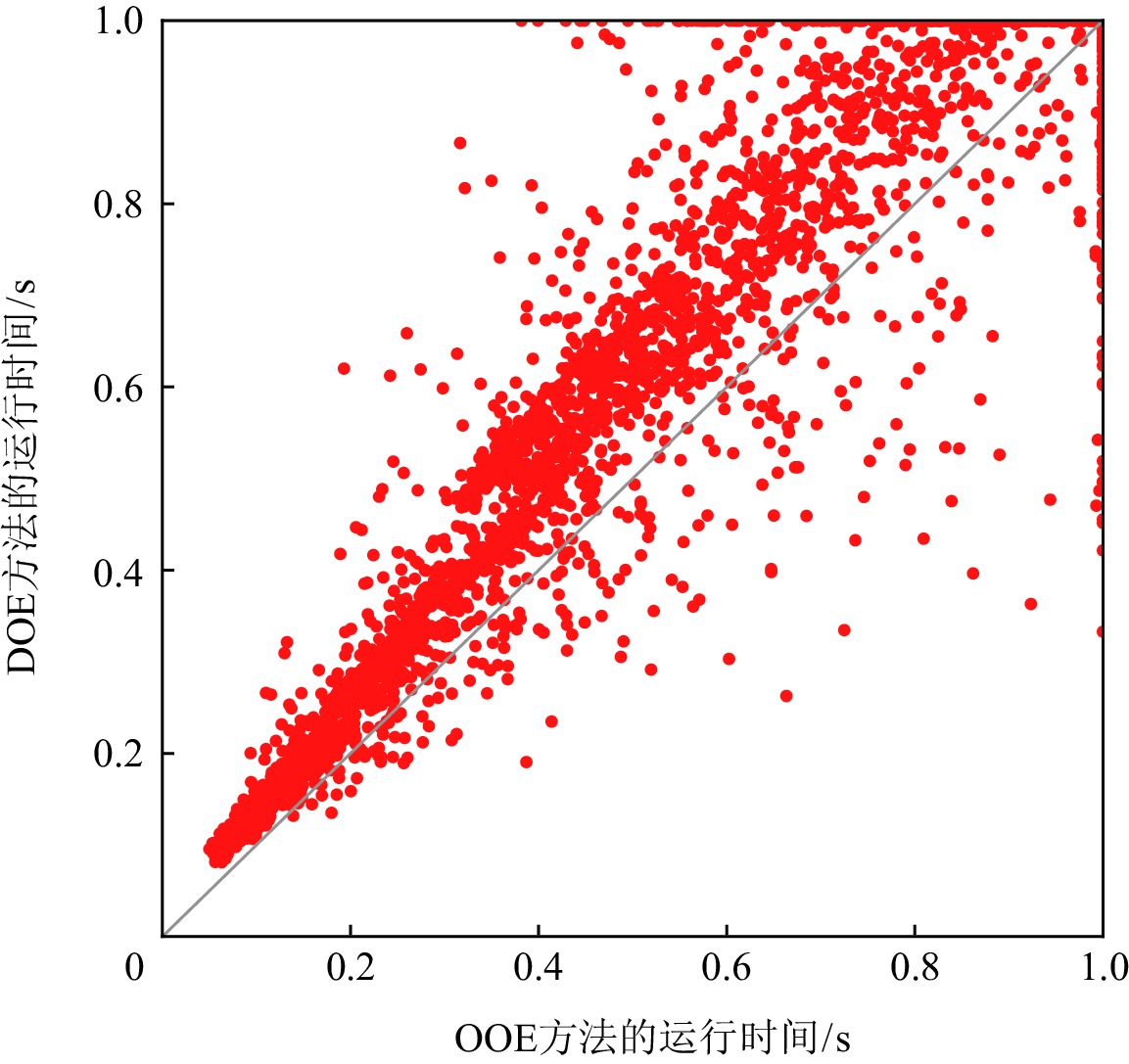
图5和图6分别显示了在ITC99实例上OOE方法与BE及DOE方法在求解诊断问题时MaxSAT求解器运行时间方面的比较.我们设置MaxSAT求解器的时间限制为1 s.坐标轴上的点表示在给定时间内无法求解的一些测试实例.使用OOE，DOE，BE方法不能得到一个解的测试实例的个数分别为4939，5197，6669.在求解实例个数上OOE方法明显优于BE和DOE方法，除此之外，在大多数情况下，相比于BE和DOE方法，使用OOE方法能在更短的时间内得到一个诊断解.

图  5  BE和OOE方法在ITC99实例上的运行时间比较

Figure  5.  The run time of BE and OOE approaches on ITC99 benchmark

下载: 全尺寸图片 幻灯片

图  6  DOE和OOE方法在ITC99实例上的运行时间比较

Figure  6.  The run time of DOE and OOE approaches on ITC99 benchmark

下载: 全尺寸图片 幻灯片

在ITC99 实例和ISCAS85实例上的详细实验结果分别如表1和表2所示：

表  1  在ITC99实例上的求解结果

Table  1.  Solved Results for ITC99 Benchmark

电路名称	观测个数	所用时间比竞争 对手短的实例个数			所用时间比竞争 对手短的实例个数
		OOE	BE		OOE	DOE[22]
b14	919	433	164		569	2
b15	995	663	188		819	2
b17	1000	946	54		1000	0
b18	1000	884	46		917	2
b19	1000	823	56		833	42
b20	997	596	222		782	0
b21	919	636	166		780	0
b22	992	722	223		932	0

下载: 导出CSV 

| 显示表格

在2组表中，我们分别列出了4组数据.第1列显示电路名称，第2列显示测试实例的数量.第3~6列显示OOE方法求解诊断时所用时间比竞争对手短的实例个数.从表1和表2可以看出，对每一个电路进行诊断问题求解时，OOE方法都是可行的，且求解结果显示，相比于DOE及 BE方法，OOE方法都有明显的优势.特别是在c880电路上，OOE方法在所有1182个测试实例中的实验结果均优于BE方法，有97.8%的实例的实验结果优于DOE方法.

表  2  在ISCAS85 实例上的求解结果

Table  2.  Solved Results for ISCAS85 Benchmark

电路名称	观测个数	所用时间比竞争 对手短的实例个数			所用时间比竞争 对手短的实例个数
		OOE	BE		OOE	DOE[22]
c17	63	48	14		56	7
c432	301	280	17		278	23
c499	835	734	96		760	71
c880	1182	1182	0		1157	20
c1355	836	719	113		832	4
c1908	864	664	182		834	12
c2670	1162	1128	34		1158	4
c3540	756	705	51		756	0
c5315	2038	2028	10		2038	0
c6288	404	246	158		398	6
c7552	1557	1536	21		1557	0

下载: 导出CSV 

| 显示表格

6.   总　　结

目前，很多基于SAT的MBD方法把MaxSAT编码作为分析MBD问题的一个基本步骤.本文在面向支配者编码的方法研究基础之上，提出一种OOE的面向观测的编码方法，显著减少了MBD编码后子句的数量，进而降低了MaxSAT求解诊断的难度，提高了求解诊断的效率.本文提出了2种方法用于提高OOE的效率.首先，根据诊断系统的输入观测和输出观测对过滤边进行约简.其次，利用基于观测的过滤节点，在编码时对一些组件进行约简，进而不被编码到MBD问题的子句中.实验结果表明，通过找到更多的基于观测的过滤节点和基于观测的过滤边，能有效减少编码后子句集规模，进而提高基于MaxSAT计算诊断解的效率.OOE方法在ISCAS85系统和ITC99系统的基准测试实例上求解诊断是高效的.在未来的研究中，将探索多观测下OOE方法的扩展算法.

作者贡献声明：周慧思负责文章主体撰写和修订，文献资料的分析、整理及文章写作；欧阳丹彤负责确定综述选题，指导和督促完成相关文献资料的收集整理；田新亮负责文献资料的收集以及部分图表数据的绘制；张立明负责提出文章修改意见, 指导文章写作.