基于自适应<i>k</i>近邻的时间序列异常模式识别

王玲; 周南; 申鹏

doi:10.7544/issn1000-1239.202111062

基于自适应k近邻的时间序列异常模式识别

北京科技大学自动化学院　北京　100083
工业过程知识自动化教育部重点实验室（北京科技大学）　北京　100083

基金项目: 国家自然科学基金项目（62076025, 61572073）

详细信息

作者简介:
王玲: 1974年生.博士，教授.主要研究方向为数据挖掘和机器学习

周南: 1997年生.硕士.主要研究方向为数据挖掘

申鹏: 2000年生.硕士研究生.主要研究方向为数据挖掘

中图分类号: TP391
计量
- 文章访问数: 225
- HTML全文浏览量: 39
- PDF下载量: 149
出版历程
- 收稿日期: 2021-10-26
- 修回日期: 2022-06-06
- 网络出版日期: 2023-02-10
- 刊出日期: 2022-12-31

Time Series Anomaly Pattern Recognition Based on Adaptive k Nearest Neighbor

School of Automation and Electrical Engineering, University of Science and Technology Beijing, Beijing 100083
Key Laboratory of Knowledge Automation for Industrial Processes(University of Science and Technology Beijing), Ministry of Education, Beijing 100083

Funds: This work was supported by the National Natural Science Foundation of China (62076025, 61572073).

摘要

摘要:
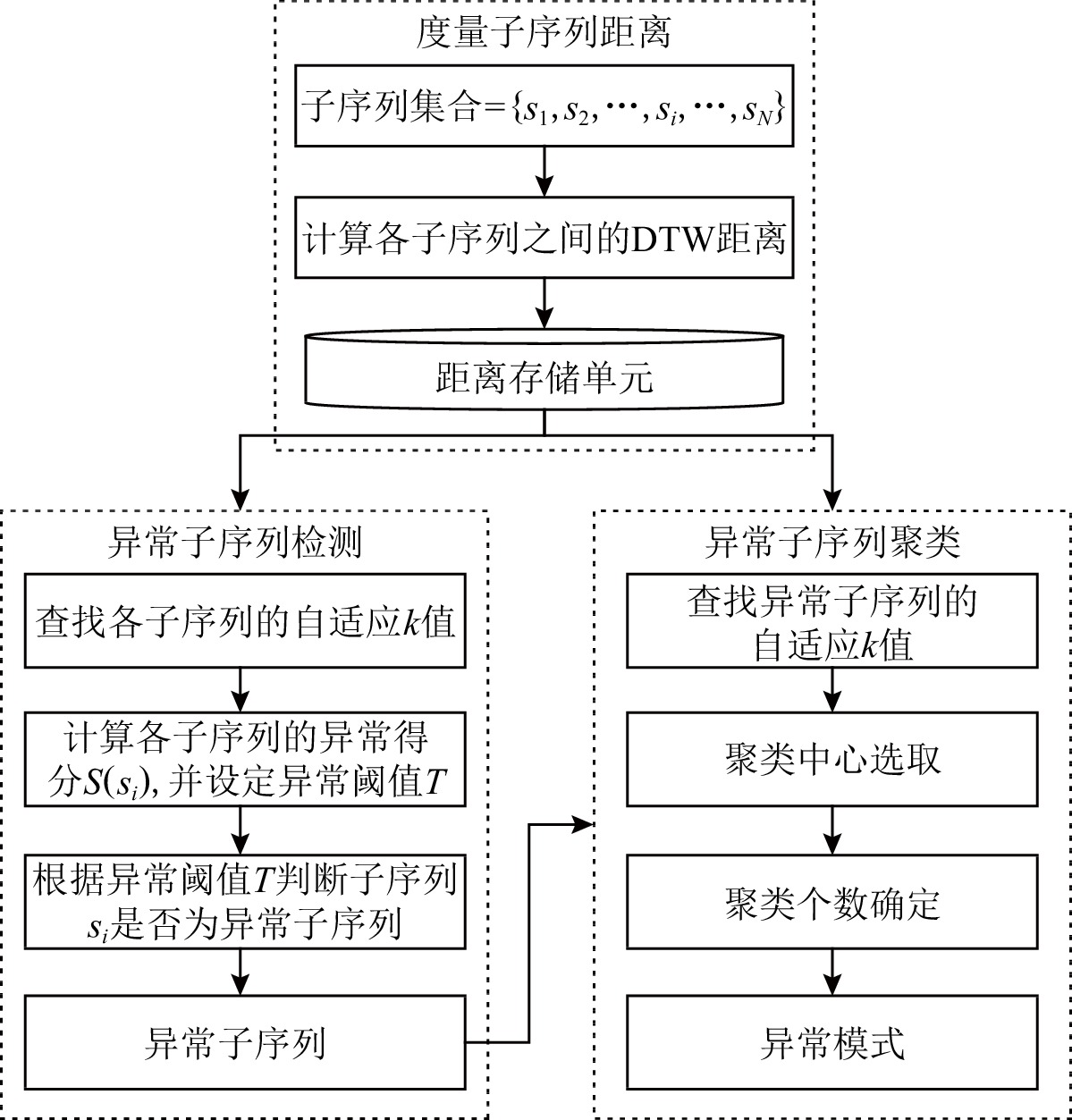
时间序列作为数据的典型代表，被广泛应用于许多研究领域. 时间序列异常模式代表了一种特殊情况的出现，在许多领域都具有重要意义. 现有的时间序列异常模式识别算法大多只是单纯检测异常子序列，忽略了异常子序列的类别区分问题，且许多参数都需要人为设置.为此提出了一种基于自适应k近邻的异常模式识别算法(anomaly pattern recognition algorithm based on adaptive k nearest neighbor, APAKN). 首先，确定各子序列的自适应k近邻值，引入自适应距离比计算子序列的相对密度,确定异常分数；然后提出一种基于最小方差的自适应阈值方法确定异常阈值，检测出所有异常子序列；最后，对异常子序列进行聚类，所得聚类中心即为具有不同变化趋势的异常模式. 整个算法过程在无需设置任何参数的情况下，不仅解决了密度不平衡问题，还精简了传统基于密度异常子序列检测算法的步骤，实现良好的异常模式识别效果. 在时间序列数据集合UCR的10个数据集上的实验结果表明, 提出算法在无需设置参数的情况下，在异常子序列检测和异常子序列聚类问题中都表现良好.
- 时间序列 /
- 异常子序列 /
- 异常模式 /
- 自适应k近邻 /
- 相对密度
Abstract:
As a typical representative of data, time series is widely used in many research fields. The time series anomaly pattern represents the emergence of a special situation, and is of great significance in many fields. Most of the existing time series anomaly pattern recognition algorithms simply detect anomaly subsequences, ignoring the problem of distinguishing the types of anomaly subsequences, and many parameters need to be set manually. In this paper, an anomaly pattern recognition algorithm based on adaptive k nearest neighbor(APAKN) is proposed. Firstly, the adaptive neighbor value k of each subsequence is determined, and an adaptive distance ratio is introduced to calculate the relative density of the subsequence to determine the anomaly score. Then, an adaptive threshold method based on minimum variance is proposed to determine the anomaly threshold and detect all anomaly subsequences. Finally, the anomaly subsequences are clustered, and the obtained cluster centers are anomaly patterns with different changing trends. The whole algorithm process not only solves the density imbalance problem without setting any parameters, but also simplifies the steps of the traditional density-based anomaly subsequence detection algorithm to achieve a good anomaly pattern recognition effect. Experimental results on the 10 data sets of UCR show that the proposed algorithm performs well in detecting anomaly subsequences and clustering anomaly subsequences without setting parameters.
- time series /
- anomaly subsequences /
- anomaly pattern /
- adaptive k nearest neighbor /
- relative density

HTML全文

计算机存储系统承载数据，是信息平台的核心基础设施. 近年来，全球数据规模爆发式增长，计算机存储系统面临着高速数据访问、海量数据存储以及存储服务质量保障的挑战. 同时，由于新型硬件（如NVMe SSD、持久内存、异构加速设备等）的发展与成熟，存储系统技术研究面临着诸多新的机遇.

基于上述背景，为促进存储领域的技术交流，《计算机研究与发展》推出了本期存储专题. 本期专题收录了6篇论文，分别展示了新硬件环境下存储系统设计和大规模数据存储服务质量保障等存储领域关注热点的研究现状和最新研究成果，希望能为从事相关工作的读者提供借鉴和帮助.

周小晖等作者的论文“基于融合学习的无监督多维时间序列异常检测”针对多维时间序列异常检测效果差的问题，提出了一种基于融合学习的无监督多维时间序列异常检测方法. 该方法同时对多维时间序列的数据局部特征和数据全局特征进行建模，并基于重构误差检测异常，提升了异常检测效果.

刘扬等作者的论文“ZB⁺ -tree：一种 ZNS SSD 感知的新型索引结构”针对传统的 B⁺ -tree 索引结构不适配 ZNS SSD 的问题，提出了ZNS SSD感知的ZB⁺ -tree索引结构. 该索引结构通过将索引节点在常规Zone和顺序Zone分散存储，实现了运行时间和空间利用率指标的提升.

屠要峰等作者的论文“UStore：面向新型硬件的统一存储系统”为适配 NVMe SSD、持久内存、异构加速设备等新型硬件的特性，提出了一种兼容多种存储介质的统一存储系统 UStore. 该存储系统包括与物理存储介质形态解耦的元数据设计、高效的数据管理机制和更新策略，充分发挥了存储硬件的特性和性能.

杨勇鹏等作者的论文“一种 wandering B+ tree 问题解决方法”针对日志结构存储系统中B+ tree树结点异地更新会导致树结构递归更新的问题，提出 IBT B+ tree 的解决方法. 该方法将树结点逻辑索引和物理地址均存放在树结构中，同时引入 dirty 链表设计和非递归更新的 IBT B+ tree 下刷算法，实现在不引入额外开销的条件下解决wandering B+ tree的问题.

文宇鸿等作者的论文“多租户固态盘服务质量保障技术综述”深入分析了多租户固态盘服务质量保障面临的性能干扰、性能不公平及总体性能损失问题，分类介绍了以保障性能隔离、性能公平、优化总体性能为目标的研究工作及技术演进方向，总结了多租户固态盘服务质量保障技术的研究现状并对未来研究方向进行了展望.

胡浩等作者的论文“新型内存硬件环境中的事务管理系统综述”全面总结了新型硬件环境下的事务管理系统，阐述了当前基于新型硬件事务管理系统的技术路线，重点剖析了硬件事务内存和非易失性存储硬件下的事务管理系统的优势和不足，指明了新型硬件环境中事务管理系统潜在的发展方向以及面临的挑战.

本专题所录用的6篇论文中，1篇论文重点关注云系统中多维时间序列的故障检测，3篇论文重点关注新硬件环境下的存储系统设计及索引结构设计，2篇论文对基于新型硬件的事务管理系统和多租户固态盘服务质量保障技术进行了综述. 由于专题篇幅有限等原因，本专题无法全面覆盖存储领域各方面的最新研究进展，不当之处请同行学者批评指正! 感谢各位作者、审稿专家和编辑部的全力支持和辛勤付出!

舒继武（清华大学）

王意洁（国防科技大学）

2023年2月

图 1 子序列分布示意图

Figure 1. Schematic diagram of subsequence distribution

下载: 全尺寸图片幻灯片

图 2 APAKN的总体工作流程

Figure 2. The overall workflow of the APAKN

下载: 全尺寸图片幻灯片

图 3 子序列在不同 $r$ 值时的近邻情况

Figure 3. Neighbors of subsequences at different values of $r$

下载: 全尺寸图片幻灯片

图 4 密度不平衡数据

Figure 4. Density imbalance data

下载: 全尺寸图片幻灯片

图 5 异常子序列分布示意图

Figure 5. Schematic diagram of anomaly subsequence distribution

下载: 全尺寸图片幻灯片

图 6 UCR部分时间子序列及其异常得分

Figure 6. UCR partial time subsequences and anomaly scores

下载: 全尺寸图片幻灯片

图 7 50words数据集在不同类别下的异常子序列示例和异常模式

Figure 7. Examples of anomaly subsequences and anomaly patterns in different categories of the 50words dataset

下载: 全尺寸图片幻灯片

图 8 CBF数据集在不同类别下的异常子序列示例和异常模式

Figure 8. Examples of anomaly subsequences and anomaly patterns in different categories of the CBF dataset

下载: 全尺寸图片幻灯片

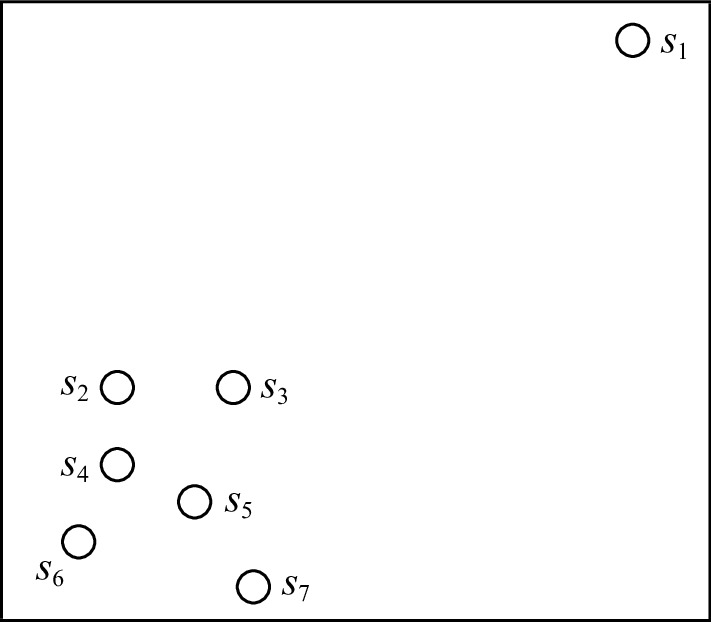
表 1 k = 4时子序列的k近邻域与反向k近邻域

Table 1 k Near Neighbors Domain and Reverse k Near Neighbors Domain of Subsequences when k = 4

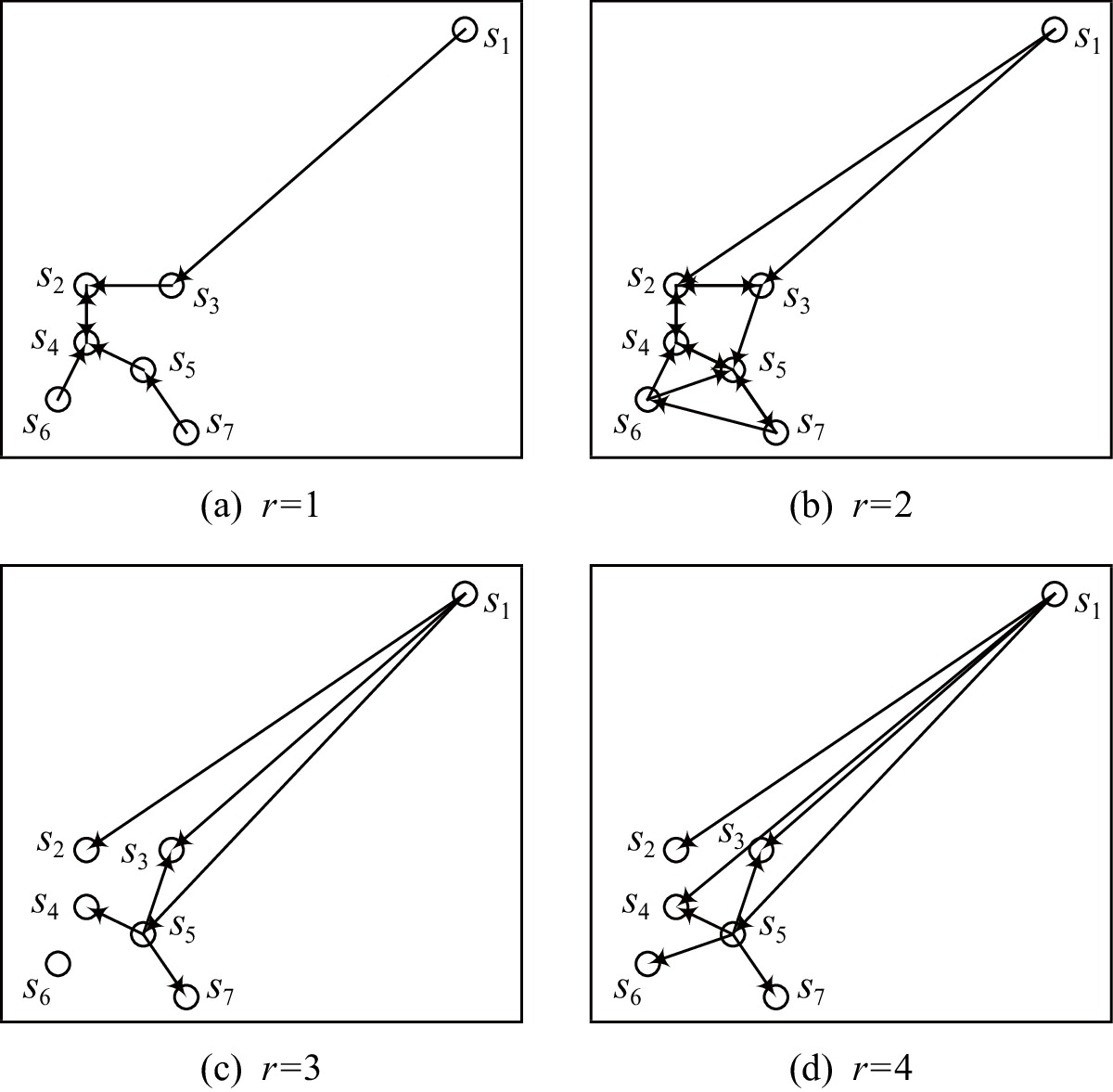
子序列	$k$ 近邻域	反向 $k$ 近邻域	反向 $k$ 近邻个数
${s}_{1}$	$\left\{{s}_{3},{\text{s}}_{2},{\text{s}}_{5},{\text{s}}_{4}\right\}$	$\mathrm{\varnothing }$	0
${s}_{2}$	$\left\{{s}_{4},{\text{s}}_{3},{\text{s}}_{5},{\text{s}}_{6}\right\}$	$\left\{{s}_{1},{\text{s}}_{3},{\text{s}}_{4},{\text{s}}_{6}\right\}$	4
${s}_{3}$	$\left\{{s}_{2},{\text{s}}_{5},{\text{s}}_{4},{\text{s}}_{7}\right\}$	$\left\{{s}_{1},{\text{s}}_{2},{\text{s}}_{4},{\text{s}}_{5},{\text{s}}_{7}\right\}$	5
${s}_{4}$	$\left\{{s}_{2},{\text{s}}_{5},{\text{s}}_{6},{\text{s}}_{3}\right\}$	$\left\{{s}_{1},{\text{s}}_{2},{\text{s}}_{3},{\text{s}}_{5},{\text{s}}_{6},{\text{s}}_{7}\right\}$	6
${s}_{5}$	$\left\{{s}_{4},{\text{s}}_{7},{\text{s}}_{3},{\text{s}}_{6}\right\}$	$\left\{{s}_{1},{\text{s}}_{2},{\text{s}}_{3},{\text{s}}_{4},{\text{s}}_{6},{\text{s}}_{7}\right\}$	6
${s}_{6}$	$\left\{{s}_{4},{\text{s}}_{5},{\text{s}}_{2},{\text{s}}_{7}\right\}$	$\left\{{s}_{2},{\text{s}}_{4},{\text{s}}_{5},{\text{s}}_{7}\right\}$	4
${s}_{7}$	$\left\{{s}_{5},{\text{s}}_{6},{\text{s}}_{4},{\text{s}}_{3}\right\}$	$\left\{{s}_{3},{\text{s}}_{5},{\text{s}}_{6}\right\}$	3

下载: 导出CSV

表 2 s₈, s₁₁, s₁₄相对于其第8近邻的自适应距离比

Table 2 Adaptive Distance Ratio of s₈, s₁₁, s₁₄ Relative to Its 8th Nearest Neighbor

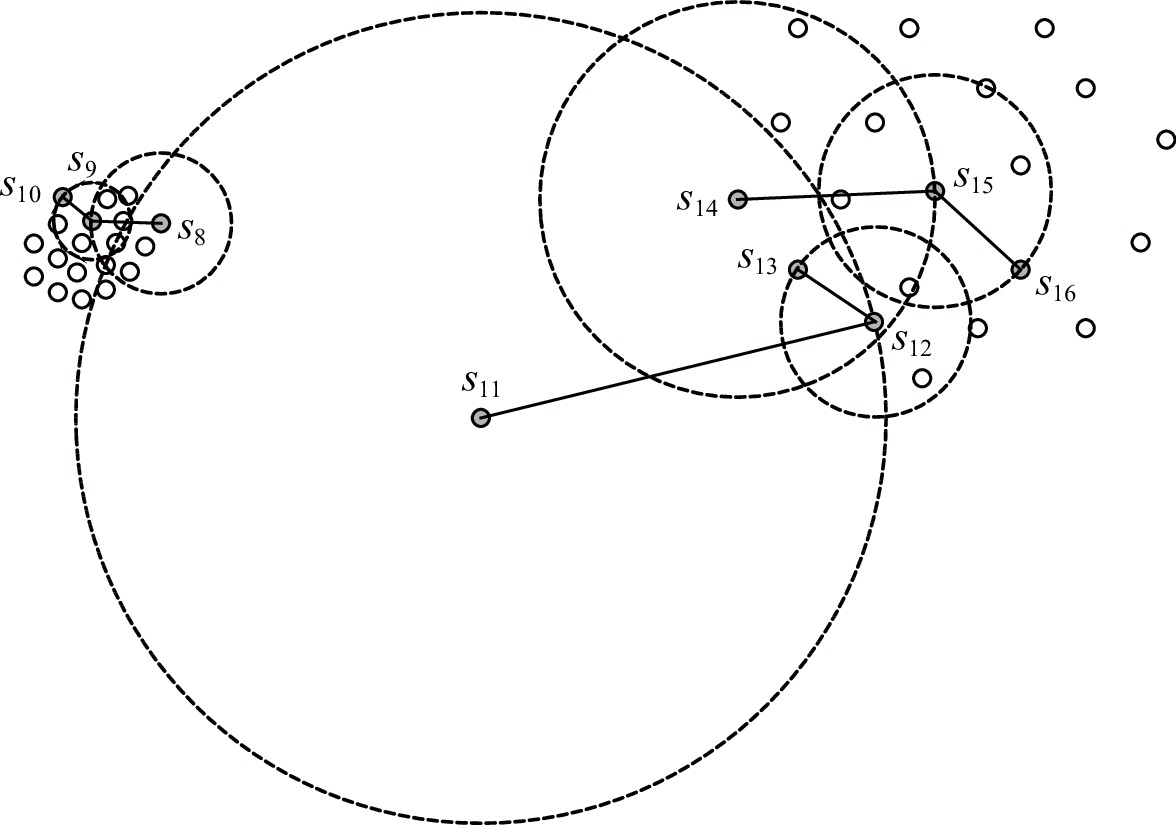
子序列 ${s}_{i}$	${s}_{i}$ 第8近邻 ${s}_{i}^{8}$	${s}_{i}^{8}$ 自适应 $k$ 近邻值 ${k}_{i}^{8}$	${s}_{i}^{8}$ 的第 ${k}_{i}^{8}$ 近邻	自适应距离比
${s}_{8}$	${s}_{9}$	6	${s}_{10}$	$adr\left({s}_{8},{s}_{9}\right)=\dfrac{{d}_{\text{dtw}}\left({s}_{8},{s}_{9}\right)}{{d}_{\text{dtw}}\left({s}_{9},{s}_{10}\right)}=1.833$
${s}_{11}$	${s}_{12}$	3	${s}_{13}$	$adr\left({s}_{11},{s}_{12}\right)=\dfrac{{d}_{\text{dtw}}\left({s}_{11},{s}_{12}\right)}{{d}_{\text{dtw}}\left({s}_{12},{s}_{13}\right)}=4.266$
${s}_{14}$	${s}_{15}$	6	${s}_{16}$	$adr\left({s}_{14},{s}_{15}\right)=\dfrac{{d}_{\text{dtw}}\left({s}_{14},{s}_{15}\right)}{{d}_{\text{dtw}}\left({s}_{15},{s}_{16}\right)}=1.722$

下载: 导出CSV

表 3 实验数据集

Table 3 Experimental Data Sets

数据集	子序列长度	类别个数	正常类别号	异常类别号	子序列个数	异常率/%
50words	270	50	2	4 $,$ 10 $,$ 43	905	20
ECG5000	140	5	1	2 $,$ 5	5000	10
FaceAll	131	14	1	2 $,$ 3 $,$ 5	2250	15
Lighting7	319	7	5	3 $,$ 4 $,$ 6	143	35
Trace	275	4	1	2 $,$ 3 $,$ 4	200	30
Two_Patterns	128	4	3	1 $,$ 2 $,$ 4	1114	13
CBF	128	3	1	2 $,$ 3	930	18
Synthetic_Control	60	6	2	1 $,$ 3 $,$ 4 $,$ 5 $,$ 6	600	25
StarLightCurves	1024	3	3	1 $,$ 2	9236	7
ElectricDevices	96	7	5	1 $,$ 2 $,$ 3 $,$ 4	16637	2

下载: 导出CSV

表 4 APAKN的 ${\mathit{k}}_{\mathit{m}}$ 值和对比算法的最佳参数值

Table 4 ${\mathit{k}}_{\mathit{m}}$ Value of APAKN and the Optimal Parameter Values of Comparison Algorithms

数据集	APAKN	DBAD	SFO	DLDE
数据集	${k}_{m}$	${t}_{\text{opt}}$	${k}_{\text{opt}}$	${h}_{\text{opt}}$
50words	18	25	9	24
ECG5000	39	31	29	30
FaceAll	25	20	9	15
Lighting7	17	15	16	15
Trace	15	11	10	16
Two_Patterns	54	27	14	18
CBF	66	33	17	30
Synthetic_Control	24	16	11	10
StarLightCurves	74	86	78	59
ElectricDevices	156	91	153	88

下载: 导出CSV

表 5 各算法在 10 个数据集上的精确率和召回率对比

Table 5 Comparison of Accuracy and Recall of Each Algorithm on 10 Data Sets

数据集	APAKN		DBAD		SFO		DLDE
数据集	精确率	召回率	精确率	召回率	精确率	召回率	精确率	召回率
50words	1.000	1.000	0.845	0.742	0.462	1.000	1.000	0.673
ECG5000	0.896	0.875	0.663	0.619	0.650	1.000	0.852	0.642
FaceAll	0.912	1.000	0.796	0.842	0.857	1.000	0.743	0.685
Lighting7	1.000	0.917	0.874	0.903	0.579	0.917	0.845	0.683
Trace	0.923	1.000	0.911	1.000	0.727	0.667	1.000	0.967
Two_Patterns	0.954	0.991	0.852	0.800	0.444	0.533	0.845	0.667
CBF	1.000	1.000	0.860	0.914	0.558	1.000	1.000	0.772
Synthetic_Control	1.000	1.000	0.757	0.637	0.735	1.000	1.000	0.700
StarLightCurves	0.912	0.896	0.912	0.845	0.774	0.685	0.875	0.689
ElectricDevices	0.923	0.851	0.845	0.798	0.855	0.762	0.796	0.744
注：黑体数值表示最佳值.

下载: 导出CSV

表 6 各算法在 10 个数据集上的准确率和F值对比

Table 6 Comparison of Accuracy and F Value of Each Algorithm on 10 Data Sets

数据集	APAKN		DBAD		SFO		DLDE
数据集	准确率	F值	准确率	F值	准确率	F值	准确率	F值
50words	1.000	1.000	0.914	0.790	0.851	0.632	0.901	0.805
ECG5000	0.996	0.885	0.923	0.640	0.973	0.788	0.865	0.732
FaceAll	0.980	0.953	0.802	0.818	0.961	0.923	0.993	0.713
Lighting7	0.974	0.957	0.826	0.888	0.769	0.710	0.875	0.755
Trace	0.971	0.960	0.871	0.953	0.800	0.696	0.963	0.983
Two_Patterns	1.000	0.972	0.836	0.825	0.876	0.485	0.896	0.746
CBF	1.000	1.000	0.931	0.886	0.940	0.716	0.875	0.871
Synthetic_Control	1.000	1.000	0.860	0.691	0.880	0.847	0.698	0.823
StarLightCurves	0.895	0.904	0.889	0.877	0.852	0.727	0.857	0.771
ElectricDevices	0.924	0.886	0.852	0.821	0.824	0.806	0.869	0.769
注：黑体数值表示最佳值.

下载: 导出CSV

表 7 各算法在 10 个数据集上的ARI和NMI对比

Table 7 Comparison of ARI and NMI of Each Algorithm on 10 Data Sets

数据集	APAKN		kmlShape		DDC		KShape
数据集	${E}_{\mathrm{A}\mathrm{R}\mathrm{I}}$	${E}_{\mathrm{N}\mathrm{M}\mathrm{I}}$	${E}_{\mathrm{A}\mathrm{R}\mathrm{I}}$	${E}_{\mathrm{N}\mathrm{M}\mathrm{I}}$	${E}_{\mathrm{A}\mathrm{R}\mathrm{I}}$	${E}_{\mathrm{N}\mathrm{M}\mathrm{I}}$	${E}_{\mathrm{A}\mathrm{R}\mathrm{I}}$	${E}_{\mathrm{N}\mathrm{M}\mathrm{I}}$
50words	0.814	0.825	0.562	0.528	0.524	0.658	0.752	0.635
ECG5000	0.827	0.768	0.662	0.612	0.586	0.693	0.825	0.698
FaceAll	1.000	1.000	0.814	0.802	0.725	0.547	0.408	0.662
Lighting7	0.836	0.905	0.635	0.620	0.433	0.623	0.689	0.814
Trace	0.522	0.734	0.586	0.532	0.425	0.389	0.368	0.647
Two_Patterns	1.000	1.000	0.633	0.396	0.362	0.412	0.453	0.504
CBF	0.925	0.814	0.755	0.852	0.615	0.578	0.847	0.689
Synthetic_Control	0.457	0.667	0.643	0.614	0.303	0.339	0.478	0.713
StarLightCurves	0.956	0.756	0.789	0.812	0.546	0.632	0.874	0.684
ElectricDevices	0.857	0.859	0.478	0.532	0.722	0.566	0.647	0.684
注：黑体数值表示最佳值.

下载: 导出CSV

参考文献(32)

[1]	O'Leary B, Reiners J J, Xu Xiaohong, et al. Identification and influence of spatio-temporal outliers in urban air quality measurements[J]. Science of The Total Environment, 2016, 573: 55−65
[2]	Qin Yu, Lou Yuansheng. Hydrological time series anomaly pattern detection based on isolation forest[C] //Proc of the 3rd Information Technology, Networking, Electronic and Automation Control Conf (ITNEC). Piscataway, NJ: IEEE, 2019: 1706−1710
[3]	Wang Jibin, Wang Ping, Wang Suping. Automated detection of atrial fibrillation in ECG signals based on wavelet packet transform and correlation function of random process[J]. Biomedical Signal Processing and Control, 2020, 55: 101662
[4]	Liang Haoran, Song Lei, Wang Jianxing, et al. Robust unsupervised anomaly detection via multi-time scale DCGANs with forgetting mechanism for industrial multivariate time series[J]. Neurocomputing, 2021, 423: 444−462
[5]	Wang Xing, Lin J, Patel N, et al. Exact variable-length anomaly detection algorithm for univariate and multivariate time series[J]. Data Mining and Knowledge Discovery, 2018, 32(6): 1806−1844 doi: 10.1007/s10618-018-0569-7
[6]	苏卫星,朱云龙,刘芳,等. 时间序列异常点及突变点的检测算法[J]. 计算机研究与发展,2014,51(4):781−788 Su Weixing, Zhu Yunlong, Liu Fang, et al. A detection algorithm of outlier and mutation points in time series[J]. Journal of Computer Research and Development, 2014, 51(4): 781−788 (in Chinese)
[7]	刘芳,齐建鹏,于彦伟,等. 基于密度的Top-n局部异常点快速检测算法[J]. 自动化学报,2019,45(9):1756−1771 doi: 10.16383/j.aas.c180425 Liu Fang, Qi Jianpeng, Yu Yanwei, et al. A fast algorithm for density-based Top-n local outlier detection[J]. Acta Automatica Sinica, 2019, 45(9): 1756−1771 (in Chinese) doi: 10.16383/j.aas.c180425
[8]	Hyndman R J, Wang E, Laptev N. Large-scale unusual time series detection[C] //Proc of the 15th IEEE Int Conf on Data Mining Workshop (ICDMW). Piscataway, NJ: IEEE, 2015: 1616−1619
[9]	Senin P, Lin J, Wang Xing, et al. Time series anomaly discovery with grammar-based compression[C] //Proc of the 18th Int Conf on Extending Database Technology(EDBT). New York: ACM, 2015: 481−492
[10]	Boniol P, Palpanas T. Series2graph: Graph-based subsequence anomaly detection for time series[J]. Proceedings of the VLDB Endowment, 2020, 13(12): 1821−1834 doi: 10.14778/3407790.3407792
[11]	Cheng Kaiwen, Chen Yietarng, Fang Wenhsien. An efficient subsequence search for video anomaly detection and localization[J]. Multimedia Tools and Applications, 2016, 75: 15101−15122
[12]	Hawkins D. Identification of outliers[M] //Monographs on Applied Probability and Statistics. Berlin: Springer, 1980: 51−73
[13]	Huo Wunjun, Wang Wei, Li Wen. Anomalydetect: An online distance-based anomaly detection algorithm[C] //Proc of the Int Conf on Web Services. Berlin: Springer, 2019: 63−79
[14]	Zhang Pengcheng, Xiao Yan, Zhu Yuelong, et al. A new symbolization and distance measure based anomaly mining approach for hydrological time series[J]. International Journal of Web Services Research, 2016, 13(3): 26−45 doi: 10.4018/IJWSR.2016070102
[15]	Zheng Dequan, Li Fenghuan, Zhao Tiejun. Self-adaptive statistical process control for anomaly detection in time series[J]. Expert Systems with Applications, 2016, 57: 324−336
[16]	Izakian H, Pedrycz W. Anomaly detection in time series data using a fuzzy c-means clustering[C] //Proc of the Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS). Piscataway, NJ: IEEE, 2013: 1513−1518
[17]	Medico R, Spina D, VandeGinste D, et al. Autoencoding density-based anomaly detection for signal integrity applications[C] //Proc of the 27th IEEE Conf on Electrical Performance of Electronic Packaging and Systems (EPEPS). Piscataway, NJ: IEEE, 2018: 47−49
[18]	Zhang Chunkai, Chen Yingyang, Yin Ao. Anomaly subsequence detection with dynamic local density for time series[G] //LNCS 11707: Proc of the 30th Int Conf on Database and Expert Systems Applications. Berlin: Springer, 2019: 291−305
[19]	Dunn J C. A fuzzy relative of the ISODATA process, and its use in detecting compact well-separated clusters[J]. Journal of Cybernetics, 1973, 3(3): 32−57 doi: 10.1080/01969727308546046
[20]	Pedrycz W, Oliveira V. A development of fuzzy encoding and decoding through fuzzy clustering[J]. IEEE Transactions on Instrumentation & Measurement, 2008, 57(4): 829−837
[21]	Genolini C, Ecochard R, Benghezal M, et al. kmlShape: An efficient method to cluster longitudinal data (time-series) according to their shapes[J]. PLoS ONE, 2016, 11(6): 1−24
[22]	Likas A, Vlassis N, Verbeek J J. The global k-means clustering algorithm[J]. Pattern Recognition, 2003, 36(2): 451−461 doi: 10.1016/S0031-3203(02)00060-2
[23]	Ma Ruizhe, Filali S B, Angryk R. Time series distance density cluster with statistical preprocessing[C] //Proc of the 20th Int Conf on Big Data Analytics and Knowledge Discovery. Berlin: Springer, 2018: 371−381
[24]	Paparrizos J, Gravano L. K-shape: Efficient and accurate clustering of time series[C] //Proc of the 42nd ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2015: 1855−1870
[25]	Breunig M M , Kriegel H P , Ng R T , et al. LOF: Identifying density-based local outliers[C] //Proc of the 28th ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2000: 93−104
[26]	Berndt D J, Clifford J. Using dynamic time warping to find patterns in time series[C] //Proc of the Workshop on Knowledge Discovery in Databases. New York: ACM, 1994: 229−248
[27]	Cover T, Hart P. Nearest neighbor pattern classification[J]. IEEE Transactions on Information Theory, 1967, 13(1): 21−27 doi: 10.1109/TIT.1967.1053964
[28]	Pukelsheim F. The three sigma rule[J]. The American Statistician, 1994, 48(2): 88−91
[29]	Pérez-Ortiz M, Durán-Rosal A M, Gutiérrez P A, et al. On the use of evolutionary time series analysis for segmenting paleoclimate data[J]. Neurocomputing, 2019, 326/327: 3−14
[30]	Dau H A, Bagnall A, Kamgar K, et al. The UCR time series archive[J]. IEEE/CAA Journal of Automatica Sinica, 2019, 6(6): 1293−1305 doi: 10.1109/JAS.2019.1911747
[31]	Qian Pengjiang, Chung Fulai, Wang Shitong, et al. Fast graph-based relaxed clustering for large data sets using minimal enclosing ball[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2012, 42(3): 672−687 doi: 10.1109/TSMCB.2011.2172604
[32]	Wang Yangtao, Chen Lihui. K-MEAP: Multiple exemplars affinity propagation with specified K clusters[J]. IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(12): 2670−2682 doi: 10.1109/TNNLS.2015.2495268